Clonal and Fine-scale Genetic Structure in Populations of a Restricted Korean Endemic, Hosta jonesii (Liliaceae) and the Implications for Conservation

Abstract

• Background and Aims In plant populations the magnitude of spatial genetic structure of apparent individuals (including clonal ramets) can be different from that of sexual individuals (genets). Thus, distinguishing the effects of clonal versus sexual individuals in population genetic analyses could provide important insights for evolutionary biology and conservation. To investigate the effects of clonal spread on the fine-scale spatial genetic structure within plant populations, Hosta jonesii (Liliaceae), an endemic species to Korea, was chosen as a study species.

• Methods Using allozymes as genetic markers, spatial autocorrelation analysis of ramets and of genets was conducted to quantify the spatial scale of clonal spread and genotype distribution in two populations of H. jonesii.

• Key Results Join-count statistics revealed that most clones are significantly aggregated at <3-m interplant distance. Spatial autocorrelation analysis of all individuals resulted in significantly higher Moran's I values at 0–3-m interplant distance than analyses of population samples in which clones were excluded. However, significant fine-scale genetic structure was still observed when clones were excluded.

• Conclusions These results suggest that clones enhance the magnitude of spatial autocorrelation due to localized clonal spread. The significant fine-scale genetic structure detected in samples excluding clones is consistent with the biological and ecological traits exhibited by H. jonesii including bee pollination and limited seed dispersal. For conservation purposes, genetic diversity would be maximized in local populations of H. jonesii by collecting or preserving individuals that are spaced at least 5 m apart.

INTRODUCTION

Clonal reproduction via vegetative spread and production of bulbils is a common characteristic of many plant species. Vegetative spread has a major effect on the genetic structure of plant populations because it determines the extent and the distribution of genetically identical individuals. In self-compatible plant species, it has been suggested that significant levels of clonal structure may increase the likelihood of self-fertilization due to cross-pollination among different ramets of the same genets, thus increasing levels of inbreeding within populations (Handel, 1985). For plant species that reproduce both sexually and vegetatively, it is expected that the magnitude and extent of spatial genetic structure of all ‘phenotypic individuals’ in populations, including clonal ramets, should be different from those of sexual individuals (genets), excluding clonal ramets (e.g. Chung and Epperson, 1999). Spatial genetic structure can be quantified using spatial autocorrelation analysis to investigate population genetic processes (Sokal and Oden, 1978; Epperson, 1989; Heywood, 1991). Methodological progress in the analysis of fine-scale genetic structure in plant populations has been ongoing. Moran's I statistic (Sokal and Oden, 1978) and the closely related co-ancestry coefficient (Loiselle et al., 1995; Kalisz et al., 2001) have been widely used and allow the analysis of spatial autocorrelation for one allele at a time (e.g. Sakai and Oden, 1983) or averaged over alleles and loci (e.g. Chung et al., 2004a). Hardy and Vekemans (2002) have introduced a particularly useful program, SPAGeDi, which permits the calculation of these and other statistics for the analysis of fine-scale genetic structure using multiallelic co-dominant and dominant loci. Also of note are the spatial autocorrelation methods of Smouse and Peakall (1999), which utilize intact multilocus genotypes (not averages over loci) and can be implemented using the program GenAlEx by Peakall and Smouse (2001). The theoretical background underlying these methods and illustrative empirical examples are described in Smouse and Peakall (1999), Hardy and Vekemans (1999) and Vekemans and Hardy (2004). Finally, to evaluate specifically the spatial distribution of clonal structure, spatial autocorrelation statistics for the total number of unlike joins among multilocus genotypes (e.g. Chung and Epperson, 1999; Chung et al., 2004a) can be calculated using the program JCSP (B. K. Epperson, Michigan State University, East Lansing, USA; the program is available upon request).

Separation of the spatial genetic structure caused by clonal reproduction from that maintained in sexually reproduced individuals within populations could provide at least two important insights for evolutionary biology and conservation. In terms of understanding evolution, the pattern and extent of the fine-scale genetic structure based on only sexually produced individuals can be used to achieve a better understanding of the underlying genetic processes shaping a population, including gene flow, random genetic drift, and differential selective pressures (Nevo et al., 1986; Barbujani, 1987; Epperson, 1993; Bjornstad et al., 1995; Chung and Epperson, 1999; Chung et al., 2004a). Furthermore, information about dispersal, pollinator behaviour, breeding system, and other processes operating within populations, and structuring them at the scale under consideration may indirectly be inferred from spatially explicit approaches (Peakall and Beattie, 1995). Spatial statistical methods can also provide powerful tools for measuring the structure of genetic diversity within populations of target plants for plant conservation biologists (Escudero et al., 2003). It is broadly accepted that knowledge of the genetic variation of a species is essential for managing a comprehensive conservation plan (Falk and Holsinger, 1991). Thus, for conservation purposes, analysis of fine-scale genetic structure within plant populations of threatened or narrowly distributed plant species could be used to provide baseline information for sampling strategies for ex situ preservation of seeds in gene banks and for selecting the sites and population sizes necessary for in situ conservation of a species (Maki and Yahara, 1997; Chung et al., 1998; Chung and Chung, 1999; Escudero et al., 2003; Chung et al., 2004b). However, most genetic studies on endangered plant species lack considerations of explicit spatial genetic structure within multiple populations (Escudero et al., 2003).

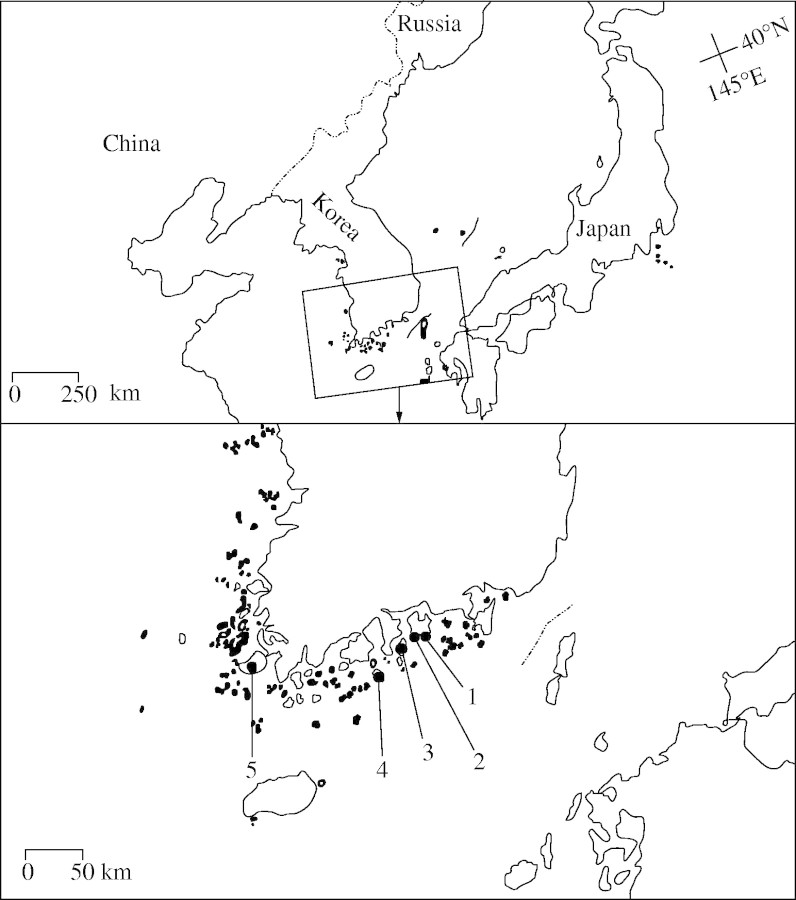
The herbaceous perennial Hosta jonesii (Liliaceae) was first described in 1989 (Chung, 1989). It has short, creeping rhizomes from which new shoots arise each year (Chung, 1989), and is an attractive species with horticultural potential. This taxon is endemic to a few southern islands in Korea, including Dolsan, Jin, Namhae and Oenaro islands (Fig. 1). One to two isolated local populations (usually 50–160 individuals in ≤400 m²) occur in a few locations on Dolsan, Jin and Namhae islands (M. Y. Chung and M. G. Chung, pers. obs.). On Oenaro Island (relatively well-preserved and the most remote island among the four islands), in contrast, local populations are relatively continuously distributed within two 0·7–0·8-ha areas across the landscape (approx. 1000–2000 clonal shoots were documented, M. Y. Chung and M. G. Chung, unpubl. res.). Unlike Oenaro Island, local populations on the other three islands could be relatively easily accessed and thus have recently been affected by anthropogenic activities and/or other ecological factors. For example, the types (holotype and isotypes) were collected from one local population on Namhae Island (number ‘1’ in Fig. 1) in 1988, but this population was revisited in 2003 and found to be extinct (M. Y. Chung and M. G. Chung, pers. obs.). The disappearance of this entire local population is attributable to unknown environmental factors or reckless collection by plant sellers. Furthermore a local population on Dolsan Island (a paratype location in 1988) does not exist any more, due to enlargement of a local coastal road. Considering these observations and data, this species may be listed as ‘endangered’ (EN) according to the following criteria of IUCN (2001): extent and area of occurrence, number of locations, observed or inferred decline in area of occupancy, area of habitat, number of subpopulations and number of mature individuals [EN B1ab (ii, iii, iv, v) and EN B2ab (ii, iii, iv, v)]. Considering the current status of the species, it is necessary to take action in order to ensure long-term genetic variability of H. jonesii by implementing appropriate conservation and management strategies.

Fig. 1.

Five known locations of Hosta jonesii in southern Korea: Numbers 1 (extinct) and 2 are populations on Namhae-do Island; number 3 is a population on Dolsan-do Island; number 4 indicates two populations (SGR and YNR) at which analysis of the fine-scale genetic structure was conducted; and number 5 is a population on Jin-do Island.

In this study, Hosta jonesii was chosen as a study species (a) to investigate the effects of clonal spread on fine-scale spatial genetic structure within plant populations and (b) to propose some in situ and ex situ conservation strategies on the basis of conservation genetics notion. To achieve these, two relatively large and well-preserved local populations of H. jonesii on Oenaro Island were investigated. Spatial autocorrelation analysis of ramets and of genets was used to quantify the spatial scale of clonal spread and its statistical significance in the populations, using allozymes as genetic markers.

MATERIALS AND METHODS

Study plant and sites

Hosta jonesii M. Chung is a perennial 35–60 cm high, which produces 3–20 whitish-purple flowers on each scape. Stamens and pistil are spatially separated (herkogamy). The fruit, a capsule, is cylindrical, 22–33 mm long and 4–6 mm wide, with black flattened seeds with wings (approx. 3 mm long). It flowers from mid-August to early September and is frequently visited by the honey bee Apis mellifera and the bumblebee Bombus diversus diversus (M. Y. Chung and M. G. Chung, unpubl. res.). Hosta jonesii is self-compatible, and the percentage of fruit set in the two local populations studied on Oenaro Island is 38·9 % (M. Y. Chung and M. G. Chung, unpubl. res.), suggesting pollinator and/or resource limitations.

A total of 291 visually identified shoots with scapes were mapped and leaf samples were collected from two undisturbed populations on Oenaro Island (southern Korea, number ‘4’ in Fig. 1). The first local population (Shinguem-ri, hereafter referred to SGR, with an area of about 20 × 20 m, altitude approx. 9 m a.s.l; 137 shoots) was located at the centre of a continuously distributed large population (40 × 200 m area) on a north-facing hillside near the coast on which Pinus thunbergii and Eurya japonica grow at low density. South of SGR by 2·1 km, the second local population (Yaenae-ri, hereafter referred to YNR, also about 20 × 20 m area, altitude approx. 125 m a.s.l.; 154 shoots) was located at the centre of a second continuously distributed large population (60 × 120 m area) on an east-facing hillside with a relatively high density of old individuals of Pinus thunbergii, Quercus acutissima and Q. serrata in the two mapped local populations and several broad-leaved evergreen shrubs. One leaf was collected from each H. jonesii individual and stored at 4 C until enzymes were extracted for allozyme analysis.

Allozyme electrophoresis

For an optimal extraction, leaves were finely cut and then crushed with a pestle and mortar in a phosphate-polyvinylpyrrolidone extraction buffer (Mitton et al., 1979). Enzyme extracts were absorbed onto 4 × 6 mm wicks of Whatman 3MM chromatography paper, and stored at −70  C until subjected to electrophoresis. Genotypes of each shoots were determined by horizontal gel electrophoresis using 11 % starch gels. Gel and electrode buffers, and enzyme staining procedures were taken from Soltis et al. (1983). Six enzyme systems were resolved: phosphoglucoisomerase (Pgi-1, Pgi-2) and phosphoglucomutase (Pgm-1, Pgm-2, Pgm-3) were resolved on system 6; 6-phosphogluconate dehydrogenase (6Pgd-1, 6Pgd-2) on system 11; and leucine aminopeptidase (Lap), triosephosphate isomerase (Tpi) and fluorescent esterase (Fe-1, Fe-2) on a modification (Haufler, 1985) of system 8. Putative loci were designated sequentially, with the most anodally migrating isozyme designated 1, the next 2, and so on. Likewise, alleles were designated sequentially with the most anodally migrating alleles designated a. All the phenotypes obtained were consistent with the quaternary structure of isozymes, subcellular localization and number of loci usually expressed in diploid plants, as documented by Weeden and Wendel (1989).

Analysis of clonal structure and population genetic structure

Given that H. jonesii reproduces both sexually and vegetatively, it is important to determine whether shoots with identical marker genotypes are clones when quantifying fine-scale genetic structure (Berg and Hamrick, 1994; Chung and Epperson, 1999; Chung et al., 2004a). To do this, the available genetic markers must have adequate statistical power to discriminate clonal genotypes from identical sexually produced genotypes. A two-locus disequilibrium (linkage) analysis was done, and no significant two-locus disequilibria for any combination of alleles were found when significance levels were adjusted with the Bonferroni procedure.

The discriminating power of the allozyme markers used was measured for each population as 1 – P_G. The P_G (the probability that two random, sexually produced genotypes are identical) was calculated using the following formula (Berg and Hamrick, 1994; Chung et al., 2004a):

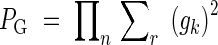where g_k is k's genotype frequency per locus, r is number of genotypes per locus, and n is the number of loci. Because power was high for both populations (1 – P_G ≈ 1; Table 1), putative clonal ramets were identified by inspection as spatially proximate, identical multilocus genotypes. Hereafter subscripts ‘r’ and ‘g’ refer to total samples (including clonal ramets) and samples restricted to genets, respectively.

Table 1.

Summary of clonal and genetic diversity and estimates of Wright's (1965) F_IS for two populations of Hosta jonesii

			Number of ramets per genet
Population	N(r)	N(g)	1	2	3	4	5	7	8	He(r) (s.e.)	He(g) (s.e.)	FIS(r) (95 % CL)	FIS(g) (95% CL)	PG
SGR	137	60	19	18	13	7	3	0	0	0·252 (0·059)	0·249 (0·061)	0·139 (0·059, 0·206)	0·167 (0·107, 0·226)	0·0042
YNR	154	57	10	19	13	13	0	1	1	0·281 (0·065)	0·274 (0·064)	0·093 (0·058, 0·127)	0·193 (0·156, 0·236)	0·0018

N_(r), Number of ramets (shoots); N_(g), number of genets (genotypes); H_e, expected heterozygosity or genetic diversity; s.e., standard error; F_IS, fixation index; 95 % CL, 95 % bootstrap CIs; P_G, probability that two random, sexually produced multilocus genotypes will be identical. Subscripts r and g refer to total samples (including clonal ramets) and samples restricted to genets, respectively.

To evaluate the spatial distribution of putative clones, spatial autocorrelation statistics (Sokal and Oden, 1978) were computed for the total number of ‘unlike’ joins among multilocus genotypes (e.g. Chung and Epperson, 1999; Chung et al., 2004a), and the standard normal deviate (SND) was calculated using the program JCSP. An SND has an asymptotically standard normal distribution under the null hypothesis of random dispersion. An SND of less than −1·96 indicates a significant (P < 0·05) deficit of pairs of unlike (and excess of like) genotypes separated by a given range of Euclidean distances (Epperson, 1993). Hence, significant negative values at short distance intervals are indicative of real clonal structure, not a lack of power of the allozyme data to distinguish genotypes. This join-count analysis was conducted at 3-m distance intervals, resulting in seven distance classes in both SGR and YNR.

To estimate genetic diversity and genetic structure, a locus was considered polymorphic when the frequency of the most common allele did not exceed 0·95. The estimated genetic diversity parameters were the following: percentage of polymorphic loci (%P), mean number of alleles per locus (A) and Nei's unbiased gene diversity (H_e).

To measure deviations from Hardy–Weinberg (H-W) equilibrium at each polymorphic locus, Wright's (1965) F statistics (F_IS, F_IT and F_ST) were calculated following Weir and Cockerham (1984). These fixation indices were used to measure deviations from H-W equilibrium attributable to individuals in local populations (F_IS), variation among local populations (F_ST, an indicator of the degree of differentiation between local populations), and individuals relative to the total population (F_IT). Means and standard errors were obtained by jackknifing over polymorphic loci. Bootstrap confidence intervals (95 % CI) were constructed around jackknifed means of the F statistics with 1500 replicates and the observed mean F statistics were considered significant when CIs did not overlap with zero. These calculations were made using the program FSTAT [version 2.9.3.2 by Goudet (2002); see Goudet (1995)]. F_IS was also calculated separately for each population with 95 % bootstrap CIs (1000 replicates) constructed using the program GDA (Lewis and Zaykin, 2001).

Analysis of fine-scale genetic structure

Moran's I statistic (Sokal and Oden, 1978) was computed for the spatial autocorrelation analysis. Based on the distance between stems, every possible pair of individuals was assigned to one of the seven distance classes with 3-m intervals as in join-count statistics. For each allele, Moran's I_k was calculated for the kth distance class using the following formula

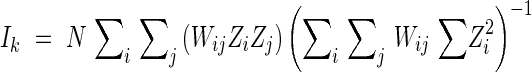where N is number of individuals; W_ij is an element of the weighting matrix, such that W_ij equals 1·0 if ith and jth individual both belong to the spatial interval k and zero otherwise; Z_i = X_i – X, Z_j = X_j – X; the variables X_i and X_j are the frequency of the allele for the ith and jth individuals, respectively; and X is the frequency of the allele in the total sample. Each I_k value was used to test for significant deviations from the expected values E(I_k) = −1/(N – 1) (Cliff and Ord, 1981).

To obtain a more powerful test of genetic structure I_k was averaged across alleles and loci (Heywood, 1991; Streiff et al., 1998; Ueno et al., 2000). To assess the statistical significance of the average I_k, each I_k value was compared with 95 % and 99 % CIs generated under the null hypothesis of no spatial genetic structure in which the expected value of I_k is E(I_k) = −1/(N – 1) (Cliff and Ord, 1981). Sample multilocus genotypes were drawn at random with replacement and assigned to occupied map locations within the study population. Resampling was repeated 999 times, and the observed I_k values represented the 1000th statistic for each distance class. CIs of 95 % and 99 % for the parameters were constructed as the interval from the 25th and the 5th to the 976th and 996th ordered permutation estimates. For a given distance class, an I_k value was considered to be significantly different from zero at P < 0·05 (or P < 0·01) when the observed value fell above or below the 95 % (or 99 %) range of this resampling method. A significant positive value of Moran's I_k indicates that pairs of individuals in the considered distance class have similar gene frequencies, whereas a significant negative value indicates that they have dissimilar gene frequencies. All calculations and resampling were performed using the program SGS (Degen et al., 2001).

Given the importance of quantifying the effects of clonal structure on the spatial patterning of genetic variation within H. jonesii populations, separate analyses of Moran's I_k were used to evaluate the effects of clonal structure. Spatial autocorrelation analyses were conducted for population samples containing all shoots [N_(r) = 137 in SGR and 154 in YNR] versus restricted data sets consisting of a single ramet per genet so as to exclude clones [N_(g) = 60 in SGR and 57 in YNR]. In this latter case, the x, y coordinates of each ramet were placed at the genet's centre of mass.

To test the overall pattern of spatial genetic structure for each data set (total samples and genets in SGR and YNR) across all distance classes, the slope (β) of pairwise Moran's I_k on the logarithm of distance (2 m distance intervals) was evaluated using a Mantel test (1000 permutations) under null hypothesis (β = 0). Standard errors of these slopes were also obtained by jackknifing across loci (as suggested in Vekemans and Hardy, 2004), permitting formal testing for differences in slopes (and hence the strength of structure) between total samples and genets, and between SGR and YNR. The approx. 95 % CIs for the slope with the logarithm of distance were thus obtained as ±1·96 times the jackknifed standard error estimates. Comparison between slopes was considered significant if 95 % CIs did not overlap each other. Finally, to test whether mean values of Moran's I_k at <2 m between total samples and genets are significantly different, the approximation of a 95 % CI (1·96 times the standard error) was used. All analyses, including estimation of jackknifed standard errors were conducted using the program SPAGeDi (Hardy and Vekemans, 2002).

RESULTS

Genetic diversity and clonal structure

Of the 11 loci examined, seven were polymorphic (Fe-1, Fe-2, 6-Pgd-1, Pgi-2, Pgm-1, Pgm-2 and Pgm-3). Allozyme variation was high and similar between populations, with a mean percentage of polymorphic loci (%P) of 64 % and mean number of alleles per locus of 1·64. Genetic diversity (or expected heterozygosity) calculated from both total population samples and samples excluding identical multilocus genotypes (and hence clones) was similar between populations ranging from 0·249 [SGR, H_e(g)] to 0·281 [YNR, H_e(r)] (Table 1).

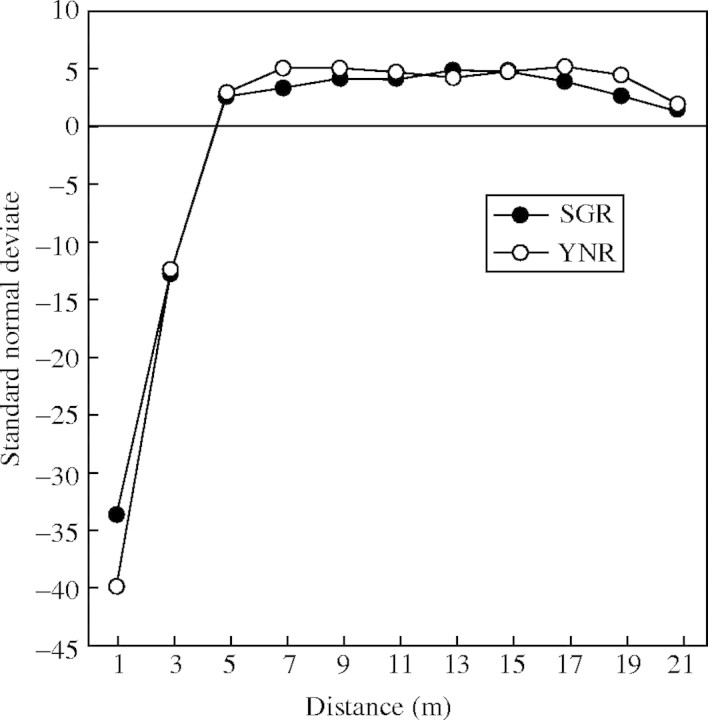
Given the variability of the markers, the power to discriminate clonal genotypes from sexually produced genotypes identical by chance alone was >0·95 for each population (mean P_G = 0·003; Table 1). Given this power, ramets sharing the same genotype were treated as putative clones, finding that, within populations, 68–82 % of genets formed clones consisting of two or more ramets (Table 1). Clones ranged in size from one to five and one to eight ramets in SGR and YNR, respectively. However, distribution of clone sizes was not significantly different between populations (contingency table chi-square of 9·55 with 6 d.f.; P = 0·145). Join-count statistics revealed a statistically significant deficit of joins between unlike multilocus genotypes (i.e. excess pairs of identical genotypes) compared with random expectation at distances (d) of 0 m < d < 1 m (standard normal deviate test statistic, SND = −33·7 for SGR, −39·9 for YNR) and for 1 m < d < 3 m (SND = −12·8 for SGR, −12·4 for YNR), but not at greater distances within the two populations (Fig. 2). Together, these results indicate the positive spatial clustering of identical genotypes consistent with the expectations of clonal structure.

Fig. 2.

Correlograms for populations SGR and YNR of Hosta jonesii showing the relationships between pairs of the total number of unlike joins among multilocus genotypes.

Population genetic structure

Wright's F_IS estimated from total samples [F_IS(r)] was significantly greater than zero for both populations, indicating significant deficits of heterozygotes compared with Hardy–Weinberg equilibrium (Table 1). When population data were constrained to exclude clonal structure, F_IS estimated from genets [F_IS(g)] increased significantly in YNR [F_IS(r) = 0·093 vs. F_IS(g) = 0·193; Table 1], whereas the two estimates were similar in SGR [F_IS(r) = 0·139 vs. F_IS(g) = 0·167; Table 1]. F_IS estimated over populations for total samples and genets were both significantly greater than zero but not significantly different from each other (Table 2; a similar pattern was observed for F_IT). At the individual locus level F_IS estimated over populations was significantly greater than zero for Pgd-1, Pgi-2 and Pgm-1 for total samples, while Pgi-2 and Pgm-1 were significant for genets (Table 2). Multilocus estimates of F_ST for both total samples and genets were significantly greater than zero but small [mean F_ST(r) = 0·006 and F_ST(g) = 0·004; Table 2], indicating relatively little allele frequency differentiation between populations, which likely reflects their close spatial proximity (SGR and YNR are separated by 2·1 km).

Table 2.

F-statistics (Wright, 1965) following the method of Weir and Cockerham (1984) and P-values (P) for seven polymorphic loci in two populations of Hosta jonesii

		FIS			P			FIT			P			FST			P
Locus	No. of alleles	r	g	r	g	r	g	r	g	r	g	r	g
Fe-1	2	−0·014	0·134	0·672	0·151	0·020	0·141	0·422	0·062	0·033	0·008	0·001	0·245
Fe-2	2	0·095	0·143	0·067	0·070	0·096	0·151	0·051	0·080	0·000	0·010	0·315	0·999
Pgd-1	2	0·116	0·162	0·034	0·060	0·117	0·166	0·023	0·032	0·001	0·006	0·270	0·525
Pgi-2	2	0·152	0·286	0·005	0·003	0·167	0·287	0·003	0·001	0·018	0·000	0·014	0·362
Pgm-1	2	0·205	0·218	0·001	0·012	0·208	0·225	0·001	0·013	0·004	0·009	0·817	0·732
Pgm-2	2	0·099	0·144	0·069	0·073	0·099	0·152	0·055	0·077	0·000	0·009	0·321	0·903
Pgm-3	2	0·077	0·132	0·114	0·112	0·082	0·138	0·073	0·076	0·005	0·007	0·140	0·250
Mean		0·114	0·178			0·120	0·181			0·006	0·004
± s.e.		0·024	0·022			0·022	0·022			0·004	0·003
95 % CI		(0·066, 0·156)	(0·142, 0·220)			(0·077, 0·159)	(0·144, 0·223)			(−0·001, 0·016)	(−0·008, 0·002)

F_IS, F_IT and F_ST represent deviations of heterozygote frequencies from Hardy–Weinberg expectations within populations, over both populations, and between populations, respectively. r and g refer to estimates obtained from total samples (including clonal ramets) and samples restricted to genets, respectively.

Clonal effects on fine-scale genetic structure

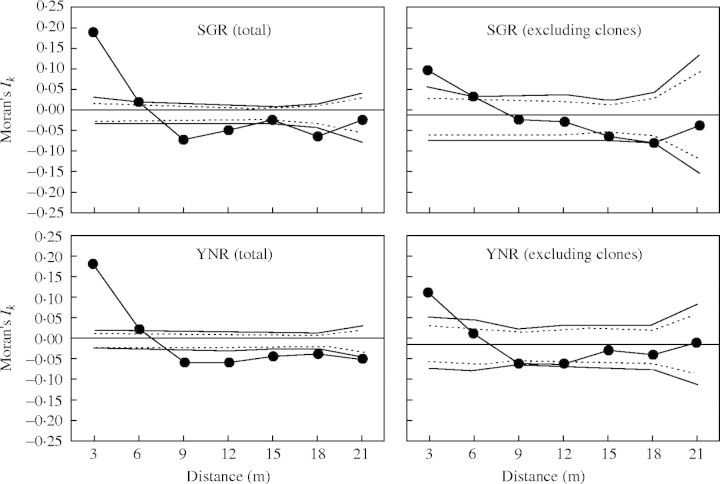
According to the criteria described in the Materials and methods, seven loci were chosen for conducting the spatial autocorrelation analysis. The spatial autocorrelation coefficients, Moran's I_k, were calculated separately for total samples and for genets in each of the two populations. For the total sample from population SGR, Moran's I_k values for individual alleles were significantly different from the expected value [E(I_k) = −0·007] in 26 (53·1 %) of 49 cases (seven independent alleles × seven distance classes) I_k averaged. For distance classes 1 and 2 (0–3 m and 3–6 m), ten significant positive values were observed, whereas only two significant negative values were detected in distance class 2 (data not shown). Taken together these results indicate that most of the genetic similarity was shared among individuals separated by <6 m. Very similar results were observed for the total samples in YNR (data not shown). Moran's I_k values were significantly different from the expected value [E(I_k) = −0·006] in 38 (77·6 %) of 49 cases and, for distance classes 1 and 2, ten positive versus three negative values were statistically significant. Moran's I_k statistic showed a reduced magnitude of spatial autocorrelation for genets as compared with total samples. For genets in SGR and YNR, the percentage of I_k values significantly different from expected was 30·6 % (15/49) and 34·7 % (17/49), respectively (data not shown). For distance classes 1 and 2, five and seven values in SGR and YNR, respectively, were significantly positive.

Similar results were found in the average correlograms, estimated across alleles per locus and across multiple genotypes for the total samples and samples excluding clones (Fig. 3). For SGR, the regression of slope on the logarithm of distance was significantly different from β = 0 with the slope of β_(r) = −0·100 (95 % CI: −0·013, 0·008) for total samples (including clonal ramets) and β_(g) = −0·065 (95 % CI: −0·026, 0·019) for genets. Very similar results were found in YNR with β_(r) = −0·094 (95 % CI: −0·009, 0·007) and β_(g) = −0·057 (95 % CI: −0·021, 0·019) for total samples and genets, respectively. Differences between slopes for total samples vs. genets and SGR vs. YNR also were not significant [SGR: β_(r) = −0·101, 95 % CI: −0·137, −0·065 and β_(g) = −0·066, 95 % CI: −0·132, 0·000 ; YNR: β_(r) = −0·094, 95 % CI: −0·134, −0·054 and β_(g) = −0·057, 95 % CI: −0·101, −0·013) since 95 % jackknifed CIs overlapped for all pairwise comparisons.

Fig. 3.

Spatial autocorrelation analyses (Moran's I_k statistic averaged over alleles and loci) in populations SGR and YNR of Hosta jonesii for total samples (including clonal ramets) and for sample genets (excluding clones). The continuous and dashed lines represent the upper and the lower 99 % and 95 % confidence envelops, respectively, around the null hypothesis of I_k = 0. The expected Moran's I_k values were lined along the x-axis.

In contrast, the magnitude of spatial autocorrelation (Moran's I_k) at the shortest distance interval (≤2 m) differed significantly between total samples and genets at SGR (jackknifed mean: 0·255, 95 % CI: 0·189, 0·325 for total; mean: 0·093, 95 % CI: −0·004, 0·185 for genets) and YNR (mean: 0·229, 95 % CI: 0·174, 0·294 for total; mean: 0·087, 95 % CI: 0·003, 0·172 for genets). Differences between populations for total samples and for genets, however, were not significantly different at this spatial scale.

The distance at which the mean Moran's I_k values first intercepts the E(I_k) value represents the diameter of a patch (Sokal and Wartenberg, 1983). For the total samples, the average intercept combining the two populations across alleles was 6·92 ± 2·18 m (average ± s.d.), with CIs at 95 % ranging from 5·66 to 8·18 m. Unlike the percentage of Moran's I_k values significantly different from the expected value, a similar value of the correlogram intercept was found in combined samples excluding clones (6·70 ± 1·92 m, 95 % CI = 5·09, 8·30) (t = 0·251; P = 0·807).

DISCUSSION

Clonal effects on genetic diversity

The levels of genetic diversity found within the total samples were very similar to those found in samples excluding clones. This indicates that clones do not significantly affect levels of genetic diversity within populations of Hosta jonesii. Although the distribution of H. jonesii is restricted to a few islands in southern Korea, this species maintains levels of genetic variation within populations that are close to its widespread congener H. minor (H_e = 0·268; Chung, 1994) and the two island endemics H. venusta and H. tsushmensis (H_e = 0·248 and 0·235, respectively; Chung, 1995), but higher than the average for taxa with restricted geographic distributions (H_e = 0·063; Hamrick and Godt, 1989). These data suggest that levels of diversity can be explained by geographical range in some taxa, but that geographical range is not a general predictor of patterns of genetic diversity (Hamrick, 1983; Weins et al., 1989; Soltis and Soltis, 1991).

Clonal effects on population genetic structure

At the population level, fixation index estimated for genets [F_IS(g)] was similar to that for total samples [F_IS(r)] in population SGR, whereas F_IS(g) in YNR for genets was 2-fold greater than F_IS(r). This indicates that in YNR heterozygous genotypes have greater clonal reproduction than homozygous genotypes, which may be indicative of viability selection against inbreeding. For total samples, estimates of F_ST indicate small but significant differences in allele frequencies between populations for two of seven loci, whereas no single locus estimates were significant when clones were excluded (Table 2). In contrast, multilocus estimates of F_ST were low for both total samples and genets, but significant for genets and insignificant for total samples.

Implications for mating system and dispersal capacity

A significant deficit of heterozygotes within populations of H. jonesii [mean F_IS(g); Table 2] may be indicative of inbreeding and/or population substructure (Hartl and Clark, 1997). Much of the deficit of heterozygotes is likely to be due to inbreeding and mating among close relatives because H. jonesii is bee-pollinated and highly self-compatible by geitonogamy (M. Y. Chung and M. G. Chung, unpubl. res.). Significant deficits of heterozygotes compared with H-W equilibrium values have been found within populations of many liliaceous species, including Hemerocallis and Hosta spp. (e.g. Chung, 1994, 1995; Kang and Chung, 2000).

At the scale of investigation, if seed and pollen dispersal is localized resulting in inbreeding and spatial clustering of full and/or half-sibs, this then would lead to the development of significant fine-scale genetic structure and inbreeding (Wright, 1943; Sokal and Wartenberg, 1983; Barbujani, 1987). Although Hosta seeds are adapted for wind dispersal, most seeds fall around maternal plants at <1 m radius (Park and Chung, 1997). The observed pollinators of H. jonesii in the populations studied were bumblebees and honey bees, which exhibited a large proportion of short flight distances (1·24 ± 1·58 s.d. m, n = 68) within patches (M. Y. Chung and M. G. Chung, unpubl. res.), though the bees certainly travel between patches as well (a leptokurtic dispersal of pollen; Roubik, 1989). Localized seed dispersal combined with random mating is expected to generate fine-scale genetic structure without the evolution of isolation by distance within populations. Evidence of restricted dispersal and significant inbreeding in H. jonesii indicate, however, that the observed fine-scale genetic structure is the result of an isolation by distance process.

How closely related are neighbouring individuals within H. jonesii populations? The coefficient of relationship (r) among plants occurring in the smallest distance class (r_d=1) can be estimated as a simple linear function of Moran's I_k calculated for the smallest distance class (I_kd=1) as r_d=1 = I_kd=1 (1 + F), where F is the population inbreeding coefficient. For populations SGR and YNR, r_d=1 is estimated to be 0·113 and 0·135, respectively. To aid in the biological interpretation of these values, it is noted that in an inbreeding population the expected coefficient of relationship for full-sibs, half-sibs and first cousins is 0·5(1 + F), 0·25(1 + F) and 0·125(1 + F), respectively, indicating that the estimates of r_d=1 for SGR and YNR are close to that expected for first cousins. While relatedness within seed shadows will be between that of full- and half-sibs, individuals produced by different mothers will often have coefficients of relationship that are close to zero. Thus the results for SGR and YNR indicate that, even over short distances, overlap of seed shadows is substantial, bringing down the relatedness of closely spaced plants to well below that expected for full- and half-sibs.

Clonal effects on fine-scale genetic structure

As seen in Fig. 3, for populations SGR and YNR, for the 0–3-m interplant distance class total samples exhibited significantly higher I_k values than genets, consistent with the expectation that clonal reproduction enhances the magnitude of spatial autocorrelation (i.e. increased genetic similarity) among neighbouring plants. Within populations, however, the distance at which the correlogram intercepts the x-axis was similar for total samples and genets, indicating that clonal reproduction effects on spatial autocorrelation are localized. Indeed, the join-count statistics revealed that most clones aggregate at interplant distances of <3 m. Thus, the exclusion of clones from the data has little effect on the patch size inferred from the correlogram intercepts. The present results for H. jonesii are different from those found in two populations of Adenophora grandiflora (Campanulaceae), an herbaceous perennial from central Korea (Chung and Epperson, 1999). Join-count statistics revealed that there were statistically significant excesses of pairs of identical genotypes compared with random distribution expectations at distances of <12 m (Chung and Epperson, 1999). Using the correlograms of Moran's I_k provided by Chung and Epperson for A. grandiflora, Diniz-Filho and Telles (2002) showed that the exclusion of clones from the total samples caused significant changes in the correlogram intercepts, which dropped from 8 ± 4·43 m to 4·8 ± 5·33 m (t = 3·696; P < 0·01). It should be noted, however, that recent work (e.g. Fenster et al., 2003) has shown that estimate of the x-intercept is sensitive to sampling scheme, calling into question the utility of comparisons made across species or studies.

Implications for conservation

Although local populations of H. jonesii maintain comparable levels of genetic diversity with its widespread congener H. minor, population sizes [N_e(g)] of H. jonesii are generally smaller than 100 and they are isolated on only four islands (Fig. 1) in southern Korea (M. Y. Chung and M. G. Chung, pers. obs.). Fragmentation and small effective sizes of populations, coupled with increasing reckless collections of endemic wild flowers, including H. jonesii, by plant sellers in South Korea, may result in a severe erosion of genetic diversity in the near future.

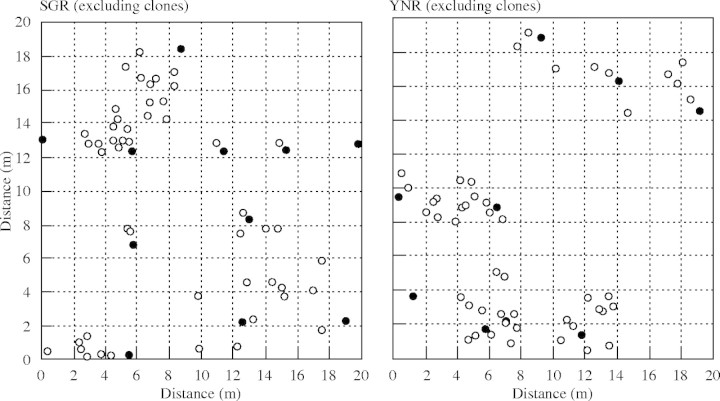
The distribution of genetic variation in space is a prime factor to consider in the conservation and management of natural plant populations (McCue et al., 1996). Achieving an adequate sampling strategy serves as an important base for the effective ex situ conservation of a plant species considered to be facing high risk of extinction in the wild. The sampling strategy for obtaining seed stocks within a population may benefit greatly from the estimation of the average intercept of each correlogram across alleles (Diniz-Filho and Telles, 2002). The average intercept across alleles for total samples (6·92 m) of H. jonesii was nearly the same as that for samples excluding clones (6·70 m). Significant genetic patch structure within populations of this species indicates that sampling strategies for ex situ preservation should maximize genetic diversity and minimize the genetic ‘pseudoreplication’ (redundant genotypes) or consanguinity within populations. To optimize sampling design and avoid pseudoreplication, it is suggested that samples are collected at interplant distances of 7 m to extract the maximum genetic diversity across an entire population. Diniz-Filho and Telles (2002), however, noted the usefulness of 95 % CIs around average intercept across alleles. These authors suggested that the upper or lower CIs could be used in a sequential sampling procedure, depending on whether the researcher is more ‘liberal’ or ‘conservative’ in the sampling strategy to be adopted (i.e. if more resources are available, the use of lower CIs permits more plants to be sampled). Following this recommendation, collections at 5-m intervals (lower CIs) would be recommended to sample the more genetically diverse individuals of H. jonesii. Based on the distribution map of sexually produced individuals (Fig. 4), it is possible to select individuals to be sampled by a ‘cascade’ procedure after one fixed point is initially established (Diniz-Filho and Telles, 2002). An individual harbouring the highest number of total alleles across seven polymorphic loci among the nearest located individuals within a genetic patch was selected. Based on these criteria, in populations SGR and YNR, approx. 11 and eight genets (which approximately correspond to one individual representing each spatial patch) could be collected to preserve most of the genetic variation within the two populations (Fig. 4). As described in Materials and methods, SGR and YNR are approximately located at the centre of continuously distributed large populations (40 × 200 m area, SGR; 60 × 120 m area, YNR). The population composition of SGR and YNR appears to be similar to the remaining area (e.g. a similar density and each local population consisting of many patches; M. G. Chung and M. Y. Chung, unpubl. res.). Thus, under the guidelines suggested above, approx. 100 to 200 genetically distinct individuals [presumably considered to be effective population size, N_e(g)] could be extracted from 0·8 ha (SGR) and 0·72 ha (YNR) for ex situ conservation. With these sample sizes, one concern may be the per-generation rate of genetic drift. The theoretical relationship between N_e and genetic drift (as measured by the per-generation increase in inbreeding) is nonlinear (e.g. Chung et al., 2004a). For example, if N_e = 1 and the initial rate of genetic drift is 0·5 per generation, then when N_e = 100 the rate of genetic drift will be 0·005 per generation. When N_e is larger than 100, then a negligible effect operates on the inferred per-generation rate of random genetic drift.

Fig. 4.

Distribution of sexually reproduced individuals in populations SGR and YNR (N_(g) = 60 in SGR and N_(g) = 57 in YNR). Closed circles represented individuals (11 in SGR and eight in YNR) to be collected for ex situ conservation according to a cascade procedure after one fixed point is initially established (Diniz-Filho and Telles, 2002).

Populations harbouring high levels of genetic diversity or allelic richness with many small genetic patches should be prioritized as targeting populations for in situ conservation, because plant populations consisting of a few, relatively large genetic patches would include fewer genotypes than a population with many, smaller genetic patches (Jin et al., 2003). In the case of H. jonesii, conserving only a fraction of a large population will not be the best choice to preserve high levels of genetic variability in natural populations since closely located individuals (patches) are genetically related. The two populations separated by 2·1 km on Oenaro Island exhibit a homogeneous genetic profile. Thus, it is recommended that large populations with many patches from each of the known locations on the four islands (Dolsan, Jin, Namhae and Oenaro islands: Fig. 1) should be preferentially targeted as in situ conservation sites. These sites could also be selected as sampling sites for ex situ germplasm collection.