Demography, not inheritance, drives phenotypic change in hunted bighorn sheep

Significance

Understanding the consequences that selective harvest has on a targeted trait, such as body size, is a great challenge. This is principally because it is difficult to evaluate the relative importance of the evolutionary and demographic factors that underlie a change in the distribution of a selected trait in a hunted population. Here we use a novel and recently developed two-sex integral projection model to tease apart the underlying demographic and evolutionary mechanisms of trait change in a trophy-hunted bighorn sheep population. We find that body size is weakly inherited and that subsequently demographic change, and not evolutionary change, as previously thought, is the principle driver of trait shifts in hunted bighorn sheep.

Abstract

Selective harvest, such as trophy hunting, can shift the distribution of a quantitative character such as body size. If the targeted character is heritable, then there will be an evolutionary response to selection, and where the trait is not, then any response will be plastic or demographic. Identifying the relative contributions of these different mechanisms is a major challenge in wildlife conservation. New mathematical approaches can provide insight not previously available. Here we develop a size- and age-based two-sex integral projection model based on individual-based data from a long-term study of hunted bighorn sheep (Ovis canadensis) at Ram Mountain, Canada. We simulate the effect of trophy hunting on body size and find that the inheritance of body mass is weak and that any perceived decline in body mass of the bighorn population is largely attributable to demographic change and environmental factors. To our knowledge, this work provides the first use of two-sex integral projection models to investigate the potential eco-evolutionary consequences of selective harvest.

Trophy hunting, can result in undesirable phenotypic change (1, 2), sometimes termed “unnatural selection” (3). Hunters may target individuals within a population that possess a trait they seek, such as large body or horn size, or a distinct color morph (4–6). If the trait is heritable, then selection against the character can result in a cross-generational decrease in the character mean (1, 6, 7). Apparent shifts in the distribution of a quantitative character, however, may not occur through genetic mechanisms alone, because hunting can also alter age and sex structure, behavior, and social hierarchies (8–10), which may in turn interact with localized density-dependent and -independent factors to accentuate, or mask, a phenotypic response (6, 11, 12).

To date, there have been some generalizations that hunting management can follow in an attempt to mimic natural mortality and limit selection against desirable traits, such as nose coloration for African lions (13). Where long-term data are available for hunted populations, then a response to unnatural selection can be detected. One relatively new method that provides a broad model framework, within which scenario tests are possible, is integral projection modeling (14, 15). These models are built from the relationships between a continuous quantitative trait such as body mass and demographic functions. Integral projection models (IPMs) are constructed from the statistical relationships between a trait and survival and fecundity, development of the trait over time, and the pattern of inheritance (15). IPMs can be used to calculate quantities useful to population and evolutionary biologists, including population structure and growth rate, net reproductive rate, generation length, and estimates of biometric heritabilities (16). IPMs also avoid the discrete classes of classic matrix models, although they can be approximated as high-dimensional matrices.

Recent theoretical development has provided for two-sex IPMs (17), allowing a more realistic assessment of sex-selective harvest, typical of trophy hunting. Moreover, long-term environmental changes and density-dependent effects can be accounted for in IPMs, allowing biologists the ability to separate these from evolutionary effects.

We generalize a two-sex IPM to include age structure, in addition to size structure, to assess the extent to which trophy hunting affects body mass in bighorn sheep (Ovis canadensis). Previous studies have shown that hunting based on 4/5 degree of horn curl resulted in artificial selection and evolutionary changes on ram horn size—a trait strongly correlated with body mass—in the Ram Mountain population (1, 18). Analyses have further revealed that bighorn ram horn size has declined over large spatial scales in trophy-hunted populations in both Alberta (19) and British Columbia (20).

Here we apply a framework to separate the relative importance of evolutionary and nonevolutionary outcomes of trophy hunting on bighorn body size. We simulate the effects of harvest on body mass instead of horn length, because we do not have adequate data for bighorn lamb horn length, although these traits are strongly correlated. Through our model we aim to assess how hunting affects body mass distribution. Because evolutionary change requires phenotypic similarity between parents and offspring, and because individuals tend to remain in the same part of the body-mass distribution throughout life (slopes of the growth function in all age classes are close to 1), we investigate the role of evolution on the population consequences of selective harvest by perturbing the inheritance slopes.

Results

Model Parameterization.

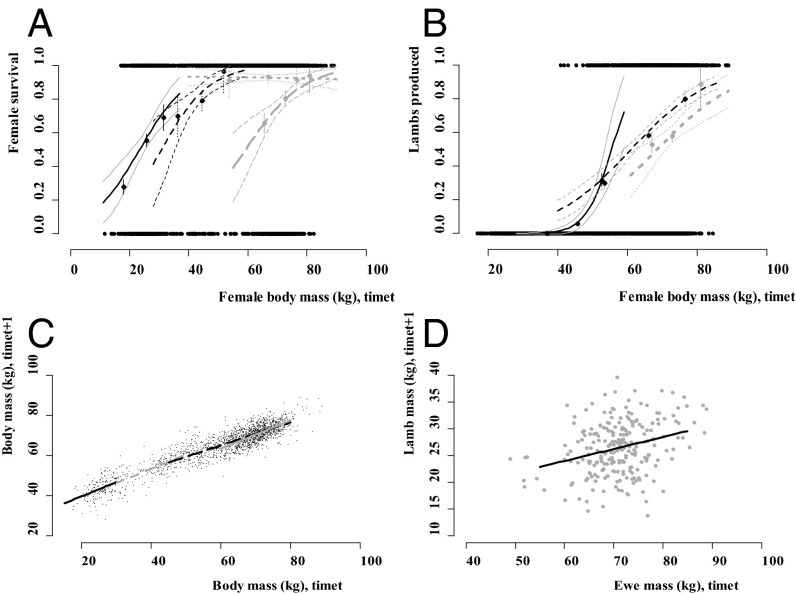
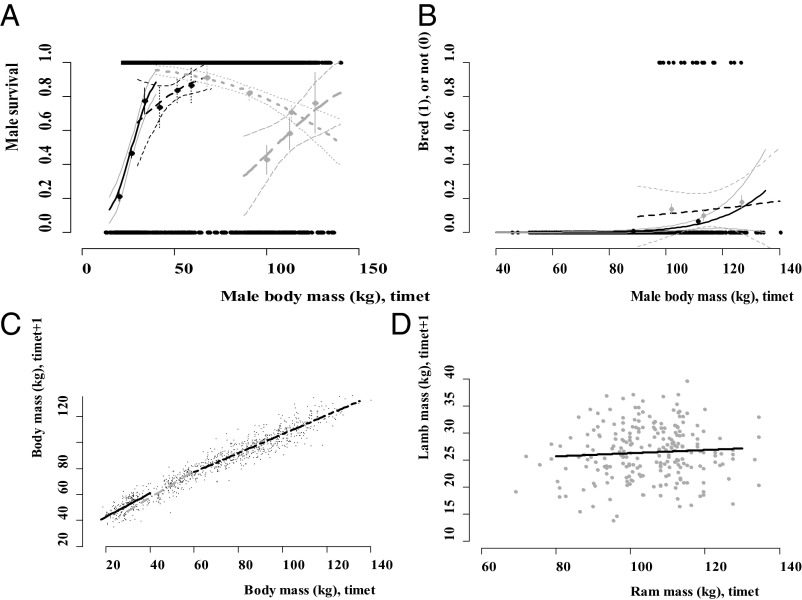
We used generalized linear mixed models to identify the functions required to construct the IPM (14). Raw data from the Ram Mountain bighorn population and generalized linear model fits are presented in Figs. 1 and 2 (for coefficients, see Tables S1–S4). These include female and male survival for all age groups (Figs. 1A and 2 A); the probability of lambing for ewe yearlings, adults, and senescents (Fig. 1B); the breeding success of adult and senescent rams (Fig. 2B); the growth of females and males across each age group (Figs. 1C and 2C); and inheritance, or lamb mass, at time t + 1 as a function of both ewe mass (Fig. 1D) and ram mass at time t (Fig. 2D). In our model, inheritance is estimated as the mass of lambs when they wean as a function of parental mass in the year of conception. The generalized linear mixed model used to determine the inheritance function in the model incorporated both parents, so lamb mass (at time t + 1) is a function of male and female mass at time t (Materials and Methods).

Fig. 1.

Statistical generalized linear model fits for survival, fertility, growth, and inheritance for female bighorn sheep (see full model coefficients in Tables S1–S4). (A) Female survival as a function of body mass (kilograms), where raw data over all years are plotted as 1 (survival) or 0 (mortality), on the y axis. The solid black line shows predicted model fit for lamb survival as a function of birth mass at time t, dotted black line yearling survival, small-dot gray line adult ewe survival, and dashed gray line senescent ewe survival. Confidence intervals are shown, along with empirical estimates of the data with SEs, taken as first, central, and last third bins for each age–size group. (B) Data and model fit for ewe reproductive success (at time t + 1), as lambed (1), or not (0), as a function of body mass at time t for yearlings (solid black line), adults (dashed black line), and senescents (dotted gray line). Confidence intervals and empirical estimates of data as in A. (C) Development data and linear model fit, where mass at time t + 1 for each age group is a function of mass at time t. Fitted black line is lamb growth, dashed gray line is yearling growth, dashed black line is adult growth, and solid gray line is senescent growth. (D) Inheritance data and linear model fit where lamb mass at time t + 1 is a function of pooled yearling, adult, and senescent ewe mass at time t. Note that the inheritance function within the IPM accounted for the mass of both parents.

Fig. 2.

Statistical model fits of survival, growth, fertility, and inheritance for male bighorn sheep (model coefficients in Tables S1–S4). (A) Raw data and binomial model fits for male survival as a function of body mass (kilograms). The solid black line shows lamb survival as a function of birth mass at time t, dashed black line shows yearling survival, dotted gray line adult ram survival, and dashed gray line senescent ram survival. Empirical estimates for these data, taken as the first, central, and last third for each age–size group, with SEs are shown as black dots and vertical lines. Confidence intervals shown for each model prediction. (B) Ram reproduced or not as a function of body mass at time t for adults (fitted solid black line) and senescents (fitted dotted black line). This figure is for illustration; mathematical notation for male mating strategy is described in SI Materials and Methods. (C) Development: The fitted black solid line is lamb growth, the dashed gray line yearling growth, and the dashed black line pooled adult and senescent males. (D) Inheritance data plotted, where lamb mass at time t + 1 is a function of pooled adult and senescent ram mass at time t, with fitted linear model as black line.

Selective Harvest.

We simulated selective harvest based on a stochastic two-sex IPM (Materials and Methods). The stochastic component is fully described in SI Materials and Methods. We simulated body mass as the targeted trait. Body mass is correlated with horn length in male bighorn sheep [correlation coefficient between male adult body mass (in June) and horn length across all cohorts was 0.752].

To simulate selective harvest, we increased the mortality rates of male adults and senescents above a body mass threshold of 100 kg. We applied varying harvest intensities, at 0.01–0.06, and then 0.1, 0.15, 0.2, and 0.25 up to 0.85 over 1,100 annual time steps. We also altered the inheritance function, simulating no inheritance of body mass from fathers (model slope at 0), observed inheritance (model slope at 0.02), and an increase in the response to selection by adjusting the paternal inheritance slope upward by 10%. We further increased the inheritance slope for the lamb–adult male relationship by 1000%, such that the slope increased from 0.02 to 0.2, similar to the slope for lamb–female inheritance (see coefficients for model fits in Table S4).

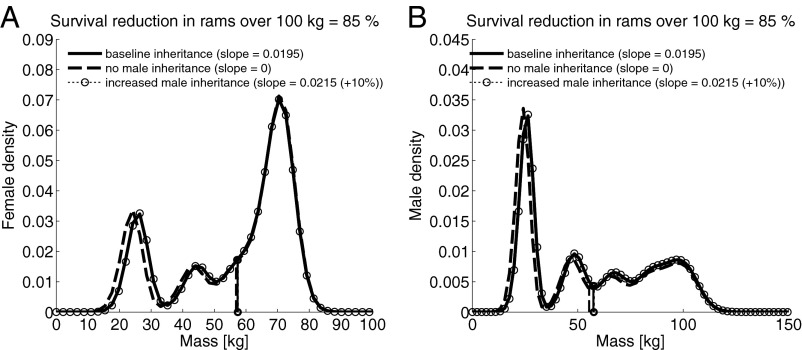
Mean body mass for all ages following harvest is shown in Fig. 3, with harvest, or mortality of males >100 kg, reduced by 0.85. Even the estimated weak inheritance of body mass from males has an effect on body mass distribution, given that when we simulate no male inheritance the distribution of body mass for lambs shifts toward smaller animals, indicating that those few adult males that do escape harvest manage to pass on some of their body size (Fig. 3). The increase in the male inheritance function slope by 10% shows little effect relative to observed inheritance. The stochastic population growth rate changes very little under varying levels of male inheritance: −0.020 where no male inheritance exists, −0.011 for the baseline value, and −0.0097 following an increase in the slope of the inheritance function for males by 10%.

Fig. 3.

Body mass distribution for a stable population of (A) female and (B) male bighorn sheep. Data show the model distribution averaged following simulation with a stochastic model over 1,100 time steps. The black dashed line indicates mass distribution with no inheritance of mass from males (slope set to 0), the black solid line distribution indicates baseline inheritance, and the small dotted line with open circles indicates body mass distribution where the inheritance slope was increased by 10%. All three lines show body weight distribution where survival rate of rams over 100 kg is reduced through harvest by 85%.

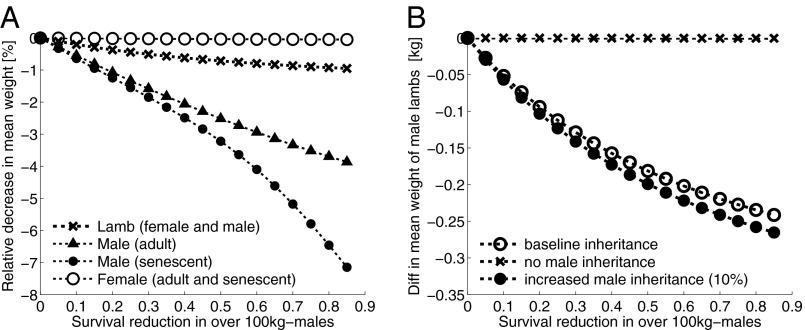
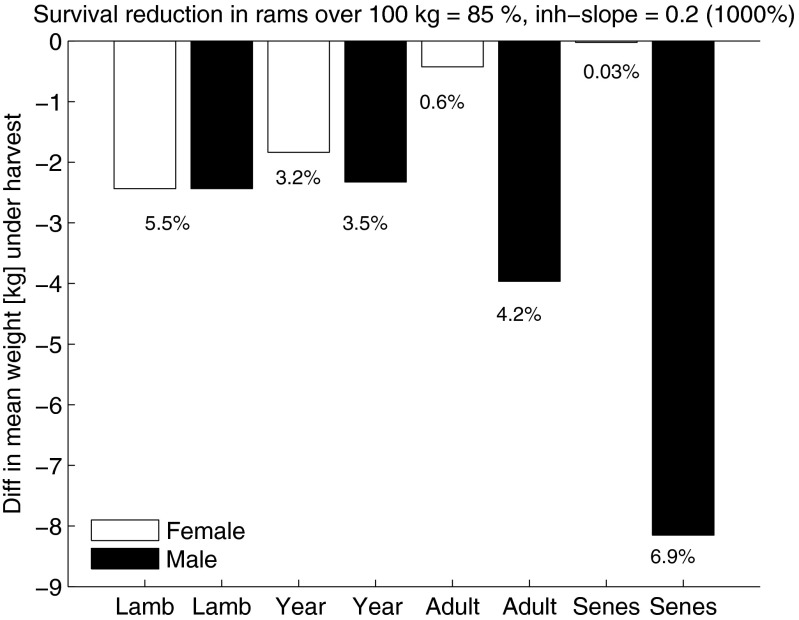
There is a shift in body mass distribution for males following harvest, but only for larger rams, as one would expect following selective harvest of larger individuals (Fig. 4A). When we consider the percentage difference in mean mass of males and females by age group following offtake, we find that despite an increased pressure of harvest the change in lamb mass is relatively low at 1% (Fig. 4A, black crosses) and at less than 0.5 kg (Fig. 4B), owing to the weak association between parental size at conception and offspring size. It is interesting to note that lambs of both sexes experience a relative decline in body mass following increased harvest; however, this does not translate to a relative decline in mass for both sexes in adulthood. If an evolutionary response to harvest were present within the population (via body mass), then there would be an obvious relative decline of adult ewe mass, and the same would likely be for males, except that these are removed through harvest. This is illustrated further when we increase the slope of the lamb–adult male inheritance function by 1,000% (Fig. 5), such that it is similar to the slope for lamb–adult female inheritance. Again the difference in the mean weight of lambs when large males are being harvested is similar, but at adulthood and senescence there is practically no shift in the mean mass of females. The shift in male adult and senescent body mass relative the shift in adult female and senescent mass implies a demographic, not evolutionary, response, which would be apparent if there were a similar shift in mean female adult mass.

Fig. 4.

The difference in mean weight of bighorn by age group following an increase in hunting intensity. (A) Hunting intensity was estimated by reducing the survival in rams over 100 kg by 5, 10, 15, 20, and 25 up to 85%. The black crosses, triangles, and circles represent the differences in mass for male and female lambs and male adults and senescents following harvest and where the male inheritance function slope is based on field data. Open circles show shifts in female adult and senescent mass following the selective harvest of large males. (B) The same harvest simulation as in A, but showing the difference in mean weight of male lambs only, based on the inheritance function slope set at 0 (no inheritance, black crosses), the inheritance slope based on field data (baseline, open circles), and an increase in the slope of that function by 10% (filled circles).

Fig. 5.

The difference in the mean mass (kilograms) of bighorn sheep, by age group and sex, following harvest of males over 100 kg and with male inheritance function slope increased by 1,000%. Data show the difference in mean mass for all age classes (lambs through senescents) following the simulated harvest of males only, set at 85% for all individuals over 100 kg. Open columns indicate females and filled black columns males, and percent values indicate change in mass away from the mean.

Further, we show that those males that do survive harvest and go on to mate have a lower mean body mass (8% decrease) than those from a nonharvested population (Fig. S1 A and B), and as a consequence, the mean mass in lambs declines by 1%. If we increase the slope of the inheritance function by 10% (Fig. 4B, black circles), then male lamb mass declines following an increase in the harvest rate of large rams, although the decline is marginal.

Thus, for the Ram Mountain bighorn sheep population, trophy hunting most likely affects mean body mass through a reduction in survival of heavy individuals. The disruption that hunting will cause for population age and sex structure is illustrated by the shift in the sex ratio (toward females) after increased levels of harvest (Fig. S2) and the proportion of older males affected (Fig. S3).

Further, we can use the framework provided through construction of the IPM to conceptually consider a priori the likely effects that the selective harvest of adult males will have on both male and female body mass distribution and population growth rate (Table S5). For example, the culling of large males will reduce female population growth rate if males limit ewe fecundity (see ref. 10) or through reduction of female survival or female lambs that are born smaller owing to inheritance. We do not find evidence of male mortality influencing female fecundity or survival here.

Discussion

Wildlife biologists have emphasized the demographic outcomes of selective harvest on populations of large vertebrates, and not always the evolutionary consequences. One reason may be because unnatural selection through the targeting of desirable traits is difficult to show (2)—in particular separating the evolutionary from nonevolutionary effects. Another may be because the demographic consequences of harvest may be catastrophic and glaring, such as the reproductive collapse of Saiga antelope (Saiga tatarica) following the removal of adult males for their horns (10). Despite this, there are a number of examples of phenotypic changes in harvested populations (3, 21), although not all of these changes may have occurred through an evolutionary response. For evolution to occur, the targeted trait needs to be passed from parents to their offspring. If the targeted trait is not inherited, then phenotypic change will most likely be demographic, or plastic.

A clear example of phenotypic change argued to have occurred through an evolutionary response to targeted selection is bighorn sheep, where the removal of “desirable” rams as trophies resulted in a subsequent shift in horn length (1, 19) and body mass (1). We argue that the observed decline in male bighorn body mass over time (see ref. 1) was a demographic, not an evolutionary, response to trophy hunting, based on the weak inheritance of size from male bighorn. Horn length and body mass are correlated in bighorn, and we expect our conclusions to hold for horn length too. Previous authors have argued that evidence of selection on horn length and body mass led to an observed trend in breeding values in bighorn (1). However, improvements in quantitative genetic methods have subsequently cast doubt on the reliability of analyses of trends in mean breeding values (22). Certainly more convincing evidence of an evolutionary response would involve a demonstration of an adaptive change in gene frequencies at loci known to influence horn size.

As a caveat, environmental factors may account for much of the variation in the inheritance function, and we did not estimate the strength of density-dependent effects here because initial analyses found the effect to be positive, owing to the unusual fluctuations in the Ram Mountain population over the last 40 y, including predator-driven Allee effects (23). A further limitation of our model relates to this: we do not include genetics explicitly. Recent work has shown how genetics can be incorporated into IPMs (24), and consequently, when the genes associated with horn length in bighorn sheep are identified, then we could extend our existing model to incorporate them, but until then our results are based on phenomenological analyses of a model of phenotypic trait dynamics. Results from Coulson et al. (24), for example, suggest that unless there are large differences in fitness between genotypes, then changes in genotype frequencies due to altering survival functions are relatively small. So, unless horn length is under relatively simple genetic control, with horn length correlating strongly with genotype, then it is unlikely that a rapid evolutionary response in horn length to selective harvest would be observed.

We do not preclude here the possibility of selective harvest leading to an evolutionary response in any species—of course it can occur. We do recommend caution, however, in interpreting a change in a phenotypic trait in a hunted population as evidence of causality, particularly where that change is very rapid, over a generation or two. Our modeling approach allows the circumstances under which evolutionary responses are likely to occur to be investigated. The models can be made more complex, or simpler, but the great power of them is the ease with which these can be parameterized.

In closing, we show that a change in distribution of body mass in wild bighorn sheep was affected largely by demographic factors, and less so through evolutionary components as a consequence of harvest. We were fortunate enough to have access to long-term, individual-based data to parameterize our model. Unfortunately, such data are typically unavailable for many harvested populations in developing nations, particularly across sub-Saharan Africa, despite the importance of the trophy-hunting industry to local African economies (25). In the absence of longitudinal data, then, informative priors based on allometrically scaled body size–demographic rate associations (26) or published demographic rates (27) may be used to parameterize IPMs, but we strongly suspect that the effects of harvest are localized (28) and that models based on longitudinal, individual-based data (see ref. 29) will be most appropriate for decision making. Once a model such as ours has been parameterized for a species it may be readily adapted for conservation decision making, as are classic matrix models (30, 31), but with the advantage of being able to explore both demographic and evolutionary outcomes of alternate strategies. Such a framework will, for example, permit an analysis of the tradeoffs around trophy income versus demographic and evolutionary change. In the absence of data or models it is probably advisable that regulatory rules mimic natural mortality schedules in males, because this should minimize the risk of undesirable consequences of demographic change, as well as evolutionary change were it sufficient to leave a population-level signature.

Materials and Methods

Individual-Based Bighorn Sheep Data.

We used data for the bighorn sheep population on Ram Mountain, Alberta, Canada. Since 1975, over 95% of the population has been individually tagged and repeatedly measured (1, 18, 32, 33). The field methods used for capture, tagging, and measurement have been documented elsewhere (18, 32).

We parameterized an age-structured two-sex IPM (see SI Materials and Methods for notation of the IPM) for bighorn sheep. The first step toward model parameterization is statistical analysis of field data, which we discuss below. See Table S6 for a complete list of model parameters and functions.

Statistical Analyses.

IPMs require just four fundamental functions that describe the association between a continuous trait and individual survival, development of the trait, recruitment, and the inheritance of the trait (14, 34). Coulson (14) provides an overview of the empirical estimation of IPMs for a similar-sized caprid, which we follow here.

To parameterize our model, we required the statistical relationship between body mass (the trait) and the dependent parameters (i) survival from time t to t + 1, (ii) trait values of surviving individuals at time t + 1, (iii) recruitment of offspring at time t + 1, and (iv) trait values of offspring at time t + 1 once recruited into the population (14).

Bighorn sheep are long-lived, and so the parameterization of model functions for each age group, or even each cohort, would have reduced model robustness and been unnecessarily time-consuming. Following a review of the literature (33, 35), we considered four age classes: juvenile (0–1 y), yearlings (1–2 y), adults (2–7 y), and senescents (7 y upward). Further, we assumed no emigration or immigration into the population.

Body mass and survival.

The survival function determines the number of individuals, and their trait values, that remain in the population at time t + 1 (15). To estimate the probability that an individual of a given body mass at time t survives from t to t + 1, we used generalized linear mixed models (GLMMs) with a binomial error structure and logit link function, within the R language (36). A binomial error structure was used because the data recorded individual survival (1), or not (0), at each year (time step). We used a mixed effects model because we accounted for temporal auto-correlation, using “year” and “ID” as crossed random effects. Analyses were done by sex and age group (Figs. 1A and 2A and Table S1). Initial mixed models accounted for density-dependent effects, using population size as a fixed effect, but we found these to be misleading; the Ram Mountain population has increased dramatically and then declined over the past 40 y, and the low-density decline phase has shown possible time-lag effects and major effects of sudden changes in cougar (Puma concolor) predation (37). Because our models detected and predicted unrealistic positive density dependence, we assumed density independence over the entire time series. We included mortality through trophy hunting as a binary fixed effect (1 for hunted and 0 for natural mortality) for adult and senescent males (Table S1).

Body mass and recruitment.

The recruitment function in the IPM describes the number of offspring produced between time t and t + 1 that survive to t + 1 (14). First, we needed to estimate the probability of a male or female producing a lamb given their mass in time t. The Ram Mountain data provided a record of reproductive success (1), or not (0), for all females all years, but not for all males. Paternity was determined by molecular genetic methods (38), and only a portion of all males were sampled, given migration. We used GLMMs with binomial error structure and logit link function to determine the probability of local reproductive success for females by age class (Figs. 1B and 2B and Table S2). We accounted for temporal influences by using year and ID as random effects, within a mixed-effects model. The male mating strategies are described in SI Materials and Methods.

Bighorn ewes in the study population never twin, so recruitment was a function of the probability of one lamb being produced by a yearling, adult, or senescent female or adult or senescent male of a given body mass (in time t) and the probability of that lamb surviving to time t + 1.

Body mass and development.

The development or growth function describes the change in trait value among surviving individuals from time t to t + 1. To statistically estimate predicted mass at time t + 1, given mass at time t, we compared body mass estimates at time t and then t + 1 for the same individuals (see ref. 14). We used GLMMs with a Gaussian error structure and identity link function with year and ID as random effects to estimate mass at time t + 1 as a function of mass at time t (Table S3), allowing the ability to predict separate changes in mass over one time step for males and females and for each age group (Figs. 1C and 2C). Squared residuals of these fits were required to develop the growth function (for explanation, see refs. 14 and 15), and to estimate these we used GLMMs where the squared growth residuals were a function of mass at time t (Table S3).

Body mass and inheritance.

Similar to the growth function, the inheritance function within the IPM describes the expected body mass of an individual produced at time step t + 1 by an individual of a given mass at time t (14).

We elaborate on the inheritance function, because it is important to our findings: Inheritance is estimated as the birth mass of lambs at weaning as a function of parental mass at conception. It is different from heritability. Heritability is an estimate of the additive genetic variance underlying a trait, usually estimated as the proportion of total variance due to additive differences (narrow-sense heritability). It is an estimate of the covariance between offspring and parental trait measured at the same age. Past heritability estimates for bighorn at Ram Mountain have been determined by regressing the mean trait values for offspring at a given age on parental values at the same age (see refs. 1 and 39). Heritability estimates often ignore the “invisible fraction” (40) when a measured trait is under selection (for example, where a trait such as mass is related to survival, then lighter lambs have higher mortality than heavier lambs), and so fail to account for those animals that have already died.

Inheritance is estimated statistically by regressing the mass of recruits at time t + 1 to the mass of their parents at conception in time t. To do this, we had to link each lamb to the body mass of both parents at time t. We then developed a GLMM where lamb mass at time t + 1 (at weaning) was a function of maternal and paternal mass at time t, accounting for temporal auto-correlation and ID as random effects (Figs. 1D and 2D and Table S4).

Two-Sex IPM.

We have included the mathematical notation for the two-sex IPM in SI Materials and Methods. Readers are encouraged to source Coulson (14) for a more detailed explanation of IPMs and Schindler et al. (17) for a further description of the two-sex IPM used here.

Mating success in bighorn rams increases with age, and older males use horn and body size as weaponry to achieve dominance over younger rams (38). Although young males do sire a substantial proportion of lambs (up to 50%), one large, older ram can sire as much as 35.5% of the lamb population (38). In our model we assume that male mating success increases linearly with male body mass and intercept and slope of that function increases with male age, thus achieving a size and age dependence of sexual selection. In reality, a few large-bodied and dominant males sire most of the offspring (38), so we attempt to simulate this by assigning 15% of successful male mating to the oldest age class and 50% to the heaviest quarter of reproducing rams. We included stochasticity as year effects (based on the random effects intercept for the generalized models for survival).

We developed a stochastic, density-independent IPM and incorporated harvest of adult and senescent rams at varying rates, from 0.01% up to 85% reduction in survival of males >100 kg. Body mass is highly correlated with horn length in bighorn, and the data showed that relatively large-bodied males in the population were more likely to be culled.