Interplay of synchronized music

Rhythmic activities are ubiquitous in nature. Synchronization of rhythmic patterns can be found in interacting inanimate systems where the mechanism of the coupling can usually be identified and understood; it is also commonly observed in living systems where the mechanisms of the interaction are less apparent, and sometimes even mysterious. To characterize the statistical properties—and to develop a simple mathematical model—of these couplings can shed some light on an important class of phenomena of interacting living systems. In PNAS, Hennig (1) examines the cross-correlation of tempo time series: that is, the time intervals between successive musical beats, between two people playing rhythmic music in synchrony. Hennig finds long-range (power-law decayed) cross-correlation between the two synchronized tempo sequences. To simulate the observed phenomenon, Hennig proposes a simple mathematical model that might also be helpful in providing some insights into other synchronization processes in nature.

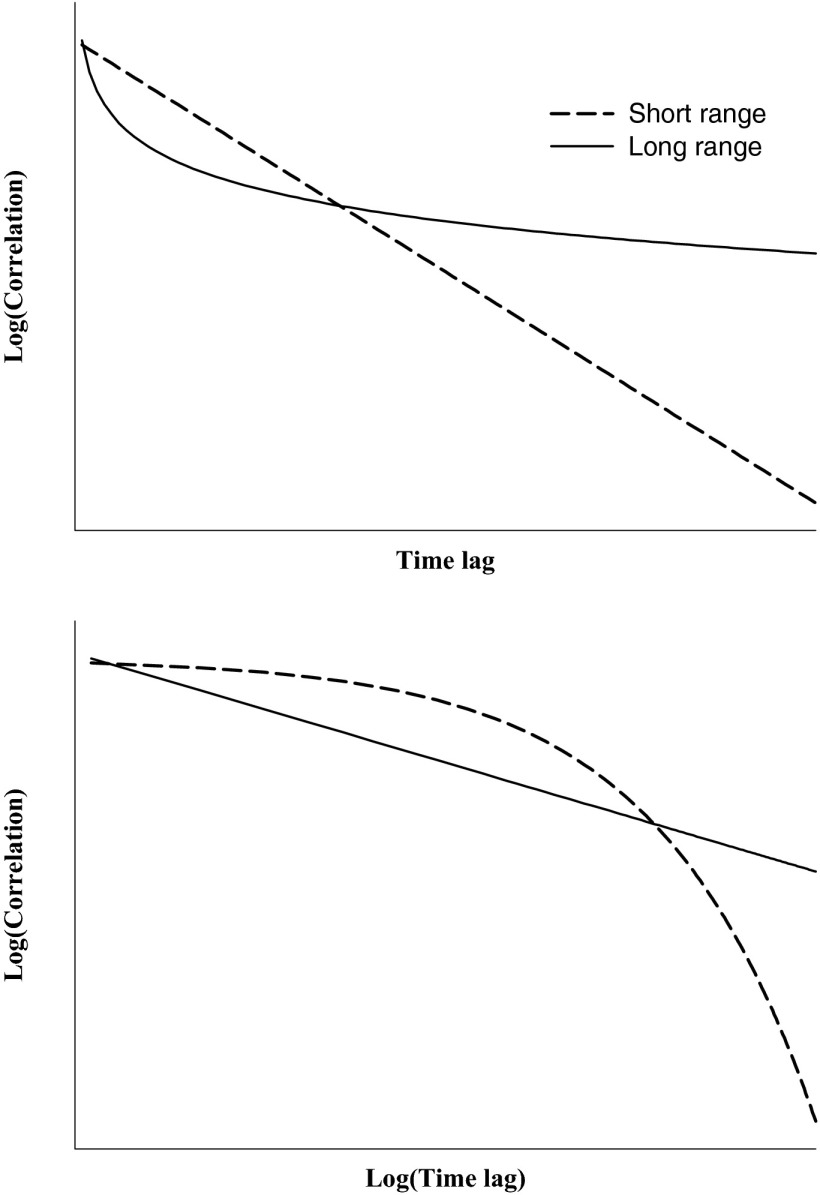
It is expected that there should be coupling in the tempo time series of musical rhythms when two people are playing the music together. The significance of Hennig’s work is the special kind of correlation that appears between two individuals playing music together. To appreciate this discovery, let us first consider the case when one person is producing musical rhythm alone. In this case, it is expected that there will be correlation in the tempo time series generated by the person who plays the music. However, what type of correlation? A simple and intuitive way to think of correlation in time is that the correlation is a result of the information propagating from one instance to the next. In the most trivial case, a certain portion of the information is lost during each propagation. As a result, an exponential decay of the correlation is expected in this type of simple process. No matter how tiny the information loss is for each propagation, this process is still considered as “short-range” correlated. A characteristic time scale, which describes the exponential decay, is associated with the decay of the correlation. Therefore, it was interesting to discover that the tempo time series of musical rhythm exhibits a different type of correlation that does not decay in an exponential fashion (2, 3). Specifically, the tempo time series show “long-range” correlation (LRC), which decays in a power-law way, and no characteristic time scale can be defined in this type of processes. See Fig. 1 for a schematic comparison of short-range vs. long-range correlation. These classes of LRC processes are also known as 1/f noise and are widely observed for complex systems in nature (4). Thus, previous discovery was not completely surprising, as many physiological processes exhibit 1/f noise fluctuations (5). One of the earliest tempo time series analyses was done by Gilden et al. (6). In their experiment, Gilden et al. presented a target time interval to the test subjects, and then asked the subjects to reproduce from memory—to the best of their ability—a temporal series that had the same interval. LRC was observed in the time series created by the test subjects; however, the mechanism of the correlation was not fully understood. It is interesting to note that decades after the discovery of these phenomena, not much progress has been achieved in understanding their origin.

Fig. 1.

Illustration of “short-range” vs. “long-range” correlations. The autocorrelation of a time series is measured as a function of the time lag. Exponential decay of the autocorrelation function (dashed line) is a straight line when plotted on a linear-log graph (Upper), whereas long-range correlation with a power law decay (solid line) is a straight line when plotted on a log-log graph (Lower).

The work by Hennig (1) is novel in two different ways. First, he was able to quantify the cross-correlation between two people playing musical rhythms together, and found that this interindividual correlation is also long-range correlated. The study requires a very careful analysis of challenging time series that are highly nonstationary. Without carefully detrending the time series, the dominant nonstationary properties could lead to spurious artifacts of apparent correlation. Second, Hennig proposed a simple mathematical model that seems to be able to reproduce the dynamics of the synchronization process. However, the model assumes that the LRC in each individual’s tempo time series is given; therefore, it does not explain the mechanism of the observed LRC of a solo player. This is a limitation to the model.

Interestingly, in statistical physics LRC shows up at the critical point of phase transition where the system is balanced between order and disorder (7), which seems to be a good analogy to music. Furthermore, previous studies demonstrated that many physiological time series, including vital signs—such as heart beat, respiration, and blood pressure—show 1/f fluctuations (8–11) that also resemble musical rhythms. Thus, it is not surprising that there have been previous attempts to convert physiologic time series to music compositions with enjoyable results (12).

Although it might be too early to forecast what impact to the real world this interesting work will bring, there are definitely reasons to think that new discoveries and applications will follow Hennig’s work (1). In addition to making more pleasant synchronizing rhythms of artificially generated music, one possible direction to apply what was discovered and proposed in Hennig’s paper is in the biomedical area. Many physiological systems can be thought of as interacting subsystems in synchrony under healthy conditions, but the synchronization degrades when the systems are under pathological perturbation. Restoring the complex interaction between subsystems can have important clinical implications. For example, one potential application is to design more intelligent life-supporting systems for critical care with built-in physiological fluctuations that can dynamically interact with the patient’s own physiological rhythms. This type of intelligent system could have great benefit to patients’ health.