Potentially singular solutions of the 3D axisymmetric Euler equations

Significance

Whether infinitely fast spinning vortices can develop in initially smooth, incompressible inviscid flow fields in finite time is one of the most challenging problems in fluid dynamics. Besides being a difficult mathematical question that has remained open for more than 250 years, the problem also attracts great attention in the physics and engineering communities due to its potential connection to the onset of turbulence in viscous flows. This paper attempts to provide an affirmative answer to this long-standing open question from a numerical point of view, by describing a class of rotationally symmetric flows from which infinitely fast spinning vortices can form in finite time. It suggests, after decades of controversies, a promising direction to the resolution of the problem.

Abstract

The question of finite-time blowup of the 3D incompressible Euler equations is numerically investigated in a periodic cylinder with solid boundaries. Using rotational symmetry, the equations are discretized in the (2D) meridian plane on an adaptive (moving) mesh and is integrated in time with adaptively chosen time steps. The vorticity is observed to develop a ring-singularity on the solid boundary with a growth proportional to ∼(t_s − t)^−2.46, where t_s ∼ 0.0035056 is the estimated singularity time. A local analysis also suggests the existence of a self-similar blowup. The simulations stop at τ₂ = 0.003505 at which time the vorticity amplifies by more than (3 × 10⁸)-fold and the maximum mesh resolution exceeds (3 × 10¹²)². The vorticity vector is observed to maintain four significant digits throughout the computations.

Whether initially smooth solutions to the 3D incompressible Euler equations

$$u_{,t}+u\cdot \nabla u=-\nabla p,\hspace{0.17em}\hspace{0.17em}\nabla \cdot u=0,\hspace{0.17em}\hspace{0.17em}\left(x,t\right)\in {\mathrm{ℝ}}^3\times {\mathrm{ℝ}}^{+},$$ [1]

can develop a singularity in finite time is one of the most fundamental problems in mathematical fluid dynamics. Standing open for more than 250 y and closely related to the Clay Millennium Prize Problem on the Navier–Stokes equations, the problem has received great attention from not only the mathematics but also the physics and engineering communities, where the formation of singularities in inviscid (Euler) flows is believed to be relevant to the creation of small scales in viscous turbulent flows (1–3). The finite-time blowup problem has been studied extensively from both mathematical and numerical points of view. On the mathematical side, a number of useful blowup/nonblowup criteria have been obtained over the years, which have greatly facilitated the numerical search of a finite-time singularity (4–10). On the numerical side, interesting numerical simulations suggesting the existence of a finite-time singularity have been reported from time to time (see, for example, refs. 11–17), but in essentially every case, evidence against a singularity was found in subsequent studies (see, for example, refs. 18–21). This casts doubt on the validity of the claimed singularity and leaves the question of finite-time blowup an unresolved puzzle.

By focusing on flows with rotational symmetry and other special properties, we have identified, through careful numerical studies, a class of potentially singular solutions to the 3D axisymmetric Euler equations in a radially bounded, axially periodic cylinder (see Eqs. 2 and 3 below). The simulations take advantage of the reduced computational complexity in cylindrical geometries, and use a specially designed adaptive mesh to achieve a maximum mesh resolution of over (3 × 10¹²)² near the point of the singularity. This results in a computed vorticity vector with four digits of accuracy (up to the stopping time) and with a (3 × 10⁸)-fold increase in magnitude. The numerical data are checked against all major blowup/nonblowup criteria to confirm the validity of the singularity. A careful local analysis also suggests the existence of a self-similar blowup in the meridian plane.

We emphasize that the 3D axisymmetric Euler equations (Eqs. 2) are different from their free-space counterpart (Eq. 1) in that they have a constant of motion that is not present in the nonsymmetric case (22). In addition, it is well known that the choice of the boundary conditions (periodic vs. no-flow) has a nontrivial impact on the qualitative behavior of the solutions of the Euler equations, especially near the solid boundaries (1, 2). In view of these differences and the fact that the singularity we discover lies right on the boundary (Fig. 1), we stress that the work described in this paper is not directly relevant to the Clay Millennium Prize Problem on the Navier–Stokes equations, which is posed either in free space or on periodic domains.* Rather, it should be viewed as an attempt at the understanding of the effect of solid boundaries in the creation of small scales and, in the case of zero viscosity, the creation of singularities in incompressible flows.

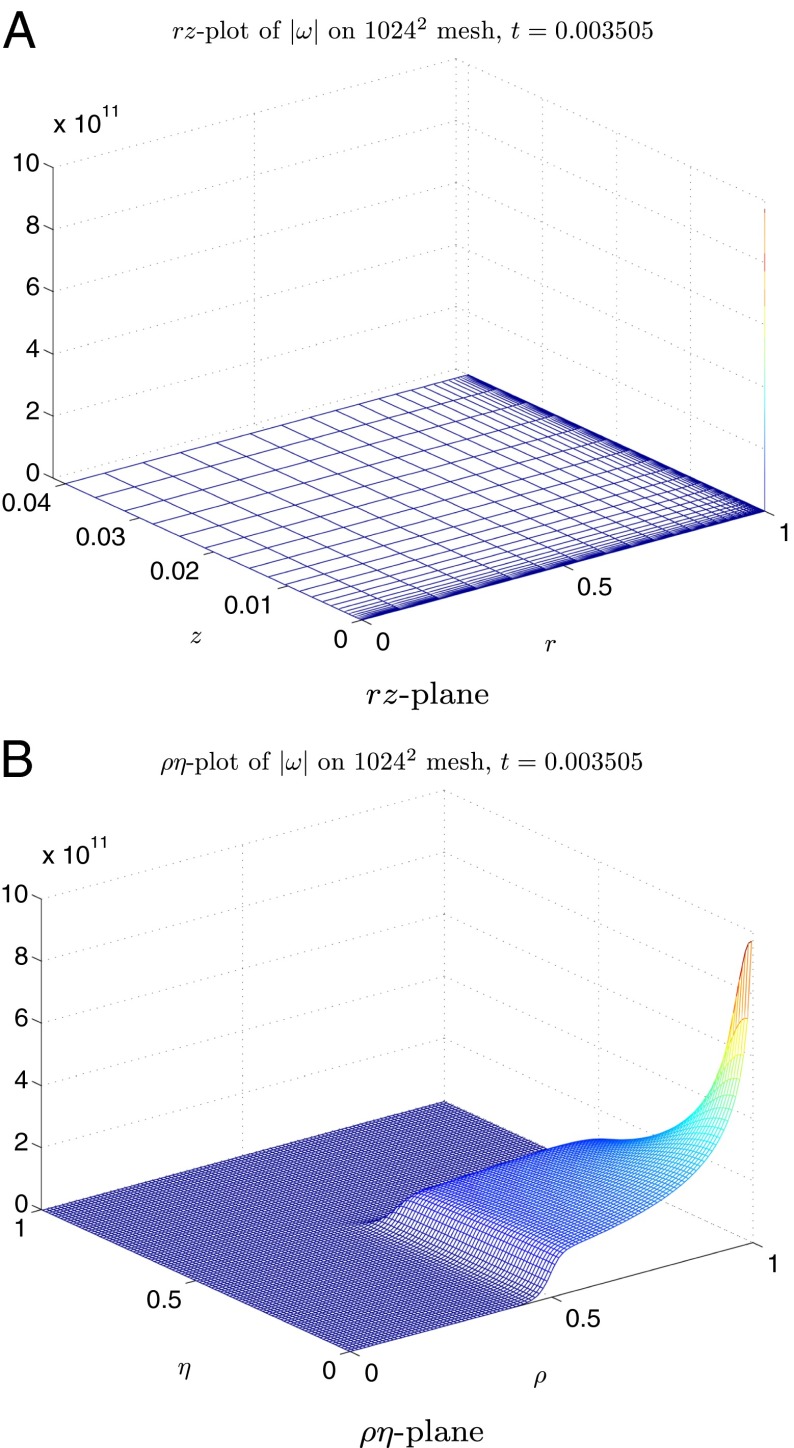
Fig. 1.

The vorticity |ω| on the 1,024 × 1,024 mesh at τ₂ = 0.003505, in (A) rz coordinates and (B) ρη coordinates, where for clarity only 1/10th of the mesh lines are displayed along each dimension.

Description of the Problem

To describe these potentially singular solutions, recall first that in cylindrical coordinates (r, θ, z), a rotationally symmetric flow u can be described by the following decomposition:

$$u\left(r,z\right)=u_r\left(r,z\right)e_r+u_{\theta }\left(r,z\right)e_{\theta }+u_z\left(r,z\right)e_z,$$

where e_r = (cos θ, sin θ, 0)^T, e_θ = (−sin θ, cos θ, 0)^T, and e_z = (0, 0, 1)^T are coordinate axes. The vorticity vector ω = ∇ × u has a similar representation:

$$\begin{array}{c}\omega \left(r,z\right)={\omega }_r\left(r,z\right)e_r+{\omega }_{\theta }\left(r,z\right)e_{\theta }+{\omega }_z\left(r,z\right)e_z,\\ {\omega }_r=-u_{\theta ,z},\hspace{0.17em}\hspace{0.17em}{\omega }_{\theta }=u_{r,z}-u_{z,r},\hspace{0.17em}\hspace{0.17em}{\omega }_z=\frac{1}{r}{\left(r{u}_{\theta }\right)}_{,r},\end{array}$$

where for simplicity we have used subscripts after commas to denote partial differentiations. The incompressibility condition ∇ ⋅ u = 0 implies the existence of a stream function:

$$\psi \left(r,z\right)={\psi }_r\left(r,z\right)e_r+{\psi }_{\theta }\left(r,z\right)e_{\theta }+{\psi }_z\left(r,z\right)e_z,$$

for which u = ∇ × ψ and ω = −Δψ. Taking the θ component of the velocity equation (Eq. 1), the vorticity equation

$${\omega }_{,t}+u\cdot \nabla \omega =\omega \cdot \nabla u,$$

and the Poisson equation −Δψ = ω gives an alternative formulation of the 3D Euler equations:

$$u_{1,t}+u_r{u}_{1,r}+u_z{u}_{1,z}=2u_1{\psi }_{1,z},$$ [2a]

$${\omega }_{1,t}+u_r{\omega }_{1,r}+u_z{\omega }_{1,z}={\left(u_1^2\right)}_{,z},$$ [2b]

$$-\left[{\partial }_r^2+\left(3/r\right){\partial }_r+{\partial }_z^2\right]{\psi }_1={\omega }_1,$$ [2c]

where u₁ = u_θ/r, ω₁ = ω_θ/r, ψ₁ = ψ_θ/r are transformed angular velocity, vorticity, and stream functions, respectively. The radial and axial components of the velocity can be recovered from ψ₁ as follows:

$$u_r=-r{\psi }_{1,z},\hspace{0.17em}\hspace{0.17em}{u}_z=2{\psi }_1+r{\psi }_{1,r},$$ [2d]

for which the incompressibility condition

$$\frac{1}{r}{\left(r{u}_r\right)}_{,r}+u_{z,z}=0$$

is satisfied automatically. As shown by ref. 24, (u_θ, ω_θ, ψ_θ) must all vanish at r = 0 if u is a smooth velocity field. Thus, (u₁, ω₁, ψ₁) are well defined as long as the corresponding solution to Eq. 1 remains smooth. The reason we choose to work with the transformed variables (u₁, ω₁, ψ₁) instead of the original variables (u_θ, ω_θ, ψ_θ) is that the equations satisfied by the latter have a formal singularity at r = 0, which is inconvenient to work with numerically.

We numerically solve the transformed equations (Eqs. 2) on the cylinder:

$$D\left(1,L\right)=\left\{\left(r,z\right):0\le r\le 1,\hspace{0.5em}0\le z\le L\right\},$$

with the initial condition:

$$u_1^0\left(r,z\right)=100\hspace{0.17em}{\text{e}}^{-30{\left(1-r^2\right)}^4}\sin \left(\frac{2\pi }{L}z\right),$$ [3a]

and ${\omega }_1^0\left(r,z\right)={\psi }_1^0\left(r,z\right)=0$. The solution is subject to a periodic boundary condition in z and a no-flow boundary condition ψ₁ = 0 on the solid boundary r = 1. The pole condition

$$u_{1,r}\left(0,z,t\right)={\omega }_{1,r}\left(0,z,t\right)={\psi }_{1,r}\left(0,z,t\right)=0$$ [3b]

is also enforced at the rotation axis r = 0 to ensure the smoothness of the solution. The initial condition (Eq. 3a) describes a purely rotating eddy in a periodic cylinder and it satisfies special odd–even symmetries at the planes $z_i=\frac{i}{4}L$, i = 0, 1, 2, 3. Specifically, $u_1^0$ is even at z₁, z₃, odd at z₀, z₂, and ${\omega }_1^0,{\psi }_1^0$ are both odd at all z_i’s. These symmetry properties are preserved by the equations (Eqs. 2), so instead of solving the problem (Eqs. 2 and 3) on the entire cylinder D(1, L), it suffices to consider the problem on the quarter cylinder $D\left(1,\frac{1}{4}L\right)$, with the periodic boundary condition replaced by appropriate symmetry boundary conditions. It is also interesting to notice that the boundaries of $D\left(1,\frac{1}{4}L\right)$ behave like “impermeable walls”:

$$u_r=0\hspace{1em}\text{on}\hspace{1em}r=1,\hspace{1em}\hspace{1em}{u}_z=0\hspace{1em}\text{on}\hspace{1em}z=0,\frac{1}{4}L,$$

which is a consequence of the no-flow boundary condition and the odd symmetry of ψ₁.

Numerical Method

The discretization of Eqs. 2 is carried out on a fixed-sized nonuniform mesh

$${\mathcal{G}}_0=\left\{\left(r_j,z_i\right):0\le i\le M,\hspace{0.5em}0\le j\le N\right\},$$

where

$$r_j=r\left(j{h}_r\right),z_i=z\left(i{h}_z\right),\hspace{0.17em}\hspace{0.17em}{h}_r=1/N,h_z=1/M,$$

and r = r(ρ), z = z(η) are analytic mesh mapping functions defined on [0, 1]. The mesh mapping functions contain a small number of parameters, which are dynamically computed from the numerical solution so that a certain fraction of the mesh points (e.g., 50% along each dimension) is always placed in a small neighborhood of the singularity. The precise definition and construction of the mesh mapping functions are outlined in Supporting Information.

Given an adaptive mesh ${\mathcal{G}}_0$ and the data (u₁, ω₁) defined on ${\mathcal{G}}_0$, the solution of Eqs. 2 is advanced using the following procedure. First, the Poisson equation (Eq. 2c) is solved for ψ₁ in the ρη-space using a sixth-order B-spline based Galerkin method, where solutions of the weak problem

$$a\left({\psi }_1,\varphi \right):={\displaystyle \underset{{\left[0,1\right]}^2}{\int }\left(\frac{{\psi }_{1,\rho }}{r_{,\rho }}\frac{{\varphi }_{,\rho }}{r_{,\rho }}+\frac{{\psi }_{1,\eta }}{z_{,\eta }}\frac{{\varphi }_{,\eta }}{z_{,\eta }}\right)r^3{r}_{,\rho }{z}_{,\eta }\hspace{0.17em}d\rho \hspace{0.17em}d\eta }={\displaystyle \underset{{\left[0,1\right]}^2}{\int }{\omega }_1\varphi r^3{r}_{,\rho }{z}_{,\eta }\hspace{0.17em}d\rho \hspace{0.17em}d\eta }=:f\left(\varphi \right),\hspace{1em}\forall \varphi \in V,$$

with

$$V=\text{span}\{\varphi \in H^1{\left[\mathrm{0,1}\right]}^2:\varphi \left(-\rho ,\eta \right)=\varphi \left(\rho ,\eta \right),\varphi \left(1,\eta \right)=0,\hspace{0.17em}\varphi \left(\rho ,\ell -\eta \right)=-\varphi \left(\rho ,\ell +\eta \right),\hspace{0.17em}\forall \ell \in \mathrm{\mathbb{Z}}\},$$

are sought in the finite-dimensional subspace of weighted uniform B-splines (25) of order k = 6:

$$V_h:=V_{w,h}^k=\text{span}\left\{w\left(\rho \right)b_{j,h_r}^k\left(\rho \right)b_{i,h_z}^k\left(\eta \right)\right\}\mathrm{\cap }V,$$

where w(ρ) = 1 − ρ² and $b_{\ell ,h}^k\left(s\right)=b^k\left(\left(s/h\right)-\left(\ell -k/2\right)\right)$ are shifted and rescaled uniform B-splines of order k. Second, the 2D velocity $\tilde{u}={\left(u_r,u_z\right)}^T$ is evaluated at the grid points using Eq. 2d, and a suitably small time step δ_t is computed on ${\mathcal{G}}_0$. Finally, the solution (u₁, ω₁) is advanced according to Eqs. 2a and 2b by δ_t using an explicit fourth-order Runge–Kutta method, where the space derivatives in Eqs. 2a and 2b are discretized in the ρη-space using a sixth-order centered difference formula. The difference scheme is complemented by symmetry boundary conditions near η = 0, 1 (symmetry planes) and ρ = 0 (rotation axis), and by extrapolation boundary conditions:

$${\left(D_{\rho ,-}^7{v}_{i,\cdot }\right)}_{N+j}=0,\hspace{0.17em}\hspace{0.17em}0\le i\le M,\hspace{0.5em}1\le j\le 3,$$

near the solid boundary ρ = 1, where D_ρ,− denotes the standard backward difference operator. Once the solution (u₁, ω₁) is advanced to the next time level, the mesh ${\mathcal{G}}_0$ is adapted to the new solution and the whole procedure is repeated until one of the stopping criteria is met (see below).

Numerical Results

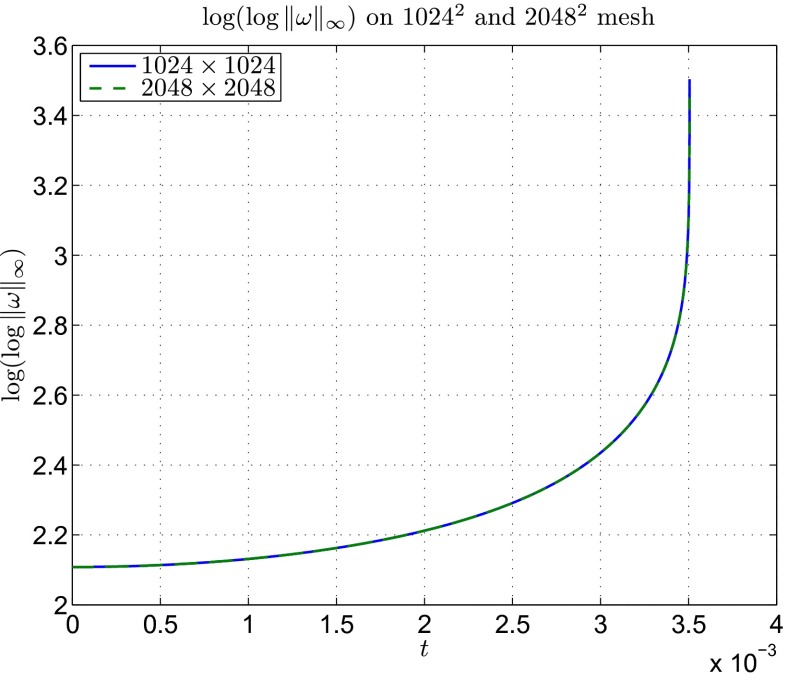
The numerical solutions of Eqs. 2 are computed using five mesh resolutions with mesh size ranging from 1,024 × 1,024 to 2,048 × 2,048. In each resolution run, the solution is advanced indefinitely in time until either the time step drops below 10⁻¹² or the minimum mesh spacing drops below 10⁻¹⁵ (in r) or ${10}^{-15}\left(\frac{1}{4}L\right)$ (in z), whichever happens first. In all five runs, the computation stops at t_e ∼ 0.00350555 and the vorticity |ω| rapidly develops a singular structure in finite time. Fig. 1 shows the vorticity |ω| computed at τ₂ = 0.003505 in both the rz coordinates (Fig. 1A) and the ρη coordinates (Fig. 1B). The rz plot suggests that the singular structure could be a point singularity at the corner ${\tilde{q}}_0={\left(\mathrm{1,0}\right)}^T$, which corresponds to a ring singularity on the solid boundary due to the rotational symmetry. The ρη plot, on the other hand, shows that a good portion of the mesh points (roughly 50% along each dimension) are consistently placed in regions where |ω| is comparable with the maximum vorticity ∥ω∥_∞, hence demonstrating the effectiveness of the adaptive mesh. The rapid growth of the vorticity is further confirmed in Fig. 2, where the maximum vorticity ∥ω∥_∞ is seen to grow much faster than double exponential, and in Fig. 3, where the nearly linear decay of the inverse logarithmic time derivative ${\left[\frac{d}{dt}\log {\Vert \omega \Vert }_{\infty }\right]}^{-1}$ suggests a power law growth of the maximum vorticity (see Eq. 4 below). The quality of the solution is ensured by a careful convergence study, which shows that ω has a pointwise relative error of 3.3212 × 10⁻⁴ at τ₂ = 0.003505 (Fig. 4), at which time the kinetic energy is conserved almost up to machine precision with a relative error of 6.6594 × 10⁻¹³. The maximum and minimum circulations along circular contours, which are known to be conserved by inviscid axisymmetric flows (22), are also monitored, and show a relative error of 3.4921 × 10⁻¹⁴ and 2.5308 × 10⁻¹⁷ at τ₂ = 0.003505. The conservation of circulation along other closed material curves C is not checked, mainly due to the lack of a clear guidance in the choice of C, but resolution studies on the velocity field indicate that the circulation is well conserved along any closed material curve, with a relative error of no more than O(10⁻⁷). Note that this error was derived from the pointwise error of the velocity field and hence is likely an overestimate of the true error.

Fig. 2.

The double logarithm of the maximum vorticity log(log∥ω∥_∞) computed on the 1,024 × 1,024 and the 2,048 × 2,048 mesh. The two curves overlap and are virtually indistinguishable from each other.

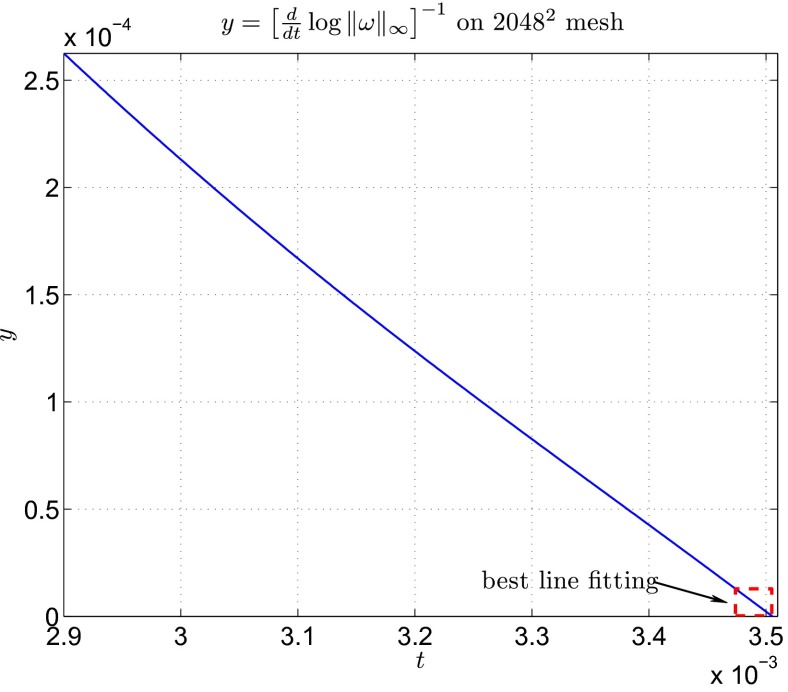
Fig. 3.

Inverse logarithmic time derivative of the maximum vorticity computed on the 2,048 × 2,048 mesh. The dashed line box represents the time interval [τ₁, τ₂] on which the line fitting (Eq. 4) is computed.

Fig. 4.

Sup-norm relative error of the vorticity vector ω. The solution on all but the finest mesh is compared with the one computed on the next finer mesh. The last time instant shown in the figure is t = 0.003504.

The existence of a finite-time singularity is confirmed using the well-known Beale–Kato–Majda (BKM) criterion (4, 6, 7). It asserts that a smooth solution of the 3D Euler equations blows up at time t_s if and only if the maximum vorticity ∥ω∥_∞ accumulates so fast in time that

$${\displaystyle \underset{0}{\overset{t_s}{\int }}{\Vert \omega \left(\cdot ,t\right)\Vert }_{\infty }dt}=\infty .$$

To apply the criterion, the maximum vorticity ∥ω∥_∞ is assumed to satisfy an inverse power law:

$${\Vert \omega \left(\cdot ,t\right)\Vert }_{\infty }\sim c{\left(t_s-t\right)}^{-\gamma },\hspace{0.17em}\hspace{0.17em}c,\hspace{0.5em}\gamma >0,$$ [4]

with unknown singularity time t_s and scaling parameters (c, γ). A careful line fitting with prudential selections of fitting intervals shows that Eq. 4 holds with γ ∼ 2.46 and t_s ∼ 0.0035056 (Fig. 5), confirming the existence of a singularity. A similar blowup criterion of Ponce (5) applies to the strain tensor $S:=\frac{1}{2}\left(\nabla u+{\nabla }^{T}u\right)$ and asserts that the divergence of the integral ${\displaystyle {\int }_0^{t_s}{\Vert S\Vert }_{\infty }dt}$ implies the blowup of the solution. For the nearly singular solution displayed in Fig. 1, it can be shown that ${\Vert S\Vert }_{\infty }\ge \frac{1}{2}{\Vert \omega \Vert }_{\infty }$, and hence the blowup of ${\displaystyle {\int }_0^{t_s}{\Vert S\Vert }_{\infty }dt}$ follows. Another useful way to check the BKM criterion is to apply the Hölder inequality Ω_2m ≤ C_m∥ω∥_∞ where

$${\mathrm{\Omega }}_{2m}:={\left({\displaystyle \underset{D\left(1,L\right)}{\int }{\left|\omega \right|}^{2m}dx}\right)}^{1/2m},\hspace{0.17em}\hspace{0.17em}m=\mathrm{1,2},\dots ,$$

are the vorticity moment integrals (21). Clearly, the divergence of the time integral of any finite-order Ω_2m implies the blowup of ${\displaystyle {\int }_0^{t_s}{\Vert \omega \Vert }_{\infty }dt}$, and in our case Ω₄ = O(t_s − t)⁻¹, which fulfills the criterion.^† Additional supporting evidence of a singularity can also be obtained from the geometric nonblowup criterion of Deng–Hou–Yu^‡ (9). It asserts that no blowup can occur along a vortex line segment L_t at time t_s provided, among other things, that

$$M\left(t\right)L\left(t\right)\le C_0,\hspace{1em}\hspace{1em}L\left(t\right)\ge c_B{\left(t_s-t\right)}^B,\hspace{0.5em}B\in \left(\mathrm{0,1}\right),$$ [5]

where L(t) is the length of L_t and

$$M\left(t\right)=\max \left\{{\Vert \nabla \cdot \xi \Vert }_{L^{\infty }\left(L_t\right)},{\Vert \kappa \Vert }_{L^{\infty }\left(L_t\right)}\right\},$$

where κ = |ξ ⋅ ∇ξ| is the curvature of L_t. Our numerical data suggest that the two conditions listed in Eq. 5 cannot be satisfied simultaneously, because the first condition implies L(t) ≤ C₀M⁻¹(t) but M⁻¹(t) is observed to scale like c(t_s − t)^2.92, which violates the second condition.^§ As is clear from Fig. 6, the z component ξ_z of the vorticity direction changes rapidly along the z dimension near the point of the maximum vorticity, indicating the formation of bundles of “densely packed” vortex lines near z = 0 and explaining the rapid growth of M(t) observed in Eq. 5.

Fig. 5.

Maximum vorticity ∥ω∥_∞ and its inverse power law fit computed on the 2,048 × 2,048 mesh. The two curves are virtually indistinguishable from each other.

Fig. 6.

The geometry of the vorticity direction: (A) the 2D vorticity direction $\tilde{\xi }={\left({\xi }_r,{\xi }_z\right)}^T$ and (B) the z-direction component ξ_z computed on the 1,024 × 1,024 mesh at τ₂ = 0.003505, shown on the region [r_l, 1] × [0, z_r], where r_l = 1 − 5.99 × 10⁻¹¹ and z_r = 2.09 × 10⁻¹². The through-plane (θ) component of ξ has a magnitude of order O(10⁻⁶) in the plotting region and hence is negligible.

The question of existence of a self-similar blowup is also of interest and is investigated numerically. In rotationally symmetric flows, a (meridian-plane) self-similar solution naturally takes the form

$$u_1\left(\tilde{x},t\right)\sim {\left[t_s-t\right]}^{{\gamma }_u}U\left(\frac{\tilde{x}-{\tilde{x}}_0}{{\left[t_s-t\right]}^{{\gamma }_l}}\right),$$ [6a]

$${\omega }_1\left(\tilde{x},t\right)\sim {\left[t_s-t\right]}^{{\gamma }_{\omega }}\mathrm{\Omega }\left(\frac{\tilde{x}-{\tilde{x}}_0}{{\left[t_s-t\right]}^{{\gamma }_l}}\right),$$ [6b]

$${\psi }_1\left(\tilde{x},t\right)\sim {\left[t_s-t\right]}^{{\gamma }_{\psi }}\mathrm{\Psi }\left(\frac{\tilde{x}-{\tilde{x}}_0}{{\left[t_s-t\right]}^{{\gamma }_l}}\right),$$ [6c]

where $\tilde{x}={\left(r,z\right)}^T$ is a point on the rz plane and (U, Ω, Ψ) are self-similar profiles. With ${\tilde{x}}_0={\left(\mathrm{1,0}\right)}^T$, the location of the maximum vorticity, the above ansatz describes a thin-tube “singularity surface” near the solid boundary of the cylinder, which shrinks to a “singularity ring” as the singularity time is approached. This is different from a Leray-type self-similar solution, which contracts along all three dimensions and which becomes a point at the singularity time. The existence of solutions of the form (Eq. 6) is partly confirmed by Fig. 7, which shows the level curves $\left|\omega \right|=\frac{1}{2}{\Vert \omega \Vert }_{\infty }$ at nine different time instants (Fig. 7A) and the same nine curves after rescaling (Fig. 7B). Clearly, the level curves all have similar shapes, indicating the existence of a self-similar solution. Additional supporting evidence of a self-similar solution can also be obtained from the primitive variables (u₁, ω₁, ψ₁) and the details are omitted here for brevity. Using a standard line fitting, the scaling exponents of the self-similar solution (Eq. 6) can be estimated from the numerical data, which gives γ_l ∼ 2.91, γ_u ∼ 0.46, γ_ω ∼ −1, and γ_ψ ∼ 4.83. In particular, it implies that ∥ω∥_∞ ∼ c(t_s − t)^−2.45, confirming again the existence of a finite-time singularity.

Fig. 7.

The level curves $\left|\omega \right|=\frac{1}{2}{\Vert \omega \Vert }_{\infty }$ at nine different time instants: (A) before rescaling, (B) after rescaling. In A, only the first three curves are visible and the other six all shrink to a point at the lower-right corner. In B, the nine rescaled curves collapse almost perfectly to a single curve.

Understanding the Blowup

For the specific initial condition (Eq. 3a) considered in our study, it is observed that $r{u}_1^0$ is monotonically increasing in both r and z within the quarter cylinder $D\left(1,\frac{1}{4}L\right)$. It turns out that this property is preserved by the equations (Eqs. 2) (for reasons yet to be determined), thus u_1,z and consequently ω₁ (Eq. 2b) remain positive for as long as the solution is smooth. The positivity of ω₁ and the homogeneous boundary condition of ψ₁ together imply the positivity of ψ₁ (Eq. 2c), which in turn implies that

$$u_z=2{\psi }_1+r{\psi }_{1,r}={\psi }_{1,r}\le 0\hspace{1em}\text{on}\hspace{1em}r=1,\hspace{0.5em}z\in \left[0,\frac{1}{4}L\right].$$

This shows that the flow has a compression mechanism near the corner ${\tilde{q}}_0={\left(\mathrm{1,0}\right)}^T$ (recall u_z is odd at z = 0), which seems to be responsible for the generation of the finite-time singularity observed at ${\tilde{q}}_0$. From a physical point of view, the blowup can be deduced from vorticity kinematics applied to the initially rotating eddy. The gradient of circulation down the tube, 2πru_θ,z, creates a θ component of vorticity (Eq. 2b). This component in turn creates the flow (u_r, u_z) (Eqs. 2c and 2d), which advects toward the symmetry plane z = 0 on the solid wall r = 1. Because vortex lines threading through the wall are carried by this flow, their points of intersection with the wall move toward the symmetry plane z = 0 and then collapse onto z = 0 in finite time (Fig. 8). This is similar to what was observed in ref. 26 in the study of a model problem, which was derived as the leading-order approximation to a stretched version of the Taylor–Green initial value problem for the 3D Euler equations. The model closely resembles the axisymmetric Euler equations except that the fluid inertia (D_tu_r) in the radial transport equation is missing. Because the variable u_θ studied in ref. 26 occurs as coefficients of the asymptotic expansions, the blowup of its z derivatives merely indicates the breakdown of the expansions and the return of the flow to 3D-ity. It does not imply the loss of regularity of the underlying solutions.

Fig. 8.

Vorticity kinematics of the 3D Euler singularity. The vortex lines (curved solid arrows) end at the wall and are brought to sections of zero circulation by the axial flow (straight dashed arrows). The curved dashed arrows indicate vortical circulation. See also figure 5 in ref. 26.

Conclusion and Future Work

We have numerically studied the 3D axisymmetric Euler equations in a periodic cylinder and have discovered a class of potentially singular solutions from carefully chosen initial data. By using a specially designed yet highly effective adaptive mesh, we have resolved the nearly singular solution with high accuracy and have advanced the solution to a point asymptotically close to the predicted singularity time. Detailed analysis based on rigorous mathematical blowup/nonblowup criteria provides convincing evidence for the existence of a singularity. Local analysis also suggests the existence of a self-similar blowup in the meridian plane.

Besides providing a promising candidate for the finite-time blowup of the 3D Euler equations, our computations also suggest a possible route to the finite-time blowup of the 2D Boussinesq equations. The Boussinesq equations describe the motion of variable-density, stratified flows under the influence of gravitational forces, and like the 3D Euler equations, the existence or nonexistence of globally regular solutions to the 2D Boussinesq equations is a well-known open problem in fluid dynamics (see, for example, ref. 27). Because the 2D Boussinesq equations are known to be qualitatively similar to the 3D axisymmetric Euler equations away from the rotation axis (22), and the singularity discovered in our Euler computations lies on the solid boundary of the cylinder, the solution of the 2D Boussinesq equations resulting from similar initial data are likely to develop a singularity in finite time. This has been confirmed in a separate computation and will be the subject of a forthcoming paper.

Motivated by the observation that the Euler/Boussinesq singularity is likely a consequence of a compression flow along the solid wall, we have derived a 1D model:

$${\theta }_{,t}+u{\theta }_{,z}=0,\hspace{0.17em}\hspace{0.17em}z\in \left(0,L\right),$$ [7a]

$${\omega }_{,t}+u{\omega }_{,z}={\theta }_{,z},$$ [7b]

where the nonlocal velocity u is defined by the following:

$$u\left(z\right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{L}{\int }}\omega \left(y\right)\log \left|\sin \left[\mu \left(z-y\right)\right]\right|dy},\hspace{0.17em}\hspace{0.17em}\mu =\pi /L.$$ [7c]

This 1D model can be viewed as the “restriction” of the 3D axisymmetric Euler equations (Eqs. 2) to the wall r = 1, with the identifications:

$$\theta \left(z\right)\sim u_1^2\left(1,z\right),\hspace{1em}\omega \left(z\right)\sim {\omega }_1\left(1,z\right),\hspace{1em}u\left(z\right)\sim {\psi }_{1,r}\left(1,z\right).$$

The detailed derivation and analysis of the model (Eqs. 7) will be reported in a separate paper.