Dynamic hydration shell restores Kauzmann's 1959 explanation of how the hydrophobic factor drives protein folding

Significance

Kauzmann's proposal that the hydrophobicity of hydrocarbons in water is caused by their hydration shells is modified here by replacing his clathrate water shell with a dynamic shell formed by van der Waals attraction, as proposed by Jorgensen et al. The hydration energetics of alkanes are then shown to be proportional to n, the number of waters in the shell given by the simulations of Jorgensen et al. The Ben-Naim standard state, which is based on solute transfer between fixed positions in the gas and liquid phases, is used for the hydration energetics. Recent experimental evidence for hydration shells is reviewed.

Abstract

Kauzmann's explanation of how the hydrophobic factor drives protein folding is reexamined. His explanation said that hydrocarbon hydration shells are formed, possibly of clathrate water, and they explain why hydrocarbons have uniquely low solubilities in water. His explanation was not universally accepted because of skepticism about the clathrate hydration shell. A revised version is given here in which a dynamic hydration shell is formed by van der Waals (vdw) attraction, as proposed in 1985 by Jorgensen et al. [Jorgensen WL, Gao J, Ravimohan C (1985) J Phys Chem 89:3470–3473]. The vdw hydration shell is implicit in theories of hydrophobicity that contain the vdw interaction between hydrocarbon C and water O atoms. To test the vdw shell model against the known hydration energetics of alkanes, the energetics should be based on the Ben-Naim standard state (solute transfer between fixed positions in the gas and liquid phases). Then the energetics are proportional to n, the number of water molecules correlated with an alkane by vdw attraction, given by the simulations of Jorgensen et al. The energetics show that the decrease in entropy upon hydration is the root cause of hydrophobicity; it probably results from extensive ordering of water molecules in the vdw shell. The puzzle of how hydrophobic free energy can be proportional to nonpolar surface area when the free energy is unfavorable and the only known interaction (the vdw attraction) is favorable, is resolved by finding that the unfavorable free energy is produced by the vdw shell.

When Kauzmann reviewed in 1959 (1) the possible sources of the free energy needed to drive protein folding, he found that that the known factors are not sufficient. He asked what the missing factor could be, and he ruled out peptide H-bonds because they do not provide enough free energy, based on Schellman's (2) analysis of the problem in 1955. Then he discovered the previously unknown hydrophobic factor after observing that known DG values for transfer of hydrocarbons out of water into other solvents could supply the missing free energy. Then he needed to assume that the interior of a folded protein is water-free and the nonpolar side chains are buried inside the protein as folding occurs. In 1960 the 2-Å structure of myoglobin by Kendrew et al. (3) confirmed these predictions.

Kauzmann's Explanation (1959, 1987) of How the Hydrophobic Factor Works in Protein Folding

Kauzmann was confident of his prediction that the hydrophobic factor should be the missing factor and he gave an explanation of how it should work. He accepted the 1945 proposal by Frank and Evans (4) that a hydrocarbon probably forms a hydration shell when it dissolves in water. Forming a hydration shell would explain why there is a large decrease in entropy (ΔS_h) and an unfavorable change in free energy (ΔG_h) when a hydrocarbon dissolves in water (see Kauzmann's Evidence for a Hydration Shell). Moreover, the hydration shell would also explain why there is a large change in heat capacity when a hydrocarbon becomes hydrated (see below). The changes in entropy and free energy explain why hydrocarbons have unusually low solubilities in water, because a hydration shell can be formed only in water. Hydrocarbons are much more soluble in semipolar solvents such as ethanol than in water (5). As the protein folds, the nonpolar side chains are removed from water, which strips off the hydration shells and supplies the favorable ΔG (i.e., −ΔG_h) needed to drive folding, according to Kauzmann's explanation. Note that the hydration shells interact with the unfolded protein, not the folded protein, and the hydration shells act indirectly to stabilize the folded protein by destabilizing the unfolded protein. The quantity ΔG_h today is termed the hydrophobic free energy, and the hydrocarbon being hydrated is gaseous, not liquid [see The Dynamic Hydration Shell Explains Why Hydrophobic Free Energy is Proportional to Nonpolar Solvent-Accessible Surface Area (Å2)].

Kauzmann's Evidence for a Hydration Shell

Some water clathrate structures that form around nonpolar molecules were known in 1959 and the X-ray structures of some water clathrates had been determined (6). Kauzmann agreed with Frank and Evans (4) that the hydrocarbon hydration shell is probably made of clathrate water (the iceberg hypothesis). However, much later (1987), when Kauzmann (7) wrote a commentary on the hydrophobic factor, he said about his 1959 explanation, “This matter has been discussed at length by many authors and is controversial.” The controversy centered around the hydrocarbon hydration shell made of clathrate water.

Kauzmann (1, 7) pointed out that large changes occur in two physical properties of the system when a hydrocarbon dissolves in water, and he argued that these large changes require some definite explanation, such as forming a hydration shell. First, the large entropy change on solution is unusual. Regular solutions (8) have solubilities that are controlled by the enthalpy changes that occur. The entropy change upon hydrocarbon hydration may be explained by a hydration shell if the water molecules in the hydration shell are more ordered than in bulk water (see below). Next, Kauzmann pointed out that the large change in specific heat that occurs when a hydrocarbon dissolves in water is especially striking. Water itself has one of the largest known specific heats: Cp = 1.0 cal deg⁻¹⋅g⁻¹. Dissolving liquid pentane in water has an even larger ΔCp = 1.2 cal deg⁻¹⋅g⁻¹ and dissolving benzene in water has ΔCp = 0.67 cal deg⁻¹⋅g⁻¹ (7). These large values of ΔCp may be explained by the presence of a hydration shell if the ordered water structure that results from forming the shell melts with increasing temperature (see Further Experimental Evidence for Hydration Shells).

Results and Discussion

Evidence Against a Hydration Shell Made of Clathrate Water.

A crystalline compound (fire ice) that has a hydration shell made of clathrate water and encloses a hydrocarbon (methane) is well-known (9) and is abundant. The clathrate structure is termed Type I water clathrate because it has been found repeatedly in various clathrates that enclose different ligands. The X-ray structure of Type I clathrate is known (10). Fire ice burns, releasing water, when exposed to a burning match; it covers the ocean floor but is difficult to bring to the surface because it melts at atmospheric pressure or at temperatures above a few degrees Celsius (9). A few other such water clathrate structures are known and enclose other small hydrocarbons, such as ethane or propane, and these clathrate structures are likewise not very stable (9). In contrast with the low stability of known water clathrates, the hydrophobic factor that helps to stabilize protein folding must be remarkably stable because some folded proteins are stable at 100 °C and an important part of the enthalpy of protein unfolding, when unfolding occurs at 100 °C, is known to be hydrophobic enthalpy (11). (As pointed out above, the hydration shell must be bound to the unfolded protein to drive protein folding when transfer occurs to a nonaqueous environment.) This disparity in stability between known water clathrate structures and the hydrophobic factor in protein folding makes it unlikely that a hydration shell made of water clathrate can explain the hydrophobic factor in protein folding.

Although Kauzmann accepted (1, 7) the iceberg hypothesis of Frank and Evans (4), he evidently hoped for a hydration shell with properties more like those of the later van der Waals (vdw) shell model (see Dynamic Hydration Shells Formed by vdw Attraction). In 1959 he said of his classic review (ref. 1, p. 41), “It seems reasonable to suppose that the structures of the Frank-Evans icebergs might resemble the polyhedral structures in the crystalline hydrates...it is more likely, however, that the crystallinity is somewhat less perfect and that correspondingly more water is involved - say one or two dozen molecules...it is very unlikely that large regions of crystalline order are produced in the icebergs.” By1965, when McMullan and Jeffrey (10) produced an accurate X-ray structure of Type I water clathrate, it was clear that the Type I clathrate structure plays the role of a structurally invariant host in host–guest structures in which the guests are different nonpolar small molecules. Such host–guest structures are quite different from the hydration shell structures that Kauzmann hoped to find, in which the hydration shell would be wrapped around and adapted to the structure of the nonpolar side chain.

Methane Gas in Water Has a Measurable Hydration Shell with 20 Water Molecules.

In 2006 Dec et al. (12) used ¹³C chemical shift data to show that CH₄ gas in water has a hydration shell with 20 water molecules. They made “magic angle” spinning experiments on crystalline fire ice at subzero temperatures and reported that CH₄ in the small domain of the Type I clathrate structure has a different chemical shift (−3.6 ppm) than the species CH₄-24 that is present in the large domain of fire ice. Species CH₄-24 has 24 waters and a ¹³C chemical shift of −5.9 ppm (12), whereas the small domain of Type I clathrate is known to contain 20 waters (10). When crystalline fire ice melts in water, only the species with a chemical shift of −3.6 ppm remains. When methane gas dissolves in water, its chemical shift is −3.6 ppm. Dec et al. concluded that methane gas in water has a hydration shell that contains 20 water molecules and they guessed that a hydration shell with even 21 water molecules would have a measurably different chemical shift than the value shown by CH₄-20.

Dynamic Hydration Shells Formed by vdw Attraction.

In 1985 Jorgensen et al. (13) made Monte Carlo simulations, for seven small alkanes, of the interaction energy (E_a) of the vdw attraction between the C atoms of an alkane and the O atoms of water. They used correlation analysis and applied a proximity criterion to find the number (n) of water molecules that are correlated with (or move with) each alkane. Then they proposed that these correlated waters form the hydration shell of the alkane. (The values of n are given in table 1 of ref. 13 in the column labeled “total,” and the values of E_a are given in table 3 of ref. 13 in the column labeled “E_ax”). An important connection between this work and the evidence for a methane hydration shell (12) is that the number (n = 20.3) of vdw-correlated waters in the methane shell (13) agrees well with the number of water molecules (20) in the hydration shell of methane found by Dec et al. (12), based on chemical shift results.

Theories of hydrophobicity before 1985, from Pierotti (14) in 1965 to Pratt and Chandler (15) in 1977, include the vdw attraction between water (O atoms) and hydrocarbon (C atoms). The presence of a dynamic hydration shell is implicit in these theories.

Testing Whether the Hydration Energetics of Alkanes Are Proportional to n.

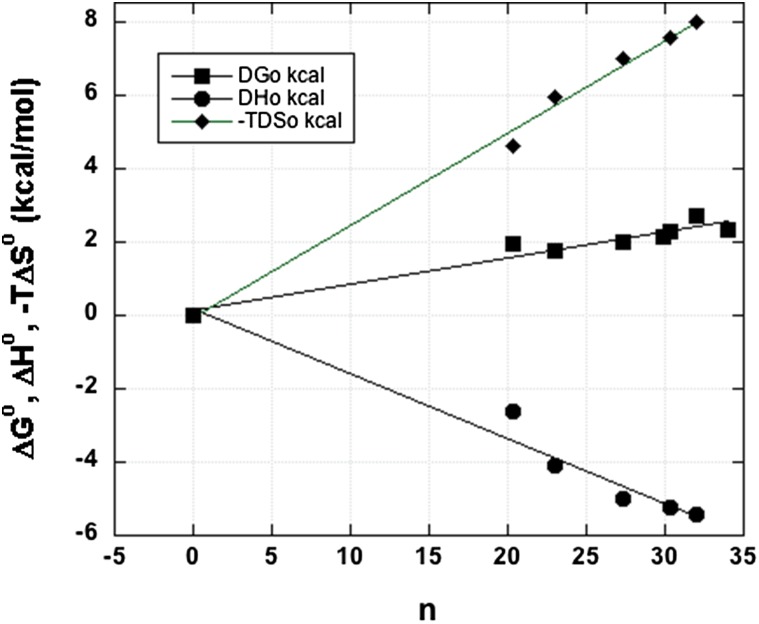
The argument is made below that a dynamic hydration shell fulfills the functions envisioned by Kauzmann: forming a hydration shell by hydrating a hydrocarbon solute stores up hydrophobic free energy and stripping the shell from the hydrocarbon by transfer to a nonaqueous environment can supply free energy that helps to drive protein folding. If this proposal is correct, then ΔG^o for hydrophobic hydration should depend strongly on n, the number of water molecules in the hydration shell. Fig. 1 shows that in fact all three thermodynamic quantities examined here (ΔG^o, ΔH^o, −TΔS^o) are proportional to n (although the results for methane are outliers).

Fig. 1.

Hydration energetics of the alkanes (ΔG^o, ΔH^o, −TΔS^o) plotted against n, the number of water molecules correlated with an alkane by vdw attraction (ref. 13). All data are from Table 1, which lists the original sources.

The results shown in Fig.1 are based on the Ben-Naim standard state (16) for the hydration energetics (see below). If, instead of using the Ben-Naim standard state, the mole fraction concentration scale is used without correction to solute transfer between fixed positions in the gas and liquid phases (which is the standard state convention commonly used earlier), then the ΔG^o values for hydrating alkanes are seen to be essentially independent of solute size, in contrast with Fig. 1 here; see also Table 1, which shows that ΔG^o is proportional to n. For example, the values of ΔG^o in figure 2 of the 1984 paper by Dec and Gill (17) are independent of alkane size and they include data for methane through hexane. The energetics data given in that paper (17) were used by Jorgensen et al. (13) to examine how ΔG^o depends on n.

Table 1.

Normalized hydration energetics (kcal/mol at 25 °C)

Solute	−TΔSo/n	ΔHo/n	ΔGo/n
Data set I
Methane	0.227	−0.128	0.098
Ethane	0.259	−0.179	0.079
Propane	0.256	−0.184	0.072
Isobutane	0.249	−0.173	0.077
Neopentane	0.249	−0.170	0.078
Data set II
Ethane	0.261	−0.182	0.080
Propane	0.249	−0.177	0.072
Butane	0.259	−0.189	0.070

Hydration free energy (ΔG^o), enthalpy (ΔH^o), and entropy (ΔS^o) for the hydration of gaseous alkanes; T is degrees K. The standard state is the one proposed by Ben-Naim (16) for solute transfer between fixed positions in the gas and liquid phases. n is the number of water molecules correlated with the alkane by vdw attraction, taken from ref. 13. ASA is the solvent-accessible surface area in Ų, using the vdw radii given in ref. 19.

A main purpose of using the Ben-Naim standard state is to eliminate the difference in translational free energy (which is very large) between the solute in the gas and liquid phases. Pollack (18) gives an illustrative example: the chemical potential, or standard free energy, of xenon gas at 20 °C is calculated to be −17.9 times thermal energy. The entropic contribution from thermal motion is calculated by the Sackur–Tetrode equation to be −20.4 times thermal energy (18), leaving the enthalpic contribution to the free energy to be just 2.5 times thermal energy. The equations and procedure for using the Ben-Naim standard state are discussed by Makhatadze and Privalov (11) and Lee (19). Note that if molar (or number density) concentration is used in both the gas and liquid phases, then it is not necessary to make a correction for solute transfer between fixed positions in the gas and liquid phases.

In Table 1 the hydration energetics per shell water molecule are the same for different alkanes, which means that the hydration shell is formed noncooperatively, in agreement with the 1985 study by Gill et al. (20), who analyzed the changes in specific heat that occur during the hydration process.

The two data sets in Table 2 (taken from refs. 19, 21) contain measurements of ΔH^o (17, 22) made by mixing alkane gas and water in a flow microcalorimeter. One study (22) was published later than the first and the values of ΔH^o for propane are somewhat different in the two data sets. The equations for measuring and interpreting the values of ΔG^o are simplest when molar (not mole fraction) concentrations are used. In Eq. 1, L is the Ostwald coefficient (18), which is the molar (or number density) alkane concentration in the liquid phase divided by that in the gas phase.

$$\mathrm{\Delta }\mathrm{G}°=-\mathrm{RT}\ln \mathrm{L}.$$ [1]

The value of TΔS^o is computed from the values of ΔH^o and ΔG^o using

$$\text{T}\mathrm{\Delta }\text{S}°=\mathrm{\Delta }\text{H}°-\mathrm{\Delta }\text{G}°.$$ [2]

Table 2.

Hydration energetics (kcal/mol, 25 °C) of some alkanes

Solute	ΔGo	ΔHo	−TΔSo	n	ASA
Data set I, ref. 19
Methane	1.98	−2.61	4.61	20.3	131
Ethane	1.82	−4.11	5.95	23.0	165
Propane	1.96	−5.02	6.98	27.3	194
Isobutane	2.32	−5.23	7.55	30.3	220
Neopentane	2.51	−5.45	7.96	32.0	240
Data set II, ref. 21
Ethane	1.84	−4.18	6.01	23.0	165
Propane	1.96	−4.83	6.79	27.3	194
Butane	2.09	−5.66	7.75	29.9	223

See footnotes to Table 1 for explanation of symbols.

Three basic points regarding the hydration energetics should be noted. First, the ΔG^o values are positive (i.e., unfavorable for solution in water) and they explain why the alkanes have very low solubilities in water. Second, the ΔH^o values are negative (favorable), which is expected from the sizable vdw attractive energies (E_a) in ref. 13. The negative ΔH^o values, which contrast with the positive ΔG^o values, confirm the energetic importance of the vdw attraction. The third point, which is the central feature of the hydration energetics, is that the values of −TΔS^o are large and positive and these values explain why ΔG^o is positive when ΔH^o is negative.

The values of (ΔG^o/n), (ΔH^o/n), and (−TΔS^o/n) are given in Table 1 to look closely at the proportionality of the hydration energetics to n, and they confirm it. In Table 1, the outlier behavior of methane is evident when the hydration energetics are divided by n. Why methane, with its symmetrical structure, should be an energetic outlier is an interesting unsolved problem in understanding the hydration energetics of alkanes.

The Dynamic Hydration Shell Explains Why Hydrophobic Free Energy is Proportional to Nonpolar Solvent-Accessible Surface Area (Ų).

Only recently has hydrophobic free energy been widely regarded as a measurable property of the hydration energetics. In the first major experimental study of the hydrophobic factor in protein folding, Nozaki and Tanford (5) in 1971 measured the transfer free energies of the various nonpolar protein side chains for transfer between two solvents, from ethanol (or dioxane) into water; they stated plainly that such measurements give the hydrophobicity values of the side chains. In 1979 their procedure was criticized by Ben-Naim (16), who believed that hydrophobicity should be measured by solvation free energy and found by transfer from the gas phase to water. Ben-Naim's criticism was rejected by Tanford (23). Nevertheless, without arguing about the question, some authors [notably Makhatadze and Privalov (11)] used gas-to-liquid transfer to find values of the hydrophobic free energy, ΔG_h. The problem of measuring ΔG_h was discussed recently (24) and the conclusion drawn that ΔG_h should be measured by gas-to-liquid transfer, as proposed by Ben-Naim (16). As used here, the term hydrophobicity may refer to results found either by gas–liquid or liquid–liquid transfer.

In 1974 Chothia (25) found that the hydrophobicity values of Nozaki and Tanford (5) for the nonpolar side chains are proportional to nonpolar solvent-accessible surface area in Ų (ASA-np), although account must be taken of any H-bonding groups. Chothia's observation was later often taken to mean that the hydrophobic free energy ΔG_h (whose values are needed in calculations of protein folding energetics) should likewise be proportional to ASA-np. As Hildebrand (26) pointed out in 1968, the only known direct interaction between water and hydrocarbons is the vdw attraction, which is favorable, so it is puzzling why there should be any strong unfavorable interaction. The explanation given here for the unfavorable interaction is based on the properties of the vdw hydration shell (see below in this section). When Pegram and Record (27) in 2008 analyzed how Hofmeister ions affect the water solubilities of hydrocarbons, they concluded there must be an unfavorable interaction between water and ASA-np.

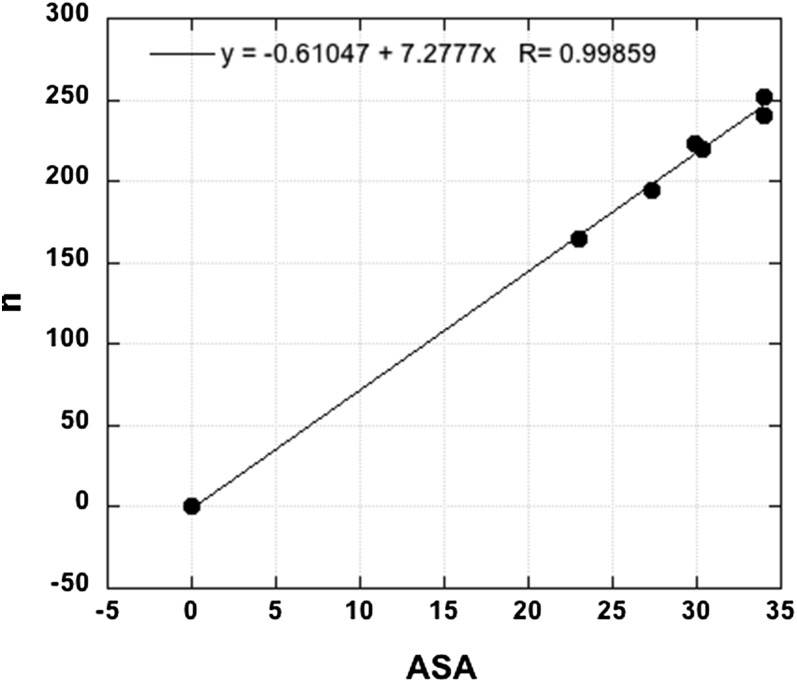
Hildebrand's (26) question is answered here by noting that n, the size of the vdw hydration shell, is proportional to ASA (Fig. 2), and it follows that the ΔG^o values of the hydration energetics are proportional to n; Fig. 1 and Table 1. Thus, ΔG_h is proportional to ASA-np, because ΔG_h = ΔG^o (24).

Fig. 2.

Plot of n (taken as the number of water molecules in the vdw hydration shell) against ASA for the alkanes discussed here; the value for methane (which is an outlier) is omitted. All data are from Table 1, which also gives the ASA value for methane.

Further Experimental Evidence for Hydration Shells.

In 2012 Ben-Amotz and co-workers (28) studied the H-bonding strength of the water within the hydration shells of some hydrophobes by using a novel technique developed in their laboratory, differential Raman spectroscopy that compares infrared spectra in the region of the water OH stretch band inside the hydration shell and in bulk water. The technique was validated in earlier studies from their laboratory. The solutes were deuterated to displace the solute CH stretch band from the water OH stretch band. If water in the solvent shell gives the same Raman spectrum as bulk water, then the solvent shell should be invisible in these experiments. Thus, the results of Ben-Amotz and co-workers show that the hydration shells of the hydrophobic solutes they studied have H-bonded structures that are different from bulk water. Note that only hydrocarbon-like solutes are expected to have hydration shells in the sense that the term is used here, because the vdw hydration shell depends on the presence of the attractive vdw interaction between hydrocarbon C atoms and water O atoms.

Ben-Amotz and co-workers obtained results over an extremely broad temperature range, 0–100 °C. They found stronger H bonding in the hydration shell than in bulk water at 20 °C but, as the temperature increased, the H bonding within the solvent shell became weaker than in bulk water. Two points should be noted here: (i) their results support the existence of hydrocarbon hydration shells, and (ii) the increased H bonding produced within the hydration shell melts out with increasing temperature, as predicted by Kauzmann's interpretation (1, 7) of the large ΔCp values when hydrocarbons dissolve in water.

Results supporting the existence of hydration shells around aliphatic hydrocarbons were found by Lin et al. (29), who used pressure perturbation calorimetry to measure the structure-making or structure-breaking behavior in water of the various amino acid side chains in proteins. They found that aliphatic amino acids (and also proline) change from being structure-making in water near 0 °C to being structure-breaking as the temperature increases above 25 °C (see their figure 3). Note that forming a hydration shell may produce increased H bonding of water molecules adjacent to the shell, as well as within the shell, according to the flickering cluster model of water structure given by Frank and Wen (30).

In 2005 Raschke and Levitt (31) used the TIP4P water model to simulate the water structures around cyclohexane and benzene at 27 °C. They computed radial distribution functions for water orientation and found that, compared with results for bulk water, the H bonding is stronger around both solutes in the first water layer but weaker between the first and second water layers. Both properties were enhanced in the results for water around the aromatic solute (benzene) that they studied, compared with cyclohexane.

Other evidence that hydrocarbon hydration shells play an important role in the interpretation of hydrophobicity was given by Wu and Prausnitz (32) in 2008. They analyzed the energetics of pairwise interactions in water between neighboring pairs of nonpolar groups in short alkanes (decanes or smaller). They were able to fit a large data set by assuming that the hydrophobic interaction in water is pairwise additive. To model their results, they assumed that the hydration shells around two neighboring hydrocarbon moieties are responsible for the hydrophobic interaction between them, and that the interaction strength depends on the distance between the two hydrophobic groups and on the overlap of the two hydration shells.

Concluding Comments.

Kauzmann's original explanation of how the hydrophobic factor drives protein folding aroused wide interest but subsequent efforts failed to find experimental evidence for a hydrocarbon hydration shell made of clathrate water. Dill's 1990 review (33) of major factors in protein folding energetics again focused interest on Kauzmann's hydrophobic factor, which Dill identified as the dominant energetic factor in folding. Also interest grew rapidly in the role of the hydrophobic factor in related problems, such as membranes: see the comprehensive review by Blokzijl and Engberts (34).

A likely reason for the later loss of interest in Kauzmann's 1959 explanation has been the success of theoretical analyses of hydrophobicity, which provided new and fruitful approaches to the study of hydrophobicity: see reviews (35, 36). This paper aims to show that Kauzmann's original explanation of how the hydrophobic factor drives protein folding can be restored by replacing the hydration shell made of clathrate water with a dynamic shell formed by vdw attraction.