Fractal branching organizations of Ediacaran rangeomorph fronds reveal a lost Proterozoic body plan

Significance

Rangeomorph fronds characterize the late Ediacaran Period (575–541 Ma), representing some of the earliest large organisms. As such, they offer key insights into the early evolution of multicellular eukaryotes. However, their extraordinary branching morphology differs from all other organisms and has proved highly enigmatic. Here we provide a unified mathematical model of rangeomorph branching, allowing us to reconstruct 3D morphologies of 11 taxa and measure their functional properties. This reveals an adaptive radiation of fractal morphologies which maximized body surface area, consistent with diffusive nutrient uptake (osmotrophy). Rangeomorphs were adaptively optimal for the low-competition, high-nutrient conditions of Ediacaran oceans. With the Cambrian explosion in animal diversity (from 541 Ma), fundamental changes in ecological and geochemical conditions led to their extinction.

Abstract

The branching morphology of Ediacaran rangeomorph fronds has no exact counterpart in other complex macroorganisms. As such, these fossils pose major questions as to growth patterns, functional morphology, modes of feeding, and adaptive optimality. Here, using parametric Lindenmayer systems, a formal model of rangeomorph morphologies reveals a fractal body plan characterized by self-similar, axial, apical, alternate branching. Consequent morphological reconstruction for 11 taxa demonstrates an adaptive radiation based on 3D space-filling strategies. The fractal body plan of rangeomorphs is shown to maximize surface area, consistent with diffusive nutrient uptake from the water column (osmotrophy). The enigmas of rangeomorph morphology, evolution, and extinction are resolved by the realization that they were adaptively optimized for unique ecological and geochemical conditions in the late Proterozoic. Changes in ocean conditions associated with the Cambrian explosion sealed their fate.

In parallel with large-scale geochemical transitions associated with ocean oxygenation (1–3), the Ediacaran Period (635–541 Ma) records a major diversification of multicellular eukaryotes. Rangeomorph fronds (575–541 Ma) dominated early Ediacaran biotas (4) and have a characteristic branching morphology, distinct from any known Phanerozoic organism (5). Although the fronds are often preserved as flattened impressions, exceptional moldic fossils preserve details of the 3D branching structure to a resolution of 30 μm (6). Qualitative classifications for rangeomorph branching patterns have been proposed (7, 8), but no quantitative model has previously been formulated. Because branching is repeated over decreasing size scales (with up to four observed orders of branching), rangeomorph fronds have been informally described as self-similar and fractal (4–6). Although this has potential implications for the functional optimality of their morphologies (5, 9), the extent to which they are formally fractal and self-similar (10, 11) has not previously been tested. Furthermore, until now, evolutionary transitions in branching patterns have not been characterized within any quantitative framework.

Rangeomorphs inhabited shallow to abyssal marine environments (1, 8, 12–14), evidently precluding photosynthesis for most taxa (12). Preservational features, including bending and overfolding (4, 15), suggest that rangeomorphs were soft-bodied. No evidence exists for either motility or active feeding (such as musculature, filter feeding organs, or a mouth). Consequently, rangeomorphs have been reconstructed as sessile, feeding on organic carbon by diffusion (or possibly endocytosis) through the body surface (3, 5, 12, 16), with a large surface area to volume ratio aiding nutrient uptake (5, 16). The adaptive potential of their different branching morphologies has, however, never been quantified.

Here, using parametric Lindenmayer systems (L-systems) (17, 18), we present a unified model to describe the branching structure of Ediacaran rangeomorph fronds. Our quantitative parameters provide a far more detailed definition of frond morphology than was previously possible. These parameters are then used to reconstruct 3D space-filling strategies within the group and evaluate potential frond functions, revealing an adaptive radiation of fractal organizations. This provides a new framework for the study of growth, functional morphology, and evolution of these lost constructions.

Results and Discussion

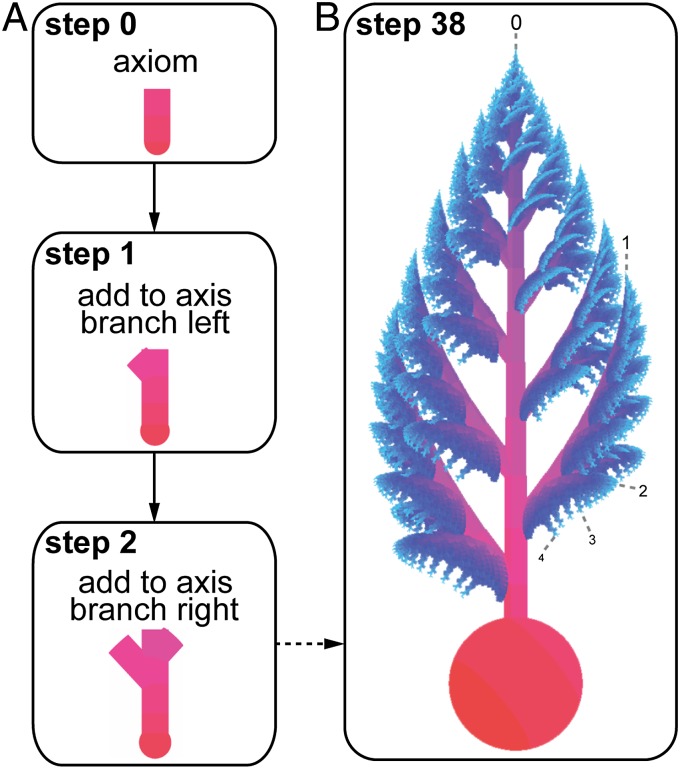
Our L-system model comprises an initial axiom (starting branch segment), production rules for axial, apical, and alternate branching; and 28 parameters which together control branch production, elongation rates, and 3D branching angles (SI Appendix, Table S1). This incorporates both (sub) apical branch production (distal extremities form the sites for subsequent branching) and expansion (branches grow in length and diameter throughout life), based on relative branch sizes and potential ontogenetic series (4, 6, 7, 20, 21). At each step in the axial branching process, an apical branch segment (e.g., the tip of the stem) produces one lateral branch segment (e.g., the beginning of a new primary lateral branch) and an additional axis segment (e.g., the new stem apex) (Fig. 1, SI Appendix, and Movies S1–S3). Lateral branches are produced alternately (e.g., left then right) along a branch axis. Reconstruction of overall morphologies that closely match the anatomy of the fossils (Fig. 2 and SI Appendix) validates this model of branching and growth. Collectively, these reconstructions demonstrate how different body shapes and symmetry patterns [characteristics relied upon by some previous comparative studies (22, 23)] emerge from variations on a shared branching pattern. Resulting body organizations include alternate-symmetry (also known as glide-symmetry) in frontal view [superficially bilateral symmetry, offset due to alternate branching on the right and left of an axis (7)], bilateral or tetraradial symmetry in apical view, and helical torsion around the main body axis (Fig. 3 and SI Appendix).

Fig. 1.

Schematic L-system model of Beothukis mistakensis. (A) First three steps of the branching process. (B) Final morphology at step 38. Segment colors indicate relative age, from oldest (red) to youngest (light blue). Numbers indicate branch order (0, stem; 1, primary; 2, secondary; 3, tertiary; and 4, quaternary).

Fig. 2.

Ediacaran rangeomorph fossils and their 3D L-system models. (A and B) Avalofractus abaculus. A reproduced with permission from ref. 4, figure 3.1. (C and D) Charnia masoni. (C) South Australia Museum specimen number P36574, described in ref. 44, image courtesy of Jim Gehling (South Australian Museum, Adelaide, Australia). (Scale bars, 1 cm.)

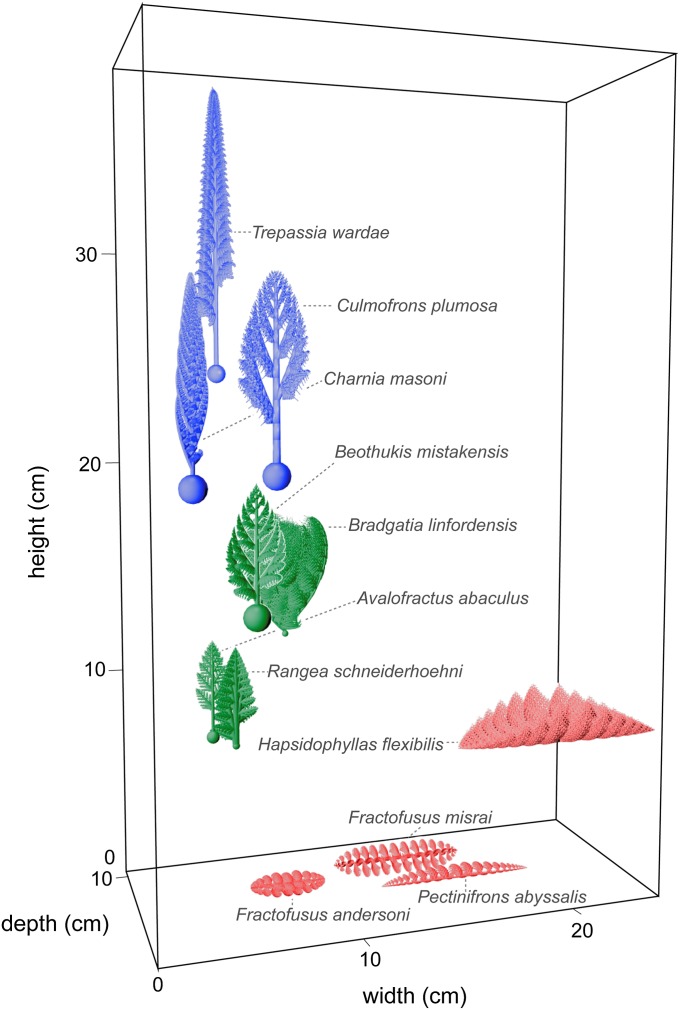
Fig. 3.

Three-dimensional space-filling by Ediacaran rangeomorph fronds (illustrated 1/2 estimated life size). Locations indicate estimated bounding box size in inferred life orientation (values in SI Appendix, Table S2). Frond colors indicate Euclidean distance-based clusters (cophenetic correlation coefficient = 0.77).

Previous descriptions (following ref. 6) informally suggested that rangeomorphs possessed a shared fractal module consisting of a centimeter-scale, self-similar frondlet (conceptually similar to the primary lateral branch and associated subbranches, as formalized here). We demonstrate that rangeomorph morphologies can be reconstructed by applying approximately self-similar branch production rules (as described above) at increasingly fine scales, although these may be modified by different parameter values to give subtle variations in the level of self-similarity (SI Appendix, Table S1). These production rules apply across the branching system of the frond [sometimes called the petalodium (8)], from the stem (the 0-order branch, which produces the first-order lateral branches) to the highest order of branching (that is, from the third-order branches) (Fig. 1). This reveals that self-similarity extends beyond the frondlet, previously hypothesized to represent the basic modular unit (6). That is to say, the entire rangeomorph frond shows approximately self-similar branching, whereas the basic unit repeated throughout the frond is a cylindrical branch segment. This branch segment can be broadly related (6) to Seilacher’s concept of the fractal pneu (24). We also show that rangeomorph fronds are approximately fractal (10) with noninteger fractal dimensions of 1.6–2.4 as determined by the 3D box counting method (SI Appendix, Fig. S13).

Shared possession of an approximately self-similar and fractal, axial, apical, and alternate branching body plan supports a rangeomorph clade (Rangeomorpha, Pflug, 1972, cited in ref. 8) but significantly increases the range of diagnostic characters [previously restricted to repeated fine-scale branching (8) only visible in exceptionally preserved specimens]. Note that this rangeomorph body plan does not extend to other enigmatic Ediacaran macroorganisms, such as Swartpuntia, Ernietta (8), or Dickinsonia (23). This suggests that the rangeomorphs were a distinct, high-ranking clade of multicellular eukaryotes (2, 6) and supports the view that the Ediacaran biota was far from homogenous but instead included diverse phylogenetic lineages and body plans (25).

More widely, approximately analogous morphologies (including alternate, axial, and apical to subapical branching patterns) are seen across the tree of life, among bacteria, protists, plants, fungi, and animals, so indicating extensive convergent evolution of fractal-like branching structures (26). Therefore, superficially similar branching arrangements are not necessarily indicative of close phylogenetic affinity. Indeed, one of the most striking features of such fractal patterns is that highly detailed structures can be described mathematically by quite simple rules (27). Correspondingly, the genetic and developmental programs of self-similar biological structures may be comparatively simple (and conceivably require a relatively small number of genetic changes to evolve) because emergent structural properties do not, in themselves, require genetic specification (9, 11, 28).

Although some exceptional rangeomorph fossils do preserve aspects of 3D morphology (4), the nature of these casts means that the full depth of the frond (perpendicular to the preserved surface) cannot be measured directly (21). However, our reconstructions of 3D branching patterns provide estimates of overall dimensions (Fig. 3), throwing new light on frond ecology. This also allows much more realistic estimates of frond surface area and volume than were possible using simple geometric models (5, 16).

Ratios of external surface area to tissue volume [assuming a 0.1-mm-thick metabolic tissue layer (5)] fall between 77 and 352 cm²/cm³ (SI Appendix, Table S2), within the range for osmotrophic giant bacteria (see also ref. 5). Absolute surface areas (SI Appendix, Table S2) also reach very high values. For example, in the large recliner Hapsidophyllas flexibilis the external surface area is equivalent to 58 m² (in the same order of magnitude as the human lung). Given their large size, rangeomorphs almost certainly relied upon aerobic metabolism (29) of organic carbon (3, 5). Among the 11 studied taxa, the vast majority of body surface area (>95%) is provided by the branching frond (rather than the buried holdfast, where present), and this would have maximized access to the water column. Thus, rangeomorphs most likely fed by the uptake of dissolved organic carbon (5) [or possibly small organic particles (3)], as well as oxygen, from the surrounding seawater, primarily through the surface of the branching frond [although subsidiary nutrient capture from the sediment, through the holdfast or reclining body surface, is a possibility (16, 23)].

The fractal branching of the rangeomorph frond is an optimal geometric solution to the problem of space-filling, maximizing surface area (and correspondingly nutrient uptake) within the boundaries of the total space occupied (9). The most planar of the fronds have fractal dimensions that range from 1.6 (for Avalofractus) to just below 2 (at 1.99 for Trepassia), as estimated by 3D box counting (SI Appendix, Fig. S13). Other taxa (Beothukis, Bradgatia, Culmofrons, and Fractofusus andersoni) have estimated fractal dimensions above 2 (up to 2.4 for Bradgatia; SI Appendix, Fig. S13), reflecting branch arrangements which provide greater 3D space-filling. For example, the helical [lettuce-like (30)] arrangement of the primary branches in Bradgatia (Fig. 3 and SI Appendix) occupies the greatest relative bounding volume (SI Appendix, Table S2) and achieves the highest fractal dimension. Space-filling by the theoretical skeleton of the rangeomorph branching frond (composed of 1D branch segments) is, therefore, so effective that its dimension approaches (or even exceeds) that of a 2D plane. In contrast to a simple plane (that is, an ellipse of comparable height and width), however, the branching frond provides up to 40 times the external surface area (SI Appendix, Table S2). Such structures (incorporating dense, planar feeding nets) maximize nutrient capture, particularly if oriented (passively or actively) with the width axis of a feeding net perpendicular to the ambient water current (31).

Cluster analysis of the total 3D space occupied by a representative of each taxon (Fig. 3 and SI Appendix, Fig. S12) suggests diversification into three major space-filling strategies: those maximizing vertical height (Fig. 3, blue), those of more moderate height including some with high volume (green), and inferred benthic recliners with an accentuated horizontal width (red). Given that the greatest variance between taxa is in height rather than width or depth (Fig. 3 and SI Appendix, Table S2), this suggests ecological tiering (32) and a strong selective pressure for greater height. The fluid dynamics that rangeomorphs experienced are likely to have depended on their local density and size, with a recent theoretical fluid flow model suggesting that dense rangeomorph communities may have created specific canopy flow conditions (16). This model predicts a strong selective advantage for increased height to maximize access to faster flowing fluid, thereby increasing nutrient absorption.

Our growth model also reveals a range of mechanisms by which modifications to a shared growth pattern can achieve different space-filling strategies (Fig. 3 and SI Appendix, Table S1). For example, height can be favored via rapid production of primary branches at angles relatively close to vertical (e.g., Charnia masoni) or by a high rate of elongation for the basal stem segment (e.g., Culmofrons plumosa). To increase frond width, primary branches are produced at a less acute angle from the stem (e.g., Beothukis and Bradgatia). Space-filling of the third dimension (i.e., adding depth if vertically oriented or height if horizontal; Fig. 3) may also be augmented, by the helical arrangement of the primary branches around the central axis [e.g., Beothukis (4) and Bradgatia (30)], by rotations of the primary branches to form a double-layered structure [e.g., Fractofusus (15)], or via primary branch curvature (e.g., Hapsidophyllas).

Some of the tallest rangeomorphs (Charnia and Trepassia) appear in the oldest part of the Avalonian sequence (1, 4). As it stands, this suggests that fronds maximizing vertical height evolved first, followed by diversification into a wider range of 3D branching and space-filling strategies (Fig. 3). However, it is possible that these large rangeomorphs [with Trepassia reaching more than 1 m in length (1, 4)] had smaller, and as yet unknown, precursors. Further to this, evolutionary transitions within the Rangeomorpha should be interpreted with some caution due to uncertainties regarding true paleobiogeographic and temporal ranges (SI Appendix, Table S3) (13).

Among the in situ communities of the earliest Avalon Assemblage, rangeomorphs are by far the most diverse and abundant macroorganisms (33). Furthermore, establishment of the major rangeomorph space-filling strategies (Fig. 3) preceded the appearance of a much wider range of macroorganisms (such as Dickinsoniomorphs and Erniettomorphs) in the White Sea Assemblage from ∼555 Ma (34), with all included rangeomorphs except Rangea itself (35) first appearing in the Avalon Assemblage, by 565 Ma (SI Appendix, Table S3). This suggests that early diversification of rangeomorph branching patterns effected a radiation in the key characters of body size and microhabitat [which are linked by the interaction between body size and access to fluid flow (16, 33)] and was driven by ecological competition between rangeomorph taxa. These features are consistent with a rapid adaptive radiation shortly after the Gaskiers glaciation [from 579 Ma (1, 4)]. Thus, evolution of the fractal branching morphology achieved unprecedented body size and elevated the rangeomorphs into the new ecological realms of the water column, enabling diversification in an environment more or less free of other macroorganisms.

Conclusions

With their terminal Proterozoic extinction and unique morphology, Ediacaran rangeomorph fronds have been described as a failed experiment in evolution (24). However, our analysis demonstrates that these intriguing fossils possessed a fractal morphology which combined programmatic [and potentially genetic developmental (9, 11, 28)] simplicity, structural versatility, and functional optimality for the uptake of organic carbon (osmotrophy) and oxygen. The appearance of rangeomorph fossils (1) occurred after a move away from anoxic, sulfidic, and ferruginous oceans, toward conditions more favorable for aerobic macroorganisms (2, 29). Their disappearance coincides with the Cambrian explosion in metazoan diversity, a dramatic increase in competition, and, crucially, decreased availability of organic carbon in ocean water (2, 12, 19, 24, 34, 36). These potentially interacting factors suggest that the Ediacaran to Cambrian transition was a bad time to be a sessile, soft-bodied osmotroph. The unique rangeomorph fronds were fractal, surface area specialists of the Ediacaran. At the Cambrian explosion, the ecological and geochemical conditions to which the rangeomorphs were optimized ceased to exist, and their extraordinary body plan was lost from life’s repertoire.

Methods

First, this study established a unified model for rangeomorph theoretical morphology using parametric (18) Lindenmayer (L) systems (17), written within the L-studio programming environment (37). L-systems are a class of parallel derivation grammar, in which specified production rules are applied in parallel to control iterative rewriting of the axiom (a starting string, here representing the first stem segments, and holdfast if present). The symbols produced are then interpreted graphically to visualize a geometry encoded by the output L-system string (representing the branching system) (18). A branching L-system is characteristically fractal, with self-similar elements visible at decreasing size scales (38). Parametric L-systems allow branching parameter values (such as branching angles and growth rates) to vary between branches (for example, of different orders or ages), enabling realistic representation of biological structures with nonuniform branching patterns (18).

Rangeomorph morphologies were modeled using formal production rules and parameters based on branching patterns of 11 studied species and quantitative measurements (of branching angles and body dimensions) from best-preserved representatives (SI Appendix). For each species, the L-system output geometry was then processed and analyzed using Blender 2.69 and MATLAB (2012b; Mathworks). For measurement comparability, L-system output was standardized to the same finite approximation (four orders of branching).

The fractal dimension of each modeled frond was estimated using box counting, the method most commonly used to analyze complex fractal shapes (10). This method determines the number (n) of boxes of a given size (r) that cover the input image. The scale (r) is incrementally decreased to determine the relationship between box size and image coverage. The slope of the line for this relationship gives the fractal dimension of the image D = −log(n)/log(r). If dimension D is not an integer, this indicates that the image is a fractal (its geometry does not correspond exactly to an integer dimension, i.e., a 1D line, 2D plane, or 3D volume). The input image for 2D box counting was a 2D binary (black or white) skeleton of the branching pattern, in frontal view (SI Appendix, Fig. S13). Input for 3D box counting was a 3D binary skeleton of the branching pattern (SI Appendix, Fig. S13). Two-dimensional box counting was conducted using ImageJ (39). Three-dimensional box counting was conducted in MATLAB with a script incorporating the Wavefront object toolbox (40), Inhull function (41), and boxcount toolbox (42). Because 3D box counting is highly computationally intensive, two large species, Fractofusus misrai and Pectinifrons abysallis, were analyzed using 2D box counting only.

Functionally relevant frond properties were calculated from the output mesh, including the surface area to tissue volume ratio [with modeled tissue depths of 0.1, 0.5, and 1 mm (comparable to ref. 5)] and the size (height, width, and depth) of a bounding box around the modeled organism. Bounding box axes for each species were oriented relative to inferred life position (based on fossil morphology and preservation). Dimensions for each species were scaled based on approximate specimen lengths recorded in the literature (SI Appendix, Table S2). A Euclidean cluster analysis of these scaled dimensions was conducted using paired group linkage in palaeontological statistics (43).