Abstract
• Background and Aims It has recently found that lowland rice grown hydroponically is exceptionally efficient in absorbing 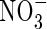 , raising the possibility that rice and other wetland plants growing in flooded soil may absorb significant amounts of
, raising the possibility that rice and other wetland plants growing in flooded soil may absorb significant amounts of 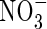 formed by nitrification of
formed by nitrification of 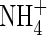 in the rhizosphere. This is important because (a) this
in the rhizosphere. This is important because (a) this 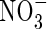 is otherwise lost through denitrification in the soil bulk; and (b) plant growth and yield are generally improved when plants absorb their nitrogen as a mixture of
is otherwise lost through denitrification in the soil bulk; and (b) plant growth and yield are generally improved when plants absorb their nitrogen as a mixture of 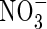 and
and 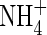 compared with growth on either N source on its own. A mathematical model is developed here with which to assess the extent of
compared with growth on either N source on its own. A mathematical model is developed here with which to assess the extent of 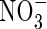 absorption from the rhizosphere by wetland plants growing in flooded soil, considering the important plant and soil processes operating.
absorption from the rhizosphere by wetland plants growing in flooded soil, considering the important plant and soil processes operating.
• Methods The model considers rates of O2 transport away from an individual root and simultaneous O2 consumption in microbial and non-microbial processes; transport of  towards the root and its consumption in nitrification and uptake at the root surface; and transport of
towards the root and its consumption in nitrification and uptake at the root surface; and transport of 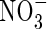 formed from
formed from 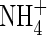 towards the root and its consumption in denitrification and uptake by the root. The sensitivity of the model's predictions to its input parameters is tested over the range of conditions in which wetland plants grow.
towards the root and its consumption in denitrification and uptake by the root. The sensitivity of the model's predictions to its input parameters is tested over the range of conditions in which wetland plants grow.
• Key Results The model calculations show that substantial quantities of 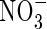 can be produced in the rhizosphere of wetland plants through nitrification and taken up by the roots under field conditions. The rates of
can be produced in the rhizosphere of wetland plants through nitrification and taken up by the roots under field conditions. The rates of 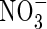 uptake can be comparable with those of
uptake can be comparable with those of 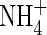 . The model also shows that rates of denitrification and subsequent loss of N from the soil remain small even where
. The model also shows that rates of denitrification and subsequent loss of N from the soil remain small even where 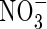 production and uptake are considerable.
production and uptake are considerable.
• Conclusions Nitrate uptake by wetland plants may be far more important than thought hitherto. This has implications for managing wetland soils and water, as discussed in this paper.
Keywords: Ammonium, flooded soil, modelling, nitrate, nitrification–denitrification, rice, rhizosphere, root aeration, soil aeration, wetland plants
INTRODUCTION
In flooded soils, 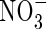 added to the soil or formed by nitrification of
added to the soil or formed by nitrification of 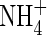 in aerobic zones near roots or at the soil surface tends to be rapidly lost through denitrification in the anoxic soil bulk, and it is therefore generally assumed that wetland plants take up little
in aerobic zones near roots or at the soil surface tends to be rapidly lost through denitrification in the anoxic soil bulk, and it is therefore generally assumed that wetland plants take up little 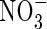 compared with
compared with 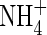 . However, in experiments using the radiotracer 13N and hydroponically grown seedlings of rice, it was found that a widely grown variety of lowland rice was exceptionally efficient in absorbing and assimilating
. However, in experiments using the radiotracer 13N and hydroponically grown seedlings of rice, it was found that a widely grown variety of lowland rice was exceptionally efficient in absorbing and assimilating 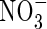 compared with
compared with  , and compared with other plant species (Kronzucker et al., 1999, 2000). This suggests a particular adaptation of rice to
, and compared with other plant species (Kronzucker et al., 1999, 2000). This suggests a particular adaptation of rice to 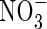 and raises the possibility that
and raises the possibility that 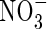 absorption by rice and perhaps other wetland plants is more important than generally thought. Since growth and yield of most plant species are superior under mixed
absorption by rice and perhaps other wetland plants is more important than generally thought. Since growth and yield of most plant species are superior under mixed 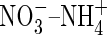 nutrition (Taiz and Zeiger, 2002), this possibility is intriguing and warrants further investigation.
nutrition (Taiz and Zeiger, 2002), this possibility is intriguing and warrants further investigation.
Three lines of evidence from Kronzucker et al. suggest unusually efficient 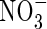 absorption. First, in the Michaelis–Menten relationships fitted to N influx data over an ecologically and agronomically relevant range of N supply, and plants of identical N status, Vmax for steady-state N influx was 40 % greater for
absorption. First, in the Michaelis–Menten relationships fitted to N influx data over an ecologically and agronomically relevant range of N supply, and plants of identical N status, Vmax for steady-state N influx was 40 % greater for 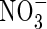 than for
than for 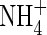 , and KM was 50 % smaller. Secondly,
, and KM was 50 % smaller. Secondly, 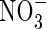 absorption was inducible and, in plants deprived of
absorption was inducible and, in plants deprived of 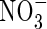 for 24 h, the induction of
for 24 h, the induction of 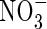 uptake was exceptionally rapid, peaking within 2 h; in comparison, in barley, which is considered a highly efficient
uptake was exceptionally rapid, peaking within 2 h; in comparison, in barley, which is considered a highly efficient 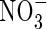 user, full induction requires up to 24 h, and in white spruce, which is considered poor at using
user, full induction requires up to 24 h, and in white spruce, which is considered poor at using 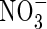 , full induction takes several days (references in Kronzucker et al., 1995, 1997, 2000). Thirdly, from the subcellular distribution of N absorbed by plants fed either
, full induction takes several days (references in Kronzucker et al., 1995, 1997, 2000). Thirdly, from the subcellular distribution of N absorbed by plants fed either 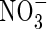 or
or 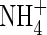 , estimated from the kinetics of 13N efflux from labelled roots, the proportion of
, estimated from the kinetics of 13N efflux from labelled roots, the proportion of  translocated to the shoot was 50 % larger, and that lost through efflux back out of the roots 50 % smaller. When
translocated to the shoot was 50 % larger, and that lost through efflux back out of the roots 50 % smaller. When 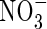 and
and 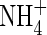 were provided together at the same total N concentration as in the single N species experiments, absorption and assimilation of
were provided together at the same total N concentration as in the single N species experiments, absorption and assimilation of 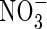 were repressed, but those of
were repressed, but those of 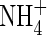 were stimulated to the extent that net N influx was doubled compared with plants fed solely on
were stimulated to the extent that net N influx was doubled compared with plants fed solely on 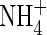 . Because very little free
. Because very little free 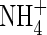 is translocated to the shoot in rice (Kronzucker et al., 1998), this indicates that
is translocated to the shoot in rice (Kronzucker et al., 1998), this indicates that 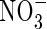 enhances
enhances 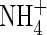 assimilation in some way, possibly through the
assimilation in some way, possibly through the 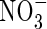 -specific induction of additional pathways for
-specific induction of additional pathways for 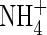 assimilation (Kronzucker et al., 1999; Britto and Kronzucker, 2004).
assimilation (Kronzucker et al., 1999; Britto and Kronzucker, 2004).
The extent of 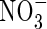 uptake by roots in flooded soil will depend on its rate of formation from
uptake by roots in flooded soil will depend on its rate of formation from 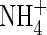 near root surfaces, its rate of transport to and absorption by the root, and its rate of transport away from the root and loss through denitrification. The rates of
near root surfaces, its rate of transport to and absorption by the root, and its rate of transport away from the root and loss through denitrification. The rates of 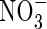 formation and subsequent denitrification will depend on reducing conditions in the soil and sinks for O2 other than nitrification. The sinks include microbial and non-microbial processes.
formation and subsequent denitrification will depend on reducing conditions in the soil and sinks for O2 other than nitrification. The sinks include microbial and non-microbial processes.
In this paper, a mathematical model of these processes is developed with which to calculate rates of formation, uptake and loss of 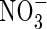 over the range of conditions in which wetland plants grow.
over the range of conditions in which wetland plants grow.
THEORY
Consider the movements of O2, 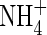 and
and 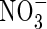 in anoxic flooded soil near a cylindrical root that simultaneously releases O2 and absorbs
in anoxic flooded soil near a cylindrical root that simultaneously releases O2 and absorbs 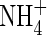 and
and 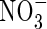 . The microbial sinks for O2 include both autotrophic processes, such as oxidation of
. The microbial sinks for O2 include both autotrophic processes, such as oxidation of 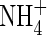 , S2− and CH4, and heterotrophic processes (Conrad and Frenzel, 2002; Kirk, 2004). The non-microbial sinks include oxidation of inorganic reductants in the soil, such as Fe(II), which may be both mobile and immobile (Howeler and Bouldin, 1971; Reddy et al., 1980; Kirk and Solivas, 1994).
, S2− and CH4, and heterotrophic processes (Conrad and Frenzel, 2002; Kirk, 2004). The non-microbial sinks include oxidation of inorganic reductants in the soil, such as Fe(II), which may be both mobile and immobile (Howeler and Bouldin, 1971; Reddy et al., 1980; Kirk and Solivas, 1994).
In initially anoxic soil, populations of aerobic microbes will be small, and therefore non-microbial processes consuming O2 will initially tend to dominate. As inorganic reductants close to the roots become exhausted, the rate of non-microbial O2 consumption will decline. Concomitantly, the rate of microbial O2 consumption will increase as aerobic populations develop. Hence the system will be complex and dynamic. We have some understanding of the kinetics of the non-microbial processes (Ahmad and Nye, 1990; Kirk et al., 1990; Kirk and Solivas, 1994), but only a weak understanding of the microbial processes and the complex interactions they involve (Bodelier et al., 2000, 2004; Brune et al., 2000; van Bodegum et al., 2001). Therefore, a very elaborate treatment of the O2-consuming processes, dissecting out the various contributors, is unjustified at this stage of our understanding, and, in our model, we therefore combine microbial and non-microbial processes. Likewise, our understanding of growth rates and activities of 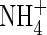 -oxidizing microbes in the rhizosphere of wetland plants and interactions with nutrients, toxins and competing substrates is insufficient for a very elaborate treatment, and hence we apply the simplest realistic treatment, with the maximum rate of nitrification as a proportion of the maximum rate of overall O2 consumption.
-oxidizing microbes in the rhizosphere of wetland plants and interactions with nutrients, toxins and competing substrates is insufficient for a very elaborate treatment, and hence we apply the simplest realistic treatment, with the maximum rate of nitrification as a proportion of the maximum rate of overall O2 consumption.
The following sections give the equations we use to describe the system. The symbols used are defined in Table 1.
Table 1.
List of symbols
| Symbol |
Meaning |
Dimensions* |
|---|---|---|
| a | Root radius | Length |
| b | Radius of zone of root influence | Length |
| bNH4 | Buffer power for 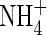 , , 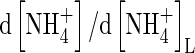
|
VolumeL volume−1 |
| DL | Solute diffusion coefficient in water, subscripted A, N or O for 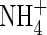 , , 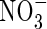 and O2 and O2
|
Area time−1 |
| FmNH4 | Maximum influx of 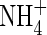 into roots into roots |
Mass area−1 time−1 |
| FmNO3 | Maximum influx of 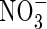 into roots into roots |
Mass area−1 time−1 |
| f | Soil diffusion impedance factor | |
| IDenit | Inhibition function for denitrification | |
| KMDenit | Michaelis constant for denitrification | 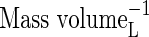 |
| KMNH4 | Michaelis constant for 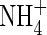 uptake uptake |
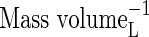 |
| KMNit1 | Michaelis constant for nitrification (re O2) | 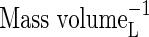 |
| KMNit2 | Michaelis constant for nitrification (re 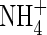 ) ) |
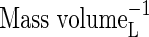 |
| KMNO3 | Michaelis constant for 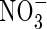 uptake uptake |
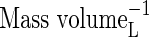 |
| KMO | Michaelis constant for O2 consumption | 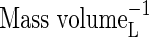 |
| LV | Root length density | Length volume−1 |
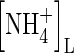 |
Concentration of 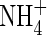 in soil solution in soil solution |
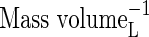 |
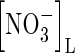 |
Concentration of 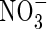 in soil solution in soil solution |
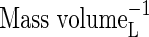 |
| [O2]L | Moncentration of O2 in soil solution | 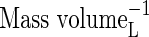 |
| VmDenit | Maximum rate of denitrification | Mass volume−1 time−1 |
| VmNit | Maximum rate of nitrification | Mass volume−1 time−1 |
| VmO | Maximum rate of O2 consumption | Mass volume−1 time−1 |
| v | Water flux into root | Length time−1 |
| λ | Root wall permeability factor | Length time−1 |
| θ | Soil water fraction by volume | VolumeL volume−1 |
Subscript L indicates soil solution; no subscript indicates whole soil.
Oxygen
The transport of O2 away from the root and its simultaneous consumption in soil processes is described by the equation
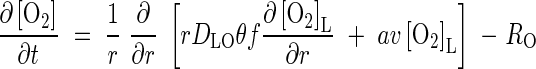 |
where RO is the rate of consumption in soil processes. The whole-soil concentration of O2 is related to the concentration in solution by [O2] = θ[O2]L. Following the reasoning above, we lump together microbial and non-microbial sinks for O2 and describe net O2 consumption using Michaelis–Menten kinetics:
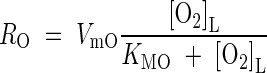 |
The boundary conditions for eqn (1) are as follows. The flux of O2 across the root surface, r = a, depends on the rate of delivery of O2 through the root, the external sink for O2 in the soil and the permeability of the root wall separating the soil solution from the root gas spaces. Following Armstrong and Beckett (1987), we define a root wall permeability factor, λ, relating the flux across the root wall to the difference in O2 concentration across it. The flux across the root wall is equal to the flux into the soil at r = a. Hence
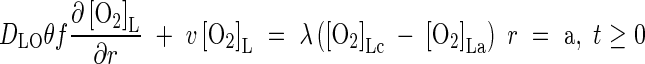 |
where subscripts c and a indicate the root cortical tissue and the soil at the root surface, respectively. Armstrong and Beckett give values of λ derived from experiments with polarographic electrodes (see Parameter Values, below). At the other boundary where the zones of influence of adjacent roots overlap, there is no transfer of O2. Thus
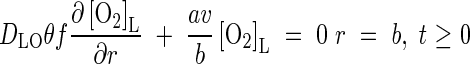 |
Ammonium
The transport of 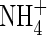 towards the root and its simultaneous consumption in nitrification is described by the equation
towards the root and its simultaneous consumption in nitrification is described by the equation
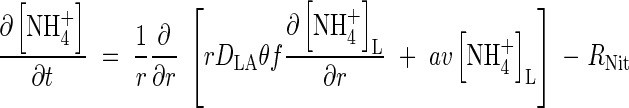 |
The whole-soil concentration of 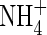 is related to the concentration in solution by the soil
is related to the concentration in solution by the soil 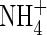 buffer power:
buffer power: 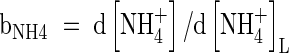 . The rate of nitrification will depend on the concentrations of O2 and
. The rate of nitrification will depend on the concentrations of O2 and  , and we describe this using dual-substrate Michaelis–Menten kinetics (see McConnaughey and Bouldin, 1985, for
, and we describe this using dual-substrate Michaelis–Menten kinetics (see McConnaughey and Bouldin, 1985, for  reduction, or Arah and Stephen, 1998, for CH4 oxidation):
reduction, or Arah and Stephen, 1998, for CH4 oxidation):
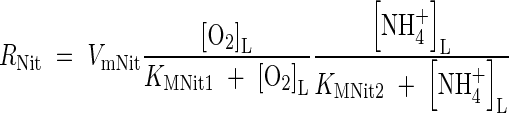 |
where VmNit is the rate in the absence of substrate limitation and KMNit1 and KMNit2 are Michaelis constants. The boundary conditions for eqn (5) are as follows. The flux of 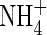 into the root will depend on the concentration of
into the root will depend on the concentration of 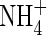 in solution at the root surface and the root
in solution at the root surface and the root 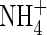 absorption properties. In accordance with conventional practice (Kronzucker et al., 1997, 2000), we describe this with a Michaelis–Menten equation:
absorption properties. In accordance with conventional practice (Kronzucker et al., 1997, 2000), we describe this with a Michaelis–Menten equation:
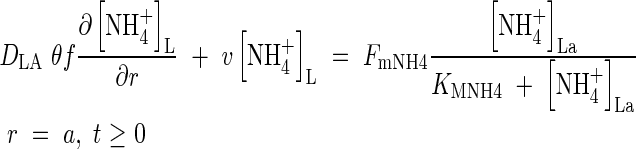 |
The quantities FmNH4 and KMNH4 are not constant during plant growth but vary with the plant's N status and other factors. However, we treat them as constants and test the model's sensitivity to them. At the other boundary, we assume there is no transfer of 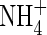 . Thus
. Thus
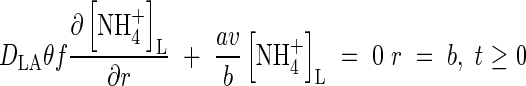 |
Nitrate
The transport of 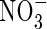 towards the root and its simultaneous production in nitrification and consumption in denitrification is described by the equation
towards the root and its simultaneous production in nitrification and consumption in denitrification is described by the equation
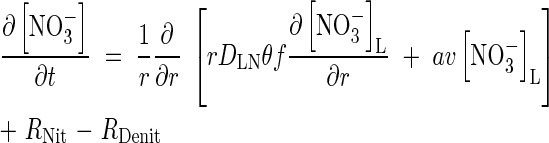 |
Because 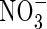 is not adsorbed on the soil solid, its concentration in the whole soil is simply related to the concentration in solution by
is not adsorbed on the soil solid, its concentration in the whole soil is simply related to the concentration in solution by 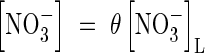 . The rate of denitrification will depend on
. The rate of denitrification will depend on 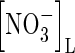 and also on the concentration of O2, which is the preferred electron acceptor. Following McConnaughey and Bouldin (1985), we describe this with a modified Michaelis–Menten equation:
and also on the concentration of O2, which is the preferred electron acceptor. Following McConnaughey and Bouldin (1985), we describe this with a modified Michaelis–Menten equation:
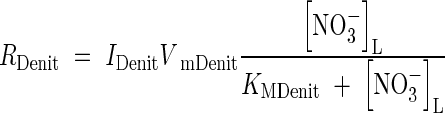 |
where IDenit is a function for inhibition by O2. We take inhibition to be linear up to a threshold concentration equal to the Michaelis constant for O2 consumption (Arah and Vinten, 1995):
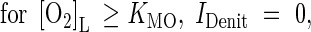 |
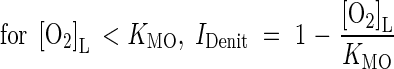 |
As for 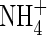 , we use a Michaelis–Menten equation for the relationship between the flux of
, we use a Michaelis–Menten equation for the relationship between the flux of 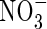 into the root and the concentration in solution at the root surface:
into the root and the concentration in solution at the root surface:
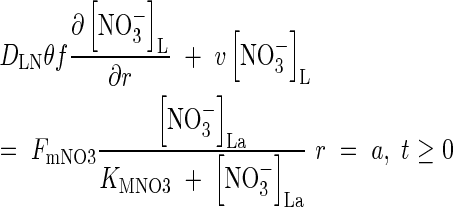 |
At the other boundary, we assume there is no transfer of 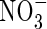 . Thus
. Thus
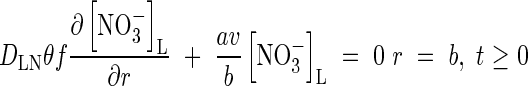 |
Numerical solutions
We expressed eqns (1)–(14) in finite-difference form using Crank–Nicholson approximations and solved the resulting sets of equations by standard numerical methods (Smith, 1985). With time steps of 0·1 h and distance steps of 0·1 mm, mass balances for all solute were conserved to within 1 % for simulations up to 10 d. Copies of the computer program for the numerical solutions, written in Fortran, are available from the first author.
PARAMETER VALUES
The standard set of parameter values used in the calculations are given in Table 2. Our reasons for choosing these values are as follows.
Table 2.
Standard parameter values
| Parameter |
Value |
Reference |
|---|---|---|
| a | 0·1 mm | Matsuo and Hoshikawa (1993) |
| b | 2 mm | Matsuo and Hoshikawa (1993) |
| bNH4 | 50 cm3 cm−3 | Kirk (2004) |
| DLA,N,O | 2 × 10−5 cm2 s−1 | Kirk (2004) |
| FmNH4 | 5 pmol cm−2 s−1 | Kronzucker et al. (1999) |
| FmNO3 | 25 pmol cm−2 s−1 | Kronzucker et al. (1999) |
| f | 0·4 | Kirk et al. (2003) |
| KMDenit | 1 µm | See text |
| KMNH4 | 50 µm | Kronzucker et al. (1999) |
| KMNit1 | 1 µm | See text |
| KMNit2 | 200 µm | See text |
| KMNO3 | 10 µm | Kronzucker et al. (1999) |
| KMO | 1 µm | See text |
 |
5 µmol cm−3 | Kirk (2004) |
| [O2]Lc | 0·18 µm | See text |
| VmDenit | 2 pmol cm−3 s−1 | See text |
| VmNit/VmO | 0·25 | See text |
| VmO | 500 pmol cm−3 s−1 | See text |
| v | 0 cm s−1 | See text |
| λ | 1 × 10−4 cm s−1 | Armstrong and Beckett (1987) |
| θ | 0·6 cm3 cm−3 | Kirk (2004) |
Rate of O2 release
The O2 budget of an individual root depends both on the rate of O2 movement and consumption within the root—which varies with position along the root and between main roots and laterals—and on the rate of O2 consumption in the surrounding soil. Measurements of rates of release, therefore, need to allow for differences across the root and its laterals and must be made under O2 sink conditions that are realistic for roots in soil. In practice, it is difficult to satisfy these conditions, and consequently reported rates of release for whole root systems vary by more than two orders of magnitude (Bedford et al., 1991; Begg et al., 1994; Sorrel and Armstrong, 1994).
However, mathematical models of root aeration show that rates of release at the upper end of the measured range can be sustained by rice roots with typical characteristics (Armstrong and Beckett, 1987; Kirk, 2003). Kirk (2003) developed a model of the steady-state diffusion of O2 through a primary rice root and its laterals and the simultaneous consumption of O2 in root respiration and loss to the soil. A sensitivity analysis showed that the basic architecture of rice root systems, i.e. a system of coarse, aerenchymatous, primary roots with gas-impermeable walls conducting O2 to short, fine, gas-permeable laterals, provides the greatest absorbing surface per unit aerated root mass. With this architecture and typical rates of root respiration, rates of O2 loss to the soil from the laterals and primary root tip can be at the upper end measured experimentally, equivalent to a flux of up to 25 pmol cm−2 (root surface) s−1.
Based on this and trial runs with the present model, we use as standard a root wall permeability factor, λ = 10−4 cm s−1 and we specify the O2 concentration in the root cortex {[O2]Lc in eqn (3)} as equal to half that in air [8·75 mol cm−3 (gas space) at s.t.p.].
Rate of O2 consumption
For ten soils with a wide range of organic matter and reducible Fe contents, Howeler and Bouldin (1971, Table 4) found steady-state rates of O2 consumption by reduced soil cores exposed to O2 equivalent to 100–1000 pmol cm−3 s−1 (mean value 500 pmol cm−3 s−1). Roughly 50 % of this was microbial. We therefore take VmO = 500 pmol cm−3 s−1 as our standard value. Heterotrophic aerobes will operate efficiently at sub micromolar O2 concentrations (Conrad and Frenzel, 2002) and we take as standard KMO = 1 µm.
Rate of nitrification
The maximum rate of nitrification is taken as a proportion of the maximum overall rate of microbial O2 consumption. From the stoichiometry of nitrification, 2 mol of O2 are consumed per mol of 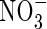 formed:
formed:
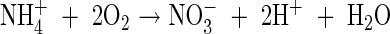 |
Therefore, an upper limit on the rate of nitrification is half the net rate of microbial O2 consumption, i.e. VmNit/VmO = 0·5. We take as standard VmNit/VmO = 0·25. Also we take as standard KMNit1 = KMO = 1 µm and KMNit2 = 200 µm based on typical concentrations of 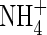 in solution in rice soils.
in solution in rice soils.
Rate of denitrification
Experiments in which 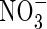 fertilizer is added to flooded soils under field conditions indicate maximum rates of N2 + N2O loss through denitrification of a few kg of N ha−1 d−1 (e.g. Lindau et al., 1990; Samson et al., 1990). Assuming denitrification to be distributed over a soil depth of 10 cm, this is equivalent to a rate of denitrification per unit soil volume of a few pmol cm−3 s−1. We therefore take as standard VmDenit = 2 pmol cm−3 s−1. Measured concentrations of
fertilizer is added to flooded soils under field conditions indicate maximum rates of N2 + N2O loss through denitrification of a few kg of N ha−1 d−1 (e.g. Lindau et al., 1990; Samson et al., 1990). Assuming denitrification to be distributed over a soil depth of 10 cm, this is equivalent to a rate of denitrification per unit soil volume of a few pmol cm−3 s−1. We therefore take as standard VmDenit = 2 pmol cm−3 s−1. Measured concentrations of 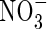 in flooded soils rarely exceed a few micromolar, unless the soil is fertilized with
in flooded soils rarely exceed a few micromolar, unless the soil is fertilized with 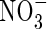 (Arth and Frenzel, 2000; Liesack et al., 2000), and therefore denitrifier populations must operate at concentrations less than this. We assign as standard KMDenit = 1 µm.
(Arth and Frenzel, 2000; Liesack et al., 2000), and therefore denitrifier populations must operate at concentrations less than this. We assign as standard KMDenit = 1 µm.
The ratio of nitrous oxide to nitrogen gas formed in denitrification will depend on the relative abundance of 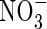 and organic substrates and on other factors influencing the rates of the sequential steps in denitrification (Kirk, 2004). Small concentrations of
and organic substrates and on other factors influencing the rates of the sequential steps in denitrification (Kirk, 2004). Small concentrations of 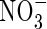 relative to organic substrates, as expected near the roots of wetland plants, will favour complete reduction to N2. Also, the slow escape of any N2O formed in flooded soil will favour its further reduction to N2. Hence, reported denitrification losses from rice fields as N2O are at least two orders of magnitude smaller than losses as N2 (Galbally and Chalk, 1987; Mosier et al., 1989; Buresh et al., 1991; Bronson et al., 1997).
relative to organic substrates, as expected near the roots of wetland plants, will favour complete reduction to N2. Also, the slow escape of any N2O formed in flooded soil will favour its further reduction to N2. Hence, reported denitrification losses from rice fields as N2O are at least two orders of magnitude smaller than losses as N2 (Galbally and Chalk, 1987; Mosier et al., 1989; Buresh et al., 1991; Bronson et al., 1997).
Root 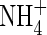 and
and 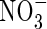 uptake properties
uptake properties
Up to a certain point, plants can regulate the inflow of N across their roots according to their need for N, and the inflow for a given external N concentration therefore depends on the plant's past supply of N. Hence, Wang et al. (1993) found for rice grown for 4 weeks in 2, 100 and 1000 µm
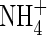 solutions, the respective values of Vmax (µmol g−1 h−1) and KM (µM) were: 12·8 and 32·2; 8·2 and 90·2; and 3·4 and 122·1, i.e. Vmax was 6-fold smaller and KM 4-fold larger for 2 µM compared with 1000 µm
solutions, the respective values of Vmax (µmol g−1 h−1) and KM (µM) were: 12·8 and 32·2; 8·2 and 90·2; and 3·4 and 122·1, i.e. Vmax was 6-fold smaller and KM 4-fold larger for 2 µM compared with 1000 µm
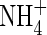 . For rice grown in 100 µm N solutions, Kronzucker et al. (1999) found that Vmax values were 8·1 and 5·7 µmol g−1 h−1 for
. For rice grown in 100 µm N solutions, Kronzucker et al. (1999) found that Vmax values were 8·1 and 5·7 µmol g−1 h−1 for 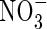 - and
- and 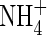 -fed plants, respectively, and KM values were 26 and 51 µm. Given that external
-fed plants, respectively, and KM values were 26 and 51 µm. Given that external 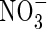 concentrations at the root surface will be far smaller than
concentrations at the root surface will be far smaller than 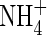 concentrations,
concentrations, 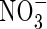 uptake will be ‘upregulated’ to a greater extent than
uptake will be ‘upregulated’ to a greater extent than 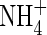 uptake, and we take as standard Fmax = 5 pmol cm−2 s−1 (calculated from Vmax in µmol g−1 h−1 using root density = 1 g cm−3 and a = 0·1 mm) and KM = 50 µm for
uptake, and we take as standard Fmax = 5 pmol cm−2 s−1 (calculated from Vmax in µmol g−1 h−1 using root density = 1 g cm−3 and a = 0·1 mm) and KM = 50 µm for 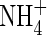 uptake, and Fmax = 25 pmol cm−2 s−1 and KM = 10 µm for
uptake, and Fmax = 25 pmol cm−2 s−1 and KM = 10 µm for 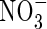 uptake.
uptake.
Root geometry
The root system of rice plants in flooded soils comprises coarse primary roots, 0·3–1 mm in diameter, supporting a dense system of fine laterals, 50–150 µm in diameter (Matsuo and Hoshikawa, 1993). Total root length densities averaged over the 15–20 cm deep puddled soil layer may be as high as 20–30 cm cm−3. Calculations with the above parameters for root 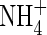 absorption properties and measured concentrations of
absorption properties and measured concentrations of 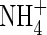 in soil solutions indicate that almost the whole of this root length is required to account for measured rates of N uptake by rice in flooded soils (Kirk and Solivas, 1997).
in soil solutions indicate that almost the whole of this root length is required to account for measured rates of N uptake by rice in flooded soils (Kirk and Solivas, 1997).
The corresponding mean inter-root distance is calculated as follows. With a regular parallel array of roots, if each root is assigned a cylinder of influence such that the whole soil volume is divided equally between roots, the radius, b, of the cylinder is given by
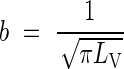 |
where LV is the root length density. The value b = 3 mm, which is realistic for half the distance between neighbouring primary roots, corresponds to LV = 3·5 cm cm−3; b = 1 mm, which is realistic for half the distance between laterals, corresponds to LV = 31·8 cm cm−3.
MODEL PREDICTIONS
Predicted concentration profiles, fluxes and rates of nitrification–denitrification
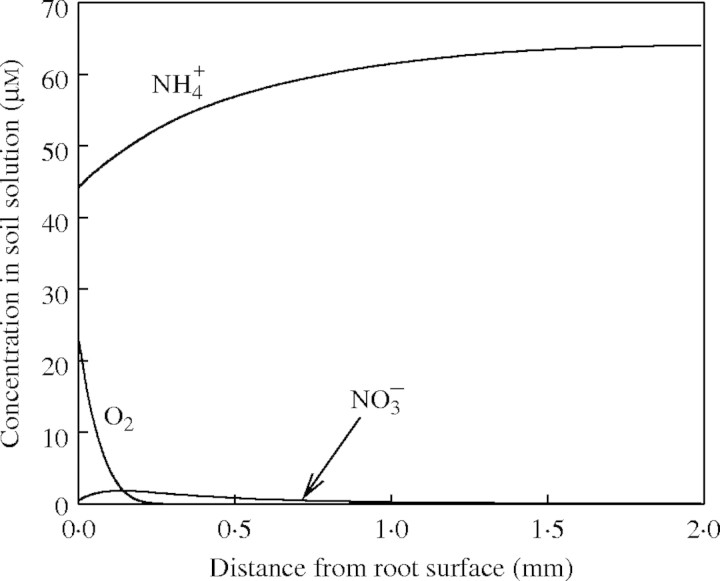
Figure 1 shows the concentration profiles of O2, 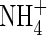 and
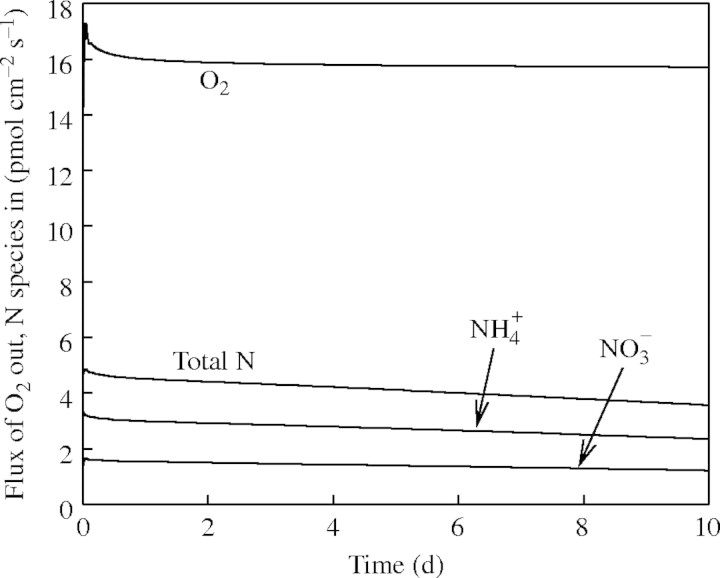
and 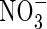 in the soil calculated with the standard set of parameter values over 10 d of root–soil contact, and Fig. 2 gives the fluxes of O2 and N species across the root over time. Figure 1 shows that only very small concentrations of
in the soil calculated with the standard set of parameter values over 10 d of root–soil contact, and Fig. 2 gives the fluxes of O2 and N species across the root over time. Figure 1 shows that only very small concentrations of 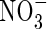 in the soil solution develop: approx. 1–2 µm within <0·5 mm of the root and 0 µm at >1 mm from the root, i.e. given the radial geometry, all but undetectable averaged over the inter-root distance. Nonetheless, the fluxes of
in the soil solution develop: approx. 1–2 µm within <0·5 mm of the root and 0 µm at >1 mm from the root, i.e. given the radial geometry, all but undetectable averaged over the inter-root distance. Nonetheless, the fluxes of 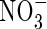 into the root shown in Fig. 2 are substantial. The accumulated uptake of nitrogen over 10 d is 1·61 µmol cm−3 of soil, or 33 % of the initial
into the root shown in Fig. 2 are substantial. The accumulated uptake of nitrogen over 10 d is 1·61 µmol cm−3 of soil, or 33 % of the initial 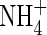 content of the soil (= 5 µmol cm−3, equivalent to 105 kg of N ha−1 over a 15 cm depth), and the concentration of
content of the soil (= 5 µmol cm−3, equivalent to 105 kg of N ha−1 over a 15 cm depth), and the concentration of 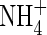 in solution in the soil bulk concomitantly falls from 100 to 64 µm. Nitrate uptake accounted for 34 % of total N uptake, and nitrification accounted for 14 % of the total O2 consumption in 10 d. The ratio of N denitrified to total N uptake was 0·20 or 6·6 % of the
in solution in the soil bulk concomitantly falls from 100 to 64 µm. Nitrate uptake accounted for 34 % of total N uptake, and nitrification accounted for 14 % of the total O2 consumption in 10 d. The ratio of N denitrified to total N uptake was 0·20 or 6·6 % of the 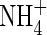 initially in the soil.
initially in the soil.
Fig. 1.
Calculated concentration–distance profiles of O2, 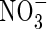 and
and 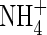 in the soil near a root after 10 d of root–soil contact. Parameter values as in Table 2.
in the soil near a root after 10 d of root–soil contact. Parameter values as in Table 2.
Fig. 2.
Fluxes of O2, 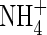 ,
, 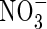 and total N across the root over time. Parameter values as in Table 2.
and total N across the root over time. Parameter values as in Table 2.
To gauge how realistic these results are, we compare the calculated rates of denitrification with published values. Measurements of denitrification in flooded rice fields made by following the emission of 15N2 and 15N2O following addition of N-fertilizer strongly labelled with 15N indicate losses in the range 1–5 % of applied ammoniacal-N over the range of soils and management conditions considered (Buresh and Austin, 1988; Mosier et al., 1989; Reddy et al., 1989; Buresh et al., 1991). Arth et al. (1998) directly measured N2 and N2O emitted by rice plants grown in chambers with an atmosphere of O2 and helium. This gave denitrification losses of the order of 6 % of added urea-N in 10 d and mean N2 + N2O emission rates of approx. 30 nmol (N) cm−2 (soil surface) h−1. The mean emission rate calculated here with the standard parameters is 14 nmol (N) cm−2 (soil surface) h−1 assuming 10 cm soil depth. We conclude that our calculated losses are realistic.
We know of no published direct measurements of rates of 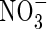 uptake by wetland plants in flooded soil under field conditions. Because the
uptake by wetland plants in flooded soil under field conditions. Because the 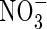 is rapidly assimilated, direct measurements of uptake are difficult.
is rapidly assimilated, direct measurements of uptake are difficult.
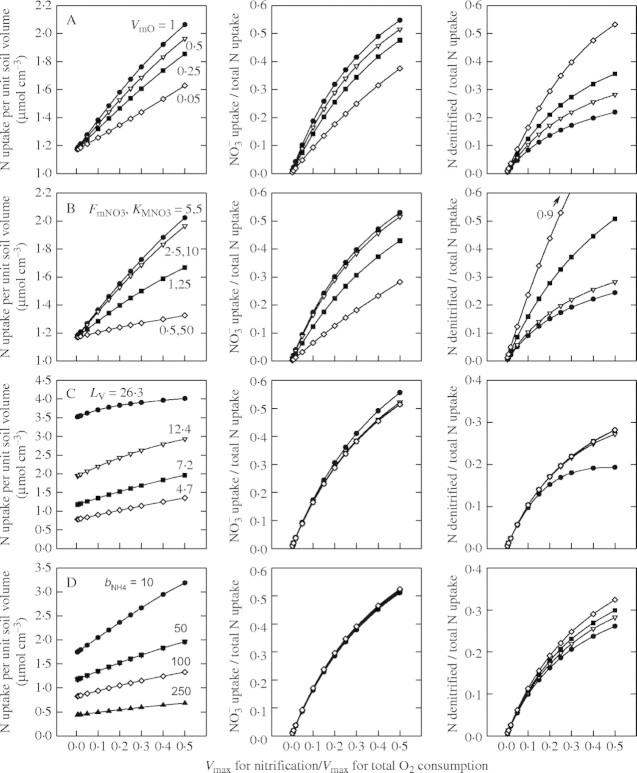
Sensitivity analysis
Figure 3 shows the sensitivity of the calculated total N and 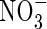 uptakes and denitrification to model parameter values over what we consider to be realistic ranges for wetland plants. As discussed above, we have some understanding of total rates of O2 consumption in flooded soils, but a much weaker understanding of the growth rates and activities of nitrifying microbes under different circumstances. We therefore show the sensitivity to different parameters in interaction with a varying nitrification potential as represented by Vmax for nitrification as a proportion of Vmax for total O2 consumption (VmNit/VmO).
uptakes and denitrification to model parameter values over what we consider to be realistic ranges for wetland plants. As discussed above, we have some understanding of total rates of O2 consumption in flooded soils, but a much weaker understanding of the growth rates and activities of nitrifying microbes under different circumstances. We therefore show the sensitivity to different parameters in interaction with a varying nitrification potential as represented by Vmax for nitrification as a proportion of Vmax for total O2 consumption (VmNit/VmO).
Fig. 3.
Sensitivity of total N uptake, uptake of 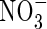 as a proportion of total N uptake and denitrification as a proportion of total N uptake to model parameter values. (A) The top three graphs indicate sensitivity to Vmax for total O2 consumption [VmO in eqn (2); numbers on curves are values in nmol cm−3 s−1]; (B) the upper middle three graphs indicate sensitivity to parameters for root
as a proportion of total N uptake and denitrification as a proportion of total N uptake to model parameter values. (A) The top three graphs indicate sensitivity to Vmax for total O2 consumption [VmO in eqn (2); numbers on curves are values in nmol cm−3 s−1]; (B) the upper middle three graphs indicate sensitivity to parameters for root 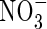 uptake [Fm, KM in eqn (13); numbers on curves are values in nmol cm−3 s−1, μm]; (C) the lower middle three graphs indicate sensitivity to root length density [LV in eqn (15); numbers on curves are values in cm cm−3]; and (D) the bottom three graphs indicate sensitivity to the soil
uptake [Fm, KM in eqn (13); numbers on curves are values in nmol cm−3 s−1, μm]; (C) the lower middle three graphs indicate sensitivity to root length density [LV in eqn (15); numbers on curves are values in cm cm−3]; and (D) the bottom three graphs indicate sensitivity to the soil 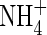 buffer power (bNH4; numbers on curves are values in cm3 cm−3). Ten d of root–soil contact. Other parameter values as in Table 2.
buffer power (bNH4; numbers on curves are values in cm3 cm−3). Ten d of root–soil contact. Other parameter values as in Table 2.
Effect of nitrification and denitrification rates
Figure 3A shows the sensitivity to the maximum total rate of O2 consumption (VmO). At a given VmNit/VmO, with increases in VmO the proportion of N uptake as 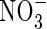 increases and total N uptake increases correspondingly. Also, the ratio of N denitrified to total N uptake decreases. This is because with a greater O2 sink, the spread of the oxygenated zone around the root is smaller and nitrification occurs closer to the root. Therefore, the concentration gradient of
increases and total N uptake increases correspondingly. Also, the ratio of N denitrified to total N uptake decreases. This is because with a greater O2 sink, the spread of the oxygenated zone around the root is smaller and nitrification occurs closer to the root. Therefore, the concentration gradient of 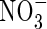 towards the root is steeper and a greater proportion of the
towards the root is steeper and a greater proportion of the 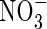 is taken up. The effect of VmO varies with VmNit/VmO: when VmNit/VmO is large, denitrification losses decrease more rapidly with increases in VmO.
is taken up. The effect of VmO varies with VmNit/VmO: when VmNit/VmO is large, denitrification losses decrease more rapidly with increases in VmO.
Effect of root 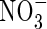 uptake properties
uptake properties
As FmNO3 increases and KMNO3 decreases, an increasing proportion of N is taken up as 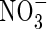 and a decreasing proportion of the
and a decreasing proportion of the 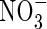 formed is denitrified (Fig. 3B). Over the range of FmNO3 and KMNO3 values shown in Fig. 3B, and other parameter values as standard,
formed is denitrified (Fig. 3B). Over the range of FmNO3 and KMNO3 values shown in Fig. 3B, and other parameter values as standard, 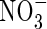 accounts for 15 to nearly 40 % of N uptake. Denitrification losses increase sharply as root
accounts for 15 to nearly 40 % of N uptake. Denitrification losses increase sharply as root 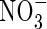 uptake decreases.
uptake decreases.
Effect of root geometry
Figure 3C shows interactions between root geometry and rates of 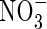 uptake and denitrification. As root length density (LV) increases, the rates of total N uptake and depletion of soil N increase. Simultaneously, with increasing LV, the inter-root distance decreases and therefore the proportion of the inter-root zone that is oxygenated increases, and so nitrification and
uptake and denitrification. As root length density (LV) increases, the rates of total N uptake and depletion of soil N increase. Simultaneously, with increasing LV, the inter-root distance decreases and therefore the proportion of the inter-root zone that is oxygenated increases, and so nitrification and 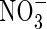 uptake increase. Superimposed on this is the effect of root radius. With large inter-root distances, increasing the root radius tends to increase the capture of
uptake increase. Superimposed on this is the effect of root radius. With large inter-root distances, increasing the root radius tends to increase the capture of 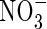 and decrease denitrification (data not shown). However, with small inter-root distances, denitrification rates are small and the capture of
and decrease denitrification (data not shown). However, with small inter-root distances, denitrification rates are small and the capture of 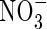 increases as the root radius decreases.
increases as the root radius decreases.
Effect of soil 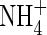 buffer power
buffer power
Figure 3D shows that uptake increases sharply as bNH4 decreases, but the proportion of uptake as 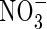 is little influenced. As bNH4 decreases, for a given total concentration of
is little influenced. As bNH4 decreases, for a given total concentration of 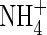 in the soil, the concentration of
in the soil, the concentration of 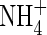 in solution increases, and hence the uptake of
in solution increases, and hence the uptake of 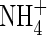 tends to increase. Simultaneously, nitrification tends to increase as
tends to increase. Simultaneously, nitrification tends to increase as 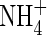 in solution increases, and hence the rate of
in solution increases, and hence the rate of 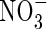 uptake increases. Thus, the sensitivity of N uptake to VmNit/VmO increases as bNH4 decreases. There is a corresponding decrease in denitrification relative to N uptake, because the gradient of
uptake increases. Thus, the sensitivity of N uptake to VmNit/VmO increases as bNH4 decreases. There is a corresponding decrease in denitrification relative to N uptake, because the gradient of 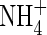 near the root is shallower at smaller bNH4, and hence a greater proportion of nitrification occurs close to the root.
near the root is shallower at smaller bNH4, and hence a greater proportion of nitrification occurs close to the root.
Effect of mass flow of the soil solution
Mass flow of solution towards the root in the transpiration stream tends to compress the zones of oxygenation and nitrification and extend the zone of 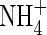 depletion. The above calculations were made with v = 0. The model shows that a rapid flux of water across the root surface (v = 10−5 cm s−1) slightly compresses the profile of
depletion. The above calculations were made with v = 0. The model shows that a rapid flux of water across the root surface (v = 10−5 cm s−1) slightly compresses the profile of 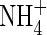 but has a negligible effect on the profiles of O2 and
but has a negligible effect on the profiles of O2 and 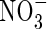 and rates of
and rates of 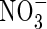 uptake and denitrification (data not shown). Approximate solutions of eqn (5) indicate that the fractional increase in
uptake and denitrification (data not shown). Approximate solutions of eqn (5) indicate that the fractional increase in 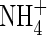 influx resulting from mass flow is about av/(0·5DLAθf) (Kirk and Solivas, 1997), or approx. 2 % for the standard parameter values and v = 10−5 cm s−1. Hence, for practical purposes, the effect of mass flow can be ignored.
influx resulting from mass flow is about av/(0·5DLAθf) (Kirk and Solivas, 1997), or approx. 2 % for the standard parameter values and v = 10−5 cm s−1. Hence, for practical purposes, the effect of mass flow can be ignored.
CONCLUDING REMARKS
Our calculations show that wetland plants growing in flooded soil can take up a large part of their nitrogen as 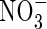 formed from
formed from 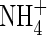 in the rhizosphere, without excessive losses of N through denitrification. The extent of this will vary greatly between soils and management regimes, being sensitive to reducing conditions in the soil and the sinks for O2 other than nitrification. Water regimes will particularly influence this. It is expected that in future rice will have to be produced with far less water across Asia as water resources are increasingly diverted to non-agricultural uses (IRRI, 2003). Therefore, water-saving irrigation methods, such as maintaining a minimal depth of standing water in the field and intermittently draining water from the field, will be increasingly widespread. This will favour increased
in the rhizosphere, without excessive losses of N through denitrification. The extent of this will vary greatly between soils and management regimes, being sensitive to reducing conditions in the soil and the sinks for O2 other than nitrification. Water regimes will particularly influence this. It is expected that in future rice will have to be produced with far less water across Asia as water resources are increasingly diverted to non-agricultural uses (IRRI, 2003). Therefore, water-saving irrigation methods, such as maintaining a minimal depth of standing water in the field and intermittently draining water from the field, will be increasingly widespread. This will favour increased 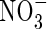 formation, and it will be important to manage conditions to maximize the capture of
formation, and it will be important to manage conditions to maximize the capture of 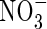 by the crop and minimize denitrification.
by the crop and minimize denitrification.
We have focused on lowland rice, but it is probable that other wetland plants are similarly efficient in capturing 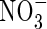 formed in the rhizosphere. This would have implications for the selection of plants for waste-water treatment in artificial wetlands.
formed in the rhizosphere. This would have implications for the selection of plants for waste-water treatment in artificial wetlands.
LITERATURE CITED
- Ahmad AR, Nye PH. 1990. Coupled diffusion and oxidation of ferrous iron in soils. I. Kinetics of oxygenation of ferrous iron in soil suspension. Journal of Soil Science 41: 395–409. [Google Scholar]
- Arah JRM, Stephen KD. 1998. A model of the processes leading to methane emission from peatland. Atmospheric Environment 32: 3257–3264. [Google Scholar]
- Arah JRM, Vinten AJA. 1995. Simplified models of anoxia and denitrification in aggregated and simple-structured soils. European Journal of Soil Science 46: 507–517. [Google Scholar]
- Armstrong W, Beckett PM. 1987. Internal aeration and the development of stelar anoxia in submerged roots New Phytologist 105: 221–245. [Google Scholar]
- Arth I, Frenzel P. 2000. Nitrification and denitrification in the rhizosphere of rice: the detection of processes by a new multi-channel electrode. Biology and Fertility of Soils 31: 427–435. [Google Scholar]
- Arth I, Frenzel P, Conrad R. 1998. Denitrification coupled to nitrification in the rhizosphere of rice. Soil Biology and Biochemistry 30: 509–515. [Google Scholar]
- Bedford BL, Bouldin DR, Beliveau BD. 1991. Net oxygen and carbon dioxide balances in solutions bathing roots of wetland plants. Journal of Ecology 79: 943–959 [Google Scholar]
- Begg CBM, Kirk GJD, MacKenzie AF, Neue H-U. 1994. Root-induced iron oxidation and pH changes in the lowland rice rhizosphere. New Phytologist 128: 469–477. [DOI] [PubMed] [Google Scholar]
- van Bodegom PM, Stams F, Mollema L, Boeke S, Leffelaar P. 2001. Methane oxidation and the competition for oxygen in the rice rhizosphere. Applied and Environmental Microbiology 67: 3586–3597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodelier PLE, Roslev P, Henckel T, Frenzel P. 2000. Stimulation by ammonium-based fertilizers of methane oxidation in soil around rice roots. Nature 403: 421–424. [DOI] [PubMed] [Google Scholar]
- Britto DT, Kronzucker HJ. 2004. Bioengineering nitrogen acquisition in rice: can novel initiatives in rice genomics and physiology contribute to global food security. BioEssays 26: 683–692. [DOI] [PubMed] [Google Scholar]
- Bronson KF, Neue H-U, Singh U, Abao EB. 1997. Automated chamber measurements of methane and nitrous oxide flux in a flooded rice soil. I. Residue, nitrogen, and water management. Soil Science Society of America Journal 61: 981–987. [Google Scholar]
- Brune A, Frenzel P, Cypionka H. 2000. Life at the oxic–anoxic interface: microbial activities and adaptations. FEMS Microbiology Reviews 24: 691–710. [DOI] [PubMed] [Google Scholar]
- Buresh RJ, Austin ER. 1988. Direct measurement of dinitrogen and nitrous oxide flux in flooded rice fields. Soil Science Society of America Journal 52: 681–688. [Google Scholar]
- Buresh RJ, De Datta SK, Samson MI, Sakorn Phongpan, Patoom Snitwonse, Fagi AM, et al. 1991. Dinitrogen and nitrous oxide flux from urea basally applied to puddled rice soils. Soil Science Society of America Journal 55: 268–273. [Google Scholar]
- Conrad R, Frenzel P. 2002. Flooded soils. In: Botten G, ed. Encyclopedia of environmental microbiology. New York: Wiley, 1316–1333. [Google Scholar]
- Galbally IE, Chalk PM. 1987. Emission of nitrogen oxides (NOx) from a flooded soil fertilized with urea: relation to other nitrogen loss processes. Journal of Atmospheric Chemistry 5: 343–365. [Google Scholar]
- Howeler RH, Bouldin DR. 1971. The diffusion and consumption of oxygen in submerged soils. Soil Science Society of America Proceedings 35: 202–208. [Google Scholar]
- IRRI. 2003.Rice almanac, 3rd edn. Manila: International Rice Research Institute. [Google Scholar]
- Kirk GJD. 2003. Rice root properties for internal aeration and efficient nutrient acquisition in submerged soil. New Phytologist 159: 185–194. [DOI] [PubMed] [Google Scholar]
- Kirk GJD. 2004.The biogeochemistry of submerged soils. Chichester, UK: Wiley. [Google Scholar]
- Kirk GJD, Solivas JL. 1994. Coupled diffusion and oxidation of ferrous iron in soils. III. Further development of the model and experimental testing. European Journal of Soil Science 45: 369–378. [Google Scholar]
- Kirk GJD, Solivas JL. 1997. On the extent to which root properties and transport through the soil limit nitrogen uptake by lowland rice. European Journal of Soil Science 48: 613–621. [Google Scholar]
- Kirk GJD, Ahmad AR, Nye PH. 1990. Coupled diffusion and oxidation of ferrous iron in soils. II. A model of the diffusion and reaction of O2, Fe2+, H+ and HCO3− in soils and a sensitivity analysis of the model. Journal of Soil Science 41: 411–431. [Google Scholar]
- Kirk GJD, Solivas JL, Alberto MA. 2003. The effects of redox conditions on solute diffusion in soil. European Journal of Soil Science 54: 617–624. [Google Scholar]
- Kronzucker HJ, Glass ADM, Siddiqi MY. 1995. Nitrate induction in spruce: an approach using compartmental analysis. Planta 196: 683–690. [Google Scholar]
- Kronzucker HJ, Siddiqi MY, Glass ADM. 1997. Conifer root discrimination against soil nitrate and the ecology of forest succession. Nature 385: 59–61. [Google Scholar]
-
Kronzucker HJ, Schjoerring JK, Erner Y, Kirk GJD, Siddiqi MY, Glass ADM.
1998. Dynamic interactions between root /article/back/ref-list/ref/citation/inline-formula
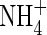 influx and long-distance N translocation in rice: insights into feedback processes. Plant and Cell Physiology
39: 1287–1293. [Google Scholar]
influx and long-distance N translocation in rice: insights into feedback processes. Plant and Cell Physiology
39: 1287–1293. [Google Scholar] - Kronzucker HJ, Siddiqi MY, Glass ADM, Kirk GJD. 1999. Nitrate–ammonium synergism in rice: a subcellular flux analysis. Plant Physiology 119: 1041–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kronzucker HJ, Glass ADM, Siddiqi MY, Kirk GJD. 2000. Comparative kinetic analysis of ammonium and nitrate acquisition by tropical lowland rice: implications for rice cultivation and yield potential. New Phytologist 145: 471–476. [DOI] [PubMed] [Google Scholar]
- Liesack W, Schnell S, Revsbech NP. 2000. Microbiology of flooded rice paddies. FEMS Microbiology Reviews 24: 625–645. [DOI] [PubMed] [Google Scholar]
- Lindau CW, Patrick WH Jr, DeLaune RD, Reddy KR. 1990. Rate of accumulation and emission of N2, N2O and CH4 from a flooded rice soil. Plant and Soil 129: 269–276. [Google Scholar]
- McConnaughey PK, Bouldin DR. 1985. Transient microsite models of denitrification: I. Model development. Soil Science Society of America Journal 49: 886–891. [Google Scholar]
- Matsuo T, Hoshikawa K. 1993.Science of the rice plant. I. Morphology. Tokyo: Food and Agriculture Policy Research Center. [Google Scholar]
- Mosier AR, Chapman SL, Freney JR. 1989. Determination of dinitrogen emission and retention in floodwater and porewater for a lowland rice field fertilized with 15N-urea. Fertilizer Research 19: 127–136. [Google Scholar]
- Reddy KR, Rao PSC, Patrick, WH Jr. 1980. Factors influencing oxygen consumption rates in flooded soils. Soil Science Society of America Journal 44: 741–745. [Google Scholar]
- Reddy KR, Patrick, WH Jr, Lindau CW. 1989. Nitrification–denitrification at the plant root–sediment interface in wetlands. Limnology and Oceanography 34: 1004–1013. [Google Scholar]
- Samson MI, Buresh RJ, De Datta SK. 1990. Evolution and soil entrapment of nitrogen gases formed by denitrification in flooded soils. Soil Science and Plant Nutrition 36: 299–307. [Google Scholar]
- Smith GD. 1985.Numerical solution of partial differential equations: finite difference methods, 3rd edn. Oxford: Oxford University Press. [Google Scholar]
- Sorrell BK, Armstrong W. 1994. On the difficulties of measuring oxygen release by root systems of wetland plants. Journal of Ecology 82: 177–183. [Google Scholar]
- Taiz L, Zeiger E. 2002.Plant physiology. Sunderland, MA: Sinauer Associates. [Google Scholar]
-
Wang YM, Siddiqi MY, Ruth TJ, Glass ADM.
1993. Ammonium uptake by rice roots. II. Kinetics of 13/article/back/ref-list/ref/citation/inline-formula
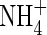 influx across the plasmalemma. Plant Physiology
103: 1259–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
influx across the plasmalemma. Plant Physiology
103: 1259–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]