Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2005 Aug 12;96(5):871–876. doi: 10.1093/aob/mci239

A Simple Model for Nitrogen-limited Plant Growth and Nitrogen Allocation

A W M VERKROOST 1, M J WASSEN 1,*
PMCID: PMC4247053  PMID: 16100225

Abstract

• Background and Aims In many studies of nitrogen-limited plant growth a linear relationship has been found between relative growth rate and plant nitrogen concentration, showing a negative intercept at a plant nitrogen concentration of zero. This relationship forms the basis of the nitrogen productivity theory. On the basis of empirical findings, several authors have suggested that there is also a distinctive relationship between allocation and plant nitrogen concentration. The primary aim of this paper is to develop a simple plant growth model that quantifies this relationship in mathematical terms. The model was focused on nitrogen allocation to avoid the complexity of differences in nitrogen concentrations in the different plant compartments. The secondary aim is to use the model for examining the processes that underlie the empirically based nitrogen productivity theory.

• Methods In the construction of the model we focused on the formation and degradation of biologically active nitrogen in enzymes involved in the photosynthetic process (photosynthetic nitrogen). It was assumed that, in nitrogen-limiting conditions, the formation of photosynthetic nitrogen is proportional to nitrogen uptake. Furthermore it was assumed that the degradation of photosynthetic nitrogen is governed by first-order kinetics. Model predictions of nitrogen allocation were compared with data from literature describing four studies of growth. Model predictions of whole plant growth were compared with the above-mentioned nitrogen productivity theory.

• Key Results Allocation predictions agreed well with the investigated empirical data. The ratio of leaf nitrogen and plant nitrogen declines linearly with the inverse of plant nitrogen concentration. Nitrogen productivity is proportional to this ratio. Predictions for whole-plant growth were in accordance with the nitrogen productivity theory.

• Conclusions The agreement between model predictions and empirical findings suggests that the derived equation for nitrogen allocation and its relationship to plant nitrogen concentration might be generally applicable. The negative intercept in the linear relationship between relative growth rate and plant nitrogen concentration is interpreted as being equal to the degradation constant of photosynthetic nitrogen.

Keywords: Plant growth, nitrogen productivity, nitrogen partitioning, Betula verrucosa (birch), Brassica oleracea var. capacitata ‘Stonehead’ (cabbage), Dactylis glomerata, Plantago lanceolata

INTRODUCTION

In many studies of nitrogen-limited plant growth, a linear relationship has been found between relative growth rate and plant nitrogen concentration, showing a negative intercept at a plant nitrogen concentration of zero (e.g. Ingestad, 1979; Ingestad and Ågren, 1992). This equation forms the basis of the nitrogen productivity theory (Ågren, 1985, 1988, 1994). On the basis of empirical studies, several authors have suggested that there is also a distinctive, but not yet mathematically quantified, relationship between allocation and plant nitrogen concentration (e.g. Van der Werf et al., 1993b; Tan and Hogan, 1998; De Pinheiro Henriques and Marcelis, 2000).

So far these empirically found relationships can not be derived from theoretical considerations. Many mechanistic models have been developed concerning the influence of nitrogen availability and/or plant nitrogen concentration on plant growth and allocation. These models are complex in the number of plant constants and variables (e.g. Van der Werf et al., 1993a; Reynolds and Chen, 1996; Bijlsma and Lambers, 2000). The detailed description of physiological processes in these models is not suitable for predicting relationships on larger levels such as plant level or plant compartment level.

In a number of models, complexity is somewhat reduced by using a combination of mechanistic and teleological (goal directed) approaches. Equations describing processes in different plant compartments are for instance combined with the use of a growth rate optimization criterion on plant level (e.g. Johnson and Thornley, 1987; Hilbert, 1990; Gleeson, 1993). However, these models are still not suitable to predict global relationships such as nitrogen allocation to plant nitrogen concentration.

Ågren (1996) formulated a simple mechanistic model to calculate plant growth, using a preliminary assumption concerning biomass allocation. He assumed a linear relationship between the ratio of leaf biomass and plant biomass and plant nitrogen concentration. However, model predictions of whole-plant growth deviated from the nitrogen productivity theory.

A simple plant growth model was constructed which is attuned to the level of detail of the empirical findings. The model quantifies nitrogen allocation (which approximates biomass allocation) in relation to plant nitrogen concentration, during nitrogen-limited growth. Nitrogen allocation was chosen instead of biomass allocation to avoid the complexity of differences in nitrogen concentrations in the different plant compartments. At equal nitrogen concentrations in these compartments nitrogen allocation coincides with biomass allocation.

In the construction of the model, the focus was on the formation and degradation of photosynthetic nitrogen. Photosynthetic nitrogen was defined in general terms as biologically active nitrogen in enzymes involved in the photosynthetic process. To avoid the complexity of a mechanistic description of allocation processes a central hypothesis was formulated in which it was assumed that the formation of photosynthetic nitrogen is proportional to nitrogen uptake. In addition, a number of mechanistic assumptions were made about the degradation of photosynthetic nitrogen and the equilibrium between photosynthetic nitrogen and other leaf nitrogen.

The primary aim of this paper is to derive a mathematical equation which predicts nitrogen allocation as a function of plant nitrogen concentration. Such an equation provides a tool for crop modellers to describe allocation in young vegetative growing plants (Van der Werf et al., 1993b). This equation for nitrogen-limited plant growth was derived from, and its general validity tested using empirical data from four growth studies of quite different plant species described in literature: Betula verrucosa (birch), Dactylis glomerata, Plantago lanceolata and Brassica oleracea var. capacitata ‘Stonehead’ (cabbage). In particular these studies were chosen because each of these studies examined a large range of nitrogen allocation patterns (large range of growth rate and plant nitrogen concentration), which was needed for an adequate testing of the validity of the derived equation for nitrogen allocation. The first three studies described steady-state experiments. The nitrogen productivity theory is primarily based on these kinds of experiments. The last study was conducted at non-steady-state conditions. It is still debated whether the nitrogen productivity theory is applicable in such conditions (e.g. Burns, 1994; Wikström and Ågren, 1995; Burns et al., 1997). Concerning nitrogen allocation there are clear indications that the partitioning functions in relation to internal plant N status are general for both steady-state and non-steady-state conditions (e.g. Van der Werf et al., 1993b; De Groot et al., 2002; Yin and Schapendonk, 2004). One non-exponential growth study was found in the literature that included a large enough range of nitrogen allocation patterns and thus was suited for an adequate testing of the validity of the model. The secondary aim of this paper is to use the constructed model to examine the processes that underlie nitrogen productivity theory.

THE MODEL

First the central hypothesis and the additional assumptions are described and formulated in four basic mathematical equations. Subsequently these basic equations are used to derive equations for whole plant growth and nitrogen allocation. Some of these equations are in bold print. Only the validity of bold equations is tested in the next paragraph by comparison with empirical data.

The model confines itself to nitrogen-limiting conditions (excluding conditions of strong deficiency). Other plant resources are non-limiting and micro-climatic conditions are presumed to be constant. Furthermore it is assumed that no loss of biomass and nitrogen occurs. To keep the model simple, photosynthetic nitrogen is defined in general terms as biologically active nitrogen in enzymes involved in the photosynthetic process.

Central hypothesis and additional assumptions

It might be argued that the formation of photosynthetic nitrogen (Nph) should be proportional to nitrogenous compounds in leaves not active in growth. However, an analysis of the supply and depletion of this pool would unnecessarily complicate the model. In any case the pool would be emptied rapidly if it was not filled continuously. Therefore, it might be argued that it is acceptable to introduce a simplification by formulating a direct relationship between nitrogen uptake and the formation of Nph. To quantify this dependency a mechanistic basis is needed. However, this mechanistic basis should include a description of the processes of allocation, which is omitted here because of the complexity involved. Instead, nitrogen is assumed to be allocated in such a way that the formation of photosynthetic nitrogen from nitrogen uptake maintains a constant efficiency in the range of nitrogen-limited uptake situations. This might well be the outcome of evolutionary and competitive processes and is in agreement with experimental evidence which suggests that under limited nitrogen availability nitrogen is used with priority for maintaining photosynthesis (De Pinheiro Henriques and Marcelis, 2000). Thus, the formation of Nph is assumed to be proportional to the uptake of nitrogen:

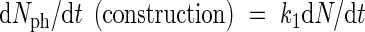graphic file with name M1.gif

in which N stands for plant nitrogen content.

Photosynthetic nitrogen has a considerable turnover (Bijlsma and Lambers, 2000). The degradation of these nitrogen compounds is assumed to be governed by first-order kinetics. This degradation contributes to the above-mentioned pool of leaf nitrogen which is not active in growth. Equation (2) describes the most simple (and most common) kinetic behaviour.

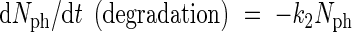graphic file with name M2.gif

It is assumed that a fast equilibrium exists between photosynthetic nitrogen and other leaf nitrogen, which means that the amount of photosynthetic nitrogen in leaves is proportional to the nitrogen content of leaves (Nl):

graphic file with name M3.gif

Growth rate on a dry weight basis is proportional to the net increment of carbon (e.g. Hilbert, 1990) and this increment is proportional to the gain of carbon in the photosynthetic process. On this basis, growth rate is assumed to be proportional to the amount of photosynthetic nitrogen.

graphic file with name M4.gif

in which B stands for biomass (dry weight).

Derivation of further model equations

Combination of eqns (3) and (4) leads to

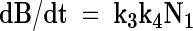graphic file with name M5.gif

Or relative growth rate (RGR) may be written as

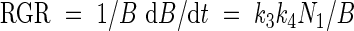graphic file with name M6.gif

To replace Nl by variables on plant level, eqns (1) and (2) are combined, leading to

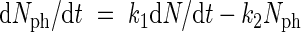graphic file with name M7.gif

Using eqn (4), Nph in the right part of eqn (7) may be substituted by (1/k4)dB/dt, leading to

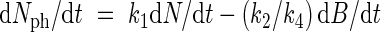graphic file with name M8.gif

In eqn (8) N includes Nph and B includes N. This equation can also be written in mutually exclusive variables (biomass of Nph, biomass of other nitrogen and the remaining biomass). Integration and subsequent reordering of variables leads to

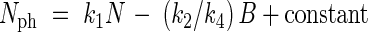graphic file with name M9.gif

When values of N and B equal zero, the value of Nph must equal zero, so

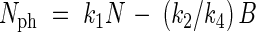graphic file with name M10.gif

Nph in eqn (10) may be substituted by (1/k4)dB/dt, which leads to the following growth equations:

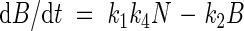graphic file with name M11.gif

or

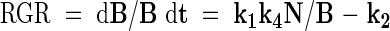graphic file with name M12.gif

Finally, to derive an equation for nitrogen allocation, eqns (3) and (10) are combined, resulting in

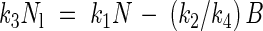graphic file with name M13.gif

or

graphic file with name M14.gif

MODEL RESULTS

Equation (12) predicts a linear relationship between relative growth rate and plant nitrogen concentration, showing a negative intercept at a nitrogen concentration of zero. This is in accordance with many experimental findings on which the earlier-mentioned nitrogen productivity (NP) theory is based (Ågren, 1985, 1988, 1994). However, it must be mentioned that some cases have been presented in which the intercept at a nitrogen concentration of zero has a positive value (e.g. Freysen and Veen, 1989).

The ratio of Nl and N is predicted by two model equations. Equation (5) predicts a proportionality between Nl/N and NP which was defined by Ingestad (1979) as 1/N dB/dt. Equation (14) predicts that Nl/N declines linearly with the inverse of plant nitrogen concentration. The validity of these equations was first tested using data from three exponential growth studies. Either eqn (5) or eqn (14) was used, depending on the available data in the publications. The first study concerns birch (Ingestad, 1979; Ingestad and Lund, 1979). The second study concerns Dactylis glomerata (Van der Werf et al., 1993a). The third study concerns Plantago lanceolata (Freysen and Veen, 1989). This study, which has already been mentioned above, showed a linear relationship between relative growth rate and plant nitrogen concentration with a positive intercept at a nitrogen concentration of zero. This is not in accordance with eqn (12). However, a positive intercept implies plant growth in the absence of photosynthetic nitrogen, which is hard to understand from a physiological point of view. For this reason, a decision was taken to test if the outcomes of the study of Plantago lanceolata in terms of nitrogen allocation complied with model predictions.

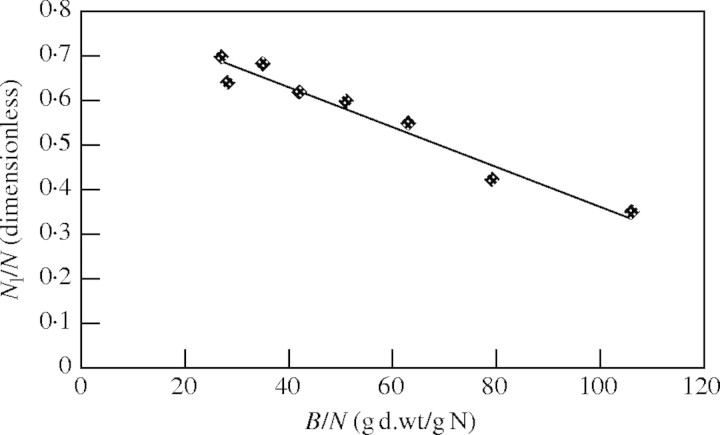
In the study of birch (Ingestad, 1979; Ingestad and Lund, 1979) the relationship between allocation and plant nitrogen concentration was not determined. However, the necessary data could be obtained from Ingestad et al. (1994). Only observations corresponding with values of RGR up to 0·20 per day were used in this analysis, to ensure N-limiting conditions (RGRmax = 0·22). Results are shown in Fig. 1, which shows that observations agree well with eqn (14).

Fig. 1.

Fig. 1.

Open in a new tab

Nitrogen allocation of birch as a function of the inverse of nitrogen concentration. The line fits to the function y = −0·0043x + 0·795 [Pearson r = 0·981; significant at 0·01 level (two-tailed)]. Linearity was tested by residual analysis and showed no reason to deviate from linearity. Data obtained from Ingestad et al. (1994).

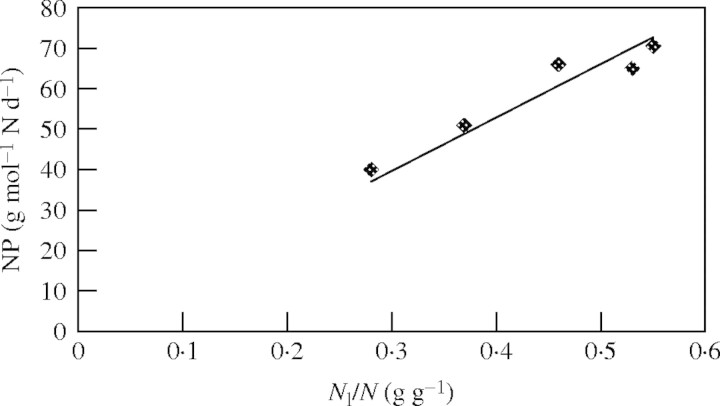
In the study of Dactylis glomerata by Van der Werf et al. (1993a), the relationship between Bl/B and NP was determined. This was shown in their fig. 5b from which, in the present study, the relationship between Nl/N and NP was determined. NP values were estimated and these values combined with corresponding values of Nl/N, which were mentioned in the legend to fig. 4b in Van der Werf et al. (1993a). The results are shown in Fig. 2. It appears that this relationship can be adequately described with eqn (5). For the derivation of this equation only basic eqns (3) and (4) were used, hence no evidence is obtained about the correctness of basic eqns (1) and (2).

Fig. 2.

Fig. 2.

Open in a new tab

Nitrogen allocation of Dactylis glomerata as a function of nitrogen productivity (NP). Best fit was obtained with the function y = 114·2x + 8·292 [Pearson r = 0·975; significant at 0·01 level (two-tailed)]. The drawn line was forced through zero and fits to the function y = 132·2x (r2 = 0·9264). Linearity was tested by residual analysis and showed no reason to deviate from linearity. Values of Nl/N and NP are based on Van der Werf et al. (1993a), as explained in the text.

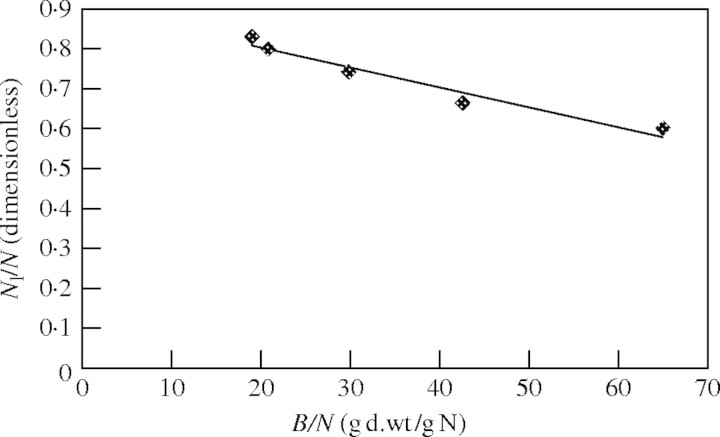
In the study of Plantago lanceolata (Freysen and Veen, 1989) the relationship between Nl/N and N/B was determined. They fitted a polynomial regression line through the observation points. The same observation points were used to analyse the relationship between Nl/N and B/N. Results are shown in Fig. 3. It appears that this relationship can be adequately described with eqn (14).

Fig. 3.

Fig. 3.

Open in a new tab

Nitrogen allocation of Plantago lanceolata as a function of the inverse of nitrogen concentration. The line fits to the function y = −0·005x + 0·9026 [Pearson r = 0·990 significant at 0·01 level (two-tailed)]. Linearity was tested by residual analysis and showed no reason to deviate from linearity. Values of Nl/N and B/N are based on fig. 4 of Freysen and Veen (1989).

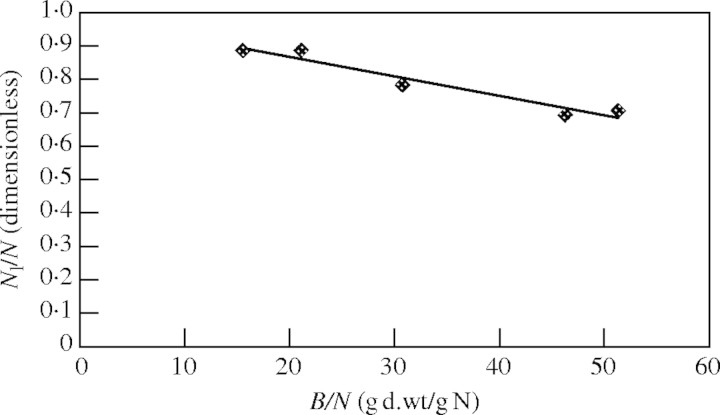
One study was found in literature (Burns, 1994) that was suitable for testing the performance of the model under non-exponential growth conditions. This study concerns cabbage. Changes in growth were measured following a total interruption of the external nitrogen supply. After this interruption the amount of nitrogen in the plant remained constant. Burns (1994) did not find a relationship between RGR and nitrogen concentration as shown in eqn (12). However this finding was questioned by Wikström and Ågren (1995). They state that observations may also be predicted with an equation which, apart from notation, is identical to eqn (12). Using data from Burns (1994) the validity of eqn (14) was tested. Nl/N was calculated as the product of Bl/B (estimated from Burns fig. 4A), Nl/Bl (estimated from Burns fig. 2B) and B/N (estimated from Burns fig. 2A). Results are shown in Fig. 4. Again expected plant behaviour agrees well with observations.

Fig. 4.

Fig. 4.

Open in a new tab

Nitrogen allocation of cabbage as a function of the inverse of nitrogen concentration. The line fits to the function y = −0·0058x + 0·9838 [Pearson r = 0·993 significant at 0·01 level (two-tailed)]. Linearity was tested by residual analysis and showed no reason to deviate from linearity. Values of Nl/N and B/N are based on Burns (1994), as explained in the text.

DISCUSSION

As mentioned before, the basic model equations are only assumed to be valid in nitrogen-limiting conditions. In particular this applies to eqns (1) and (3). Equation (1) assumes a proportionality between the formation of photosynthetic nitrogen and nitrogen uptake. Equation (3) assumes an equilibrium between photosynthetic nitrogen and other leaf nitrogen with a single equilibrium constant. At high plant nitrogen concentrations one might expect that these equations are no longer valid, as plants invest relatively more nitrogen in non-photosynthetic compounds.

The constructed model offers no insight in the physiological processes by which allocation is realized. For this reason, apart from the above, the model cannot be compared with complex mechanistic models such as mentioned in the Introduction. These models have a different purpose than the simple model that is proposed in this paper. They aim at a better understanding of the physiological processes that regulate growth and allocation. On the other hand, the intricate structure of these models is not attuned to finding simple general relationships between plant nitrogen concentration and relative growth rate or allocation.

Model equations can be used to examine the processes that underlie the empirically based nitrogen productivity theory. In agreement with this theory, eqn (12) describes a linear relationship between relative growth rate and plant nitrogen concentration, showing a negative intercept at a nitrogen concentration of zero. In the nitrogen productivity theory k1k4 is designated as a single constant. In this paper it is described as the product of two constants: one describing the efficiency of formation of photosynthetic nitrogen from nitrogen uptake, the other describing the efficiency of biomass formation in relation to the amount of photosynthetic nitrogen.

As may be seen from basic eqn (2), the negative intercept k2 is interpreted as being equal to the degradation rate constant of photosynthetic nitrogen. Due to this degradation, growth rate equals zero when N/B equals k2/(k1k4). The reconstruction of degraded proteins is one of the major (residual) maintenance respiration costs (e.g. Cannell and Thornley, 2000). Hence the parameter k2 can also be linked to respiratory costs. The validity of the interpretation of k2 could be checked by comparing reported k2 values to data about the degradation of active photosynthetic nitrogen, if the latter data were available from literature. In the model, photosynthetic nitrogen was not chemically defined, but it is known that Rubisco is the principal enzyme involved in the photosynthetic process (Lambers et al., 1998). However, the degradation mechanism of Rubisco is still a mystery in plant physiology (Yamauchi et al., 2002). Yamauchi et al. (2002) have suggested that the glycation of Rubisco, with ascorbic acid as a glycating agent, might be important for the loss of activity and degradation of Rubisco. They performed experiments which showed that the activity of Rubisco in the presence of ascorbic acid declined with approx. 50–75 % at an incubation time of 20 d (Yamauchi et al., 2002, fig. 6a, b). In the study of birch (Ingestad, 1979) a k2 value of approx. 0·02 d−1 was reported. In 20 d this would lead to a degradation of the initial active Nph by approx. 35 %. It is concluded that the order of magnitude of k2 corresponds fairly well with the measured decline of active Rubisco. However, firm conclusions can only be drawn when further research has unequivocally determined the degradation mechanism rate of photosynthetic nitrogen.

Equation (5) predicts that the quotient of growth rate and the amount of nitrogen in leaves is constant. This quotient resembles nitrogen productivity (NP), which is defined as the quotient of growth rate and the total amount of nitrogen (Ingestad, 1979):

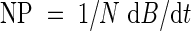graphic file with name M15.gif

Using eqn (11), eqn (15) may be written as:

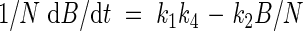graphic file with name M16.gif

which means that NP varies with internal nitrogen concentration.

Ågren (1985) gives three alternative interpretations of the nitrogen productivity concept. In his first interpretation NP is defined as in eqn (15) and NP varies with internal nitrogen concentration as in eqn (16). In the other interpretations, two alternative definitions of NP are formulated in which NP is independent of internal nitrogen concentration. This is done by applying correction factors to eqn (15), respectively for maintenance costs (respiration) or for nitrogen not contributing to growth. Due to the unclear meaning of k2 (it is only a means of fitting experimentally found growth curves), Ågren (1985) does not opt for the first interpretation. Instead, he provisionally opts for a constant NP in combination with the latter correction factor. However, in this paper k2 has a biochemical meaning as defined above. Perhaps an NP which is independent of plant nitrogen concentration is unlikely. Allocation depends on plant nitrogen concentration and only nitrogen in leaves contributes directly to growth. In fact from eqn (5) it appears that NP is proportional to Nl/N.

CONCLUSIONS

The agreement between model outcomes and empirical findings suggests that the derived equation for nitrogen allocation in relation to plant nitrogen concentration might be generally applicable. In accordance with the central hypothesis in the construction of the model, nitrogen seems to be allocated in such a way that the formation of photosynthetic nitrogen from nitrogen uptake maintains a constant efficiency in the range of nitrogen-limiting conditions.

The model gives a biochemical meaning to the observed negative intercept between relative growth rate and plant nitrogen concentration. This intercept is interpreted as being equal to the degradation constant of photosynthetic nitrogen.

Acknowledgments

We thank Dr G. I. Ågren for his constructive comments on earlier versions of this paper and for the provision of data from the original experiments of T. Ingestad. We also thank an anonymous referee for his critical remarks. We thank Dr F. M. Klis for stimulating discussions.

LITERATURE CITED

  1. Ågren GI. 1985. Theory for growth of plants derived from the nitrogen productivity concept. Physiologia Plantarum 64: 17–28. [Google Scholar]
  2. Ågren GI. 1988. The ideal nutrient productivities and nutrient proportions. Plant, Cell and Environment 11: 613–620. [Google Scholar]
  3. Ågren GI. 1994. The interaction between CO2 and plant nutrition: comments on a paper by Coleman, McConnaughay and Bazzaz. Oecologia (Berlin) 98: 239–240. [DOI] [PubMed] [Google Scholar]
  4. Ågren GI. 1996. Nitrogen productivity or photosynthesis minus respiration to calculate plant growth? Oikos 76: 529–535. [Google Scholar]
  5. Bijlsma RJ, Lambers H. 2000. A dynamic whole-plant model of integrated mechanism of nitrogen and carbon. 2. Balanced growth driven by C fluxes and regulated bij signals from C and N substrate. Plant and Soil 220: 71–87. [Google Scholar]
  6. Burns IG. 1994. Studies of the relationship between the growth rate of young plants and their total-N concentration using nutrient interruption techniques: theory and experiments. Annals of Botany 74: 143–157. [Google Scholar]
  7. Burns IG, Walker RL, Moorby J. 1997. How do nutrients drive growth? Plant and Soil 196: 321–325. [Google Scholar]
  8. Cannell MGR, Thornley JHM. 2000. Modelling the components of plant respiration: some guiding principles. Annals of Botany 85, 45–54. [Google Scholar]
  9. De Groot CC, Marcelis LFM, van den Boogaard R, Lambers H. 2002. Interactive effects of nitrogen and irradiance on growth and partitioning of dry mass and nitrogen in young tomato plants. Functional Plant Biology 29: 1319–1328. [DOI] [PubMed] [Google Scholar]
  10. De Pinheiro Henriques AR, Marcelis LFM. 2000. Regulation of growth at steady-state nitrogen nutrition in lettuce (Lactuca sativa L.): interactive effects of nitrogen and irradiance. Annals of Botany 86, 1073–1086. [Google Scholar]
  11. Freysen AHJ, Veen BW. 1989. Phenotypic variation in growth as affected by N-supply: nitrogen productivity. In: Lambers H, Cambridge ML, Konings H, et al eds. Causes and consequences of variation in growth rate and productivity of higher plants. The Hague: SPB Academic Publishing, 19–33. [Google Scholar]
  12. Gleeson SK. 1993. Optimization of tissue nitrogen and root–shoot allocation. Annals of Botany 71: 23–31. [Google Scholar]
  13. Hilbert DW. 1990. Optimization of plant root:shoot ratios and internal nitrogen concentration. Annals of Botany 66: 91–99. [Google Scholar]
  14. Ingestad T. 1979. Nitrogen stress in birch seedlings. 2. N, K, P, Ca and Mg nutrition. Physiologia Plantarum 45: 149–157. [Google Scholar]
  15. Ingestad T, Ågren GI. 1992. Theories and methods on plant nutrition and growth. Physiologia Plantarum 84: 177–184. [Google Scholar]
  16. Ingestad T, Lund AB. 1979. Nitrogen stress in birch seedlings. 1. Growth technique and growth. Physiologia Plantarum 45: 137–148. [Google Scholar]
  17. Ingestad T, Hellgren O, Ingestad Lund AB. 1994.Data base for birch plants at steady state. Performance of birch plants (Betula pendula Roth) under non-limiting conditions and under limitation by nitrogen and light. Report 75. Department of Ecology and Environmental Research, Swedish University of Agricultural Sciences. [Google Scholar]
  18. Johnson IR, Thornley JHM. 1987. A model of shoot:root partitioning with optimal growth. Annals of Botany 60: 133–142. [Google Scholar]
  19. Lambers H, Stuart Chapin III F, Pons TL. 1998.Plant physiological ecology. Springer-Verlag, Berlin, 13. [Google Scholar]
  20. Reynolds JF, Chen J. 1996. Modelling whole-plant allocation in relation to carbon and nitrogen supply: coordination versus optimization: opinion. Plant and Soil 185: 65–74. [Google Scholar]
  21. Tan W, Hogan GD. 1998. Dry weight and N partitioning in relation to substrate N supply, internal N status and developmental stage in jack pine (Pinus banksiana Lamb.) seedlings: implications for modelling. Annals of Botany 81: 195–201. [Google Scholar]
  22. Van der Werf A, Visser AJ, Schieving F, Lambers H. 1993. Evidence for optimal partitioning of biomass and nitrogen at a range of nitrogen availabilities for a fast- and slow-growing species. Functional Ecology 7: 63–74. [Google Scholar]
  23. Van der Werf A, Enserink T, Smit B, Booij, R. 1993. Allocation of carbon and nitrogen as a function of the internal nitrogen status of a plant: Modelling allocation under non-steady-state situations. Plant and Soil 155/156: 183–186. [Google Scholar]
  24. Wikström F, Ågren GI. 1995. The relationship between the growth rate of young plants and their total- N concentration is unique and simple: a comment. Annals of Botany 75: 541–544. [Google Scholar]
  25. Yamauchi Y, Ejiri Y, Tanaka K. 2002. Glycation of ascorbic acid causes loss of activity of ribulose-1,5-bisphosphate carboxylase/oxygenase and its increased susceptibility to proteases. Plant Cell Physiology 43: 1334–1341. [DOI] [PubMed] [Google Scholar]
  26. Yin X, Schapendonk AHCM. 2004. Simulating the partitioning of biomass and nitrogen between roots and shoot in crop and grass plants. NJAS–Wageningen Journal of Life Sciences 51: 407–426. [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES