Loss of Genetic Variation in Geographically Marginal Populations of Atriplex tatarica (Chenopodiaceae)

Abstract

• Background and Aims Genetic variability was estimated for Atriplex tatarica from 25 populations in the Czech Republic. Since its north-western range margin is in central Europe, a relationship between marginality and low within-population genetic diversity was tested in accordance with the Central–Marginal Model.

• Methods Population genetic diversity was expressed by assessing patterns of variation at 13 putatively neutral allozyme loci (comprising 30 putative alleles) within and between 25 natural populations of A. tatarica along a north-west–south-east transect in the Czech Republic.

• Key Results Atriplex tatarica is a species of human-made habitats with a mixed mating system and wide geographic distribution. Overall, A. tatarica displayed moderate levels of genetic diversity in comparison with other herbaceous plants. The percentage of loci that were polymorphic was 47·1 %, with average values of 1·55, 0·151 and 0·155 for the average number of alleles per polymorphic locus (A), observed heterozygosity (H_o) and expected heterozygosity (H_e), respectively. There was only weak evidence of inbreeding within populations (F_IS = 0·031) and significant population differentiation (F_ST = 0·214). Analysis of the data provides no evidence for isolation-by-distance for the whole study area. However, Mantel tests were highly significant for the marginal Bohemian region and non-significant for the central Moravian region. While northern populations of A. tatarica showed significantly lower allelic richness (A = 1·462) than populations from the southern part of the study area (A = 1·615), they did not differ in observed heterozygosity (H_o), gene diversity (H_S), inbreeding within populations (F_IS) or population differentiation (F_ST), despite generally lower values of particular genetic measurements in the marginal region.

• Conclusions Genetic diversity, with the exception of allelic richness, was not significantly lower at the margins of the species' range. This, therefore, provides only weak support for the predictions of the Central–Marginal Model.

INTRODUCTION

Genetic variation and population structure reflect both the influence of present-day evolutionary forces (e.g. natural selection, genetic drift, and gene flow) and historical processes associated with patterns of colonization and migration (Barrett, 1982). The study of historical plant invasions reveals differing levels of genetic variation within colonizing species, mainly due to founder effects, number of population bottlenecks, the mating system or ability to hybridize (Barrett, 1982).

Both the founder effect, when numbers of immigrants are important, and population bottlenecks lead to lowered amounts of genetic information present in the new population, as compared with the source population. This sampling error causes random fluctuations in allele frequencies called genetic drift. The extent of the loss of genetic variation in comparison to the source population depends on the size of the founder population, the number of times a founder event occurs and the severity of a population bottleneck (Nei et al., 1975; Goodnight, 1987, 1988). For example, multiple introductions of ornamental species such as Lathyrus latifolius (Godt and Hamrick, 1991), Lonicera japonica (Schierenbeck et al., 1995) or Pueraria lobata (Pappert et al., 2000) resulted in higher levels of genetic variability compared with single introductions such as for Bromus tectorum (Novak and Mack, 1993) or Reynoutria japonica var. japonica (Hollingsworth and Bailey, 2000; Mandák et al., 2003, 2005).

The importance of the mating system has been repeatedly documented for a variety of invasive species. For example, species with a predominantly autogamous mode of reproduction usually exhibit low levels of genetic variation and often form highly homozygous populations composed of a few genotypes, e.g. Capsella bursa-pastoris (Bosbach and Hurka, 1981), Lolium temulentum (Hayward and Zaruk, 1982), Polygonum pensylvanicum (Kubetin and Schaal, 1979) and Senecio viscosus (Koniuszek and Vereij, 1982). On the other hand, invading species with predominantly allogamous modes of reproduction may possess a high level of genetic diversity, e.g. Echium plantagineum (Brown and Burdon, 1983).

Hybridization can increase genetic variability and generate both novelty and variation (Rieseberg et al., 2003). In alien plants, it can occasionally be followed by the spread of hybrid gene combinations (Ellstrand and Schierenbeck, 2000; Vila et al., 2000). Hence, hybridization can lead to adaptive evolution in a number of ways, for example, through the generation of novel genotypes and variation, fixed heterosis stabilized by apomixis or clonality and dumping of genetic load (Ellstrand and Schierenbeck, 2000). However, not all hybridization events lead to increased fitness or adaptive evolution (Arnold, 1997). The hybridization process is important not only at the interspecific level but it can also act as a stimulus for the evolution of invasiveness within plant species (Ellstrand and Schierenbeck, 2000), i.e. hybridization between previously isolated populations of the same species, in the case of multiple introductions from various sites within the native distribution range.

In plant species with continuous distributions, genetic variation among geographic regions may result from the presence of barriers to gene flow among populations (e.g. a mountain range) or as a result of historical events such as glaciations (Hewitt, 1996, 1999; Ibrahim et al., 1996; Chauvet et al., 2004; Persson et al., 2004). On the basis of the concept of recolonization of new areas typically constructed for patterns of genetic variation in a colonized area after glaciations, two models for recently spreading species can be introduced. The ‘gradual expansion scenario’, when migration proceeds from a gradually expanding continuous front, assumes that most genetic diversity will be retained through the course of an expansion. In contrast, the ‘satellite population scenario’ assumes many spatially isolated and initially small marginal populations, which in turn become the source of new founding events. In the latter case, an enhanced potential for founder effects that reduce allelic diversity within populations (Nei et al., 1975) will occur and, as a consequence, these marginal populations will constitute a number of small demes representing only part of the genetic variation of the central populations. The classical view, often referred to as the Central–Marginal Model (Da Cunha and Dobzhansky, 1954), shows that patterns of genetic variation between central and marginal populations may thus depend on the degree to which markers are under selection, rates of gene flow into marginal populations, and the amount of habitat variability and rates of population growth in central and marginal areas (Franks et al., 2004).

Species that have increased their range recently are particularly appropriate for addressing questions regarding patterns of spatial genetic structuring and comparison of genetic variation between central and marginal areas. This is due to their fragmented distribution in the marginal areas, when populations are often restricted to the most ecologically suitable habitats only, as opposed to the naturally continuous distribution in the central area. Here, using polymorphism at allozyme loci, the genetic diversity of A. tatarica in the Czech Republic was investigated to address the following specific questions: (a) what is the pattern of genetic variation within and among populations of A. tatarica and is there evidence of inbreeding and population differentiation; and (b) is there evidence of reduced genetic diversity in the north-western marginal populations of A. tatarica compared with the south-eastern central populations, due to the likely migration north-west from the south-eastern area of continuous distribution?

MATERIALS AND METHODS

The plant studied

Atriplex tatarica L. (syn. A. laciniata L., A. sinuata Hoffm., A. veneta Willd.) (Chenopodiaceae) is one of two annual, heterocarpic, diploid species of the section Sclerocalymma Aschers in the Czech Republic (Mandák, 2003a). Atriplex tatarica has spread from its native Central Asia, Asia Minor and eastern Europe (Aellen, 1960) to central Europe (Fig. 1) where it is abundant in urban areas, on disturbed sites, along railways and roads mainly in the warmer areas of the Czech Republic, with a tendency towards spreading further (Mandák, 2003a). It grows well in nitrogen-rich soils and tolerates a high content of NaCl (Mandák, 2003b). The north-west border of its continuous European distribution lies partly in the Czech Republic. The species is very common in the south-eastern part of the Czech Republic (south Moravia), which probably represents part of the native continuous area of distribution from south-eastern Europe through the Pannonian lowland. In the rest of the Czech Republic, i.e. the western part (Bohemia), the species is only found in several localities geographically isolated from the Moravian sites and from one another (Fig. 1).

Fig. 1.

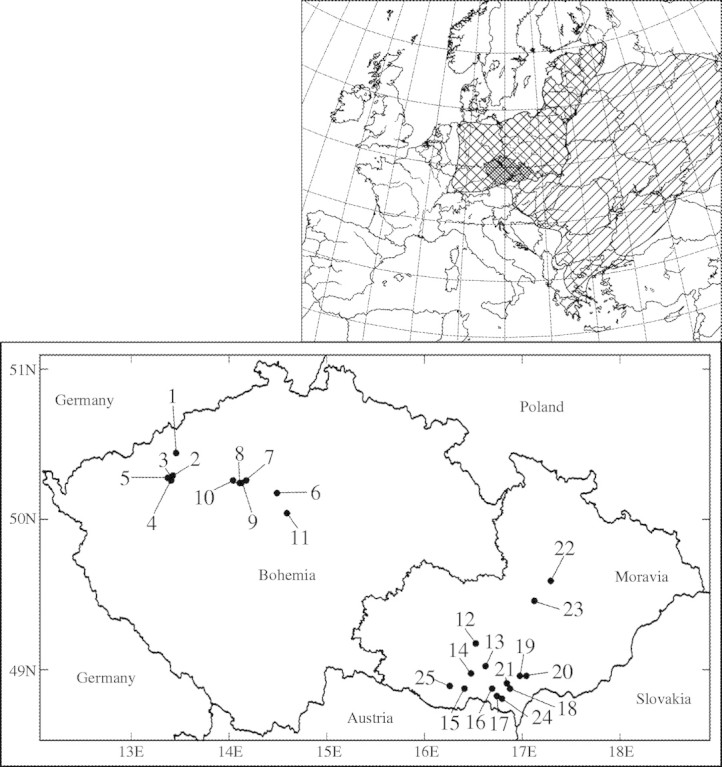
Map showing the total distribution of Atriplex tatarica in Europe (redrawn from Jalas and Suominen, 1988). The shaded area indicates native area distribution of A. tatarica and the cross-hatched area indicates secondary area distribution in Europe (Jalas and Suominen, 1988). The detailed map of the Czech Republic shows the location of the 25 populations of A. tatarica used in this study.

The populations studied

Twenty-five populations were studied along a geographical gradient through the Czech Republic; 11 populations from Bohemia and 14 from Moravia (Table 1 and Fig. 1). Samples for genetic analysis were collected from June to August in 2002–2003. A 50-m transect was located in each of the selected populations and ten different individuals were collected in each population at 5-m intervals. Samples were transported in a cool box and the youngest expanded leaf of each plant analysed within 24 h.

Table 1.

Summary of genetic diversity within 25 populations of Atriplex tatarica based on nine putative allozyme loci (enzyme systems AAT, LAP, MDH, SKDH and SOD) and mean species values

Population*	Latitude	Longitude	n	PL	A	Ae	Ho	He	f (=FIS)
B1	50°25′85″	13°26′68″	6	53·9	1·54	1·31	0·192	0·195	0·013
B2	50°16′75″	13°24′65″	3	46·2	1·46	1·26	0·169	0·168	−0·005
B3	50°15′83″	13°23′21″	6	53·9	1·54	1·22	0·162	0·150	−0·080
B4	50°14′79″	13°24′17″	4	53·9	1·54	1·32	0·208	0·201	−0·034
B5	50°16′25″	13°21′69″	6	23·1	1·23	1·16	0·077	0·088	0·135
B6	50°10′35″	14°29′06″	5	30·8	1·31	1·10	0·054	0·070	0·241
B7	50°15′25″	14°09′64″	1	38·5	1·38	1·26	0·139	0·157	0·124
B8	50°14′25″	14°07′18″	2	38·5	1·46	1·24	0·131	0·136	0·044
B9	50°14′15″	14°05′80″	5	30·8	1·38	1·18	0·131	0·111	−0·191
B10	50°15′07″	14°02′08″	3	46·2	1·54	1·28	0·162	0·178	0·096
B11	50°02′43″	14°35′18″	2	38·5	1·69	1·32	0·123	0·135	0·094
M12	49°10′40″	16°30′76″	2	69·2	1·85	1·27	0·169	0·185	0·092
M13	49°01′44″	16°36′75″	4	46·2	1·46	1·25	0·177	0·161	−0·107
M14	48°58′18″	16°27′86″	4	61·5	1·77	1·42	0·231	0·253	0·094
M15	48°52′09″	16°24′04″	2	38·5	1·46	1·10	0·085	0·075	−0·138
M16	48°52′05″	16°41′14″	6	38·5	1·38	1·24	0·123	0·139	0·122
M17	48°49′09″	16°44′52″	6	69·2	1·85	1·29	0·162	0·166	0·026
M18	48°51′69″	16°52′23″	2	53·9	1·62	1·27	0·162	0·156	−0·038
M19	48°56′84″	16°58′51″	2	53·9	1·62	1·32	0·154	0·186	0·182
M20	48°57′57″	17°02′43″	5	38·5	1·38	1·14	0·108	0·097	−0·115
M21	48°54′02″	16°50′34″	4	46·2	1·77	1·45	0·192	0·189	−0·018
M22	49°35′39″	17°17′59″	6	30·8	1·31	1·16	0·108	0·103	−0·050
M23	49°26′80″	17°06′86″	6	69·2	1·77	1·35	0·177	0·226	0·228
M24	48°47′78″	16°46′84″	6	53·9	1·69	1·31	0·208	0·177	−0·182
M25	48°53′14″	16°15′23″	6	53·9	1·69	1·31	0·169	0·180	0·062
Mean				47·1	1·55	1·26	0·151	0·155	0·024
(±SD)				(12·6)	(0·18)	(0·09)	(0·043)	(0·046)	(0·120)

Number of individual sampled from each population was ten.

PL = percentage of polymorphic loci; A = average number of alleles per polymorphic locus; A_e = effective allele number; H_o = observed heterozygosity; H_e = expected heterozygosity; f = Weir and Cockerham's estimate (Weir and Cockerham, 1984) of F_IS (Wright's fixation index) per population over loci.

Populations were assigned to six partly arbitrary classes, in which n = estimated total number of individuals: 1, n ≤ 50; 2, 50 < n ≤ 100; 3, 100 < n ≤ 200; 4, 200 < n ≤ 300; 5, 300 < n ≤ 400; 6, n > 400.

^*The first letter of each population name refers to the province in which the population was found, i.e. B = Bohemia and M = Moravia.

To examine the relationship between population size and population genetic structure, populations were assigned to six partly arbitrary classes, ranging from populations with <50 individuals to populations with >400 individuals (Table 1).

Allozyme procedures

Twelve enzymatic systems were tested and those which provided the best results in the given group were selected for further analysis, i.e. AAT (EC 2.6.1.1), LAP (EC 3.4.11.1), MDH (EC 1.1.1.37), SKDH (EC 1.1.1.25) and SOD (EC 1.15.1.1).

Electrophoresis was performed on crude protein extracts of leaf material. The tissue was ground in ice-cold TRIS–HCl extraction buffer [0·1 m TRIS–HCl, pH 8·0; 70 mm 2-mercaptoethanol, 26 mm sodium metabisulfite, 11 mm ascorbic acid, 4 % (w/v) polyvinylpyrrolidone]. Roughly 80 mg of fresh leaf material, along with Dowex.Cl (1-X8), was homogenized on ice in 0·75 mL of extraction buffer. Extracts were centrifuged for 10 min at 21 150 g and the clear supernatants were stored at −75 °C. Isozymes were separated on native-PAGE and 30 μL of each sample were employed for electrophoresis in a Hoefer vertical unit.

All enzyme systems (AAT, LAP, MDH, SKDH and SOD) were investigated on polyacrylamide gels [8 % acrylamide, discontinuous TRIS–glycine buffer system (pH 8·3)]. The staining procedures followed Vallejos (1983) for LAP and AAT and Wendel and Weeden (1989) for SKDH, MDH, ME and SOD, with certain modifications. Two staining solutions were prepared for AAT (20 mL 0·1 m TRIS–HCl (pH 8·4), 240 mg aspartic acid, 40 mg α-ketoglutaric acid and 20 mL 0·1 m TRIS–HCl (pH 8·4), 50 mg Fast Blue BB Salt, 50 mg Fast Violet B, 25 mg pyridoxal-5-phosphate). The gel was rinsed in water and then in TRIS–HCl pH 7 buffer. The solutions were then mixed and poured on the gel. The gel was incubated in the dark at 32 °C until bands appeared, and then rinsed and fixed with a 1 : 1 : 3 : 5 solution of glycerine, acetic acid, H₂O and methanol. The gel stained for LAP was rinsed in buffer [0·2 m TRIS–maleate (pH 6)] and incubated for 10 min with 40 mg l-leucyl-β-naphthylamide.HCl (in 50 % acetone) and 60 mg MgCl₂ (both dissolved in 30 mL buffer). Afterwards, a solution of 25 mg Fast Black K Salt in 30 mL buffer was added. For SKDH ingredients, 30 mg of shikimic acid, 5 mg of NADP, 6 mg of MTT and 2 mg of PMS were combined and dissolved in 30 mL of 0·1 m TRIS–HCl (pH 8·4). A standard staining solution for ME was prepared by dissolving 150 mg malic acid in 25 mL 0·05 m TRIS–HCl (pH 8·0) and adjusted to pH 7·5 with 1 n NaOH; to this was added a solution of 10 mg of MTT, 5 mg of NADP and 2 mg of PMS in 25 mL of 0·05 m TRIS–HCl (pH 8·0), and the resulting staining solution was poured over the gel. A parallel gel was stained for MDH [50 mL 0·1 m TRIS–HCl (pH 7·5), 150 mg malic acid, 15 mg NAD, 10 mg MTT, 2 mg PMS], as some MDH isozymes were active with NADP as a co-factor and, hence, were visualized with this stain. Best results were obtained with ME staining. All gels were incubated in the dark at 32 °C until bands appeared. For SOD ingredients, 50 ml of 0·05 m TRIS–HCl (pH 8·2), 5 mg of EDTA, 5 mg of NBT and 2 mg of riboflavin were combined and poured over the gel. This was incubated for 20 min in the dark at 32 °C then removed and illuminated under a lamp until bands appeared on the blue background. Afterwards, all gels were thoroughly rinsed in distilled water, dried between two cellophane sheets and stored.

Statistical analyses

To estimate genetic diversity and genetic structure, a locus was considered polymorphic if the frequency of the most common allele did not exceed 0·95. Genetic diversity parameters, i.e. percentage polymorphic loci (PL), average number of alleles per locus (A), effective number of alleles (A_e), observed heterozygosity (H_o) and Nei's unbiased heterozygosity (H_e), were estimated using the POPGEN program (Yeh et al., 1999). In addition, Weir and Cockerham's parameter f(F_IS), a measure of inbreeding within populations (Weir and Cockerham, 1984), was calculated for each population with FSTAT (Goudet, 1995).

Genetic variation among populations was analysed in several ways. First, genetic structure was investigated via Nei's measures of genetic diversity (Nei, 1973), which include total genetic diversity (i.e. total expected heterozygosity) at a polymorphic locus (H_T), mean genetic diversity within populations (H_S), and the proportion of genetic diversity occurring among populations [G_ST = (H_T – H_S)/H_T] (Culley et al., 2002). Secondly, Weir and Cockerham's estimates (Weir and Cockerham, 1984) of Wright's F statistics (Wright, 1965) were generated for each polymorphic locus. Significant deviations from the null expectation of F = 0 were determined by 5000 bootstrap replicates, calculations being undertaken using the FSTAT program (Goudet, 1995). In the bootstrap analysis, F (corresponding to Wright' F_IT) was estimated by alleles permutated among populations, f(F_IS) was estimated by the permutation of alleles within samples, and f(F_ST) was estimated by the permutation of alleles among samples. The average gene flow among populations (N_m) was estimated from f-values as f = 1/(4N_mα + 1) where α = [n/(n – 1)]² and n is number of populations (Crow and Aoki, 1984). Measures of within-population variation were related to latitude and population size using Spearman rank correlation (r_s). Probability values for differences between regions are given for the two-sided t-test, after 10 000 permutations. All analyses were performed using FSTAT software (Goudet, 1995).

A Mantel test was used to assess the model of isolation-by-distance using the genetic distance for pairs of populations (Nei, 1978) and geographic distance among these populations. The Nei's genetic distance was also employed to obtain a UPGMA phenogram, after 1000 bootstrap samples (calculated using TFPGA; Miller, 1997).

RESULTS

Allozyme polymorphism

Altogether, five enzyme systems (AAT, LAP, MDH, SKDH and SOD) were consistently resolved and scored for 13 putative loci (Aat-1, Aat-2, Lap-1, Lap-2, Mdh-1, Mdh-2, Mdh-3, Skdh-1, Sod-1, Sod-2, Sod-3, Sod-4 and Sod-5). Four loci (Aat-1, Sod-1, Sod-2 and Sod-5) turned out to be monomorphic across the study area. Nine polymorphic (at the 0·05 level) loci (Aat-2, Lap-1, Lap-2, Mdh-1, Mdh-2, Mdh-3, Skdh-1, Sod-3 and Sod-4), with a total of 30 alleles, were evaluated further. The allelic frequencies of each polymorphic locus (for all populations) are given in Appendix 1. Enzyme systems ADH, EST, G-6-PDH, IDH, ME, PGI, PGM, 6-PGDH and locus Skdh-2 were not consistently resolved.

Variation in allele frequencies and levels of inbreeding

The average number of alleles per polymorphic locus (A) ranged from 1·23 (locality 5) to 1·85 (localities 12 and 17), with a mean of 1·55. The effective number of alleles per locus (A_e) was 1·26 and the mean percentage of polymorphic loci (PL), evaluated at the 95 % confidence level, was 47·1 %. The interpopulation differences in observed heterozygosity (H_o) are due to deviations from the Hardy–Weinberg equilibrium, as shown by the average fixation indices per populations (Table 1). The H_o ranged from 0·054 (locality 6) to 0·231 (locality 14), with a mean of 0·151, while the expected heterozygosity (H_e) ranged from 0·070 (locality 6) to 0·253 (locality 14), with a mean of 0·155.

The value of f(F_IS) was highest in population 6 (0·241) and lowest in population 9 (–0·191), indicating the presence of both populations with an excess of heterozygotes (f < 0) compared with expected Hardy–Weinberg allelic frequencies and populations showing an excess of homozygous individuals, suggesting high levels of inbreeding (Table 1).

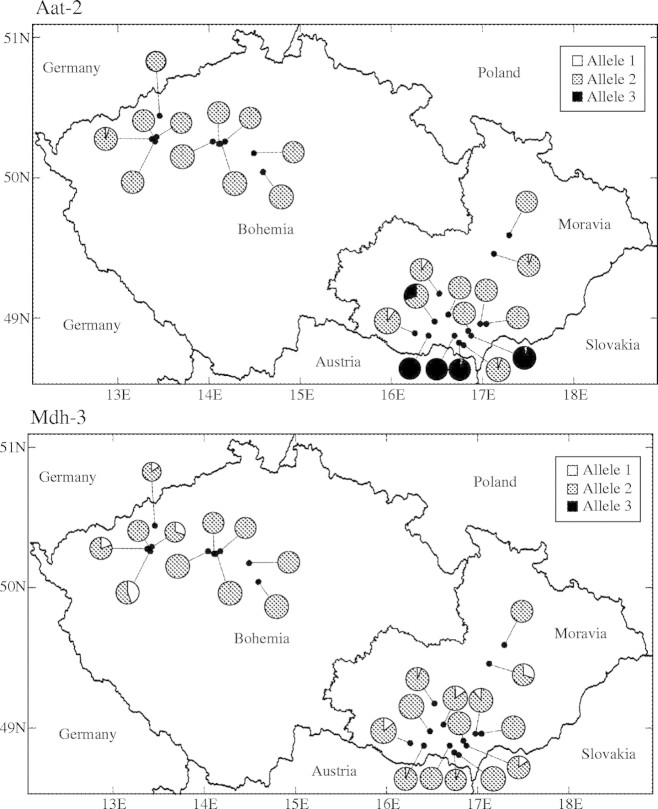
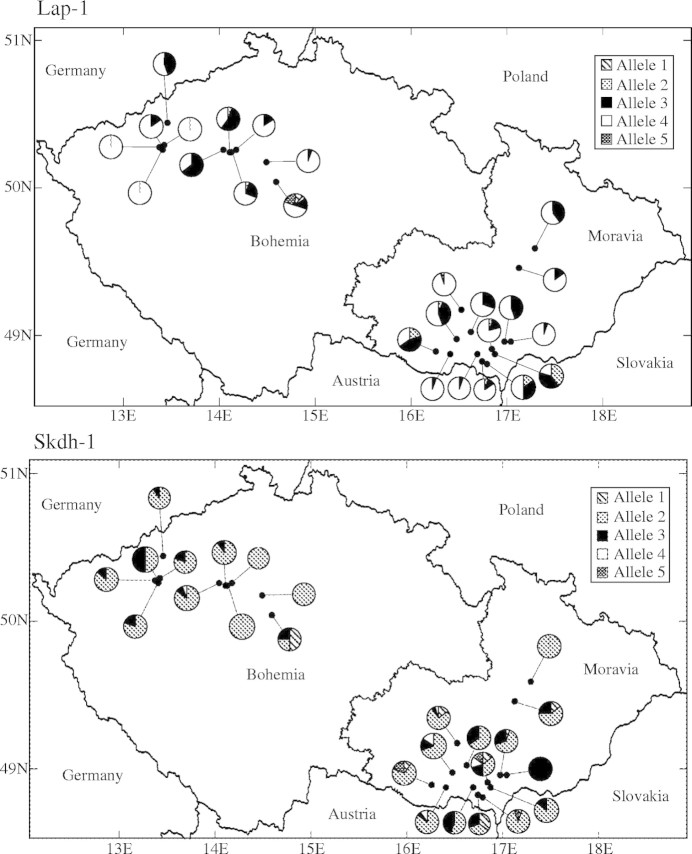
Frequency maps for representative loci (Fig. 2) revealed little variation in allele frequencies between regional populations, a majority of the alleles occurring in all regions and with few alleles completely absent from the Bohemian marginal region. While there was only weak geographical structure in allele frequencies, the average number of alleles per polymorhic locus (A) was negatively correlated with latitude (r_s = −0·40, P = 0·045). Other genetic diversity measures, i.e. percentage of polymorphic locus (PL), observed heterozygosity (H_o), expected heterozygosity (H_e) and Weir and Cockerham's estimate (Cockerham, 1984) of F_IS(f), were not correlated with latitude (r_s = −0·28, P = 0·183; r_s = −0·06, P = 0·758; r_s = −0·03, P = 0·870; r_s = −0·18, P = 0·384, respectively). When the population size was taken into account, no significant correlation was found between population size and A, PL, H_o, H_e and F_IS (f) (data not shown).

Fig. 2.

Allele frequencies at four polymorphic loci (Aat-2, Mdh-3, Lap-1 and Skdh-1) for samples taken from the 25 localities in the Czech Republic.

Hierarchical partitioning of diversity

Estimates of the total genetic diversity (H_T) reached a mean value of 0·196, ranging from 0·103 to 0·434, and the within-population genetic diversity (H_S) reached a mean value 0·156, ranging between 0·053 and 0·347 (Table 2). The between-population component of diversity showed a mean value of 0·208, ranging from 0·051 to 0·789 (Table 2).

Table 2.

Statistics for genetic variation and structure for nine polymorphic loci (enzyme systems AAT, LAP, MDH, SKDH and SOD) identified in 25 Atriplex tatarica populations

	Nei's					Wright's
Locus (alleles)	HT	HS	GST	f(FIT)	f(FIS)	f(FST)	Nm
Lap-1 (5)	0·434	0·347	0·200	0·196*	−0·013	0·207*	0·88
Lap-2 (2)	0·342	0·289	0·153	0·244*	0·101	0·158*	1·23
Sod-3 (2)	0·184	0·168	0·083	0·327*	0·264*	0·086*	2·45
Sod-4 (2)	0·303	0·275	0·093	−0·222	−0·352	0·096*	2·17
Mdh-1 (2)	0·367	0·314	0·146	0·080	−0·084	0·151*	1·30
Mdh-2 (2)	0·103	0·097	0·051	0·961*	0·959*	0·053*	4·12
Mdh-3 (3)	0·155	0·132	0·144	0·178*	0·034	0·150*	1·31
Skdh-1 (5)	0·413	0·346	0·161	0·191*	0·029	0·167*	1·15
Aat-2 (3)	0·253	0·053	0·789	0·832*	0·175	0·796*	0·06
Over all loci	0·196	0·156	0·208	0·239*	0·031	0·214*	0·85

H_T = total genetic diversity for the species; H_S = mean within-population genetic diversity; G_ST = proportion of total genetic diversity among populations; F, f, f = Weir and Cockerham's estimates of Wright's F statistics (F_IT, F_IS and F_ST, respectively), which represents deviations from Hardy–Weinberg expectations over all populations, deviations within individual populations, and the proportion of total genetic diversity partitioned among populations.

N_m was approximated from f using Crow and Aoki's formula (Crow and Aoki, 1984).

^*Significant deviation (P < 0·05) from the null expectation of F = 0.

The mean overall f(F_IS) of 0·031 was not statistically different from zero, only Sod-3 and Mdh-2 exhibiting significant levels of inbreeding (f > 0) (Table 2). f(F_ST) was high (0·214), and significantly different from zero (Table 2), indicating significant genetic differentiation among populations, i.e. 21·4 % of the total genetic variation was due to differences among populations and 78·6 % of the total genetic variability was found within populations. In this case, all individual loci had significant f(F_ST) values. As a consequence, F(F_IT) = 0·239 was significantly positive (Table 2).

Genetic differentiation

To further understand the pattern of inbreeding and differentiation, the 25 populations were divided into two geographic groups (Table 1): Bohemia (localities 1–11) and Moravia (localities 12–25) (Fig. 1). The mean values of f(F_IS) were not significantly different from zero and increased from the geographically marginal populations in Bohemia to populations situated in the area of continuous distribution in Moravia (Table 3). Significant differentiation among populations in both regions was detected. Higher values of f(F_ST) were reached by populations in the area of continuous distribution (Moravia) and lower values were detected in the marginal populations of Bohemia (Table 3).

Table 3.

Nei's and Wright's statistics and estimates of N_m per regions of Atriplex tatarica from Bohemia (1–11) and Moravia (12–25)

	Nei's					Wright's
Region	HT	HS	GST	f(FIT)	f(FIS)	f(FST)	Nm
Bohemia	0·175	0·145	0·172	0·210*	0·029	0·186*	1·01
Moravia	0·208	0·164	0·213	0·251*	0·033	0·225*	0·79

See Table 2 for definitions of the symbols used and Table 1 and Fig. 1 for population locations.

^*Significant deviation (P < 0·05) from the null expectation of F = 0.

The multi locus estimate of the mean number of migrants per generation (N_m) was low (Table 2, average number 0·85), suggesting that gene flow is probably restricted in A. tatarica. In considering both of our geographic regions separately (Table 3), N_m declines from Moravia to Bohemia, suggesting lower levels of gene flow among Moravian populations.

Comparison of the two regions studied revealed significant differences in allelic richness (A), with populations in the area of continuous distribution (Moravia) containing more alleles per polymorphic locus (Table 4). In contrast, there were no significant differences between regions for the observed heterozygosity, gene diversity, or F_IS and F_ST estimates (Table 4), in spite of generally lower values of particular genetic measurements in the marginal region of Bohemia.

Table 4.

Comparison of population polymorphism between Bohemia (n = 11 populations) and Moravia (n = 14

Diversity measure	Bohemia	Moravia	P
A	1·462	1·615	0·032
Ho	0·141	0·159	0·309
Hs	0·145	0·164	0·314
FIS	0·029	0·033	0·947
FST	0·186	0·225	0·629

See Table 2 for definitions of the symbols used and Table 1 and Fig. 1 for population locations.

A = average number of alleles per polymorphic locus, H_o = observed heterozygosity, H_S = gene diversity, F_IS and F_ST are estimated according to Weir and Cockerham (1984).

Probability values for differences between regions are given for two-sided t-test, after 10 000 permutations. Analysis was performed with FSTAT software.

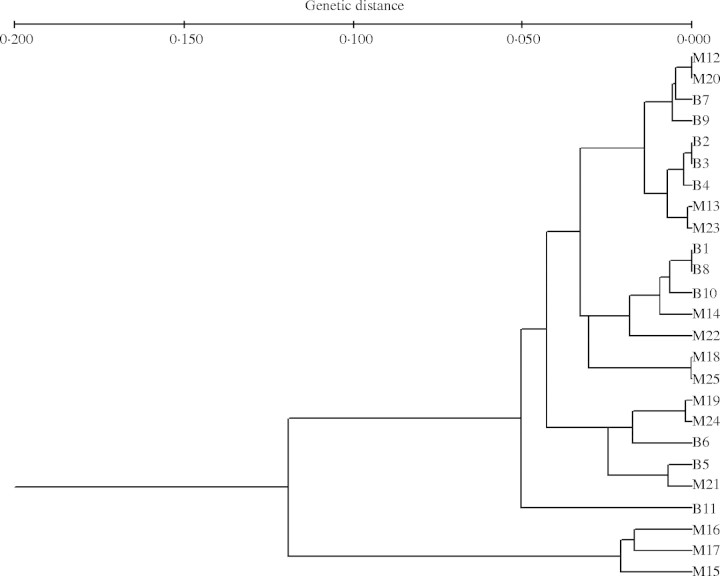
Cluster analysis (Fig. 3), based on Nei's genetic distances (Nei, 1978), did not show any clear geographic structure. There was no consistent association between genetic and geographic distances, as indicated by the Mantel test (r = 0·017, R² = 0·03, P = 0·758), for the whole study area. However, Mantel tests were significant for the Bohemian marginal region (r = 0·356, R² = 0·13, P = 0·009) and non-significant for the Moravian central ones (r = 0·0002, R² = 0, P = 0·999).

Fig. 3.

UPGMA phenogram constructed on the basis of five enzyme systems (AAT, LAP, MDH, SKDH and SOD) using Nei's genetic distances (Nei, 1978) for 25 populations of Atriplex tatarica in the Czech Republic. Populations were coded by region: B, Bohemia; M, Moravia (see Table 1 and Fig. 1 for population locations).

DISCUSSION

The present study investigated genetic diversity at allozyme loci in an annual herb common in human-made habitats, A. tatarica, from a sample of populations through the north-eastern margin of the species' range. The possibility of comparing genetic variation of A. tatarica with other Atriplex species is limited due to the low number of species examined for allozyme diversity. Indeed, the genus Atriplex has been studied with respect to its physiology and ecology (Osmond et al., 1980) much more than for genetic variability, the only published genetic work being on A. halimus in North Africa (Haddioui and Baaziz, 2001). Unfortunately, Atriplex halimus is a perennial desert halophyte species that has been classified as an outcrossing wind-pollinated species on the basis of allozyme data, making it difficult to compare it with annual species of disturbed habitats. Hamrick and Godt (1996) characterized Chenopodiaceae as the species with the lowest percentage of polymorphic loci and genetic diversity within species and the highest amount of genetic diversity found among populations. Although it was stated that ‘genetic diversity and its distribution are more closely associated with individual species’ life history traits than with their phylogenetic status', genetic variation measures are in agreement with a predominant autogamous reproduction mode in Chenopodiaceae, leading to higher population differentiation and lower within-population variability. Hamrick and Godt (1996) further identified mating system and geographical range as important correlates of the levels of genetic variation. Considering both its wide range, from central Europe to central Asia, and mixed mating system, the annual A. tatarica tends to be less variable (H_S = 0·156) than expected based on the estimated mean level of genetic variation in this group (H_S = 0·206; Hamrick and Godt, 1996), and the overall G_ST estimate for A. tatarica (0·208) is higher than that normally found in widespread species with a mixed-mating system (G_ST = 0·169) (Hamrick and Godt, 1996). Based on the regional analysis (Tables 3 and 4), these patterns can be attributed to the deviating estimates for populations in the central region, rather than consistent differences in the structuring of variation between A. tatarica and other widespread species with mixed-mating systems.

Previous work has shown conflicting results as regards the relationship between marginality and measures of within-species variation. Several authors have found marginal populations to be less variable than populations representing more central regions (Mahy et al., 1997; Broyles, 1998; Jorgensen et al., 2002; Griffin and Barrett, 2004; Persson et al., 2004), whereas a number of studies report no or weak effects (e.g. Levin, 1977; Yeh and O'Malley, 1980; Comps et al., 1990; Betancourt et al., 1991; Schiemann et al., 2000).

The populations in the area of continuous distribution of A. tatarica showed significantly higher allelic richness, but observed heterozygosity, gene diversity, and F_IS and F_ST estimates were not significantly higher (Table 4). This result is not surprising, considering the small sizes of the marginal populations and the typical loss of variability in many small isolated populations (Cole, 2003). The significant reduction of A, but non-significant reduction of H_S was predicted by Nei et al. (1975). If population size increases rapidly after going through a bottleneck, the reduction in average heterozygosity is small compared with the reduction in the average number of alleles. This difference occurs mainly because genetic drift eliminates low frequency alleles. However, the pattern of population sub-division showed that populations from central areas are more divergent from each other than those from the marginal area (Table 4). It might be argued that the similarity among the marginal populations has been generated by a single population giving rise to the others in this marginal area. This would seem especially likely if the marginal populations were adjacent to each other and isolated from the central ones as in the case of A. tatarica. The scenario that marginal populations have a greater likelihood of gene flow from central populations than from other adjacent marginal populations has lower probability due to the geographical distance (>200 km) of the central population of A. tatarica. This view is also encouraged by the non-significant correlation between geographical and genetic distances within the whole study area and by the significant result in the case of the Bohemian marginal region as opposed to the Moravian central regions.

Theoretically, repeated founding events associated with metapopulation dynamics may decrease genetic diversity within, and increase genetic differentiation among, local populations (Ingvarsson et al., 1997). These effects will be strongest where the colonists are derived from single rather than multiple demes and where rates of gene exchange among extant demes are low relative to the rates of population turnover (Whitlock and McCauley, 1990).

Atriplex tatarica is a species of early succession stages that does not survive for >3 years due to proceeding ecological succession; therefore, the species has high spatio-temporal variation across its range. The spreading of A. tatarica to new areas, with consequent formation of isolated populations, is probably due to both human building activity, which moves fruits over long distances through transportation of soil, (Mandák, 2003a) and salt treatment of roads in winter, A. tatarica being a facultative halophilic species (Mandák, 2003b) that is able to grow and spread on habitats with higher salt concentrations. Thus, treating roads with salt in winter results in several halophytic species being spread for long distances to climatically less favourable conditions where they survive in salty habitats without surrounding vegetation, forming small isolated populations (Mandák, 2003a). These specific ‘urban’ niches promote the spread of this species and enable it to occupy relatively large areas. The present analysis of population structure of A. tatarica revealed considerable population differentiation at allozyme loci. However, there was no clear geographical clustering of populations in the UPGMA analysis or evidence for isolation-by-distance over the whole study area.

In summary, several conclusions can be drawn from the patterns of genetic variation and structure in A. tatarica. First, A. tatarica, as a species of human-made habitats with a mixed mating system and wide geographic distribution, possesses moderate genetic diversity, which is consistent with the expectation for that type of organism. Secondly, when considering the whole study area, there were no consistent associations between genetic and geographic distances, probably due to occasional long-distance dispersal, disturbance events, or to anthropogenic factors. Thirdly, genetic diversity, with the exception of allelic richness, was not significantly lower at the margins of the species' range, in spite of generally lower values of particular genetic measurements in the marginal region, thus only weakly supporting the predictions of the Central–Marginal Model.