Sensitivity of near-infrared spectroscopy and diffuse correlation spectroscopy to brain hemodynamics: simulations and experimental findings during hypercapnia

Abstract.

Near-infrared spectroscopy (NIRS) and diffuse correlation spectroscopy (DCS) are two diffuse optical technologies for brain imaging that are sensitive to changes in hemoglobin concentrations and blood flow, respectively. Measurements for both modalities are acquired on the scalp, and therefore hemodynamic processes in the extracerebral vasculature confound the interpretation of cortical hemodynamic signals. The sensitivity of NIRS to the brain versus the extracerebral tissue and the contrast-to-noise ratio (CNR) of NIRS to cerebral hemodynamic responses have been well characterized, but the same has not been evaluated for DCS. This is important to assess in order to understand their relative capabilities in measuring cerebral physiological changes. We present Monte Carlo simulations on a head model that demonstrate that the relative brain-to-scalp sensitivity is about three times higher for DCS (0.3 at 3 cm) than for NIRS (0.1 at 3 cm). However, because DCS has higher levels of noise due to photon-counting detection, the CNR is similar for both modalities in response to a physiologically realistic simulation of brain activation. Even so, we also observed higher CNR of the hemodynamic response during graded hypercapnia in adult subjects with DCS than with NIRS.

1. Introduction

Near-infrared spectroscopy (NIRS) and diffuse correlation spectroscopy (DCS) are two noninvasive diffuse optical technologies that provide information about microvascular cerebral hemodynamic processes. NIRS is sensitive to variations in absorption by oxy- and deoxy-hemoglobin of near-infrared light propagating diffusively in the head, providing a measure of cerebral blood volume (CBV) and oxygenation changes.^1–4 DCS uses a long coherence length source and measures the decorrelation time scale of the intensity fluctuations of the multiple-scattered light, which relates to the motion of moving scattering centers, mostly consisting of red blood cells.^5–7 Unlike indocyanine green bolus tracking methods that require the injection of a contrast agent,^8–10 DCS provides a noninvasive and fast measure of blood flow relative changes. It quantifies a blood flow index that has been shown to correlate with cerebral blood flow (CBF) as assessed by other modalities such as transcranial Doppler (TCD) ultrasonography,^11–13 phase-encoded velocity mapping magnetic resonance imaging (MRI),¹⁴ and Xenon-enhanced computed tomography.¹⁵ NIRS, and more recently and sporadically DCS, has been applied to a broad range of functional imaging and monitoring studies, including developmental studies in infants and children,^16–19 cognitive and memory assessment in mental disorders,^20–22 and monitoring of cerebrovascular health in brain injured patients.^15,23–26

Both modalities seek to monitor cortical hemodynamics, but are based on light injection and detection on the surface of the head. As a consequence, while they are sensitive to changes in the cortex, the information of interest from the brain is contaminated by hemodynamic processes in the extracerebral vasculature. However, this extracerebral contamination and the contribution from the brain itself differ between the two modalities, due to different contrast mechanisms (light absorption versus temporal decorrelation) and sensitivity to different physiological parameters (blood volume and oxygenation versus blood flow). Although the sensitivity of NIRS to cerebral physiology and extracerebral contamination has been extensively characterized through modeling and phantom and in vivo experiments (see for instance Refs. ^27–30 for the most recent works), only a few studies have started to investigate the same questions for DCS.^7,31–33

In this study, we compare the sensitivity of continuous-wave (CW) NIRS and DCS to brain hemodynamics. We quantify the sensitivity to brain of both technologies under different physiological conditions, using Monte Carlo simulations, with added empirically derived noise. We show that DCS yields higher sensitivity to brain and less contamination from scalp vasculature, but is also hindered by higher noise levels. These combined effects result in a similar contrast-to-noise ratio (CNR) for both technologies in response to functional activation. Finally, we performed in vivo measurements combining both modalities during graded hypercapnia in adults, and we demonstrated the higher sensitivity of DCS to this physiological event.

2. Methods

2.1. Monte Carlo Simulations

We assessed the sensitivity of NIRS and DCS to cerebral hemodynamics through Monte Carlo simulations on a realistic MRI-based three-dimensional (3-D) head structure. Specifically, we compared two metrics of brain sensitivity at different source-detector (SD) separations. The first metric was the sensitivity to brain and to extracerebral tissue, for a change of blood volume or blood flow occurring in one compartment only. The second metric is the CNR for each modality elicited by a physiologically realistic event, mimicking functional activation or response to hypercapnia.

2.1.1. Head structure and baseline properties

We used a 3-D head structure obtained from an MRI scan of a healthy adult.³⁴ The internal structure was segmented into four tissue types:³⁵ scalp and skull, cerebrospinal fluid (CSF), gray matter, and white matter. These were subsequently combined into two compartments: brain (CSF, gray, and white matters), and extracerebral tissue (scalp and skull), sometimes simply referred to as “scalp” below. For the simulations, unless specified otherwise, the baseline total hemoglobin concentrations were fixed at ${[\mathrm{HbT}]}_{\text{Scalp}}=30\mu \text{M}$ and ${[\mathrm{HbT}]}_{\text{Brain}}=75\mu \text{M}$, in the extracerebral tissue and the brain, respectively, with oxygen saturation set at 65% in both compartments. Different studies in the literature report a wide range of ${[\mathrm{HbT}]}_{\text{Brain}}$ as estimated by time-domain or frequency-domain NIRS, with values as low as 40 μM and as high as 120 μM.^36–39 We chose a value approximately in the middle of this range. Water content was set to 75% in both tissue types.⁴⁰ Using published extinction coefficients for hemoglobin⁴¹ and water,⁴² we obtained the corresponding absorption coefficients at the wavelengths of interest in our experimental data, namely 690 and 830 nm for NIRS and 785 nm for DCS. The resulting optical properties are reported in Table 1. The reduced scattering coefficient was set to $12{\mathrm{cm}}^{-1}$ in the whole head for all wavelengths.

Table 1.

Baseline physiological and optical parameters for the Monte Carlo simulations.

					Optical properties
	Physiology				Scattering ${{\mu }_{\mathrm{s}}}^{\prime }$	Absorption ${\mu }_{\mathrm{a}}$
	[HbT] (μM)	${\mathrm{SO}}_2$ (%)	Water content (%)	Blood flow index (${\mathrm{mm}}^2{\mathrm{s}}^{-1}$)	All $\lambda$ (${\mathrm{cm}}^{-1}$)	690 nm (CW-NIRS) (${\mathrm{cm}}^{-1}$)	785 nm (DCS) (${\mathrm{cm}}^{-1}$)	830 nm (CW-NIRS) (${\mathrm{cm}}^{-1}$)
Scalp	30	65	75	$1\times {10}^{-6}$	12	0.066	0.073	0.082
Brain	75	65	75	$6\times {10}^{-6}$	12	0.159	0.158	0.173

For DCS, it was necessary to assign baseline values for blood flow in the extracerebral and cerebral regions. The flow of moving scatterers can be characterized by the effective Brownian motion coefficient $D_{\mathrm{B}}$, previously shown to best describe the DCS signal.^6,13,31,43 DCS yields a blood flow index $\mathrm{BFI}=\alpha D_{\mathrm{B}}$, where $\alpha$ is the ratio of moving scatterers to total scatterers. BFI is expressed in ${\mathrm{mm}}^2{\mathrm{s}}^{-1}$ and has been demonstrated to correlate well with CBF (traditionally expressed in $\mathrm{mL}/100\mathrm{g}/\min$) as assessed by other modalities.^11–15 Based on positron emission tomography (PET) data in healthy adults,⁴⁴ we used a relative brain-to-scalp flow ratio of 6, with BFI set to ${1\times 10}^{-6}{\mathrm{mm}}^2{\mathrm{s}}^{-1}$ in the extracerebral layer and to ${6\times 10}^{-6}{\mathrm{mm}}^2{\mathrm{s}}^{-1}$ in the brain.

We also investigated the dependence of our results on these baseline parameters. Specifically, we varied the brain baseline total hemoglobin ${[\mathrm{HbT}]}_{\text{Brain}}$ from 50 to 100 μM, with a constant brain-to-scalp blood volume ratio of 2.5. We varied CBF index ${\mathrm{BFI}}_{\text{Brain}}$ from ${2\times 10}^{-6}$ to ${10\times 10}^{-6}{\mathrm{mm}}^2{\mathrm{s}}^{-1}$, with a constant brain-to-scalp blood flow ratio of 6. Finally, at constant baseline cerebral total hemoglobin ${[\mathrm{HbT}]}_{\text{Brain}}=75\mu \text{M}$ and flow ${\mathrm{BFI}}_{\text{Brain}}{=6\times 10}^{-6}{\mathrm{mm}}^2{\mathrm{s}}^{-1}$, we varied the brain-to-scalp baseline blood volume ratio ${[\mathrm{HbT}]}_{\text{Brain}}/{[\mathrm{HbT}]}_{\text{Scalp}}$ from 1 and 4, and the baseline flow ratio ${\mathrm{BFI}}_{\text{Brain},0}/{\mathrm{BFI}}_{\text{Scalp},0}$ from 1 and 10.

2.1.2. Monte Carlo simulations of NIRS and DCS signals

We considered eight probe locations, four on the forehead and four on the left temporal region, each consisting of one source and three aligned detectors approximately 1, 2, and 3 cm away. The precise locations of the optodes were obtained from a larger probe wrapped onto the surface of the head as described in a previous study.⁴⁵ The median values of the true SD direct-line separations, i.e., without following the curvature of the head, were 0.98, 1.96, and 2.94 cm. The true individual direct-line SD separations were used for each subject in the subsequent data analysis.

We used a Monte Carlo code modified in-house from the version described by Boas et al.⁴⁶ The partial pathlength in each tissue type, i.e., “brain” and “scalp,” was recorded for every detected photon, enabling the postprocessing computation of the fluence⁴⁶ at each detector for any absorption coefficient value ${\mu }_{\mathrm{a}j}$ in tissue type $j$. For the simulation of DCS data, we also recorded the total momentum transfer, summed over all scattering events, for each photon.^5,47 This allows the postsimulation computation of the electric field autocorrelation function $g_1(\tau )$, where $\tau$ is the autocorrelation delay for any value of the Brownian diffusion coefficient ${\mathrm{BFI}}_j$ characterizing moving scatterers in tissue type $j$. We launched ${10}^9$ photons at the source, resulting in approximately ${2\times 10}^6$, ${2\times 10}^5$, and ${7\times 10}^4$ photons detected at the three SD separations, respectively.

2.1.3. Sensitivity to scalp and brain

The first metric we computed is the sensitivity of both NIRS and DCS to brain versus extracerebral layers. Specifically, we simulated a true variation in the parameter of interest (blood volume for NIRS, blood flow for DCS) in the brain only, and in the extracerebral tissue only. Next, we fit this simulated data as if it were a semi-infinite medium instead of a layered medium, as is done in our experimental analysis, in order to compute a bulk measured change in the parameter of interest. Finally, we defined the sensitivity to each region (brain and scalp) as the ratio of the measured change over the true change. We also studied the relative brain-to-scalp sensitivity $S_{\text{Brain}/\text{Scalp}}$, defined as the ratio of sensitivities to both compartments.

For NIRS, we independently simulated in each tissue type (brain or scalp) a 5% increase in blood volume with no change in oxygen saturation, so that ${\mathrm{\Delta }[\mathrm{HbT}]}_{\mathrm{Tiss}}/{[\mathrm{HbT}]}_{0,\mathrm{Tiss}}{=\mathrm{\Delta }[\mathrm{HbO}]}_{\mathrm{Tiss}}/{[\mathrm{HbO}]}_{0,\mathrm{Tiss}}{=\mathrm{\Delta }[\mathrm{HbR}]}_{\mathrm{Tiss}}/{[\mathrm{HbR}]}_{0,\mathrm{Tiss}}$, where ${[\mathrm{HbT}]}_0$, ${[\mathrm{HbO}]}_0$, and ${[\mathrm{HbR}]}_0$ are the baseline concentrations in total, oxy-, and deoxy-hemoglobin, respectively, and $\mathrm{\Delta }[\mathrm{HbT}]$, $\mathrm{\Delta }[\mathrm{HbO}]$, and $\mathrm{\Delta }[\mathrm{HbR}]$ are their corresponding absolute changes from baseline. We computed the corresponding change in measured optical density at the two wavelengths of interest for the NIRS signal, i.e., 690 and 830 nm. Finally, using the modified Beer–Lambert law,^48,49 we retrieved the measured changes ${\mathrm{\Delta }}_{\mathrm{m}}{[\mathrm{HbT}]}_{\text{Brain}}$ and ${\mathrm{\Delta }}_{\mathrm{m}}{[\mathrm{HbT}]}_{\text{Scalp}}$ in [HbT], for a brain-only change and for a scalp-only change, respectively. We used differential pathlength factors (DPFs) of 6.5 at 1 cm, 7 at 2 cm, and 7.5 at 3 cm, at both wavelengths. These values were obtained from the Monte Carlo simulations as the average of the true DPF over all probe locations, for the default baseline optical properties. The NIRS sensitivity to brain $S_{\mathrm{CW},\text{Brain}}$ and to scalp $S_{\mathrm{CW},\text{Scalp}}$ was finally computed as $S_{\mathrm{CW},\text{Brain}}={\mathrm{\Delta }}_{\mathrm{m}}{[\mathrm{HbT}]}_{\text{Brain}}/\mathrm{\Delta }{[\mathrm{HbT}]}_{\text{Brain}}$ and $S_{\mathrm{CW},\text{Scalp}}{=\mathrm{\Delta }}_{\mathrm{m}}{[\mathrm{HbT}]}_{\text{Scalp}}/\mathrm{\Delta }{[\mathrm{HbT}]}_{\text{Scalp}}$.

For DCS, we simulated a true 20% relative increase in blood flow ${r\mathrm{BFI}}_{,\mathrm{Tiss}}=\mathrm{\Delta }{\mathrm{BFI}}_{\mathrm{Tiss}}/{\mathrm{BFI}}_{0,\mathrm{Tiss}}$ in the brain or in the scalp only. We fit the resulting $g_1(\tau )$ curve with the analytical solution of the correlation diffusion equation for a semi-infinite homogeneous medium,⁵ at each SD separation independently, at baseline and after the flow increase. This resulted in the measured blood flow index relative change $r_{\mathrm{m}}\mathrm{BFI}$. The sensitivities to brain and to scalp for DCS were defined as $S_{\mathrm{DCS},\text{Brain}}=r_{\mathrm{m}}{\mathrm{BFI}}_{\text{Brain}}/r{\mathrm{BFI}}_{\text{Brain}}$, and $S_{\mathrm{DCS},\text{Scalp}}=r_{\mathrm{m}}{\mathrm{BFI}}_{\text{Scalp}}/r{\mathrm{BFI}}_{\text{Scalp}}$. Additionally, we compared the sensitivity of DCS when fitting the whole autocorrelation curve (maximal delay ${\tau }_{\mathrm{Max}}=10\mathrm{ms}$), or only the early delays, as illustrated in the insets of Fig. 1. For the latter, we restricted the fit to the early portion of the curve for which the normalized function $g_1(\tau )$ was greater than 0.7. Restricting the fit to the early delays $\tau$ is known to give more weight to longer photon pathlengths and to higher blood flow, therefore increasing the cerebral contribution to the signal.¹⁴

Fig. 1.

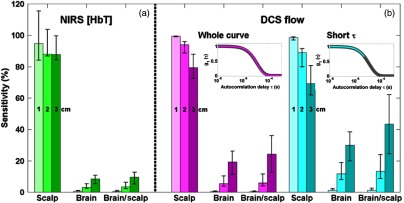
Sensitivity of near-infrared spectroscopy (NIRS) (a) and diffuse correlation spectroscopy (DCS) (b) as simulated with Monte Carlo simulations on an MRI-based head structure, for source–detector separations of 1, 2, and 3 cm. We present the sensitivity to scalp (measured-over-true scalp change), sensitivity to brain (measured-over-true brain change), and the relative brain-to-scalp sensitivity. The NIRS sensitivity is based on a blood volume change only, and that of DCS is based on a blood flow change only. For DCS, we present the cases where the whole autocorrelation curve $g_1(\tau )$ is fit (magenta, see first inset), and when only the early delays corresponding to $g_1(\tau )>0.7$ are fit (cyan, see second inset). In all cases (NIRS and DCS), the reconstruction is done using a homogeneous semi-infinite model. The bar heights present the median value across all eight probe locations, and the error bars extend from the 25th to 75th percentile of the values.

For all sensitivities, we present the median, and 25th and 75th percentiles of the data over the eight probe locations.

2.1.4. Contrast-to-noise ratio

Our second metric is the CNR for a physiologically realistic change in CBF and volume. We chose two representative physiological activations, namely functional activation and hypercapnia.

Physiological change—functional activation

We simulated a functional activation by inducing a 50% increase in CBF from baseline ${\mathrm{CBF}}_0$ and a 20% increase in cerebral metabolic rate of oxygen (${\mathrm{CMRO}}_2$), corresponding to a flow-consumption ratio of 2.5. This value was chosen to fall within the range of 2 to 4 typically reported in the PET and fMRI literature,⁵⁰ with values as low as 1.5 observed by NIRS approaches.^16,51 We estimated the corresponding change in CBV using the Grubb relationship:⁵² $\mathrm{CBV}/{\mathrm{CBV}}_0={(\mathrm{CBF}/{\mathrm{CBF}}_0)}^{\alpha }$. The Grubb’s coefficient $\alpha$ was set to 0.25,^53–56 resulting in an 11% increase in CBV. To estimate the corresponding changes in [HbO] and [HbR], we used the expression of Mayhew et al.⁵⁷ for relative changes in the cerebral metabolic rate of oxygen ${\mathrm{CMRO}}_2$, under the approximation that arterial saturation ${\mathrm{SaO}}_2=1$:

$$1+\frac{\mathrm{\Delta }{\mathrm{CMRO}}_2}{{\mathrm{CMRO}}_{2,0}}=(1+\frac{\mathrm{\Delta }\mathrm{CBF}}{{\mathrm{CBF}}_0})(1+{\gamma }_{\mathrm{R}}\frac{\mathrm{\Delta }[\mathrm{HbR}]}{{[\mathrm{HbR}]}_0}){(1+{\gamma }_{\mathrm{T}}\frac{\mathrm{\Delta }[\mathrm{HbT}]}{{[\mathrm{HbT}]}_0})}^{-1},$$

where ${\gamma }_{\mathrm{R}}$ and ${\gamma }_{\mathrm{T}}$ factors relate the fractional changes in deoxy- and total hemoglobin, respectively, in the venous compartment to those across all vascular compartments. For simplification, we used ${\gamma }_{\mathrm{R}}={\gamma }_{\mathrm{T}}=1$. We, therefore, simulated the following changes: $\mathrm{\Delta }[\mathrm{HbO}]=+11\mu \text{M\hspace{0.17em}}(+23\%)$, $\mathrm{\Delta }[\mathrm{HbR}]=-3\mu \text{M\hspace{0.17em}}(-11\%)$, and $\mathrm{\Delta }[\mathrm{HbT}]=+8\mu \text{M\hspace{0.17em}}(+11\%)$.

Physiological change—hypercapnia

The hemodynamic response to hypercapnia, i.e., to an increase in the fraction of inspired ${\mathrm{CO}}_2$ to approximately 5%, was simulated with the same model as above, but assuming a 60% increase in CBF, and no change in ${\mathrm{CMRO}}_2$. Hypercapnia is widely believed in the fMRI community to induce purely vascular effects without metabolic changes for inspired ${\mathrm{CO}}_2$ concentrations of 5% or less.^58,59 Under this assumption, we simulated $\mathrm{\Delta }[\mathrm{HbO}]=+17\mu \text{M\hspace{0.17em}}(+35\%)$, $\mathrm{\Delta }[\mathrm{HbR}]=-8\mu \text{M\hspace{0.17em}}(-30\%)$, and $\mathrm{\Delta }[\mathrm{HbT}]=+9\mu \text{M}(+12\%)$. The CBF and CBV increases we simulate are consistent with the values reported by Chen and Pike,⁵⁶ where a moderate hypercapnic event (end-tidal ${\mathrm{CO}}_2$ elevated 9 mm Hg above baseline) resulted in a 65% increase in CBF and a 12% increase in CBV, as assessed by MRI modalities.

NIRS contrast and noise

The NIRS contrast was defined as the retrieved changes in oxy-, deoxy-, and total hemoglobin concentrations, ${\mathrm{\Delta }}_{\mathrm{m}}{[\mathrm{HbO}]}_{\text{Brain}}$, ${\mathrm{\Delta }}_{\mathrm{m}}{[\mathrm{HbR}]}_{\text{Brain}}$, and ${\mathrm{\Delta }}_{\mathrm{m}}{[\mathrm{HbT}]}_{\text{Brain}}$, respectively, using the modified Beer–Lambert law at each separation independently, with the same DPFs described before. We estimated the NIRS noise using experimental data obtained on the forehead of four subjects during two 10 min resting runs. The signal was bandpass filtered between 0.05 and 0.5 Hz to remove high frequency instrumental noise, the cardiac pulse, and low frequency instrumental drifts and physiological oscillations. The noise for each hemoglobin species was quantified as the median, over all runs, of the standard deviation of their time traces. Note that our estimation of noise therefore includes both instrumental and physiological sources. The resulting noise levels were 0.30, 0.25, and 0.20 μM on [HbO] and [HbT] for separations of 1, 2, and 3 cm, respectively, and 0.05 μM on [HbR] at all separations.

DCS contrast and noise

For DCS, the autocorrelation curve was simulated at all SD separations for the baseline flow and for the flow increase, also taking into account the increase in absorption due to hemoglobin concentration changes. Each curve was fit with the analytical solution of the electric field autocorrelation diffusion equation for a semi-infinite medium,^5,60 and the contrast was defined as the measured relative change in retrieved BFI. As before we compared fitting the whole autocorrelation curve, or only the early delay [$g_1(\tau )>0.7$]. Similar to NIRS, we estimated the noise on the DCS signal using experimental recordings during the same resting runs described above. The autocorrelation curves were integrated over 2 s, and then further averaged over three time points for an effective integration time of 6 s. The retrieved BFI time series were high-pass filtered at 0.05 Hz. The DCS noise was defined as the median over all runs of the standard deviation of BFI normalized by its mean. This resulted in a noise level of approximately 3%, 4%, and 5% at 1, 2, and 3 cm, respectively, increasing to 3%, 7%, and 10% when considering only the early correlation times.

2.2. In Vivo Human Measurements During Hypercapnia

Data were collected on adult subjects as part of another study (results not yet published). We report here the results on a subset of four subjects who were measured simultaneously with NIRS and DCS with good signal quality. The study was approved by the Partners Healthcare Institutional Review Board, and all subjects provided written informed consent to participate in the study before data acquisition.

2.2.1. Protocol

CW-NIRS and DCS data were simultaneously acquired on all subjects. For the NIRS measurements, we used a laser-diode based TechEn device (TechEn Inc., Medford, Massachusetts). The NIRS probe was located on the left side of the forehead, and consisted of one source (690 and 830 nm) and two detectors along a line at 0.8 and 3 cm. The NIRS data were acquired at 50 Hz. The DCS device is custom-built with one 785-nm long coherence length laser source (CrystaLaser, Reno, Nevada) and eight single photon counting avalanche photodiode detection channels (PerkinElmer/Excelitas, Waltham, Massachusetts, SPCM-AQRH series).^6,60 The DCS probe was located on the right side of the forehead and consisted of one source and two detection locations along a line at 0.8 and 3 cm. Seven single-mode fibers were bundled together and placed at the 3 cm separation in order to improve the signal-to-noise ratio at this location. The DCS autocorrelation curves were acquired over an integration time of 2 s.

The recordings analyzed in this study were part of a longer protocol that we do not describe here. Relevant to this study is the hypercapnic runs. The subjects breathed through a mouthpiece connected to a specialized breathing circuit that minimized spontaneous breath-to-breath fluctuations in end-tidal ${\mathrm{CO}}_2$.⁶¹ End-tidal ${\mathrm{CO}}_2$ (${\mathrm{etCO}}_2$) was monitored continuously, and recorded synchronously with the optical data. Periods of hypercapnia were achieved by adding ${\mathrm{CO}}_2$ to the inspired air. Each subject underwent two 11-min trials that comprised six hypercapnic episodes during each trial. Each hypercapnic episode was sustained for 30 s, during which inspired ${\mathrm{CO}}_2$ was briskly increased to elevate ${\mathrm{etCO}}_2$ to either 4 or 8 mm Hg above each subject’s habitual baseline ${\mathrm{etCO}}_2$, in a predefined order (4-4-8-4-8-8 mm Hg). Each hypercapnic episode of 4 and 8 mm Hg was followed by a recovery/wash-out period of 60 and 90 s, respectively.

2.2.2. Data analysis

From the NIRS intensities at 690 and 830 nm for both SD pairs, we computed the relative changes in optical density at each wavelength, applied a wavelet motion correction algorithm,⁶² low-pass filtered the motion-corrected optical density at 0.5 Hz, and converted them to relative changes in oxy- and deoxy-hemoglobin using the modified Beer–Lambert law. We used a DPF of 6 at both separations and both wavelengths. We did not apply any partial volume correction factor. Finally, we applied a 6-s sliding window averaging of the hemoglobin time series for consistency with the temporal processing of the DCS data described below.

For DCS, a weighted average of the seven autocorrelation curves for the 3 cm SD separation was computed, using weights equal to the integrated intensities of the DCS signal for each fiber. The DCS autocorrelation curves were further averaged using a moving window of 6 s (three curves) prior to fitting. This resulted in two time series of autocorrelation curves, for 0.8 and 3 cm. The intensity autocorrelation curves were fit at each time point with the analytical solution of the correlation diffusion equation for a semi-infinite homogeneous medium. We fixed the unknown absorption and reduced scattering coefficient values to ${\mu }_{\mathrm{a}}=0.15{\mathrm{cm}}^{-1}$ and ${{\mu }_{\mathrm{s}}}^{\prime }=10{\mathrm{cm}}^{-1}$, respectively. We compared three different delay ranges: $g_1{(\tau )}^2>0.01$, $g_1{(\tau )}^2>0.1$, and $g_1{(\tau )}^2>0.5$ [i.e., $g_1(\tau )>0.1$, $g_1(\tau )>0.3$, and $g_1(\tau )>0.7$, respectively). The whole intensity autocorrelation curve $g_2(\tau )=1+\beta$. $g_1{(\tau )}^2$ was first fitted, then the threshold delay was computed on the fitted $g_1{(\tau )}^2$ curve to reduce noise. Time points for which the short separation curve fit resulted in a $R^2$ below 0.95 were discarded from the time series. The resulting BFI time traces were interpolated to the same time points as the NIRS signal before further analysis.

We computed the hemodynamic response function (HRF) to the hypercapnic episodes for each modality and each hypercapnic strength (4 and 8 mm Hg). The time of onset of each hypercapnic event was manually identified on the ${\mathrm{etCO}}_2$ time traces. Block averages over a period of $-20$ to $+85\mathrm{s}$ from stimuli onsets of both runs were performed on [HbO], [HbR], and [HbT] for NIRS, and on relative changes in BFI for DCS. At each time point, we also computed the standard deviation of the signal over the six successive blocks of a specific hypercapnic strength. We computed the CNR of the 4- and 8-mm Hg HRFs for each subject. The contrast was defined as the change in the block-averaged signal between a baseline period (time $-20$ to 0 s from hypercapnia onset), and an “active” period (time $+45$ to $+65\mathrm{s}$ from onset). The noise was defined as the average of the HRF standard deviation over all time points.

3. Results

3.1. Monte Carlo Simulations

3.1.1. Sensitivity to brain and scalp

The sensitivity to brain and scalp obtained from the Monte Carlo computations are shown in Fig. 1, where the bar height is the median, and the error bars extend from 25th to 75th percentile of the values over all eight simulated probe locations. The NIRS sensitivities at 1, 2, and 3 cm are 95%, 88%, and 88%, respectively, for scalp, and 0.6%, 3%, and 8% for brain. This results in brain-to-scalp sensitivities of 0.7%, 4%, and 10% at these same separations. For DCS, the sensitivities to scalp when fitting the whole autocorrelation curve are 100%, 94%, and 80%, and the sensitivities to brain are 0.4%, 6%, and 19%, resulting in relative brain-to-scalp sensitivities of 0.4%, 6%, and 24%. When fitting only the early portion of the curve [$g_1(\tau )>0.7$], the DCS sensitivity to scalp decreases to 99%, 89%, and 69%, and the sensitivity to brain increases to 1%, 12%, and 30%, resulting in higher brain-to-scalp sensitivities of 1%, 13%, and 43% at the three separations.

The NIRS Monte Carlo simulations rely on the Beer–Lambert law, which assumes a linear relationship between the optical density change and the absorption change. This assumption holds true for small variations in blood volume. For our computation, we used a 5% increase in blood volume, but the resulting sensitivity to brain and scalp is independent of this value. Note that, at each wavelength, the relative sensitivity to brain and scalp is simply the ratio of the partial pathlengths in both tissue types. Our computations are performed for the sensitivity in HbT, incorporating two wavelengths, as opposed to optical density sensitivity at a single wavelength. For comparison, the brain-to-scalp ratios of partial pathlengths at these same separations were 0.9%, 4%, and 10% at 690 nm, and 0.7%, 3%, and 9% at 830 nm.

Contrary to the NIRS signal simulations, the DCS signal has a nonlinear dependence on blood flow changes, and the sensitivity to each compartment depends weakly on the amplitude of the flow change. In particular, the relative contribution of scalp is slightly stronger for higher relative flow changes in the brain. The results of Fig. 1 correspond to a 20% increase in CBF, but the orders of magnitude of the sensitivities remain the same for a large range of relative flow increase. Specifically, we tested CBF increases of 1% and 100%, and the brain sensitivity varied from 0.4% to 0.3% at 1 cm, 6% to 5% at 2 cm, and 20% to 17% at 3 cm, while the scalp sensitivity varied from 100% to 100% at 1 cm, 94% to 93% at 2 cm, and 80% to 78% at 3 cm (data not shown).

Figure 2 shows the dependence of the sensitivities of both modalities on the baseline parameters. At a constant brain-to-scalp blood volume ratio, the sensitivity to brain of both NIRS and DCS decreases with increasing brain blood volume (Fig. 2, column 1). This can be intuitively understood by the increased absorption of the whole head, which reduces the depth of photon penetration and, therefore, the sensitivity to the brain. Note that at low CBV, NIRS presents a sensitivity to scalp above 100% for the 1 cm SD separation. This can be simply explained by the fact that we kept the same DPF as was computed for ${[\mathrm{HbT}]}_{\text{Brain}}=75\mu \text{M}$. Changes in the scalp are, therefore, slightly overestimated because the DPF is slightly underestimated. However, the choice of DPF has no effect on the relative brain-to-scalp sensitivity. For DCS, we do not correct for the change of absorption due to blood volume change in the autocorrelation fits, i.e., we assume constant absorption. For cerebral total hemoglobin increasing from 40 to 120 μM, the relative brain-to-scalp sensitivity is approximately divided by two for both modalities.

Fig. 2.

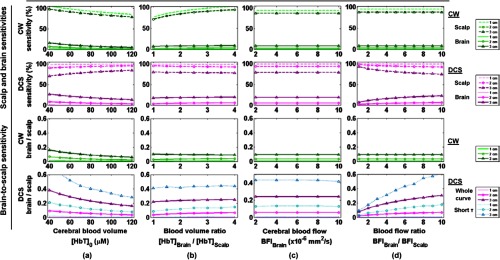
Dependence on the baseline physiological parameters of NIRS and DCS sensitivities: (a) varying CBV, at constant brain-to-scalp volume $\text{ratio}=2.5$; (b) varying brain-to-scalp volume ratio, at constant $\mathrm{CBV}=75\mu \text{M}$; (c) varying CBF, at constant brain-to-scalp $\text{flow ratio}=6$; (d) varying brain-to-scalp flow ratio, at constant ${\mathrm{CBF}=6\times 10}^6{\mathrm{mm}}^2{\mathrm{s}}^{-1}$. The dotted lines show the sensitivity to scalp, and the solid lines the sensitivity to brain. For DCS brain-to-scalp sensitivity, we present the results when the whole autocorrelation curve is fit (thick magenta lines), and when only the early delays corresponding to $g_1(\tau )>0.7$ are included (thin cyan lines).

At constant CBV (${[\mathrm{HbT}]}_{\text{Brain}}=75\mu \text{M}$), varying the brain-to-scalp blood volume ratio from 1 to 4 (i.e., decreasing the scalp blood volume from 75 to 18.8 μM) slightly increases the sensitivity of NIRS to both scalp and brain (Fig. 2, column 2). For DCS, the sensitivity to scalp slightly increases and that to brain slightly increases. The resulting impact of decreasing scalp blood volume depends on the SD separation for NIRS: at 1 and 2 cm, the relative brain-to-scalp sensitivity increases from 0.3% to 0.9% and from 2.6% to 3.9%, respectively, while at 3 cm it decreases slightly from 10% to 9%. For DCS, the effect of decreasing the scalp blood volume is a slight increase in the relative scalp-to-brain sensitivity.

For a constant brain-to-scalp blood flow ratio of 6, varying the baseline CBF has no effect on the sensitivity of NIRS to cerebral or extracerebral layers (Fig. 2, column 3). This is expected since the sensitivity of this modality depends solely on scattering and absorption properties, and not flow parameters. The variation of baseline CBF also has a negligible effect on the sensitivity of DCS to brain and scalp, provided that the brain-to-scalp flow ratio is kept constant.

Similarly, at constant CBF, varying the scalp flow has no effect on NIRS sensitivity (Fig. 2, column 4). On the contrary, the sensitivity of DCS to scalp and brain depends strongly on their relative flow values. As an example, at a typical SD separation of 3 cm, the relative brain-to-scalp sensitivity is only 8% for identical baseline flows in both compartments. In contrast, when considering a brain flow 10 times that of scalp, the relative brain-to-scalp sensitivity increases almost four times, up to 30%. This relative brain-to-scalp sensitivity further increases to 48% when fitting only the early portion of the autocorrelation curves.

3.1.2. Contrast-to-noise ratio

Figure 3 shows the contrast and CNR of both modalities in response to a simulated functional activation and to hypercapnia. We simulated a similar flow change in both cases, 50% and 60% CBF increase, respectively, which leads to a similar DCS contrast: for the 3 cm channel, a flow increase of about 10% is detected (when taking into account the absorption change in the autocorrelation fitting). When this change in absorption is not taken into account, the retrieved change in flow decreases from 10% to 6.5% for both physiological events (data not shown). Similarly, the modeled increase in CBV being almost identical for both physiological events, the NIRS contrast on [HbT] is identical in both cases, with a detected increase of approximately 0.25 μM at 3 cm. On the contrary, the contrast on [HbO] and [HbR] differs between the simulated functional activation and hypercapnia because oxygen consumption increases during functional activation but not during hypercapnia. For the functional activation, the measured increase in [HbO] ($+0.38\mu \text{M}$ at 3 cm) is three to four times the amplitude of the [HbR] decrease ($-0.11\mu \text{M}$ at 3 cm). In contrast, in the case of hypercapnia, the measured [HbO] increase ($+0.62\mu \text{M}$ at 3 cm) is only twice the amplitude of the [HbR] decrease ($-0.33\mu \text{M}$ at 3 cm).

Fig. 3.

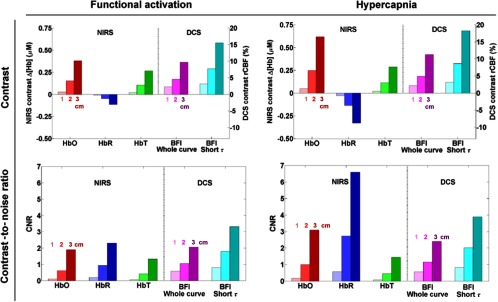
Monte Carlo simulations of the contrast (top) and CNR (bottom) of NIRS and DCS, in response to functional activation (left) and hypercapnia (right). The bar heights show the median value across the eight probe locations. For each parameter, the three bars of increased darkness in the same color show the results at 1, 2, and 3 cm, respectively. For DCS, we present the cases where the whole autocorrelation curve $g_1(\tau )$ is fit (magenta), and when only the early delays corresponding to $g_1(\tau )>0.7$ are fit (cyan).

When considering the NIRS and DCS noise levels, we find a very similar CNR for both modalities during cerebral activation. Specifically, the CNR on [HbO] ($\mathrm{CNR}=1.9$ at 3 cm), [HbR] ($\mathrm{CNR}=2.3$ at 3 cm), and BFI ($\mathrm{CNR}=2.1$ at 3 cm) are all within 20% of each other, with a slight advantage to [HbR]. Because of lower contrast on [HbT], the resulting CNR is also lower ($\mathrm{CNR}=1.3$ at 3 cm).

For the simulated hypercapnia, our model results in high CNR on [HbR] ($\mathrm{CNR}=6$ at 3 cm), two times larger than that for [HbO] ($\mathrm{CNR}=3$) and four times larger than that for [HbT] ($\mathrm{CNR}=1.5$). The CNR on the DCS retrieved flow ($\mathrm{CNR}=2.5$ at 3 cm) is similar to that on [HbO] and lower than that of [HbR].

3.2. In Vivo Human Measurements During Hypercapnia

3.2.1. End-tidal ${\mathsf{C}\mathsf{O}}_{\mathsf{2}}$ data

Table 2 shows, for each subject, the mean increase in ${\mathrm{etCO}}_2$ from their individual baseline, across all 4 and 8 mm Hg hypercapnic episodes. The ${\mathrm{etCO}}_2$ increase as manually identified on the ${\mathrm{etCO}}_2$ time traces is slightly higher than the targeted values.

Table 2.

Mean increase in end-tidal ${\mathrm{CO}}_2$ for each subject from their individual baseline, as manually identified on the ${\mathrm{etCO}}_2$ time traces.

	Target: 4 mm Hg	Target: 8 mm Hg
Subject 1	5.1 mm Hg	8.6 mm Hg
Subject 2	5.1 mm Hg	8.6 mm Hg
Subject 3	4.2 mm Hg	8.1 mm Hg
Subject 4	5.9 mm Hg	10.2 mm Hg

3.2.2. Hemodynamic response functions

Figure 4 shows the hemodynamic response we observed with NIRS (upper row) and with DCS (lower row) on subject 1, after independently block-averaging all 4 mm Hg events (left) and all 8 mm Hg events (right). For DCS, the three curves were obtained with the three different ranges of delays corresponding to $g_1{(\tau )}^2>0.01$, $g_1{(\tau )}^2>0.1$, and $g_1{(\tau )}^2>0.5$. For this subject, we observed a response with both modalities at 3 cm to both grades of hypercapnia, specifically an increase in blood flow as measured with DCS, as well as a decrease in [HbR] and increase in [HbO] as measured by CW-NIRS. No significant change in [HbT] was detected. The changes are qualitatively identical for both hypercapnic strengths but present higher amplitude at 8 mm Hg.

Fig. 4.

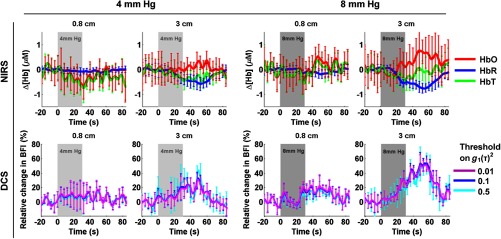
Hemodynamic response function (HRF) to hypercapnia measured in subject 1, with NIRS (top) and DCS (bottom). The targeted hypercapnia duration is indicated with the shaded gray area. For DCS, the three colors indicate different range of delays included in the fit, corresponding to different thresholds on $g_1{(\tau )}^2$ (0.01, 0.1, and 0.5).

Figure 5 displays the HRF at 3 cm for the 8 mm Hg hypercapnia for all four subjects. Although an increase in flow was detected by DCS in all subjects (bottom row), albeit with varying amplitude, changes in the NIRS signals were not consistently observed (top row). In fact, while two subjects show the expected response described above, one subject displays the inverse response (decrease in [HbO] and small increase in [HbR]) and the CNR in one subject was too low to observe any hemoglobin change.

Fig. 5.

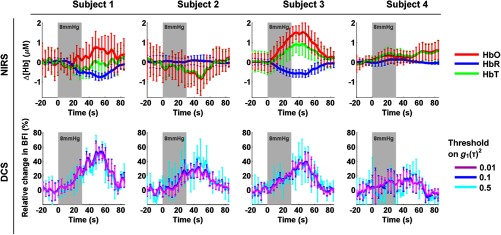
NIRS and DCS HRF to hypercapnia (8 mm Hg above baseline) measured at 3 cm for all four subjects.

3.2.3. Contrast and contrast-to-noise ratio

Figure 6(a) reports the median contrast for both modalities over the four subjects. For the 4 mm Hg hypercapnia, we observed an increase in blood flow at 0.8 and 3 cm of 9% and 15%, respectively, an increase in [HbO] of $+0.23$ and $+0.44\mu \text{M}$, a decrease in [HbR] of $-0.11$ and $-0.29\mu \text{M}$, and a small increase in HbT of $+0.14$ and $+0.17\mu \text{M}$. For the 8 mm Hg hypercapnia, we observed increase an in blood flow at 0.8 and 3 cm of 11% and 27%, respectively, an increase in [HbO] of $+0.08$ and $+0.25\mu \text{M}$, a decrease in [HbR] of $-0.07$ and $-0.25\mu \text{M}$, and a small increase in [HbT] of $+0.01$ and $+0.03\mu \text{M}$. For both hypercapnia responses, when fitting only the early portion of the autocorrelation curves, the flow response decreases slightly at 0.8 cm and increases slightly at 3 cm.

Fig. 6.

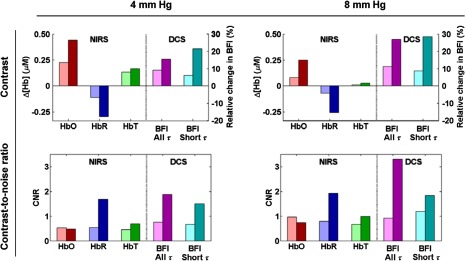
Median across four subjects of contrast (top) and CNR (bottom) of the HRF to 4 mm Hg hypercapnia (left) and 8 mm Hg hypercapnia (right). For each parameter, we present the results at 0.8 cm (light color) and at 3 cm (dark color). The DCS results are presented for two different ranges of delays incorporated in the fit, corresponding to two thresholds of the autocorrelation curve: $g_1{(\tau )}^2>0.01$ (“All $\tau$,” magenta), and $g_1{(\tau )}^2>0.5$ (“Short $\tau$,” cyan).

The corresponding median CNR is shown in Fig. 6(b). For both hypercapnic strengths, the CNR was low ($<1$) for HbO and HbT at both separations, as well as for the 0.8 cm HbR signal and DCS signal. In contrast, at the long 3 cm separation, the CNR on [HbR] was almost 2 at both hypercapnic strengths, and the CNR on flow was about 2 for 4 mm Hg and above 3 for 8 mm Hg. Even though the contrast itself was slightly increased when fitting only the early portion of the curve [$g_1{(\tau )}^2>0.5$], the CNR on the 3 cm DCS blood flow nonetheless decreased to about 1.5 and 1.8 for 4 and 8 mm Hg, respectively, because of increased noise.

4. Discussion

4.1. DCS Sensitivity to Brain and Extracerebral Tissue

From our simulations, we find that the sensitivity of DCS to the extracerebral layers decreases with the SD separation, from almost 100% at 1 cm, down to 80% and 70% at 3 cm for the whole autocorrelation curve and the early correlation times only, respectively. This is in contrast to the NIRS sensitivity to extracerebral layers which is almost constant around 90% at all SD separations. Conversely, we find that the DCS sensitivity to brain increases more sharply with an SD separation than that of NIRS, from a few percent at 1 cm, up to 20% and 30% at 3 cm for the whole curve and the early curve, respectively.

It is interesting to compare these results to the approach described by Mesquita et al. to experimentally estimate the extracerebral contribution to the DCS signal.⁶³ By increasing the pressure of the DCS probe on the forehead, they decrease the inflow of blood under the probe. It is assumed that the extracerebral flow contribution to the signal will reduce to zero at a sufficiently high pressure. Although they use a semi-infinite homogeneous model of light propagation to recover the blood flow index, they further describe this flow as the sum of two terms: a pressure-dependent and separation-independent contribution from the extracerebral layer, and a pressure-independent but separation-dependent contribution from the brain. With this model applied to in vivo data, they estimate the absolute brain blood flow contribution to the signal to be about 3%, 9%, and 40% at 0.5, 1.5, and 2.5 cm, which is reasonably close to our values. Although they model the contribution of the extracerebral layer to be independent of SD separation, this is not supported by their experimental results, which show a decrease of the superficial contribution to the signal with separation, in agreement with our simulated data.

4.2. Higher Sensitivity to Brain of DCS Compared to NIRS

According to our simulation results, for the same 3 cm SD separation, DCS retrieves a higher fraction of the true brain hemodynamics changes than NIRS. Conversely, DCS is less sensitive to extracerebral changes than NIRS. As a result, the relative brain-to-scalp sensitivity of DCS is about three times that of NIRS at a 3 cm SD separation, for a brain-to-scalp flow ratio of 6.

This higher sensitivity of DCS can be intuitively understood by examining the contrast mechanism of the two technologies. The NIRS signal arises from the absorption of light by hemoglobin, while the DCS signal arises from the momentum transfer accumulated by photons scattering from moving red blood cells along their trajectories. Therefore, photons with long pathlengths, i.e., those with a higher probability of reaching the brain, contribute little to the NIRS signal as they are more likely to be absorbed. On the contrary, these photons undergo a larger number of scattering events and accumulate more momentum transfer along their path, which amplifies their contribution to the DCS signal. This effect is further enhanced at small autocorrelation delays, because the longer paths with more momentum transfer will more promptly decay the autocorrelation function. This property renders DCS similar in concept to time-domain NIRS, where the ability to distinguish the arrival times of photons provides some depth sensitivity.^64,65

Physiological factors also favor DCS in terms of brain-to-scalp sensitivity. First, baseline flow is about six times higher in the brain than in the scalp as reported by a PET study in adult humans,⁴⁴ while baseline blood volume is typically only twice that of scalp, as reported by PET and NIRS studies.^36,37,44 As observed in Fig. 2, when the baseline brain-to-scalp flow ratio increases, the relative sensitivity of DCS to brain increases, and that to scalp decreases. This higher blood flow in the brain also explains why restricting the analysis of the autocorrelation curves to their early part, corresponding to fast decorrelation processes, increases the sensitivity to brain and decreases the contribution from lower scalp flow. Second, the hemodynamic response to neuronal activation or to hypercapnia typically induces a relative increase in CBF, to which DCS is primarily sensitive, three to seven times that in CBV.^52–56

By varying baseline blood volume, we effectively studied the dependence of our results on baseline absorption (see Fig. 2, first column) and observed a small decrease in NIRS and DCS brain-to-scalp sensitivity with increased absorption. However, we did not investigate the influence of baseline scattering on the results. It is well known that there is a strong cross-talk between BFI and the reduced scattering coefficient ${{\mu }^{\prime }}_{\mathrm{s}}$ which DCS cannot retrieve independently.⁶⁶ Therefore, several experimental studies combine the DCS modality with a method such as frequency-domain NIRS that enables the characterization of the medium’s absolute optical properties.^16,67 In this study, we did not seek to retrieve the absolute flow values, but instead their relative changes over time. In this case, a commonly employed and reasonable assumption is that ${{\mu }^{\prime }}_{\mathrm{s}}$ is constant during the measurements,³ so that the observed relative changes only arise from changes in BFI. Nonetheless, the sensitivity of DCS to scalp and brain, as well as the simulated contrast to cerebral hemodynamics, depends on the baseline scattering coefficients of the head, which we assumed constant across regions. To estimate the effect of different reduced scattering coefficients, recall that the decay of the autocorrelation curve is determined by a factor $K(\tau )$ which depends on ${{\mu }^{\prime }}_{\mathrm{s}}\alpha D_{\mathrm{B}}={{\mu }^{\prime }}_{\mathrm{s}}$ BFI,⁶⁶ so that the effect of baseline reduced scattering ${{\mu }^{\prime }}_{\mathrm{s}}$ is similar to that of baseline BFI. The last panel of Fig. 2 is, therefore, useful to estimate the effect of a change in scattering. In our case, the brain-to-scalp flow ratio was set to 6, with identical ${{\mu }^{\prime }}_{\mathrm{s}}=12{\mathrm{cm}}^{-1}$ in both regions. In a more realistic case, where scattering is higher in the brain than in the scalp, the same curve can be used to estimate the updated brain and scalp contributions. For instance, if ${{\mu }^{\prime }}_{\mathrm{s},\text{Scalp}}=8{\mathrm{cm}}^{-1}$ and ${{\mu }^{\prime }}_{\mathrm{s},\text{Brain}}=12{\mathrm{cm}}^{-1}$, the brain-to-scalp flow ratio would effectively increase to $6\times 12/8=9$, leading to increased brain-to-scalp sensitivity (30% versus 20%). Although not a rigorous investigation of the effect of a heterogeneous baseline scattering coefficient, the above considerations permit a fast estimate of the dependence of our results on different baseline optical properties.

4.3. Partial Volume Correction Factors

This sensitivity study also provides partial volume correction factors for NIRS and DCS, for different baseline physiological values. The computations and measurements of DPFs for NIRS have been extensively documented, as well as their dependence on wavelength, SD separation, and location.^30,68–71 The use of a partial volume correction factor is more difficult to implement quantitatively, as it depends on knowledge of the activation spatial extent.^30,69 A typical value of 50 is sometimes used⁷² or the correction is simply dropped because of its arbitrary value³ and concentration results are sometimes expressed in units of μM cm. Here, our sensitivity to brain is about 8.5% at 3 cm, corresponding to a partial volume correction factor of $1/0.085$, i.e., approximately 12. This value is relatively low because we did not simulate a localized activation, but a global change in the whole brain. Note that we are not able to comment on the dependence of this correction factor with wavelengths since we assumed a constant scattering coefficient at both NIRS wavelengths in our Monte Carlo simulations.

For DCS, our sensitivity to brain at 3 cm is almost 20%, which translates to a partial volume correction factor of 5. This correction factor varies between 4 and 9 (25th to 75th percentile) depending on the probe location. The sensitivity also increases to 30% when fitting only the early portion of the curve, i.e., a median partial volume correction factor of 3. This result is in good agreement with previously published values. Durduran et al. obtained a correction factor of 5 from a simple two-layer model.⁶ Similarly, Gagnon et al. found, through Monte Carlo simulations at one location on a realistic head structure, that a homogeneous model underestimated the brain CBF change by a factor of $\sim 8$ for a 3 cm SD separation.³³ Note that, similarly to NIRS, this correction factor assumes a homogeneous CBF change in the whole cortical compartment and would, therefore, underestimate a focal change in CBF.

4.4. Similar CNR for CW-NIRS and DCS

Despite the higher sensitivity of DCS to brain compared to CW-NIRS, both modalities yielded similar CNR in response to a simulated functional activation and response to activation. This result stems from the fact that DCS has higher noise levels as determined through experimental in vivo measurements on adults.

We chose to estimate the noise empirically based on in vivo recordings, so that it encompasses both instrumental and physiological sources. The sensitivity of both modalities to physiological noise, notably arising from the scalp vasculature, is probably fairly similar. For NIRS, our estimate of the noise amplitude on HbR is about four times less than that on HbO and HbT. This difference is due to the fact that our noise is dominated by physiological sources. Low-frequency systemic oscillations arising from blood pressure fluctuations have consistently been reported to have a higher amplitude (two to 10 times) in oxy- than in deoxy-hemoglobin.^25,73,74 This is expected from the higher HbO content in the vasculature, especially in the arterial compartment subject to higher magnitude volume oscillations in response to arterial blood pressure fluctuations.⁷⁵ Although our preprocessing bandpass filtering between 0.05 and 0.5 Hz removes very-low frequency oscillations and cardiac pulse, low-frequency (around 0.1 Hz) physiological oscillations remain a major contribution to our noise estimate.

On the other hand, the instrumental noise of NIRS is much lower than that of DCS in our experimental setup. Although both modalities are shot-noise limited, NIRS systems employ optical fibers or fiber bundles with diameters typically ranging from 200 μm to a few millimeters. In contrast, DCS systems operate in photon counting mode, with detection through single-mode fibers ($\sim 5\mu \text{m}$ in diameter). At each location, the collection area for DCS is, therefore, several orders of magnitude less, resulting in fewer detected photons and higher shot noise level. This noise is even higher when restricting the analysis to the early portion of the autocorrelation curve. Zhou et al. have developed a model of the DCS noise,⁷⁶ and Dong et al. demonstrated its experimental validity in semi-infinite media.⁶⁶ The model depends on the photon counts, the correlator bin time interval, and the exponential decay of the correlation function. We compared this shot-noise limited model to our experimentally derived noise levels. For this, we applied the DCS noise model of Zhou et al.⁷⁶ to our experimental parameters and generated 50 autocorrelation curves with different instances of noise, from which we obtained the standard deviation on BFI. With this model, we obtained noise levels at 1, 2, and 3 cm of 0.9%, 2.5%, and 4%, respectively. This is lower than the noise we measured experimentally (3%, 4%, and 5% respectively), suggesting that, even though it is dominated by shot noise at longer separations, our experimental DCS signal also encompasses other sources of noise, probably both instrumental and physiological.

It is expected that other devices with different parameters would yield slightly different noise levels. In our case, it appears that NIRS is dominated by physiological noise at all three separations, while DCS presents a mixture of different noise sources at short separations and is dominated by shot noise at 3 cm due to low photon counts. Dietsche et al. proposed a novel DCS instrumentation and demonstrated improved signal-to-noise ratio (SNR) with the use of a bundle of up to 32 single-mode fibers, enabling them to measure the BFI changes at a high frequency sufficient for resolving the cardiac waveform.⁷⁷ A similar multichannel setup could also be used at a lower temporal resolution to increase the SNR. The placement of a diffuser in front of the DCS laser source has also been implemented to allow a higher power to be safely delivered on the tissue⁶⁷ and, therefore, increase the SNR. In summary, there are instrumental options to reduce the DCS instrumental noise. Our results are, therefore, generalizable to other systems, but higher DCS performance in terms of SNR is potentially available.

4.5. NIRS and DCS Measures of Functional Activation

To our knowledge, there have only been a very few studies combining CW-NIRS and DCS measurements of functional activation.^6,16,78 Our simulations of contrast and CNR are in good qualitative agreement with these published results. The first report of simultaneous NIRS and DCS was published by Durduran et al.,⁶ who combined the two modalities in seven subjects performing a finger tapping task. Before partial volume correction, for an SD separation of 3 cm, they observed on average a $+0.63\mu \text{M}$ ($\pm 0.14\mu \text{M}$) increase in [HbO], a $-0.19\mu \text{M}$ ($\pm 0.04\mu \text{M}$) decrease in [HbR], a $+0.42\mu \text{M}$ ($\pm 0.12\mu \text{M}$) increase in [HbT], and a 7.8% ($\pm 2\%$) increase in flow (these values were computed from the results reported in the article, after division by the partial volume correction factor of 20 for NIRS and five for DCS that the authors employed). When dividing the contrast by the variability assessed as the standard deviation of the response over all subjects, this results in CNR of 4.5 for HbO, 4.8 for HbR, 3.6 for HbT, and 3.9 for flow. These results agree with our simulated results, both in terms of contrast and CNR. In particular they demonstrate similar CNR for both modalities, albeit slightly better for NIRS.

Roche-Labarbe et al. combined both NIRS and DCS modalities in preterm neonates during passive tactile stimulation of the hand.¹⁶ The difference in head size, and potentially in the premature brain physiology, forbids direct comparison with our simulations on the adult head. It is nonetheless interesting to note that their functional results are also in qualitative agreement with our findings, with similar CNR for DCS and NIRS.

Further, Mesquita et al. used the combined NIRS/DCS modalities to study the response to repetitive transcranial magnetic stimulation (rTMS) of the motor cortex in eight subjects.⁷⁸ For an SD separation of 2.5 cm, they reported a median increase in CBF in the side ipsilateral to the stimulation of 33%, an increase in [HbO] of 5.4 μM, a nonsignificant decrease in [HbR] of $-0.15\mu \text{M}$, and an increase in [HbT] of $+5.1\mu \text{M}$, after correction by wavelength-dependent DPFs. For each subject, they report the maximum change measured by both modalities, as well as an error estimated by the standard deviation of the fluctuations during the rTMS duration. From these numbers, we computed a CNR for each subject. Over all subjects, this results in a median CNR of 2.5 for [HbO], 0.3 for [HbR], 1.7 for [HbT], and 1.9 for CBF. Except for the low CNR on HbR, these values are also in good quantitative agreement with our simulations during functional activation.

Although these results are in generally good quantitative agreement with our simulations, minor discrepancies arise that can be explained by a number of parameters: the chosen baseline parameters, the head geometry, and different instruments resulting in different noise levels. In particular, our noise level is defined as the standard deviation of the signal during a resting run, while the variability of the results in the studies described above arise from group averaging of the data. Additionally, note that the parameters of the data acquisition and processing for our noise estimation (e.g., fiber diameter, integration time, photon counts, filtering frequencies) reflect typical experimental conditions, but differ between the two modalities, and are probably different from the other studies as well. Our aim is not to compare the absolute noise of both modalities in identical conditions (e.g., for the same number of detected photons and integration time), but rather to estimate their level in realistic experimental conditions. Importantly, our simulations show a good quantitative agreement with the published studies in terms of contrast, as well as a good qualitative agreement in terms of CNR.

4.6. NIRS and DCS Measures of Response to Hypercapnia

In contrast to the functional activation studies, our simulated hypercapnia results present a mix of agreement and disagreement with our experimental findings. In agreement with our modeled data are the facts that, experimentally, HbR yields the higher CNR of the hemoglobin species, and that the increase in [HbO] is about twice the amplitude of the decrease in [HbR]. On the other hand, we observed a high CNR for DCS experimentally; almost twice that for [HbR], while our simulations predicted the CNR on [HbR] to be three times that of CBF. This discrepancy arises from both a higher than expected DCS response and a lower than expected NIRS response compared to the model.

4.6.1. NIRS measure of hypercapnia

Interestingly, our NIRS experimental results are consistent with the previous hypercapnia studies that reported low or inconsistent responses to hypercapnia^79,80 for a 3 cm SD separation. Leung et al. combined NIRS and TCD ultrasound measurements in healthy adults during hypercapnia (about a 6% increase in inspired ${\mathrm{CO}}_2$).⁷⁹ Over 14 subjects, they report an average flow increase of 15%, but only a 1% increase in the tissue hemoglobin index representative of CBV. In fact, 13 out of 14 subjects showed an increase in CBF as measured by TCD, but four presented a decrease in CBV during hypercapnia. Virtanen et al.⁸⁰ presented NIRS measurements of hypercapnia (2% to 3% ${\mathrm{CO}}_2$ increase from rest level). For a 3 cm SD separation, the response to hypercapnia is barely visible in the HbO signal, but appears in the HbR time trace. However, at a 5-cm interoptode distance, the response to hypercapnia is clearly visible in both species. A rough estimate from their figures shows a CNR of about 1 on HbR and 0.3 on HbO at 3 cm, and about 1.5 and 0.7, respectively, at a 5 cm separation. Similarly to our own NIRS experimental findings, these results show higher CNR on HbR than on HbO, and lower CNR absolute values than we modeled. Alderliesten et al. observed a consistent response to hypercapnia in a study combining NIRS and fMRI imaging.⁸¹ They used a 4-cm SD separation which could explain their higher sensitivity to brain. However, they also found that the NIRS measure of CBV changes was systematically about four times lower than its fMRI-derived measure. Smielewski et al.⁸² consistently observed a response to hypercapnia as measured by CW-NIRS with a 6-cm interoptode separation. Successful measures of responses to hypercapnia with NIRS in adults have, therefore, been obtained with long SD separations ($>4\mathrm{cm}$), while a shorter (3 cm) interoptode distance produced inconsistent results similar to the present study.

The question arises of why our simplified model, while qualitatively consistent with experimental results, fails to quantitatively describe the NIRS signal reported by multiple hypercapnia studies. Specifically, it predicts a response on HbO, and even more so on HbR, much higher than was experimentally observed. The flow and volume responses we model are based on the Grubb relationship, and are consistent with multiple PET and MRI studies during hypercapnia.^54,56 Reported values for the Grubb coefficient vary widely, typically from 0.12 to 0.38.^52–56 We used a relatively low value of 0.25. Chen et al. even report a lower value, specific to venous-weighted fMRI, of 0.12 in the frontal cortex in response to hypercapnia (value not significantly different from the rest of the head value of 0.17). If we use a lower value of 0.15 for the Grubb coefficient, our simulations result in a lower HbT contrast, in better agreement with our experimental results. However, because we assume a constant ${\mathrm{CMRO}}_2$ in the relationship, such as that of Maydew et al. [Eq. (1)], this in turn results in a higher contrast on HbR, further away from our experimental results. Conversely, using a higher $\alpha$ value in our simulations decreases the contrast on HbR, in better agreement with our experimental results. Our simplified model lumps all microvasculature into a single compartment to which NIRS is homogeneously sensitive. It is possible that we are more sensitive than modeled to the arterial compartment, where we expect a smaller decrease in HbR. For instance, Sakadzic et al. observed in a rat model a smaller increase in ${\mathrm{SO}}_2$ in the arterioles than in the venules in response to hypercapnia.⁸³

4.6.2. DCS measure of hypercapnia

We report in this study a high increase in blood flow in response to a short ($\sim 30\mathrm{s}$) period of approximately 5% inspired ${\mathrm{CO}}_2$ (${\mathrm{etCO}}_2$ about 8 mm Hg above baseline), with a median value of 27% before applying any partial volume correction, or 3.4% per mm Hg of ${\mathrm{etCO}}_2$. From our simulations, a correction factor of approximately 5 is required on the adult head. This would correspond to an actual CBF increase of 135%, or 17% per mm Hg of ${\mathrm{etCO}}_2$. This value is physiologically too high compared to numerous other studies of response to hypercapnia as assessed by other modalities for a comparable amount of inspired ${\mathrm{CO}}_2$.^45,47,84 We expect an increase in CBF on the order of 60% for 5% inspired ${\mathrm{CO}}_2$. Note, however, that our results are consistent with one publication that reported DCS measurements of hypercapnia in adults.⁸⁵ Durduran et al. observed an average 2.4% increase in CBF per mm Hg of ${\mathrm{etCO}}_2$ in five adult subjects. Buckley et al. performed DCS measurements in children undergoing hypercapnia and validated their results through comparison with phase-encoded velocity mapping MRI.¹⁴ They observed an average increase in blood flow of 49% in response to a 30-min long hypercapnia episode (approximately a 3% fraction of the inspired ${\mathrm{CO}}_2$). Note that these results cannot be directly compared to our simulations and experimental data as the subjects were children with a thinner extracerebral layer than adults.

One explanation for the high CBF increase we observe is the possible contribution of some extracerebral systemic blood flow increase. Indeed, the short separation DCS measurement (0.8 cm) shows a small blood flow increase (11% on average) which probably arises from the scalp, since the sensitivity to brain at 1 cm is very low ($<1\%$). This hypothesis is also supported by the fact that subjects with the highest flow increase at 3 cm also have a higher contribution at 0.8 cm (data not shown). This observation is, however, in contrast to the results of Durduran et al.,⁸⁵ who reported no change in scalp flow during hypercapnia as measured with laser Doppler flowmetry. It is also surprising that we did not observe a stronger response with NIRS if there is indeed a systemic superficial contribution to the signal. Further studies incorporating a more rigorous multilayer model will be needed to distinguish the cerebral and superficial contributions to the DCS signal.

5. Conclusion

In summary, we show through Monte Carlo simulations that DCS has about three times higher brain sensitivity than NIRS for a 3 cm SD separation, and for a typical brain-to-scalp flow ratio of 6. However, because of higher noise in DCS, both modalities yield a similar CNR under typical physiological and instrumental conditions. This is an important result to understand the relative capabilities of both modalities in measuring cerebral physiological changes. Additionally, we combined NIRS and DCS measurements during graded hypercapnia in adults, and report inconsistent responses as measured with NIRS, but highly consistent and sensitive responses as measured with DCS.

Biographies

Juliette Selb received her PhD degree in 2002 from the Université Paris Sud in France for her work on acousto-optic imaging. She is an instructor in the Optics Division of the Athinoula A. Martinos Center for Biomedical Imaging at Massachusetts General Hospital, Harvard Medical School. Her current research focuses on diffuse optical modalities for brain imaging in humans.

David A. Boas is a PhD physicist and professor of radiology at Massachusetts General Hospital, Harvard Medical School. He has published more than 150 peer-review papers in the field of biomedical optics. He is the founding editor-in-chief of Neurophotonics.

Suk-Tak Chan is an instructor in radiology at Massachusetts General Hospital, Harvard Medical School. She is the author of more than 30 journal papers and two book chapters. Her interests include vascular physiology, ultrasound imaging, and magnetic resonance imaging.

Karleyton C. Evans is a director of the Laboratory for Neuroimaging of Anxiety and Respiratory Psychophysiology at Massachusetts General Hospital and assistant professor of psychiatry at Harvard Medical School. His current research involves studies of neural and cerebral vascular responses to elevated carbon dioxide (hypercapnia) in health and disease.

Erin M. Buckley received her PhD degree in physics from the University of Pennsylvania in 2011, and then spent a year as a postdoctoral fellow in the division of neurology at the Children’s Hospital of Philadelphia before coming to the Martinos Center. She is a research fellow at the Athinoula A. Martinos Center for Biomedical Imaging at Massachusetts General Hospital. Her current research focuses on the application of NIRS and DCS to neonates at high risk for brain injury.

Stefan A. Carp received his BS degrees in chemistry and chemical engineering from Massachusetts Institute of Technology in 2000, and his PhD degree in biomedical optics from University of California, Irvine, in 2005. He is a PhD biomedical engineer and instructor in radiology at Massachusetts General Hospital, Harvard Medical School. He is the author of 20 peer-reviewed journal articles and three book chapters. His current research focuses on noninvasive physiology quantification using near-infrared light.