Iterative total-variation reconstruction versus weighted filtered-backprojection reconstruction with edge-preserving filtering

Abstract

Iterative image reconstruction with the total-variation (TV) constraint has become an active research area in recent years, especially in x-ray CT and MRI. Based on Green’s one-step-late algorithm, this paper develops a transmission noise weighted iterative algorithm with a TV prior. This paper compares the reconstructions from this iterative TV algorithm with reconstructions from our previously developed non-iterative reconstruction method that consists of a noise-weighted filtered backprojection (FBP) reconstruction algorithm and a nonlinear edge-preserving post filtering algorithm. This paper gives a mathematical proof that the noise-weighted FBP provides an optimal solution. The results from both methods are compared using clinical data and computer simulation data. The two methods give comparable image quality, while the non-iterative method has the advantage of requiring much shorter computation times.

1. Introduction

Total-variation (TV) minimization has been shown to be useful in constructing piecewise constant images with sharp edges, and has been widely used in x-ray CT and MRI applications (Sidky et al 2006, Candes et al 2006, Sidky and Pan 2008, Tang et al 2009, Bian et al 2010, Han et al 2011, Ritschl et al 2011, Han et al 2012). TV-based iterative image reconstruction algorithms are effective in noise reduction especially when the measurements are undersampled or noisy. Bruder et al (2010) suggested to use an edge image to control the smoothing filter in an iterative algorithm, less filtering is performed at edges.

Fourteen years ago our group developed an iterative TV algorithm based on the emission Poisson model, using Green’s one-step-late algorithm (Green 1990, Panin et al 1999). In this paper, we show that this one-step-late algorithm can be extended to any noise model. As an example, we present a version that uses the transmission noise model. We realize that iterative TV algorithms are computationally expensive. This paper also considers an alternative non-iterative method to reach the same goal.

The filtered backprojection (FBP) algorithm has been in use for several decades (Radon 1917, Bracewell 1956, Vainstein 1970, Shepp and Logan 1974, Zeng 2010). It is the workhorse of x-ray CT image reconstruction. A drawback of the FBP algorithm is that it produces very noisy images. Algorithms based on optimization of an objective function are able to incorporate the projection noise model and produce less noisy images than the FBP algorithm. Usually these algorithms are iterative algorithms (Dempster et al 1977, Shepp and Vardi 1982, Langer and Carson 1984, Geman and McClure 1987, Hudson and Larkin 1994). In order to shorten the computation time of an iterative algorithm, effort has been made to transform a regular iterative algorithm into an iterative FBP algorithm (Delaney and Bresler 1996). Another approach to noise control is to apply an adaptive filter or nonlinear filter to the projection measurements (Hsieh 1998, Kachelrieß et al 2001). We recently developed a non-iterative FBP-MAP (maximum a posteriori) algorithm that can model the projection noise on a view-by-view basis and in which an average or a maximum noise variance is used for all projection rays in each view (Zeng 2012). It was an initial attempt to use the FBP algorithm to model data noise. In the view-by-view weighted FBP (vFBP) algorithm, a single weighting factor, w(view), is assigned to all projection rays in a view. This noise-weighting scheme is not as accurate as ray-by-ray noise weighting which we recently proposed. The resulting algorithm is denoted as the ray-by-ray noise-weighted FBP (rFBP) algorithm (Zeng and Zamyatin 2013).

One drawback of the vFBP and rFBP algorithms is that the Bayesian prior must be in the form of a quadratic function, which does not enforce sharp edges. However, the rFBP paper also considered a special bilateral nonlinear filter to further smooth out the noise and preserve the edges (Aurich and Weule 1995, Zeng and Zamyatin 2013).

This paper has three goals: to develop an iterative one-step-late TV algorithm, to present a mathematic proof of our previously suggested noise-weighted FBP algorithm, and to compare the results with the above two algorithms.

The iterative TV algorithm will be presented in detail in section 2. In order to make this paper self-contained, the non-iterative rFBP algorithm, and the edge-preserving bilateral filter are also presented in section 2. Computer implementation issues will be presented in section 3. Clinical and computer simulated data will be used to compare the proposed methods. The results will be reported in section 4. Some issues are discussed in section 5, and conclusions are drawn in section 6. Due to the complex mathematical derivation, the proof of the noise-weighted FBP algorithm will be presented in the appendices.

2. Methods

2.1. Iterative Green-type TV algorithm with a general noise model

Green’s one-step-late ML-EM(maximum likelihood expectation maximization) MAP iterative algorithm for emission measurements was extended to incorporate the TV norm 14 years ago (Panin et al 1999). The extended algorithm can be expressed as

$$x_i^{\text{new}}=\frac{x_i}{\sum _j{a}_{ij}+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}\sum _j\frac{a_{ij}{p}_j}{\sum _k{a}_{kj}{x}_k}$$ (1)

where the image is presented by a one-index array x_i, the projections p_j also use one index j, a_ij is the contribution from image pixel i to projection j, γ is a weighting parameter controlling the influence of the TV prior on the image, and TV(X) is the TV norm of the current image X. The mathematical expressions for TV(X) and its partial derivative will be given in the implementation section of this paper.

In order to extend algorithm (1) to a general noise model, an array of weighting factors q_j is introduced to the backprojection summations. In (1), the backprojection of a constant 1 is given as ∑_j a_ij = ∑_j a_ij1, which becomes ∑_j a_ijq_j after weighting factors q_j are inserted. In (1), the backprojection of the ratio p_j/∑_k a_kjx_k is given as ∑_j a_ijp_j/(∑_k a_kjx_k), which becomes ∑_j a_ijq_jp_j/(∑_k a_kjx_k) after weighting factors q_j are inserted. Therefore (1) becomes

$$x_i^{\text{new}}=\frac{x_i}{\sum _j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}\sum _j\frac{a_{ij}{q}_j{p}_j}{\sum _k{a}_{kj}{x}_k}.$$ (2)

To understand how the weighting factors q_j can be selected for noise modeling, the multiplicative update scheme (2) is re-written as an additive update scheme as follows:

$$x_i^{\text{new}}=\frac{x_i}{{\sum }_j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}\times (\sum _j{a}_{ij}{q}_j\frac{p_j-{\sum }_k{a}_{kj}{x}_k+{\sum }_k{a}_{kj}{x}_k}{{\sum }_k{a}_{kj}{x}_k}-\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i})=\frac{x_i}{{\sum }_j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}\times (\sum _j{a}_{ij}{q}_j\frac{p_j-{\sum }_k{a}_{kj}{x}_k}{{\sum }_k{a}_{kj}{x}_k}+{\sum }_j{a}_{ij}{q}_j-\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i})=\frac{x_i}{{\sum }_j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}\times \left[\right(\sum _j{a}_{ij}{q}_j\frac{p_j-{\sum }_k{a}_{kj}{x}_k}{{\sum }_k{a}_{kj}{x}_k}-\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i})+({\sum }_j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}\left)\right]=x_i+\frac{x_i}{{\sum }_j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}[\sum _j{a}_{ij}\frac{q_j}{{\sum }_k{a}_{kj}{x}_k}(p_j-{\sum }_k{a}_{kj}{x}_k)-\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}].$$ (3)

In the first line of (3), $\frac{p_j}{{\sum }_k{a}_{kj}{x}_k}$ is replaced by $\frac{p_j-{\sum }_k{a}_{kj}{x}_k+{\sum }_k{a}_{kj}{x}_k}{{\sum }_k{a}_{kj}{x}_k}$, and $-\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}$ is inserted without affecting anything. The second and third lines of (3) simply re-group some terms from the previous line. The last line of (3) is obtained by multiplying the factor $x_i/[{\sum }_j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}]$ to both terms in the brackets.

Let us consider an objective function:

$$\text{Objective function}=\frac{1}{2}\sum _j{w}_j{(\sum _k{a}_{kj}{x}_k-p_j)}^2+\gamma \mathrm{T}\mathrm{V}(\mathbf{X}),$$ (4)

and a typical gradient-type iterative algorithm to minimize (4) can be expressed as

$$x_i^{\text{new}}=x_i+s_i\left[\sum _j{a}_{ij}{w}_j\right(p_j-\sum _k{a}_{kj}{x}_k)-\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}],$$ (5)

where s_i is the iteration step size, $[{\sum }_j{a}_{ij}{\omega }_j(p_j-{\sum }_k{a}_{kj}{x}_k)-\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}]$ is the negative gradient of the objective function to be minimized, w_j is the noise weighting factor for projection p_j, and w_j is usually chosen as the reciprocal of the variance of the noise in p_j. Comparing (3) with (5), we have

$$\text{Step size}:s_i=\frac{x_i}{\sum _j{a}_{ij}{q}_j+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}},\text{and}$$ (6)

$$\text{Noise weighting factor}:w_i=\frac{q_j}{\sum _k{a}_{kj}{x}_k}.$$ (7)

Once the noise variance model is known, q_j can be selected accordingly as

$$q_i=w_j\sum _k{a}_{kj}{x}_k=\frac{\sum _k{a}_{kj}{x}_k}{\text{noise variance of}{p}_j}.$$ (8)

For example, for emission projection, the Poisson noise model is assumed and the variance of p_j can be approximated by p_j or ∑_k a_kjx_k. Thus, w_i ≈ 1/p_j or w_j ≈ 1/ ∑_k a_kjx_k. Therefore, q_j can be chosen as a constant 1.

For transmission measurements, also using the Poisson noise model, the variance of line-integral p_j can be approximated by $\frac{1}{N_0\text{exp}(-p_j)}$ or $\frac{1}{N_0\text{exp}(-{\sum }_k{a}_{kj}{x}_k)}$. Thus, w_i ≈ N₀ exp(−p_j) or w_i = N₀ exp(−∑_k a_kjx_k). Therefore, q_j can be chosen as

$$q_i=N_0\text{exp}(-p_j)\sum _k{a}_{kj}{x}_k\text{or}{q}_i=N_0\text{exp}(-\sum _k{a}_{kj}{x}_k)\sum _m{a}_{mj}{x}_m.$$ (9)

Since weighting factors for measurements are relative, if the incoming flux N₀ is stable, it does not need to be included in factors q_j. In other words, q_j can be chosen as

$$q_i=\text{exp}(-p_j)\sum _k{a}_{kj}{x}_k\text{or}{q}_i=\text{exp}(-\sum _k{a}_{kj}{x}_k)\sum _m{a}_{mj}{x}_m.$$ (10)

Therefore, two iterative transmission-data noise-weighted TV algorithms are obtained from (2) and (10) as

$$x_i^{\text{new}}=\frac{x_i}{\sum _j[a_{ij}\text{exp}(-p_j)\sum _k{a}_{kj}{x}_k]+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}\sum _j[a_{ij}{p}_j\text{exp}(-p_j)];$$ (11a)

$$x_i^{\text{new}}=\frac{x_i}{\sum _j\left[a_{ij}\text{exp}\right(-\sum _k{a}_{kj}{x}_k\left)\sum _m{a}_{mj}{x}_m\right]+\gamma \frac{\partial \mathrm{T}\mathrm{V}(\mathbf{X})}{\partial x_i}}\sum _j\left[a_{ij}{p}_j\text{exp}\right(-\sum _k{a}_{kj}{x}_k\left)\right].$$ (11b)

In this section, a new iterative TV algorithm with a general noise-model is obtained as (2). As a special case, for transmission measurements algorithm (2) has been further written as (11a) or (11b).

Algorithms (11a) and (11b) are not equivalent. The difference between (11a) and (11b) is due to different selections of the weighting factors. Noise weighting is a double-edged sword. It can improve the image quality and it can also introduce artifacts. Our experience teaches us that a smoother weighting function introduces fewer artifacts. The weighting function in (11b) is smoother than that in (11a). Another option is to use a lowpass filter to smooth ‘exp(–p_j)’ before it is used in (11a).

2.2. Ray-by-ray noise-weighted FBP algorithm

A fundamental difference between an analytical FBP algorithm and an iterative algorithm is that the iterative algorithm requires a discrete presentation of the image to perform forward projection at each iteration while the analytical algorithm can be formulated in the continuous function space. Solving for an optimal solution in the continuous function space requires the calculus of variations (van Brunt 2004), which is more complicated than solving for an optimal discrete parameter or optimal discrete pixilated image. Due to the high level of complexity of the mathematical derivation, the weighted FBP algorithm is derived in appendices A and B at the end of this paper.

Similar to a conventional FBP algorithm, the weighted FBP algorithm reconstructs an image in two steps: projection domain filtering and backprojection. The only difference between the weighted FBP algorithm and the conventional FBP algorithm is that the conventional ramp filter |ω | is replaced by a more general ramp-filter as given by (A.19) in appendix A:

$$H(\omega )=\frac{|\omega |}{1+\beta ·\frac{M_{1D}(\omega )·|\omega |}{w(\theta )}}$$

where β is a control parameter for the contribution of the Bayesian prior, w(θ) is the weighting function at view angle θ, and M_1D(ω) is the Fourier domain transfer function associated with a spatial domain quadratic prior. If a minimal-norm solution is assumed to be the prior, then M_1D(ω) = 1. Thus, (A.19) becomes

$$H(\omega )=\frac{|\omega |}{1+\beta ·\frac{|\omega |}{w(\theta )}}.$$ (12)

In (A.19) and (12), the weighting function w(θ) is determined by the noise variance of the projection at detector view angle θ (Zeng 2012).

This view-by-view noise-weighting scheme can be extended to a ray-by-ray noise weighting scheme in an ad hoc manner (Zeng and Zamyatin 2013). For ray-based noise weighting, w is a function of the ray: w = w(ray). At each view angle, we quantize the ray-based weighting function into n + 1 values: w₀, w₁, …, w_n, which in turn give n + 1 different filters as defined in (12). That is,

$$H_k(\omega )=|\omega |/(1+\beta ·|\omega |/w_k),\text{for}k=0,1,\dots ,n.$$ (13)

Using these n + 1 filters, n + 1 sets of filtered projections are obtained. Before backprojection, one of these n + 1 projections is selected for each ray according to its proper weighting function. Only one backprojection is performed using the selected filtered projections.

This noise weighted rFBP algorithm is the first stage of the proposed non-iterative image reconstruction algorithm. Its purpose is to reconstruct the image while suppressing the noise texture.

2.3. Nonlinear edge-preserving bilateral post filtering

One drawback of the rFBP algorithm is that its Bayesian prior must be quadratic, thus it is unable to incorporate edge-preserving filtering during image reconstruction. Our strategy is to apply a nonlinear, edge-preserving, bilateral filter to rFBP reconstructed images.

Bilateral filters are a class of nonlinear filters that are specified by both domain (G_domain) and range (G_range) functions (Aurich and Weule 1995). A general form of the input/output relationship of a bilateral filter can be given as

$$x_k^{\text{output}}=\frac{\sum _{j\in \mathrm{\Omega }(k)}{x}_j^{\text{input}}{G}_{\text{domain}}(k,j)G_{\text{range}}(x_k^{\text{input}}-x_j^{\text{input}})}{\sum _{j\in \mathrm{\Omega }(k)}{G}_{\text{domain}}(k,j)G_{\text{range}}(x_k^{\text{input}}-x_j^{\text{input}})},$$ (14)

where $x_j^{\text{input}}$ represents the jth pixel of the input (unfiltered) image, $x_j^{\text{output}}$ represents the kth pixel of the output (filtered) image, Ω(k) is a neighborhood around pixel k,G_domain is a ‘domain’ function, and G_range is a ‘range’ function. In many applications, G_domain and G_range are chosen to be Gaussian functions.

In this paper, functions G_domain and G_range are chosen as binary functions, with their function values as 0 and 1. Our strategy is to use the average value to replace the original image value. Not every image pixel is allowed to participate in the ‘average’ operation. To be qualified, a pixel x_j must satisfy two conditions: it must be in the close neighborhood of the pixel k, and its value x_j is close enough to the value of x_k. A larger neighborhood Ω(k) is more effective in noise reduction. However, a larger filtering neighborhood Ω(k) results in a higher computation cost.

This image domain bilateral filtering is the second stage of the proposed non-iterative image reconstruction algorithm. Its purpose is to perform edge preserving smoothing to further suppress noise.

3. Implementation and data sets

3.1. Implementation of the iterative TV algorithm

Implementation of the iterative TV algorithm (11b) is almost the same as implementation of the conventional ML-EM algorithm, except for the evaluation of the partial derivative of the TV measure of the current image X. For 2D image reconstruction, it is easier to use double index to label the image pixels. Then the TV measure of the image is defined as (Panin et al 1999)

$$\mathrm{T}\mathrm{V}(X)=\sum _{k,l}\sqrt{{(x_{k,l}-x_{k-1,l})}^2+{(x_{k,l}-x_{k,l-1})}^2+{\epsilon }^2}$$ (15)

and its partial derivative can be calculated as

$$\frac{\partial \mathrm{T}\mathrm{V}(X)}{\partial x_{k,l}}=\frac{x_{k,l}-x_{k-1,l}}{\sqrt{{(x_{k,l}-x_{k-1,l})}^2+{(x_{k-1,l+1}-x_{k-1,l})}^2+{\epsilon }^2}}+\frac{x_{k,l}-x_{k,l-1}}{\sqrt{{(x_{k+1,l-1}-x_{k,l-1})}^2+{(x_{k,l}-x_{k,l-1})}^2+{\epsilon }^2}}-\frac{x_{k+1,l}+x_{k,l+1}-2x_{k,l}}{\sqrt{{(x_{k+1,l}-x_{k,l})}^2+{(x_{k,l+1}-x_{k,l})}^2+{\epsilon }^2}},$$ (16)

where a small non-zero value ε is to prevent the denominators from becoming zero.

The iterative TV reconstruction is time consuming. In our clinical data study and computer simulations, only the central axial slice of the image volume was reconstructed, using a 2D fan-beam geometry. The image size was 840 × 840. The clinical data had 1200 views and the computer simulation had 900 views, both over 360°. Each view had 896 channels (i.e., detector bins). Algorithm (11b) was implemented and γ = 10 and ε = 0.1 were chosen. The number of iterations was 1000.

3.2. Implementation of the new rFBP algorithm

The rFBP algorithm consists of a filtering procedure and backprojection. The backprojection is the same as that in the conventional FBP algorithm. However, the filtering procedure is different because the new modified ramp filter (13) depends on the ray-based noise-weighting factor w(d,θ), with w(d, θ) ≈ w_k, where θ is the detector view angle, d is the coordinate along the detector, and k is an index from {0, 1, …, n}.

Our strategy to implement (13) is to quantize the weighting function w(d, θ) as w_k = exp(−0.1 · k · p_max), where p_max is the maximum projection value, and k = 0, 1, 2, …, 10. Then efficient Fourier domain filtering is used to perform the filtering and the fast Fourier transform routine can be used. The detailed implementation steps are given below.

Before projection data are ready to process, form 11 Fourier domain filter transfer functions H_k(ω) as defined in (13) with w_n = exp(−0.1 · k · p_max), k = 0, 1, 2, …, 10, respectively. Note: in implementation, ω is a discrete frequency index and takes discrete values of 0, 1/N, 2/N, …, 0.5N/N, where N is twice the number of channels, this is a detector row.

Step 1: At each view angle θ, find the 1D Fourier transform of projection p(d, θ) with respect to d, obtaining P(ω, θ).

Step 2: Form 11 versions of Q_k(ω, θ) = P(ω, θ) H_k(ω) with k = 0, 1, …, 10.

Step 3: Take the 1D inverse Fourier transform of Q_k(ω, θ) with respect to ω, obtaining q_k(d, θ) with k = 0, 1, …, 10.

Step 4: Construct the filtered projection q(d,θ) by letting q(d,θ) = q_k(d,θ) if p(d, θ) ≈ 0.1 · k · p_max.

The Bayesian term was chosen as the minimal norm prior (i.e.,M_1D(ω) = 1), to encourage aminimal norm solution, and the controlling parameter β was selected as 10⁻⁵. To be consistent with the iterative reconstruction, only the central slice of the cone-beam data was used for image reconstruction.

For the purposes of comparison, the central slice was also reconstructed with the conventional fan-beam FBP algorithm. The image size and the data were identical to those for the iterative reconstruction.

The reconstruction times for the rFBP algorithm and the conventional FBP algorithm are almost the same, which is about 1/3 of the computation time of one iteration of the iterative algorithm (11b).

3.3. Implementation of the bilateral filter

Bilateral filters can be specially designed according to the application. The edge-preserving bilateral filter in this paper is suggested by (Zeng and Zamyatin 2013) and can be implemented as follows.

• Specify a neighborhood Ω(k) around pixel k in the image domain. For each image pixel, filtering is performed only in this region.

• Specify a threshold value t. This value t represents the smallest edge jump or smallest detectable contrast. Image variation smaller than this value t is considered as noise.

• At each image pixel k, the filtered image value at x_k is the average value of all pixels in the set {x_j: j ∈ Ω(k) and |x_k − x_j| <t}.

Using the notation in (14), in our case,

$$\mathrm{\Omega }(k)=\text{an}r\times r\text{region},\text{centered at pixel}k;$$ (17)

$$G_{\text{domain}}(k,j)=1\text{if}j\in \mathrm{\Omega }(k),\text{and}{G}_{\text{domain}}(k,j)=0\text{if}j\notin \mathrm{\Omega }(k);$$ (18)

$$G_{\text{range}}(x_k-x_j)=1\text{if}|x_k-x_j|<t,\text{and}{G}_{\text{range}}(x_k-x_j)=0\text{if}|x_k-x_j|\ge t.$$ (19)

A drawback of this bilateral filter is that if the noise influence is larger than the smallest contrast t, the noise influence cannot be filtered out. The threshold t in our implementation was selected as 0.001 for the clinical data, 0.0025 for the computer simulation phantom shown in figure 2, and 0.0005 for the computer simulation phantom shown in figure 3. Parameter r in (17) was chosen as 2 in the cadaver study, and as 19 in the computer simulations.

Figure 2.

Image reconstruction using computer simulation data. (A) conventional FBP reconstruction. (B) Proposed iterative TV reconstruction. (C) Non-iterative rFBP reconstruction. (D) Non-iterative rFBP reconstruction with bilateral post filtering. (E) Gold-standard: conventional FBP reconstruction using noiseless data.

Figure 3.

Image reconstruction using computer simulation data. (A) conventional FBP reconstruction. (B) Proposed iterative TV reconstruction. (C) Non-iterative rFBP reconstruction. (D) Non-iterative rFBP reconstruction with bilateral post filtering. (E) Gold-standard: conventional FBP reconstruction using noiseless data.

3.4. Low-dose cadaver CT data

To compare the results of the iterative TV algorithm and the non-iterative rFBP/bilateral algorithm, a cadaver torso was scanned using an x-ray CT scanner with a low-dose setting, and the images were reconstructed with the conventional fan-beam FBP algorithm, the rFBP/bilateral algorithm, as well as the proposed iterative TV algorithm. Data were collected with a diagnostic scanner (Aquilion ONE™, Toshiba America Medical Systems, Tustin, CA, USA; raw data courtesy of Leiden University Medical Center).

The imaging geometry was cone-beam, the x-ray source trajectory was a circle of radius 600 mm. The detector had 320 rows, the row-height was 0.5 mm, each row had 896 channels, and the fan angle was 49.2°. A low-dose noisy scan was carried out. The tube voltage was 120 kV and current was 60 mA. There were 1200 views uniformly sampled over 360°. The reconstructed image array was 840 × 840. The noise weighting factor for this data set was chosen as w = exp(−p), where p is the line-integral measurement.

3.5. Computer simulation data

Two computer generated elliptical 2D torso phantoms were used to generate transmission projections. One of the phantoms (shown in figure 2) was elongated on purpose to illustrate the worst body shape, which generates severe streak artifacts. For both phantoms, the x-ray flux N₀ was 10⁵, the detector pixel size was 0.575 mm, the number of views was 900 over 360°, the number of detection channels (i.e., detector bins) was 896, and the focal length (i.e., the distance from the x-ray source to the curved detector) was 600 mm. The reconstructed image array was 840 × 840. The noise weighting factor for this data set was chosen as w = exp(−0.8p), where p is the line-integral measurement.

4. Results

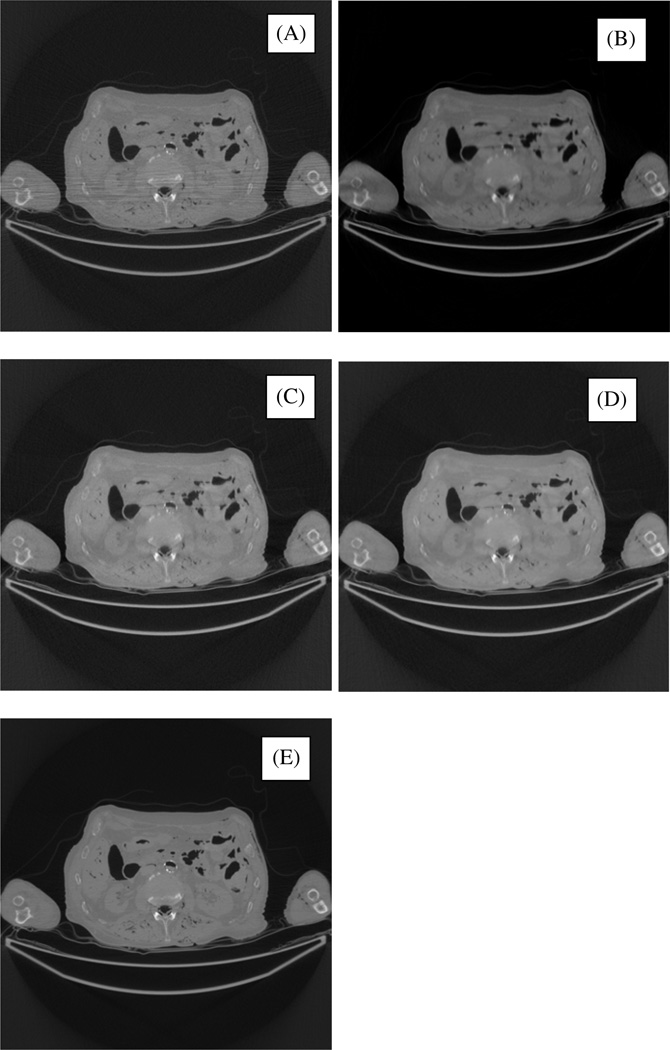
Figure 1(A) shows the conventional fan-beam FBP reconstruction of a transverse slice in the abdominal region of the cadaver. The x-rays through the arms are attenuated more than x-rays in other orientations, and create the left-to-right streak artifacts in the middle of the image.

Figure 1.

Image reconstruction using low-dose CT clinical cadaver data. (A) conventional FBP reconstruction. (B) Proposed iterative TV reconstruction. (C) Non-iterative rFBP reconstruction. (D) Non-iterative rFBP reconstruction with bilateral post filtering. (E) Gold-standard: conventional FBP reconstruction using regular dose CT data.

Figure 1(B) shows the cadaver data result from 1000 iterations of the proposed iterative TV algorithm using a transmission noise model. The noise modeling effectively removes the streak artifacts. The TV prior further reduces the noise fluctuation.

Figure 1(C) shows the rFBP reconstruction using the cadaver data. The streak artifacts are removed as well. The bilateral post filtering further reduces the noise fluctuation as shown in figure 1(D).

Figure 1(E) is the gold standard image, which is the conventional fan-beam FBP reconstruction using the standard dose CT data.

Figures 2 and 3 have the same arrangement as figure 1, except that the data were computer simulated. The gold standard images, figures 2(D) and 3(D), respectively, are the conventional FBP reconstruction using noiseless simulation data. Streak artifacts that appeared in the conventional FBP reconstruction have been significantly reduced in the rFBP reconstruction and the iterative reconstruction, when noise related weighting is incorporated during the reconstruction. The TV prior and the bilateral post filtering are effective in further reducing the noise while maintaining the edges. The image sharpness using both iterative and non-iterative methods is comparable. However, the non-iterative method is much more computationally efficient.

The computer generated phantom in figure 2 was dramatically elongated, and the noise distribution for this phantom is extremely anisotropic. It is very difficult to reduce the streak artifacts for this phantom. The effort in reducing the streak artifacts has some size effects of generating an image with non-isotropic resolution. The side-effects appear as shadows and directional blurring.

The phantom in figure 3 had a shape that was similar to a patient body. The shadow and directional blurring side-effects are not visualized. The computer simulated x-ray flux was the same for these two phantom studies.

Figure 3(E) was treated as the standard image for other images to compare with. The discrepancy of X from X_E is calculated as

$$\text{Dis}(X,X_E)=\frac{\text{norm}(X-X_E)}{\text{norm}(X_E)},$$ (20)

where ‘norm’ is the usually Euclidian matrix norm, X_E is the standard good image, and X is the image under investigation. The discrepancy values are labeled in the figures. If the discrepancy is used as the figure of merit, for the phantom shown in figure 2, the iterative TV algorithm gave the best result. For the phantom shown in figure 3, all images are equally good and the rFBP algorithm combined with the bilateral edge-preserving filtering gave the best image.

5. Discussion

The iterative TV algorithm is a gradient based optimization algorithm. This algorithm can only be used to search for a local minimum. Our objective function for the iterative one-step-late TV algorithm consists of a quadratic data-fidelity term and a small TV regularization term. As long as the parameter γ is small enough, the quadratic term dominates the shape of the objective function, which has only one minimum. Otherwise, the objective function may have many local minima. When an objective function has multiple local minima, no simple optimization algorithm guarantees its convergence to the global minimum.

This paper gave two forms of the iterative TV algorithm for transmission data; they are (11a) and (11b). One (11b) has been implemented in this paper. Notice that each iteration of (11b) requires one forward-projection (i.e., the summation over index k) and two backprojections (i.e., the summations over index j).

For the noise weighted FBP algorithm, its derivation in the appendices uses a quadratic objective function, which does not have the local minima issue.

The iterative TV algorithm enforces the piecewise constant constraint at each iteration, while the non-iterative algorithm enforces the piecewise constant constraint only once at the end. These two approaches are not equivalent. The iterative approach is much more effective. If one applies an edge-preserving bilateral filter to the result of a conventional FBP algorithm, the performance of the edge-preserving bilateral filter is very poor when the image is noisy. This is the reason that a noise-weighted FBP algorithm must be applied first to remove some noise textures such as the streak artifacts and produce a not-so-noisy image, and then the edge-preserving bilateral filter can further reduce the low magnitude noise.

These two algorithms are not equivalent. They may give similar results for some practical and useful applications. For other applications, their performance can be significantly different. For example, the current non-iterative algorithm cannot handle few-view tomography and limited angle tomography. Only in some sufficient data sampling situations, both can give similar results.

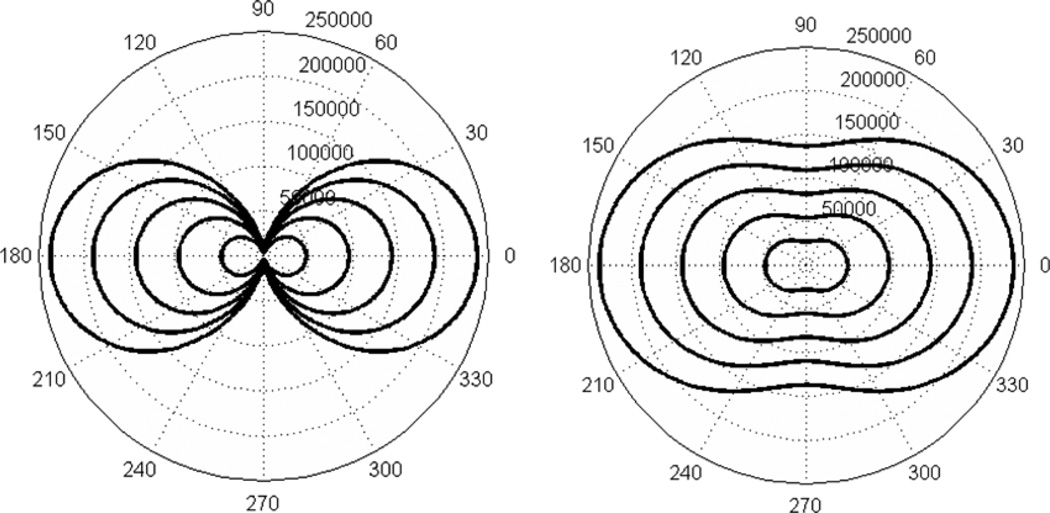
When anisotropic noise weighting is modeled in an image reconstruction (either iterative or non-iterative) algorithm, the PSF of the resultant image is also anisotropic (see figure 4). Figure 2 shows a dramatically elongated phantom that produces highly anisotropic Poisson noise distribution at different directions. Highly anisotropic noise distribution causes streak artifacts. The noise weighted (either iterative or non-iterative) reconstruction algorithm removes the streak artifacts by essentially applying heaviest lowpass filtering in the noisiest views and lightest lowpass filtering in the least noisy views, thus resulting in anisotropic PSF. This is the price to pay to remove noise textures.

Figure 4.

The gain level curves for the PSF transfer functions for the two computer simulation studies: (Left) for the phantom shown in figure 2 and (Right) for the phantom shown in figure 3.

By comparing the results in figures 2 and 3, the images in figure 2 suffer from poor resolution in the vertical direction. This is because we use a specially elongated phantom in figure 2 that gives anisotropic measurement noise. The phantom was chosen for the worst case scenario study, which you do not see in daily clinical studies. In transmission tomography, the noise variance is proportional to the exponential function of the line integral measurement. Usually, a longer path length gives a noisier measurement. The noise textures in this case are streak artifacts. The noise weighted reconstruction algorithm removes the streak artifacts by applying different levels of lowpass filtering at different orientations, and the image frequency bandwidth at a certain direction is inversely proportional to the noise variance in the projections when the detector is at that direction.

In order to see this, figure 4 shows two Fourier domain polar plots to illustrate the gain level curves for the situation of phantom in figures 2 and 3, respectively. The gain is defined by writing H(ω) in (12) as the ramp filter |ω| times the gain. Thus gain

$$\text{gain}(\omega ,\theta )=\frac{1}{1+\beta ·\frac{|\omega |}{w(\theta )}}.$$ (21)

A gain level curve is the curve of gain (ω, θ) = constant. The weight w(θ) is an exponential function e^−0.8p, where p is the line-integral of the attenuation coefficients along the x-ray path. When the path is long, the exponential function makes the weight w(θ) very small. The plots in figure 4 show that for the dramatically elongated phantom the bandwidth is much narrower in the vertical direction than the horizontal direction. The bandwidth in the vertical direction is significantly increased by using the phantom that is closer to the patient’s torso shape.

6. Conclusions

This paper introduces a new iterative TV image reconstruction algorithm, and a non-iterative algorithm. The iterative algorithm is based on Green’s one-step-late maximum a posteriori algorithm. The non-iterative algorithm consists of two stages: the ray-by-ray noise weighted FBP reconstruction and the 2D edge-preserving post-filtering. The mathematic derivation presented in the appendices is a proof the noise weighted FBP algorithm, which does not enforce edge-preserving smoothing.

These algorithms can incorporate a general noise model.We implemented these algorithms using the transmission data noise model. Both clinical low-dose CT data and computer simulation data were used to validate the proposed algorithms.

It is shown that the noise model in both iterative and non-iterative algorithms is able to reduce/remove the streak artifacts. The TV prior and the special bilateral filter are able to further reduce the noise while maintaining edges. The non-iterative method has an obvious advantage of fast reconstruction time, which is almost the same as that of a conventional FBP algorithm.

Appendix A

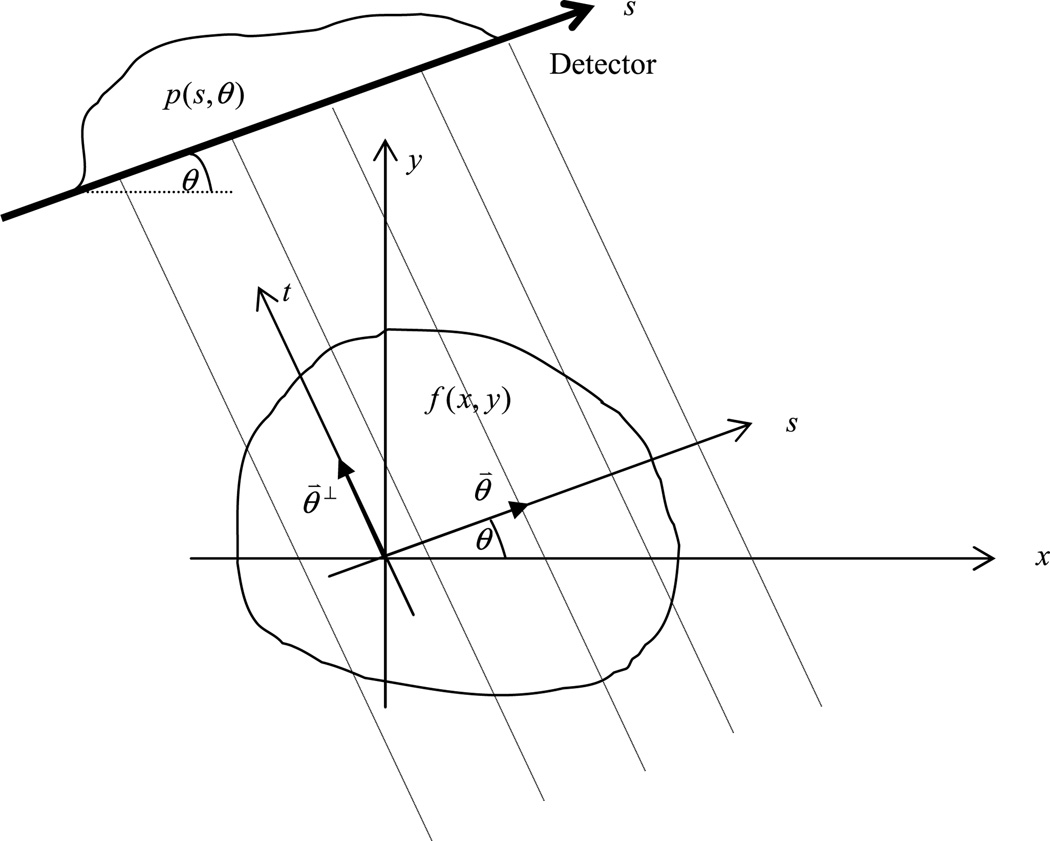
In this appendix, we use the two-dimensional (2D) parallel-beam Radon transform to derive an rFBP algorithm. The principle presented can be readily extended to fan-beam and cone-beam imaging geometries. Let the image to be reconstructed be f (x, y) and its Radon transform be [Rf](s, θ), defined as

$$[Rf](s,\theta )={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f(x,y)\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}x\mathrm{d}y,$$ (A.1)

where δ is the Dirac delta function, θ is the detector rotation angle, and s is the line-integral location on the detector. The Radon transform [Rf](s, θ) is the line-integral of the object f (x, y). Image reconstruction is to solve for the object f (x, y) from its Radon transform [Rf](s, θ).

A popular image reconstruction method is the FBP algorithm, which consists of two steps. In the first step, [Rf](s, θ) is convolved with a kernel function h(s) with respect to variable s, obtaining q(s, θ). The Fourier transform of the kernel h(s) is the ramp-filter |ω|. The second step performs backprojection, which maps the filtered projection q(s, θ) into the image domain as

$$f(x,y)={\int }_0^{\pi }q(s,\theta ){|}_{s=x\text{cos}\theta +y\text{sin}\theta }\mathrm{d}\theta .$$ (A.2)

This appendix applies a noise-variance-derived weighting function on the projections and enforces a prior term in the objective function, and this approach is commonly used in iterative algorithms.

Let the noisy line-integral measurements be p(s, θ). The objective function is a functional υ depending on the function f (x, y) as follows.

$$\upsilon (f)={\Vert [Rf](s,\theta )-p(s,\theta )\Vert }_w^2+\beta {\Vert f(x,y)**c(x,y)\Vert }^2,$$ (A.3)

where the first term enforces data fidelity, the second term imposes prior information about the image f, the parameter β controls the level of influence of the prior information to the image f, and w is a weighting function satisfying w(θ) = w(θ ± π) in the fidelity norm. In (A.3), c(x,y) is a symmetric image domain convolution kernel and ‘**’ represents the image domain 2D convolution. If c(x,y) is a Laplacian, the regularization term encourages a smooth image. If c(x,y) is a constant 1, the regularization term encourages a minimum norm solution. Using integrals, υ in (A.3) can be written as

$$\upsilon (f)={\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }{[{\int }_{x=-\infty }^{\infty }{\int }_{y=-\infty }^{\infty }f(x,y)\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}y\mathrm{d}x-p(s,\theta )]}^2\mathrm{d}sw(\theta )\mathrm{d}\theta +\beta {\int }_{x=-\infty }^{\infty }{\int }_{y=-\infty }^{\infty }{[{\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)c(x-\mathrm{x̂},y-ŷ)\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}]}^2\mathrm{d}y\mathrm{d}x.$$ (A.4)

of variations (van Brunt 2004) will be used to find the optimal function f (x, y) that minimizes the functional υ(f) in (A.4). The initial step in the method is to replace the function f (x, y) in (A.4) by the sum of two functions: f (x, y) + εη(x, y). The next step is to evaluate the derivative ${\frac{\mathrm{d}\upsilon }{\mathrm{d}\epsilon }|}_{\epsilon =0}$ and set it to zero. That is,

$$0=2{\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }\left\{\right[{\int }_{x=-\infty }^{\infty }{\int }_{y=-\infty }^{\infty }f(x,y)\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}y\mathrm{d}x-p(s,\theta )]·[{\int }_{x=-\infty }^{\infty }{\int }_{y=-\infty }^{\infty }\eta (x,y)\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}y\mathrm{d}x\left]\right\}\mathrm{d}sw(\theta )\mathrm{d}\theta +2\beta {\int }_{x=-\infty }^{\infty }{\int }_{y=-\infty }^{\infty }\left\{\right[{\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)c(x-\mathrm{x̂},y-ŷ)\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}]·[{\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }\eta (\mathrm{x̂},ŷ)c(x-\mathrm{x̂},y-ŷ)\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}\left]\right\}\mathrm{d}y\mathrm{d}x.$$ (A.5)

In practice, the function f (x, y) is compact, bounded, and continuous almost everywhere. After changing the order of integrals, we have

$$0={\int }_{x=-\infty }^{\infty }{\int }_{y=-\infty }^{\infty }\eta (x,y)\left\{{\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }\right[{\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)\delta (\mathrm{x̂}\text{cos}\theta +ŷ\text{sin}\theta -s)\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}-p(s,\theta )]\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}sw(\theta )\mathrm{d}\theta +\beta {\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ){\int }_{\mathrm{x̆}=-\infty }^{\infty }{\int }_{\mathrm{y̆}=-\infty }^{\infty }c(\mathrm{x̆}-\mathrm{x̂},\mathrm{y̆}-ŷ)c(\mathrm{x̆}-x,\mathrm{y̆}-y)\mathrm{d}\mathrm{y̆}\mathrm{d}\mathrm{x̆}\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}\}\mathrm{d}y\mathrm{d}x.$$ (A.6)

Equation (A.6) is in the form of ∫ ∫ η(x, y)g(x, y) dy dx = 0. Since η(x, y) can be any arbitrary function, one must have g(x, y) = 0, which is the Euler–Lagrange equation (van Brunt 2004). The Euler–Lagrange equation in our case is

$${\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }[{\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)\delta (\mathrm{x̂}\text{cos}\theta +ŷ\text{sin}\theta -s)\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}-p(s,\theta )]\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}sw(\theta )\mathrm{d}\theta +\beta {\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)m(x-\mathrm{x̂},y-ŷ)\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}=0$$ (A.7)

with

$$m(x-\mathrm{x̂},y-ŷ)={\int }_{\mathrm{x̆}=-\infty }^{\infty }{\int }_{\mathrm{y̆}=-\infty }^{\infty }c(\mathrm{x̆}-\mathrm{x̂},\mathrm{y̆}-ŷ)c(\mathrm{x̆}-x,\mathrm{y̆}-y)\mathrm{d}\mathrm{y̆}\mathrm{d}\mathrm{x̆}={\int }_{\mathrm{x̆}=-\infty }^{\infty }{\int }_{\mathrm{y̆}=-\infty }^{\infty }c(\mathrm{x̆},\mathrm{y̆})c((x-\mathrm{x̂})-\mathrm{x̆},(y-ŷ)-\mathrm{y̆})\mathrm{d}\mathrm{y̆}\mathrm{d}\mathrm{x̆}.$$ (A.8)

By moving the term containing p(s, θ) to the right-hand-side, equation (A.7) can be further rewritten as

$${\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)[{\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }\delta (\mathrm{x̂}\text{cos}\theta +ŷ\text{sin}\theta -s)\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}sw(\theta )\mathrm{d}\theta ]\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}+\beta {\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)m(x-\mathrm{x̂},y-ŷ)\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}={\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }p(s,\theta )\delta (x\text{cos}\theta -y\text{sin}\theta -s)\mathrm{d}sw(\theta )\mathrm{d}\theta .$$ (A.9)

Notice that

$${\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }p(s,\theta )\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}sw(\theta )\mathrm{d}\theta ={\int }_{\theta =0}^{\pi }p(s,\theta ){|}_{s=x\text{cos}\theta +y\text{sin}\theta }w(\theta )\mathrm{d}\theta =b_w(x,y)$$ (A.10)

is the weighted backprojection of the projection data p(s, θ) with a view-angle dependent weighting function w(θ), and the backprojection is denoted as b_w(x, y). It must be pointed out that b_w(x, y) is not the same as f (x, y) even when p(s, θ) is noiseless and w(θ) = 1, because no ramp filter has been applied to p(s, θ).

Also notice that

$${\int }_{\theta =0}^{\pi }{\int }_{s=-\infty }^{\infty }\delta (\mathrm{x̂}\text{cos}\theta +ŷ\text{sin}\theta -s)\delta (x\text{cos}\theta +y\text{sin}\theta -s)\mathrm{d}sw(\theta )\mathrm{d}\theta ={\int }_{\theta =0}^{\pi }w(\theta )\delta ((x-\mathrm{x̂})\text{cos}\theta +(y-ŷ)\text{sin}\theta )\mathrm{d}\theta =\mathrm{P}\mathrm{S}{\mathrm{F}}_w(x-\mathrm{x̂},y-ŷ)$$ (A.11)

is the point spread function (PSF) of the projection/weighted-backprojection operator at point (x, y) if the point source is at (x̂, ŷ) and the view-based weighting function is w(θ).

In appendix B, we show that

$$\mathrm{P}\mathrm{S}{\mathrm{F}}_w(x,y)=\frac{w({\text{tan}}^{-1}\frac{y}{x}\pm \frac{\pi }{2})}{\sqrt{x^2+y^2}}.$$ (A.12)

When w(θ) is set to 1, the point spread function reduces to the familiar expression (Zeng 2010):

$$\mathrm{P}\mathrm{S}{\mathrm{F}}_{w=1}(x,y)=\frac{1}{\sqrt{x^2+y^2}}.$$ (A.13)

Using (A.10) and (A.11), (A.9) becomes

$${\int }_{\mathrm{x̂}=-\infty }^{\infty }{\int }_{ŷ=-\infty }^{\infty }f(\mathrm{x̂},ŷ)[\mathrm{P}\mathrm{S}{\mathrm{F}}_w(x-\mathrm{x̂},y-ŷ)+\beta ·m(x-\mathrm{x̂},y-ŷ)]\mathrm{d}ŷ\mathrm{d}\mathrm{x̂}=b_w(x,y).$$ (A.14)

The left-hand-side of (A.14) is a 2D convolution. Taking the 2D Fourier transform of (A.14) yields

$$F({\omega }_x,{\omega }_y)\times [\frac{w(\phi )}{\sqrt{{\omega }_x^2+{\omega }_y^2}}+\beta ·M({\omega }_x,{\omega }_y)]=B_w({\omega }_x,{\omega }_y),$$ (A.15)

or

$$F({\omega }_x,{\omega }_y)=B_w({\omega }_x,{\omega }_y)/[\frac{w(\phi )}{\sqrt{{\omega }_x^2+{\omega }_y^2}}+\beta ·M({\omega }_x,{\omega }_y)].$$ (A.16)

Here the capital letters are used to represent the Fourier transform of their spatial domain counterparts, which are represented in lowercase letters; ω_x and ω_y are the frequency variables for x and y, respectively, and tan⁻¹(ω_y/ω_x) = φ. The expression $w(\phi )/\sqrt{{\omega }_x^2+{\omega }_y^2}$ is the 2D Fourier transform of the point spread function PSF_w(x, y) as derived in appendix B. Notice that the Fourier transform B_w(ω_x, ω_y) of weighted backprojection can be related to the Fourier transform B(ω_x, ω_y) of un-weighted backprojection as

$$B_w({\omega }_x,{\omega }_y)=B({\omega }_x,{\omega }_y)w(\phi ).$$ (A.17)

Then (A.16) becomes

$$F({\omega }_x,{\omega }_y)=w(\phi )B({\omega }_x,{\omega }_y)/[\frac{w(\phi )}{\sqrt{{\omega }_x^2+{\omega }_y^2}}+\beta ·M({\omega }_x,{\omega }_y)]=B({\omega }_x,{\omega }_y)\sqrt{{\omega }_x^2+{\omega }_y^2}/[1+\beta ·\frac{M({\omega }_x,{\omega }_y)\sqrt{{\omega }_x^2+{\omega }_y^2}}{w(\phi )}].$$ (A.18)

Equation (A.18) is in the form of ‘backprojection first, then 2D filter’ reconstruction approach and the Fourier domain 2D filter is $\sqrt{{\omega }_x^2+{\omega }_y^2}/[1+\beta ·M({\omega }_x,{\omega }_y)\sqrt{{\omega }_x^2+{\omega }_y^2}/w(\phi )]$. By using the central slice theorem, an FBP algorithm, which performs 1D filtering first, then backprojects, can be obtained. The Fourier domain 1D filter for the FBP algorithm is the central slice of the 2D filter $\sqrt{{\omega }_x^2+{\omega }_y^2}/[1+\beta ·M({\omega }_x,{\omega }_y)\sqrt{{\omega }_x^2+{\omega }_y^2}/w(\phi )]$, which gives

$$\text{Fourier domain filter for the}\mathrm{F}\mathrm{B}\mathrm{P}-\mathrm{M}\mathrm{A}\mathrm{P}\text{algorithm}=\frac{|\omega |}{1+\beta ·\frac{M_{ID}(\omega )·|\omega |}{w(\phi )}}.$$ (A.19)

When β = 0, (A.19) reduces to the ramp filter |ω| of the conventional FBP algorithm.

Appendix B

This appendix proves (A.12) and derives its 2D Fourier transform. The vector notation will be used in this appendix, and the derivation steps are similar to those in example 4 of chapter 1 in the textbook (Zeng 2010).

Using the coordinate system depicted in figure B1, let us consider the weighted backprojection of δ(x · θ) with x = (x, y) and θ = (cos θ, sin θ):

$$\mathrm{P}\mathrm{S}{\mathrm{F}}_w(\mathbf{x})={\int }_0^{\pi }w(\theta )\delta (\mathbf{x}·\mathit{\theta })\mathrm{d}\theta$$ (B.1)

where δ(x · θ) is the Radon transform of a point source function δ(x) and can be written as

$$\delta (\mathbf{x}·\mathit{\theta })={\int }_{-\infty }^{\infty }\delta (\mathbf{x}-t{\theta }^{\perp })\mathrm{d}t$$ (B.2)

with θ^⊥ = (−sin θ, cos θ). Equation (B.1) can then be written as

$$\mathrm{P}\mathrm{S}{\mathrm{F}}_w(\mathbf{x})={\int }_0^{\pi }{\int }_{-\infty }^{\infty }w(\theta )\delta (\mathbf{x}-t{\theta }^{\perp })\mathrm{d}t\mathrm{d}\theta$$ (B.3)

which can be viewed using the polar coordinate system. Let x̂ = tθ^⊥ with ‖x̂‖ = |t|, dx̂ = |t|dtdθ, and ∠x̂^⊥ = θ. The double integral using the polar coordinate system in (B.3) can be expressed using the Cartesian system as

$$\mathrm{P}\mathrm{S}{\mathrm{F}}_w(\mathbf{x})={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\frac{w(\angle {\mathbf{x̂}}^{\perp })\delta (\mathbf{x}-\mathbf{x̂})}{\Vert \mathbf{x̂}\Vert }\mathrm{d}\mathbf{x̂}=\frac{w(\angle {\mathbf{x}}^{\perp })}{\Vert \mathbf{x}\Vert }.$$ (B.4)

Next, we use the 2D Fourier transform in the polar coordinate system to find the transfer function, TF_w(ω) with ω = ρe^iφ, of (B.4) as follows:

$$T{F}_w(\rho {\mathrm{e}}^{\mathrm{i}\phi })={\int }_0^{\pi }{\int }_{-\infty }^{\infty }\mathrm{P}\mathrm{S}{\mathrm{F}}_w(\mathrm{r}{\mathrm{e}}^{\mathrm{i}\theta }){\mathrm{e}}^{-\mathrm{i}2\pi r\rho \text{cos}(\theta -\phi )}r\mathrm{d}r\mathrm{d}\theta ={\int }_0^{\pi }{\int }_{-\infty }^{\infty }\frac{w(\theta \pm \pi /2)}{|r|}{\mathrm{e}}^{-\mathrm{i}2\pi r\rho \text{cos}(\theta -\phi )}|r|\mathrm{d}r\mathrm{d}\theta ={\int }_0^{\pi }w(\theta \pm \pi /2)\left[{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{i}2\pi r\rho \text{cos}(\theta -\phi )}\mathrm{d}r\right]\mathrm{d}\theta ={\int }_0^{\pi }w(\theta \pm \pi /2)\delta (\rho \text{cos}(\theta -\phi ))\mathrm{d}\theta .$$ (B.5)

To evaluate the integral with a δ-function in (B.5), we need to consider the zeros of r cos(θ − φ). The zeros are θ = φ ± π/2 and only one of these zeros is between 0 and π. The normalization factor at this zero is given by 1/|[ρ cos(θ − φ)]′|_θ=φ±π/2| = 1/|ρ|. Recalling that w(φ) = w(φ ± π), (B.5) becomes

$$\mathrm{T}{\mathrm{F}}_w(\rho {\mathrm{e}}^{\mathrm{i}\phi })={\int }_0^{\pi }w(\theta \pm \frac{\pi }{2})\frac{1}{|\rho |}\delta (\theta -(\phi \pm \frac{\pi }{2}\left)\right)\mathrm{d}\theta =\frac{w(\phi )}{|\rho |}.$$ (B.6)

Figure B1.

Coordinate systems for 2D Radon transform.