On species sampling sequences induced by residual allocation models

Abstract

We discuss fully Bayesian inference in a class of species sampling models that are induced by residual allocation (sometimes called stick-breaking) priors on almost surely discrete random measures. This class provides a generalization of the well-known Ewens sampling formula that allows for additional flexibility while retaining computational tractability. In particular, the procedure is used to derive the exchangeable predictive probability functions associated with the generalized Dirichlet process of Hjort (2000) and the probit stick-breaking prior of Chung and Dunson (2009) and Rodriguez and Dunson (2011). The procedure is illustrated with applications to genetics and nonparametric mixture modeling.

1. Introduction

An exchangeable sequence of random variables X₁, X₂, … defined on a probability space $(\mathcal{X},\mathcal{B})$ follows a species sampling model (SSM) if its joint distribution can be characterized by a sequence of predictive rules where X₁ ~ G₀ and

$$p(X_{n+1}\in B\mid X_{1,\dots ,X_n})=\sum _{k=1}^{K^n}{q}_k^n\left({\mathbf{m}}^n\right){\delta }_{{\tilde{X}}_k}\left(B\right)+q_{K^n+1}^n\left({\mathbf{m}}^n\right)G_0\left(B\right),$$

for some non-atomic measure G₀ on $(\mathcal{X},\mathcal{B})$ and for all $\mathit{B}\in \mathcal{B}$. In the previous expression, δ_a denotes the degenerate probability measure placing probability 1 on a, ${\mathbf{m}}^n=(m_1^n,\dots ,m_{K^n}^n)$ with $m_k^n={\sum }_{j=1}^{n}I(X_j={\tilde{X}}_k)$ being the number of values among X₁, … , X_n that are equal to ${\tilde{X}}_k$, $K^n=\max \{k:m_k^n>0\}$ being the number of unique values among X₁, … , X_n, and $q_k^n$ for k ≤ n and n = 1, 2, … being a collection of functions of mⁿ (usually called the predictive probability functions, or PPFs) which for all n and mⁿ satisfy

$$q_k^n\left({\mathbf{m}}^n\right)\ge 0,\sum _{k=1}^{K^{n+1}}{q}_k^n\left({\mathbf{m}}^m\right)=1.$$

The name species sampling model comes from the application of this type of models in ecology and genetics (Fisher et al., 1943; Ewens, 1972; Engen, 1978). Indeed, we could think of sequentially sampling individuals in an infinite population with an unknown (and potentially infinite) number of species. When the first individual is sampled, its species is assigned a random tag generated according to G₀. Subsequently, individual n either belongs to one of the previously observed Kⁿ species with respective probabilities $q_1^n,\dots ,q_{K^n}^n$, or to a new species (which is again given a random tag according to G₀) with probability $q_{K^n+1}^n$.

A well-defined set of PPFs implies a symmetric joint probability distribution $p(m_1^n,\dots ,m_{K^n}^n)$ for the number of species and the sample sizes associated with each one of them, which can be obtained through a recursion where p(1) = 1,

$$p(m_1^n,\dots ,m_k^n+1,\dots ,n_{K^n})=q_k^n(m_1^n,\dots ,m_{K^n}^n)p(m_1^n,\dots ,m_k^n,\dots ,m_{K^n}^n)$$

for k ≤ Kⁿ, and

$$p(m_1^n,\dots ,m_{K^n}^n,1)=q_{K^n+1}^n(m_1^n,\dots ,m_{K^n}^n)p(m_1^n,\dots ,m_{K^n}^n)$$

(for example, see Pitman, 1995 and Lee et al., 2013). The function p is often called the exchangeable partition probability function (EPPF). Alternatively, this can be written as

$$q_k^n(m_1^n,\dots ,m_{K^n}^n)=\{\begin{array}{cc}\frac{p(m_1^n,\dots ,m_k^n+1,\dots ,n_{K^n})}{p(m_1^n,\dots ,m_k^n,\dots ,m_{K^n}^n)}\hfill & k\le K^n\hfill \\ \frac{p(m_1^n,\dots ,m_{K^n}^n,1)}{p(m_1^n,\dots ,m_{K^n}^n)}\hfill & k=K^n+1.\hfill \end{array}\phantom{\}}$$ (1)

In principle, constructing EPPFs is a difficult task, as ensuring that X₁, X₂, … is an exchangeable sequence implies quite strict conditions on the PPFs (for a discussion, see for example Pitman, 1995, Pitman, 1996b and Lee et al., 2013). As a consequence, the number of species sampling models available in the literature is rather small, with the most popular ones arguably being those associated with the Dirichlet process (DP) (Ferguson, 1973; Blackwell and MacQueen, 1973), the two-parameter Poisson-Dirichlet process (PDP) (Pitman, 1995), and the normalized inverse Gaussian measures (NIGM) (Lijoi et al., 2005).

The previous list suggests that there is a close link between the class of nonparametric priors on almost-surely discrete distributions often used in nonparametric Bayesian modeling and the class of SSMs. Indeed, a well known result due to Pitman (1996b) establishes that the de Finetti measure of any SSM can be written as

$$G(\cdot )=\sum _{k=1}^{\infty }{\omega }_k{\delta }_{X_k^{\ast }}(\cdot )+{\mathit{RG}}_0$$ (2)

for some sequence of positive random variables ω₁, ω₂, … and R such that $1-R={\sum }_{k=1}^{\infty }{\omega }_k\le 1$ almost surely, $X_1^{\ast },X_2^{\ast }$,… is a random sample from a non-atomic G₀, and the sequences ω₁, ω₂, … and $X_1^{\ast },X_2^{\ast },\dots$ are independent. The resulting SSM is termed proper if R = 0 with probability 1. This connection can be exploited to generate novel SSMs, in particular, we study the SSM induced by a class of residual allocation models, as well as the special cases associated with the generalized Dirichlet process (GDP) of Hjort (2000), and the probit stick-breaking processes (PSBP) (Rodriguez et al., 2009; Chung and Dunson, 2009; Rodriguez and Dunson, 2011). In addition to model construction, we discuss computational issues associated with Bayesian estimation in this class of models.

The remainder of the paper is organized as follows. Section 2 discusses the EPPF for a class of species sampling models, specifically, independent residual allocation models, giving a general expression and analyzing some special well-known particular cases. Section 3 applies the results to the probit stick-breaking priors of Chung and Dunson (2009) and Rodriguez and Dunson (2011) and to the generalized Dirichlet process of Hjort (2000). Section 4 discusses Bayesian inference for the parameter controlling the allocation distribution and the probability of discovery of a new species for the class of models considered here. Section 5 illustrates our methods using both simulated and real datasets. Final comments are given in Section 6. An Appendix contains proofs of some auxiliary results.

2. Exchangeable partition probability functions and predictive probability functions derived from residual allocation models

A random probability measure G defined on a probability space $(\mathcal{X},\mathcal{B})$ is said to follow an independent residual allocation prior if it can be represented as

$$G(\cdot )=\sum _{k=1}^N{\omega }_k{\delta }_{X_k^{\ast }},$$ (3)

where $N\in \mathbb{N},X_1^{\ast },X_2^{\ast },\dots$ is a sequence of independent and identically distributed realizations from some distribution G₀ and ω_k = z_k ∏_ℓ<k{1 – zℓ} where $z_k~H_k^{\theta }$ independently for all k = 1, 2, … (with the convention z_N = 1 if N < ∞), and $H_k^{\theta }$ is a probability distribution on [0, 1] indexed by the vector of parameters θ. Two of the best-known examples of residual allocation priors are the Dirichlet process (where N = ∞, θ = b, and z_k ~ Beta(1, b) for some b > 0) and the Poisson-Dirichlet process (for which θ = (a, b), z_k ~ Beta(1 – a, b, + ka) and either N = ∞, 0 ≤ a < 1 and b > –a or N < ∞, a < 0 and b = –aN). It follows that (3) is a special case of SSM (2). It should be also noted that for the case N = ∞, the resulting residual allocation model defines a probability model (i.e. the SSM is proper) if and only if ${\sum }_{k=1}^N\log (1-E_{\theta }(z_k\left)\right)=-\infty$, which is for instance the case of the PDP. See Barrientos et al. (2012).

Kingman (1978) and Pitman (1996b) discuss in more generality the relationship between almost surely discrete random distributions and SSMs. In particular, note that if X₁, … , X_n is an independent and identically distributed sample from G which follows a stick-breaking prior, then it is exchangeable and there is a positive probability of ties among the X_is. In fact, the EPPF associated with this prior can be computed as

$$p(m_1^n\dots ,m_{K^n}^n\mid \theta )=\sum _{(j_1,\dots ,j_{K^n})\in {\mathcal{J}}_{K^n}}{\mathsf{E}}_{\theta }\left\{\prod _{k=1}^{K^n}{\omega }_{\mathit{jk}}^{m_k^n}\right\},$$ (4)

where $\mathcal{J}$ represents the set of all possible sequences of distinct (not necessarily consecutive) positive integers of length Kⁿ. Briefly, this formula simply states that to compute the EPPF we need to consider all possible allocations of the observed species to Kⁿ of the atoms $X_1^{\ast },X_2^{\ast },\dots$ in (3), and compute the expected value of the probability of obtaining the sample under each of these orderings. Note that once the EPPF has been obtained, the PPFs necessary to define the associated SSM can be obtained using (1).

Example 1 (The Ewens sampling formula and the Dirichlet process)

Consider the case n = 2. When computing p(2) (i.e., the probability that the first two samples belong to the same species), Equation (4) reduces to $p\left(2\right)={\sum }_{k=1}^{\infty }{\mathsf{E}}_{\theta }\left\{{\omega }_k^2\right\}$. More generally, the probability that all the samples belong to the same species is simply $p\left(n\right)={\sum }_{k=1}^{\infty }{\mathsf{E}}_{\theta }\left\{{\omega }_k^n\right\}$. In the case of the Dirichlet process, this implies

$$p(m_1^n=n\mid b)=\sum _{k=1}^{\infty }{\mathsf{E}}_b\left\{{\omega }_k^n\right\}=\sum _{k=1}^{\infty }{\mathsf{E}}_b\left\{z_k^n\prod _{s<k}{(1-z_l)}^n\right\}=b\frac{\Gamma \left(b\right)\Gamma \left(n\right)}{\Gamma (b+n)},$$

which is a well known result.

The residual allocation construction associated with the weights in equation (3) provides a very general mechanism to define priors on random measures and, implicitly, on the associated SSMs. In the sequel, we will focus on the special case where all the stick-breaking ratios z_k are not only independent but also identically distributed, i.e., z_k ~ H for all k = 1, 2, …. Note that this type of construction leads to weights that are stochastically ordered. Indeed, when $z_k\underset{~}{\text{iid}}H$ we have w_k+1/w_k = (1 – z_k)_zk+1/zk for al k ≥ 1. Since P(z_k ≤ t) = P(z_k+1 ≤ t) and P((1 – z_k)_zk+1 ≤ z_k+1) = 1 then z_k+1 ≤ t implies (1 – z_k)_zk+1 ≤ t, so that P(z_k+1 ≤ t) ≤ P((1 – z_k)_zk+1 ≤ t), from which stochastic order follows. However, in spite of this property, this class of models still affords a great deal of flexibility while retaining some tractability.

Lemma 1

The EPPF induced by the stick breaking prior in (3) is given by

$$p(m_1^n,\dots ,m_{K^n}^n\mid \theta )=\sum _{\sigma \in {\mathcal{P}}_{K^n}}\left\{\prod _{k=1}^{K^n}\frac{{\gamma }_{\theta }\left(m_{{\sigma }_k}^n,{\Sigma }_{j=k+1}^{K^n}{m}_{{\sigma }_j}^n\right)}{1-{\gamma }_{\theta }\left(0,{\Sigma }_{j=k}^{K^n}{m}_{{\sigma }_j}^n\right)}\right\},$$ (5)

where ${\mathcal{P}}_{K^n}$ denotes the set of all permutations of {1, … , Kⁿ}, $\sigma =({\sigma }_1,\dots ,{\sigma }_K^n)$ and γ_θ(x, y) = E_θ{z^x(1 – z)^y} with z ~ H.

For a proof, see the Appendix. Note that, for the case where the stick-breaking ratios are i.i.d., we only need to consider the order in which the species arise during sampling, and not the actual identity of the atoms. From (5) it is easy to see that for $m_1^n=n$ (i.e., all samples belong to the same species, or Kⁿ = 1) we have

$$p(m_1^n=n\mid \theta )=\frac{{\gamma }_{\theta }(n,0)}{1-{\gamma }_{\theta }(0,n)},$$ (6)

while in the case $m_1^n=m_2^n=\cdots =m_n^n=1$ (i.e., each sample belongs to a different species, or Kⁿ = n) we have

$$p(m_1^n=1,\dots ,m_n^n=1\mid \theta )=n!\prod _{k=1}^n\frac{{\gamma }_{\theta }(1,n-k)}{1-{\gamma }_{\theta }(0,n-k+1)}=n!\prod _{k=0}^{n-1}\frac{{\gamma }_{\theta }(1,k)}{1-{\gamma }_{\theta }(0,k+1)}.$$ (7)

Furthermore, equation (7) corresponds to equation (5.2) from Hjort (2000).

Example 2 (The Ewens sampling formula and the Dirichlet process continued)

Again, if z_k ~ Beta(1, b) we have θ = b and

$${\gamma }_b(x,y)={\int }_0^1{z}^x{(1-z)}^{y}b{(1-z)}^{b-1}{d}_z=b\frac{\Gamma (x+1)\Gamma (y+b)}{\Gamma (x+y+b+1)}.$$

Hence,

$$\prod _{k=1}^{K^n}{\gamma }_b\left(m_{{\sigma }_k}^{K^n}\sum _{j=k+1}^{K^n}{m}_{{\sigma }_j}^n\right)=b^{K^n}\frac{\Gamma \left(b\right)}{\Gamma (b+n)}\left[\prod _{k=1}^{K^n}\Gamma m_{{\sigma }_k}^n\right]\left[\prod _{k=1}^{K^n}\frac{m_{{\sigma }_k}^n}{b+{\Sigma }_{j=k}^{K^n}{m}_{{\sigma }_j}}\right],$$ (8)

while

$$\prod _{k=1}^{K^n}\left\{1-{\gamma }_b\left(0,\sum _{j=k}^{K^n}{m}_{{\sigma }_j}^n\right)\right\}=\prod _{k=1}^{K^n}\frac{\sum _{j=1}^{K^n}{m}_{{\sigma }_j}^n}{b+\sum _{j=1}^{K^n}{m}_{{\sigma }_j}^n}.$$ (9)

Putting (8) and (9) together we have

$$\begin{array}{cc}\hfill p(m_1^n,\dots ,m_{K^n}^n\mid b)& =b^{K^n}\frac{\Gamma \left(b\right)}{\Gamma (b+n)}\left[\prod _{k=1}^{K^n}\Gamma \left(m_k^n\right)\right]\sum _{\sigma \in {\mathcal{P}}_{K^n}}\prod _{k=1}^{K^n}\frac{m_{{\sigma }_k}^n}{\sum _{j=1}^{K^n}{m}_{{\sigma }_j}}\hfill \\ \hfill & =b^{K^n}\frac{\Gamma \left(b\right)}{\Gamma (b+n)}\left[\prod _{k=1}^{K^n}\Gamma \left(m_k^n\right)\right],\hfill \end{array}$$

which is a well known formula for the Dirichlet process. The fact that ${\sum }_{\sigma \in {\mathcal{P}}_{K^n}}{\prod }_{k=1}^{K^n}\frac{m_{{\sigma }_k}^n}{{\sum }_{j=k}^{K^n}{m}_{{\sigma }_j}}=1$ can be shown by induction (see the Appendix).

Note that the function

$$g_{\theta }\left(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_{K^n}}^n\right)=\prod _{k=1}^{K^n}\frac{{\gamma }_{\theta }\left(m_{{\sigma }_k}^n,\sum _{j=k+1}^{K^n}{m}_{{\sigma }_j}^n\right)}{1-{\gamma }_{\theta }\left(0,\sum _{j=k}^{K^n}{m}_{{\sigma }_j}^n\right)}$$

satisfies g_θ(1) = 1, but is in general not symmetric on its arguments and depends on the permutation σ, which encodes the order of the indices that identify the components that generate the unique labels associated with the observed species. Indeed, in the future it will be convenient to interpret $g_{\theta }(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_{K^n}}^n)$ as describing the joint probability distribution of the exchangeable vector $(m_1^n,\dots ,m_{K^n}^n)$ and the permutation σ, $p(m_1^n,\dots ,m_{K^n}^n,\sigma \mid \theta )$. This joint probability can be potentially factorized as

$$p\left(m_1^n,\dots ,m_{K^n}^n,\sigma \mid \theta \right)=p\left(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_{K^n}}^n\mid \sigma ,\theta \right)p(\sigma \mid \theta ).$$

Example 3 (The Ewens sampling formula and the Dirichlet process continued)

Since the Dirichlet process is invariant to size-biased permutations of the components, for the Ewens sampling formula we have

$$p(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_{K^n}}^n\mid \sigma ,b)=p(m_1^n,\dots ,m_{K^n}^n\mid b)=b^{K^n}\frac{\Gamma \left(b\right)}{\Gamma (b+n)}\left[\prod _{k=1}^{K^n}\Gamma \left(m_k^n\right)\right],$$

and

$$p(\sigma \mid b)=p\left(\sigma \right)=\prod _{k=1}^{K^n}\frac{m_{{\sigma }_k}^n}{\sum _{j=k}^{K^n}{m}_{{\sigma }_j}}.$$

This probability is maximized for the permutation σ’ such that m_σ’(1) ≥ m_σ’(2) ≥ ⋯ ≥ m_σ’(Kⁿ). Indeed, since in the Dirichlet process the weights are stochastically ordered, we do not expect that all possible permutation of the labels should be equiprobable. Instead, permutations that assign larger groups to lower indexes should be preferred.

The interpretation of g_θ as a joint probability distribution will be helpful later in developing computational algorithms for these species sampling models.

3. Two new species sampling models

3.1. The probit stick-breaking process

Consider the class of probit stick-breaking priors (Chung and Dunson, 2009; Rodriguez and Dunson, 2011) where z_k = Φ(u_k) and u_k ~ N(μ, τ²). Note that if μ = 0 and τ² = 1, then z_k ~ Uni[0, 1] and we recover the Dirichlet process as a special case.

For any integers c and d, we can write

$$z_k^c{(1-z_k)}^d=z_k^c\sum _{j=0}^d\left(\begin{array}{c}\hfill d\hfill \\ \hfill j\hfill \end{array}\right){(-z_k)}^j=\sum _{j=0}^d{(-1)}^j\left(\begin{array}{c}\hfill d\hfill \\ \hfill j\hfill \end{array}\right)z_k^{j+c}.$$

Rodriguez and Dunson (2011) show that, for any integer q, $\mathsf{E}(z_k^q\mid \mu ,{\tau }^2)=\text{Pr}({\mathbf{T}}_q\in {\Omega }_q)$ where ${\Omega }_q=\left\{\right(x_1,\dots ,x_q)\in {\mathbb{R}}^q:x_i\ge 0\}$, and T_q = (T₁, … , T_q)’ follows a q-variate normal distribution with mean E(T_i) = μ and covariance matrix satisfying Var(T_i) = τ² + 1 and Cov(T_i, T_j) = τ². Hence

$${\gamma }_{\mu ,\tau }(c,d)=\sum _{j=0}^d\left(\begin{array}{c}\hfill d\hfill \\ \hfill j\hfill \end{array}\right){(-1)}^j\text{Pr}({\mathbf{T}}_{j+c}\in {\Omega }_{j+c}).$$

Alternatively, noting that $(1-u)\underset{=}{D}{u}^{\ast }$, where u* = Φ(z*) and z* ~ N(–μ, τ²), we could also write

$${\gamma }_{\mu ,\tau }(c,d)=\sum _{j=0}^c\left(\begin{array}{c}\hfill c\hfill \\ \hfill j\hfill \end{array}\right){(-1)}^j\text{Pr}({\mathbf{T}}_{j+d}^{\ast }\in {\Omega }_{j+d})$$

where ${\mathbf{T}}_q^{\ast }\underset{=}{D}-{\mathbf{T}}_q$. Computationally, the first expression would be preferred if d < c and the second if d > c (if d = c both formulas have the same computational complexity).

3.2. A generalized Dirichlet processes

Hjort (2000) defined a new class of residual allocation priors by letting N = ∞ and u_k ~ Beta(a, b). Since a = 1 implies that G follows a Dirichlet process, he called this construction a generalized Dirichlet processes (GDP). To compute the EPPF associated with the GDP, note that

$$\mathrm{E}\left\{z_k^c{(1-z_k)}^d\right\}=\frac{\Gamma (a+b)}{\Gamma \left(a\right)\Gamma \left(b\right)}\frac{\Gamma (a+c)\Gamma (b+d)}{\Gamma (a+b+c+d)}.$$

Hence

$$p(m_1^n,\dots ,m_{K^n}^n\mid a,b)={\left\{\frac{\Gamma (a+b)}{\Gamma \left(a\right)\Gamma \left(b\right)}\right\}}^{K^n}\frac{\Gamma \left(b\right)}{\Gamma (b+n)}\sum _{\sigma \in {\mathcal{P}}_{K^n}}\prod _{k=1}^{K^n}\frac{\Gamma \left(a+m_k^n\right)}{\left\{\frac{\Gamma \left(a+b+\sum _{j=k}^{K^n}{m}_{{\sigma }_j}^n\right)}{\Gamma \left(b+\sum _{j=k}^{K^n}{m}_{{\sigma }_j}^n\right)}-\frac{\Gamma (a+b)}{\Gamma \left(b\right)}\right\}}.$$

Example 4

Note that if a = 1 this expression leads to

$$p(m_1^n,\dots ,m_{K^n}^n\mid b)=b^{K^n}\frac{\Gamma \left(b\right)}{\Gamma (b+n)}\prod _{k=1}^{K^n}\Gamma \left(m_k^n\right),$$

as expected.

As the following result shows, the GDP is particularly appealing as the basis for creating species sampling models because it allows for a multitude of asymptotic behaviors for the expected number of species.

Lemma 2

The expected number of clusters E_a,b(Kⁿ) for the species sampling model induced by a generalized Dirichlet process where z_k ~ Beta(a, b) is given by

$${\mathrm{E}}_{a,b}\left(K^n\right)=\sum _{i=1}^n\frac{\mathit{ia}\Gamma (a+b)\Gamma (b+i-1)}{\Gamma \left(b\right)\Gamma (a+b+i)-\Gamma (a+b)\Gamma (b+i)}.$$ (10)

For a proof, see the Appendix. Note that for a = 1, equation (10) simplifies to ${\mathsf{E}}_{a,b}\left(K^n\right)={\sum }_{i=1}^n\frac{b}{b+i-1}~o\left(\log n\right)$, a well known result for the Dirichlet process (Antoniak, 1974). For more general values of a, Stirling’s approximation can be used to show that

$$\frac{\mathit{na}\Gamma (a+b)\Gamma (b+n-1)}{\Gamma \left(b\right)\Gamma (a+b+n)-\Gamma (a+b)\Gamma (b+n)}\approx C(a,b)n^{-a},$$

where C(a, b) = {aΓ(a + b)/Γ(b)} exp{−2(a + 1)}. Hence, for a ≤ 1 the expected number of distinct species will grow slowly but without bound as n increases, with E_a,b(Kⁿ) ~ o(n^1–a). This behavior is similar to the one associated with the Poisson-Dirichlet process (for example, see Pitman, 2006 and Sudderth and Jordan, 2009). However, for a > 1 the expected number of species instead converges to a finite constant, a result that is similar to the one obtained from a hierarchical specification for the Poisson-Dirichlet process in which a < 0, b = –aL for some integer L, and L is given a prior with support over $\mathbb{N}$ and having a finite mean.

4. Bayesian inference for species sampling models

In this section we discuss practical issues associated with Bayesian inference for species sampling models with a EPPF defined by (5). In particular we focus on estimation of the parameter θ and prediction of probability of discovery for new species in a new sample using simulation based algorithms.

4.1. Parameter estimation

Given a prior p(θ), the posterior distribution of the parameters of the SSM is trivially given by

$$p(\theta \mid m_1^n,\dots ,m_{K^n}^n)\propto p_{\theta }(m_1^n,\dots ,m_{K^n}^n)p\left(\theta \right),$$

where $p_{\theta }(m_1^n,\dots ,m_{K^n}^n)$ was given in (5). Since θ is typically a low dimensional vector, exploring this posterior distribution using a Markov chain Monte Carlo algorithm should be in principle straightforward. However, for realistic applications, evaluating the sum over all possible permutations of the set {1, 2, … , Kⁿ} is infeasible (for example, with only Kⁿ = 10 species, the number of terms in the sum is 10! = 3, 628,800, all of which need to be evaluated each time the likelihood is calculated).

In a Bayesian setting we can get around this issue by reinterpreting $g_{\theta }(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_{K^n}}^n)$ as describing a joint distribution over both the permutation σ and the vector of observations $m_1^n,\dots ,m_K^n$, and treating σ as a latent variable to be imputed as part of an augmented sampler. Once we augment the model by introducing the permutation σ, the joint posterior distribution can be written as

$$p(\theta ,\sigma \mid m_1^n,\dots ,m_{K^n}^n)\propto g_{\theta }\left(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_{K^n}}^n\right)p\left(\theta \right).$$

This posterior distribution can be explored by alternatively sampling from the full conditional associated with the parameters θ that control the prior size of the weights, and the full conditional distribution of the permutation σ controlling the assignment of species to atoms:

1. Randomly initialize the values of the model parameters to θ⁽⁰⁾ and σ⁽⁰⁾.

2. For each b = 1, … , B repeat the following two steps:

   • (a) Sample θ^(b) from the full conditional distribution p (θ ∣ m, σ^(b–1)), possibly using a Metropolis Hastings step.
   • (b) Sample σ^(b) from the full conditional distribution p (σ ∣ m, θ^(b)), possibly using a Metropolis Hastings step.

For sampling θ we favor a Metropolis-Hasting step with a multivariate Gaussian random walk proposal on a suitable transformation of θ (for example, in the case of a SSM induced by the generalized Dirichlet process prior, we use a bivariate Gaussian random walk on log a and log b as our proposal distribution). The covariance matrix for the proposal is chosen on the basis of an estimate of Cov(θ ∣ m) obtained from a preliminary run that uses uncorrelated proposals. The covariance matrix obtained in this way is then rescaled to obtain an overall acceptance rate of around 35%. The acceptance ratio for these proposals reduces to

$${\Delta }_1=\min \left\{1,\frac{g_{{\theta }^{\ast }}\left(m_{{\sigma }^{(b-1)}\left(1\right)}^n,\dots ,m_{{\sigma }^{(b-1)}\left(K^n\right)}^n\right)p\left({\theta }^{\ast }\right)\mid J\left({\theta }^{(b-1)}\right)\mid }{g_{{\theta }^{(b-1)}}\left(m_{{\sigma }^{(b-1)}\left(1\right)}^n,\dots ,m_{{\sigma }^{(b-1)}\left(K^n\right)}^n\right)p\left({\theta }^{(b-1)}\right)\mid J\left({\theta }^{\ast }\right)\mid }\right\},$$

where ∣J(θ)∣ is the Jacobian of the transformation applied to θ.

For sampling σ, the most obvious proposal involves generating a new permutation σ^* from the current state of the Markov chain, σ^(b–1), by randomly selecting two indexes i, j ∈ {1, … , Kⁿ} and setting σ^*(i) = σ^(b–1)(j) and σ^*(j) = σ^(b–1)(i), while keeping all other entries of σ^* identical to those of σ^(b–1). The acceptance ratio for this proposal reduces to

$${\Delta }_2=\min \left\{1,\frac{g_{{\theta }^{\left(b\right)}}\left(m_{{\sigma }^{\ast }\left(1\right)}^n,\dots ,m_{{\sigma }^{\ast }\left(K^n\right)}^n\right)}{g_{{\theta }^{\left(b\right)}}\left(m_{{\sigma }^{(b-1)}\left(1\right)}^n,\dots ,m_{{\sigma }^{(b-1)}\left(K^n\right)}^n\right)}\right\}.$$

Although this is a natural approach, our numerical experiments suggest that this simple scheme mixes too slowly to be practical. Instead, we consider sampling algorithms that simultaneously update blocks of r randomly selected components of the permutation σ. More specifically, note that for any set of indexes Ξ = {ξ₁, … , ξ_r} with ξ_i ∈ {1, … , Kⁿ} and ξ_i ≠ ξ_j for i ≠ j, and for any permutation π of Ξ, the full conditional probability given by p {(σ_ξ1, … , σ_ξr) = (σ_πξ1, … , σ_πξr) ∣ m, ⋯ } is proportional to

$$g_{\theta }\left(m_{{\sigma }_1},\dots ,m_{{\sigma }_{{\xi }_1-1}},m_{{\sigma }_{{\pi }_{{\xi }_1}}},m_{{\sigma }_{{\xi }_1+1}},\dots ,m_{{\sigma }_{{\xi }_r-1}},m_{{\sigma }_{{\pi }_{{\xi }_r}}},m_{{\sigma }_{{\xi }_r+1}},\dots ,m_{{\sigma }_{K^n}}\right).$$

For small values of r (say, in the range of 4 to 6) an algorithm that uniformly selects the indexes in ξ at each iteration can sample from this full conditional distribution in a reasonable amount of time. In particular note that the computation of p (σ_ξ1, … , σ_ξr ∣ m, ⋯ ) can be easily parallelized. Furthermore in the case r = 2 this scheme is essentially equivalent to the naive algorithm described before.

The proposal described above works well when the values m₁, … , m_Kⁿ are, for the most part, distinct. However, when there are multiple ties among the counts this proposal can be very inefficient, as permutations that involve swapping positions for species that have the same size lead to the same value of g_θ. In those cases, we use stratified sampling instead of random sampling to select the set Ξ. More specifically, the set Ξ is selected by first selecting r cluster sizes among the unique values of m₁, … , m_Kⁿ, and then each ξ_i is selected uniformly among the indexes that correspond to each of the unique values previously selected. If m₁, … , m_Kⁿ are all distinct, this scheme is equivalent to randomly sampling ξ₁, … , ξ_K without replacement form the set {1, … , Kⁿ}. However, when ties are present, the algorithm will avoid considering swaps that involve two species with the same number of observations.

Finally, in addition to the local updates for σ just described, we incorporate a global update σ that consists on randomly proposing a completely new permutation from an independent proposal with

$$q\left({\sigma }^{\ast }\right)=\prod _{k=1}^{K^n}\frac{m_{{\sigma }_k^{\ast }}}{\sum _{j=k}^{K^n}{m}_{{\sigma }_j^{\ast }}}.$$

(Recall that this is the probability of a permutation of the indexes associated with a Dirichlet process prior, and it favors permutations in which larger groups are assigned to lower indexes). The acceptance probability for this proposal is

$${\Delta }_3=\min \left\{1,\frac{g_{{\theta }^{\left(b\right)}}\left(m_{{\sigma }_1^{\ast }}^n,\dots ,m_{{\sigma }_{K^n}^{\ast }}^n\right)}{g_{{\theta }^{\left(b\right)}}\left(m_{{\sigma }_1^{(b-1)}}^n,\dots ,m_{{\sigma }_{K^n}^{(b-1)}}^n\right)}\prod _{k=1}^{K^n}\frac{m_{{\sigma }_k^{(b-1)}}}{m_{{\sigma }_k^{\ast }}}\frac{\sum _{j=k}^{K^n}{m}_{{\sigma }_j^{\ast }}}{\sum _{j=k}^{K^n}{m}_{{\sigma }_j^{(b-1)}}}\right\}.$$

This long-range move is used sparingly. We select q, the number of steps between attempts to perform a global move, so that the probability of covering any specific position with the short-range moves discussed before over q moves, (1 – r/K)^q, is high (in our numerical experiments, 0.999).

4.2. Predicting the number of new species

The previous MCMC algorithm can be easily extended to estimate the predictive distribution of ${\tilde{K}}^{\tilde{n}}$, the number of new species to be observed if the current sample size is extended from n to $n+\tilde{n}$. This can be done by computing an “order-dependent” EPPF, as described below.

Consider first the probability that a single newly sampled individual belongs to one of the existing species. In this case, the addition of a new species does not affect the permutation σ. Furthermore, for the species identified by σ_k, it is clear that such probability is proportional to

$$g_{\theta }(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_k}^n+1,\dots ,m_{{\sigma }_{K^n}}^n).$$

On the other hand, the probability that a new species appears will depend on the position in the order where that new species resides. Hence, to compute this probability we need to consider an extended permutation $\tilde{\sigma }$ of the elements of {1, … , Kⁿ + 1} where ${\tilde{\sigma }}_{K^n+1}$ (which indicates the relative position of the newly observed species) can take any value on {1, … , Kⁿ + 1}, while ${\tilde{\sigma }}_1,\dots ,{\tilde{\sigma }}_{K^n}$ must respect the same order of the elements induced by the original permutation σ. In particular, the permutation the assigns ${\tilde{\sigma }}_{K^n+1}=k$ has probability proportional to

$$g_{\theta }(m_{{\sigma }_1}^n,\dots ,m_{{\sigma }_k}^n,1,m_{{\sigma }_{k+1}}^n,\dots ,m_{{\sigma }_{K^n}}^n).$$

In the context of our MCMC algorithm, these probabilities can be used to sample the species of a new individual by extending the vector mⁿ to mⁿ⁺¹ and (if required) the permutation σ to $\tilde{\sigma }$. Furthermore, by sequentially applying the same ideas we can simulate from the distribution of new $\tilde{n}$ individuals over species, allowing for inferences over ${\tilde{K}}^{\tilde{n}}$, as well as any other functionals of interest.

5. Illustrations

5.1. Simulation study 1

We begin by considering four simulated datasets, which are presented in Table 1. The first two datasets were simulated from a species sampling model induced by a DP with precision parameter b = 2.0. These two datasets differ in terms of the total number of observations (n = 500 in the first case and n = 5000 in the second). On the other hand, the last two datasets were generated from the species sampling model induced by a GDP with parameters a = 0.2, b = 1.5, and a = 2.0, b = 0.3. These parameters correspond to situations in which the prior expected number of species either grows at an exponential rate with the number of observations, or converges to a finite value as n grows. In addition to estimating the parameters of the GDP, we also predict ${\tilde{K}}^{\tilde{n}}$, the expected number of species if the sample is extended from n to $n+\tilde{n}$. These results are compared against those obtained by fitting species sampling models based on the Dirichlet process (fitted using the data-augmentation algorithm of Escobar and West, 1995) and/or the Poisson-Dirichlet process (fitted using a joint random walk Metropolis-Hastings algorithm). All results are based on 250000 iterations of the respective algorithms, which were obtained after a burn-in period of 20000 iterations. Priors for the parameters of the SSM associated with the GDP and DP are exponentials with mean 1, while for the PDP we use a uniform prior on the interval [0, 1] for the intensity parameter and an exponential with mean 1 for the concentration parameter.

Table 1.

Four datasets used in our first simulation study.

ID	True a	True b	m
1	1.0	2.0	(36, 160, 49, 85, 35, 57, 63, 10, 1, 1, 3)
2	1.0	2.0	(2552, 1, 919, 624, 327, 227, 131, 129, 12, 5, 8, 30, 21, 1, 9, 3, 1)
3	0.2	1.5	(120, 19, 20, 19, 2, 22, 1, 2, 173, 21, 56, 2, 7, 2, 5, 2, 1, 4, 4, 12, 1, 4, 1)
4	2.0	1.5	(353, 81, 30, 16, 9, 6, 5)

Table 2 presents posterior means and 95% posterior symmetric credible intervals for the parameters of the SSM induced by the GDP, along with the associated equivalent sample sizes (ESS). Overall, we are capable of recovering the true values of the parameters in all four examples, although the level of uncertainty associated with them is relatively high. Furthermore, we note that the equivalent sample sizes are relatively small, with the ESS tending to be smaller when the number of components is higher. This is likely a consequence of the need to sample the permutation of the groups using a Metropolis step, which increases the overall autocorrelation in the chain.

Table 2.

Results from our simulation study. The last four columns show the posterior mean and the posterior 95% symmetric credible intervals for the parameters of the SSM induced by a generalized Dirichlet process, along with the equivalent sample sizes associated with the MCMC sample.

ID	n	K	True a	True b	E(a ∣ m) under GDP	ESS(a)	E(b ∣ m) under GDP	ESS(a)
1	500	11	1.0	2.0	0.98 (0.07, 2.63)	11,817	1.70 (0.45, 4.00)	12,136
2	5000	17	1.0	2.0	1.09 (0.04, 3.30)	2,979	2.07 (0.51, 5.12)	3,394
3	500	23	0.2	1.5	0.35 (0.01, 1.14)	3,963	2.26 (0.82, 4.96)	5,497
4	500	7	2.0	1.5	1.47 (0.09, 4.41)	15,801	1.31 (0.28, 3.46)	13,616

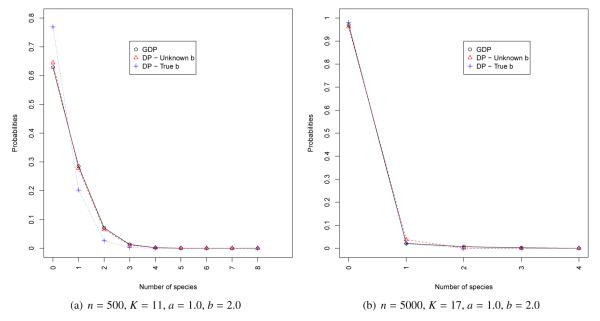
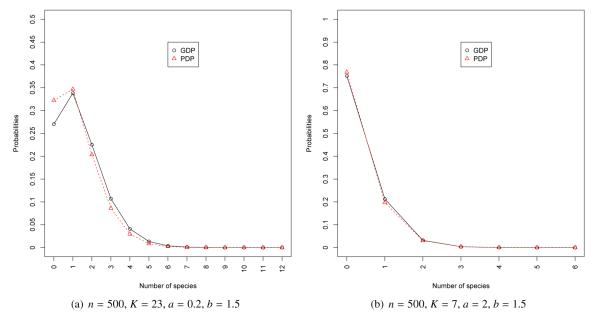
Figure 1(a) and 1(b) present estimates of the predictive distribution of the number of new species in a sample of 100 observation for our first two datasets. In this setting we compare the distribution generated by the SSM associated with the GDP with unknown parameters, with that generated by the SSM associated with a DP with unknown parameter b (recall that this is equivalent to setting a = 1 in the GDP), and that associated with a DP with known (true) parameter b = 2. Note that, even though there is substantial uncertainty associated with the estimate of a and b, in both cases the prediction of the number of species from the GDP are essentially identical to those generated by the DP with unknown parameter. Similarly Figures 2(a) and 2(b) show the predictive distributions for the number of species under the SSMs associated with the GDP and the PDP for the last two datasets. Interestingly enough, the predictions from these two models (which, should be emphasized, are not nested) are very similar in these examples.

Figure 1.

Distribution of the number of new species in a new sample of 150 individuals for datasets 1 and 2. We compare the distribution under the true parameter with the posterior distribution under the species sampling model induced by a Dirichlet process with precision parameter b, and under a species sampling model induced by a generalized Dirichlet process model with parameters a and b.

Figure 2.

Posterior distribution of the number of new species in a new sample of 150 individuals for datasets 3 and 4. We compare the posterior distribution under the species sampling model induced by a Dirichlet process with precision parameter b and under a species sampling model induced by a generalized Dirichlet process model with parameters a and b.

5.2. Simulation study 2

In this section we consider two datasets, both with K = 8 and n = 1200 (see Table 3). None of the two datasets were simulated according to a known species sampling model. Instead, they were selected to represent two opposite situations in terms of the relative size of the observed species. Indeed, while the first dataset corresponds to a situation where species are uniformly represented, the second corresponds to a very non-uniform distribution.

Table 3.

Two datasets used in our second simulation study.

ID	m
5	(150, 150, 150, 150, 150, 150, 150, 150)
6	(800, 300, 80, 16, 1, 1, 1, 1)

Figure 3(a) shows the posterior expected number of new species for each of the two datasets under a generalized Dirichlet process with parameters a = 0.2 and b = 0.7 as a function of the new sample size $\tilde{n}$. These curves were constructed using 40000 samples of our MCMC algorithm obtained by burning the first 200000 iterations of the chain and by skipping every 50 iterations. The differences between the two curves illustrate that, unlike the Poisson-Dirichlet process, predictions under the generalized Dirichlet process depend not only on the number of species observed so far, but also on the relative sizes of the species. To further illustrate the differences between the methods, we also present in Figure 3(b) the expected number of species for each of the two samples sizes under the generalized Dirichlet process when the values of a and b are estimated from the data. These estimates are complemented with the expected values under a Poisson-Dirichlet process, which are also treated as unknown.

Figure 3.

Posterior expected number of new species in an additional sample of size $\tilde{n}$ for the datasets in Table 3.

5.3. Modeling expressed sequence tag data

As a final illustration we consider a real dataset discussed in Mao and Lindsay (2002), Mao (2004), and Lijoi et al. (2007). The data consist of n = 2574 randomly selected expressed sequence tags taken form a large cDNA library made from the 0 mm to 3 mm buds of tomato flowers. The number of distinct tags observed in this sample is K = 1814; Table 4 shows the number of times each species size was observed in the sample (e.g., 1423 tags were observed only once).

Table 4.

Data on the number of expressed sequence tags from a cDNA library made from the 0 mm to 3 mm buds of tomato flowers.

Size	1	2	3	4	5	6	7	8	9	10	11	12	13	14	16	23	27
Frequency	1423	253	71	33	11	6	2	3	1	2	2	1	1	1	2	1	1

We compare the species sampling model associated with the GDP against the species sample models induced by the DP and the PDP. For this illustration, the algorithm described in Section 4 was used to generate of 20000 samples from the posterior distribution, obtained after a burn-in of 100000 iterations and thinning every 80 observations. The parameters a and b of the GDP are given exponential prior distributions with means 0.1 and 1000 respectively; the corresponding posterior means are E(a ∣ m) = 0.053 and E(b ∣ m) = 1345, while the respective 95% symmetric credible intervals are (0.001, 0.186) and (1172, 1584). The equivalent sample sizes for these parameters are 3385 for a and 5431 for b. In the case of the PDP, the parameters are given a uniform distribution on the (0, 1) interval and an exponential prior with mean 800; the corresponding posterior means are 0.61 and 735.9, with 95% credible intervals of (0.53, 0.67) and (515.6, 1017.4). Finally, for the DP an exponential prior with mean 1000 is employed for the concentration parameters, which leads to a posterior mean of 2724.9 and 95% posterior credible interval of (2491.3, 2972.1).

Figure 4 presents the distribution of the number of unique species in a new sample of size 500 taken from this population under these three models, while Figure 4(b) shows the posterior expected number of species for a new sample of size $\tilde{n}$. Not surprisingly given the large number of singleton species, the PDP favors a larger number of new species than the DP. On the other hand, the GDP seems to offer a compromise between both predictions, with a forecast of the number of species that seems to be in between those generated by the DP and the PDP.

Figure 4.

Prediction for the number of new species for the expressed sequence tag data of Mao and Lindsay (2002). Panel (a) shows the posterior distribution of the number of new species in a new sample of 500 individuals under each of three competing models: the generalized Dirichlet process (GDP), the Poisson-Dirichlet process (PDP) and the Dirichlet process (DP). Panel (b) shows the posterior expected number of species for a new sample of size $\tilde{n}$ under each of the three competing models.

6. Discussion

We have discussed the structure of species sampling models that arise from residual allocation models with independent and identically distributed stick-breaking ratios. The approach we propose avoids an explicit truncation of the process and the need to directly infer the underlying probabilities of the different species.

One interesting observation from our example is that, for small samples, there is little difference between the GDP and other similar models. However, for large samples with a large numbers of individuals belonging to unique species, the results can be quite different. Another interesting observation relates to the relatively high levels of uncertainty associated with posterior estimates of the parameters of the species sampling models. As pointed out by one referee, this is particularly noteworthy in situations such as dataset 4, where the posterior credible interval for a in the GDP encompasses situations that correspond to both finite and infinite prior expected number of species. To us, this highlights the importance of using model-averaged predictions (in which we integrate over the posterior distribution of the parameters) instead of just “plugging in” point estimators. It also highlights the difficulties of differentiating, in practice, between models that assume an infinite number of species and models with a finite but unknown number of them.

Although we do not consider an explicit example because of space constraints, it is worthwhile noting that, besides being used to model data directly, species sampling models are widely used as priors on partition structures in the context of (nonparametric) mixture models (e.g., see Escobar and West, 1995). In that context, a closed form for the EPPF provides the basis for the so-called “collapsed” Gibbs samplers, which act on the space of equivalence classes implied by the partitions (e.g., see Escobar, 1994, Neal, 2000 and references therein). In such cases, sampling over the permutations plays the same role as the label-switching moves commonly used in “blocked” and “retrospective” Gibbs samplers that explicitly represent the mixture distribution (for example, see Roberts and Papaspiliopoulos, 2008). Because of the invariance to size-biased permutations inherent to DP and PDP priors (Pitman, 1996a), that type of label-switching moves are not required in collapsed Gibbs samplers for mixture models based on those processes. However, for more general general priors on the weights, label-switching moves seem to be required for both collapsed and blocked samplers.

The approach discussed in this paper could potentially be extended to residual allocation models for which residuals are not identically distributed. Indeed, our key observation is that Bayesian inference on general species sampling models can be carried out using a data augmentation approach that considers the identity of the atoms to which each species is assigned. When the weights are independent and identically distributed this is relatively straightforward because only the order in which the different species appear matters. For more general models we also need to consider the separation between species, considerably increasing the computational burden.

Devising specific sampling algorithms for the parameters associated with the SSM is highly model-dependent and we have just discussed simple random walk Metropolis algorithms. In order to improve the efficiency of our algorithm, adaptive techniques such as those introduced in Roberts and Rosenthal (2009) might be worthwhile pursuing. However, we do note that the reason for a slow mixing seems to be the need to sample the permutations; designing better algorithms for this particular step might have a stronger impact on the efficiency of the algorithm.

Highlights for Review.

• We discuss fully Bayesian inference for a class of models induced by residual allocation priors.

• We give a generalization of the Ewens sampling formula for the class under study.

• We derive the exchangeable partition probability function for generalized Dirichlet and probit stick-breaking priors.

• A suitable computational strategy for fitting the models is described.

Appendix. Proofs of Theoretical Results

Proof of Lemma 1

From (4) we have

$$p(m_1^n,\dots ,m_{K^n}^n)=\sum _{j_1}\sum _{j_2\ne j_1}\cdots \sum _{j_{K^n}\notin \{j_1,\dots ,j_{K^n-1}}\mathsf{E}\left\{\prod _{k=1}^{K^n}{\left(z_{j_k}\prod _{r<j_k}\{1-z_r\}\right)}^{m_k^n}\right\}.$$

This sum can be broken into Kⁿ! pieces according to the ordering of the indexes j₁, … , j_Kⁿ. Because of the symmetry of the problem, it is enough to work with a particular ordering of the variables, for example j₁ < j₂ < … < j_Kⁿ. In that case

$$\begin{array}{cc}\hfill \prod _{k=1}^{K_n}{\omega }_{j_k}^{m_k^n}=& {(1-z_1)}^{{\Sigma }_{j=1}^{K^n}{m}_j^n}{(1-z_2)}^{{\Sigma }_{j=1}^{K^n}{m}_j^n}\cdots {(1-z_{s1})}^{{\Sigma }_{j=1}^{K^n}{m}_j^n{z}_{j1}^{m_1}}{(1-z_{j_1})}^{{\Sigma }_{j=2}^{K^n}{m}_j^n}\hfill \\ \hfill & {(1-z_{j_1+1})}^{{\Sigma }_{j=2}^{K^n}{m}_j^n}{(1-z_{j_1+2})}^{{\Sigma }_{j=2}^{K^n}{m}_j^n}\cdots {(1-z_{j_1+s_2})}^{{\Sigma }_{j=2}^{K^n}{m}_j^n{z}_{j^1}^{m_2}}{(1-z_{j_2})}^{{\Sigma }_{j=3}^{K^n}{m}_j^n}\cdots \hfill \\ \hfill & \cdots {(1-z_{j_{K^n-1}+1})}^{m_{K^n}^n}{(1-z_{j_{K^n-1}+2})}^{m_{K^n}^n}\cdots {(1-z_{j_{K^n-1+s_{K^n}}})}^{m_{K^n}^n{z}_{j_{K^n}}^{m_{K^n}}},\hfill \end{array}$$

where s_i = j_i – j_i–1 – 1 for i = 1, … , Kⁿ are the sizes of the “gaps” between the labels of two consecutive observed species, with the convention j₀ = 0. Now, since z₁, z₂, … are assumed to be independent and identically distributed, we have

$$\mathsf{E}\left\{\prod _{k=1}^{K^n}{\omega }_{j_k}^{m_k^n}\right\}=\prod _{k=1}^{K^n}{\left[\mathsf{E}\left\{{(1-z)}^{{\Sigma }_{j=k}^{K^n}{m}_j^n}\right\}\right]}^{s_k}\mathsf{E}\left\{z^{m_k^n}{(1-z)}^{{\Sigma }_{j=k+1}^{K^n}{m}_j^n}\right\},$$

where z ~ H, and

$$\begin{array}{cc}\hfill \sum _{s_1=0}^{\infty }\cdots \sum _{s_{K^n}=0}^{\infty }\mathsf{E}\left\{\prod _{k=1}^{K^n}{\omega }_{j_k}^{m_k^n}\right\}=& \prod _{k=1}^{K^n}\mathsf{E}\left\{z^{m_k^n}{(1-z)}^{{\Sigma }_{j=k+1}^{K^n}{m}_j^n}\right\}\sum _{s_k=0}^{\infty }{\left[\mathsf{E}\left\{{(1-z)}^{{\Sigma }_{j=k}^{K^n}{m}_j^n}\right\}\right]}^{s_k}\hfill \\ \hfill =& \prod _{k=1}^{K^n}\frac{\mathsf{E}\left\{z^{m_k^n}{(1-z)}^{{\Sigma }_{j=k+1}^{K^n}{m}_j^n}\right\}}{1-\mathsf{E}\left\{{(1-z)}^{{\Sigma }_{j=k}^{K^n}{m}_j^n}\right\}}.\hfill \end{array}$$

The proof is completed by noting that the results for the other Kⁿ! – 1 terms can be obtained through a similar calculation that involves permuting the order of the counts $m_1^n,\dots ,m_{K^n}^n$.

The distribution over permutations for the Ewens sampling formula

Lemma 3

For all K ≥ 1 and m₁, … , m_K ≥ 1 write

$$r_K(m_1,\dots ,m_K)=\sum _{\sigma \in {\mathcal{P}}_K}\prod _{i=1}^K\left\{\frac{m_{\sigma \left(i\right)}}{{\Sigma }_{j=1}^K{m}_{{\sigma }_j}}\right\},$$ (.1)

where ${\mathcal{P}}_K$ denotes the set of all K! permutations of the indices (1, 2, … , k). Then r_k(m₁, … , m_K) = 1 for all k ≥ 1.

Proof

We proceed by induction on k. When k = 1, ${\mathcal{P}}_k$ contains only one element, namely, (1), and the only term within brackets in (.1) trivially becomes 1, and so r₁(m₁) = 1. Assuming now that r_K(m₁, … , m_K) = 1 for a given K, we consider r_K+1(m₁, … , m_k, m_K+1). Write any ${\sigma }^{(K+1)}\in {\mathcal{P}}_{K+1}$ as σ^(K+1) = (σ^(K+1)(1),…,σ^(K+1)(K + 1)). For s = 1, … , K + 1 define ${\mathcal{L}}_s^{(K+1)}=\{{\sigma }^{(K+1)}\in {\mathcal{P}}_{K+1}:{\sigma }^{(K+1)}(1)=s\}$ i.e., ${\mathcal{L}}_s^{(K+1)}$ is the set of all permutations of 1, … , K + 1 whose first element is s. Denote also $m_{+}^{(K+1)}=m_1+\cdots +m_{k+1}$. The first term in the product involved in (.1) for K + 1 is $m_{\sigma }{(K+1)}_{\left(1\right)}∕m_{+}^{(K+1)}$, while the remaining terms are precisely those involved in the definition of r_K(m₁, … , m_s−1, m_s+1, … , m_K+1). Therefore, the summation over all permutations in ${\mathcal{P}}_{K+1}$ can divided into K + 1 sums running over all possible values for σ^(K+1)(1). Then

$$\begin{array}{cc}\hfill r_{K+1}(m_1,\dots ,m_{K+1})=& \sum _{s=1}^{K+1}\frac{m_s}{m_{+}^{(K+1)}}{r}_K(m_1,\dots ,m_{s-1},m_{s+1},\dots ,m_{K+1})\hfill \\ \hfill =& \sum _{s=1}^{(k+1)}\frac{m_s}{m_{+}^{(K+1)}}=1,\hfill \end{array}$$

where the first equality in the second line holds by the induction hypothesis.

Proof of Lemma 2

Let W₁, W₂, … be a sequence of binary variables such that W_i = 1 if observation i corresponds to a species that had not been observed in the past, and W_i = 0 otherwise. Note that $K^n={\sum }_{i=1}^n{W}_i$ and that, conditionally on the random weights, these random variables are independent (although not identically distributed). Hence,

$$\mathsf{E}\left(K^n\right)=\sum _{i=1}^n\mathsf{E}\left(W_i\right),$$

where, from Hjort (2000),

$$\mathsf{E}\left(W_i\right)=i\frac{\mathsf{E}\left\{u{(1-u)}^{i-1}\right\}}{1-\mathsf{E}\left\{{(1-u)}^i\right\}}=\frac{\mathit{ia}\Gamma (a+b)\Gamma (b+i-1)}{\Gamma \left(b\right)\Gamma (a+b+i)-\Gamma (a+b)\Gamma (b+i)},$$

which completes the proof.