Estimation of Optimal Dynamic Treatment Regimes

Abstract

Background

Recent advances in medical research suggest that the optimal treatment rules should be adaptive to patients over time. This has led to an increasing interest in studying dynamic treatment regimes (DTRs), a sequence of individualized treatment rules, one per stage of clinical intervention, which map present patient information to a recommended treatment. There has been a recent surge of statistical work for estimating optimal DTRs from randomized and observational studies. The purpose of this paper is to review recent methodological progress and applied issues associated with estimating optimal DTRs.

Methods

We discuss Sequential Multiple Assignment Randomized Trials (SMARTs), a clinical trial design used to study treatment sequences. We use a common estimator of an optimal DTR that applies to SMART data as a platform to discuss several practical and methodological issues.

Results

We provide a limited survey of practical issues associated with modeling SMART data. We review some existing estimators of optimal dynamic treatment regimes and discuss practical issues associated with these methods including: model building; missing data; statistical inference; and choosing an outcome when only non-responders are re-randomized. We mainly focus on the estimation and inference of DTRs using SMART data. DTRs can also be constructed from observational data, which may be easier to obtain in practice, however, care must be taken to account for potential confounding.

Introduction

In practice, clinical and intervention scientists adapt treatment according to the evolving health status of each patient. Dynamic treatment regimes (DTRs), also known as adaptive treatment strategies, formalize this process as a sequence of individualized treatment rules, one per stage of clinical intervention, which map up-to-date patient information to a recommended treatment. A DTR is said to be optimal if it maximizes the average of a desirable clinical outcome when applied to a population of interest. Note that the outcome of interest could be a measure of efficacy, side-effects, or even a composite of multiple outcomes combined into a single utility function; throughout, we assume that the outcome has been coded so that higher is better. There has been a recent surge of methodological work for estimating optimal DTRs from randomized and observational studies [1–14]. However, less attention has been given to applied issues associated with estimating optimal DTRs including model building, dealing with missing data, and choosing outcomes that define optimality. We discuss these issues within the context of data collected in a randomized clinical trial.

To review the motivation for DTRs we briefly consider an example. The treatment of advanced non-small cell lung cancer typically involves two or more lines of treatment. First-line treatments primarily consist of platinum-based doublets which include: cisplatin; gemcitabine; pemetrexed; paclitaxel; carboplatin; and vinorelbine [15]. Docetaxel, pemetrexed and erlotinib are approved second-line treatments. The question of which first-line treatment, or combination of treatments, is best depends both on patient individual characteristics and the protocol for choosing a second-line treatment as there are thought to be interactive effects between first-line and second-line treatments [15]. By considering sequences of treatments we can capture not only synergies between the first- and second-line treatments but also delayed or carry-over effects of the first-line treatment [1]. Another important consideration is the timing of the second-line therapy [16]. Figure 1 shows a schematic for treatment protocol for non-small cell lung cancer indicating where treatment choices must be made. There is interest in optimizing these treatment choices using data from a randomized clinical trial.

Figure 1.

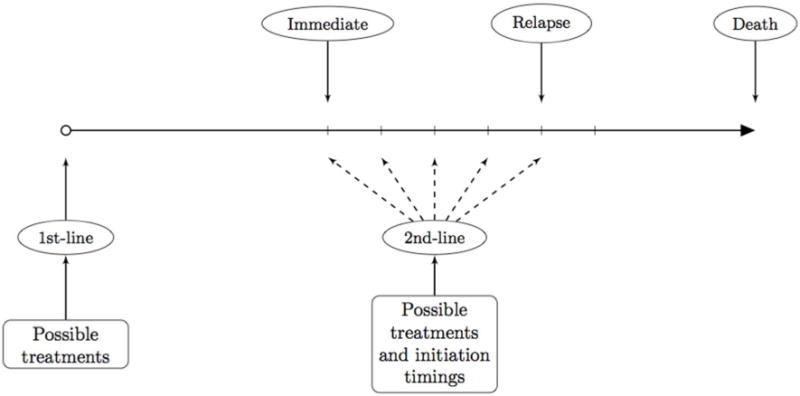
Non-small Cell Lung Cancer. There are multiple possible 1^st-line treatments to start with. As a follow-up, multiple possible 2^nd –line treatments exist. In addition, there are many choices for when to initiate the 2^nd-line treatment. For example, it can be initiated once the 1^st-line treatment is finished (immediate); it can be initiated when the disease progresses (progression); or any time inbetween.

One type of randomized clinical trial, which provides data useful for estimating optimal DTRs, is the Sequential Multiple Assignment Randomized Trial (SMART) [17–22]. Optimal DTRs have been estimated from SMARTs for a wide range of chronic conditions including: attention deficit hyperactivity disorder [23, 24]; depression [25]; HIV infection [26, 27, 13]; schizophrenia [28]; and cigarette addiction [5]. In a SMART, subjects are randomized multiple times according to the progression of their health status. A common feature of a SMART is that the pool of available treatments depends on subject-specific characteristics. For example, in the CATIE Schizophrenia Trial [29], subjects with tardive dyskinesia could not be randomized to receive perphenazine. Another common feature of SMARTs is to first randomize subjects to a first-line therapy and subsequently re-randomize only a subset of the subjects according to their health status [30–36]. Figure 2 shows a schematic for such SMART for school-aged children with attention deficit hyperactivity disorder [37]; in this trial responders, operationalized by adequate response on the impairment rating scale [38] and individualized list of target behaviors [39], were not re-randomized. As we will show, these features present novel challenges for building high-quality and interpretable outcome models.

Figure 2.

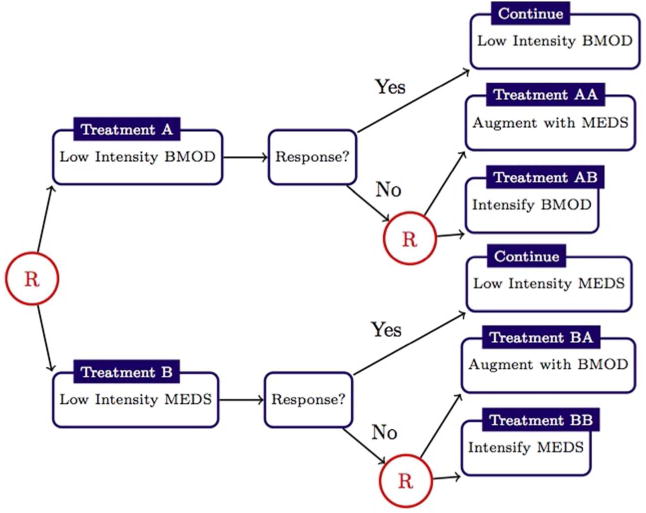
Schematic describing the Adaptive Pharmacological and Behavioral Treatments for Children with ADHD SMART [W. Pelham (PI)]; randomizations, denoted by a circled letter ’R,’ were with equal probability. Responder status is based on subject Impairment Rating Scale [38] and Individualized List of Target Behaviors [39]. see [22] for additional details.

In the next section we introduce basic concepts underpinning two common classes of DTRs estimators using data from SMARTs. Later we discuss some practical issues that arise in applying DTRs estimators, and we finish with some concluding remarks.

Estimating optimal DTRs from SMARTs

To simplify notation, we consider two-stage SMARTs with binary treatment options at each randomization. Data available from such a trial takes the form ${\{({\mathrm{X}}_{1\mathrm{i}},{\mathrm{A}}_{1\mathrm{i}},{\mathrm{X}}_{2\mathrm{i}},{\mathrm{A}}_{2\mathrm{i}},{\mathrm{Y}}_1)\}}_{i=1}^n$ comprising n independent and identically distributed trajectories, one for each subject. A generic trajectory (X₁, A₁, X₂, A₂, Y) is composed of ${\mathrm{X}}_1\in {\mathrm{R}}^{{\mathrm{p}}_1}$ which denotes baselines subject information; A₁ ∈ {−1, 1} which denotes the initial (first-line) treatment; ${\mathrm{X}}_2\in {\mathrm{R}}^{{\mathrm{p}}_2}$ which denotes interim subject information collected during the course of the first treatment; A₂ ∈ {−1, 1} which denotes the second (second-line) treatment; and Y ∈ R which denotes an outcome coded so that higher values are better. Sample size formulae exist for sizing a SMART to compare fixed (i.e., not data-driven) treatment strategies [20, 40, 41]; see [42] for designing SMART pilots. In a trial where only “non-responders” are re-randomized, A₂ can be conceptualized as missing by design. Define H₁ = X₁ and ${\mathrm{H}}_2={(X_1^T,{\mathrm{A}}_1,X_2^T)}^{\mathrm{T}}$ so that H_j denotes the available information before the j^th treatment assignment.

A DTR is a pair of functions d = (d₁, d₂) where d_j is a function mapping the covariate space to the treatment space. Under d, a patient with history h_j is recommended with treatment d_j(h_j). Let E^d denote expectation under the restriction that A₁ = d₁(H₁) and A₂ = d₂(H₂) for those re-randomized at the second stage. The optimal DTR, d^opt, satisfies ${\mathrm{E}}^{{\mathrm{d}}^{\mathrm{opt}}}\mathrm{Y}\ge {\mathrm{E}}^{\mathrm{d}}\mathrm{Y}$ for all DTRs d. Define Q₂(h₂, a₂) = E(Y | H₂ = h₂, A₂ = a₂) and ${\mathrm{Q}}_1({\mathrm{h}}_1,{\mathrm{a}}_1)=\mathrm{E}({\max }_{{\mathrm{a}}_2}{\mathrm{Q}}_2({\mathrm{H}}_2,{\mathrm{a}}_2)|{\mathrm{H}}_1={\mathrm{h}}_1,{\mathrm{A}}_1={\mathrm{a}}_1)$; Q_j is called the stage-j Q-function. The stage-2 Q-function measures the quality of assigning treatment A₂ = a₂ to a patient presenting at the second stage with history H₂ = h₂. The stage-1 Q-function measures the quality of assigning treatment A₁ = a₁ to a subject presenting at the first stage with history H₁ = h₁ if he/she were treated according to the $d_2^{\mathit{opt}}$ at stage-2. From dynamic programming [43] it follows that $d_j^{\mathit{opt}}({\mathrm{h}}_{\mathrm{j}})={\mathrm{argmax}}_{{\mathrm{a}}_{\mathrm{j}}}{\mathrm{Q}}_{\mathrm{j}}({\mathrm{h}}_{\mathrm{j}},{\mathrm{a}}_{\mathrm{j}})$. This formulation suggests several strategies for estimating d^opt from SMART data. Estimators can be broadly classified into three categories: (i) regression-based methods; (ii) value maximization methods; and (iii) planning methods. Regression-based methods attempt to first estimate the Q-functions via regression models and subsequently use a plug-in estimator of d^opt. Regression based estimators include Q- and A-learning [1, 2, 25, 44, 45]; regret regression [6]; threshold methods [5, 4, 11]; and interactive Q-learning [46]. Regression-based estimators for censored data, discrete outcomes, continuous treatments [47, 48], and quantiles have also been developed [45, 49, 50]. We give a version of the Q-learning algorithm in the following section. Value maximization methods are based on forming an estimator of V(d) = E^dY and then directly maximizing this estimator over d in some class of DTRs, say D. Value maximization methods include outcome weighted learning [9, 14], augmented value maximization [10, 12, 13], and structural mean models [7]. We give a version of outcome weighted learning in the subsequent section. Planning methods rely on systems dynamics models to simulate patient trajectories under different DTRs to find an optimum [51–53]. These models rely strongly on biological or behavioral theory, which are absent or incomplete in the settings we consider and thus we will not discuss them further.

Q-learning

In this section we assume that all subjects are re-randomized at the second stage. The Q-learning algorithm requires postulated models for the Q-functions; we consider linear working models of the form ${\mathrm{Q}}_{\mathrm{j}}({\mathrm{H}}_{\mathrm{j}},{\mathrm{A}}_{\mathrm{j}};{\mathrm{\theta }}_{\mathrm{j}})=H_j^T{\mathrm{\alpha }}_{\mathrm{j}}+{\mathrm{A}}_{\mathrm{j}}{H}_j^T{\mathrm{\beta }}_{\mathrm{j}}$, where ${\mathrm{\theta }}_{\mathrm{j}}={({\alpha }_j^T,{\beta }_j^T)}^{\mathrm{T}}$, H_j1, H_j2 are known features constructed from H_j. Q-learning algorithm mimics the dynamic programming solution using a sequence of regressions to obtain the estimates $\widehat{{\theta }_J}$, and subsequently the estimated DTRs. The algorithm is summarized in the Appendix. Thus, Q-learning can be easily implemented in almost any statistical software package. Q-learning is available in packages qLearn and iqLearn of the R programming language (cran.us.r-project.org), which is freely available and callable from both SAS and SPSS. Other advantages of Q-learning include: (i) that it can be extended to accommodate discrete outcomes [45, 50], censored outcomes [49], and competing outcomes [54, 55]; (ii) measures of goodness of fit and visual diagnostics can be used to assess the quality of the fitted regression models in each stage; and (iii) the estimated Q-functions are prognostic, i.e., ${\mathit{max}}_{a_j}{Q}_j(h_j,a_j;\widehat{{\theta }_J})$, is a prediction for the outcome for a patient presenting at stage j and receiving optimal treatment thereafter.

Despite the foregoing advantages, Q-learning presents a number of challenges in practice. First, as the result of the maximization in the intermediate step (step Q2 in the appendix), modeling the stage-1 Q-function requires modeling a nonsmooth, nonmonotone transformation of the data. Even under simple generative models, it can be shown that the form of the stage-1 Q-function can be quite complex [25, 46] making it difficult to correctly specify a model. One potential remedy is to use flexible regression models, say, support vector regression or generalized additive models, to estimate the Q-functions [15, 45]; however, such models are difficult to interpret, limiting their ability to generate new scientific content. Another potential solution is to modify the Q-learning algorithm to avoid modeling after maximization [46].

A second challenge associated with Q-learning is statistical inference. Coefficients indexing the stage-1 Q-function are statistically nonregular [5, 23, 56]. A consequence is that standard methods for inference, e.g., the bootstrap or normal approximations, cannot be applied without modification. Proposed solutions include subsampling [56] and adaptive confidence intervals [23]. Both of these methods have been shown to perform well in simulations but may be conservative in small samples.

Value maximization methods

Q-learning is often called an indirect method because it estimates the optimal DTR indirectly through the estimated Q-functions. A more direct approach is to postulate an estimator of V(d) = E^dY, say $\widehat{V}(\mathrm{d})$, and then estimate the optimal DTR by searching for $\widehat{d}={\mathrm{argmax}}_{\mathrm{d}\in \mathrm{D}}\widehat{V}(\mathrm{d})$, where D is a prespecified class of DTRs. Estimators of this form are called value maximization methods or policy search methods and have received a great deal of attention recently [7, 9, 10, 12–14]. A potential advantage of value maximization methods is that, because they need not rely on models for the Q-function, they may be more robust to model specification. Conversely, fewer assumptions about the trajectory distribution may lead to estimators with higher variability.

Methods for estimating V(d), include: inverse probability-weighting [9, 14]; augmented inverse probability-weighting [10, 13]; and marginal structural mean models [7]. Marginal structural mean models are most effective with low-dimensional histories and a small class of potential regimes D. Inverse probability-weighting and augmented inverse probability-weighting estimators can be applied with high-dimensional histories and very large classes of regimes, however, they are nonsmooth functions of the observed data making the search for the optimal regime within D computationally challenging. Both [9] and [10] connected the problem of maximizing inverse probability-weighting and augmented inverse probability-weighting estimators of V(d) with weighted classification problems and were thereby able to leverage existing classification algorithms to approximately compute ${\mathrm{argmax}}_{\mathrm{d}\in \mathrm{D}}\widehat{V}(\mathrm{d})$. We briefly review a simple value maximization algorithm.

Assume that binary treatments are equally randomized at each stage. Then, under mild regularity conditions, it can be shown that $\mathrm{V}(\mathrm{d})=4E(Y{1}_{A_1=d_1(H_1)}{1}_{A_2=d_2(H_2)})$ where 1_z equals one if z is true and zero otherwise [14]. The inverse probability weighted estimator is based on the foregoing expression for V(d) and is given by $\widehat{V}(\mathrm{d})=4n^{-1}{{\displaystyle \sum }}_{i=1}^n{Y}_i{1}_{A_{1i}=d_1(H_{1i})}{1}_{A_{2i}=d_2(H_{2i})}$.

For illustration, assume D is the space of all linear decision rules. Then, for an d ∈ D, we may associate a vector $\mathrm{\beta }={({\beta }_1^T,{\beta }_2^T)}^{\mathrm{T}}$ so that ${\mathrm{d}}_{\mathrm{j}}({\mathrm{h}}_{\mathrm{j}})=\mathrm{sign}(h_j^T{\mathrm{\beta }}_{\mathrm{j}})$ where sign(x)=1 if x>0 and sign(x)=−1 if x<0, and write

$$\widehat{V}(d)=\widehat{V}(\beta )=4n^{-1}{\displaystyle \sum }_{i=1}^n{Y}_i{1}_{A_{1i}{H}_{1i}^T{\beta }_1>0}{1}_{A_{2i}{H}_{2i}^T{\beta }_2>0}.$$

An estimator of the optimal DTR is obtained by solving for $\stackrel{\sim }{\beta }={\mathit{argmax}}_{{\beta }_2}\widehat{V}(\beta )$. However, the indicator functions make this a mixed integer linear program, which is known to be computationally burdensome. Approaches to finding $\stackrel{\sim }{\beta }$ include employing a stochastic search algorithm, for example simulated annealing or a generic algorithm [13], or using a concave surrogate for the indicator functions [14]. Depending on the optimization method, additional constraints on 9 may be required to ensure a unique solution.

Value maximization methods are appealing because they avoid strong and potentially incorrect assumptions about the outcome distribution. Furthermore, the class of regimes D can be restricted to only include regimes which are logistically feasible, parsimonious, interpretable, or otherwise desirable. Drawbacks of value maximization methods include: computational complexity; the lack of a prognostic model; the potential lack of a scientifically meaningful estimand; and, as mentioned previously, potentially higher variability.

Additional practical considerations

In addition to the issues raised in the foregoing section, there are a number of important practical considerations associated with estimating optimal DTRs from SMART data. Here, we provide an overview of those that we have found to be most common.

Missing data

SMARTs, like any clinical trial, are prone to missing data. Dealing with missing data in SMARTs is complicated by the sequential design and the fact that treatment randomizations depend on evolving subject status. For example, in a trial where only responders are re-randomized at the second stage, a subject that is lost to follow-up during the first stage will be missing: second stage history which contains his/her responder status; second stage treatment; and outcome. Whether the second stage treatment is truly missing or missing by design depends on the subject’s unobserved responder status. Another complication is that the timing and number of clinic visits may be dependent on patient outcomes [29]; thus, a natural approach is to use multiple imputation and sequentially impute missing data as needed. For example, if clinic visits are dependent on patient status, one would first impute patient status, then, conditional on the imputed status, one would subsequently impute the next visit time, etc. Shortreed et al. provide a sequential multiple imputation strategy for SMARTs that can be used with existing multiple imputation software [57].

Both regression-based and value-maximization methods for estimating optimal DTRs can be extended for use with multiply imputed datasets by either aggregation or concatenation. In the aggregation approach one first estimates the optimal DTR separately for each imputed data set and then take a majority vote. For example, if ${\widehat{d}}^{(1)},\dots ,{\widehat{d}}^{(M)}$ are M stage-j decision rules estimated across M multiply imputed datasets, then the aggregated rule is ${\widehat{d}}_j^A\left(h_j\right)=\mathit{sign}({{\displaystyle \sum }}_{m=1}^M{\widehat{d}}_j^{(m)}(h_j))$. Note that in the case of linear decision rules, the aggregated decision rule is equivalent to simply averaging the coefficients indexing the decision rules to form a single linear decision rule. Alternatively, concatenation involves stacking the M imputed datasets on top of each other to form a single large dataset and then estimating a single decision rule. This is advantageous if fitting the model on each imputed dataset is computationally expensive or if it is desired that the final decision be sparse (the average of sparse vectors need not be sparse). However, concatenation may preclude estimation of between-imputation variance estimation used in standard multiple imputation variance formulas [58].

Choosing an outcome in responder trials

SMARTs where only a subset of subjects, which we generically term ‘non-responders,’ are re-randomized at the second stage are common, especially in cancer clinical trials. We assume responders are followed until the end of the study.

Let R be an indicator of response, which takes the value 1 if the subject is a responder and 0 otherwise, then R is contained in H₂ for all subjects. We assume that R is assessed at the end of a fixed time-period, e.g., six-months from baseline. Those deemed non-responders are immediately re-randomized. For responders, Y is collected prior to the assignment of A₂ and hence is part of H₂; indeed, H₂ will contain different information for responders and non-responders. Thus, Q₂(H₂, A₂) = Y R + E (Y | H₂, R = 0, A₂). In Q-learning one would thus estimate the stage-2 Q-function by regressing Y on H₂ and A₂ only using the non-responder data. Let $Q_2(H_2,a_2;\widehat{{\theta }_2})$ denote this estimator. The second step of the Q-learning algorithm, Q₂, is to compute $\widehat{Y}=RY+(1-R){\mathit{max}}_{a_2}{Q}_2(H_2,a_2;\widehat{{\theta }_2})$. However, note that $\widehat{Y}$ will typically be more variable for responders than non-responders since non-responder data has been projected onto H₂. This can complicate building high-quality models of the stage-1 Q- function. One approach to alleviate this problem is to regress Y on information collected prior to classification of responder status. Let $\stackrel{\sim }{H_2}$ denote information collected prior to responder classification and let $\stackrel{\sim }{Y}$ be an estimator of $\mathrm{E}(\mathrm{Y}|\stackrel{\sim }{H_2})$ built using only responder data. Then, $\widehat{Y}\ast =R\stackrel{\sim }{Y}+(1-R){\mathit{max}}_{a_2}{Q}_2(H_2,a_2;\widehat{{\theta }_2})$ is used in place of $\widehat{Y}$ in the first stage regression of Q-learning. Note that this does not affect the validity of the Q-learning algorithm since H₁ and A₁ are contained in $\stackrel{\sim }{H_2}$ so that $\mathrm{E}(\mathrm{YR}|{\mathrm{H}}_1,{\mathrm{A}}_1)=\mathrm{E}\{\mathrm{E}(\mathrm{YR}|\stackrel{\sim }{H_2},\mathrm{R})|{\mathrm{H}}_1,{\mathrm{A}}_1\}$.

Conclusions

We have tried to provide a limited survey of practical issues associated with estimation of optimal DTRs from SMART data. While estimation of and inference for DTRs is a rapidly growing area of statistics methodological research, it is equally important to address more practical issues associated with modeling SMART data. Given the rapidly growing interest in estimating optimal DTRs from SMARTs we believe a crucial open issue is the development of valid sample size formulae for testing data-driven DTRs.

Appendix

Q-learning algorithm is as follows:

• Q1Find $\widehat{{\theta }_2}={\mathit{argmin}}_{{\theta }_2}{\sum }_{i=1}^n{(Y_i-Q_2(H_{2i},A_{2i};{\theta }_2))}^2$;
• Q2Define $\widehat{Y}={\mathit{max}}_{a_2}{Q}_2\left(H_2,a_2;\widehat{{\theta }_2}\right)$;
• Q3Find $\widehat{{\theta }_1}={\mathit{argmin}}_{{\theta }_1}{\sum }_{i=1}^n{(\widehat{Y_i}-Q_1(H_{1i},A_{1i};{\theta }_1))}^2$;

then ${\widehat{d}}_j^Q\left(h_j\right)={\mathit{argmax}}_{a_j}{Q}_j\left(h_j,a_j;\widehat{{\theta }_J}\right)$. Q-learning, in the simple case considered, requires fitting two linear regressions (steps Q1 and Q3) and making linear predictions for each subject (step Q2).