Multidimensional reaction rate theory with anisotropic diffusion

Abstract

An analytical expression is derived for the rate constant that describes diffusive transitions between two deep wells of a multidimensional potential. The expression, in contrast to the Kramers-Langer formula for the rate constant, is valid even when the diffusion is highly anisotropic. Our approach is based on a variational principle for the reactive flux and uses a trial function for the splitting probability or commitor. The theoretical result is validated by Brownian dynamics simulations.

I. INTRODUCTION

Langer¹ generalized Kramers’ seminal work² on reaction rates to many dimensions.³ Assuming that the rate-limiting step is crossing the saddle point region, he derived an analytic expression for the rate constant for escape from a deep potential well. The problem appeared to have been completely solved until Berezhkovskii and Zitserman (BZ) pointed out that Langer's formula failed for potential surfaces of a certain shape when the friction/diffusion was highly anisotropic.⁴ They developed a formalism, based on reaction-diffusion equations, to obtain the rate constant in the regime where Langer's formula was incorrect,^4–6 but did not give a general analytic expression for the rate constant.

In this paper, we derive such an expression using a variational principle for the reactive flux.⁷ We consider diffusive dynamics in a two-dimensional potential U(x, y) with two deep wells separated by a high saddle-shaped barrier, when diffusion coefficients along x and y are arbitrary (D_x ≠ D_y). We assume that the matrix of diffusion coefficients, denoted by D, is diagonal, the potential U(x, y) is non-separable, and the potentials of mean force along x and y each have a double-well form. Our goal is to find an expression for the rate constant of the transition from one well to the other that is valid for all values of the diffusion coefficients. If the potential U(x, y) is not symmetric, then the rate constants for transitions in the two directions differ. Since the theory presented here is equally applicable to both rate constants, we will focus only on the transition from the reactant to the product. For the sake of concreteness, we assume that progress along x describes the breaking of a chemical bond or the unfolding of a protein, and refer to this coordinate as chemical or molecular. We call y the environmental coordinate, assuming that it describes the influence of the solvent⁸ or the tip of an atomic force microscope in a single-molecule pulling experiment.⁹

When the potentials of mean force along x and y have a double-well shape, expressions for the rate constant can be readily obtained in the limiting cases of fast and slow relaxation of the environment (D_y → ∞ and D_y → 0, respectively) using Kramers’ theory. When D_y → ∞ the two-dimensional diffusion equation reduces to a one-dimensional one for diffusion along x in the potential of mean force denoted by U_∞(x) and defined (to within a constant) by

$$e^{-U_{\infty }\left(x\right)}={\int }_{-\infty }^{\infty }{e}^{-U(x,y)}dy,$$ (1a)

where we have set the product of the Boltzmann constant and absolute temperature to unity. The corresponding rate constant, k_∞, obtained using the one-dimensional Kramers theory involving the potential U_∞(x) with a high parabolic barrier, is given by

$$k_{\infty }=\frac{D_x}{2\pi }\sqrt{K_{\infty }{K}_{\infty }^R}{e}^{-\Delta U_{\infty }},$$ (1b)

where K_∞ = −U″_∞(x_b), $K_{\infty }^R=U_{\infty }^{\prime \prime }\left(x_w\right)$, with double prime denoting the second derivative, x_b and x_w are the locations of the barrier top and the reactant well bottom of the potential U_∞(x), and ΔU_∞ = U_∞(x_b) − U_∞(x_w).

In the opposite limit (D_y → 0), where the environment responds so slowly that its adjustment becomes the rate-limiting step, the two-dimensional reaction dynamics reduces to one-dimensional diffusion along y in the presence of a double-well potential of mean force denoted by U₀(y) and defined (to within a constant) by

$$e^{-U_0\left(y\right)}={\int }_{-\infty }^{\infty }{e}^{-U(x,y)}dx.$$ (2a)

The corresponding rate constant, k₀, is given by

$$k_0=\frac{D_y}{2\pi }\sqrt{K_0{K}_0^R}{e}^{-\Delta U_0},$$ (2b)

where K₀ = −U″₀(y_b), $K_0^R=U_0^{\prime \prime }\left(y_w\right)$, ΔU₀ = U₀(y_b) − U₀(y_w), with y_b and y_w denoting the locations of the barrier top and the reactant well bottom of the potential U₀(y).

To write Langer's rate constant for arbitrary D_x and D_y, we assume, without loss of generality, that the saddle point of the potential surface U(x, y) is located at the origin and U(0, 0) = 0. In the vicinity of the saddle point, U(x, y) can be approximated by a quadratic expansion, U(x, y) = (K_xxx² + 2K_xyxy + K_yyy²) / 2, where K_xx, K_xy = K_yx, and K_yy are elements of the symmetric matrix, K, of second derivatives of U(x, y) at the saddle point. From the definition of the saddle point it follows that $\det \mathbf{K}=K_{xx}{K}_{yy}-K_{xy}^2<0$. The corresponding matrix of force constants for the reactant well is denoted by K_R, with $\det {\mathbf{K}}_R>0$. In the diffusive regime Langer's rate constant for the reactant-to-product transition, denoted by k_L, is given by

$$k_L=\frac{1}{2\pi }{\left(\frac{\det {\mathbf{K}}_R}{\left|\det \mathbf{K}\right|}\right)}^{1/2}\lambda e^{-\Delta U},$$ (3)

where ΔU is the energy difference between the saddle point and the reactant well bottom, and −λ is the only negative eigenvalue of matrix KD, corresponding to the only positive root of the equation $\det \left(\lambda \mathbf{I}+\mathbf{KD}\right)=0$.

If Langer's result were valid for all D_x and D_y, one would expect that it would reduce to k_∞ and k₀ in the D_y → ∞ and D_y → 0 limits,

$$\underset{D_y\to \infty }{lim}{k}_L=k_{\infty }\propto D_x,\underset{D_y\to 0}{lim}{k}_L=k_0\propto D_y,$$ (4)

where, as above, k_∞ and k₀ are the rate constants corresponding to the potentials of mean force U_∞(x) and U₀(y), respectively. When K_yy > 0, BZ⁴ showed that Langer's formula is valid for all D_x and D_y only when K_xx > 0, i.e., when the force constant along the chemical/molecular coordinate at the saddle point is also positive. This means that the potential along x for any fixed y near the barrier top has a single-well form. When K_xx < 0, the potential along x at fixed y has a double-well form, and Eq. (3) leads to (see Appendix A)

$$\underset{D_y\to 0}{lim}{k}_L=k_{\infty }\frac{K_{xx}{K}_{yy}}{\det \mathbf{K}}\propto D_x,$$ (5)

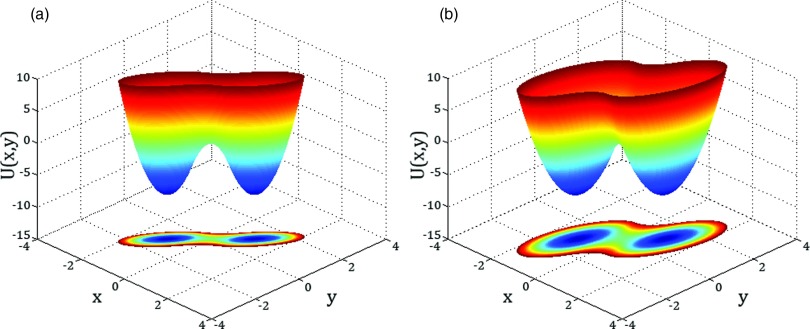
which is obviously an unphysical result. Instead of predicting that the rate constant vanishes as D_y → 0, Langer's formula predicts that it approaches a constant proportional to D_x. The physical reason for this failure is the change in the nature of the reactant-to-product transition when D_y → 0. Langer's theory postulates that the transition rate is determined by the passage through the saddle point region. If K_xx < 0, the potential U(x, y = const) has two minima along x for some range of fixed y values. Therefore, when D_y → 0, the system, before it moves along y, makes many transitions between the two wells. As a consequence, the motion along the slow environmental coordinate is governed by the potential of mean force U₀(y), which is determined by the local minima and not by the saddle point region. Examples of potentials for which Langer's theory works and does not work are shown in Figs. 1(a) and 1(b), respectively.

FIG. 1.

Whether Langer's generalization of Kramers’ theory is valid for all values of the diffusion coefficients depends on the shape of the two-dimensional potential. The potentials shown are given by Eqs. (8) and (19) at ΔU = 8, with γ = 2 in (a) and 1/3 in (b). When the potential along x for y = 0 has a single-well form (i.e., one minimum), as shown in (a), Langer's formula is always valid; when the potential along x for y = 0 has a double-well form (i.e., two minima), as shown in (b), Langer's formula fails as D_y → 0.

II. RESULTS

The main result of this paper is an analytical expression for the rate constant k, derived using a variational principle, which is valid for all D_x and D_y. It correctly reduces to k_∞ and k₀ in the limiting cases of fast and slow response of the environment irrespective of the sign of K_xx. Our result for the rate constant is

$$k=\frac{k_L{k}_0-{\chi }^2}{k_L+k_0-2\chi },$$ (6)

where Langer's rate constant, k_L, depends on both D_x and D_y, the rate constant k₀ for escape from the reactant well of the potential of mean force U₀(y) is proportional to D_y, and χ is a cross term given by

$$\begin{array}{ccc}\hfill \chi & =& \frac{D_y{e}_y\sqrt{K_0\left|\det \mathbf{K}\right|}}{2\pi \left(\mathbf{e}·\mathbf{D}·\mathbf{e}\right)\sqrt{K_L}}{k}_L\hfill \\ & & \times \int \underset{I}{\int }{e}^{-U(x,y)-K_L{\left(x{e}_x+y{e}_y\right)}^2/2-K_0{\left(y-y_b\right)}^2/2}dxdy.\hfill \end{array}$$ (7)

Here, e is the unit eigenvector of the matrix KD corresponding to the only negative eigenvalue −λ (i.e., KDe = −λe), e_x and e_y are the x- and y-components of e, K_L is a force constant defined as K_L = −(e · K⁻¹ · e)⁻¹ = λ /(e · D · e). The integration in Eq. (7) is over the intermediate region I that separates the reactant region from the product region.

The expression for χ can be simplified for a double-well potential U(x, y) of the form

$$U(x,y)=U_{\infty }\left(x\right)+\Gamma {\left(y-x\right)}^2/2,$$ (8)

which nevertheless contains the essential physics of the problem. Using Eq. (1a), one can check that U_∞(x) is indeed the potential of mean force along x. Let us further assume that U_∞(x) is symmetric, U_∞(x) = U_∞(−x), with the barrier top located at the origin, x_b = 0, and the barrier energy equal to zero, U_∞(x_b) = 0. The double-well potential of mean force along y, U₀(y), defined by Eq. (2a), depends on the sign of the matrix element K_xx = Γ−K_∞. For K_xx > 0, it can be shown that $K_0^R=\Gamma K_{\infty }^R/\left(\Gamma +K_{\infty }^R\right)$, K₀ = ΓK_∞ / (Γ − K_∞), and $\Delta U_0=\Delta U_{\infty }-\left(1/2\right)\ln \left[\left(\Gamma +K_{\infty }^R\right)/\left(\Gamma -K_{\infty }\right)\right]$. Using these relations one can check that Eq. (2b) leads to k₀ = D_yΓk_∞ / [D_x(Γ − K_∞)], which is identical to the D_y → 0 limit of k_L. When K_xx < 0, the condition where Langer's theory fails, the potential along x at constant y, U(x, y = const), has a double-well form for y near y_b = 0. Then the main contribution to the integral in Eq. (2a) comes from the vicinities of the two minima. Using quadratic expansion of U_∞(x) near its minima and evaluating the resulting Gaussian integrals, we obtain

$$U_0\left(y\right)=-\ln \left(e^{-K_0^R{\left(y-x_w\right)}^2/2}+e^{-K_0^R{\left(y+x_w\right)}^2/2}\right),$$ (9)

where again $K_0^R=\Gamma K_{\infty }^R/\left(\Gamma +K_{\infty }^R\right)$. Now we have $K_0=K_0^R\left(K_0^R{x}_w^2-1\right)$ and $\Delta U_0=K_0^R{x}_w^2/2-\ln 2$. The rate constant k₀ is again given by Eq. (2b). Langer's formula for the rate constant in this case is

$$k_L=k_{\infty }\left[\sqrt{{\left(\gamma -1+\varepsilon \gamma \right)}^2+4\varepsilon \gamma }-\left(\gamma -1+\varepsilon \gamma \right)\right]/2,$$ (10)

where γ = Γ/K_∞ and ɛ = D_y/D_x.

For the potential in Eq. (8), when U_∞(x) is symmetric and y_b = 0, we carry out the integration over y in Eq. (7) and find that the cross term becomes relatively simple,

$$\chi =k_L\sqrt{\frac{A}{2\pi }}{\int }_{-\infty }^{\infty }{e}^{-U_{\infty }\left(x\right)-K_{\infty }{x}^2/2-A{x}^2/2}dx,$$ (11)

where the force constant A is given by

$$A=\frac{\delta {\varepsilon }^2{\gamma }^3}{\left(\delta +\gamma \right){\left(\varepsilon \gamma +\mu \right)}^2-\delta \gamma {\mu }^2}{K}_{\infty }$$ (12)

with δ = K₀/K_∞ and μ = k_L/k_∞. When K_xx > 0 (i.e., Γ > K_∞), the force constant A remains finite over the entire range of D_y. Then the main contribution to the integral in Eq. (11) comes from the barrier region near x = 0 where U_∞(x) ≈ −K_∞x²/2 so that the integrand can be approximated by exp ( − Ax²/2). This leads to χ = k_L. Consequently, it follows from Eq. (6) that k = k_L, i.e., we recover Langer's formula for the entire range of D_y. When Γ < K_∞, Eq. (12) shows that the force constant A vanishes as D_y (or ɛ) tends to zero. Here, χ approaches k_L and hence k approaches k_L only when D_y is large enough for the integrand in Eq. (11) to be still well approximated by exp (−Ax² / 2). When D_y → 0, this approximation fails, and χ becomes proportional to D_y. Consequently, the rate constant k approaches k₀, as it should. Thus, Eq. (6) recovers Langer's formula for the rate constant over the entire range of D_y for K_xx > 0 and corrects the defect of this formula when D_y → 0 for K_xx < 0.

III. OUTLINE OF DERIVATION

To derive the expressions in Eqs. (6) and (7), we use the fact that the rate constant is the ratio of the unidirectional reactive flux through the intermediate region (I) to the reactant well population at equilibrium. The flux, in turn, can be expressed in terms of the splitting probability (or commitor) ϕ(x, y), which is the probability of reaching the reactant region before the product region from a point (x, y) in the intermediate region.^7,10 Consequently, the rate constant k can be expressed as

$$k=\frac{1}{2\pi }\sqrt{\det {\mathbf{K}}_R}{e}^{-\Delta U}\int \underset{I}{\int }\left(\nabla \varphi ·\mathbf{D}·\nabla \varphi \right)e^{-U(x,y)}dxdy.$$ (13)

We now exploit the E and Vanden-Eijnden⁷ variational principle for the reactive flux: the reactive flux is greater than or equal to $\int \underset{I}{\int }\left(\nabla f·\mathbf{D}·\nabla f\right)e^{-U(x,y)}dxdy/\int \int e^{-U(x,y)}dxdy$ for any function f(x, y) that is unity and zero at the two boundaries of the intermediate region. The equality occurs when f(x, y) is the splitting probability ϕ(x, y).

We determine the rate constant by minimizing the expression for k in Eq. (13) with respect to the parameter α in the trial function for the splitting probability,

$$\varphi (x,y)=\alpha {\varphi }_L(x,y)+(1-\alpha ){\varphi }_0\left(y\right).$$ (14)

Here, ϕ_L(x, y) and ϕ₀(y) are the splitting probabilities which, when substituted into Eq. (13), yield k_L and k₀, respectively, and α is a variational parameter, with 0 ⩽ α ⩽ 1. Substituting the trial function in Eq. (14) into Eq. (13), we arrive at

$$k={\alpha }^2{k}_L+{(1-\alpha )}^2{k}_0+2\alpha (1-\alpha )\chi ,$$ (15)

where χ is the cross-term given by

$$\chi =\frac{1}{2\pi }\sqrt{\det {\mathbf{K}}_R}{e}^{-\Delta U}\int \underset{I}{\int }\left(\nabla {\varphi }_L·\mathbf{D}·\nabla {\varphi }_0\right)e^{-U(x,y)}dxdy.$$ (16)

The optimal value of the variational parameter, α*, is found by minimizing the rate constant in Eq. (15) with respect to α. The result is α* = (k₀ − χ)/(k_L + k₀ − χ). Substituting α* into Eq. (15), we arrive at the expression for the rate constant in Eq. (6).

To complete the derivation we use the gradient of the splitting probability that leads to Langer's rate constant k_L,¹¹

$$\nabla {\varphi }_L(x,y)=-\sqrt{\frac{K_L}{2\pi }}{e}^{-K_L{\left(x{e}_x+y{e}_y\right)}^2/2}\mathbf{e},$$ (17)

and its one-dimensional counterpart leading to Kramers’ rate constant k₀,

$$\nabla {\varphi }_0\left(y\right)=-\sqrt{\frac{K_0}{2\pi }}{e}^{-K_0{\left(y-y_b\right)}^2/2}\mathbf{y},$$ (18)

where y is a unit vector in the y-direction. Substituting these gradients into Eq. (16), after considerable algebra, we arrive at the expression for the cross-term given in Eq. (7).

IV. VALIDATION VIA SIMULATIONS

To check the accuracy of our formula for the rate constant in Eq. (6), we compare its predictions with the results obtained from Brownian dynamics simulations. This is done for the potential U(x, y) in Eq. (8) with a symmetric piecewise parabolic potential U_∞(x) of the form

$$U_{\infty }\left(x\right)=\Delta U·\left\{\begin{array}{cc}\begin{array}{c}-2x^2,\hfill \\ -1+2{\left(\right|x|-1)}^2,\hfill \end{array}& \begin{array}{c}\hfill 0\le \left|x\right|\le 1/2\\ \hfill 1/2\le \left|x\right|\end{array}\end{array}\right.$$ (19)

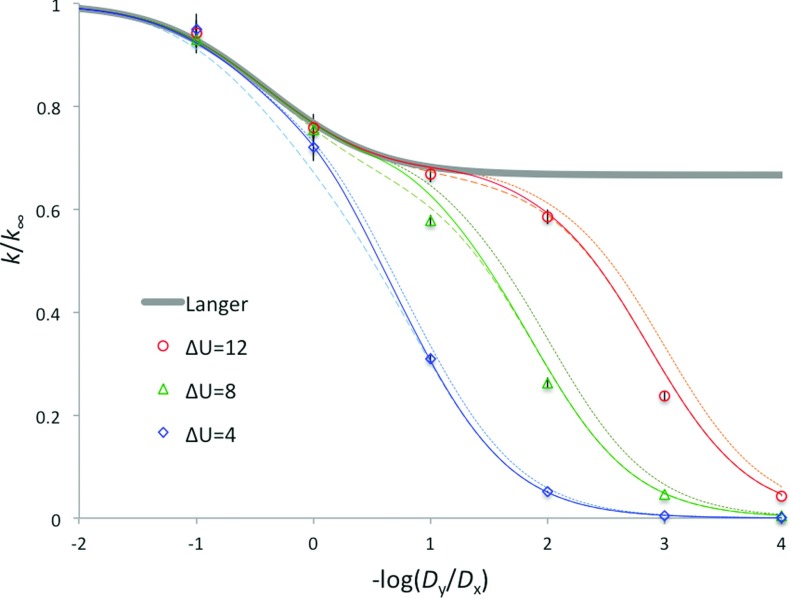
and Γ = 4ΔU / 3, so that γ = Γ / K_∞ = 1/3 (see Fig. 1(b) with ΔU = 8). The comparison is made for ΔU = 4, 8, and 12 and diffusion anisotropy ɛ = D_y / D_x ranging from 10 to 10⁻⁴. In Fig. 2, the simulation results (see Appendix B) are shown as symbols whereas our theoretical predictions are given by dotted curves. The systematic difference between the two for small D_y is due to the fact that the potential of mean force U₀(y) near the barrier top is parabolic only in a very short range. Therefore, the formula for k₀ in Eq. (2b), which assumes a parabolic barrier, is inaccurate. Consequently, we replace k₀ in Eq. (6) by the rate constant obtained from the mean first passage time to the barrier top (y = 0) starting from the equilibrium distribution in the reactant well of U₀(y),¹²

$$k_0=\frac{{\int }_{-\infty }^0{e}^{-U_0\left(y\right)}dy}{2{\int }_{-\infty }^0{e}^{U_0\left(y\right)}dy{\left({\int }_{-\infty }^y{e}^{-U_0\left(z\right)}dz\right)}^2}.$$ (20)

The dependence of the resulting rate constant on the diffusion anisotropy is shown in Fig. 2 as solid curves. One can see that our theoretical predictions are in good agreement with the simulation results. We also notice that a simple interpolation formula,

$$k=\frac{k_L{k}_0}{k_L+k_0},$$ (21)

which follows from Eq. (6) if χ² is much smaller than the product, k_Lk₀, of the rate constants, works remarkably well. The resulting dependence of k, with k₀ given in Eq. (20), on diffusion anisotropy is shown in Fig. 2 as dashed curves. To show the failure of Langer's formula, we also display the prediction of Eq. (10) as a thick solid curve.

FIG. 2.

Comparison of predictions of Eqs. (6) and (21) for the rate constant of the transition between two wells in a two-dimensional potential with simulation results over a wide range of diffusion anisotropy. The simulation results for the ratio k/k_∞ are shown as symbols with error bars representing standard deviations obtained from 10 independent simulations; note that many error bars are smaller than the corresponding symbols. The predictions of Eq. (6) with k₀ given by Eqs. (2b) and (20) are shown as dotted and solid curves, respectively. The predictions of Eq. (21) with k₀ given by Eq. (20) are shown by dashed curves. The thick solid curve shows the rate constant given by Langer's formula, Eq. (10).

V. CONCLUDING REMARKS

In summary, our main results are the expression for the reactant-to-product rate constant given by Eq. (6) and its simplified version in Eq. (21). They are applicable for arbitrary diffusion anisotropy, thus correcting the defect of Langer's formula for potential surfaces with K_xx < 0 when the diffusion is highly anisotropic. Our results can be generalized to more than two dimensions. For example, when there is only one slow mode, the expression for the rate constant in Eq. (6) remains unchanged, but χ in Eq. (7) becomes a multiple integral over x, y, z, … with xe_x + ye_y replaced by xe_x + ye_y + ze_z + …. Our results do not correct the defect of Langer's formula when applied to the irreversible escape from a single metastable well to the continuum, since there is no longer a potential of mean force along the slow coordinate. For this case, BZ^4,5 showed that in the regime where Langer's formula fails, the two-dimensional Smoluchowski equation can be reduced to a one-dimensional one along the slow coordinate with a sink term equal to the escape rate constant at fixed y. Approximate solutions to this equation have been found, but the problem of finding an analytical expression for the rate constant in the irreversible case, valid for all diffusion coefficients, remains open.

APPENDIX A: DERIVATION OF EQ. (5)

The two-dimensional potential U(x, y) has the reactant well bottom located at (x_R,y_R) and the saddle point located at the origin. In the vicinities of these points, U(x, y) can be approximated by quadratic expansions. Near the reactant well bottom the potential is

$$\begin{array}{ccc}\hfill U(x,y)& =& -\Delta U+\frac{1}{2}[K_{xx}^R{\left(x-x_R\right)}^2+2K_{xy}^R\left(x-x_R\right)\left(y-y_R\right)\hfill \\ & & +K_{yy}^R{\left(y-y_R\right)}^2],\hfill \end{array}$$ (A1)

with $\det {\mathbf{K}}_R>0$, while near the saddle point the potential is given by

$$U(x,y)=\frac{1}{2}\left(K_{xx}{x}^2+2K_{xy}xy+K_{yy}{y}^2\right),$$ (A2)

with $\det \mathbf{K}<0$. Substituting these expressions into Eq. (1a) and integrating over y, we obtain

$$e^{-U_{\infty }\left(x\right)}=\sqrt{2\pi }\times \left\{\begin{array}{c}\frac{1}{\sqrt{K_{yy}^R}}{e}^{\Delta U-\frac{\det {\mathbf{K}}_R}{2K_{yy}^R}{\left(x-x_R\right)}^2},\mathrm{near}x=x_R\hfill \\ \frac{1}{\sqrt{K_{yy}}}{e}^{\frac{\det \mathbf{K}}{2K_{yy}}{x}^2},\mathrm{near}x=0\hfill \end{array}\right..$$ (A3)

It then follows that

$$K_{\infty }=\frac{\left|\det \mathbf{K}\right|}{K_{yy}},K_{\infty }^R=\frac{\det {\mathbf{K}}_R}{K_{yy}^R},$$ (A4)

and

$$\Delta U_{\infty }=U_{\infty }\left(0\right)-U_{\infty }\left(x_R\right)=\Delta U+\frac{1}{2}\ln \left(\frac{K_{yy}}{K_{yy}^R}\right).$$ (A5)

Applying Eqs. (A4) and (A5) in Eq. (1b), we obtain

$$k_{\infty }=\frac{D_x}{2\mathit{\pi }{K}_{yy}}{\left(\left|\det \mathbf{K}\right|\det {\mathbf{K}}_R\right)}^{1/2}{e}^{-\Delta U}.$$ (A6)

To show that the same expression for k_∞ follows from Eq. (3) for k_L when D_y → ∞, we note that in this limiting case the equation $\det \left(\lambda \mathbf{I}+\mathbf{KD}\right)=0$ leads to

$$\lambda =\frac{D_x}{K_{yy}}\left|\det \mathbf{K}\right|,D_y\to \infty .$$ (A7)

Substituting this into Eq. (3), we arrive at the expression for k_∞ in Eq. (A6). When D_y → 0, the equation $\det \left(\lambda \mathbf{I}+\mathbf{KD}\right)=0$ leads to different expressions for λ depending on the sign of the force constant K_xx,

$$\lambda =\left\{\begin{array}{c}\frac{\left|\det \mathbf{K}\right|}{K_{xx}}{D}_y,K_{xx}>0\hfill \\ \left|K_{xx}\right|D_x,K_{xx}<0\hfill \end{array}\right..$$ (A8)

Inserting the second line of Eq. (A8) in Eq. (3) and using Eq. (A6), one obtains the limiting behavior of k_L given in Eq. (5).

APPENDIX B: VALUES OF THE RATE CONSTANT FROM BROWNIAN DYNAMICS SIMULATIONS

Our model system consists of N point-like particles that reside in a symmetric two-dimensional double-well potential of the form given in Eqs. (8) and (19). Here, the ratio Γ/(4ΔU), denoted as γ, is set to 1/3. The particles are allowed to diffuse along x and y. A particle is considered to be in the left well if x is less than zero and in the right well otherwise.

When the diffusion along one of the coordinates becomes infinitely fast, the dynamics can be reduced to one dimension. In the case of infinitely fast diffusion along y, the system becomes one-dimensional in x, with the potential of mean force given by U_∞(x) and the boundary between the wells still at x = 0.

For infinitely fast diffusion along x or, equivalently, infinitely slow diffusion along y, the system becomes one-dimensional in y. The potential of mean force, U₀(y), is now given by [see Eq. (9)]

$$\begin{array}{ccc}& & \exp \left[-U_0\left(y\right)\right]\approx \exp \left[-\Delta U{\left(y+1\right)}^2/2\right]\hfill \\ & & +\exp \left[-\Delta U{\left(y-1\right)}^2/2\right],\hfill \end{array}$$ (B1)

and the well boundary is at y = 0.

Two-dimensional Brownian dynamics simulations were carried out to determine the rate constant k. The simulations began with the N particles initially positioned in the left well (x < 0) according to the Boltzmann distribution, exp[−U(x, y)]. This was done by first choosing x according to the Boltzmann distribution exp[−U_∞(x)] and then choosing y according to the conditional probability p(y|x) ∝ exp[−Γ(y − x)²/2]. To choose x, the fractions of particles that would begin in the x < −1/2 and −1/2 < x < 0 regions were determined according to their respective Boltzmann weights. These fractions were compared to a random number uniformly distributed between 0 and 1 in order to determine which region a particle would start in. If the particle was to start in the x < −1/2 region, a normally distributed random number was generated via the Box-Muller method, and linearly transformed to produce the initial x value with the desired mean of −1 and standard deviation of $1/\left(2\sqrt{\Delta U}\right)$; any initial x value greater than −1/2 was discarded and the process was repeated until an x value less than −1/2 was produced. If a particle was to start in the −1/2 < x < 0 region, its initial x value was generated by the rejection method. Specifically, a random x was generated according to the exponential distribution exp(ΔUx), and whether that x was accepted was determined by comparing a random number uniformly distributed between 0 and 1 to the ratio of the desired distribution exp[−U_∞(x)] = exp(2ΔUx²) and the reference exp(ΔUx). Once the initial x was assigned, the initial y was generated via the Box-Muller method and linearly transformed to have the desired mean of x and standard deviation of $1/\left(2\sqrt{\gamma \Delta U}\right)$.

After the initial coordinates of a particle were generated, its diffusion was followed according to the Ermak-McCammon algorithm

$$\begin{array}{c}x=x_0+F_x\left(x_0,y_0\right)D_x\Delta t+{\left(2D_x\Delta t\right)}^{1/2}{R}_x,\hfill \\ y=y_0+F_y\left(x_0,y_0\right)D_y\Delta t+{\left(2D_y\Delta t\right)}^{1/2}{R}_y.\hfill \end{array}$$ (B2)

Here, x₀ is the current x, x is the position after a timestep of Δt, F_x(x₀, y₀) is the x component of the force calculated at the current position from the potential U(x,y), D_x is the diffusion constant along x, and R_x is a normally distributed random number. The description of the quantities in the y direction is similar. The number of particles remaining in the left well was recorded as a function of time throughout the simulation until this number first became one half of N.

In addition to the two-dimensional simulations outlined above, simulations were also carried out for one-dimensional diffusion along either x (to determine k_∞) or y (to determine k₀). For the simulations along x, the initial x coordinates were generated the same way as described above in the two-dimensional case. The movement of x was also nearly the same as above, except now the force was calculated from U_∞(x) instead of U(x, y). The same type of data was recorded and each simulation was again ended when the number of particles in the initial well became N/2.

For the simulations along y, the initial y coordinates were generated according to the first term, exp [−ΔU(y + 1)²/2], of the Boltzmann distribution exp[−U₀(y)], via the Box-Muller method and a linear transformation to have the correct mean of −1 and standard deviation of $1/\sqrt{\Delta U}$. The contribution of the second term, exp [−ΔU(y − 1)²/2], was captured by a reflection of the initial y value (to −y) if y generated by the foregoing procedure was greater than 0. The movement of y was the same as described in the two-dimensional case, except that the force was calculated from the potential U₀(y). The rest of the simulation process was the same as described above.

Three different values of ΔU, i.e., 4, 8, and 12, were studied. In each simulation, the number of particles was 5000. For the two-dimensional simulations and the one-dimensional simulations in x, D_x was fixed at 1; in the former case six D_y values were used: 10, 1, 10⁻¹, 10⁻², 10⁻³, and 10⁻⁴. For the one-dimensional simulations in y, D_y was fixed at 1. In all cases, final data were produced using a timestep of 5 × 10⁻⁴. This timestep was chosen after running simulations at a series of timesteps in the two one-dimensional cases. It was found that there was no significant difference in the rate constant obtained from the simulations (see below) with a tenfold change in timestep. The latter results for ΔU = 12 are listed in Table I.

Table I.

Effects of the timestep on the simulation results for the rate constants.

Δt	k0/Dy	k∞/Dx
1.0 × 10−3	(2.25 ± 0.08) × 10−2	(4.67 ± 0.09) × 10−5
5.0 × 10−4	(2.27 ± 0.10) × 10−2	(4.70 ± 0.19) × 10−5
1.0 × 10−4	(2.29 ± 0.05) × 10−2	(4.69 ± 0.13) × 10−5

The middle timestep was chosen for the balance of accuracy and speed. These results can be compared with the predictions of Kramers’ theory, k₀/D_y = 3.14 × 10⁻² and k_∞/D_x = 4.69 × 10⁻⁵. The simulation result for k_∞ agrees very well with the Kramers prediction, but there is a significant discrepancy between the two for k₀. As explained in the main text, due to the narrow parabolic region of U₀(y) near the barrier, the Kramers prediction for k₀ is inaccurate. A better prediction is given by half the inverse of the mean-first-passage-time for reaching the barrier from the reactant well [Eq. (20)], yielding k₀/D_y = 2.30 × 10⁻², which is in excellent agreement with the simulation result.

The data recorded from each simulation were the number of particles remaining in the left well over time, n(t), up to the time when the number of particles in the initial well dropped to one half for the first time. For the two high energy barriers (ΔU = 8 and 12), the decay of n(t) to its equilibrium value N/2 could be fit well to a single exponential function, 2n(t)/N − 1 = exp(−t/τ), where τ is the relaxation time. For the lowest barrier (ΔU = 4), n(t) in the two-dimensional simulations with small D_y (i.e., ≤ 10⁻²) exhibited a rapid initial decay before the slow decay. The initial decay came from particles initially near the boundary between the wells, and only the slow decay represented inter-well transitions. To account for the presence of the initial decay, for ΔU = 4 the amplitude of the exponential function was treated as a floating parameter rather than fixed at unity. In all the cases, the value of 1/τ was equated to twice the rate constant for the transition from the reactant well to the product well.

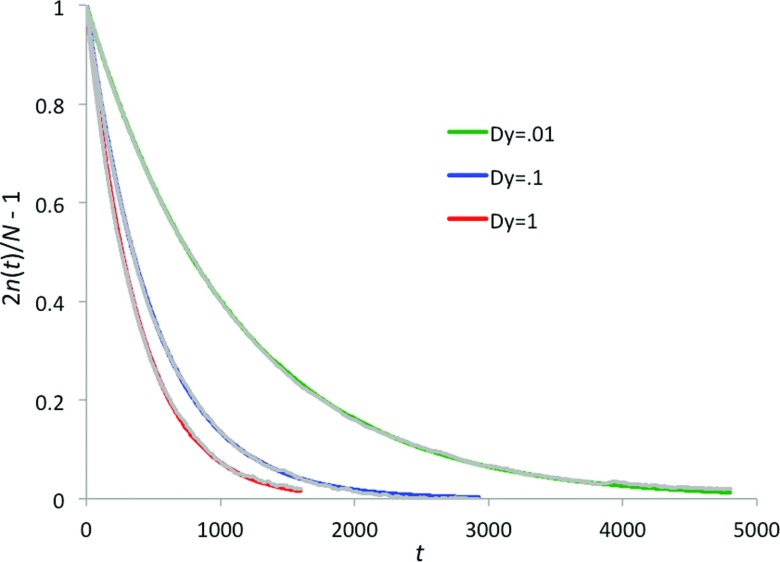
Sample data for the two-dimensional problem at ΔU = 8 and D_y = 1, 10⁻¹, and 10⁻² are shown in Fig. 3 to illustrate the exponential fitting. For each set of parameters, simulations were repeated ten times with different random number seeds. The averages and standard deviations of the rate constant calculated among the 10 repeat simulations are taken as the simulated rate constant and the simulation error, respectively.

FIG. 3.

The decay of the number of particles in the initial well toward the equilibrium value. The gray curves are data averaged over 10 repeat simulations, and red, blue, and green curves are exponentials with the average rate constants for D_y = 1, 10⁻¹, and 10⁻², respectively, at ΔU = 8.