Electrically generated eddies at an eightfold stagnation point within a nanopore

Abstract

Electrically generated flows around a thin dielectric plate pierced by a cylindrical hole are computed numerically. The geometry represents that of a single nanopore in a membrane. When the membrane is uncharged, flow is due solely to induced charge electroosmosis, and eddies are generated by the high fields at the corners of the nanopore. These eddies meet at stagnation points. If the geometry is chosen correctly, the stagnation points merge to form a single stagnation point at which four streamlines cross at a point and eight eddies meet.

I. INTRODUCTION

Streamline patterns reveal the topology of a flow field: we sketch streamlines, eddies, and stagnation points in order to develop our understanding of flows.^1,2 Stagnation points away from solid walls usually occur at the intersection of two streamlines, which divide the fluid into four separate regions. Such stagnation points can be generated in many ways, e.g., by a four-roll mill³ or by opposed fluid jets in a cross-slot device.^4,5 More complicated stagnation points are harder to generate. Berry and Mackley⁶ built a six-roll mill and investigated the flow field. When exact symmetry was achieved, six eddies met at a central point, and the various ways in which symmetry could be broken were described by Berry and Mackley⁶ in terms of catastrophe theory. Here, we report an electrically generated flow field in which four streamlines cross at a point and divide the flow into eight regions.

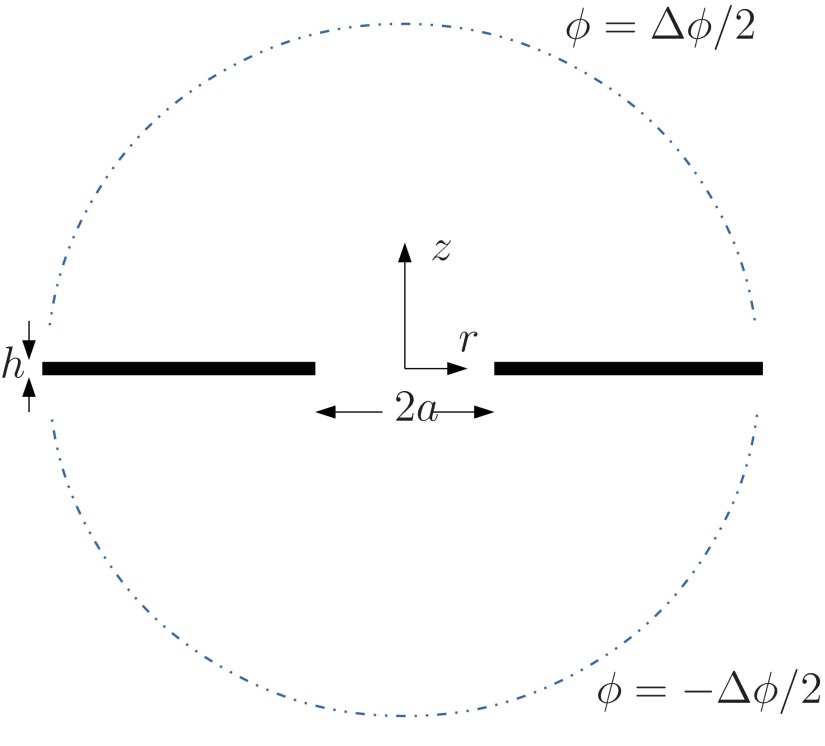
The axisymmetric flow geometry is shown in Figure 1. A cylindrical hole of radius a passes through an uncharged thin dielectric plate of thickness h: the hole represents a nanopore in a membrane, and we are interested in the induced charge electroosmotic flow generated by an electric potential difference applied between the two sides of the membrane.^7–9 We set up cylindrical polar coordinates, with z axis along the axis of symmetry and with the plane surfaces of the membrane at r > a, z = ±h/2.

FIG. 1.

The (infinite) dielectric plate of thickness h, pierced by a hole of radius a and surrounded by an electrolyte solution. The axisymmetric geometry represents a nanopore in a membrane. An electrical current is driven through the hole by a potential difference Δϕ between the two sides, at infinity.

In Sec. II, we consider the electric field passing through a circular hole in a membrane of zero thickness. We then (Sec. III) show how the field is modified at the edge of the hole when the membrane thickness h is small but non-zero. In Sec. IV, we review the fluid jets that are created by the electrical forces on the fluid near the corners of the membrane, and then in Sec. V we present numerical computations that show how the geometry of eddies created by these jets depends on the geometry of the hole in the membrane. As the ratio h/a increases, three stagnation points merge to form a stagnation point at which four streamlines cross. The stagnation points separate again as h/a increases further.

II. THE IMPOSED ELECTRIC FIELD

The pore and the two regions on either side of the membrane are occupied by an incompressible, electrically conducting Newtonian electrolyte solution with viscosity μ and electrical permittivity ε_f. The membrane is non-conducting, with permittivity ε_s. The electrical potential ϕ is continuous at the boundary between the solid membrane and the fluid. The surface charge density on the membrane is zero, so that εn · ∇ϕ is continuous, where n is the unit normal to the membrane and the permittivity ε takes values ε_s and ε_f on the two sides of the boundary. If (as is usually the case) ε_s ≪ ε_f, then to a first approximation we set ε_s = 0, and n · ∇ϕ = 0 in the fluid adjacent to the membrane.

We assume that the electrolyte solution contains N ionic species, with valence z_i and number density nⁱ. Far from any charged surfaces, the ionic number densities are $n^i=n_{\infty }^i$, with ${\sum }_i{z}_i{n}_{\infty }^i=0$ to ensure electrical neutrality of the bulk electrolyte. The electrical potential satisfies the Poisson equation

$${\nabla }^2\varphi =-\rho /{\epsilon }_f=-\sum _{i=1}^{N}e{z}_i{n}^i/{\epsilon }_f,$$ (1)

where ρ is the charge density.

Ions are convected with the fluid velocity u, and move relative to the fluid under the influence of electric fields and thermal diffusion. The conservation equation for the number density nⁱ of the ith ionic species, in steady state, is therefore

$$\nabla ·\left[n^i\mathbf{u}-{\omega }_i(kT\nabla n^i+e{z}_i{n}^i\nabla \varphi )\right]=0,$$ (2)

where ω_i is the mobility of the ith species of ion, kT is the Boltzmann temperature, and e is the elementary charge. In the absence of any reactions at the surface of the membrane, the flux of ions normal to the membrane is zero at the membrane surface.

When ε_s = 0, there is a steady solution of the ion conservation equation (2) in which the fluid is at rest (u = 0), the ionic number densities are unperturbed ($n^i=n_{\infty }^i$), and the electrical potential ϕ = ϕ₀ within the electrolyte is given by the solution of the Laplace equation

$$\begin{array}{c}\hfill {\nabla }^2{\varphi }_0=0,\end{array}$$ (3a)

$$\begin{array}{ccc}\hfill \mathbf{n}·\nabla {\varphi }_0& =& 0\text{on}\text{the}\text{membrane}\text{surface,}\hfill \end{array}$$ (3b)

$$\begin{array}{c}\hfill \varphi \to \pm \Delta \varphi /2,\text{as}\mathbf{r}\to \infty \text{in}z\gtrless 0\text{.}\end{array}$$ (3c)

This represents Ohmic conduction through an electrolyte with uniform electrical conductivity. The solution ϕ₀ = Φ₀ of the Laplace equation (3) when h = 0 is given by Morse and Feshbach¹⁰ (p. 1292) in terms of oblate spherical coordinates (ξ, η) where −∞ < ξ < ∞, 0 ⩽ η ⩽ π/2 such that

$$z=a\sinh \xi \cos \eta ,r=a\cosh \xi \sin \eta ,$$ (4)

and is

$$\begin{array}{ccc}\hfill {\varphi }_0={\Phi }_0(r,z)& =& \frac{\Delta \varphi }{2}\left[1-\frac{2}{\pi }{\tan }^{-1}\left(\frac{1}{\sinh \xi }\right)\right],z>0,h=0,\hfill \end{array}$$ (5a)

$$\begin{array}{c}\hfill =-{\Phi }_0(r,-z),z<0.\end{array}$$ (5b)

On the surface z = 0₊ of the membrane

$${\Phi }_0(r,0_{+})=\frac{\Delta \varphi }{2}\left[1-\frac{2}{\pi }{\tan }^{-1}\left(\frac{a}{{(r^2-a^2)}^{1/2}}\right)\right],r>a,$$ (6)

and for r = a(1 + δ), with δ ≪ 1,

$${\Phi }_0(r,0_{+})\approx \frac{\Delta \varphi }{\pi }{\left(2\delta \right)}^{1/2},$$ (7)

with Φ₀(r, 0₋) = −Φ₀(r, 0₊). The electric field in the plane of the hole is

$$\mathbf{E}=-\frac{\Delta \varphi \widehat{\mathbf{z}}}{\pi a{\left(1-r^2/a^2\right)}^{1/2}},r<a,$$ (8)

and if the conductivity of the electrolyte is Σ, the total current through the hole is 2aΣΔϕ. However, real membranes have a non-zero thickness h > 0. We shall show in Sec. III that when 0 < h ≪ a, the potential ϕ₀ differs from the potential Φ₀ for h = 0 by an amount O((h/a)^1/2). We neglect this perturbation for the moment, and assume ϕ₀(r, h/2) ≈ Φ₀(r, 0₊). The leading order potential ϕ₀ leads to an electric field of strength

$$\widehat{\mathbf{z}}·\nabla \varphi =\frac{2{\varphi }_0(r,h/2)}{h}\approx \frac{2{\Phi }_0(r,0_{+})}{h}$$ (9)

within the membrane.

If ε_s = 0 (as assumed so far), the electric field (9) within the membrane and the electric field (3b) outside the membrane satisfy the requirement that εn · ∇ϕ should be continuous at the boundary. However, in the real world, ε_s is at least as large as the permittivity of free space, ε₀, so that ε_s ⩾ ε₀ > 0, and the normal electric field outside the membrane must be perturbed at O(ε_sΔϕ/(ε_fh)) in order to ensure continuity of εn · ∇ϕ. Ions move toward (or away from) the membrane under the influence of this perturbation until equilibrium, with zero flux of ions into the membrane, is achieved. In order to determine this perturbation to the field, we assume that

$$\gamma =\frac{{\epsilon }_s}{{\epsilon }_f}\ll 1$$ (10)

and use γ as the basis for a perturbation expansion

$$\begin{array}{ccc}\hfill \varphi & =& {\varphi }_0+\gamma {\varphi }_1+\cdots ,\hfill \end{array}$$ (11a)

$$\begin{array}{ccc}\hfill n^i& =& n_0^i+\gamma n_1^i+\cdots ,\hfill \end{array}$$ (11b)

$$\begin{array}{ccc}\hfill \mathbf{u}& =& \gamma {\mathbf{u}}_1+\cdots ,\hfill \end{array}$$ (11c)

where the subscript 0 refers to the uniform ion density $n_0^i=n_{\infty }^i$ and to the potential (3c) for ε_s = 0. The O(γ) terms in the steady-state ion conservation equation give

$${\mathbf{u}}_1·\mathbf{\nabla }{n}_0^i={\omega }_i\mathbf{\nabla }·\left[e{z}_i{n}_0^i\mathbf{\nabla }{\varphi }_1+e{z}_i{n}_1^i\mathbf{\nabla }{\varphi }_0+kT\mathbf{\nabla }{n}_1^i\right].$$ (12)

Since $n_0^i$ is uniform, the left-hand side of (12) is zero.

On the surface of the membrane (except close to the edge of the hole), the potential ϕ₀ varies on a length scale r > a, whereas we expect the perturbation potential ϕ₁ to vary on the Debye length scale

$${\kappa }^{-1}={\left(\frac{{\epsilon }_{f}kT}{{\sum }_{i=1}^N{e}^2{z}_i^2{n}_{\infty }^i}\right)}^{1/2}.$$ (13)

Hence, if r − a ≫ κ⁻¹ so that we are much further than a Debye length away from the edge of the hole, we may neglect the second term on the right-hand side of (12), which reduces to

$$\mathbf{\nabla }·\left[e{z}_i{n}_0^i\mathbf{\nabla }{\varphi }_1+kT\mathbf{\nabla }{n}_1^i\right]=0.$$ (14)

The perturbed ionic number densities are therefore given by a Boltzmann distribution

$$n_1^i=n_{\infty }^i{\text{e}}^{-e{z}_i{\varphi }_1/kT}$$ (15)

and ϕ₁ satisfies the Poisson equation

$${\nabla }^2{\varphi }_1=-\frac{{\rho }_1}{{\epsilon }_f}=-\frac{e}{{\epsilon }_f}\sum _{i=1}^N{z}_i{n}_1^i=-\frac{e}{{\epsilon }_f}\sum _{i=1}^N{z}_i{n}_{\infty }^i{\text{e}}^{-e{z}_i{\varphi }_1/kT}.$$ (16)

The perturbation potential ϕ₁ varies in the z direction over the Debye length scale κ⁻¹, and we neglect its slow variation with r. We assume that γeϕ₁/(kT) is small, and linearize the Poisson-Boltzmann equation (16), which becomes

$$\frac{{\text{d}}^2{\varphi }_1}{\text{d}{z}^2}=-{\kappa }^2{\varphi }_1.$$ (17)

The solution of (17) that ensures that the potential ϕ = ϕ₀ + γϕ₁ satisfies the jump boundary condition [εn · ∇ϕ] = 0 at the surface of the membrane is

$$\begin{array}{ccc}\hfill \varphi & =& {\varphi }_0-\frac{2{\Phi }_0(r,0_{+}){\epsilon }_s}{h\kappa {\epsilon }_f+2{\epsilon }_s}\exp [-\kappa (z-h/2)],z>h/2,\hfill \end{array}$$ (18a)

$$\begin{array}{ccc}\hfill \varphi & =& {\varphi }_0+\frac{2{\Phi }_0(r,0_{+}){\epsilon }_s}{h\kappa {\epsilon }_f+2{\epsilon }_s}\exp \left[\kappa (z+h/2)\right],z<-h/2,\hfill \end{array}$$ (18b)

with

$$\varphi =\frac{2{\Phi }_0(r,0_{+})\kappa {\epsilon }_{f}z}{h\kappa {\epsilon }_f+2{\epsilon }_s},\left|z\right|<h/2,$$ (19)

inside the solid membrane. We see from (18) that the perturbation γϕ₁ is only small compared to ϕ₀ if γ/(hκ) ≪ 1. We also note that (18) does not represent the first terms of a systematic expansion, and is incorrect at O((γ/hκ)²). However, we prefer to leave the expansion in the form (18) since it shows explicitly how the expansion fails in the limit h → 0. In particular, far from the hole we recover the uniform charge cloud that would be induced in the absence of any hole. A detailed analysis of induced charge electroosmotic flow around an uncharged dielectric sphere (or cylinder) of radius a in the limit aκ ≫ 1 has been provided by Schnitzer and Yariv.¹¹

The perturbation potential (18) outside the membrane can be described in terms of an effective induced zeta potential

$${\zeta }_i=-\frac{2{\epsilon }_s{\Phi }_0(r,0_{+})}{h\kappa {\epsilon }_f+2{\epsilon }_s}.$$ (20)

The tangential electric field −∂ϕ/∂r acts on the charge cloud adjacent to the membrane and causes a tangential velocity. Immediately outside the double layer (assuming r ≫ a + κ⁻¹, so that flow can be assumed to be locally one-dimensional), the leading-order radial fluid velocity outside the charge cloud is given by the Smoluchowski slip velocity

$$u=\frac{\partial \varphi }{\partial r}\frac{{\epsilon }_f{\zeta }_i}{\mu },$$ (21)

and using the expansion (7) at r = a(1 + δ), together with (20), we obtain, in the limit ε_s ≪ hκε_f,

$$u=-\frac{2{\epsilon }_{\mathrm{s}}}{ah\kappa \mu }{\left(\frac{\Delta \varphi }{\pi }\right)}^2,z=0_{+}.$$ (22)

The radial velocity created by the induced charge is toward the hole on both sides of the membrane.

This solution (18), (19), and (22) is clearly inappropriate within a distance O(κ⁻¹) of the edge of the hole, where the electric field can no longer be assumed to vary slowly with r. In Sec. III, we find a local solution to the Laplace equation in the neighbourhood of the edge, for the case ε_s = 0 for which the electric field satisfies a Neumann boundary condition (3b) at the surface of the membrane.

III. MEMBRANE OF UNIFORM THICKNESS: A CONFORMAL MAPPING SOLUTION

We now study in detail the electric field at the edge of the membrane of thickness h > 0 near r = a, for the case ε_s = 0. Sufficiently close to the edge (Figure 2(b)) we neglect the azimuthal curvature, and seek a local solution of the two-dimensional Laplace equation. In the limit h ≪ a, the outer limit of the local solution can then be matched to the inner limit (7) of the outer solution for a membrane of zero thickness.

FIG. 2.

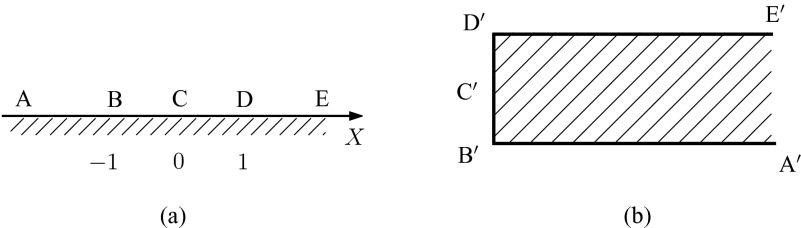
(a) The Z plane, with origin at C. D is at Z = 1 and B at Z = −1. (b) The w plane, with origin at D^′. C^′ is at w = −iHπ/2 and B^′ is at w = −iHπ. The w plane represents the edge of the hole in the membrane.

We map the upper half of the Z-plane Z = X + iY (Figure 2(a)) onto the region outside a rectangular edge in the w plane w = u + iv (Figure 2(b)) by means of the conformal mapping¹²

$$w=H\left[Z{(Z^2-1)}^{1/2}-{\cosh }^{-1}\left(Z\right)\right],$$ (23)

where the constant H will be determined later, and the branch of the square root is chosen such that

$$w=H\left[X{(X^2-1)}^{1/2}-\ln (X+{(X^2-1)}^{1/2})\right],Z=X\ge 1,$$ (24)

along the real axis. The rectangular edge (Figure 2(b)) represents the right-hand edge of the hole in the membrane (Figure 1), seen on a scale at which the membrane thickness can be observed, and the constant H in (23) will eventually be chosen to ensure that the membrane has thickness h.

If Z = X ≫ 1 (E on Figure 2(a)),

$$w\sim H{X}^2.$$ (25)

If Z = 1 + ɛ, with |ɛ| ≪ 1 (near D on Figure 2(a)), then

$$w=H\left(\frac{4\sqrt{2}}{3}\right){\varepsilon }^{3/2},$$ (26)

so that if Z = 1 − ɛ_R, with 0 < ɛ_R ≪ 1 real,

$$w=-H\left(\frac{4\sqrt{2}}{3}\right){\varepsilon }_R^{3/2}\text{i},$$ (27)

and if Z = ɛ with |ɛ| ≪ 1 (near C on Figure 2(a)),

$$w=-\text{i}H\left[\frac{\pi }{2}-2\varepsilon \right].$$ (28)

Finally, since cosh ⁻¹(−Z) = πi − cosh ⁻¹Z, we note that when Z = −1 (at B),

$$w=-H{\cosh }^{-1}Z=-\text{i}H\pi .$$ (29)

In order to map the upper half Z plane into the space outside a semi-infinite rectangular slab of thickness |D^′B^′| = h, we see from (26) and (29) that we should choose H = h/π.

We now consider the (harmonic) function

$$\varphi =C{H}^{1/2}\Re \left(Z\right)=C{H}^{1/2}X.$$ (30)

This satisfies the Neumann boundary condition (3b) on the boundary ABCDE in the Z plane, and after transformation to the w plane leads to a solution¹⁰ of the Laplace equation that satisfies the Neumann boundary condition on the transformed boundary A^′B^′C^′D^′E^′, i.e., on the boundary of the membrane near the edge of the hole. In the far field of the w plane,

$$\varphi =C\Re \left(w^{1/2}\right),$$ (31)

which matches with the inner expansion of the outer solution (7) for the electric potential at the edge of the hole in a membrane of zero thickness if

$$C={\left(\frac{2}{a}\right)}^{1/2}\frac{\Delta \varphi }{\pi }.$$ (32)

Close to the corner D^′ of the slab, at w = s e^iθ with s ≪ 1,

$$\varphi =C{H}^{1/2}\left\{1+{\left(\frac{3s}{4H\sqrt{2}}\right)}^{2/3}\cos \left(\frac{2\theta }{3}\right)\right\}.$$ (33)

Thus, the electrical potential at the corner D^′ is CH^1/2 = Δϕ(2h/a)^1/2π^−3/2, together with an eigensolution proportional to s^λ, with λ = 2/3, and the potential difference between the two corners D^′ and B^′ (Figure 2) is

$$\Delta {\varphi }_c=\Delta \varphi {\left(\frac{2}{\pi }\right)}^{3/2}{\left(\frac{h}{a}\right)}^{1/2}.$$ (34)

In Sec. IV, we compare the magnitude of the electroosmotic flow generated at the corner by the potential (33) with the magnitude of the flow (22) generated along the surface of the membrane away from corners at the edge of the hole.

IV. INDUCED CHARGE AT A CORNER

The theory of electro-osmotic flow at a dielectric corner is discussed by Thamida and Chang¹³ and Yossifon et al.¹⁴ We consider a plane 2-dimensional wedge of internal angle 2α = 2(π − θ₀), and adopt plane polar coordinates (s, θ), as shown in Figure 3. The solution of the Laplace equation for the potential ϕ outside the electrical double layer, antisymmetric in θ outside the wedge, has the form

$$\varphi =A{s}^{\lambda }\sin \lambda \theta .$$ (35)

Zero flux of ions into the solid wedge requires

$$\mathbf{n}.\nabla \varphi =\frac{1}{s}\frac{\partial \varphi }{\partial \theta }=A\lambda s^{\lambda -1}\cos \lambda \theta =0,\theta ={\theta }_0=\pi -\alpha ,$$ (36)

so that

$$\lambda =\frac{(2n+1)\pi }{2{\theta }_0},n=0,\pm 1,\pm 2\cdots .$$ (37)

If θ₀ = π, the least singular eigensolution (35) corresponds to λ = 1/2, in agreement with (7). If α = π/4, so that θ₀ = 3π/4, then λ = 2/3, as found in (33), and

$$A=\frac{3^{2/3}}{2^{5/3}}C{H}^{-1/6}=\frac{3^{2/3}}{2^{7/6}}\frac{\Delta \varphi }{\pi a^{1/2}}{\left(\frac{\pi }{h}\right)}^{1/6}.$$ (38)

Within the solid wedge, the potential is

$$\varphi ={\varphi }_w=A{s}^{\lambda }\frac{\sin \lambda {\theta }_0}{\sin \lambda \alpha }\sin \left[\lambda (\pi -\theta )\right],$$ (39)

which is antisymmetric about θ = π. As in Sec. II, we conclude that there will be an induced surface charge, corresponding to an induced zeta potential

$$\begin{array}{ccc}\hfill {\zeta }_i=-\frac{{\epsilon }_s}{\kappa {\epsilon }_f}\frac{\partial {\varphi }_w}{\partial n}& =& -\frac{{\epsilon }_s}{{\epsilon }_f}\frac{A{s}^{\lambda -1}}{\kappa }\lambda \cot \lambda \alpha \sin \lambda {\theta }_0,\theta ={\theta }_0,\hfill \end{array}$$ (40a)

$$\begin{array}{ccc}\hfill & =& \frac{{\epsilon }_s}{{\epsilon }_f}\frac{A{s}^{\lambda -1}}{\kappa }\lambda \cot \lambda \alpha \sin \lambda {\theta }_0,\theta =-{\theta }_0.\hfill \end{array}$$ (40b)

FIG. 3.

A dielectric wedge, of angle 2α, with local cylindrical coordinates (s, θ).

Note that this potential becomes large as s → 0 close to the apex of the wedge, and an analysis based on linearized Poisson-Boltzmann theory therefore breaks down. Large induced potentials on the surface of a spherical particle are discussed by Yariv and Davis.¹⁵

The tangential electric field immediately outside the wall is

$$\begin{array}{c}\hfill E_s=-\frac{\partial {\Phi }_l}{\partial s}=\lambda A{s}^{\lambda -1}\sin \lambda {\theta }_0,\theta ={\theta }_0,\end{array}$$ (41a)

$$\begin{array}{ccc}\hfill & =& -\lambda A{s}^{\lambda -1}\sin \lambda {\theta }_0,\theta =-{\theta }_0,\hfill \end{array}$$ (41b)

and, as discussed in Sec. II, this acts upon the charge cloud associated with the induced zeta potential ζ_i (40). If the Debye length κ⁻¹ is sufficiently small, we expect a Smoluchowski slip velocity just outside the charge cloud, of magnitude

$$u_s=-\frac{{\epsilon }_f{E}_s{\zeta }_i}{\mu }=-\frac{{\epsilon }_s}{\kappa \mu }{A}^2{s}^{2\lambda -2}{\lambda }^2\cot \lambda \alpha {\sin }^2\lambda {\theta }_0,\theta =\pm {\theta }_0.$$ (42)

For the corner of the membrane at the entrance to the pore, α = π/4 and λ = 2/3, with A given by (38), so that the velocity is

$$u_s=-\frac{{\epsilon }_s}{a\kappa \mu }{s}^{-2/3}{\left(\frac{\Delta \varphi }{\pi }\right)}^2{\left(\frac{\pi }{h}\right)}^{1/3}{3}^{-1/6}{2}^{-1/3},\theta =\pm {\theta }_0.$$ (43)

We can seek a solution of the Stokes equations for fluid flow around the corner which has the required radial velocity u_s ∝ s^{2λ − 2}, and look for a stream function ψ of the form² (for m ≠ 0, 1, 2)

$$\psi =s^m\left[B_1{\text{e}}^{\text{i}m\theta }+B_2{\text{e}}^{\text{i}(m-2)\theta }\right],$$ (44)

where the B_i are constants. The fluid velocity is then

$$u_s=\frac{1}{s}\frac{\partial \psi }{\partial \theta },u_{\theta }=-\frac{\partial \psi }{\partial s}.$$ (45)

However, we shall not proceed further with this local solution, since in Sec. V we consider full numerical solutions of the governing equations.

Note that a direct comparison between u_s (43) and the slip velocity u (22) away from the the edge of the hole indicates that u > u_s for s > 0.337h, so that any solution of the form (44) is only useful very close to the corner.

V. NUMERICAL COMPUTATION OF EDDIES

The set of time-independent equations governing the electrical potential ϕ, the ionic number densities nⁱ, the fluid velocity u, and fluid pressure p consists of the Poisson equation (1), the ion conservation equation (2), and the Stokes equations

$$\begin{array}{ccc}\hfill -\nabla p+\mu {\nabla }^2\mathbf{u}-\nabla \varphi \sum _{i=1}^N{z}_{i}e{n}^i& =& 0,\hfill \end{array}$$ (46)

$$\begin{array}{ccc}\hfill \nabla ·\mathbf{u}& =& 0.\hfill \end{array}$$ (47)

We solve the coupled equations (1), (2), (46), and (47) by means of a finite volume numerical scheme based upon the OpenFOAM CFD library.¹⁶ The surface charge density σ_m in the absence of any imposed field is set to zero, and a symmetrical electrolyte (N = 2, z₁ = −z₂ = 1) is considered, with identical cationic and anionic mobilities. There is therefore complete symmetry about the plane of the membrane, and no net flow through the hole. The relative permittivity of the electrolyte is ε_f /ε₀ = 80, where ε₀ is the permittivity of free space, and that of the membrane is set in the computations to be either ε_s/ε₀ = 3.9, corresponding to silica, or ε_s = 0. The hole has radius $a=5\mathrm{nm}$ (a typical hole size in silica¹⁷ or graphene^18,19), with aκ = 5, corresponding to an electrolyte of strength 95 mM (at 300 K). The results presented here were performed with a mesh spacing that varied smoothly from κ⁻¹/10 close to the membrane and hole, to κ⁻¹ at the far outer boundary. The potential difference applied to generate the flow was $\Delta \varphi =1\mathrm{mV}$, so that eΔϕ/kT ≈ 0.04: fluid velocities are everywhere proportional to (Δϕ)² as long as eΔϕ/kT is sufficiently small for the linearized Poisson-Boltzmann equation to be valid, in which case the streamlines are independent of Δϕ. Further details of the computational scheme are given by Mao et al.⁸

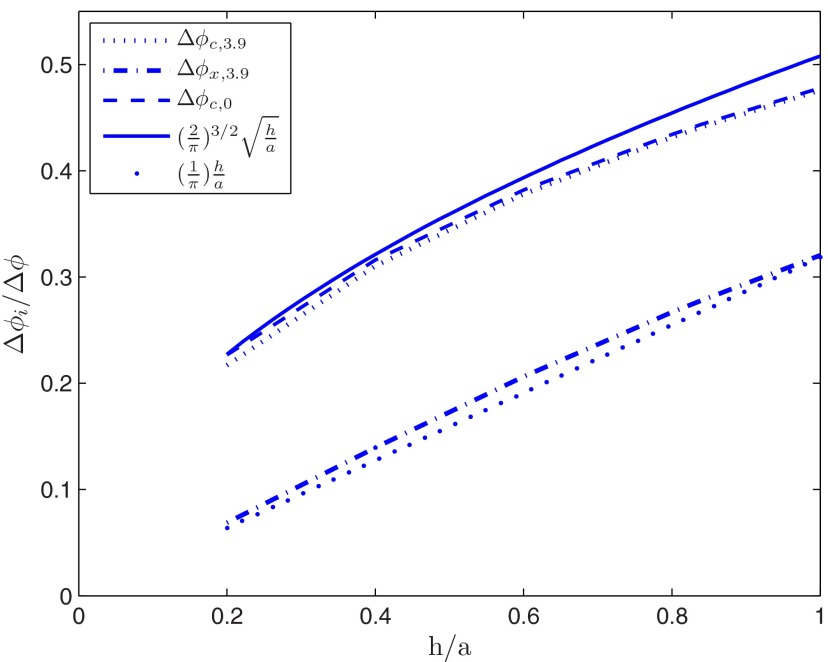
The difference in electrical potential between the two ends of the pore, at the wall of the cylindrical pore, is Δϕ_c (34) when h ≪ a and this analytic prediction is shown in Figure 4 as a function of h/a. We see that the analytic result is in good agreement with computed results Δϕ_{c, 0} (ε_s = 0) for h/a < 0.4. Also shown are computations for a membrane with relative permittivity ε_s/ε₀ = 3.9, which differ little from those for ε_s/ε₀ = 0. If h/a is sufficiently small, the resistance of the pore changes only slightly⁹ from that predicted for the electric field (5b) when h = 0. We therefore expect the current along the centreline of the pore, well away from the edges, to be little changed, and the electric field along the centreline is still (to a first approximation) $-\widehat{\mathbf{z}}\Delta \varphi /\left(a\pi \right)$ (8). The potential difference between the ends (z = ±h/2) of the pore along the centreline should therefore be

$$\Delta {\varphi }_x=\frac{\Delta \varphi }{\pi }\left(\frac{h}{a}\right),h\ll a.$$ (48)

This too is shown in Figure 4, and we see reasonable agreement between theory and computation.

FIG. 4.

The potential difference across the cylindrical pore, scaled by the total potential difference Δϕ between the two sides of the membrane. Potential difference along the pore wall: ——— theoretical prediction Δϕ_c (34); – – – – Δϕ_{c, 0} computed for ε_s = 0; ⋯ computed for ε_s/ε₀ = 3.9. Potential difference along the pore axis: - - - - - - - Δϕ_{c, 3.9} theoretical prediction Δϕ_x (48); – - – - – computed Δϕ_{x, 3.9} for ε_s/ε₀ = 3.9.

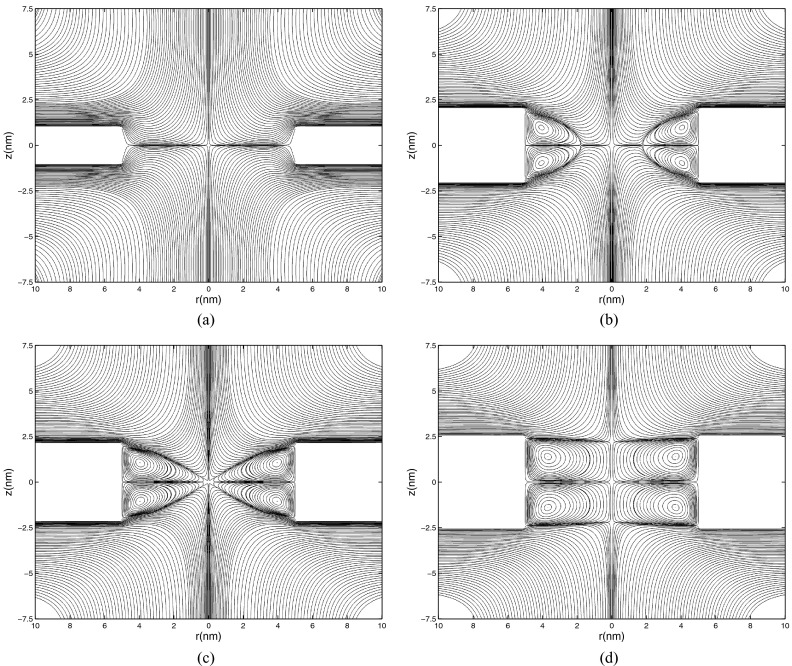
When ε_s/ε₀ = 3.9, induced charges lead to electro-osmosis. Streamlines computed for the case h = 0.4a are shown in Figure 5(a) and take the form shown schematically in Figure 6(a). Axial symmetry implies that ABD and GFH in Figure 6(a) are cross-sections of the same toroidal eddy (and similarly for CBD and EFH). However, the eddy pairs ABCD and EFGH in Figure 5(a) are very small. Flow near the corners A,C,E,G is a combination of the horizontal velocity (22) predicted on the upper and lower surfaces of the membrane, and the local corner flow (43), which flows upwards along BA and FG, thereby causing the horizontal flow to separate at A and G (and similarly at C and E). At fixed position, the uniform flow (22) varies as h⁻¹, whereas the corner flow (43) varies as h^−1/2. As h increases, the ratio of the corner flow to horizontal flow increases, and the eddies become larger, so that the stagnation points D and H (or more correctly, stagnation lines, since the flow has axial symmetry) move toward the central stagnation point at O. This is seen in Figure 5(b) for h = 0.8a.

FIG. 5.

Numerically computed streamlines in the neighbourhood of the hole, aκ = 5, ε_s/ε₀ = 3.9. Uncharged membrane of thickness: (a) h = 0.4a; (b) h = 0.8a; (c) h = 0.84a; (d) h = a.

FIG. 6.

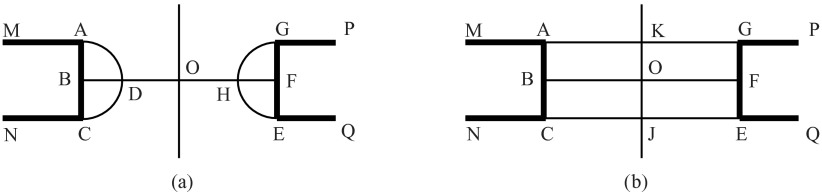
Schematic showing the boundaries of eddies in Figure 5. MA and GP represent the membrane surface at z = h/2; NC and EQ the surface at z = −h/2. ABC and GFE represent the cylindrical surface of the nanopore. Stagnation points within fluid (away from the walls) are at (a) O,D,H and (b) O,J,K. Axial symmetry implies that the eddies ABD and GFH in (a) are cross-sections of the same toroidal eddy.

When h ≈ 0.84a the stagnation points D and H merge into O, and 8 eddies meet at O, as seen in Figure 5(c). Any further increase in h causes the stagnation point to bifurcate into three points, at O, J, and K, as seen in Figure 5(d) and shown schematically in Figure 6(b). Figure 5(c) shows eddies for h = 0.84a, and the precise value for h at which the 8-fold stagnation point is formed lies within the range 0.83a < h < 0.85a. Computations with larger grid size κ⁻¹/5 in the vicinity of the membrane gave streamlines that could not be distinguished from those in Figure 5, and the 8-fold stagnation point was still formed at h ≈ 0.84a,

The Debye length when h = 0.84a and aκ = 5 is κ⁻¹ = 0.238h. The corner flow discussed in Sec. IV is valid only outside the charge cloud (i.e., for s > κ⁻¹), in which region the corner flow (45) is swamped by the velocity (22) parallel to the plane of the membrane. We are therefore unable to see in Figure 5 regions close to the corners in which streamlines are symmetric about the local coordinate θ = 0 (Figure 3).

Any asymmetry in the flow caused by a non-zero surface charge density σ_m or by differences between the mobilities of the ions causes a net flow from one side of the membrane to the other. If this is weak, the eddies seen in Figure 5 persist, and the net flow has to snake its way between them, as discussed by Jeffrey and Sherwood,² Thamida and Chang,¹³ and Yossifon et al.¹⁴

VI. CONCLUDING REMARKS

We have shown that the system of induced charge electro-osmotic eddies in a cylindrical pore can have a rich structure that varies markedly with pore aspect ratio. If flows created by induced charge electroosmosis are strong compared to net motion through the pore, there is a danger that fluid trapped in the eddies may become contaminated (or may degrade) over time, and lead to contamination of samples passing through the pore. Such problems can be reduced by suitable choice of pore geometry and imposed electric field strength, in order to control the ratio of eddy velocity to volumetric flow rate through the pore.