Shrinkage prediction of seed-voxel brain connectivity using resting state fMRI

Abstract

Resting-state functional magnetic resonance imaging (rs-fMRI) is used to investigate synchronous activations in spatially distinct regions of the brain, which are thought to reflect functional systems supporting cognitive processes. Analyses are often performed using seed-based correlation analysis, allowing researchers to explore functional connectivity between data in a seed region and the rest of the brain. Using scan–rescan rs-fMRI data, we investigate how well the subject-specific seed-based correlation map from the second replication of the study can be predicted using data from the first replication. We show that one can dramatically improve prediction of subject-specific connectivity by borrowing strength from the group correlation map computed using all other subjects in the study. Even more surprisingly, we found that the group correlation map provided a better prediction of a subject's connectivity than the individual's own data. While further discussion and experimentation are required to understand how this can be used in practice, results indicate that shrinkage-based methods that borrow strength from the population mean should play a role in rs-fMRI data analysis.

Introduction

Spontaneous low-frequency fluctuations in the blood oxygenation level-dependent (BOLD) signal, measured using functional magnetic resonance imaging (fMRI), promise to provide critical information about the functional organization of the brain. Resting-state functional connectivity research has already revealed large-scale spatial patterns of coherent signals in the brain (Biswal et al., 1995; Fox et al., 2005; Greicius et al., 2003; Lowe et al., 1998). These resting-state networks have been shown to consist of regions co-activated during tasks (Smith et al., 2009), and have been consistently observed both across groups of subjects and in repeated scanning sessions (Damoiseaux et al., 2006; Shehzad et al., 2009).

Various methods exist for analyzing resting-state data, including independent component analysis (Beckmann et al., 2005; Kiviniemi et al., 2003), partial correlation (Fransson and Marrelec, 2008), and clustering (Cordes et al., 2002). However, perhaps the most common approach to explore functional connectivity within the brain is to use seed-based correlation analysis (Biswal et al., 1995; Fox et al., 2005; Greicius et al., 2003). Seed analysis is based on the a priori selection of a region from which time series data are extracted, and connectivity is calculated as the correlation of the time series for the a priori seed with the time courses for all other voxels in the brain. This technique has proven useful in revealing the connectivity properties of many seed areas, and has been used extensively in recent years (Fox et al., 2005; Greicius et al., 2003; Margulies et al., 2007) due to its efficacy and ease of implementation.

In the statistics literature, shrinkage estimators (Efron and Morris, 1975; James and Stein, 1961) have been shown to improve upon many traditional estimators, in terms of mean squared error (MSE), by shrinking the estimators towards some fixed constant value. For example, shrinkage is implicit in Bayesian inference, penalized likelihood inference and multi-level models (Lindquist and Gelman, 2009), and is directly related to the so-called empirical Bayes estimators used in neuroimaging data analysis (Friston and Penny, 2003; Friston et al., 2002; Su et al., 2009). Charles Stein's early work on this phenomenon (Stein, 1956) is generally considered by the statistics community to be one of the seminal results of the twentieth century (Efron, 2010).

In this paper, we investigate whether the use of shrinkage-based methods can improve estimates of resting-state functional connectivity using seed-based analysis. To illustrate our point, we analyze a data set consisting of scan–rescan resting-state fMRI runs from 20 healthy adults. For each of the 40 fMRI scanning sessions (20 participants, each with 2 replicates), using a seed-based analysis we obtain different connectivity maps and ask a simple question: how well can we predict the correlation map of the second replicate for each subject using data from the first replicate?

A natural predictor of the connectivity of the second replicate would be to use the same subject's correlation map from the first scanning session. However, somewhat surprisingly, our results illustrate that one can dramatically improve prediction of subject-specific correlation maps by borrowing strength from the group correlation map, estimated using the first scan from all other subjects in the study. Therefore, we propose a weighted predictor of the subject-specific correlation map and the group correlation computed using all other subjects in the study. Using measurement error approaches (Carroll et al., 2006; Di et al., 2009; Shou et al., 2013; Zipunnikov et al., 2011), the weights are voxel-specific and the amount of shrinkage depends upon each voxel's reliability. The greater the uncertainty, the less the connectivity estimate for the voxel is trusted and the more it will be pulled towards the group estimate. The smaller the uncertainty, the more the individual estimate is trusted and the less it will be pulled towards the group estimate. This process leads to estimates that lie closer together than those obtained using a standard analysis. Even more surprisingly, we find that the group correlation map is a better predictor of the connectivity patterns for an individual than the subject's own data.

These results indicate that individual subject results can be improved by shrinking their estimates towards the mean of the population. The proposed shrinkage approach is very easy to implement in practice, and simply requires the calculation of a weighted average of connectivity maps. Though these results are presented for standard seed-based analysis, the idea promises to have impact on other analyses, as well.

Methods

Estimators

Let Y_ij(v, t) denote the fMRI time series for subject i = 1, ,...,, I at replication j = 1, ,...,, J_i at voxel v and time t. While the replication experiment used in this paper is simple with J_i = 2, for each of the I = 20 subjects, other studies may have different experimental designs with a different number of replicates per subject. Let us denote the seed time course as

$$Y_{ij}^{\mathrm{S}}\left(t\right)=\frac{1}{\mid \mathrm{S}\mid }\sum _{v\in \mathrm{S}}{Y}_{ij}(v,t),$$

where S and |S| denote the collection of voxels and the total number of voxels in the seed region, respectively. For a given subject i, replicate j, and voxel v, the seed-based connectivity map is defined as the correlation between Y_ij(v, t) and Y $Y_{ij}^{\mathrm{S}}\left(t\right)$(t) over t, that is

$$W_{ij}\left(v\right)=\frac{{\sum }_{t=1}^T\{Y_{ij}(v,t)-{\overline{Y}}_{ij}(v,\cdot )\}\{Y_{ij}^{\mathrm{S}}\left(t\right)-{\overline{Y}}_{ij}^{\mathrm{S}}(\cdot )\}}{\sqrt{{\sum }_{t=1}^T{\{Y_{ij}(v,t)-{\overline{Y}}_{ij}(v,\cdot )\}}^2\sqrt{{\sum }_{t=1}^T{\{Y_{ij}^{\mathrm{S}}\left(t\right)-verline{Y}_{ij}^{\mathrm{S}}(\cdot )\}}^2}}},$$

where ${\overline{Y}}_{ij}(v,\cdot )$ and ${\overline{Y}}_{ij}^{\mathrm{S}}(\cdot )$ are the averages over t of Y_ij(v, t) and $Y_{ij}^{\mathrm{S}}\left(t\right)$, respectively. Thus, the connectivity map does not depend on time and can be calculated for each subject, replicate and voxel, including all voxels in the seed region.

To illustrate the fact that by “borrowing strength” between subjects we can obtain a better estimate of the seed-based correlation maps, we propose a series of estimators for the correlation map which incorporate varying amounts of information from other subjects. Our goal is to estimate the second replication connectivity maps for each subject i₀, W_i02(v), based on data from the first replication, W_i1(v), for i = 1, ,..., 20, and v = 1, ,..., V.

The first, and perhaps most natural, potential estimator of the second replication connectivity map, W_i02(v), is to use the first replica tion connectivity map, ${\widehat{W}}_{i_{0}2}^{\mathrm{raw}}=W_{i_{0}1}\left(v\right)$. We will refer to this as the “Raw” estimator. The second potential estimator for W_i02 (v) is the average of the first replication connectivity maps for all subjects:

$${\widehat{W}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)=\frac{1}{I}\sum _{i=1}^I{W}_{i1}\left(v\right).$$

Note that this estimator is the same for all subjects and the index i₀ from ${\widehat{W}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)$ could be dropped. We keep the index for consistency with the other estimators and refer to this as the “mean” estimator.

We also investigate the class of shrinkage estimators, that is, estimators that take the first replication subject-specific connectivity data and shrink it towards the average connectivity of all subjects' first replicate. As all entries we consider are correlations, we first transform them using Fisher's z-transformation $r\to \frac{1}{2}\log \frac{1+r}{1-r}=\mathrm{arctanh}\left(r\right)$, whose inverse is $z\to \frac{\exp \left(2z\right)-1}{\exp \left(2z\right)+1}=\tanh \left(z\right)$. More precisely, we calculate

$$V_{ij}\left(v\right)=\frac{1}{2}\log \frac{1+W_{ij}\left(v\right)}{1-W_{ij}\left(v\right)},$$

apply shrinkage estimation to the transformed data, V_ij(v), and then apply the inverse transformation to the shrinkage estimator. Using the same notation as with the untransformed data, we define ${\widehat{V}}_{i_{0}2}^{\mathrm{raw}}=V_{i_{0}1}$ and ${\widehat{V}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)={\sum }_{i=1}^I{V}_{i1}\left(v\right)∕I$.

The connectivity shrinkage estimator on the transformed scale is defined as

$${\widehat{V}}_{i_{0}2}^{\gamma }\left(v\right)=\gamma \left(v\right){\widehat{V}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)+\{1-\gamma \left(v\right)\}{\widehat{V}}_{i_{0}2}^{\mathrm{raw}}\left(v\right),$$

where γ(v) can take any value in [0, 1] and is a shrinkage factor at the voxel level. When γ(v) = 1, the subject-specific data ${\widehat{V}}_{i_{0}2}^{\mathrm{raw}}$ are considered completely unreliable and the estimator is reduced to the mean ${\widehat{V}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)$, whereas when γ(v) = 0, the subject-specific data ${\widehat{V}}_{i_{0}2}^{\mathrm{raw}}$ are perfectly reliable and there is no shrinkage towards the population average. The estimator of connectivity on the original scale of the correlation is then obtained as ${\widehat{W}}_{i_{0}2}^{\gamma }\left(v\right)=\tanh \left\{{\widehat{V}}_{i_{0}2}^{\gamma }\left(v\right)\right\}$. In practice, data are seldom perfectly reliable, which makes shrinkage towards the population mean a good alternative. A major question is how to estimate the shrinkage function γ(v). A very simple approach for fMRI connectivity is to use γ(v) = γ = 0.1 that is, very strong and equal shrinkage at all voxels towards the population mean. This value is close to the average reliability over all voxels (Shou et al., 2013) and performs well in practice. However, we would like to have an estimator of γ(v) that takes into account the potential differences in the reliability of connectivity maps across brain voxels v.

The optimal amount of shrinkage at every voxel can be calculated based on the replication data. In this case, we are still interested in shrinking estimators of the type ${\widehat{V}}_{i_{0}2}^{\gamma }\left(v\right)$, though γ(v) can be estimated from the replication studies for the other subjects, i ≠ i₀. To avoid cases of data predicting itself, we use only the replication data for subjects i ≠ i₀ and do not use V_i02 . Indeed, subject i₀ only contributes their data from the first replicate, V_i through ${\widehat{V}}_{i_{0}2}^{\mathrm{raw}}$, and ${\widehat{V}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)$, and V_i02(v is not used. Before we describe the conceptual model, we provide the intuition: at every voxel, we estimate γ(v) as the reliability or intra class correlation coefficient (ICC) of the connectivity maps of the other 19 subjects at every voxel v.

More specifically, we start with the classical measurement error (ME) model (Carroll et al., 2006)

$$V_{ij}\left(v\right)=X_i\left(v\right)+U_{ij}\left(v\right)$$ (1)

where {X_i(v), i = 1, 2,..., I} is the true unobserved correlation at voxel v and U_ij(v) is replication-specific error. We assume that X_i(·) and U_ij(·) are mutually uncorrelated and that E{X_i(v)} = μ_X(v), E{U_ij(v)} = 0 for every i, j, and v, respectively. With these assumptions, the Best Linear Unbiased Predictor (BLUP) of X_i0(v) using only information at the voxel v is ${\widehat{V}}_{i_{0}2}^{\gamma }\left(v\right)={\widehat{X}}_i\left(v\right)=\gamma \left(v\right){\widehat{V}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)+\{1-\gamma \left(v\right)\}{\widehat{V}}_{i_{0}2}^{\mathrm{raw}}\left(v\right)$ where

$$\gamma \left(v\right)=\frac{\mathrm{Var}\left\{X_i\left(v\right)\right\}}{\mathrm{Var}\left\{X_i\left(v\right)\right\}+\mathrm{Var}\left\{U_{i1}\left(v\right)\right\}}.$$ (2)

These variances can be estimated from the data as (Carroll et al., 2006)

$$\mathrm{Var}\left\{U_{ij}\left(v\right)\right\}=\sum _{i\ne i_0}\sum _{j=1}^{J_i}{\left\{v_{ij}\left(v\right)-{\overline{V}}_i.\left(v\right)\right\}}^2∕\sum _{i\ne i_0}(J_i-1),$$

Thus, an estimator of γ(v) can be obtained by replacing the parameters in Eq. (2) with their estimators in Eq. (3). Here ${\overline{V}}_i.\left(v\right)$ over the replicates, j, and $\overline{V}..\left(v\right)$ is the average of all V_ij(v) over subjects, i, and visits, j. The shrinkage estimator obtained using this estimator of γ will be denoted ${\widehat{V}}_{i_{0}2}^{\gamma ,\mathrm{P}}\left(v\right)$, while the original scale estimator of the connectivity is then ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{P}}\left(v\right)=\tanh \left\{{\widehat{V}}_{i_{0}2}^{\gamma ,\mathrm{P}}\left(v\right)\right\}$. This is labeled as the pointwise shrinkage estimator.

An inspection of the brain map of the γ(v) estimators using pointwise estimation (web appendix) reveals large voxel-to-voxel variability, as there is no information borrowed from neighboring voxels. One way to resolve this is to think about the model (1) as a joint model over a neighborhood of each voxel. Here we use a cube of size m³, where m = 6. With such a choice, the model becomes the multilevel functional principal component (MFPCA) model introduced by Di et al. (2009) and Zipunnikov et al. (2011) where γ(·) is viewed as a function over the entire neighborhood. In this joint model γ(v) is equal to

$$\mathrm{Var}\left\{X_i\left(v\right)\right\}=\frac{{\sum }_{i\ne i_0}{J}_i{\{{\overline{V}}_i.\left(v\right)-\overline{V}..\left(v\right)\}}^2-(I-1)\mathrm{Var}\left\{U_{ij}\left(v\right)\right\}}{{\sum }_{i\ne i_0}{J}_i-{\sum }_{i\ne i_0}{J}_i^2∕{\sum }_{i\ne i_0}{J}_i.}$$ (3)

where K_X(u, v) is the covariance operator of X_i(·) and K_U(u, v) is the covariance operator of U_ij(·). To estimate γ(v), we apply the algorithm described in Di et al. (2009) cube by cube. More specifically, we first obtain the method of moments estimators for K_X(u, v) and K_U(u, v) as two covariance matrices for voxels within a cube. After conducting a bivariate smoothing on the covariance matrices, γ(v) is estimated as the ratio between the diagonal elements of K_X(u, v) versus the diagonal elements of K_X(u, v) plus K_U(u, v). The shrinkage estimator obtained using this estimator of γ will be denoted ${\widehat{V}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)$, while the original scale estimator of the connectivity is then ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)=\tanh \left\{{\widehat{V}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)\right\}$. This is labeled as the local shrinkage estimator.

We note that, by definition, γ(v) ∈ [0, 1], while the method of moment estimators of γ(v) can fall outside of this range, especially in situations when reliability is very small, as is the case in our rs-fMRI study. Thus, all estimators of γ(v) that were negative were set to 0 and all those that exceeded 1 were set to 1, while all other estimators were left unchanged. This had a large effect on the MSE, as many voxels had very low replication-to-replication reliability. While the justification for each estimator is more or less complicated, all estimators are very simple to calculate in practice. In the next section we will show that for the Kirby21 data (Landman et al., 2011), the proposed methods are significantly better than using the first replication data for the same subject. This is surprising and raises a host of interesting questions related to how to best estimate resting-state correlation maps.

Experimental data

We reanalyze the “Multi-Modal MRI Reproducibility Resource” (www.nitrc.org) data set, which is publicly known as “Kirby21” (Landman et al., 2011). The data set contains scan–rescan multi-parametric magnetic resonance images (MRI) from 21 healthy adults. For the purposes of this experiment, we use the two 7-min resting-state scans that were acquired from each participant using a single-shot, partially parallel (SENSE) gradient-recalled echo planar sequence with an ascending slice order (TR/TE, 2000/30 ms; FA, 75; SENSE acceleration factor, 2; 3-mm axial slices with a 1-mm slice gap) and an 8-channel head coil. Participants are instructed to relax and fixate on a centrally presented cross while remaining as still as possible. The two resting-state scans are separated by a short break during which the participant exits the scanner; the T1-weighted anatomical images are also acquired to be used as a template for spatial registration of the functional images.

Image processing is performed using SPM8 (Wellcome Department of Imaging Neuroscience) and custom MATLAB scripts. Anatomical images are registered to the first functional volume and normalized to MNI space using unified segmentation/normalization (SPM8). Functional data are adjusted for slice time acquisition as well as participant motion and are transformed to MNI space. Nuisance covariates from white matter and CSF are estimated using a CompCor Behzadi et al. (2007) and regressed from the data along with the motion realignment estimates, their derivatives (computed by backward differences), global mean signal, and linear trends. Data are then spatially smoothed (6-mm kernel) and temporally filtered using a 0.01–0.10 pass-band filter. Data from one participant are excluded from analysis due to a misalignment of the first and second resting-state scans.

To assess the reliability of functional connectivity estimates (and as a proxy, our ability to predict a future subject-specific connectivity map from a previous rs-fMRI scan), we choose to focus on the precentral gyrus, a key component of the motor control network. This is one of the most consistently identified and well-characterized functional networks in the brain. Given the potential influence of region of interest (ROI) selection on functional connectivity estimates, we also analyze connectivity estimates for 11 additional ROIs distributed throughout the brain. All ROIs are selected using the “Type II Eve Atlas,” which is based on the manual segmentation of a high-resolution, T1-weighted anatomical image (Oishi et al., 2009). The same unified segmentation/ normalization approach used on the anatomical images for the Kirby21 data is used to transform the Eve template to MNI space, and the resulting transformation is applied to the various ROIs by neighbor interpolation.

Results

Results for the precentral gyrus

Due to an absence of a gold standard, we use a jackknife approach (Quenouille, 1949; Quenouille, 1956; Tukey, 1958) to evaluate the various estimators. More precisely, we use the correlation maps from the first replication of subject i₀ and the two replicates from the remaining 19 subjects to predict the second replicate correlation map W_i02 (v) of subject i₀. Prediction performance is evaluated using the mean square repeated for each subject i₀ = 1, 2, ···, 20 and the MSEs are shown in Table 1. Simply using the first replicate connectivity to predict second replicate connectivity is labeled as “Raw” (column 2 in the table). This corresponds to estimator ${\widehat{W}}_{i_{0}2}^{\mathrm{raw}}\left(v\right)$. The sample average of the first replicates from all 20 subjects is called “Mean” (column 3 in the table) which corresponds to ${\widehat{W}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)$(v). Both shrinkage estimators (columns 4 and 5) show sizeable improvement in MSEs for almost all subjects with two exceptions for the pointwise shrinkage estimator and one for the local shrinkage estimator. On average, the reduction in MSE (or, equivalently, improvement in prediction) was approximately 30% for the local estimator, ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)$, and 27.5% for the pointwise estimator, ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{P}}\left(v\right)$. Percent improvement was calculated as the percent MSE reduction (indicated by positive percentages) or increase (indicated by negative percent-ages) over the MSE of the “Raw” estimator, ${\widehat{W}}_{i_{0}2}^{\mathrm{raw}}\left(v\right)$. Surprisingly, by simply incorporating the information from the first replicates of the other 19 subjects, ${\widehat{W}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)$ reduces the average MSE by 25%, improving prediction in 18 subjects out of the 20 subjects.

Table 1.

MSEs averaged among all voxels in the brain for multiple estimators that predict correlation maps for each subject. “Raw” corresponds to the estimator based on the first visit connectivity map, ${\widehat{W}}_{i_{0}2}^{\mathrm{raw}}\left(v\right)$. “Mean” is the estimator obtained as the average of all first replicates from the 20 subjects, ${\widehat{W}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)$. “Pointwise” and “Local” are the shrinkage estimators ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{P}}\left(v\right)$ and ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)$, respectively. “Red. %” is the reduction of MSE relative to the MSE for the Raw estimator.

	Raw	Mean		Pointwise		Local
Subject	MSE	MSE	Red.%	MSE	Red. %	MSE	Red.%
1	0.035	0.023	35.28	0.022	37.32	0.022	38.33
2	0.044	0.031	27.97	0.032	27.68	0.031	28.85
3	0.062	0.049	20.99	0.047	23.31	0.046	25.70
4	0.051	0.045	11.73	0.043	15.01	0.042	17.56
5	0.031	0.039	–27.94	0.036	–17.65	0.032	– 4.85
6	0.054	0.047	12.05	0.046	15.13	0.044	17.55
7	0.059	0.031	47.04	0.031	46.47	0.032	45.95
8	0.049	0.041	15.39	0.040	17.17	0.039	19.59
9	0.037	0.026	28.78	0.026	29.26	0.026	30.30
10	0.041	0.025	39.12	0.025	40.02	0.024	40.98
11	0.070	0.027	62.19	0.028	60.40	0.030	57.76
12	0.045	0.033	27.52	0.032	28.83	0.031	32.18
13	0.049	0.022	55.35	0.022	54.41	0.023	52.36
14	0.036	0.034	5.65	0.033	9.25	0.031	13.34
15	0.062	0.030	50.96	0.031	49.74	0.033	47.40
16	0.063	0.036	43.29	0.035	44.14	0.036	43.43
17	0.030	0.035	– 16.83	0.032	– 8.66	0.029	1.04
18	0.037	0.025	30.62	0.026	30.05	0.025	31.10
19	0.044	0.030	32.10	0.029	34.00	0.028	36.42
20	0.031	0.029	9.39	0.027	14.89	0.026	19.00
Average	0.047	0.033	25.53	0.032	27.54	0.032	29.70

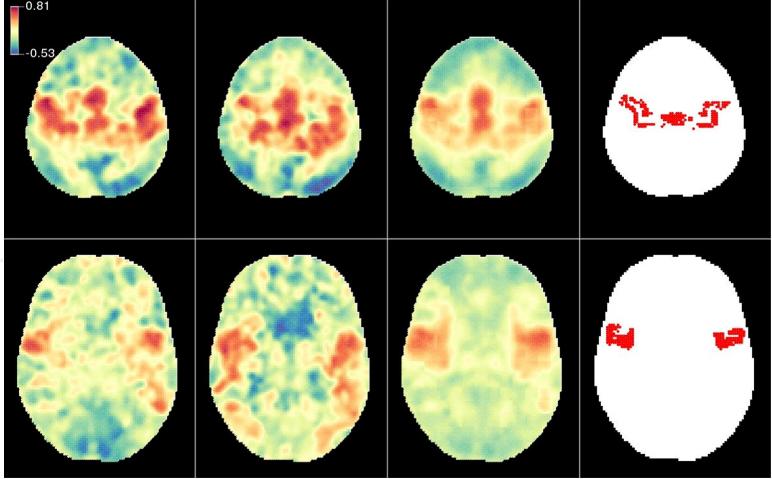
To illustrate this improvement, we display results for one subject in Fig. 1. We choose the subject labeled ‘2’ in Table 1 because the improvement in MSE for its local shrinkage estimator, ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)$, was 29%, which is almost identical with the average MSE improvement over all subjects. Each row in the image corresponds to a different slice. The first two columns represent the estimated precentral gyrus seed brain connectivity for the first replicate and second replicate, respectively. The problem we considered was to predict the second column from the first. The third column displays the local shrinkage estimator of the brain connectivity map at the second replication. The much smoother appearance of the shrinkage estimators is due to the strong shrinkage of the images towards the visit one mean for the remaining 19 subjects, which is much smoother than the replication-specific maps. For this subject, the average shrinkage coefficient over all voxels in the brain is 0.15, though it differed quite substantially across the brain. From a statistical perspective, this is a classic example of bias and variance trade-off, where reduction in variance is more important for low reliability cases. The fourth column indicates the precentral gyrus seed used to calculate voxel-wise connectivity with the rest of the brain. The local shrinkage estimator of the connectivity map is spatially smoother, has less extreme values and more closely resembles the seed region.

Fig. 1.

First column: correlation map estimated using the first replication of subject 2; second column: correlation map estimated using the second replication of subject 2. Third column: predicted correlation map using the local shrinkage estimator. Blue indicates negative correlation, while red and yellow indicate positive correlations. Fourth column: the mask for the precentral gyrus used as the seed region.

An important question is to quantify the effect of the sample size on the improvement in shrinkage towards the mean correlation map. To address this issue we repeat the same analysis using a smaller number of subjects. More specifically, we examine a series of a different sample sizes n = 3, 5, 10, 15 and 20, where 20 is the maximum number of subjects available in the Kirby21 dataset. Given a sample size n, for each subject i₀, we sample sets of n-1 subjects, which form a new population of data. We apply the same estimators used for the entire data set and compare their performance. For each estimator, we calculate the MSE over all voxels in the brain. For n = 3 and n = 20 we enumerate all possible combinations, whereas for n = 5, 10 and 15, we randomly sample without replacement 20 combinations of the subjects to make up the population data for every subject i₀.

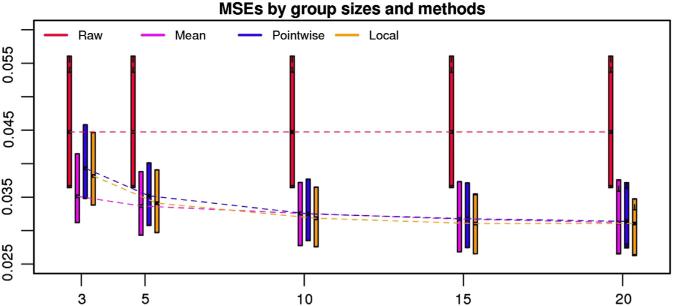
Fig. 2 displays the boxplots of MSE as a function of estimator (shown as different colors) and sample size (indicated on the x-axis). Here, smaller MSE indicates better performance of the estimator. The “Raw” estimator (shown in red) does not change with the sample size, because it does not depend upon the other subjects. The “Mean” estimator (the one that averages the visit 1 correlation maps from the subject i₀ with the visit 1 data of the other n-1 subjects) is shown in purple. It performs better than the other estimators when n = 3 and n = 5, and improves with increased n, though improvements are quite minor after n = 10. While the “Pointwise” and “Local” shrinkage estimators (shown in blue and orange) do not perform as well as the “Mean” estimator for n = 3 and 5, they improve rapidly and become slightly better for n = 10, 15 and 20. This is probably due to the fact that the shrinkage parameter, γ(v), is not easy to estimate in very small samples.

Fig. 2.

The boxplots of MSE for 4 different prediction methods under various sample sizes. The x-axis indicates sample size ranging from 3 to 20 and the y-axis indicates the MSE averaged across all voxels in the brain for each prediction. The length of the bar represents the interquartile range of the estimation accuracy (MSE) across multiple sets of the image data with a fixed sample size and under a particular prediction method. The dashed lines connect the median values of the MSEs when the sample size increases. ‘Raw’ is the naive estimator with the visit 1 data from the same subject. ‘Mean’ corresponds to the mean of all visit 1 correlation maps in the population with a particular sample size. ‘Pointwise’ and ‘Local’ are two shrinkage estimators.

Results for 11 additional brain regions

The precentral gyrus was initially selected because it was the first ROI used to investigate functional connectivity (Biswal et al., 1995) and is commonly evaluated in many studies, such as, in comparing typically developing children and children with autism (Nebel et al., 2014). However, the methods and results are not restricted by the choice of ROI. To investigate the generalizability of these improvements, we conduct similar analyses on multiple seed regions (Faria et al., 2012). More precisely, we investigate several regions in the visual cortex including the cuneus, superior occipital gyrus (SOG), middle occipital gyrus (MOG) and inferior occipital gyrus (IOG). We have also investigated the middle frontal gyrus (MFG) and the cingulate. These seed choices belong to a range of functional networks, and are spatially distributed throughout the brain, covering posterior, middle and frontal regions. Table 2 displays the MSEs using the five estimation methods averaged over 20 subjects when predicting the second-visit correlation map from one of the 12 seed regions; we have repeated the precentral gyrus results for ease of interpretation. Thus, the effects of estimators that we described for the precentral gyrus results are far from being specific to this area. If anything, the improvements in estimation are smaller in the precentral gyrus with much larger improvements in the right and left SOG (~ 50%) and right and left MOG (im45%). The improvements in the cuneus and the precentral gyrus were among the smallest observed (range ~ 25 to ~ 30%). The relative estimation accuracy and ordering of estimator performance is also consistent with the findings for the precentral gyrus seed analysis.

Table 2.

MSEs averaged over all voxels in the brain and 20 subjects for multiple estimators that predict correlation maps generated based on 12 seed regions. The superior occipital gyrus (SOG), middle occipital gyrus (MOG) and inferior occipital gyrus (IOG) and cuneus are all part of the visual system and are in the occipital lobecortex. The middle frontal gyrus (MFG) is in the frontal lobe, while the cingulate spans regions from the frontal and parietal lobes. For the five estimation methods, “Raw” corresponds to the estimator based on the first visit connectivity map, ${\widehat{W}}_{i_{0}2}^{\mathrm{raw}}\left(v\right)$. “Mean” is the average of all first replicates from the 20 subjects, ${\widehat{W}}_{i_{0}2}^{\mathrm{mean}}\left(v\right)$ “pointwise” and “Local” are the shrinkage estimators ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)$ and ${\widehat{W}}_{i_{0}2}^{\gamma ,\mathrm{L}}\left(v\right)$, respectively. ‘Reduction %’ shows the reduction of MSE relative to the MSE for the ‘Raw’ estimator. The values are multiplied by 100 to show the percentage of improvement.

Seed	Raw	Mean		Pointwise		Local
	MSE	MSE	Reduction %	MSE	Reduction %	MSE	Reduction %
Left SOG	0.070	0.037	47.96	0.036	49.85	0.035	50.30
Right SOG	0.074	0.036	50.95	0.035	52.76	0.035	53.13
LeftMOG	0.065	0.034	45.91	0.033	48.11	0.033	48.71
Right MOG	0.068	0.036	45.80	0.035	47.36	0.034	48.05
LeftIOG	0.072	0.040	43.48	0.038	45.59	0.038	46.30
Right IOG	0.070	0.039	42.55	0.038	43.76	0.038	44.50
Cuneus	0.052	0.037	25.03	0.036	26.77	0.035	28.36
LeftMFG	0.073	0.040	45.42	0.039	47.34	0.039	47.70
Right MFG	0.076	0.041	46.74	0.040	48.48	0.040	48.87
Left cingulate	0.068	0.039	43.02	0.037	45.74	0.037	46.19
Right cingulate	0.072	0.042	43.40	0.039	46.35	0.039	46.77
Precentral gyrus	0.046	0.033	24.10	0.033	24.53	0.032	26.99

Conclusions

One of the most counter-intuitive results in the field of statistics is the so-called “Stein phenomenon” (Stein, 1956), which states that if one is interested in estimating more than 3 means, then the simple Maximum Likelihood Estimate (MLE) (labeled “Raw” for the purpose of this paper) can be uniformly outperformed by another estimator. Even more importantly, it was shown that taking the individual means and shrinking them (James and Stein, 1961) towards their common mean provides a better estimate, in terms of overall mean square error, than the simple MLE of each individual observation. Stein's foundational contribution forms the basis of many different practical approaches to estimation including smoothing, shrinkage, mixed-effects models, massive prediction problems, and even predicting batting averages for baseball players (Efron and Morris, 1975). The amount of shrinkage needed in any specific application varies, however some degree of shrinkage is guaranteed to improve prediction.

This paper shows another facet of this surprising result, this time with an application to brain connectivity. When data show large replication-to-replication variability, one can dramatically improve prediction of subject-specific connectivity by “borrowing strength” from the mean of other subjects. Of course, this borrowing needs to be done carefully and reasonably, and may not work in high reliability cases or when the measurement error mechanism is unknown or hard to describe. Even more surprisingly, we have found that the simple group mean of all the other subjects in the study provides a better predictor of the connectivity patterns of an individual subject than actually collecting another fMRI on that subject. Clearly, much discussion and experimentation are required to understand how this can be used in practice or to better inform experimental designs for estimating connectivity at the subject level.

Using the Kirby21 replication data, we obtained the connectivity maps for each of 20 subjects (one subject was excluded) using a seed-based correlation analysis. A natural predictor of the estimated connectivity of the second replicate connectivity is the first replicate of the same subject. Here we show that for the precentral gyrus the average of the first replicate connectivity of all subjects is a better predictor of the second replicate subject-specific connectivity in 18 out of the 20 subjects by an average of 25% in terms of mean square error. We also introduced a shrinkage estimator of the second replicate subject-specific connectivity as a voxel-specific weighted average of the subject-specific first replication connectivity and the first replication average connectivity of all subjects. This predictor is better in 19 out of the 20 subjects by an average of 30% in terms of MSE. Similar results were obtained for the other 11 seed regions (Table 2). One of the main reasons for these findings is no doubt the low reproducibility of subject-specific connectivity maps; see, for example, Shou et al. (2013) who found the reliability of the seed-based whole brain connectivity maps to be in the range of 10–30%.

It is worth discussing the practical relevance of the findings in this paper. First, the results discussed here will be relevant in all contexts when subject-level inference or analysis is necessary. When analyzing subject-level rs-fMRI data, there is an implicit assumption that the connectivity estimates we obtain represent a stable characteristic of some underlying process that can be replicated. In a study without replication, it appears that one could improve the reliability of subject-specific connectivity measures by calculating subject-specific connectivity maps and then simply shrinking them 80% towards the population connectivity map. This would be especially relevant when one is interested in clustering, segmentation, or inference at the subject-level, which is crucial to the development of reliable imaging biomarkers of disease. These shrunken estimators will probably also have better within-subject prediction properties for future rs-fMRI replicates than the subject's previous scans alone.

Another important application of the results is that one could calculate the sample size necessary to produce a reliable seed-voxel connectivity map at the subject level. Such questions and calculations may prove crucial if and when fMRI will be used for clinical purposes including surgery planning. Irrespective of the number of replications at the subject level, it appears that shrinking connectivity maps towards their population average may help systematically improve prediction and reliability. However, if one is interested in population level parameter estimation or testing, then shrinking will probably not help analyses or increase power. For example, while the estimation of subject-specific connectivity maps will improve, the population average of or the group differences between connectivity maps will not change by first shrinking the connectivity maps and then averaging them. The intuition is that “the average of averages is the average.” Similarly, if one is interested in prediction of health outcomes using fMRI data, then the performance of predictors will probably not improve, though the estimated associations may exhibit smoother spatial patterns.

Further, the results suggest that, at least with regard to seed-based correlation analysis, the unique subject-specific measurement of functional connectivity beyond the population mean may, in fact, be largely due to noise or some other session-dependent source of variability. If this result is true, this could have profound impact on the manner in which seed-based functional connectivity studies are interpreted and future experiments designed.

In sum, this paper illustrates that one can dramatically improve prediction of subject-specific connectivity by borrowing strength from the population of subjects. This clearly illustrates that shrinkage estimators, that allow individual subject data to be shrunk towards the population mean, should play a critical role in future rs-fMRI data analyses.