Controlled Incremental Filtration: A simplified approach to design and fabrication of high-throughput microfluidic devices for selective enrichment of particles

Abstract

The number of microfluidic strategies aimed at separating particles or cells of a specific size within a continuous flow system continues to grow. The wide array of biomedical and other applications that would benefit from successful development of such technology has motivated the extensive research in this area over the past 15 years. However, despite promising advancements in microfabrication capabilities, a versatile approach that is suitable for a large range of particle sizes and high levels of enrichment, with a volumetric throughput sufficient for large-scale applications, has yet to emerge. Here we describe a straightforward method that enables the rapid design of microfluidic devices that are capable of enriching/removing particles within a complex aqueous mixture, with an unprecedented range of potential cutoff diameter (below 1µm to above 100µm) and an easily scalable degree of enrichment/filtration (up to 10-fold and well beyond). A simplified model of a new approach to crossflow filtration – controlled incremental filtration – was developed and validated for its ability to generate microfluidic devices that efficiently separate particles on the order of 1–10µm, with throughputs of tens of µL/min, without the use of a pump. Precise control of the amount of fluid incrementally diverted at each filtration “gap” of the device allows for the gap size (~20µm) to be much larger than the particles of interest, while the simplicity of the model allows for many thousands of these filtration points to be readily incorporated into a desired device design. This new approach should enable truly high-throughput microfluidic particle-separation devices to be generated, even by users only minimally experienced in fluid mechanics and microfabrication techniques.

Introduction

The ability to efficiently recover (or eliminate) particles of a specified size from a complex aqueous suspension or slurry has widespread applications across a number of fields. In some applications, the particles of interest are retained for subsequent processing (e.g. concentration of algae or fungal spores^{1, 2}), or diagnostic testing (e.g. enrichment of circulating tumor cells^{3, 4}). In others, particles are removed because they are less valuable than the small molecules within the mixture (e.g. extraction of antibiotics from fermentation broth,⁵ DNA purification⁶) or are simply an undesirable component to be removed (e.g. blood cleansing,⁷ wastewater treatment^{8, 9}).

Conventional macroscopic methods such as dead-end filtration and centrifugation can be time-consuming, as they must be run serially or in batch mode, and can cause the particles to be exposed to large shear forces and prolonged contact with foreign surfaces. These techniques have additional negative properties such as membrane fouling/clogging (for filtration), and a need for bulky, expensive equipment (for centrifugation). Tangential- (or cross-) flow filtration mitigates some of these issues, but typically requires specialized membranes and flow systems that are not cost-effective for many applications – particularly those which limit the filtration elements to one-time use due to the contamination or sterility concerns present in most biomedical applications.¹⁰

Several microfluidic approaches have been developed to concentrate particulate suspensions in a continuous flow regime.^1–12 “Active” microfluidic devices rely on the application of an outside force (e.g. magnetic,^{7, 13} acoustic,¹⁴ dielectrophoretic¹⁵) to direct particles to the desired output collection channel, however they require complex equipment and/or undesirable sample preparation steps, and are still generally low throughput. “Passive” microfluidics approaches typically either (i) exploit the unique phenomena associated with fluidic streamlines that have been manipulated by the device’s microchannel architecture, in order to divert (or simply retain) finite-sized particles within this complex flow profile for selective enrichment and collection (e.g. deterministic lateral displacement (DLD),^{1, 13, 16} microfluidic crossflow filtration,^{2, 17–19} plasma skimming,^{20, 21} pinched flow fraction,²² hydrodynamic filtration²³), or (ii) make use of the natural tendency of particles of different sizes to migrate to distinct positions within the cross-section of the velocity profile (e.g. the tubular pinch effect²⁴ and Dean flow fractionation,²⁵ both of which fall into the general area of “inertial focusing ”^{4, 8, 9}).

Separation of very small particles with diameters less than ~5µm, however, has been particularly challenging for even the most promising of microfluidic approaches. The difficulties typically manifest in constraints on throughput (e.g. due to the requirement for DLD-based and crossflow filtration microfluidic devices to employ very small gaps or other feature dimensions^{18, 26}), or in a need to raise the driving pressure to an extreme degree (up to several hundred kPa) in order to separate particles <5µm in size (as is the case with inertial focusing, which is a phenomenon with a highly-nonlinear dependence on the dimensions of both the particles and the channels through which they are driven⁹). The resulting high shear flow regimes can have unwanted adverse effects on sensitive biological particles (e.g. shear-induced activation of platelets^{27, 28}), in addition to the practical complications associated with constructing prototype devices to withstand the necessary pressures.²⁵

One way to reduce the level of shear, at a given volumetric flow rate, is to increase the depth of microchannels within a device. Designing and producing these devices is a particularly daunting task because of the difficulties one encounters when trying to account for all of the relevant fluid mechanical phenomena associated with highly-branched networks of high aspect ratio microchannels, much of which do not have analytical solutions, as well as the unavoidable impact of imperfect fabrication on device performance. The design of microfluidic devices with complex architecture is often guided by customized computational fluid dynamics (CFD) simulations, particularly when geared toward the filtration/enrichment of particles of a specified size. While this approach can be successfully employed by those experienced in the field,^{2, 19} CFD simulations are not a readily accessible tool to the majority of researchers that may be interested in using these devices in their research. Given the fact that even the most comprehensive models are encumbered by the inherent issues of (especially biological) particle heterogeneity and finite computing power, the accuracy of the filtration size cutoff predictions as well as the total filtration fraction that can be designed for and practically achieved using this approach are limited.

Our objective was to develop a simple yet reliable approach, which we have termed “controlled incremental filtration” – that does not rely on CFD simulations nor complex microfabrication capabilities (e.g. deep reactive ion etching) – for generating crossflow-style filtration microfluidic devices with relatively high aspect ratio microchannels and large feature sizes, designed for the efficient concentration of particles in a continuously flowing suspension with high throughput and low shear. In this paper we describe the initial validation of this approach using suspensions of beads, and demonstrate its practical utility by producing a high-throughput device for concentrating platelets in platelet-rich plasma.

Results

Semi-empirical approach to designing microfluidic devices based on controlled incremental filtration (CIF)

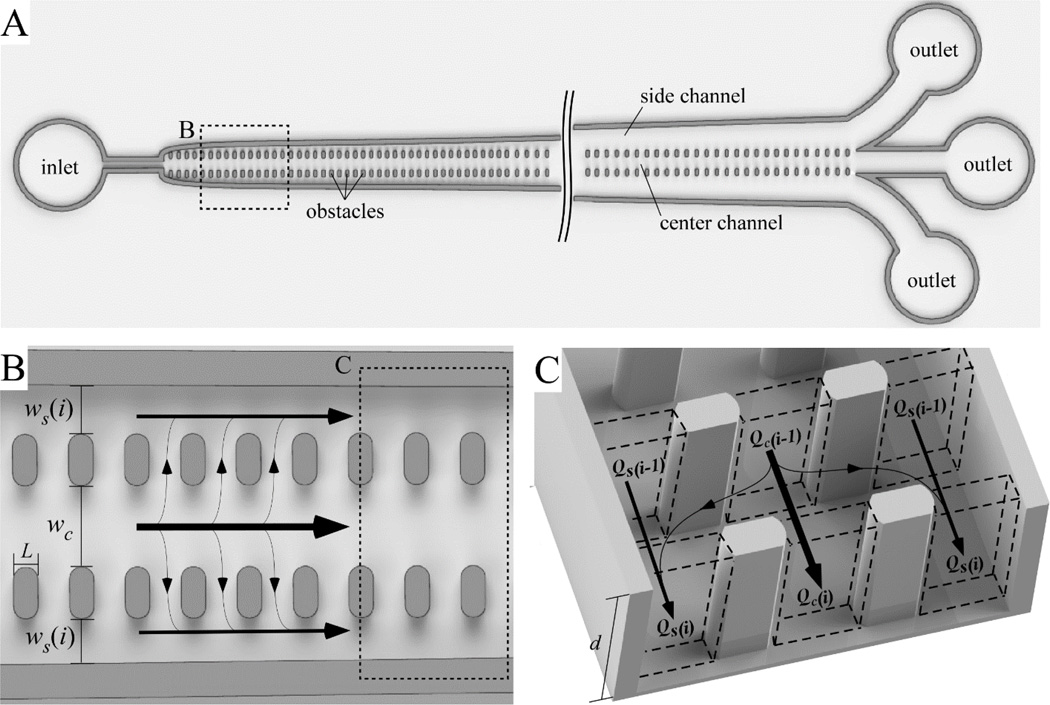
Generally, devices employing the crossflow filtration principle concentrate particles by removing a small fraction of the main channel flow though each filtration point (pore)located along the length of the device, and excluding particle passage through these pores (typically simply by using pores smaller than the size of the particles of interest). In our devices, “controlled incremental filtration” (CIF) is implemented using short gaps that are relatively wide (~20µm in practice), which separate a central flow channel (where particles are concentrated) from two adjacent side channels (which carry the filtrate along the length of the device) (see Fig. 1A). The width of these side channels gradually increases along the length of the device. The rate of this increase – and not the size of the gaps in the device – ultimately determines the size cutoff of filtered particles. This architecture dramatically simplifies the calculation of the channel dimensions necessary to ensure the filtration fraction at each gap, f_gap, is the same, as opposed to approaches that progressively alter the length of the gap separating the filtrate- and permeate-carrying channels.² In this approach, the central flow channel has a constant width, w_c, and is flanked on either side by channels whose width at gap i, w_s(i) (Fig. 1B), is ultimately calculated merely by the desired value of f_gap, and their width at the previous gap, w_s(i − 1), as discussed in detail below.

Figure 1.

Schematic illustration of a controlled incremental filtration (CIF) array. (A) Overall design of a CIF-based device comprising a central flow channel which retains the particles being concentrated, and two side channels which carry the filtrate. The width of the side channels, w_s(i), gradually increases with increasing gap row number, i, while the width of the central channel, w_c, remains constant throughout the length of the device. (B) A close-up view of the CIF array showing the overall geometry of the obstacle placement in the device. (C) A 3D rendering of the CIF array. Arrows indicate the direction of flow.

This recursive approach to calculating the side channel width allows a CAD drawing of a functional device to be generated very quickly (in under 2 minutes on an ordinary desktop computer), using only a small number of governing equations. The key simplifying assumption that enables such an easily-implementable approach is that we treat the gaps between the flow channels of the array as nodes which allow equalization of pressure across the width of the device. The rationale for this assumption is that: (a) we use relatively wide (~20µm) gaps (which present a relatively small amount of resistance to the flow of fluid that equilibrates this pressure, given main channel widths on the order of 100–150µm), and (b) most practical applications of this approach will involve devices that remove less than 0.05% of the fluid from the central channel at each gap, i.e. f_gap < 5×10⁻⁴ (which means the net fluid flux through a given gap is exceedingly small). This assumption has been validated by observations of fluid flow in this geometry, which show that a single gap is sufficient to enable the lateral movement of fluid caused by a slight, incremental change in side channel width.

Implementation of this approach yields a simple recursive equation (1) for the volumetric flow rate in the central, Q_c(i), and the side, Q_s(i), channels following gap row i (Fig. 1C).

$$Q_s(i)=Q_s(i-1)+f_{\mathit{\text{gap}}}·Q_c(i-1)$$ (1)

If expressed in terms of the pressure differential, ΔP(i), the resistance of a side channel segment, R_s(i), and the central channel segment resistance, R_c, between gap rows i − 1 and i, eqn (1) can be written as eqn (2).

$$\frac{\mathrm{\Delta }P(i)}{R_s(i)}=\frac{\mathrm{\Delta }P(i-1)}{R_s(i-1)}+f_{\mathit{\text{gap}}}·\frac{\mathrm{\Delta }P(i-1)}{R_c}$$ (2)

Because the fluid is assumed incompressible, the total volumetric flow within the device before and after each gap must be constant, yielding eqn (3).

$$\frac{\mathrm{\Delta }P(i)}{\mathrm{\Delta }P(i-1)}=1-2f_{\mathit{\text{gap}}}$$ (3)

Using eqn (3), eqn (2) can be reformulated as eqn (4).

$$R_s(i)=\frac{(1-2f_{\mathit{\text{gap}}})R_c{R}_s(i-1)}{R_c+f_{\mathit{\text{gap}}}{R}_s(i-1)}$$ (4)

The fluidic resistance of each channel segment between the rows of gaps (of which there are typically several thousand) can be estimated using the approximation of each of the individual segments as rectangular channels. While this is undoubtedly a simplification of the actual geometry, and does not take into the complex fluidic effects resulting from the close proximity of each channel segment to the filtration gaps, it nevertheless produces effective devices with practical utility (please see further below). The fluidic resistance of a rectangular channel is given by eqn (5), in which L is the length, w is the width and d is the depth of the channel, and μ is the viscosity of the fluid.²⁰

$$R(w,d,\mu ,L)=\frac{12\mu L}{d{w}^3}{[1-\frac{192w}{d}·{\sum }_{n=1,3,5,\dots }^{\infty }\frac{\mathit{\text{tan}}h\left(\frac{n\pi d}{2w}\right)}{{(n\pi )}^5}]}^{-1}$$ (5)

To determine w_s(i) using these equations, one would begin with the desired value for w_s(i = 1), which may be made close to or equal to zero, depending on the device production capabilities available, and a value for R_s(i = 1) calculated using eqn (5). Eqn (4) can then be used to numerically determine the width of the side channel at subsequent rows, w_s(i), simply by adding a small amount to the value of w_s(i − 1) until the resultant value of R_s(i) (calculated using eqn (5)) is lowered sufficiently to satisfy eqn (4).

Practical implementation of the approach

The recursive design approach described above can be easily encoded in any number of software packages – here we used MATLAB (The MathWorks Inc, Natick, MA). We performed these calculations with an iterative stepsize of 0.5nm, using the first 50 terms in eqn (5) to calculate resistance. In eqn (5), L is equal to the size (along the direction of flow) of an obstacle in the device (Fig. 1B). Importantly, we assumed that the viscosity of fluid in each channel segment remained constant along the entire length of the device. Although suitable in the cases presented below, this assumption should be accounted for appropriately in particulate solutions that become highly concentrated in the central channel and depleted in the side channels along the length of the device. Finally, it is worth noting that d and w can be reversed in eqn (5) without affecting its validity, thus making the solution aspect ratio independent, as opposed to more simplified treatments of R(w).¹⁹

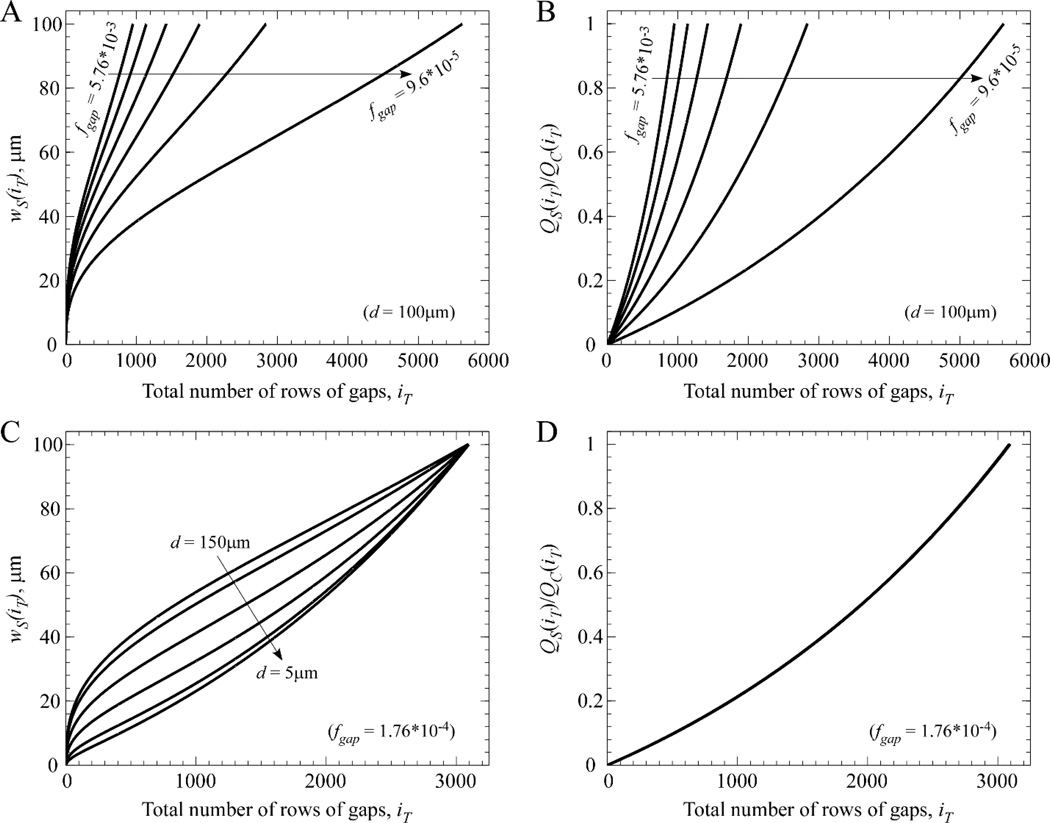
Figure 2 illustrates the complex relationship between the progressive increase in the width of the side channel along the length of a device, as a function of device depth and f_gap. Each curve in Fig. 2 was generated using only eqns (4) and (5), with the initial side channel width, w_s(0), set to zero.

Figure 2.

Dependence of device length and side channel width on input parameters. The desired degree of filtration per gap, f_gap, dictates how long a device must be (represented by the total number of rows of gaps comprising the CIF array) to achieve the desired endpoint condition (here: w_s(i) = w_c = 100µm). (A) For a fixed value of depth (d = 100µm), there is an expected inverse relationship between the necessary total number of rows of gaps, i_T, and the value of f_gap (which decreases linearly from 5.76×10⁻³ to 9.6×10⁻⁵ in the curves from left-to-right). (B) As w_s(i) increases at each subsequent gap, the corollary is that the ratio of side channel flow, Q_S(i_T), to central channel flow, Q_C(i_T), increases toward unity (the set endpoint condition). (C) The complex dependence of the w_s(i) curve on device depth is shown for a variety of depths (left-to-right: 150µm, 100µm, 50µm, 25µm, 10µm, 5µm), while f_gap is held constant at 1.76×10⁻⁴. (D) Since f_gap is held constant, the six cases in panel C each generate the same relative flow fraction curve that does not depend on device depth.

A practical application of our approach is ideally performed in two stages. First, one may experimentally examine a range of f_gap values in an array of short-length (several centimeter long) test devices to determine the appropriate f_gap with respect to the given application and width of the central channel. This typically involves identifying the maximum value of f_gap that maintains the particles of interest in the central (concentration) channel to the desired purity. Second, this value of f_gap may then be used to generate the pattern of a much longer (tens of cm long) device with the width of the side channels gradually increasing to the level necessary to fully achieve the desired degree of particle enrichment by the end of the device.

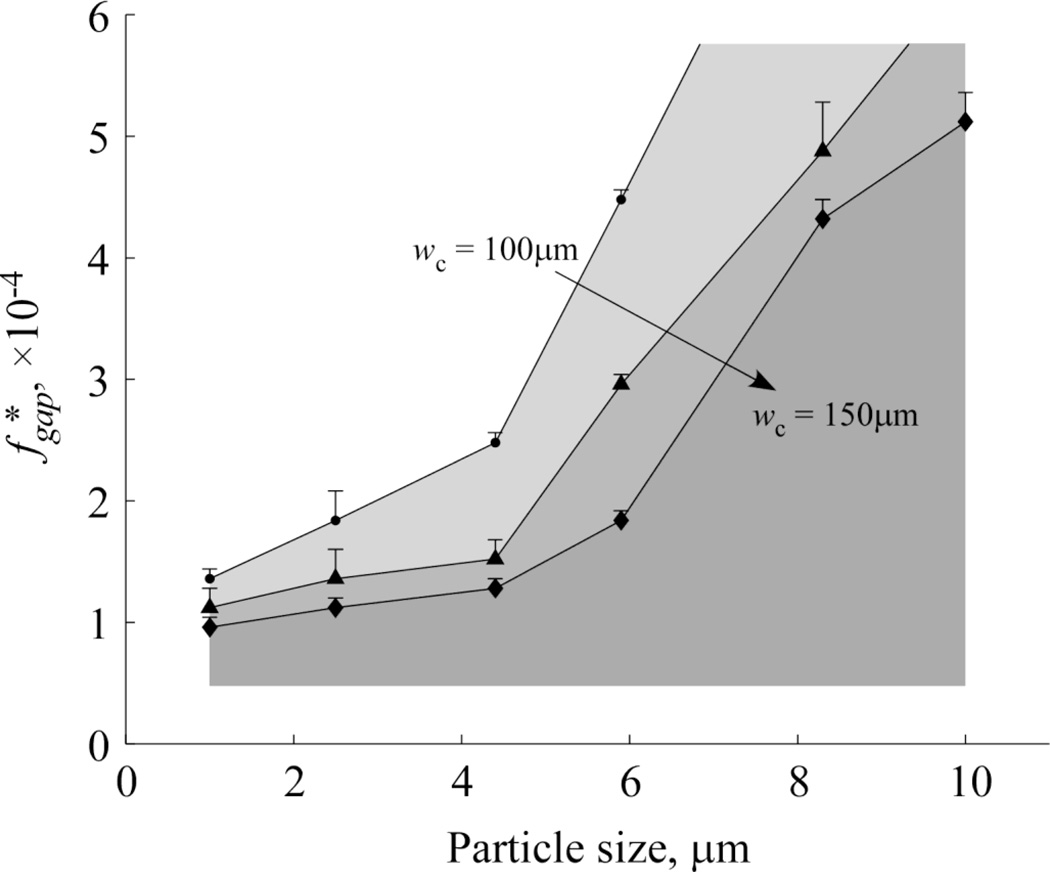
Figure 3 shows the results of performing stage one testing on beads of various diameter (ranging 1 – 10µm) in three microchannel arrays with different central channel widths (w_C = 100µm, 125µm, and 150µm) in order to experimentally determine the threshold value of the filtration fraction per gap for each bead size. To perform these experiments, we designed a parallel array of 33 test devices to explore a wide range of f_gap values ranging linearly from 6.40×10⁻⁵ (device #1) to 5.76×10⁻⁴ (device #33). The values of the f_gap cutoff threshold $(f_{\mathit{\text{gap}}}^{*})$ for beads of various diameter – that is, the filtration fraction per gap below which the beads of a specific diameter are consistently maintained in the central flow channel – were then determined visually. As expected, we found that as the width of the central channel increased, or the diameter of the beads decreased, the fraction of the flow that can be diverted to the side channels at each gap (before beads began to be noticeably “dragged” along) decreased (Fig. 3).

Figure 3.

Effect of central channel width (w_C = 100µm, 125µm, 150µm) on the threshold value of the filtration fraction per gap, $f_{\mathit{\text{gap}}}^{*}$, observed for particles of different size.

Figure 4 demonstrates operation of a CIF device designed to concentrate particles that are above a certain size, within an overall complex mixture. We selected a value of f_gap = 3.34×10⁻⁴ (using the data from Fig. 3) to retain particles with diameter 8.3µm in the central channel, while allowing smaller 4.7µmparticles to follow the filtrate into the side channels. We used that value of f_gap to design a full-length device, and ran a mixture of 4.7µm and 8.3µm polystyrene beads through the device. As expected, the beads of smaller size were pulled into the side channels with the flow of filtered fluid, while the larger beads were maintained in the central (concentration) channel (Fig. 4 inset). The depth of the device shown in Fig. 4 was 80µm; the width of the central channel was 100µm and the final width of the side channels was 300µm, resulting in ~10× enrichment by the end of the device for particle populations that are maintained in the central channel.

Figure 4.

CIF-based device for separation of particles with different size. A value of f_gap = 3.34×10⁻⁴ was chosen in-between those observed to retain beads with diameter 4.7µm and diameter 8.3µm and used to pattern a full-length device. Overall design of the device is shown schematically on the left. The inset shows an image of the second and fourth legs of the device during operation. Selective retention and concentration of only the larger-size particles in the central channel is clearly visible. The depth of the device was 80µm ± 3µm; the width of the central channel was 100µm and the final width of the side channels was 300µm. Arrows indicate direction of flow. Scale bar is 300µm.

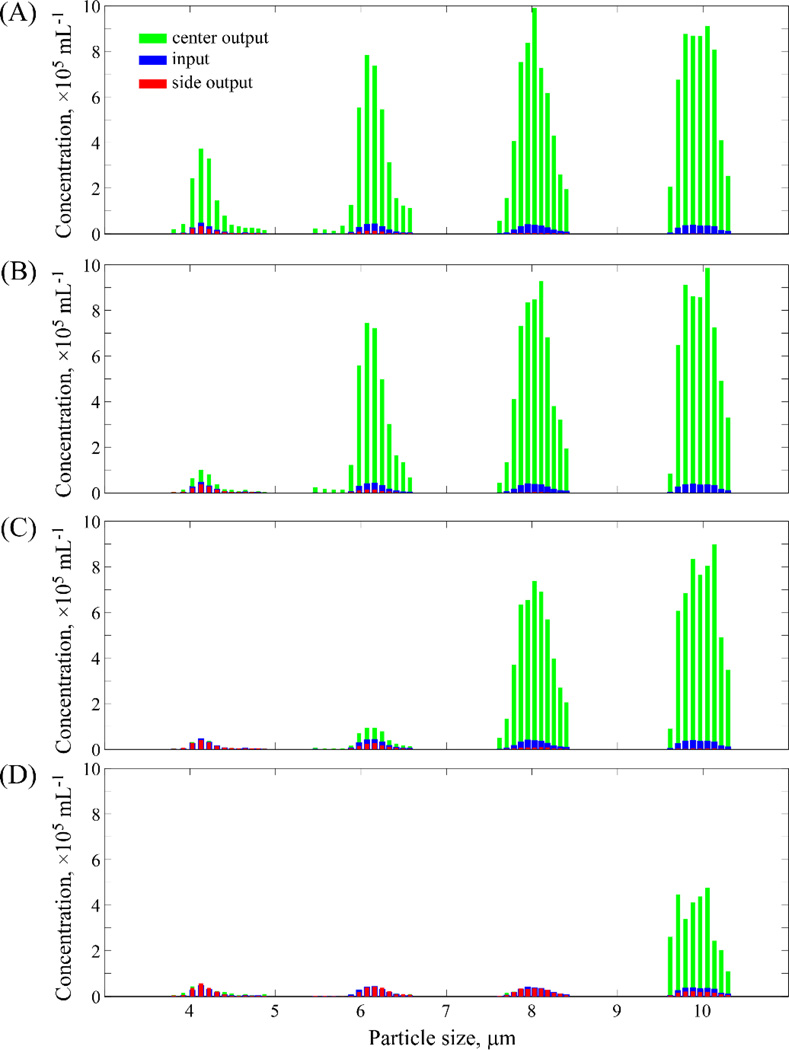
Further testing of the ability of the CIF approach to separate particles of specific size, with significantly higher filtration ratios than previously reported in this area,² was performed by creating four individual devices with a range of values of f_gap (2.2 – 10.0×10⁻⁴). A mixture of four different sizes of beads (4 – 10µm in diameter) suspended in GASP buffer (with 0.1% Tween added) was flowed through each device at a rate of 25 µL/min, and 50 µL of the center channel and side channel outputs were collected for analysis on a coulter counter. As shown in Figure 5, as the value of f_gap increases, the threshold cutoff size of particles that continue to be retained in the central channel also increases, as expected. These results reinforce those presented in Figs. 3 and 4 above, although here we have fabricated devices with a final side channel width of 450µm. Thus the ratio of cumulative output flow of the two side channels to that of the (100µm wide; 125µm deep) center channel in these devices is theoretically ~23:1 (as calculated via eqn. 5), provided the hydrostatic pressures in the output collection areas are kept equal.

Figure 5.

Relationship of the degree of particle enrichment to the filtration fraction per gap, for high filtration ratio devices. Four 125µm-deep CIF devices with values of f_gap ranging 2.2–10.0×10⁻⁴ were tested for their ability to enrich beads of various sizes (nominal diameter 4, 6, 8 and 10µm) present within a heterogeneous mixture. For all devices, the width of central channel was 100µm and the width of side channel final was 450µm, equivalent to a theoretical 24.4× enrichment of particles in the central channel (relative to the input). (A) The device with f_gap = 2.2×10⁻⁴ was able to produce 8.6× enrichment for 4µm beads, 17.7× for 6µm beads, 22.2× for 8µm beads, and 24.1× for 10µm beads. (B) The device with f_gap = 3.5×10⁻⁴ produced 2.3× enrichment for 4µm beads, 16.9× for 6µm beads, 22.6× for 8µm beads, and 24.2× for 10µm beads. (C) The device with f_gap = 6.0×10⁻⁴ could no longer enrich 4µm beads, but was able to produce 2.3× enrichment for 6µm beads, 19.3× for 8µm beads, and 22.7× for 10µm beads. (D) The device with f_gap = 10.0×10⁻⁴ could only produce enrichment of 12.0× for the largest 10µm beads.

In the case when the bead diameter is approaching that of the threshold cutoff size, there are invariably places in a device where some fraction of these beads will be lost (e.g. the 4µm beads in the device represented in panel A of Fig.5) – often owing to imperfections introduced during device mold fabrication and/or a slight shifting of device features during the final bonding step of the PDMS replicas, both of which can serve to elevate the effective value of f_gap in the affected areas of a device. These issues could be mitigated by fabricating devices directly in solid substrates, rather than the soft lithography approach we’ve employed here. However it is apparent from Fig.5 that when a value of f_gap is chosen that generates an array with a cutoff size several microns below a given particle size, that the vast majority of those particles are indeed retained in the central channel of the device, very close to the level of enrichment predicted by fluidic resistance estimates of the final channel widths.

Enrichment of platelets via high-throughput controlled incremental filtration

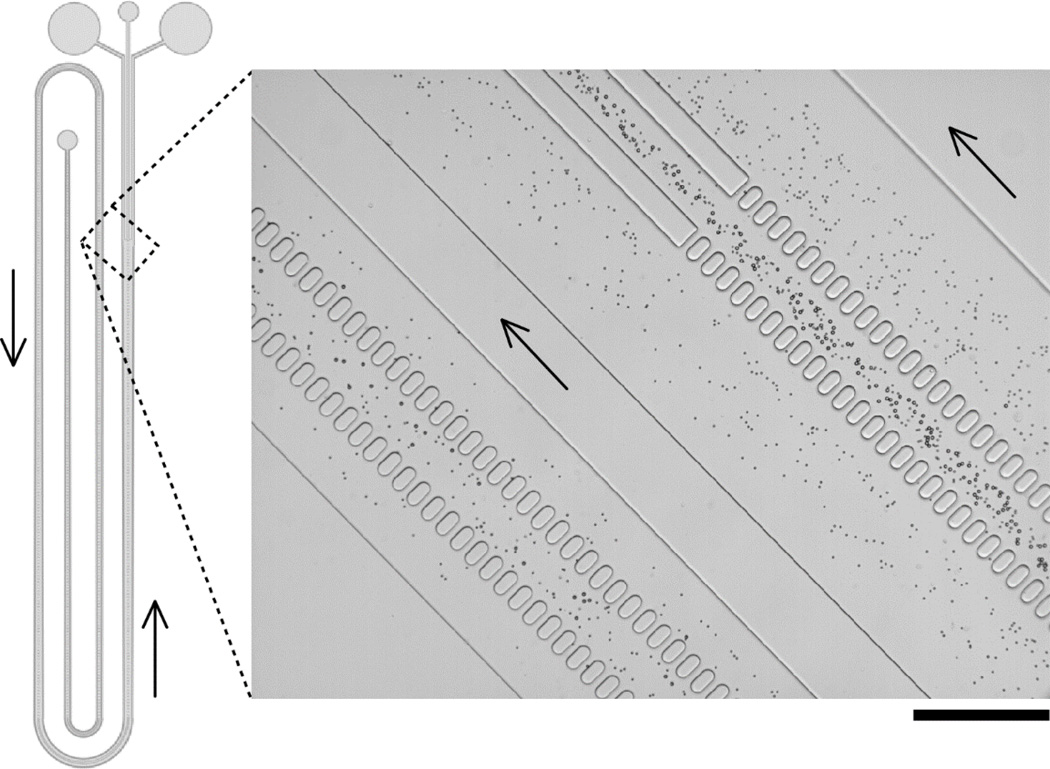
The values of $f_{\mathit{\text{gap}}}^{*}$ shown in Fig. 3 give approximate values around which one can focus their search when developing devices for enrichment / separation of particles other than simple polystyrene beads. One such application of keen practical interest is the ability to further enrich platelets in a suspension of platelet-rich plasma (PRP), to levels above the AABB standard for “platelet concentrate” blood product.²⁹ Human platelets have an approximately discoid—but also highly variable, non-uniform and, in fact, dynamically changing—shape, with effective diameters ranging ~1.5 – 4.0 µm.³⁰ In order to determine the $f_{\mathit{\text{gap}}}^{*}$ suitable for platelet concentration, we observed the behavior of PRP flowing through the same three arrays that were used to generate the data in Fig. 3, with particular attention to devices representing the f_gap range of 1×10⁻⁴ – 2×10⁻⁴. We found that the majority of platelets of most studied subjects remained in the central flow channel for devices with $f_{\mathit{\text{gap}}}^{*}$ values of 1.92×10⁻⁴ (w_c = 100µm), 1.76×10⁻⁴ (w_c = 125µm) and 1.28×10⁻⁴ (w_c = 150µm), however a subset of smaller-sized platelets could still be observed to be pulled into the side channels of these devices.

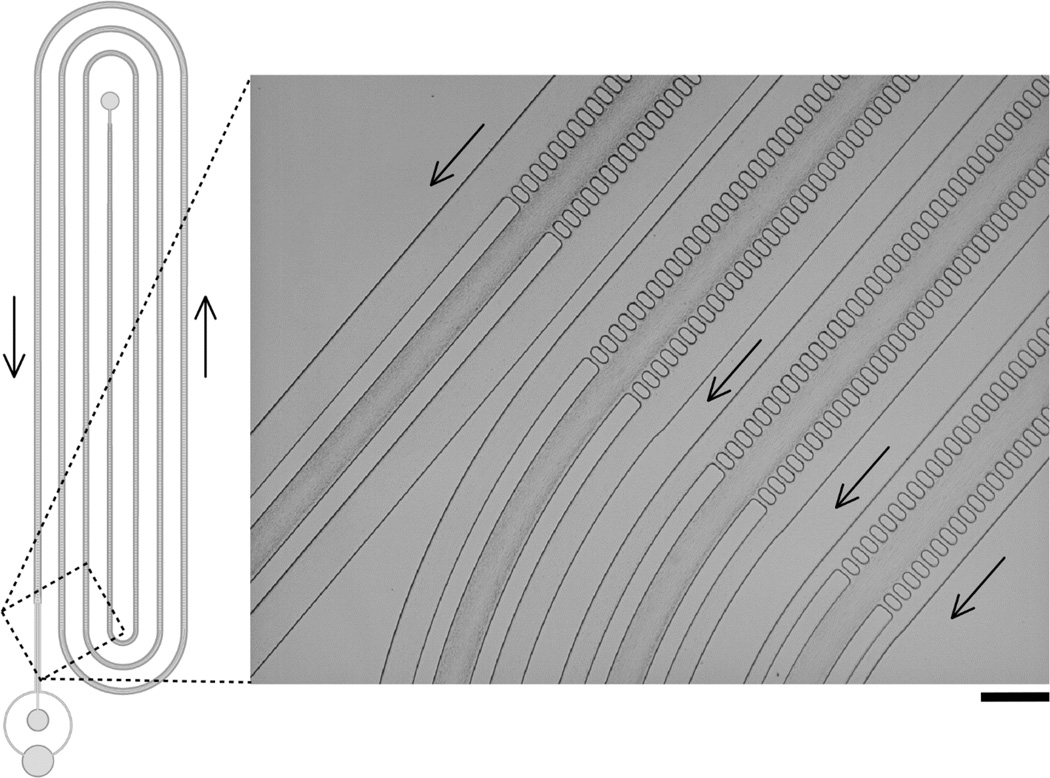
We patterned a full-length (~40cm, in total) CIF device with f_gap =1.04×10⁻⁴ (w_c = 125µm, d = 150µm) in order to reliably concentrate the vast majority of platelets in a flowing suspension of PRP into the central channel. We selected the final width of the side-channels (w_s(i) = 144µm) to achieve our ultimate desired level of platelet enrichment after a single pass through the device, however other levels of enrichment are easily selected and implemented by setting the final value of w_s(i) during the recursive design process. Figure 6 illustrates the overall design and operation of this device, which consistently produced ~3× enrichment of platelets with 80–85% yield. In a typical experiment (shown in Fig. 6), the input platelet count (PLT) was 384×10³/µL, and the output PLT for the central channel was 1039×10³/µL (enriched platelets) and for the side channels PLT was 93×10³/µL (purified plasma). The yield of platelets in the central (enrichment) channel was 83.2%, with a total throughput of 55µL/min, generated simply from hanging the PRP reservoir at a height of 5ft above the CIF device (i.e. no pump required). The throughput of this device design can be increased to several hundred µL/min when fluid flow is pump-driven (please see videos S1, S2, and S3 in the ESI†, which show red blood cells flowing through the device at flow rates of 100µL/min, 250µL/min, and 500µL, respectively), depending on the structural and bonding limitations of the materials used in its fabrication, and shorter devices (i.e. those having larger values of f_gap and/or smaller values of w_s(i_T)) of course show correspondingly higher throughput levels. Despite its relatively long total length, the footprint of this platelet enrichment device was below 6cm² (Fig. 4 and 6 are not drawn to scale, for clarity), enabling several multiplexed devices to be fabricated in parallel on a typical (3” or 4”) wafer mold.

Figure 6.

CIF-based device for enrichment of platelets in platelet-rich plasma (PRP). Overall design of the device is shown schematically on the left. The value of f_gap for this device was 1.04×10⁻⁴. A close-up view of a representative functional device in operation, showing incremental concentration of platelets in successive legs of the CIF array, is shown on the right. The depth of the device was 150µm ±5µm; the width of the central channel was 125µm and the final width of the side channels was 140µm such that the ratio of total flow into the side channel collection port was ~2.5× that into the central collection port. The device consistently retained >80% of platelets in the central channel, representing a ~3× enrichment in platelet concentration overall. Arrows indicate direction of flow. Scale bar is 250µm.

Discussion

Earlier modeling work by Inglis & Herman illustrates the difficulties one encounters when developing a comprehensive analytical framework of the fluid flow in highly-branched microchannel networks.² Invariably there are factors that cannot be readily accounted for in a finite model, from purely a physics perspective (e.g. the precise effect of bifurcation shape/dimensions on fluid flow, or the nonlinear dependence of the flow profile on channel depth³¹), as well as from a practical standpoint (e.g. the variation in feature size and cross-section due to inherent limitations in the fidelity of photolithography^{32, 33}). The particles of interest, which are flowing in these already complex fluidic streams, themselves complicate the overall modeling process: inter-particle interactions, as well as confounding behavioral patterns even of isolated particles in very low Reynolds number flow, also serve to reduce the accuracy of in silico predictions of particle-size cutoffs at microfluidic bifurcations.^{2, 34}

In addition to these fundamental issues associated with producing a completely accurate fluid dynamics model for a given filtration design, practical implementation of any such model is also far from straightforward. For example, CFD simulations run in COMSOL Multiphysics (COMSOL, Inc., Burlington, MA) – previously used to iteratively optimize the dimensions of fluid-skimming side channels in crossflow filtration devices – appear to be limited to the inclusion of just a few dozen such channels for a given design, in order to be completed within a reasonable amount of (desktop computer) processing time.^{2, 19} Further, as nearly all practical applications of crossflow filtration involve the removal and/or concentration of heterogeneous particle populations, each having non-uniform distributions of multiple properties, any advanced model of this type of system would have to attempt to account for all of the relevant sources of variability. The addition of particle properties (e.g. shape, density, drag) to a more comprehensive computer simulation – while useful for gaining insights into certain aspects of particulate solution flows,^{35, 36} and likely necessary for achieving a truly predictive model – would be prohibitive for achieving an easily-implementable, simple approach to the rapid design of crossflow filtration devices.

As Inglis & Herman,² we believe that the appropriate design consideration for crossflow filtration should be to remove a consistent fraction of the main channel flow though each filtration point of the device (as opposed to earlier work by Sethu et al,¹⁹ which strove to remove a consistent amount of absolute volume). Using this approach (which also applies to the DLD-style “bumping” arrays), one anticipates that the so-called “critical diameter” (or the threshold that dictates the lower limit on the size of particles that will be concentrated via passage through these devices) will be maintained at each filtration point, in order to maximize device efficiency. However, due to the modeling and manufacturing complexities discussed above, it is often the case that even the best theoretical estimates for critical diameter do not completely agree with results observed in practice, even for perfectly spherical test particles.^{2, 26} Thus, a simplified method for rapidly generating a new style of crossflow filtration device designs that can be readily tested for their true, real-world efficiency was clearly needed – particularly for very small biological particles, which may require several thousand filtration points to be concentrated to the desired degree. This paper described the development and practical validation of such a method.

Analytical and/or computational predictions used by other methods often fail due to the conceptual difficulties discussed above. Our approach naturally circumvents this limitation because it does not rely on CFD simulations for determining the critical parameters needed to design a device. A hallmark of our method is the two stage design process that involves (1) identifying the appropriate value of the filtration fraction per gap parameter experimentally, and then (2) using that value of f_gap and the desired microchannel depth to generate the architecture of a fully functional device with the required amount of total filtration or enrichment (Fig. 2). In practice, the choice of f_gap should be made conservatively, especially for biological particles that may exhibit significant intra- and inter-subject variability and/or have considerable particle interactions at the desired concentrated volume fraction near the exit of the device (e.g. Fig.6, and supplementary videos S1, S2, and S3 in the ESI†). Further, the slight deviations invariably occurring during photolithographic, or other methods of, microchannel fabrication often serve to increase the effective value of f_gap in places on the device mold where they occur, thus the nominal value chosen should also take into account the precision of the mold manufacturing capabilities available.

Due to its computational simplicity, the modelling framework of our method (represented by eqns (1) – (5)) can be used to quickly and efficiently generate CAD drawings of crossflow filtration devices comprising many thousands of filtration points (for example, the devices shown in Fig. 4 and 6) – a necessary capability for creating devices able to highly concentrate very small particles. The dramatically reduced number of parameters used in our method makes it very easy to implement numerically (as a recursive algorithm). Other approaches employing either more complex analytical solutions or intricate CFD simulations are much more difficult to perform, making them largely inaccessible to non-experts in the field. Our method significantly simplifies the design process in particular for high throughput devices, which is a key toward finally translating numerous microfluidic devices from small-volume, lab-on-a-chip applications to large (even industrial) scale processing of biological particles, realizable in a manageable footprint. Given that the readily-achievable depth of our devices (150µm, or more) is at least 3–4 times deeper than in most conventional microfluidic systems based on general crossflow filtration principles,^{2, 19} the overall throughput of our devices is several fold higher, at a given driving pressure and level of particle enrichment. Even the rather flexible PDMS devices used in this work were capable of supporting ~250µL/min volumetric flow rates, in designs that produced ~3× enrichment of particles with effective diameters as low as 1–2µm, before channel deformation started to become significant (please see supplementary videos S1, S2, and S3 in the ESI†). This combined level of throughput and enrichment capability opens up a wide range of potential practical applications including concentration of blood cells for storage and transfusion, therapeutic removal of leukocytes from whole blood, or enrichment of circulating tumor cells for further analysis.

The ability to now easily manufacture high-throughput microfluidic devices implementing CIF, puts this approach in a highly competitive position with respect to conventional, macroscopic crossflow filtration technology. Traditional crossflow filters rely on steric size-exclusion, and therefore often foul and/or clog with use over time. The effective ‘pore size’ for the new type of microfluidic crossflow filtration devices described here can be made much larger than the particulates to be concentrated in the center (retentate) channel (Figs. 3–6), and the size cutoff is determined primarily by the width of the streamlines diverted into the side (filtrate) channels, thus the potential for plugging is essentially eliminated in normal operation. The relatively large (> 15µm) typical pore size for the microfluidic method we describe enables the production of correspondingly deep devices (i.e. >150µm, assuming a 10:1 aspect ratio limitation). Thus, a high-throughput system of multiplexed devices could be produced out of comparatively inexpensive materials (e.g. thermoplastics), versus expensive specialty membranes, while providing a superior degree of ‘tunability’ and resistance to fouling than macroscopic tangential filters.

Conclusions

Here we presented a straightforward methodology that enables rapid development of highly-efficient, high-throughput “controlled incremental filtration” devices for the enrichment and/or separation of small biological particles. The primary advantage of this CIF approach to the design process is its ease of implementation for a wide range of practical applications, making it (i) much more accessible to non-experts in the field, and (ii) capable of producing devices with significantly higher levels of filtration/enrichment, even for very small (~1µm) particles of interest, as compared to other existing methods. Further, our use of wide filtration gaps allows for the creation of comparatively deep microchannel constructs, which in turn provides higher throughput, and makes the manufacture of devices designed using our approach much more feasible relative to conventional microfluidics.

Materials and methods

Fabrication and operation of microfluidic devices

Chrome-on-glass photomasks (Photo Sciences, Inc., Torrance CA) of the CAD device designs were used to transfer the negative of the microchannel patterns into photoresist (SU8 3050; MicroChem Corp, Newton, MA) spun onto 4” silicon wafers (University Wafer, South Boston, MA), via UV (i-line) exposure (ETI/6/350/NUV/DCCD/M mask aligner, Evergreen Technology Inc, San Jose, CA). In order to produce 150µm deep structures of sufficient planarity, two 75µm layers of SU-8 were sequentially applied, each followed by a modified softback protocol of 2hours at 65°C followed by 1 hour at 95°C, on a leveled hotplate (Torrey Pines Scientific, Inc., Carlsbad, CA), with the wafers covered by glass petri dishes slightly elevated by glass slides, to create ventilation. Following exposure and development of the photoresist, wafers were exposed to tridecafluoro (1,1,2,2 tetrahydrooctyl) trichlorosilane (CAS# 78560-45-9, GelestInc, Morrisville, PA) under vacuum in a desiccator overnight. Lateral device design dimensions were adjusted during the CAD process to account for the predictable increase in SU-8 feature size arising from the relatively large UV exposure dose required for such deep devices.³²

Poly(dimethylsiloxane) (PDMS; SylGard 184, Dow Corning Corp, Midland, MI) casts of the wafer/photoresist masters were created and sealed to PDMS-coated glass slides via air plasma oxidation (PDC-3xG, Harrick Plasma, Ithaca, NY). Input and output fluidic ports were created in the ~5mm thick PDMS via biopsy punches prior to sealing. 7:1 PDMS mixtures were used to increase the rigidity of the molds and reduce feature-to-feature adherence during demolding. Removal of silica particles, to produce clearer images for publication, was accomplished by slowly filtering PDMS mixtures through 0.2µm syringe filters (cellulose acetate, Whatman / GE Healthcare Bio-Sciences, Pittsburgh, PA) prior to pouring.

Assembled PDMS devices were treated with a 1% (w/v) aqueous solution of mPEG-silane (MW 5000, Laysan Bio Inc, Arab, AL) for 30 minutes, followed by GASP buffer (9 mM Na₂HPO₄, 1.3 mM NaH₂PO₄, 140 mM NaCl, 5.5 mM glucose, 1% w/v bovine serum albumin, 290 mmol/kg, pH 7.4) for one hour, prior to the introduction of the particles of interest. Fluid was driven through the devices by inserting into the input port an appropriate length of 1.5mm O.D. polyethylene tubing, which was attached to a 3 mL plastic syringe with its plunger removed, hung at height of 1 inch to 5 feet above the device. Both the tubing and vessel were filled with GASP buffer or PRP, as appropriate. After a sufficient volume of fluid had passed through a given device, samples were collected from each of the output ports for analysis.

Sample Preparation and Analysis

Fresh human blood was collected via venipuncture from healthy consenting volunteers into Vacutainer tubes (8 mL, K₂EDTA, BD, Franklin Lakes, NJ). To separate PRP for testing, blood samples were spun at 50×g for 10–15 minutes, and the supernatant removed. Packed RBCs or polystyrene beads (Bangs Laboratories, Inc., Fishers, IN) were re-suspended in GASP buffer at the amounts required to produce test samples with the desired particle volume fraction. Platelet counts were measured with a hematology analyzer (Medonic M-Series, Boule Diagnostics Int AB, Stockholm, Sweden). Bead concentrations were measured with a coulter counter (Z2™ COULTER COUNTER®, Beckman Coulter Inc., Brea, California).