Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2014 Dec;24(12):2050–2058. doi: 10.1101/gr.176214.114

A formal perturbation equation between genotype and phenotype determines the Evolutionary Action of protein-coding variations on fitness

Panagiotis Katsonis 1, Olivier Lichtarge 1,2,3,4,✉
PMCID: PMC4248321  PMID: 25217195

Abstract

The relationship between genotype mutations and phenotype variations determines health in the short term and evolution over the long term, and it hinges on the action of mutations on fitness. A fundamental difficulty in determining this action, however, is that it depends on the unique context of each mutation, which is complex and often cryptic. As a result, the effect of most genome variations on molecular function and overall fitness remains unknown and stands apart from population genetics theories linking fitness effect to polymorphism frequency. Here, we hypothesize that evolution is a continuous and differentiable physical process coupling genotype to phenotype. This leads to a formal equation for the action of coding mutations on fitness that can be interpreted as a product of the evolutionary importance of the mutated site with the difference in amino acid similarity. Approximations for these terms are readily computable from phylogenetic sequence analysis, and we show mutational, clinical, and population genetic evidence that this action equation predicts the effect of point mutations in vivo and in vitro in diverse proteins, correlates disease-causing gene mutations with morbidity, and determines the frequency of human coding polymorphisms, respectively. Thus, elementary calculus and phylogenetics can be integrated into a perturbation analysis of the evolutionary relationship between genotype and phenotype that quantitatively links point mutations to function and fitness and that opens a new analytic framework for equations of biology. In practice, this work explicitly bridges molecular evolution with population genetics with applications from protein redesign to the clinical assessment of human genetic variations.

Each birth introduces about 70 new human genetic mutations (Keightley 2012) that have led, over generations, to the current four million DNA differences among randomly chosen individuals. Besides insertions, deletions, copy number variations, and chromosomal rearrangements, genetic alterations include single nucleotide substitutions that translate into nearly 10,000 amino acid substitutions per human exome (Ng et al. 2008; Lupski et al. 2010). These protein-coding variants can affect fitness (Eyre-Walker and Keightley 2007), account for 85% of known disease mutations (Choi et al. 2009), and are associated with more than 2500 ailments (Botstein and Risch 2003; Bodmer and Bonilla 2008). Nevertheless, association studies explain only a fraction of disease susceptibility (McCarthy and Hirschhorn 2008), and the role of both private and common mutations remains unclear (Ng et al. 2008). Computational approaches therefore aim to identify which coding variations cause disease (Ng and Henikoff 2001; Stone and Sidow 2005; Adzhubei et al. 2010) within the limitations of biophysical, statistical, and machine-learning models of protein function (Chun and Fay 2009; Hicks et al. 2011). In parallel, a large body of theory models the spread and fixation of mutations (Orr 2005), their distribution for various population sizes and fitness effects (Eyre-Walker and Keightley 2007), and whether selection or drift dominates their fate (Nei 2007). However, without a practical measure of the action of mutations on fitness, the theory cannot be applied to the massive inflow of genetic information (Orr 2005; Losos et al. 2013).

Here, we follow the perspective that evolution proceeds in infinitesimal mutational steps (Fisher 1930; Orr 2005) to propose an equation for the Evolutionary Action of a mutation on fitness. This action equation is derived from a model of the genotype-phenotype relationship that is simpler than current models (Choi et al. 2008; Kleinman et al. 2010; Grahnen et al. 2011) and that is compatible with the theory of nearly neutral evolution (Ohta 1992) and with fundamental variational principles of physics describing how physical systems evolve to follow paths of least action. The computed Evolutionary Action consistently topped the most sophisticated, homology-based or machine-learning methods that predict the impact of mutations in both retrospective and prospective assessments. Retrospective validation included large data sets of (1) experimental assays of molecular function; (2) human disease association; and (3) population-wide polymorphisms. Prospective validation involved the CAGI (Critical Assessment of Genome Interpretation) community contest, which challenged predictors to estimate the impact of 84 mutations on enzymatic activity of the cystathionine beta-synthase.

Results

A genotype-phenotype perturbation equation

To assess mutations, we treat each one as a small genotype perturbation that may disturb the phenotype. For a protein P, the genotype γ is the sequence of n residues (r1, r2, …, rn)P, and the global fitness phenotype is a scalar quantity ϕ that integrates all the structural, dynamic, and other functional attributes of P that affect the survival and reproduction of the organism in its milieu (Wright 1932; Smith 1970). As species drift or adapt over time, γ and ϕ vary, coupled to each other by a multivariate evolutionary fitness function f, such that f(γ) = ϕ, where time and natural selection constraints are implicit. Our central hypothesis is that f exists and is differentiable. If so, a small genotype perturbation dγ will trigger a global fitness phenotype variation dϕ given by

graphic file with name 2050equ1.jpg

where ∇f is the gradient of f and • denotes the scalar product.

In practice, we consider the phenotype variation for a single missense mutation from amino acid X to any other amino acid Y at sequence position i. Then, the genotype perturbation reduces to the magnitude of that substitution, denoted Δri,X→Y, and the gradient reduces to the partial derivative of the evolutionary fitness function for its ith component, denoted ∂f/∂ri. This last term is the sensitivity of the global fitness phenotype to variations at position i and implicitly accounts for part of the context-dependence at i, that is, the structural and functional role of that position. The remainder of the context-dependence should reside in higher order terms that explicitly represent epistatic interactions with other mutations (Breen et al. 2012). To simplify, we neglect these terms so that the Evolutionary Action (EA, or action for short) of a single substitution on the reference genotype of a species becomes, to a first order:

graphic file with name 2050equ2.jpg

In this reduced form, the Evolutionary Action equation states that a point mutation displaces fitness from its current state in proportion to the magnitude of the mutation and to the evolutionary fitness gradient at that site (Fig. 1A). This differential expression is useful because its terms may be evaluated from evolutionary data.

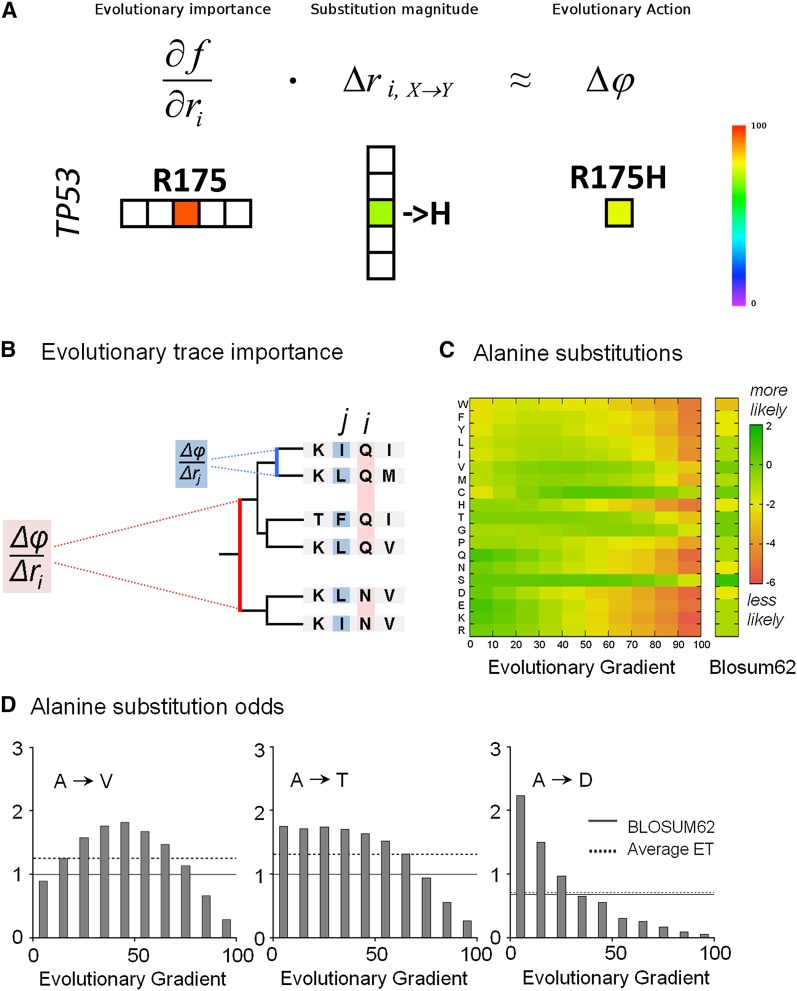
Figure 1.

Figure 1.

Open in a new tab

Computation of the Evolutionary Action equation. (A) An illustration of computing the Evolutionary Action of a mutation, such as the R175H in the TP53 gene, from the evolutionary importance of the residue R175 and the arginine-to-histidine substitution magnitude at that position. (B) A sequence alignment and the associated evolutionary tree show that the evolutionary fitness gradient of a protein residue, which is defined as the phenotypic fitness change due to an elementary genotypic change, will be larger (in red), or smaller (in blue), depending on the phylogenetic distance between evolutionary branches that differ at that position. Since the Evolutionary Trace ranks the functional importance of sequence positions by correlating residue variations with phylogenetic branching (Lichtarge et al. 1996; Mihalek et al. 2004), we can estimate the evolutionary fitness gradient with ET. (C) A color matrix, computed from nearly 67,000 protein sequence alignments, displays the relative substitution odds from alanine to any other amino acids (in single-letter code) depending on the evolutionary gradient decile at the mutation site (most likely substitutions are green, least likely ones are in red), and compared to the standard BLOSUM62. (D) The gradient-specific (gray bars), the nonspecific (dashed lines), and the BLOSUM62 (solid lines) substitution odds are illustrated for alanine substitutions to valine (V), threonine (T), and aspartate (D). The code is (A) alanine, (W) tryptophan, (F) phenylalanine, (Y) tyrosine, (L) leucine, (I) isoleucine, (V) valine, (M) methionine, (C) cysteine, (H) histidine, (T) threonine, (G) glycine, (P) proline, (Q) glutamine, (N) asparagine, (S) serine, (D) aspartic acid, (E) glutamic acid, (K) lysine, (R) arginine.

To measure the evolutionary fitness gradient ∂f/∂ri, we rank the importance of every sequence position with the Evolutionary Trace (ET) method (Lichtarge et al. 1996; Mihalek et al. 2004; Wilkins et al. 2013). By definition, a gradient is the ratio of the sensitivity of a function with respect to its coordinates. Here, ∂f/∂ri is the sensitivity of the global fitness phenotype with respect to a mutational step, or simply the fitness difference observed upon variation. This definition points to ET, which ranks every position in a sequence alignment of a protein family as more (or less) important if it varies mostly among major (or minor) evolutionary branches. Since evolutionary branch distances reflect fitness (Coyne and Orr 1998), in effect ET and evolutionary gradient are equivalent concepts and we may choose ET ranks to approximate ∂f/∂ri (Fig. 1B). A frequent and simpler measure of evolutionary importance is residue conservation (Livingstone and Barton 1993; Pei and Grishin 2001; Valdar 2002; Mihalek et al. 2004), but conservation is an average rather than a derivative and is less accurate than ET in practice. In that light, prior ET studies have already shown the broad applications of evolutionary gradients: They identify functional sites and allosteric pathway residues (Yao et al. 2003), guide mutations that block or reprogram function (Rodriguez et al. 2010), and define structural motifs that predict function on a large scale (Ward et al. 2009; Erdin et al. 2010), such as substrate specificity (Amin et al. 2013).

To measure the magnitude of a substitution Δri,X→Y, we use the relative evolutionary odds of these substitutions (Henikoff and Henikoff 1992; Overington et al. 1992; Koshi and Goldstein 1995). For example, the amino acid alanine is substituted to serine more often than to aspartate, in line with greater biophysical and chemical similarities to the former. Although conceptually independent, we find that the gradient of a position strongly biases its substitution odds. For example, compared to standard, uniform substitution values (Henikoff and Henikoff 1992), alanine positions with large gradients mostly tolerate substitutions to small neutral amino acids, whereas alanine positions with small gradients strongly favor substitutions to large polar or charged amino acids (Fig. 1C). These trends are specific to every amino acid pair: Alanine to valine substitution odds form a bell-shaped distribution as the evolutionary gradient at the mutated position varies from minimum to maximum; those of alanine to threonine begin flat then tail off, whereas those of alanine to aspartate decay steadily (Fig. 1D). These findings are also distinct and complementary to the dependence of substitutions on structural features (Supplemental Fig. 1; Overington et al. 1992; Koshi and Goldstein 1995) and show that the evolutionary gradient at each sequence position is an important factor in substitution bias. Accordingly, we approximate Δri,X→Y by the evolutionary gradient-sensitive substitution odds.

The Evolutionary Action correlates with experimental loss of protein function

For any mutation in a protein with a sufficiently large evolutionary tree, typically more than 20 sequences from a variety of species, we can now apply these approximations for ∂f/∂ri and Δri,X→Y to evaluate a normalized Evolutionary Action, from a neutral value of 0 to a maximum impact value of 100, and then compare this action to the relative changes in function and fitness observed experimentally. First, the Evolutionary Action correlates linearly with the average loss of DNA recombination measured in vivo by P1 phage-mediated transduction in 31 E. coli RecA point mutants relative to wild type (Adikesavan et al. 2011), with a Pearson R2 correlation coefficient of 0.87 (Fig. 2A). More broadly, in larger and independent data sets, correlations between the Evolutionary Action and the fraction of dysfunctional mutants in vivo or the average loss of activity in vitro range from 0.73 to 0.96 (Fig. 2B–E) in 4041 lac repressor mutations in E. coli assayed for their impact on β-galactosidase repression (Markiewicz et al. 1994); 2015 lysozyme mutations in bacteriophage T4 assayed for plaque formation due to degradation of the host cell walls by lysozyme (Rennell et al. 1991); 336 HIV-1 protease mutations assayed by the cleavage products (Loeb et al. 1989); and 2314 TP53 mutants assayed for transactivation (see Methods) (Kato et al. 2003). The Spearman’s rank correlation coefficient is at least 0.98. In lysozyme, two regimes were apparent: Low action mutations minimally affect the phenotype (or the assay), and then there is a steep linear response past some action threshold (Fig. 2C). This lag may be due to the relative insensitivity of the lysozyme assay, which only classified 16% of mutations overall as being deleterious compared to 62%, 53%, and 30% in the lac repressor, HIV protease, and TP53 assays, respectively. In TP53 there is also a lag, but it is small and may reflect the experimental error of averaging small differences in transactivation. As a reference, the sensitivity and specificity of common alternative measures of mutational impact (Ng and Henikoff 2001; Stone and Sidow 2005; Adzhubei et al. 2010) are lower on the same data sets (Fig. 3A). Moreover, blind predictions assessed by independent judges also showed that the action equation identified deleterious mutations better than state-of-the-art predictions of mutational effect (Fig. 3B). Together these data span 8500 mutations in eukaryotic, prokaryotic, and viral proteins, and they show that the Evolutionary Action equation quantifies the impact of mutations on assays of function and fitness.

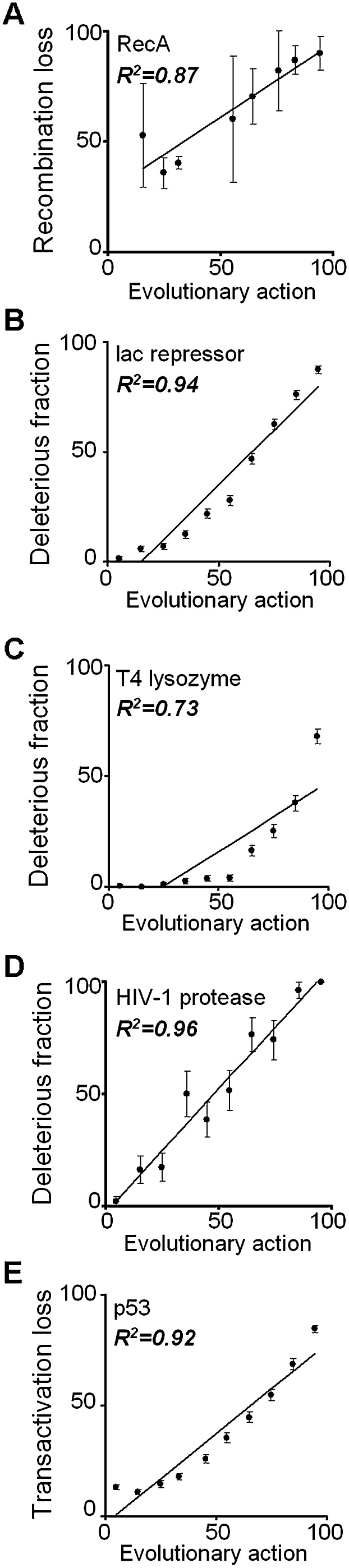
Figure 2.

Figure 2.

Open in a new tab

Mutational action correlates with experimental impact. Each panel shows along the x-axis the action predicted from Equation (2) and along the y-axis the fractional activity or fitness measured experimentally as (A) the average loss of recombination activity in 31 point mutants of E. coli RecA protein; (B) the nonfunctional fraction of 4041 point mutants in E. coli lac repressor in a β-galactosidase repression assay (Markiewicz et al. 1994); (C) the nonfunctional fraction of 2015 point mutants in bacteriophage T4 lysozyme in a plaque formation assay (Rennell et al. 1991); (D) the nonfunctional fraction of 336 HIV-1 protease point mutants in substrate cleavage (Loeb et al. 1989); and (E) the average transactivation activity of 2314 human TP53 point mutants assayed in yeast over eight response-elements (Petitjean et al. 2007). The data are binned into action deciles, the R2 values indicate Pearson product-moment correlation coefficients following linear fitting, and the standard error of the mean is shown with error bars.

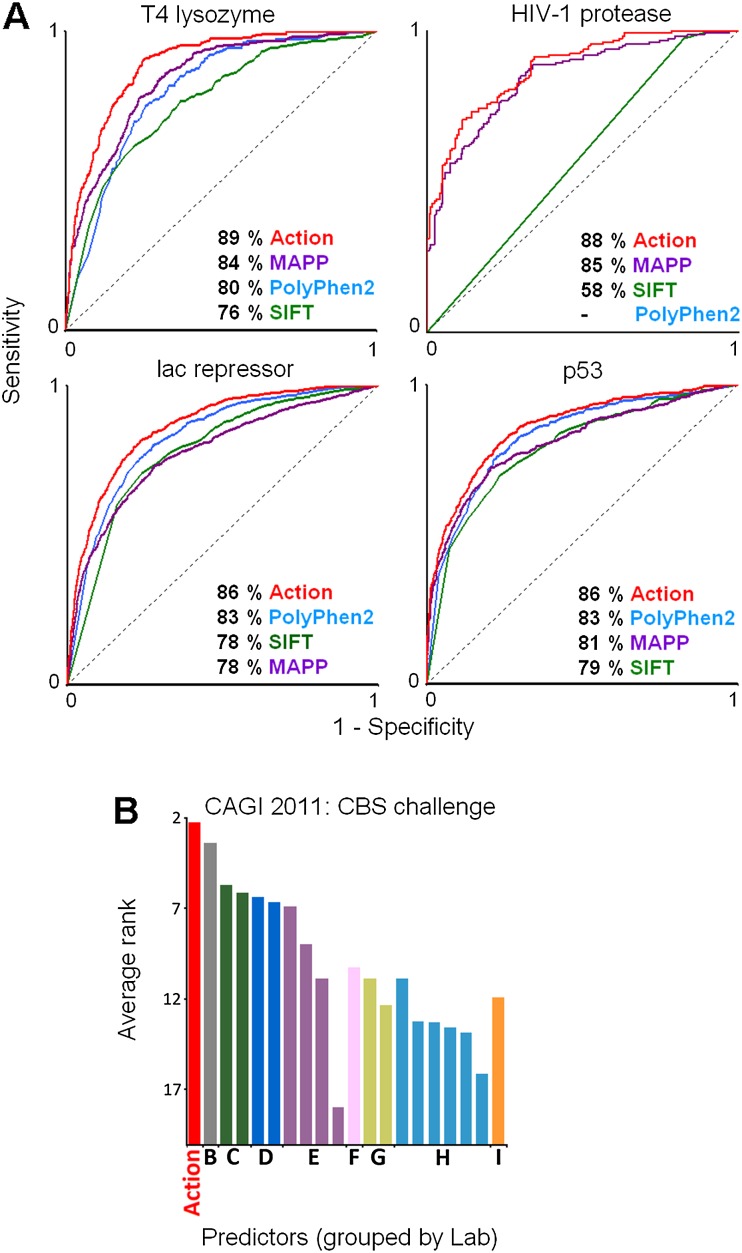
Figure 3.

Figure 3.

Open in a new tab

The performance of the Evolutionary Action method was compared to state-of-the-art methods. (A) The area under the receiver operating characteristic curve (AUC) of the relative sensitivity and specificity to separate harmful from harmless mutations for the Evolutionary Action, PolyPhen-2, SIFT, and MAPP was calculated for each of the data sets: 2015 bacteriophage T4 lysozyme mutants to break the host cell walls; 4041 E. coli lac repressor mutants to repress β-galactosidase more than 20-fold; 336 HIV-1 protease mutants to cleave the Gag and Gag-Pol precursor proteins (PolyPhen-2 returned no predictions for the HIV-1 protease mutations); and 2314 human TP53 mutants to transactivate eight TP53 response-elements in yeast. (B) The average rank of current methods (bars), from different groups (letters), to predict the activity of cystathionine beta-synthase (CBS) mutants was assessed by the Critical Assessment of Genome Interpretation (CAGI) of 2011. The CBS activity was assayed for the ability of each mutant to restore growth in yeast cells lacking the normal CYS4 ortholog under two different growth conditions (high and low concentrations of pyridoxine cofactor) (Mayfield et al. 2012). Twenty methods from nine groups were assessed over nine criteria (precision, recall, accuracy, harmonic mean f1, Spearman’s rank correlation coefficient, Student’s t-test P-value, root mean square deviation [RMSD], RMSD over Z-scores, and the AUC) for each cofactor concentration, and then their rank was averaged. Evolutionary Action is shown in red, and a taller bar is a better rank. Raw data and assessment details are available at the CAGI website (https://genomeinterpretation.org/) and from the CAGI organizers Susanna Repo, John Moult, and Steven E. Brenner. The Evolutionary Action analysis files are available at http://mammoth.bcm.tmc.edu/KatsonisLichtargeGR.

The Evolutionary Action correlates with severity in inherited diseases

Since protein variations of unknown significance (VUS) are a recurring problem in exome interpretation, we asked whether the Evolutionary Action could be a biomarker for the impact of protein mutations on human diseases. We first assembled a set of 218 genes from the UniProt database that were each annotated with both benign and harmful coding polymorphisms (see Methods). The Evolutionary Action distribution was strikingly different between the mutations that were benign and those that were harmful, with the former strongly biased to low action and the latter strongly biased to large action (Wilcoxon rank-sum P-value < 10−16) (Fig. 4A). As a result, the action separated the two types of mutations with better specificity and sensitivity than other methods: The area under a receiver operating characteristic curve was 85% overall, and it rose above 90% when only the mutations with the greatest or the least action were considered (Supplemental Fig. 2A,B). A second test aimed to distinguish harmful mutations within a single protein family. Starting from a collection of 26,597 human tumors (Petitjean et al. 2007), we compared TP53 mutations seen in 10 or more different cases, and thus more likely to play a role in pathogenesis, to those seen in fewer cases. The Evolutionary Action of the frequent mutations was significantly larger (χ2 P-value = 9 × 10−34), and these mutations were also typically nonfunctional in vitro (Fig. 4B). In contrast, the less frequent mutations had no action bias (Fig. 4C). The subgroup of less frequent mutations that impaired function in vitro, however, was biased to large action (χ2 P-value = 2 × 10−47). These data show that the action values of clinically harmful and of benign polymorphisms are not random. In many disease-associated proteins, low action polymorphisms are typically benign and those with high action are typically harmful.

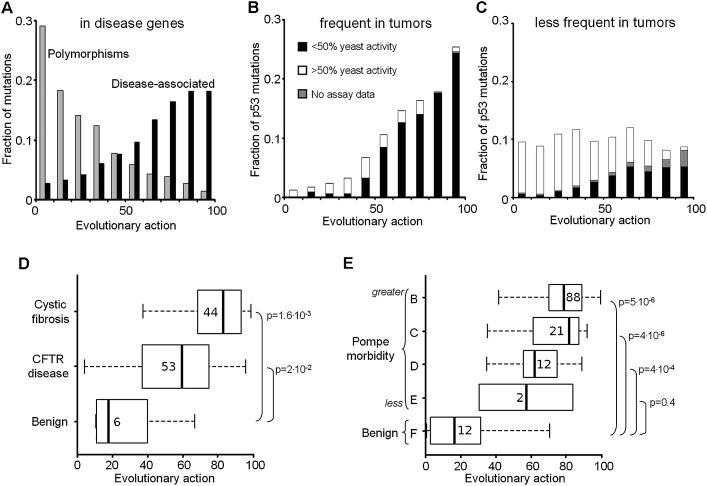
Figure 4.

Figure 4.

Open in a new tab

Mutational action correlates with morbidity. (A) The action distributions of coding polymorphisms from 218 genes for the 8553 cases that are disease-associated (in black) compared to the 794 that are benign (in gray). Each of these genes, obtained from the UniProt database, is linked to at least one disease. (B) The action distribution of 343 somatic TP53 mutations found frequently in tumor samples (at least ten times in 26,597 cases tallied in the IARC database), compared to (C) the remaining 1026 sporadic TP53 mutations. The fraction with less (more) than 50% of the wild-type transactivation activity in yeast assays is black (white), and those for which these data are unknown is gray. (D) The action distribution of 103 mutations in the CFTR gene binned by the severity of clinical presentation: full-blown cystic fibrosis (top), CFTR-related disorders (middle), and no symptoms (bottom) (Dorfman et al. 2010). Vertical bars indicate median action; numbers refer to the total mutations in each group; box sizes match the quartiles of the distributions, and the error bars indicate the spread of variation. (E) The action distribution of 135 Pompe disease mutations in the GAA gene binned into decreasing severity classes from Class B, the most severe, to Class F, which contains the asymptomatic patients.

These distribution biases suggest that action may be prognostic of morbidity in diseases that depend directly on a gene defect. Therefore, we turned to two autosomal recessive monogenic disorders. First, a curated and well-characterized study of 103 mutations of the CFTR gene linked them to cystic fibrosis (44 cases); CFTR related disease (53 cases); or benign presentations (six cases) (Dorfman et al. 2010). The median action between these groups was significantly different (Wilcoxon rank-sum P-value = 1.6 × 10−3) (Fig. 4D), such that high, intermediate, and low action values separated them. Second, Pompe’s disease is a clinically heterogeneous disorder, caused by a deficiency of acid alpha-glucosidase, an enzyme encoded by the GAA gene. Known missense mutations of GAA were classified by order of decreasing severity into types B, C, D, and E, ending with nonpathogenic type F (Kroos et al. 2008). The median action of GAA mutations rose significantly with clinical severity (Wilcoxon rank-sum P-value = 5 × 10−6), being in the top half for pathogenic types B–E, but in the bottom half for nonpathogenic type F (Fig. 4E). These data show that in two different diseases the Evolutionary Action of mutations in causative genes is related to morbidity.

Action reflects the fitness effect of population-wide polymorphisms

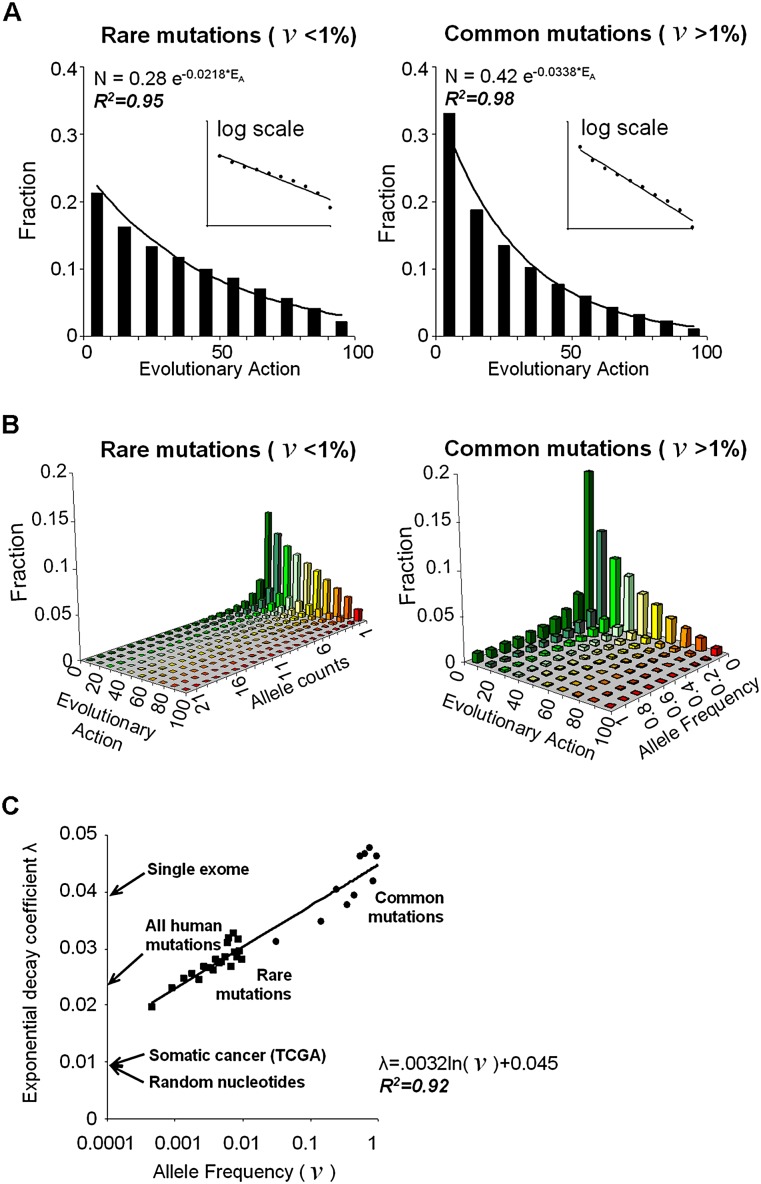
If action is a general biomarker of morbidity or fitness effect, then we would expect the population to carry fewer coding polymorphisms with larger action. Indeed, long-standing population genetics models suggest that the probability of polymorphisms to remain in a population decreases nearly exponentially with their fitness effects (Fisher 1930), although without a practical measure for the size of the phenotypic effect, validation in genomic data has been lacking (Orr 2005). Thus, to test the generality of the action equation, we tallied the frequency of coding polymorphisms from the 1000 Genomes Project (The 1000 Genomes Project Consortium 2012) as a function of their action. The 261,899 unique coding variations were divided into common mutations (36,379 SNPs with allele frequencies above 1%) and into rare mutations (225,520 SNVs, with allele frequencies below 1%). Without special regard for zygosity, dominance, genetic background, or trait associations, and in contrast to other measures of deleterious impact (Supplemental Fig. 3A,B), we found that the action distribution was nearly exponential in both groups (R2 = 0.98 and 0.95, respectively) (Fig. 5A), but the decay or loss rate, denoted by λ, was larger for common than for rare mutations. To investigate these different loss rates, the variations were grouped more finely by their allele frequency, denoted by ν (Fig. 5B). This revealed a family of exponential distributions with loss rates that were log-linear in ν:

graphic file with name 2050equ3.jpg

where α = 4.5 × 10−2 and β = 3.2 × 10−3 fit these distributions with correlation coefficient R2 = 0.92 (Fig. 5C). These data support the Evolutionary Action as a general measure of fitness effect and show that the human coding variations from the 1000 Genomes Project are distributed as a nearly exponential function of the action modulated by a power law function of allele frequency:

graphic file with name 2050equ4.jpg

where N is the fraction of mutations of a given allele frequency, N0 = 0.2, and the loss rate λ is a scaling factor for the selective constraints on mutations with different actions (Hartl and Taubes 1996).

Figure 5.

Figure 5.

Open in a new tab

Nearly exponential action distributions of human coding polymorphisms. (A) Coding polymorphisms from the 1000 Genomes Project (including 1092 individuals) were separated into 225,751 rare variants (left) and 36,354 common mutations (right), based on an allele frequency (ν) threshold of 1%. Both groups fit exponential distributions with Pearson coefficients R2 of 0.95 and 0.98 and decay rates of 2.18 × 10−2 and 3.38 × 10−2, respectively, when binned into action deciles. The insets show equivalent log-linear plots. (B) These groups were further fractionated by allele count or frequency. The action distribution of polymorphisms in the same tranche of allele count, or frequency, also fit an exponential with R2 values from 0.87 to 0.99. The colors represent different Evolutionary Action (green for low and red for high). (C) The action decay rate for these exponentials varies linearly with the logarithm of their allele frequency (R2 value of 0.92). Arrows indicate the observed decay rates for all nonsynonymous coding mutations from a single individual’s exome; for the rare and the common mutations of the 1000 Genomes Project; for somatic cancer mutations retrieved from TCGA (http://tcga-data.nci.nih.gov); and for nonsynonymous mutations obtained by the translation of random nucleotide changes following the standard genetic code (random nucleotides).

Coding variations found in single cells, in individuals, and in populations are ensembles of variants that span a wide range of different allele frequencies. The overall action distribution of these different ensembles, however, is also nearly exponential with a loss rate λ unique to each one (Supplemental Fig. 3C). For example, λ is largest in an individual’s exome, but it decreases by 40% over a group of individuals, such as the entire set of variations from 1092 individuals sequenced in the 1000 Genomes Project, and it decreases by 73% over the set of all somatic cancer mutations described in The Cancer Genome Atlas (TCGA) (The Cancer Genome Atlas Research Network et al. 2013). These data show that ensemble-specific loss rates are dominated by common polymorphisms for an individual’s exome, by rare variants over a population such as the group of the 1000 Genomes Project exomes, and by random nucleotide changes in somatic cancer tissue from TCGA (Fig. 5C).

Discussion

A fundamental problem in evolution is to quantify how genotype variations drive phenotype variations. This work therefore applied elementary mathematical concepts from differential analysis to formulate an equation of evolution. The result is a computable first order Evolutionary Action equation for the effect of genotype perturbations on fitness. At the molecular level, the action estimates the deleterious impact of substitutions in proteins from viruses, bacteria, and eukaryotes. In individuals, this deleterious impact measured by the Evolutionary Action correlates with the pathogenicity and clinical course of mutations in disease-causing genes, and it separates genes with harmful versus neutral mutations by their different action distributions. The action threshold for clinical consequences may differ depending on the essentiality, allelic dominance, and external factors specific to each protein. Finally, over a population, the greater clinical harm associated with larger Evolutionary Action governs the purifying selection of coding polymorphisms, notably recovering the distribution of fitness effect anticipated by Fisher in 1930 and consistent with population genetics models (Fisher 1930; Orr 2005). Thus, the Evolutionary Action equation quantitatively bridges the phenotypic fitness effects of mutations across molecular, clinical, and population genetics data.

This Evolutionary Action equation rests on the fact that ∇f(x)·dx = dy for any differentiable function f(x) = y and on the postulate that the genotype γ and the fitness phenotype ϕ can stand for x and y, respectively, and be related by a differentiable evolutionary function f. For missense mutations, the genotype variation dγ is the difference in amino acid similarity, estimated by substitution odds, and the partial derivative components of the gradient ∇f is the sensitivity of fitness to mutations, estimated by the evolutionary importance of each sequence residue. Although evolutionary importance is often conflated with conservation, in the context of differential analysis, an average, such as conservation, is less accurate than ET, which directly uses phylogenetic analysis to couple variations in sequence to variations in fitness, as a derivative should, since by definition derivatives are ratios of variations. The fact that ET measures a fundamental evolutionary quantity, ∇f, is consistent with its accuracy and versatility to predict, selectively block, redesign, or mimic protein function by pinpointing the amino acid determinants of specificity (Yao et al. 2003; Rodriguez et al. 2010; Amin et al. 2013). To improve substitution odds, we likewise used phylogenetic analysis by considering the evolutionary gradient of the substituted site. Both terms, ∇f and dγ, contribute to the impact of a mutation since each one separates deleterious from neutral mutations if the other is held nearly constant (Supplemental Fig. 4).

It is noteworthy that the evolutionary fitness function f between genotype and phenotype is never solved for. It suffices to evaluate ∇f because the perturbation approach treats mutations as infinitesimal displacements from the current fitness state of a species. This shifts the focus from discovering global evolutionary paths in the fitness landscape, tantamount to solving f and predicting protein structure and function from sequence, to evaluating the path divergences dϕ as a sequence mutates and “jumps” in the fitness landscape. Computing these jumps requires solving Eq. (2), which is simpler because the phylogenetic divergence tree provides an integrative summary of the impact of mutations over all past relevant molecular, cellular, systemic, and environmental interactions even if the details of these features remain unknown. In the future, it may be possible to improve accuracy with additional higher-order perturbation terms that account for epistatic effects. Another source for improvements is that, although ∇f and dγ are computed over the past evolutionary record, their product informs on the Evolutionary Action of mutations dϕ at any point in time, including today. In other words, the fitness metric and the action of a mutation are assumed to be time-invariant. This is an approximation since divergent proteins can develop new functional sites, a phenomena that leads to branch-specific evolutionary gradient variations and accounted for by differential ET (Lichtarge et al. 1997), for example, to identify ligand-specific sites (Madabushi et al. 2004; Rodriguez et al. 2010).

Despite its simplicity and these limitations, the Evolutionary Action equation matches experimental data as well as or better than the most sophisticated current machine-learning and statistical methods, and when applied to the 1000 Genomes Project data, it brings to light fine details and new parameters for the distribution of polymorphisms. First, the strength of selective constraints against mutations with large fitness effects is specified by λ, the exponential loss rate constant of the Evolutionary Action distribution. This loss rate is greatest in individuals, consistent with selective pressure to carry few detrimental mutations. It is smaller in a population, where rare variations may accumulate in unrelated individuals for better overall adaptive potential. And λ is least and reaches the lower limit set by the codon bias itself in diverse cancer cells, in which the large background of random passenger mutations obscures the rare cancer driving mutations. Second, as polymorphisms spread in a population the loss rate λ grows linearly at a rate of β until it peaks, at fixation, with λmax = α, when ν = 1. Thus, α and β are basic parameters of evolutionary drift and adaptation. For the same value of α, species with larger β experience less selective forces against new, larger deviations from neutral alleles, which may increase the pool of variations underlying genetic drift and possible adaptation. Reciprocally, for the same value of β, species with larger α have relatively greater selective forces against larger deviations from neutral alleles, lowering possibilities for drift and adaptation. Since the mutation rate is subject to molecular and selection factors (Shee et al. 2012), one may speculate whether similar factors might modulate α and β, and underlie shifts between evolutionary quiescence and bursts.

More certain is that mutations with greater action are at increasing selective disadvantage and that fixation should mostly favor polymorphisms with least action (Fig. 5A,B), consistent with the nearly neutral theory of molecular evolution (Ohta 1992). This is also true when comparing the Evolutionary Action differences among pairs of homologous proteins as they diverge further apart. Indeed, homologs that are evolutionarily closer, based on sequence identity, consistently exhibit lower overall, as well as average, action differences (Supplemental Fig. 5). Therefore the genotype-phenotype trajectory should follow a path of nearly least Evolutionary Action, with the frequency of larger deviations from least action attenuating exponentially as dictated by the loss rate λ. The emergence of least action as a fundamental evolutionary constraint is intriguing and suggests a convergence between evolution in biological systems and familiar variational principles in physics.

For now, starting with elementary calculus and a reductive view of biology that ϕ = f(γ), we show a first principle perturbation equation for the Evolutionary Action of genotype variations on functional fitness phenotype that robustly matches data across biological scales and clades. This opens new directions for the formal analysis of evolution and, in practice, sheds light on the analysis of coding variations, with applications to biological engineering, to genome interpretation, and to disease surveillance and personalized therapy based on individual and comparative mutational action profiles.

Methods

Calculation of action

The action Δϕ was calculated by the product of the evolutionary gradient ∂f/∂ri and the perturbation magnitude of the substitution, Δri,X→Y. These two terms, ∂f/∂ri and Δri,X→Y, were measured by importance ranks of the Evolutionary Trace method and by amino acid substitution odds, respectively, as described below. We normalized both terms and their product to become percentile scores for each protein. Therefore, high or low action indicated deleterious or neutral assessment, respectively, such that, for example, an action of 68 implied that the impact was higher than 68% of all possible amino acid substitutions in a protein.

To compute the evolutionary gradient for position i of protein P, we retrieved its homologs in three databases (NCBI nr, the UniRef100, and the UniRef90 [Suzek et al. 2007]) with blastall 2.2.15. Up to 5000 homologous sequences were selected each time with an e-value cutoff set to 10−5, the minimum sequence identity set to 30%, and all other parameters set to default values. Sequences were aligned with MUSCLE (Edgar 2004) (http://drive5.com/muscle/), and the columns with gap in the query sequence were removed. Then, we ran the rvET method (Mihalek et al. 2004), which optimizes sequence selection by maximizing the spatial clustering among top-ranked residues (Madabushi et al. 2002) and their rank information (Yao et al. 2006), and we averaged the ET scores produced on each of these three alignments. We computed substitution log-odds following the BLOSUM methodology (Henikoff and Henikoff 1992), with the difference that the odds were computed separately depending on the evolutionary gradient of the substituted position. For this, we assembled as above over 67,000 multiple sequence alignments for proteins available in the PDB database (http://www.rcsb.org/pdb/), and we computed an evolutionary gradient for each position of each alignment. These positions were divided into 10 groups (gradient deciles), and the substitution odds were computed for each group, as described below. An additional structure-dependent set of substitution matrices further divided each gradient decile into nine groups: into low (< 10 Å2), medium (10–50 Å2), and high solvent accessibility (> 50 Å2), and also into helical, stranded, and coiled secondary structure elements. Finer bins of substitution odds may better distinguish the selection constraints that are less common in protein evolution, such as for transmembrane patches (Soyer et al. 2003).

Calculation of the substitution log-odds

Let fijc be the total number of matches between amino acid i (1 ≤ i ≤ 20) to any amino acid j (1 ≤ j ≤ 20) when i is the most frequent amino acid in a column of class c (1 ≤ c ≤ 10 or 1 ≤ c ≤ 90). Then the observed frequency, qijc, for substituting the amino acid i by j in class c is

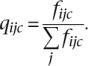graphic file with name 2050equ5.jpg

The probability of occurrence of the amino acid j in the data set is

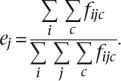graphic file with name 2050equ6.jpg

The log-odds for the substitution of i is then calculated with entries

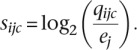graphic file with name 2050equ7.jpg

Unlike the BLOSUM methodology, log-odds were not rounded to the nearest integer.

Current predictors of mutation impact

SIFT predictions were obtained using “SIFT BLink” (http://sift.jcvi.org/). MAPP predictions were obtained after installing the software (http://mendel.stanford.edu/SidowLab/downloads/MAPP/) using sequence alignments from the UniRef90 database as input. The “P-value interpretations of the MAPP scores” were used as the impact. PolyPhen-2 predictions were obtained using the default parameters of the batch query tab at http://genetics.bwh.harvard.edu/pph2/.

Statistics

The χ2 test was used to calculate the P-value of the overlap between action and clinical association or yeast assay activity of TP53 mutations. The Wilcoxon rank-sum test was used to compare the distributions of disease and benign polymorphisms for the data set of UniProt mutations and of the TP53, CFTR, and GAA genes.

Experimental data sets

The set of 31 E. coli RecA mutations was assayed in Adikesavan et al. (2011) for its recombination activity as a percent of the wild-type activity. The mutations were binned in 10 action groups and the average recombination was calculated. The set of 2015 bacteriophage T4 lysozyme mutations was assayed in Rennell et al. (1991) by the amount of formed plaque, due to lysozyme’s break-up of the host cell walls. Mutants with no (−) and difficult to discern (−/+) plaque formation were considered as deleterious, while mutants with normal (+) and small plaque formation (+/−) were considered as neutral. The set of 4041 E. coli lac repressor mutations were assayed in Markiewicz et al. (1994) by the protein’s repression activity. Mutations with phenotypes less than 20-fold (− and −/+) repression activity were considered as deleterious, while mutants with more than 20-fold (+ and +/−) repression activity were considered as neutral. The set of 336 HIV-1 protease mutations were assayed in Loeb et al. (1989) by the amount of cleavage products of Gag and Gag-Pol precursor proteins. Mutants with no (−) and some (−/+) product were considered as deleterious, while mutants with normal (+) function were considered as neutral. The set of 2314 TP53 mutations were assayed in yeast for transactivation on eight TP53 response-elements (Kato et al. 2003). Values > 100% in any assay were treated as equal to 100%. Then, we calculated the average transactivation, and we grouped the mutants with < 50% of wild-type activity as deleterious and the rest as neutral.

The 26,597 TP53 tumor mutations were obtained from the IARC TP53 database (version R14) (Petitjean et al. 2007), and they were divided into 342 recurrent mutations (at least 10 times) and 1023 nonrecurrent mutations (nine times or less). The 9347 human mutations on disease-associated genes were obtained from the UniProt database (http://www.uniprot.org/) after we roughly classified each as neutral if it was annotated by the keywords “dbSNP,” “polymorphism,” and “VAR_” or as disease-associated otherwise. From 20,343 human genes, 70% (11,995) had at least one SNP entry and only 15% (3023) had at least one disease-association entry. We selected genes with at least 10 mutations associated with the same disease, which had at most 10 mutations marked as “Uncertain pathogenicity.” For the resulting 218 genes, we inspected and corrected the rough classification and removed mutations associated with uncertain pathogenicity and sporadic cancers. The GAA missense mutations and their Pompe’s disease severity classification were obtained from http://cluster15.erasmusmc.nl/klgn/pompe/mutations.html. The 278,179 human polymorphisms were obtained from the phase 1 analysis of the 1000 Genomes Project, at http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase1/analysis_results/input_call_sets/. The somatic cancer mutations were obtained from The Cancer Genome Atlas (TCGA) at http://cancergenome.nih.gov/.

The output files of the Evolutionary Action analysis for the above proteins may be found at http://mammoth.bcm.tmc.edu/KatsonisLichtargeGR.

An Evolutionary Action server is accessible at http://mammoth.bcm.tmc.edu/EvolutionaryAction.

Supplementary Material

Supplemental Material
supp_24_12_2050__index.html (1.1KB, html)

Acknowledgments

We would like to thank Benjamin J. Bachman and Rhonald C. Lua for their technical assistance in building the Evolutionary Action server: B.J.B. contributed a visual representation of the action scores for all possible substitutions in a protein sequence and R.C.L. implemented a robust queuing system. This work is supported by the National Institutes of Health (GM079656 and GM066099) and the National Science Foundation (DBI-1356569).

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.176214.114.

Freely available online through the Genome Research Open Access option.

References

  1. The 1000 Genomes Project Consortium 2012. An integrated map of genetic variation from 1,092 human genomes. Nature 491: 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Adikesavan AK, Katsonis P, Marciano DC, Lua R, Herman C, Lichtarge O. 2011. Separation of recombination and SOS response in Escherichia coli RecA suggests LexA interaction sites. PLoS Genet 7: e1002244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Adzhubei I, Schmidt S, Peshkin L, Ramensky V, Gerasimova A, Bork P, Kondrashov A, Sunyaev S. 2010. A method and server for predicting damaging missense mutations. Nat Methods 7: 248–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Amin S, Erdin S, Ward R, Lua R, Lichtarge O. 2013. Prediction and experimental validation of enzyme substrate specificity in protein structures. Proc Natl Acad Sci 110: 45. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bodmer W, Bonilla C. 2008. Common and rare variants in multifactorial susceptibility to common diseases. Nat Genet 40: 695–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Botstein D, Risch N. 2003. Discovering genotypes underlying human phenotypes: past successes for Mendelian disease, future approaches for complex disease. Nat Genet 33: 228–237. [DOI] [PubMed] [Google Scholar]
  7. Breen MS, Kemena C, Vlasov PK, Notredame C, Kondrashov FA. 2012. Epistasis as the primary factor in molecular evolution. Nature 490: 535–538. [DOI] [PubMed] [Google Scholar]
  8. The Cancer Genome Atlas Research Network, Weinstein JN, Collisson EA, Mills GB, Mills Shaw KR, Ozenberger BA, Ellrott K, Shmulevich I, Sander C, Stuart JM. 2013. The Cancer Genome Atlas Pan-Cancer analysis project. Nat Genet 45: 1113–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Choi SC, Redelings BD, Thorne JL. 2008. Basing population genetic inferences and models of molecular evolution upon desired stationary distributions of DNA or protein sequences. Phil Trans R Soc B 363: 3931–3939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Choi M, Scholl UI, Ji W, Liu T, Tikhonova IR, Zumbo P, Nayir A, Bakkaloglu A, Ozen S, Sanjad S, et al. . 2009. Genetic diagnosis by whole exome capture and massively parallel DNA sequencing. Proc Natl Acad Sci 106: 19096–19101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chun S, Fay J. 2009. Identification of deleterious mutations within three human genomes. Genome Res 19: 1553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Coyne JA, Orr HA. 1998. The evolutionary genetics of speciation. Phil Trans R Soc B 353: 287–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dorfman R, Nalpathamkalam T, Taylor C, Gonska T, Keenan K, Yuan X, Corey M, Tsui L, Zielenski J, Durie P. 2010. Do common in silico tools predict the clinical consequences of amino-acid substitutions in the CFTR gene? Clin Genet 77: 464–473. [DOI] [PubMed] [Google Scholar]
  14. Edgar RC. 2004. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res 32: 1792–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Erdin S, Ward R, Venner E, Lichtarge O. 2010. Evolutionary trace annotation of protein function in the structural proteome. J Mol Biol 396: 1451–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Eyre-Walker A, Keightley PD. 2007. The distribution of fitness effects of new mutations. Nat Rev Genet 8: 610–618. [DOI] [PubMed] [Google Scholar]
  17. Fisher RA. 1930. The genetical theory of natural selection. Oxford University Press, Oxford, UK. [Google Scholar]
  18. Grahnen JA, Nandakumar P, Kubelka J, Liberles DA. 2011. Biophysical and structural considerations for protein sequence evolution. BMC Evol Biol 11: 361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hartl DL, Taubes CH. 1996. Compensatory nearly neutral mutations: selection without adaptation. J Theor Biol 182: 303–309. [DOI] [PubMed] [Google Scholar]
  20. Henikoff S, Henikoff J. 1992. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci 89: 10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hicks S, Wheeler DA, Plon SE, Kimmel M. 2011. Prediction of missense mutation functionality depends on both the algorithm and sequence alignment employed. Hum Mutat 32: 661–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kato S, Han S, Liu W, Otsuka K, Shibata H, Kanamaru R, Ishioka C. 2003. Understanding the function–structure and function–mutation relationships of p53 tumor suppressor protein by high-resolution missense mutation analysis. Proc Natl Acad Sci 100: 8424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Keightley PD. 2012. Rates and fitness consequences of new mutations in humans. Genetics 190: 295–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kleinman CL, Rodrigue N, Lartillot N, Philippe H. 2010. Statistical potentials for improved structurally constrained evolutionary models. Mol Biol Evol 27: 1546–1560. [DOI] [PubMed] [Google Scholar]
  25. Koshi JM, Goldstein RA. 1995. Context-dependent optimal substitution matrices. Protein Eng 8: 641–645. [DOI] [PubMed] [Google Scholar]
  26. Kroos M, Pomponio RJ, van Vliet L, Palmer RE, Phipps M, Van der Helm R, Halley D, Reuser A. 2008. Update of the Pompe disease mutation database with 107 sequence variants and a format for severity rating. Hum Mutat 29: E13–E26. [DOI] [PubMed] [Google Scholar]
  27. Lichtarge O, Bourne H, Cohen F. 1996. An evolutionary trace method defines binding surfaces common to protein families. J Mol Biol 257: 342–358. [DOI] [PubMed] [Google Scholar]
  28. Lichtarge O, Yamamoto KR, Cohen FE. 1997. Identification of functional surfaces of the zinc binding domains of intracellular receptors. J Mol Biol 274: 325–337. [DOI] [PubMed] [Google Scholar]
  29. Livingstone CD, Barton GJ. 1993. Protein sequence alignments: a strategy for the hierarchical analysis of residue conservation. Comput Appl Biosci 9: 745–756. [DOI] [PubMed] [Google Scholar]
  30. Loeb D, Swanstrom R, Everitt L, Manchester M, Stamper S, Hutchison C. 1989. Complete mutagenesis of the HIV-1 protease. Nature 340: 397–400. [DOI] [PubMed] [Google Scholar]
  31. Losos JB, Arnold SJ, Bejerano G, Brodie E III, Hibbett D, Hoekstra HE, Mindell DP, Monteiro An, Moritz C, Orr HA. 2013. Evolutionary biology for the 21st century. PLoS Biol 11: e1001466. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lupski JR, Reid JG, Gonzaga-Jauregui C, Rio Deiros D, Chen DCY, Nazareth L, Bainbridge M, Dinh H, Jing C, Wheeler DA. 2010. Whole-genome sequencing in a patient with Charcot–Marie–Tooth neuropathy. N Engl J Med 362: 1181–1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Madabushi S, Yao H, Marsh M, Kristensen DM, Philippi A, Sowa ME, Lichtarge O. 2002. Structural clusters of evolutionary trace residues are statistically significant and common in proteins. J Mol Biol 316: 139–154. [DOI] [PubMed] [Google Scholar]
  34. Madabushi S, Gross AK, Philippi A, Meng EC, Wensel TG, Lichtarge O. 2004. Evolutionary trace of G protein-coupled receptors reveals clusters of residues that determine global and class-specific functions. J Biol Chem 279: 8126–8132. [DOI] [PubMed] [Google Scholar]
  35. Markiewicz P, Kleina L, Cruz C, Ehret S, Miller J. 1994. Genetic studies of the lac repressor. XIV. Analysis of 4000 altered Escherichia coli lac repressors reveals essential and non-essential residues, as well as “spacers” which do not require a specific sequence. J Mol Biol 240: 421. [DOI] [PubMed] [Google Scholar]
  36. Mayfield JA, Davies MW, Dimster-Denk D, Pleskac N, McCarthy S, Boydston EA, Fink L, Lin XX, Narain AS, Meighan M, et al. . 2012. Surrogate genetics and metabolic profiling for characterization of human disease alleles. Genetics 190: 1309–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. McCarthy MI, Hirschhorn JN. 2008. Genome-wide association studies: potential next steps on a genetic journey. Hum Mol Genet 17: R156–R165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mihalek I, Res I, Lichtarge O. 2004. A family of evolution-entropy hybrid methods for ranking protein residues by importance. J Mol Biol 336: 1265–1282. [DOI] [PubMed] [Google Scholar]
  39. Nei M. 2007. The new mutation theory of phenotypic evolution. Proc Natl Acad Sci 104: 12235–12242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Ng P, Henikoff S. 2001. Predicting deleterious amino acid substitutions. Genome Res 11: 863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Ng PC, Levy S, Huang J, Stockwell TB, Walenz BP, Li K, Axelrod N, Busam DA, Strausberg RL, Venter JC. 2008. Genetic variation in an individual human exome. PLoS Genet 4: e1000160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ohta T. 1992. The nearly neutral theory of molecular evolution. Annu Rev Ecol Syst 23: 263–286. [Google Scholar]
  43. Orr HA. 2005. The genetic theory of adaptation: a brief history. Nat Rev Genet 6: 119–127. [DOI] [PubMed] [Google Scholar]
  44. Overington J, Donnelly D, Johnson MS, Sali A, Blundell TL. 1992. Environment-specific amino acid substitution tables: tertiary templates and prediction of protein folds. Protein Sci 1: 216–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Pei J, Grishin NV. 2001. AL2CO: calculation of positional conservation in a protein sequence alignment. Bioinformatics 17: 700–712. [DOI] [PubMed] [Google Scholar]
  46. Petitjean A, Mathe E, Kato S, Ishioka C, Tavtigian S, Hainaut P, Olivier M. 2007. Impact of mutant p53 functional properties on TP53 mutation patterns and tumor phenotype: lessons from recent developments in the IARC TP53 database. Hum Mutat 28: 622–629. [DOI] [PubMed] [Google Scholar]
  47. Rennell D, Bouvier S, Hardy L, Poteete A. 1991. Systematic mutation of bacteriophage T4 lysozyme. J Mol Biol 222: 67–86. [DOI] [PubMed] [Google Scholar]
  48. Rodriguez G, Yao R, Lichtarge O, Wensel T. 2010. Evolution-guided discovery and recoding of allosteric pathway specificity determinants in psychoactive bioamine receptors. Proc Natl Acad Sci 107: 7787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Shee C, Gibson JL, Rosenberg SM. 2012. Two mechanisms produce mutation hotspots at DNA breaks in Escherichia coli. Cell Rep 2: 714–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Smith JM.1970. Natural selection and the concept of a protein space. Nature 225: 563–564 [DOI] [PubMed] [Google Scholar]
  51. Soyer OS, Dimmic MW, Neubig RR, Goldstein RA. 2003. Dimerization in aminergic G-protein-coupled receptors: application of a hidden-site class model of evolution. Biochemistry 42: 14522–14531. [DOI] [PubMed] [Google Scholar]
  52. Stone E, Sidow A. 2005. Physicochemical constraint violation by missense substitutions mediates impairment of protein function and disease severity. Genome Res 15: 978–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Suzek BE, Huang H, McGarvey P, Mazumder R, Wu CH. 2007. UniRef: comprehensive and non-redundant UniProt reference clusters. Bioinformatics 23: 1282–1288. [DOI] [PubMed] [Google Scholar]
  54. Valdar WS. 2002. Scoring residue conservation. Proteins 48: 227–241. [DOI] [PubMed] [Google Scholar]
  55. Ward RM, Venner E, Daines B, Murray S, Erdin S, Kristensen DM, Lichtarge O. 2009. Evolutionary Trace Annotation Server: automated enzyme function prediction in protein structures using 3D templates. Bioinformatics 25: 1426–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Wilkins AD, Venner E, Marciano DC, Erdin S, Atri B, Lua RC, Lichtarge O. 2013. Accounting for epistatic interactions improves the functional analysis of protein structures. Bioinformatics 29: 2714–2721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Wright S.1932. The roles of mutation, inbreeding, crossbreeding, and selection in evolution. In Proceedings of the 6th International Congress of Genetics, Vol. 1, pp. 356–366. Genetics Society of America, Ithaca, NY. [Google Scholar]
  58. Yao H, Kristensen D, Mihalek I, Sowa M, Shaw C, Kimmel M, Kavraki L, Lichtarge O. 2003. An accurate, sensitive, and scalable method to identify functional sites in protein structures. J Mol Biol 326: 255–261. [DOI] [PubMed] [Google Scholar]
  59. Yao H, Mihalek I, Lichtarge O. 2006. Rank information: a structure-independent measure of evolutionary trace quality that improves identification of protein functional sites. Proteins 65: 111–123. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
supp_24_12_2050__index.html (1.1KB, html)
supp_gr.176214.114_Supplemental_Material.pdf (301.1KB, pdf)

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES