Abstract
Bone strains resulting from physical activity are thought to be a primary driver of bone adaptation, but cannot be directly noninvasively measured. Because bone adapts nonuniformly, physical activity may make an important independent structural contribution to bone strength that is independent of bone mass and density. Our objective was to create and validate methods for subject-specific finite element (FE) model generation that would accurately predict the surface strains experienced by the distal radius during an in vivo loading task, and to apply these methods to a group of 23 women age 23-35 to examine variations in strain, bone mass and density, and physical activity. Four cadaveric specimens were experimentally tested and specimen-specific FE models were developed to accurately predict periosteal surface strains (Root mean square error=16.3%). In the living subjects, when a 300 N load was simulated, mean strains were significantly inversely correlated with BMC (r=−0.893), BMD (r=−0.892) and physical activity level (r=−0.470). Although the group of subjects was relatively homogenous, BMD varied by two-fold (range: 0.19 – 0.40 g/cm3) and mean energy-equivalent strain varied by almost six-fold (range: 226.79 – 1328.41 με) with a simulated 300 N load. In summary, we have validated methods for estimating surface strains in the distal radius that occur while leaning onto the palm of the hand. In our subjects, strain varied widely across individuals, and was inversely related to bone parameters that can be measured using clinical CT, and inversely related to physical activity history.
Keywords: cadaver testing, strain gage, finite element, bone, human, bone adaptation, physical activity
Introduction
Fractures are a common consequence of falls in older adults that occur when the applied load exceeds bone strength. Bone strength is influenced by extrinsic factors such as physical activity and the bone’s habitual mechanical loading environment. Frost proposed that bone adaptation occurs to maintain strains within a particular biological set point (Frost, 2003). Consistent with this theory, prospective in vivo animal loading models have shown that mechanical loads eliciting strain above a specific threshold initiate bone formation that improves bone strength (e.g., Turner et al., 1991; Gross et al., 1997). In growing children, exercise that loads the skeleton leads to long-term increases in bone mineral content (BMC; Gunter et al., 2008). Mechanical loading causes measures of bone strength and stiffness to increase more than measures of bone mass or density (Miller et al., 2007). This implies that physical activity may make an important structural contribution to bone strength independent of these measures. Based on this evidence, exercise-based interventions have been proposed to maintain and improve bone strength in older adults (Gomez-Cabello et al., 2012).
Although it is understood that adaptation is driven by mechanical strain, or some consequence thereof, a direct relationship between the adaptive response and mechanical strain has not been quantified in humans. This is partly due to difficulties in non-invasively quantifying bone strain. External forces and accelerations have been proposed as surrogate measures of strain (Ahola et al., 2010, Weeks and Beck, 2008); however, the relationship between external force and bone strain is often difficult to interpret. In addition to the applied load (i.e., external and muscle contractile force), strain is affected by bone size, shape, mineral distribution, and material properties. Biological variation in these parameters is large and experimentally measured strains vary widely (Földhazy et al., 2005). The ability to measure or accurately predict bone strain non-invasively could contribute towards the development and evaluation of personalized exercise programs to improve bone health and reduce the occurrence of fractures.
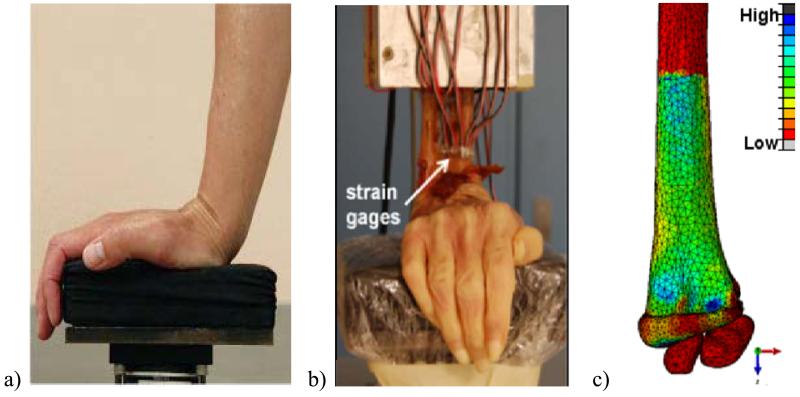
We have developed an in vivo loading paradigm to prospectively study the interaction between strain and bone adaptation in humans (Troy et al., 2013). The loading task involves leaning on to the palm of the hand with the wrist extended to apply an axial force through the radius (Figure 1a). As a practical matter, subjects are assigned a target force, however, to understand the strain/adaptation relationship it is necessary to obtain some measure of in vivo strain within the radius and ideally, to manipulate strain directly. Subject-specific finite element (FE) models have been successfully used to predict bone strains during specific loading scenarios (e.g., Keyak et al., 1993; Schileo et al., 2008). The accuracy of such models depends on factors such as the accuracy with which individual anatomic features and boundary conditions are replicated, and the equations chosen to relate bone density to elastic modulus (Edwards and Troy, 2011).
Figure 1.
a) Targeted loading protocol, b) Experimental testing setup, c) Minimum Principal Strain map of the finite element model.
The objective of this study was to validate methods for generating subject-specific FE models to accurately predict the surface strains in the distal radius while leaning onto the palm of the hand with the wrist extended. The methods were then used to predict in vivo strains at the distal radius of subjects performing the loading task. We expected strain to vary inversely with bone measures and physical activity history.
Methods
Finite element model validation
Specimens
Four female cadaveric forearms with hand intact (age: 82–89 years) were obtained through anatomical gift. Specimens were freshly-frozen and stored at −20°C but were thawed to room temperature for: 1) Computed tomography (CT) data acquisition; 2) dissection and potting; and 3) strain gage application and mechanical testing. The distal 12 cm of the forearms were imaged with CT (BrightSpeed; GE Medical Systems, Milwaukee, WI, 120 kV, 180 mA, voxel size: 0.234 × 0.234 × 0.625 mm) and reconstructed using a low frequency convolution kernel. A calibration phantom (QRM, Moehrendorf, Germany) with known calcium hydroxyapatite equivalent concentrations was included in each scan and used to establish the following average relationship between Hounsfield units (Hu) and hydroxyapatite equivalent density (ρha) in g/cm3:
Specimen Preparation and Mechanical testing
The details of the cadaver mechanical testing have been previously reported (Troy et al., 2013). Briefly, soft tissue proximal to the wrist joint capsule was removed and a radioulnar osteotomy was performed 14 cm proximal to the distal dorsal tubercle. The proximal 8 cm of the forearms was potted in polymethyl-methacrylate and six strain gage rosettes (TS1N-K120M-PK06-LE, Micro-Flextronics Ltd, Coleraine, N. Ireland) were adhered circumferentially to the periosteal surface. Three gages were mounted distally just proximal to the distal dorsal tubercle and three gages were mounted 3 cm proximal to the distal gage locations (Figure 1b).
Specimens were aligned on a uniaxial materials testing machine (MiniBionix 858, MTS Systems, Eden Prairie, MN) with the radius and ulna oriented vertically and the palm of the hand placed on a padded load cell with the wrist in 80 degrees extension (Figure 1b). The actuator was driven at a fixed displacement rate of 0.3 mm/sec to a load of 300 N. This magnitude was selected to create periosteal surface strains of 1000-2000 με, consistent with other in vivo loading models (Srinivasan et al, 2002). Force, displacement, and strain gage recordings were collected at 100 Hz.
FE modeling
CT images were segmented by a single investigator (VAB) to identify periosteal surfaces of the radius, scaphoid, and lunate, using a density threshold of ρha≥0.165 g/cm3. This value best visually defined the surface and minimized the need to manually edit voxels. Surfaces were used to create FE geometry of the three bones using Mimics v15.0 (Materialise, Leuven, Belgium). Articular cartilage was created by expanding the distal surface of the radius and performing a Boolean subtraction with the intersecting carpal bones so that the lunate and scaphoid were seated within the cartilage (cartilage thickness: 1.4±0.4 mm). The geometries were exported to 3Matic v7.0 (Materialise, Leuven, Belgium), and a quadratic tetrahedral element mesh was generated for each specimen. For all models, the scaphoid and lunate were meshed with a mean element volume of 0.5 mm3, and cartilage with mean element volume of 0.25 mm3. A mesh convergence analysis was performed for the radius with mean element volumes of 0.25, 0.5, 0.75, or 1.25 mm3.
Three cartilage material properties and four density-elasticity relationships were investigated. Cartilage was defined as either 1) linear elastic with modulus (E)=10 MPa and Poisson’s ratio (ν)=0.45, 2) linear elastic with E=50 MPa and ν=0.45, or 3) neo-Hookean hyperelastic with E=10 MPa and ν=0.45 (Anderson et al., 2008; Armstrong et al., 1984). The radius was assigned inhomogeneous linearly-isotropic material properties based on four previously established density-elasticity relationships:
| (i) |
| (ii) |
| (iii) |
| (iv) |
where E is the modulus expressed in MPa, ρash (ash density) and ρapp (apparent density) are expressed in g/cm3. Calcium hydroxyapatite equivalent density (ρha) was converted to ρapp and ρash using:
Each element density was assigned as the mean of its enclosed voxels, and then grouped by density into 200 evenly spaced bins. Elements within each bin were assigned material properties based on the bin mean density. Bins had ranges of approximately 150 MPa, and all materials were assigned ν= 0.4 (Reilly et al., 1975; Keyak et al., 1993). Elements with ρha < 0.01 g/cm3 (located primarily within the medullary canal) were reassigned a value of 0.01 g/cm3 to prevent negative elastic modulus values. To account for partial volume effects at the periosteal surface, the material assignment was based on an area corresponding to the segmented radius eroded by 1 voxel. The <0.1% of elements that were entirely outside this volume were assigned ρha=0.01 g/cm3 (i.e they were effectively eliminated from the analysis).
The FE analyses were performed using Abaqus 6.10 (Simulia, Providence, RI). The proximal nodes in the radius at the potting location were fully constrained. The scaphoid and lunate were rotated about their centroids in the anterior-posterior direction by 70° and 53° to simulate a wrist extension of 80° (Moojen et al., 2002; Kobayashi et al., 1997; Wolfe et al., 2000). Radio-carpal ligaments and the wrist joint capsule were assumed to keep the carpal bones seated within the cartilage. Hence, a tied interface contact model was defined wherein the carpal bones could not slide or rotate once they were seated into the cartilage. A ramped force was applied to the centroid of the scaphoid (180N) and lunate (120N) based on the assumption that 60% of the load transmitted through the wrist is borne by the scaphoid (Majima et al., 2007). The line of action of the resultant force vector was determined for each specimen using unsymmetrical beam theory based on proximal strain gage and CT information (Edwards and Troy, 2012).
Application of the Model
Twenty-three healthy women ages 21-35 (22.7±3.5 years, height 156±6 cm, mass 60±7 kg and BMI 18.5-25) were recruited for this institutionally approved study, which was part of a larger long-term experiment (Troy et al., 2013). All subjects gave written informed consent prior to participation. Subjects were generally physically active, but none at the collegiate or professional level or in sports specific to the upper extremities such as tennis. Seventeen of the subjects completed a validated bone loading history survey, the Bone Physical Activity Questionnaire (BPAQ; Weeks and Beck, 2008), which produces a unitless score that ranges from 0 (no bone loading activity) to over 120. Since the anatomic site of interest was the distal radius, an upper-extremity BPAQ was also scored by including only the subset of activities that would load the upper extremities (e.g. volleyball but not running). Clinical CT data were collected on the non-dominant arm of each participant in an identical fashion to the cadaver specimens. The data were analyzed quantitatively using methods previously described (Troy et al., 2013) to measure the following three-dimensional parameters for a 9.375 mm “ultra-distal” region immediately proximal to the subchondral plate (automatically identified as the location of maximum cross sectional area): integral bone volume (BV; cm3, defined as the volume enclosed by the periosteal surface), volumetric bone mineral density (BMD; g/cm3, the average ρha of the volume), and bone mineral content (BMC; g). A laboratory precision study in which ten scans were randomly rotated in three dimensions four times each before analysis yielded root-mean squared coefficients of variance (CV) of 0.9%, 0.9% and 0.5% for ultra-distal BV, BMC, and BMD, respectively. As an additional measure of precision, a small tube packed with powdered hydroxyapatite was included in 45 scans acquired over a 28 week period, and was found to have a density CV of 1.38%. The CT data were also the basis for FE models that were created using the parameters that produced the most accurate results based on cadaver testing. For each subject, mean and median values for energy equivalent strain were calculated at the ultra-distal region for an applied force of 300N.
where E=elastic modulus, and U=strain energy density, εn and σn are the strain and stress values in the principal direction. Energy equivalent strain was chosen because it is a single dimensionless scalar quantity that has been associated with bone adaptation (e.g., Szwedowski et al., 2012). FE models generated from the precision study data mentioned above illustrated a root mean squared CV of 0.3% for energy equivalent strain.
Statistical analysis
Descriptive statistics were calculated for all variables to assess normality. For FE convergence analysis, strain energy density (SED), magnitude of peak displacement, and principal strains for a 5 mm transverse section within the ultra-distal region were calculated for each element size for all specimens. To determine the sensitivity of the model to cartilage material properties, principal strains were calculated for all elements within the same 5 mm section. To determine the best density-elasticity relationship, FE model predicted strains were compared to the experimentally-measured strains. Strains in the elements corresponding to each rosette location were transformed into the local surface coordinate system. Maximum and minimum principal strains were calculated at the surface (Figure 1c), and the values averaged for all elements within each rosette location, yielding 12 values for comparison per specimen (maxima and minima at each gage location). The predicted and measured strains were compared using a mixed effects linear model wherein specimen was treated as a repeated measure. Slope, intercept, root mean square error (RMSE), and maximum error were assessed.
The FE methods that produced the most accurate results were applied to each participant in the human study. To examine the relationships between in vivo predicted strain, bone parameters, and physical activity history, correlations were calculated for the BV, BMD, BMC, and BPAQ scores, versus mean ε within the ultra-distal radius. Spearman’s correlations were used for non-normally distributed variables. To evaluate the scatter in bone parameters versus strain measures, CV and ratio of maximum/minimum were calculated. Finally, to determine the degree to which bone parameters and physical activity were predictive of bone strain, we examined a stepwise linear regression model with BV, BMD, BMC, and BPAQ as potential explanatory variables, and dependent variable of mean ε.
Results
Finite element modeling validation
The mean principal strains recorded at each of the strain gage locations have been previously reported in detail (Troy et al., 2013). Briefly, strains ranged from −2601 to 1427 με with the highest strains at the distal radius on the dorsal surface near the ulna. For the convergence analysis, the two highest resolution models (0.25 and 0.5 mm3/element) showed only a 2% difference in SED, whereas the two coarser models had SED 11% and 42% lower. All other measured parameters converged at either 0.5 or 1.0 mm3/element size. Based on these results an element size of 0.5mm3 (35508 ± 3375 elements) was selected.
The principal strains within the radius were relatively insensitive to cartilage material properties. The within-specimen mean principal strain values for the 5 mm test section varied by 0.7 to 6.3% with the differing definitions, with linear elastic E=10 MPa, ν=0.45 producing slightly higher strains than the other two definitions. Based on these results and physiologic relevance, the hyperelastic material definition was selected.
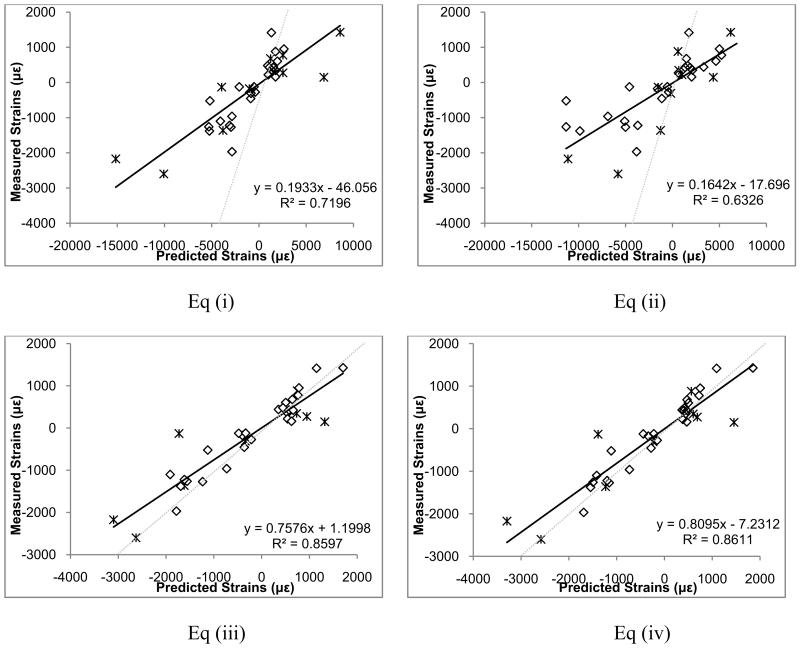
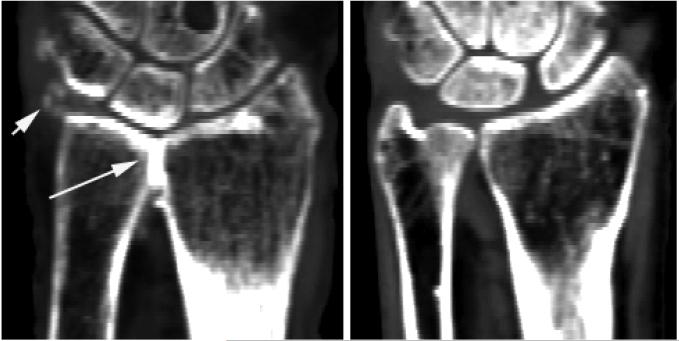
Predicted versus measured principal strains for the four density-elasticity equations are shown in Figure 2, with Eq (iv) producing the best results. These models had a slope of 0.81 (95% CI: 0.70, 0.92) and an intercept of −7.3 (95% CI: −135.4, 120.9) and RMSE of 424.3 με (Table 1). One specimen illustrated substantial error (RMSE=713.8 με) relative to the other three specimens. Visual examination of the specimen and its radiographic data suggested that the radius and ulna were fused at the distal radio-ulnar joint, possibly due to osteoarthritis (Figure 3). This assessment was confirmed by a rheumatologist who viewed the scan. Using Eq (iv), exclusion of this specimen resulted in a slope of 0.98 (95% CI: 0.88, 1.09), intercept of 51.1 (95% CI: −39.1, 141.3), and RMSE of 219.6 με (11.1% of maximum measured strain). Based on these results, Eq. (iv) was selected for application.
Figure 2.
Predicted versus measured principal strains at 300 N for the four tested density-elasticity equations. * symbols correspond to points of osteoarthritic subject. Dashed lines show a y=x line, which would indicate a perfect prediction.
Table 1.
Slope, intercept, root mean square error (RMSE), and RMSE as a percentage of the maximum absolute measured strain, for the four density-elasticity relationships.
| Eq (i) | Eq (ii) | Eq (iii) | Eq (iv) |
Eq (iv) excluding subject with OA |
|
|---|---|---|---|---|---|
| slope | 0.193a (95% CI: 0.151 0.236) |
0.164a (95% CI: 0.12 0.209) |
0.758a (95% CI: 0.649 0.866) |
0.809a (95% CI: 0.694 0.925) |
0.984ns (95% CI: 0.874 1.094) |
| Intercept | −46.1ns (95% CI: −233.1 140.9) |
−17.7ns (95% CI: −234 198.6) |
1.2ns (95% CI: −132 134.5) |
−7.2ns (95% CI: −139.5 125.1) |
51.1ns (95% CI: −43.4 145.5) |
| RMSE (ue) | 3557.4 | 4117.2 | 472.3 | 424.3 | 219.6 |
| RMSE (%) | 136.8 | 158.4 | 18.2 | 16.3 | 11.1 |
Significantly different,
not significantly different from 1 (slope) or 0 (intercept)
Figure 3.
Coronal CT image of the arthritic specimen (left) compared to another cadaver specimen (right). The arrows highlight areas of increased mineralization in the arthritic specimen, in which radius and ulna appear to be fused.
Application of the Model
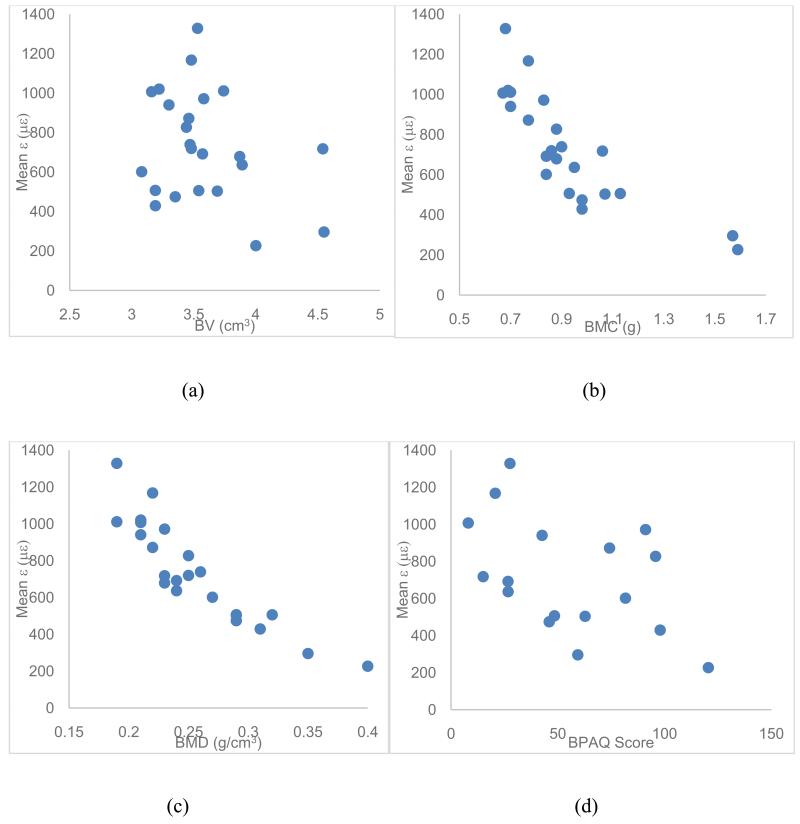
In vivo predicted strains at 300 N of applied load, bone mineral parameters, and physical activity data are summarized in Table 2. The most common physical activities reported by subjects were walking and running. BV, BMC, and upper extremity BPAQ scores were non-normally distributed (Shapiro-Wilk p≤0.008). The strains were negatively correlated with BMD, BMC, and total BPAQ score (Table 3), but BMC and BMD exhibited considerably less scatter than mean ε. CVs were 0.26, 0.20, and 0.38, and maximum/minimum ratios were 2.37, 2.10, and 5.85, for BMC, BMD, and mean ε, respectively (Figure 4). BMD alone explained 79.5% of the variance in mean ε. Both BPAQ and BMC were significantly correlated with BMD (r=0.618 p=0.008 and r=0.881 p<0.001, respectively).
Table 2.
Mean and standard deviations of mean and median energy equivalent strain, BV, BMC, and BMD calculated at the ultra-distal radius, and Total and Upper Extremity BPAQ scores.
| N | Mean | Std. Deviation | Range | |
|---|---|---|---|---|
| Mean Energy Equivalent Strain (με) | 23 | 733.74 | 277.98 | 226.79 – 1328.41 |
| BV (cm3) | 23 | 3.58 | 0.39 | 3.08 – 4.55 |
| BMD (g/cm3) | 23 | 0.26 | 0.05 | 0.19 – 0.40 |
| BMC (g) | 23 | 0.93 | 0.24 | 0.67 – 1.59 |
| Total BPAQ | 17 | 55.5 | 33.4 | 8.1 – 120.5 |
| Upper Extremity BPAQ | 17 | 28.1 | 29.4 | 0.2 – 101.6 |
Table 3.
Correlation coefficients for the bone mineral parameters, physical activity data, and energy equivalent strain. Pearson correlations were used for normally distributed variables, and Spearman’s ranked correlations for non-normal variables. N=23 for all comparisons except for those with BPAQ or Upper Extremity BPAQ, where n=17.
| BMD | BMC# | Energy Equiv. Strain |
BPAQ | Upper Extremity BPAQ# |
|
|---|---|---|---|---|---|
| BV# | 0.096 | 0.463* | −0.199 | −0.061 | 0.017 |
| BMD | 0.881** | −0.892** | 0.618* | 0.328 | |
| BMC# | −0.893** | 0.377 | 0.189 | ||
| Energy Equiv. Strain |
−0.470* | −0.299 | |||
| BPAQ | 0.610* |
non-normally distributed variable
p<0.05
p<0.01
Figure 4.
(a) BV versus ε, (b) BMC versus ε, (c) BMD versus ε, and (d) BPAQ versus ε for the subjects who participated in the experiment.
Discussion
Non-invasive subject-specific methods to quantify bone strain are necessary to understand the mechanical environment experienced by bone during physical activity. Here, we validated methods for subject-specific FE model generation to predict the surface strains experienced by the distal radius when leaning onto the palm of the hand. The methods were applied to a group of subjects to examine the relationship between bone parameters and strain.
Of the four density-elasticity relations analyzed, Eq. (iv) most accurately predicted experimentally measured strains. However, this relationship over-predicted strains by an average of 418 με in one specimen believed to be osteoarthritic. The discrepancy suggests that partial joint fusion may have redirected force through the ulna, which was not modeled here. A recent study estimated that 2% of the force applied to the palm of the hand was transmitted through the ulna in healthy extended wrists (Majima et al., 2008). The clinical consequence of altered load transmission pathways is not known.
Previous in vitro FE validation studies have shown similar agreement to that of the present study, with r=0.77 (Keyak et al., 1993), r = 0.91 (Taddei et al., 2006), r = 0.90 (Gupta et al., 2004), r = 0.91 (Anderson et al., 2005), and r = 0.95 (Schileo et al., 2007). Our results can be compared with an earlier model validation of the human distal radius from our group, in which periosteal surface strains were predicted with r = 0.90 and RMSE = 13.4% (Edwards and Troy, 2012). Our previous study simulated a fall onto the hands, while the present study built upon this knowledge to estimate surface strains during our loading task in an experimental population. The present validation was limited by a single boundary condition, small number of specimens, and the omission of tendons, ligaments, and other soft tissue.
A large range of radius strains was predicted in the experimental subjects (Table 2). Although subjects were relatively homogenous in terms of age and BMI, they came from a variety of genetic backgrounds, which has been related to variation in areal BMD (Pocock et al., 1987). In the present group, bone measurements varied by a factor of two and strain measurements varied by nearly six. The surface strains estimated here were lower than those measured in vivo during a push-up (Földhazy et al., 2005). This may be attributed to differences in measurement site and methods, subject age, and boundary conditions. In our data set, predicted strains were strongly and negatively correlated to BMD and BMC. Basic mechanics dictate that strain should decrease as area and modulus increase. However, strain cannot be predicted based on BMD and area alone, since bone is an inhomogeneous medium with complex geometry. A strength of the modeling procedure used here is that the effects of bone structure are explicitly accounted for. Thus, while bone parameters are closely related to strain, variation in these parameters may underestimate the variation in strain.
One explanation for large variation in observed strain compared to BMD is that bone mass was distributed in a mechanically advantageous manner in those subjects who were most active. At cortical sites physical activity has been associated with increased bone area (humerus; Kontulainen et al., 2003) and moment of inertia but not bone density (tibia; Milgrom et al., 2012). However, at trabecular sites such as the distal radius, increased cortical thickness and trabecular density may dominate the response (Kontulainen et al., 2003). Related, moments of inertia increase exponentially with bone size, and bones with higher BMC tend to be larger.
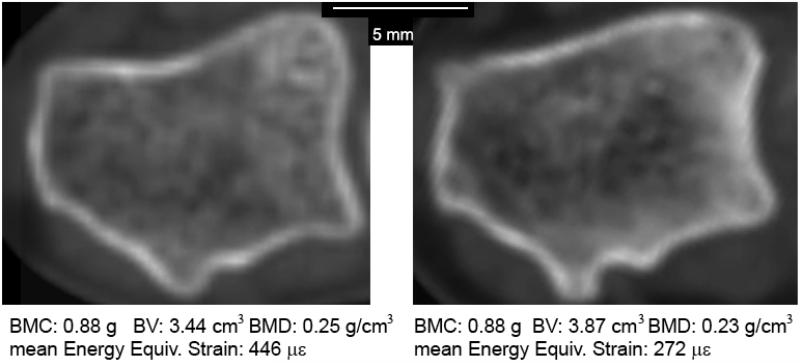
In the present data set, BPAQ was negatively correlated with radius strain, although it was not sufficiently independent from BMD to be included in the stepwise regression. The BPAQ is limited by the design of the survey, which assigns weighting factors to activities based on ground reaction forces, which may not be relevant to upper extremity bone loading. Thus, the present analysis may underestimate the degree to which physical activity history can explain variance in radius strain. Physical activity may cause changes to bone structure (primarily by affecting the distribution of mineral within the bone and through subtle changes in bone geometry) without increasing BMC or average BMD. Figure 5 illustrates a counterintuitive example of two radii with equal BMC, with the less dense bone having 40% lower strain. Mechanically and metabolically, it is logical that bone adaptation be directed towards a more efficient structure rather than increased BMC or BMD.
Figure 5.
Cross-sections of the distal radius 0.625 mm proximal to the subchondral plate from two subjects with identical BMC. The radius on the right had strains that were only 60% of that on the left for a simulated 300 N load.
The variability in strain observed here highlights a key limitation of previously reported exercise-based interventions targeting bone health. If strain is a key driver of bone adaptation and subjects are assigned force-based tasks (such as in resistance training), it is not surprising that inconsistent responses would be observed (e.g., Bailey and Brooke-Wavell, 2010; Rantalainen et al., 2011). Indeed, one might expect that those individuals with the weakest bones would experience the largest strains and, therefore, benefit the most from the intervention.
This study has limitations related to small sample size and measurement methods. The cadaver donors were older than the subjects participating in the experiment, however, age-related changes in bone structure and density are explicitly accounted for in the FE models. The experiment involved exposing healthy subjects to ionizing radiation, with an effective dose of 3 mrem (Biswas et al., 2009), or 3% of the recommended maximum annual voluntary exposure. Nevertheless, any exposure involves risk, and for this reason a rigorous in vivo repeatability study for the QCT measures was not performed. The laboratory precision study, while imperfect, demonstrates our methods to be both objective and repeatable, with all CVs less than 1.4%.
In summary, we have validated methods for generating subject-specific FE models for the purpose of estimating surface strains in the distal radius that occur while leaning onto the palm of the hand. The methods allow models to be objectively created and are suitable for application to larger clinical data sets. We applied these techniques to the radii of subjects participating in a bone-loading experiment and demonstrated that strain varies widely across individuals, and is inversely related to bone parameters that can be measured using clinical CT, and inversely related to physical activity history. Bone strain is thought to be a primary driver of bone adaptation and is highly variable between individuals for a given loading scenario. The ability to predict bone strain non-invasively is important in understanding the strain/adaptation process in humans and we plan to use these methods to assign strain-based activities to study the relationship between strain environment and bone adaptation in humans. Eventually, these techniques may facilitate the development of personalized exercise prescriptions for bone health.
Acknowledgements
Research reported in this publication was supported by NIAMS of the National Institutes of Health under award number R01AR063691, and by the University of Illinois at Chicago Department of Kinesiology and Nutrition. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Joshua Johnson, PhD, assisted with the repeatability study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References Cited
- Ahola R, Korpelainen R, Vainionpaa A, Jamsa T. Daily impact score in long-term acceleration measurements of exercise. Journal of Biomechanics. 2010;43:1960–1964. doi: 10.1016/j.jbiomech.2010.03.021. [DOI] [PubMed] [Google Scholar]
- Anderson AE, Ellis BJ, Maas SA, Peters CL, Weiss JA. Validation of finite element predictions of cartilage contact pressure in the human hip joint. Journal of Biomechanical Engineering. 2008;130(5):051008. doi: 10.1115/1.2953472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson DD, Deshpande BR, Daniel TE, Baratz ME. A three-dimensional finite element model of the radiocarpal joint: distal radius fracture step-off and stress transfer. The Iowa orthopaedic journal. 2005;25:108. [PMC free article] [PubMed] [Google Scholar]
- Armstrong CG, Lai WM, Mow VC. An analysis of the unconfined compression of articular cartilage. Journal of biomechanical engineering. 1984;106(2):165. doi: 10.1115/1.3138475. [DOI] [PubMed] [Google Scholar]
- Bailey CA, Brooke-Wavell K. Optimum frequency of exercise for bone health: randomised controlled trial of a high-impact unilateral intervention. Bone. 2010;46:1043–1049. doi: 10.1016/j.bone.2009.12.001. [DOI] [PubMed] [Google Scholar]
- Biswas D, Bible JE, Bohan M, Simpson AK, Whang PG, Grauer JN. Radiation exposure from musculoskeletal computerized tomographic scans. J Bone Joint Surg Am. 2009;91:1882–1889. doi: 10.2106/JBJS.H.01199. [DOI] [PubMed] [Google Scholar]
- Carter DR, Hayes WC. The compressive behavior of bone as a two-phase porous structure. The Journal of bone and joint surgery. American volume. 1977;59(7):954–962. [PubMed] [Google Scholar]
- Dalstra M, Huiskes R, Odgaard A, Van Erning L. Mechanical and textural properties of pelvic trabecular bone. Journal of Biomechanics. 1993;26(4):523–535. doi: 10.1016/0021-9290(93)90014-6. [DOI] [PubMed] [Google Scholar]
- Edwards WB, Troy KL. Simulating distal radius fracture strength using biomechanical tests: a modeling study examining the influence of boundary conditions. J Biomech Eng. 2011;133(11):114501. doi: 10.1115/1.4005428. [DOI] [PubMed] [Google Scholar]
- Edwards WB, Troy KL. Finite element prediction of surface strain and fracture strength at the distal radius. Med Eng Phys. 2012;34(3):290–8. doi: 10.1016/j.medengphy.2011.07.016. [DOI] [PubMed] [Google Scholar]
- Edwards WB, Schnitzer TJ, Troy KL. Torsional stiffness and strength of the proximal tibia are better predicted by finite element models than DXA or QCT. J Biomech. 2013;46(10):1655–62. doi: 10.1016/j.jbiomech.2013.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Földhazy Z, Arndt A, Milgrom C, Finestone A, Ekenman I. Exercise-induced strain and strain rate in the distal radius. J Bone Joint Surg Br. 2005;87(2):261–6. doi: 10.1302/0301-620x.87b2.14857. [DOI] [PubMed] [Google Scholar]
- Frost HM. Bone’s Mechanostat: A 2003 Update. Anat. Rec A. 2003;275A:1081–1101. doi: 10.1002/ar.a.10119. [DOI] [PubMed] [Google Scholar]
- Gómez-Cabello A, Ara I, González-Agüero A, Casajús J. Effects of Training on Bone Mass in Older Adults. Sports Medicine. 2012;42(4):301–325. doi: 10.2165/11597670-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Gross TS, Edwards JL, Mcleod KJ, Rubin CT. Strain gradients correlate with sites of periosteal bone formation. Journal of Bone and Mineral Research. 1997;12(6):982–988. doi: 10.1359/jbmr.1997.12.6.982. [DOI] [PubMed] [Google Scholar]
- Gunter K, Baxter-Jones AD, Mirwald RL, Almstedt H, Fuchs RK, Durski S, Snow C. Impact exercise increases BMC during growth: an 8-year longitudinal study. Journal of Bone and Mineral Research. 2008;23(7):986–93. doi: 10.1359/JBMR.071201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta S, van der Helm FC, Sterk JC, Van Keulen F, Kaptein BL. Development and experimental validation of a three-dimensional finite element model of the human scapula. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 2004;218(2):127–142. doi: 10.1243/095441104322984022. [DOI] [PubMed] [Google Scholar]
- Hsieh YF, Wang T, Turner CH. Viscoelastic response of the rat loading model: implications for studies of strain-adaptive bone formation. Bone. 1999;25(3):379–82. doi: 10.1016/s8756-3282(99)00181-7. [DOI] [PubMed] [Google Scholar]
- Keller TS. Predicting the compressive mechanical behavior of bone. Journal of biomechanics. 1994;27(9):1159–1168. doi: 10.1016/0021-9290(94)90056-6. [DOI] [PubMed] [Google Scholar]
- Keyak JH, Fourkas MG, Meagher JM, Skinner HB. Validation of an automated method of three-dimensional finite element modelling of bone. Journal of Biomedical Engineering. 1993;15(6):505–509. doi: 10.1016/0141-5425(93)90066-8. [DOI] [PubMed] [Google Scholar]
- Kobayashi M, Berger RA, Nagy L, Linscheid RL, Uchiyama S, Ritt M, An KN. Normal kinematics of carpal bones: a three-dimensional analysis of carpal bone motion relative to the radius. Journal of biomechanics. 1997;30(8):787–793. doi: 10.1016/s0021-9290(97)00026-2. [DOI] [PubMed] [Google Scholar]
- Kontulainen S, Sievanen H, Kannus P, Pasanen M, Vuori I. Effect of long-term impact-loading on mass, size, and estimated strength of humerus and radius of female racquet-sports players: a peripheral quantitative computed tomography study between young and old starters and controls. Journal of Bone and Mineral Research. 2003;18:352–359. doi: 10.1359/jbmr.2003.18.2.352. [DOI] [PubMed] [Google Scholar]
- Majima M, Horii E, Matsuki H, Hirata H, Genda E. Load transmission through the wrist in the extended position. The Journal of hand surgery. 2008;33(2):182–188. doi: 10.1016/j.jhsa.2007.10.018. [DOI] [PubMed] [Google Scholar]
- Milgrom C, Constantini N, Milgrom Y, Lavi D, Appelbaum Y, Novack V, Finestone A. The effect of high versus low loading on bone strength in middle life. Bone. 2012;50:865–869. doi: 10.1016/j.bone.2012.01.001. [DOI] [PubMed] [Google Scholar]
- Miller LE, Wootten DF, Nickols-Richardson SM, Ramp WK, Steele CR, Cotton JR, Carneal JP, Herbert WG. Isokinetic training increases ulnar bending stiffness and bone mineral in young women. Bone. 2007;41(4):685–9. doi: 10.1016/j.bone.2007.07.004. [DOI] [PubMed] [Google Scholar]
- Moojen TM, Snel JG, Ritt MJPF, Kauer JMG, Venema HW, Bos KE. Three-dimensional carpal kinematics in vivo. Clinical Biomechanics. 2002;17(7):506–514. doi: 10.1016/s0268-0033(02)00038-4. [DOI] [PubMed] [Google Scholar]
- Morgan EF, Bayraktar HH, Keaveny TM. Trabecular bone modulus–density relationships depend on anatomic site. Journal of biomechanics. 2003;36(7):897–904. doi: 10.1016/s0021-9290(03)00071-x. [DOI] [PubMed] [Google Scholar]
- Pockock NA, Eisman JA, Hopper JL, Yeates MG, Sambrook PN, Eberl S. Genetic Determinants of Bone Mass in Adults: A Twin Study. J Clin Invest. 1987;80:706–710. doi: 10.1172/JCI113125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reilly DT, Burstein AH. The elastic and ultimate properties of compact bone tissue. Journal of biomechanics. 1975;8(6):393–405. doi: 10.1016/0021-9290(75)90075-5. [DOI] [PubMed] [Google Scholar]
- Rantalainen T, Hoffren M, Linnamo V, Heinonen A, Komi PV, Avela J, Nindl BC. Three month bilateral hopping intervention is ineffective in initiating bone biomarker response in healthy elderly men. European Journal of Applied Physiology. 2011 doi: 10.1007/s00421-011-1849-8. [DOI] [PubMed] [Google Scholar]
- Schileo E, Dall’Ara E, Taddei F, Malandrino A, Schotkamp T, Baleani M, Viceconti M. An accurate estimation of bone density improves the accuracy of subject-specific finite element models. Journal of Biomechanics. 2008;41(11):2483–2491. doi: 10.1016/j.jbiomech.2008.05.017. [DOI] [PubMed] [Google Scholar]
- Schileo E, Taddei F, Malandrino A, Cristofolini L, Viceconti M. Subject-specific finite element models can accurately predict strain levels in long bones. Journal of biomechanics. 2007;40(13):2982–2989. doi: 10.1016/j.jbiomech.2007.02.010. [DOI] [PubMed] [Google Scholar]
- Srinivasan S, Weimer DA, Agans SC, Bain SD, Gross TS. Low-magnitude mechanical loading becomes osteogenic when rest is inserted between each load cycle. J Bone Miner Res. 2002;17:1613–1620. doi: 10.1359/jbmr.2002.17.9.1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szwedowski TD, Taylor WR, Heller MO, Perka C, Muller M, Duda GN. Generic rules of mechano-regulation combined with subject specific loading conditions can explain bone adaptation after THA. PLoS One. 2012;7(5):e36231. doi: 10.1371/journal.pone.0036231. doi: 10.1371/journal.pone.0036231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddei F, Cristofolini L, Martelli S, Gill HS, Viceconti M. Subject-specific finite element models of long bones: an in vitro evaluation of the overall accuracy. Journal of biomechanics. 2006;39(13):2457–2467. doi: 10.1016/j.jbiomech.2005.07.018. [DOI] [PubMed] [Google Scholar]
- Troy KL, Edwards WB, Bhatia VA, Bareither ML. In vivo loading model to examine bone adaptation in humans: A pilot study. Journal of Orthopaedic Research. 2013;31(9):1406–13. doi: 10.1002/jor.22388. [DOI] [PubMed] [Google Scholar]
- Turner CH, Akhter MP, Raab DM, Kimmel DB, Recker RR. A noninvasive, in vivo model for studying strain adaptive bone modeling. Bone. 1991;12(2):73–79. doi: 10.1016/8756-3282(91)90003-2. [DOI] [PubMed] [Google Scholar]
- Weeks BK, Beck BR. The BPAQ: a bone-specific physical activity assessment instrument. Osteoporosis International. 2008;19(11):1567–1577. doi: 10.1007/s00198-008-0606-2. [DOI] [PubMed] [Google Scholar]
- Wolfe SW, Neu C, Crisco JJ. In vivo scaphoid, lunate, and capitate kinematics in flexion and in extension. The Journal of hand surgery. 2000;25(5):860–869. doi: 10.1053/jhsu.2000.9423. [DOI] [PubMed] [Google Scholar]