Abstract
This study demonstrates a method for alternating current (AC) susceptibility imaging (ASI) of magnetic nanoparticles (mNPs) using low cost instrumentation. The ASI method uses AC magnetic susceptibility measurement to create tomographic images using an array of drive coils, compensation coils and fluxgate magnetometers. Using a spectroscopic approach in conjunction with ASI, a series of tomographic images can be created for each frequency measurement and is termed sASI. The advantage of sASI is that mNPs can be simultaneously characterized and imaged in a biological medium. System calibration was performed by fitting the in-phase and out-of-phase susceptibility measurements of an mNP sample with a hydrodynamic diameter of 100 nm to a Brownian relaxation model (R2 = 0.96). Samples of mNPs with core diameters of 10 and 40 nm and a sample of 100 nm hydrodynamic diameter were prepared in 0.5 ml tubes. Three mNP samples were arranged in a randomized array and then scanned using sASI with six frequencies between 425 and 925 Hz. The sASI scans showed the location and quantity of the mNP samples (R2 = 0.97). Biological compatibility of the sASI method was demonstrated by scanning mNPs that were injected into a pork sausage. The mNP response in the biological medium was found to correlate with a calibration sample (R2 = 0.97, p <0.001). These results demonstrate the concept of ASI and advantages of sASI.
Keywords: AC susceptibility, imaging, nanoparticles, modeling, spectroscopy
1. Introduction
The use of magnetic nanoparticles (mNPs) in medicine is an active area of research with several promising therapies currently under study [1, 2]. One of the most promising uses of mNPs in medicine is as an imaging contrast agent. Significant research has resulted in the development of methods such as magnetic particle imaging (MPI) [3–6], magnetic resonance imaging MRI methods such as Sweep Imaging with Fourier Transform (SWIFT) [7, 8], magnetic relaxometry (MRX) [9–17] and AC susceptibility detection [18–23]. A particularly relevant study to the present work describes the use of magnetic relaxometry and an array of SQUID sensors and drive coils to spatially localize mNPs using excitation fields in the microtesla range [9]. Magnetic nanoparticles can also be used to detect tumors using either targeted or untargeted mNPs. This approach has been demonstrated in preclinical trials of cancer detection in lymph nodes [24].
Magnetic susceptibility imaging relies on the inherent magnetic susceptibility of mNPs to provide imaging contrast. When a magnetically susceptible material is subjected to an external magnetic field H, the resulting magnetic field will be B = μ0 (H+M), where μ0 is the magnetic permeability in a vacuum, B is the magnetic induction or B-field, H is the externally applied magnetic field strength, and M is the magnetization field from the magnetic material. The magnetization field arises from the magnetically susceptible material as M = Hχv, where χv is the volume magnetic susceptibility. Although the M-field only exists inside of the magnetic material, it gives rise to additional external B-field that contributes to the magnetic field detected by a sensor such as a fluxgate magnetometer. Studying this additional B-field from the magnetically susceptible material requires that it be distinguished from the directly coupled applied magnetic field and from background noise.
We previously introduced a method that we have called susceptibility magnitude imaging (SMI) that achieves mNP imaging with an array of drive coils, fluxgate magnetometers, and compensation coils [25]. SMI scans localize and quantify mNPs with known alternating current (AC) magnetic susceptibility properties within the field of view of the system. If the supplied AC susceptibility properties of the mNPs are incorrect then SMI results will become distorted and inaccurate. The AC susceptibility imaging (ASI) method demonstrated in the present work overcomes this limitation of SMI. This use of susceptibly properties enables a new contrast type for mNP imaging that was previously not possible with SMI. In addition, using a multi-frequency approach, it is possible to implement sASI to enable yet another contrast type in which it is possible to classify mNPs within the imaging zone.
AC susceptibility has several important applications in biological imaging. It has been shown that the AC susceptibility contrast of mNPs changes between bound and unbound states [20, 26–29]. AC susceptibility can be exploited to distinguish multiple mNPs situated inside an imaging region [30] and may allow multiple mNP tracers to be simultaneously imaged inside a tumorous region. In addition, AC susceptibility imaging (ASI) can be optimized to provide maximal contrast for particular mNPs by choosing specific imaging frequencies.
Biological AC susceptibility measurement methods for mNPs have been extensively studied [20, 22, 31–33]. Many studies have applied Brownian relaxation models for immunoassay applications [11, 26, 29, 34]. AC rotational magnetic fields have been exploited to enhance the measurement of the out-of-phase susceptibility component of mNPs [19, 35, 36]. A study has looked into simultaneous quantification of multiple mNPs [37] in which the authors and were able to accurately quantify three mNPs using mNP saturation harmonics. Another group has attempted to distinguish nanobeads [38, 39] where the authors quantified the derivatives of the nth order magnetic induction field with respect to the magnetic field in order to create magnetic signatures for different nanobeads. The authors were then able to quantify mixtures of nanobeads. A recent AC susceptibility study [30] distinguished mNPs in a mixture based on their out-of-phase susceptibility components. The authors were also able to detect susceptibility differences based on mNP binding states. These prior studies have not combined methods for distinguishing mNPs with imaging as we undertake in the present study.
Mathematical models for magnetic susceptibility imaging have been developed previously. The magnetic inverse problem has been described in detail [40]. Two-dimensional magnetic susceptibility tomography (MST) methods have been developed for use on samples of uniform thickness [41]. Three-dimensional methods of MST have not been implemented, but the analytical groundwork for the method has been developed [42, 43]. Further developments of MST for biological imaging [44], non-destructive evaluation (NDE) [45], diamagnetic and paramagnetic objects [46] and in a non-uniform magnetic field [47] have also been reported. Models including a system of voxels containing magnetically susceptible material, an array of excitation coils, and an array of sensors have been developed for magnetic relaxometry [48] and brain hemodynamics [49]. The susceptibility-imaging model presented in this study relies empirically upon calibration data rather than models of field theory. This empirical approach is necessary for our approach to digital magnetic field compensation and is tolerant of imprecise knowledge of model elements such as coil and sensor geometry. The model presented in this work also incorporates AC susceptibility effects and accounts for the delays that result from electrical components such as inductors and capacitors. By accounting for AC susceptibility and imaging in the same model, the proposed ASI approach simultaneously images and distinguishes mNPs.
In the present study, we introduce a contrast type called ASI and extend the concept to a multi-frequency approach called sASI. We first introduce a model for ASI and then validate the model by performing sASI on three different mNP samples in three voxels using six excitation frequencies. We experimentally show the limitations of MSI and demonstrate how sASI can be used to distinguish different mNP types by exploiting their AC magnetic susceptibility properties. We then show results of a biological demonstration experiment where mNPs were injected into a pork sausage and compare the sASI scans from the mNPs in the biological medium to mNPs in a calibration sample. This new contrast type and its spectroscopic extension enable new possibilities for imaging applications with multiple mNP types or biological interaction with mNPs.
2. Methods
2.1. Hardware
2.1.1. Coil and Sensor Configuration
In an AC susceptibility method (figure 1), a sinusoidal current generates a multiple-frequency applied magnetic field with a drive coil. The applied magnetic field interacts with the magnetically susceptible mNPs. The induced magnetic field is then measured by a fluxgate magnetometer. This measured magnetic field will also be sinusoidal but will have a different amplitude and phase relative to the applied magnetic field. The fluxgate measurement axis is oriented orthogonally to the applied field to minimize direct coupling of the applied field in the measurements. In practice, this geometric field compensation is imperfect making the fluxgate measurement a combination of the directly coupled magnetic field from the drive coil and the induced magnetic field of the mNPs. In our system, we additionally generate a compensation field (not shown) to actively cancel the drive coil field along the axis of the fluxgate. In order to be effective, the digital and geometric compensation must be sufficient to lower the directly coupled magnetic fields to within the dynamic range of the sensors and analog-to-digital converter (ADC) without injecting noise into the measurements that exceeds the induced magnetic field signal. This requirement limits the applied fields that can be achieved before the compensation methods start to increase the noise measured by the sensors. Details of the compensation scheme are explained in a prior study [25].
Figure 1.
Conceptual diagram of AC susceptibility measurements. A sinusoidal current produces a magnetic field with a drive coil that interacts with magnetic nanoparticles. The induced magnetic field is detected by a fluxgate magnetometer. The detected magnetic field will have a different amplitude and phase from the applied magnetic field.
2.1.2. Analog and Digital Systems
The prototype design used three drive coils, two fluxgate sensors and two compensation coils. The drive coils (Jantzen-1258, 0.3 mm diameter wire, 5 mH, 10.1 Ω at DC, 15 mm inner diameter × 15 mm height × 25 mm outer diameter, Jantzen, Praestoe, Denmark) were arranged orthogonally to the fluxgate axes to create a higher condition number for matrix inversion while still producing magnetic fields at the sample that produced a magnetization field that resulted in a signal above the noise floor when measured by the sensor. To measure the magnetic field, FLC-100 fluxgate magnetometers (Stefan-Mayer Instruments, Dinslaken, Germany) were used. This fluxgate has an on-axis sensing range of ±100 μT, a cross field operating range of ±1 mT, a cutoff frequency of 1 kHz, noise specification <50 pT/√ Hz at 10 Hz, and size of 44 mm × 14 mm × 5.5 mm. Compensation coils (Jantzen-1814, 0.3 mm diameter wire, 0.15 mH, 1.3 Ω at DC, 15 mm inner diameter × 8 mm height × 18 mm outer diameter) were aligned on a common axis with the fluxgates.
Figure 2 shows the experimental grid for test cases A–D. In figure 2, an Eppendorf tube is located in voxel v3. Also shown are the fluxgate sensors, the drive coils and the compensation coils.
Figure 2.

A: Photo of the current prototype with labels indicating the fluxgates, drive and compensation coils, imaging grid, and mNP samples. B: 0.5 ml Eppendorf tube containing an mNP sample.
As shown in figure 3, software was used to produce five sinusoidal waves that controlled an array of digital-to-analog converters (DACs) (CS4334, Cirrus Logic Inc., Austin, TX, USA). The ADC array was used to produce AC currents at frequencies between 425–925 Hz for the drive and compensation coils. The compensation coils were driven at six frequencies while the drive coils were driven with pairs of frequencies that were time-division multiplexed over the drive coils. The frequency amplitudes of the compensation coils were updated at each frequency rotation. Operational amplifiers (LM 412, Texas Instruments, Dallas, TX, USA) were then used to amplify to current amplitudes of 30 mA peak-to-peak. The applied fields from the drive coils at this current produced magnetic fields of 1 mT at the center of the drive coils and 10 μT at a sample point 0.5 cm in front of a fluxgate sensor. In addition, the DAC also produced a reference current for each frequency being used. Each fluxgate field measurement was then amplified and low pass filtered by a 4th order analog Butterworth filter with a cutoff frequency of 3.3 kHz. Data was acquired at 20 kS/s with an 18-bit analog to digital array (ADC) (NI-USB 6289, National Instruments, Austin, TX, USA). A digital lock-in amplifier was used to find the in-phase and out-of-phase components of the measured magnetic fields.
Figure 3.
Flowchart of the system. Software commands the frequency components for each of the five coil channels of the DAC and a reference signal. The DAC array then produces a current that is amplified and used to generate magnetic fields in the drive coils (dc1–dc3) and compensation coils (cc1, cc2). This field composed of frequencies (f1–f6) interacts with the mNPs and the resulting magnetic induction field along with any uncompensated field is detected by the fluxgates (fg1, fg2). This field is amplified and sampled by an ADC array. A digital lock-in amplifier determines the in-phase and out-of-phase field components for each field measurement for subsequent imaging algorithms.
2.2. Mathematical Model
2.2.1. Measurement of Induced Fields
The magnetic field strength H at the n th sample volume V of mNPs is the sum of contributions from drive coils D and compensation coils C
| (1) |
At reference frequency f0, the field strength corresponding to the i th drive coil and all compensation coils is modeled as
| (2) |
where the A values indicate the amplitudes commanded with the DAC for sine (A″) and cosine ( A′) reference components of the modulated signals, geometric gain factors G account for coupling between the drive or compensation coils and the voxels, and the phase angles ϕ account for unknown but constant phase lags from analog electronic components between the timing of the commanded reference signals from the DAC and the sensor signals recorded by the ADC. The magnetic induction per unit volume V of the sample combines the influence of the applied fields and the volume magnetic susceptibility of the n th sample volume
| (3) |
The magnetic induction field from the sample as measured at the fluxgate sensors S includes a geometric gain GVnSk that relates the n th sample volume to the scalar measurement of the k th sensor along its measurement axis
| (4) |
The magnetic induction of the sample from the AC fields will have an in-phase, or real, component
| (5) |
and an out-of-phase, or complex, component
| (6) |
where the magnitude of the susceptibility and the phase lag . Accounting for the phase lag of the susceptibility response in the magnetic induction field results in the expression
| (7) |
It is convenient to introduce a reference sine and cosine, defined as
| (8) |
and
| (9) |
Expanding the magnetic induction expression and substituting in for the reference sine and cosine and the in-phase and out-of-phase magnetic susceptibility we obtain
| (10) |
Mixing the model of the measured induction field with the reference sine and averaging over time converges to the scalar quantity
| (11) |
Alternatively mixing the measured induction field with a reference cosine and averaging converges to
| (12) |
Computation of and from the two equations above requires calibration measurements of the electronic component phase delays ϕDiSk and ϕCjSk, and also requires model-based calculations or measured estimates of the geometric gains from the drive coils to sample volumes GDiVn, compensation coils to sample volumes GCjVn, and sample volumes to fluxgate sensors GVnSk. Rearranging the above expression into a matrix form allows for the definition of linear set of equations regarding the complex susceptibility
| (13) |
where a matrix rotation operator Φ is defined as,
| (14) |
Equation 13 can be further condensed by defining 3-point geometric gains that account for the coupling from drive or compensation coils to sample volumes and from sample volumes to fluxgate sensors
| (15) |
and
| (16) |
The constant factors can also be arranged into 4×4 matrices K pertaining to the drive or compensation coils
| (17) |
and
| (18) |
The resulting expression concisely expresses the relationship between the complex susceptibility in a sample volume and the measured induction fields mixed with the reference signals and time averaged
| (19) |
The complex susceptibility values can then be calculated from the linear inverse of the above equation using prior knowledge of the 3-point gains from the drive or compensation coils to the sample volumes to the fluxgate sensors and prior knowledge of the system phase lags in K. Methods for obtaining these gains and phase lags are described in the next section.
2.2.2. Coil-to-Voxel-to-Sensor Geometric Gains
The 3-point geometric gains that relate the drive or compensation coils to the sample volumes and then to the sensors can be obtained from additional calibration measurements or by modeling the generated, induced, and measured fields. The following approach is based on calibration measurements. These 3-point geometric gains are needed to reconstruct tomographic images of the magnetic susceptibility in multiple volumes (a.k.a. voxels) that comprise the imaging field of view.
The calibration measurements for imaging should be performed using a sample that has a known magnetic susceptibility magnitude. Inaccuracy in prior knowledge of the reference sample will uniformly alter the scale of subsequently calculated tomographic images. In our experiments, we assumed a Brownian relaxation model for magnetic susceptibility for a 0.5 ml sample of 100 nm Fe3O4 nanoparticles based on literature values described by [30, 50, 51]. The AC susceptibility for mNPs undergoing Brownian relaxation can be modeled by
| (20) |
and
| (21) |
where ω is the frequency in radians and TB is the Brownian relaxation time constant. Using the reported time constant it was possible to tune our calibration results to find the experimental time constant and determine the susceptibility magnitude scaling at each frequency.
The first calibration measurement was performed on a single drive coil, voxel, and sensor. The measurement was mixed with sine and cosine references and time averaged to relate the data to the complex susceptibility of the sample
| (22) |
The 3-point geometric gain was then calculated from the measurements by taking the L2-norm of the constant factor matrix inverse and the measurement vector
| (23) |
This geometric gain was then used to calculate the susceptibility of the reference sample at all other frequencies that are used in the coil array by activating the same drive coil with each frequency in turn. The measured volume susceptibility magnitudes as a function of frequency were then used to obtain 3-point geometric gain factors for all remaining voxel locations and all remaining drive and compensation coils. Since negative gains are mathematically possible but not physically permissible with the calculation in equation 23, the phase between each sensor to voxel was also determined. If the phase was negative, the gain was made negative.
2.2.3. Coil-to-Sensor Phase Lags
The phase delays between the drive coils and fluxgate sensors can be calculated using measurement data obtained using data driven by the sine amplitude calibration data
| (24) |
or equivalently from the cosine amplitude calibration data
| (25) |
It should be noted that these phase lags and gains result from the practical implementation of the system model, which is from digital input to digital output and encompasses all of the hardware and geometric conditions in between. The phase lags relating the compensation coils to the fluxgate sensors are obtained in the same manner as the calculations above. An alternative to this measure-based approach is to use a model of the drive and compensation coils and circuitry to calculate the generated fields and phase lags, and to use the relative positions, orientations and system characteristics of the fluxgate sensors to obtain the geometric gains and any addition to the phase lags from the sensors.
2.2.4. Tomographic Imaging
The challenge of working with arrays of drive coils, fluxgate sensors, and sample volumes is that there is mixing of the induced fields from magnetically susceptible material in the measurements. The benefit of the array measurement approach is that the information contained in these mixed measurements can be inverted to form spatial images of the complex susceptibility of the samples. Solving this inverse problem is referred to as tomographic imaging.
When multiple sample volumes are present, the magnetic induction field associated with the i th drive coil and measured by the k th fluxgate sensor results from the sum of the induction fields from all of the sample volumes, which are indexed by n in the following expression
| (26) |
Assuming that the magnetic susceptibility response stays in the linear regime then by superposition, the mixing of the fluxgate measurements with the sine and cosine reference signals and averaging over time yields sum of contributions from all sample volumes
| (27) |
If the product of the number of drive coils and sensors equals the number of sample volumes, then the above summation can be arranged into a matrix form linear model that can be inverted to solve for the complex susceptibility values of the sample volumes. For example, given two sensor measurements and a single drive coil, it is possible to resolve the complex susceptibility of two sample volumes
| (28) |
If the number of measurements exceeds the number of sample volumes then the susceptibility values can be solved using a least squares approach. If there are too few measurements, then the problem is mathematically ill posed and the solution requires prior assumptions that are typically cast as a regularized inverse problem. Regularization can also become necessary if the available measurements are dominated by noise making the problem ill conditioned.
2.3. Nanoparticles
Testing was performed using mNPs of three different sizes. The largest mNPs had a hydrodynamic diameter of 100 nm and were Fe3O4 starch coated nanoparticles (10-00-102, micromod Partikeltechnologie GmbH, Rostock, Germany). Two samples of these mNPs were prepared. The first was a full concentration sample and the second sample was diluted to 3.125 mg Fe/ml. Both samples were placed in 0.5 ml Eppendorf tubes. The magnetic properties of these mNPs have been characterized by [51, 52]. The intermediate size mNPs had a core diameter of 40 nm and were Fe3O4 nanoparticles with 10 nm polyethylene glycol (PEG) coatings (SHP-40, Ocean NanoTech LLC, Springdale, AR, USA). The smallest sized mNPs were also from Ocean Nanotech and had a core diameter of 10 nm with a 10 nm PEG coatings (SHP-10). Both of the Ocean Nanotech mNPs were concentrated at 5 mg Fe/ml and also placed in 0.5 ml Eppendorf tubes. The magnetic properties of this line of mNPs have been studied previously [30, 50].
2.4. Experimental Procedures
Experiments were performed to validate the model and to perform ASI and sASI scans of 10, 40 and 100 nm mNPs. In order to show the limitations of a prior method, an MSI scan was also performed.
2.4.1. MNP Frequency Response
A frequency response calibration was performed using the fully concentrated sample of 100 nm mNPs. One of the drive coils was driven with the six imaging frequencies components (425–925 Hz, spaced at 100 Hz) and one of the fluxgate magnetometers measured the magnetic field for 20 s. The mNP sample was then placed in an imaging voxel 0.5 cm in front of the sensor for 20 s. Using the magnetic field measurement without the sample present, it was possible to determine the drive coil to sensor phase lags as described in equation 24. Using the system phase, the susceptibility response of the mNP sample was fit to a Brownian relaxation model as described in equations 20 and 21 by tuning the time constant TB until the best fit was obtained. Since the magnitude of the susceptibility of the calibration sample was unknown it was necessary to scale the experimental susceptibility values by the theoretical magnitudes to obtain the best fit. Once the best fit was obtained, it was then possible to model the susceptibility phase and amplitude gains needed for imaging calibration as described in section 2.2.2.
Using an average of the reconstructed susceptibility values from sections 3.3 and 3.4, a susceptibility response was determined for each of the mNP samples used for imaging. The standard deviation of these susceptibility values was added to the plot as error bars.
2.4.2. Imaging calibration
To perform susceptibility imaging calibration it was first necessary to run the compensation algorithm as described in section 2.2.1 of Ficko, Nadar et al. [25]. The six frequencies used for imaging were 425, 525, 625, 725, 825 and 925 Hz. The compensation algorithm determined the compensation fields at each frequency in each of the compensation coils. The goal of the imaging calibration algorithm was to measure the mNP response to each frequency across all imaging voxels. These voxels were at a depth of 0.5 cm and two of the voxels were placed in front of each sensor with a third halfway between. This middle voxel was spaced 1.5 cm from each of the other two voxels. To minimize imaging time and maximize magnetic field strength, frequencies were paired such that each drive coil produced a magnetic field with two frequency components. The pairings were (425, 725), (525, 825) and (625, 925). The calibration sample was the 100 nm mNPs at full concentration.
To perform calibration, each drive coil was assigned a pair of frequency components and the sample was placed in the first imaging voxel. After 20 s, each drive coil was time-division multiplexed to a new pair of frequencies and after another 20 s each drive coil was multiplexed to the remaining pair of frequencies. The drive coils were then multiplexed to the original frequency pair and the sample was moved to the next imaging voxel and the steps repeated. This was then repeated for the remaining voxel. To determine the magnetic field at each sensor without an mNP sample present, a final cycle of time-division multiplexing across drive coils was performed. Using the model derived in section 2.2.2 it was then possible to determine the drive coil gain needed for susceptibility imaging. Since the calibration sample was nominally eight times more concentrated than the 100 nm imaging sample, the calibration gains were scaled by a factor of eight.
After preliminary testing it was determined that the contributions of the compensation coils (GCjVnSk) in equation 27 were insignificant and therefore these terms were ignored for image reconstruction.
2.4.3. Susceptibility Magnitude Imaging (SMI)
To demonstrate the limitations of SMI scanning across multiple mNPs, the imaging calibration from section 2.2.2 was modified to determine the gain terms of section 2.2.4 as described in Ficko, Nadar et al. [25]. Figure 4 illustrates mNP testing sequences. In the first test sequence (A), the 10 nm sample was placed in voxel 1, then placed in voxel 2 and finally in voxel 3. Data collection was performed as described in the prior section. Each drive coil produced a magnetic field with two frequency components for 20 s before switching to the next frequency pair. After 60 s all data was collected for a voxel and the mNP sample was moved to the next voxel in the test sequence. The test was repeated in sequences B and C with 40 nm and 100 nm samples respectively. The 10 nm and 40 nm samples were concentrated at 5 mg Fe/ml, while the 100 nm sample was concentrated at 3.125 mg Fe/ml. In addition, because the calibration sample was nominally eight times more concentrated than the 100 nm imaging sample the calibration matrix was scaled by a factor of eight. SMI scans were performed by talking the third multiplexed 20 s time blocks and only using drive coil frequencies of 525, 725 and 925 Hz. The third time-division was chosen because these drive coil frequencies produced the most mismatched signal with respect to the calibration. An R2 value was computed between the known and measured susceptibility magnitudes using a model function with the SMI reconstruction mean for the three sample locations and a mean of zero everywhere else. In figure 4, this would be represented by using the mean of the diagonal magnitudes for the diagonal locations and zeros everywhere else.
Figure 4.
Test sequences A, B, and C for SMI and ASI scans. Each test sequence is labeled on top, each voxel (v) is labeled on the side, and the cells contain the mNP size in nm. Test sequence A was performed on 10 nm mNPs, B was performed on 40 nm mNPs, and C was performed on 100 nm mNPs. Within each test sequence, the mNP sample was placed first in voxel v1, voxel v2 and then voxel v3.
2.4.4. AC Susceptibility Imaging (ASI) and spectroscopic ASI (sASI)
To demonstrate ASI and sASI, the data collected from test sequences A, B, and C was re-analyzed using the ASI model. This produced images with an in-phase and an out-of-phase amplitude, rather than a susceptibility magnitude scaling.
2.4.5. Nanoparticle Identification through sASI
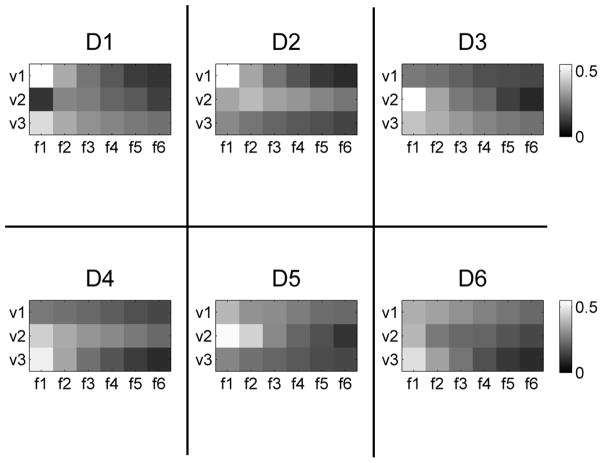
To demonstrate one of the potential applications of sASI, nanoparticle identification was performed by imaging all three mNP samples simultaneously. The test sequence D is shown in figure 5 and corresponds to each of the six possible combinations of placing one of the mNP samples in each of the voxels. sASI scans were performed using the same procedure as described for test sequences A, B, and C. To determine the quantity and type of mNP sample in each voxel, a mixing matrix was constructed using the in-phase and out-of-phase values obtained from test sequences A, B, and C. This mixing matrix contained the susceptibility values for each mNP sample located in each voxel. Then, using the in-phase and out-of-phase susceptibility values obtained from the sequence described in figure 5, the concentration of each mNP sample in each voxel was determined through a least squares linear inversion. To help reduce reconstruction errors, a non-negative linear least squares algorithm was used (Matlab LSQNONNEG function).
Figure 5.
Test sequence D for mNP identification from sASI scans. Each test in the sequence is labeled on top and each voxel is labeled on the side. Test sequence D1 through D6 for nanoparticle identification corresponds to placing 10 nm, 40 nm, and 100 nm mNPs in voxel v1, v2, and v3 as shown.
2.4.6 Biological Demonstration
To demonstrate that sASI scans can be performed on mNPs in a biological medium, an approximately 28 g uncooked pork sausage (Product code 2378, McKenzie Maple Breakfast Link Sausage, Burlington, VT, USA) was used as a background medium. The side of the sausage was located a distance of 0.5 cm from the sensor and contained in a 2 cm wide × 2 cm deep × 10.5 cm long plastic holder. Three wells were created in the sausage corresponding approximately to each of the three voxel locations. The distance from the sensor to each of these wells was approximately 0.5 cm. The sausage and mNP samples for injection were allowed to equilibrate to room temperature. A calibration run was then performed using 0.25 ml of 12.5 mg Fe/ml in an Eppendorf tube by placing the tube in each of the three wells in the sausage. During the imaging experiment, direct injections of 0.2 ml of 100 nm mNPs concentrated at 12.5 mg Fe/ml and 0.2 ml of saline were delivered into wells 1 and 3 while an mNP control sample was located in well 2. A sASI scan was then immediately performed. It was originally conceived that 0.25 ml of mNP and saline would be injected into each well but the sausage deformed during the experiment and only 0.2 ml was able to be injected.
3. Results
3.1. MNP Frequency Response
The normalized experimental susceptibility for the calibration sample is shown in figure 6 along with the modeled magnetic susceptibility. The experimental susceptibility required calculation of the system phase and also relied on susceptibility magnitude scaling obtained through modeling. The model and the experimental data were matched by tuning the time constant TB until the two plots came into agreement. From the literature it is known that the peak out-of-phase susceptibility should be between 325–350 Hz. The experimental phase initially indicated an out-of-phase peak at 515 Hz but this led to a systematic error in the susceptibility measurements. Using a system phase correction of 0.17 radians, the peak was then found to match a time constant of 455 μs, corresponding to a peak out-of-phase susceptibility at 350 Hz. It was observed that background noise was high at 425 Hz compared with the other frequencies. Table 1 shows the root-mean squared (RMS) noise for 30 s of 10 Hz amplitude estimates for each of the frequencies, measured by one of the fluxgates. The R2 value for the full model is 0.956, while if 425 Hz is removed the model has an R2 value of 0.998.
Figure 6.
Experimental and modeled magnetic susceptibility for the calibration sample. The sample was a 100 nm mNP sample concentrated at 25 mg Fe/ml in a 0.5 ml vial. The experimental result used an experimental system phase but relied on the model for its magnitude scaling. The best fit was to a Brownian relaxation model with a time constant TB = 455 μs.
Table 1.
Noise at each imaging frequency. RMS noise calculations were taken from 30 s of amplitude estimates at each of the frequencies. Amplitudes were estimated at a 10 Hz frame rate.
| 425 Hz | 525 Hz | 625 Hz | 725 Hz | 825 Hz | 925 Hz | |
|---|---|---|---|---|---|---|
| Noise amplitude (nT RMS) | 0.40 | 0.18 | 0.11 | 0.08 | 0.10 | 0.15 |
Using the susceptibility values obtained from the sASI scans for test sequences A, B, and C, mean and standard deviation estimates were computed across the imaging voxels for each of the mNP samples (figure 7). As expected, the 100 nm imaging sample has the same susceptibility curve as the calibration sample. The 10 and 40 nm samples have a larger in-phase than out-of-phase component, with the in-phase amplitude of the 10 nm sample is larger than the in-phase amplitude of the 40 nm sample across all frequencies. The out-of-phase amplitude of the 40 nm sample is larger than the out-of-phase amplitude of the10 nm sample. Error bars indicate the standard deviation of the nine measurements used to compute the mean values shown.
Figure 7.
Scaled susceptibility for mNP samples. The in-phase and out-of-phase amplitudes are plotted for each of the imaging samples. The error bars indicate the standard deviations.
3.2. Susceptibility Magnitude Imaging
SMI scanning results are shown in figure 8 and labeled as test sequences A, B, and C as defined in figure 4. In these tests, only one of the mNP samples is present at a time in only one of the imaging voxels. The ideal result would be a nonzero value in v1 (A1, B1 and C1), then the same value in v2 (A2, B2 and C2) and the same value in v3 (A3, B3 and C3) with zeros in the rest of the imaging locations. The SMI scans show the reconstructed susceptibility magnitudes in each of the three voxels. In sequence A, the 10 nm sample exhibits crosstalk between the voxels and has an R2 of 0.800 when compared to the true values. In test sequence B, the 40 nm sample also exhibits crosstalk and has an even poorer R2 of 0.696. In test sequence C, the 100 nm sample is used for the SMI scan. In this case, the calibration corresponds to the imaging sample so there is no apparent crosstalk in this case (R2 is 0.998).
Figure 8.

SMI for each of the three mNP samples at each of the voxels. Test sequences A, B, and C are defined in figure 4. The SMI scans results are shown for each voxel. In sequences A and B, crosstalk between voxels is apparent. In test sequence C, the 100 nm is consistent with the calibration so there is no apparent crosstalk.
3.3. AC Susceptibility Imaging and spectroscopic AC Susceptibility Imaging
SASI scaning results for test sequences A, B, and C are shown in figures 9 and 10. The in-phase susceptibility images are shown in figure 9 while the out-of-phase images are shown in figure 10. As in the SMI results shown in figure 8, each of these images represents one of the mNP samples placed in one of the imaging voxels. Unlike the SMI results, the sASI scans show the susceptibility values across the six frequencies simultaneously. The ideal result would be a nonzero value in v1 (A1, B1 and C1), then the same value in v2 (A2, B2 and C2) and the same value in v3 (A3, B3 and C3) with zeros in the rest of the imaging locations.
Figure 9.
In-phase susceptibility sASI scaning results for test sequences A, B, and C as defined in figure 4. In each image, one of the mNP samples is placed in one of the voxels and the in-phase susceptibility is computed for each of the six frequencies (f1 through f6).
Figure 10.
Out-of-phase susceptibility sASI scanning results for test sequences A, B, and C as defined in figure 4. In each image, one of the mNP samples is placed in one of the voxels and the out-of-phase susceptibility is computed for each of the six frequencies (f1 through f6).
3.4. Nanoparticle Identification through sASI
The sASI scanning results for test sequence D, as described in figure 5, are shown in figures 11 and 12. Figure 11 shows the in-phase susceptibility sASI scanning results while figure 12 shows the out-of-phase sASI results. The ideal result would be a nonzero value in v1, v2 and v3 that changes with each plot but remains consistent according to the sample locations defined in figure 5.
Figure 11.
In-phase sASI scanning results for test sequence D as defined in figure 5. In each test, the mNP locations are varied to cover the six possible arrangements of the 3 samples. The images show the in-phase sASI scans for the three voxels over the six frequencies (f1 through f6).
Figure 12.
Out-of-phase sASI scanning results for test sequence D as defined in figure 5. In each test, the mNP locations are varied to cover the six possible arrangements of the 3 samples. The sASI scans show the out-of-phase sASI scans for the three voxels over the six frequencies (f1 through f6).
To distinguish between mNP samples, a mixing matrix was constructed using the in-phase and out-of-phase susceptibility values across the five highest frequencies (f2 through f6) for the sASI scans in figures 9 and 10. Using the in-phase and out-of-phase susceptibility values from figures 11 and 12 as input values, relative mNP concentration values were determined for each of the mNP samples in each of the voxels for each test sequence. The relative mNP concentrations and coefficient of determination R2 between the phantom placement and reconstructions are shown in figure 13. In each case the mNP with the highest concentration in a voxel is the correct mNP sample for that voxel indicating the goodness of fit between the phantom placement and reconstruction. The comparison between the computed concentrations and the expected concentrations has an R2 value of 0.97.
Figure 13.
Comparison of phantom placement and image reconstruction. Voxel brightness indicates the relative mNP concentrations in the voxels for each test in Sequence D of figure 5. In each case the mNP sample reconstruction with the highest concentration is the mNP phantom that is actually present in that voxel (R2 = 0.97).
3.5 Biological Demonstration
Figure 14 shows the sASI scanning results of injecting pork sausage with saline and mNPs. In figure 14A, the susceptibility response of mNPs and saline are taken from the 3-voxel sASI reconstructions and compared with the AC susceptibility response of the calibration sample. In figure 14B, the sASI-reconstructed in-phase and out-of-phase responses of the mNPs and saline are plotted against the 0.25 ml calibration sample response. The in-phase and out-of-phase mNP sample in sausage is significantly correlated to the calibration sample (R2 = 0.97, p < 0.001 and R2 = 0.99, p < 0.001) whereas the in-phase and out-of-phase saline sample does not correlate significantly with the calibration sample (R2 = 0.55, p = 0.09 and R2 = 0.31, p = 0.25)
Figure 14.

Demonstration of sASI scanning of mNPs and saline samples injected into a biological medium. A: sASI reconstructions of the in-phase and out-of-phase responses of a calibration sample, mNPs, and saline plotted as spectra. B: mNP and saline responses compared to the calibration sample responses.
4. Discussion and Conclusion
This study demonstrates a method for AC susceptibility imaging of mNPs and demonstrates one of the applications of spectroscopic AC susceptibility imaging. We first developed an empirical model for magnetic susceptibility imaging and then validated the model with spectroscopic susceptibility imaging of three different mNP samples at six frequencies over three voxels. Initially the model was calibrated with a 100 nm sample that was assumed to undergo Brownian relaxation. Our experimental susceptibility agreed with the Brownian model (R2 = 0.956). We then showed that SMI exhibits cross talk between voxels when mNPs of multiple sizes are used (R2 = 0.80 and R2 = 0.70). This limitation of SMI was compared with sASI methods, which was shown to be able to distinguish different mNP types through their magnetic susceptibility properties. The sASI scans were used to separate mNP concentration images with an R2 = 0.97. We also demonstrated that sASI scanning of mNPs is possible in a biological medium by showing that measurements of mNPs injected into a pork sausage are consistent with a calibration sample.
The ability of ASI to overcome the loss of image quality of SMI for the 10 and 40 nm mNP samples demonstrates the primary advantage of imaging in ASI. Unlike SMI, ASI can be used to effectively image mNPs with unknown magnetic susceptibility response characteristics. SASI also presents a number of advantages over ASI, including the potential to track changes in the susceptibility responses over time. Some practical biological applications of these capabilities of sASI could be imaging the dynamics of tumor uptake of targeted nanoparticles for cancer therapy and imaging the temperature changes over time of different regions of a tumor being heated in magnetic hyperthermia therapy.
Several technical aspects of our ASI prototype could be improved. We demonstrated separation of sASI into mNP concentration images with an R2 = 0.97. However, we only used five of the six sASI frequencies to perform these calculations. The lowest frequency at 425 Hz was dropped from the image reconstruction because the noise of its in-phase and out-of-phase amplitudes were significantly higher than at the other frequencies. By using a digital lock-in amplifier and digital frequency selection it may be possible to find alternative frequencies with less noise. It is also apparent that at higher frequencies, the 10 and 40 nm mNPs start to have more distinct magnetic susceptibility responses. Performance of the sASI method may be improved by using higher applied field frequencies, such as 1025 Hz to better differentiate mNPs in this size range. The strength of the applied fields could also be increased to improve the imaging depth but also cannot exceed the linear response regime of the mNPs for the ASI model to remain valid. Currently, the imaging model does not use regularization to help reduce noise during image reconstruction. Due to the small amplitudes of the out-of-phase components of the 10 and 40 nm samples, sASI and mNP identification could potentially be improved if the noise levels of the in-phase and out-of-phase components were taken into account.
This study has demonstrated the concept and potential advantages of using spectroscopic AC susceptibility imaging for biological applications. There are several important factors to consider when comparing the potential for clinical translation of the proposed method. These include the contrast type, cost, complexity, imaging resolution and acquisition time. The present study has shown the methodological concept of ASI without attempting to establish the ultimate limitations associated with scale-up to a clinical system. Extrapolating based on our experience with the existing prototype, the imaging resolution of ASI at scale-up will be approximately determined by the number of sensors and coils that can be situated in proximity to the imaging zone. This is because the product of sensors and coils determines the maximum number of measurements for image reconstruction. Expanding on its current form with fluxgate sensors and voice coils, this could conceivably lead to an imaging field of view of roughly 10 cm × 10 cm × 5 cm, with 0.5-cm isotropic imaging voxels. In a previous report on susceptibility magnitude imaging, we demonstrated sensitivity to less than 1 mg Fe/ml and depth sensitivity up to 2.5 cm [25]. While these specifications do not represent the performance limits of the ASI method, they are in an appropriate range for medical applications that use mNP concentrations in the range of several mg Fe/ml. One advantage of ASI compared with other imaging methods is that many imaging measurements can be acquired simultaneously. In our prototype, multiple frequency measurements are required and sASI cycles through each frequency sequentially leading to an acquisition time of 60 seconds. However, depending on the sensitivity requirements this cycling time can be optimized to minimize acquisition time while maintaining acceptable image quality. One application for sASI could be intraoperative surgical guidance for mNP hyperthermia cancer therapy in which high concentrations of mNPs are often used [53]. This application could tolerate lower imaging resolution and acquisition times of several minutes. Due to the interactions of mNPs and tissue, spectroscopic information contained in the sASI contrast type could become important parameters for procedural guidance.
Several other experimental imaging methods are in development that relate to ASI. These other experimental methods have contrast types that are different than ASI but all measure mNP concentrations in tissue. One of the most promising methods is MPI. MPI has the potential for millimeter-scale imaging resolution if a magnetic gradient of several T/m can be created. For instance, [5] show an image with a resolution of 3.8 mm and an acquisition time of 8 seconds. The sensitivity of their device is also high and could approach 10−9 mol Fe/L. Magnetic relaxometry methods using SQUID arrays have also shown promise. For instance a recent study [10] has shown that it is possible to localize 0.09 mg Fe located in two mouse tumors from roughly 2.5 cm away. This method requires 3 s to magnetize the mNPs and acquire a relaxation signal. Perhaps even more interesting is an array of sequentially activated coils that has recently been proposed for increased imaging resolution [48]. This method could lead to images with several thousand voxels by using a SQUID array for detection and an array of magnetic coils for magnetization. Another promising method for imaging mNPs is MRI SWIFT. For instance, a recent report [8] used SWIFT imaging to measure cells labeled with SPIOs injected into a rat heart. The imaging field of view was 7 cm × 7 cm × 14 cm, the resolution was 0.5 mm × 0.5 mm × 1 mm and the acquisition time was 27 minutes. In two cases, 2 million labeled cells were injected into a rat with an iron content of 5 pg/cell. All of these methods have shown promise for imaging mNPs but ultimately clinical applications will require a tradeoff between various parameters such as cost, complexity, resolution and acquisition time. These parameters have yet to be determined for each method and will determine how the methods will be used in a clinical setting. With these factors in mind, it is difficult to directly compare ASI to other experimental methods at this stage of development. However, ASI does have certain advantages such as its AC susceptibility contrast type, use of low cost components, low instrumentation complexity and reasonable acquisition time, while having some drawbacks such as poorer sensitivity and lower resolution when compared with these other methods.
The potential applications of ASI and sASI scanning are significant in mNP medical imaging. SASI has the potential to distinguish between different mNPs and different mNP states based on their AC susceptibility response characteristics. This could significantly advance the use of mNPs in clinician therapies and diagnostics by enabling clinicians to simultaneously image and characterize the AC susceptibility properties of mNPs.
Highlights.
Development of an AC susceptibility imaging model
Comparison of AC Susceptibility Imaging (ASI) and Susceptibility Magnitude Imaging (SMI)
Demonstration of ASI and spectroscopic ASI (sASI) using three different magnetic nanoparticle types
SASI scan separation of three different magnetic nanoparticles samples using 5 spectroscopic frequencies
Demonstration of biological feasibility of sASI
Acknowledgments
This work was supported in part by the Dartmouth Center of Cancer Nanotechnology Excellence (DCCNE) NIH NCI U54-CA151662-04, the Center for the Translation of Rehabilitation Engineering Advances and Technology (TREAT) 5-R24-HD065703-04, and NIH NIBIB 1R21EB016241-01A1. The authors thank E.K. Wirta, A. Hartov, K.E. Griswold, and P.J. Hoopes.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
6. Bibliography
- 1.Pankhurst QA, et al. Applications of magnetic nanoparticles in biomedicine. Journal of Physics D-Applied Physics. 2003;36(13):R167–R181. [Google Scholar]
- 2.Pankhurst QA, et al. Progress in applications of magnetic nanoparticles in biomedicine. Journal of Physics D-Applied Physics. 2009;42(22):224001. [Google Scholar]
- 3.Gleich B, Weizenecker R. Tomographic imaging using the nonlinear response of magnetic particles. Nature. 2005;435(7046):1214–1217. doi: 10.1038/nature03808. [DOI] [PubMed] [Google Scholar]
- 4.Borgert J, et al. Fundamentals and applications of magnetic particle imaging. Journal of Cardiovascular Computed Tomography. 2012;6(3):149–153. doi: 10.1016/j.jcct.2012.04.007. [DOI] [PubMed] [Google Scholar]
- 5.Goodwill PW, et al. X-Space MPI: Magnetic nanoparticles for safe medical imaging. Advanced Materials. 2012;24(28):3870–3877. doi: 10.1002/adma.201200221. [DOI] [PubMed] [Google Scholar]
- 6.Saritas EU, et al. Magnetic particle imaging (MPI) for NMR and MRI researchers. Journal of Magnetic Resonance. 2013;229:116–126. doi: 10.1016/j.jmr.2012.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hoopes PJ, et al. Imaging and modification of the tumor vascular barrier for improvement in magnetic nanoparticle uptake and hyperthermia treatment efficacy. Energy-Based Treatment of Tissue and Assessment Vii. 2013:8584. doi: 10.1117/12.2008689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhou R, et al. SWIFT detection of SPIO-labeled stem cells grafted in the myocardium. Magnetic Resonance in Medicine. 2010;63(5):1154–1161. doi: 10.1002/mrm.22378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Steinhoff U, et al. Spatially Resolved Measurement of Magnetic Nanoparticles Using Inhomogeneous Excitation Fields in the Linear Susceptibility Range (<1mT) In: Buzug TM, Borgert J, editors. Magnetic Particle Imaging. Springer; Berlin Heidelberg: 2012. pp. 295–300. [Google Scholar]
- 10.Adolphi NL, et al. Imaging of Her2-targeted magnetic nanoparticles for breast cancer detection: comparison of SQUID-detected magnetic relaxometry and MRI. Contrast Media & Molecular Imaging. 2012;7(3):308–319. doi: 10.1002/cmmi.499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Enpuku K, et al. Characterization of Magnetic Markers for Liquid-Phase Immunoassays Using Brownian Relaxation. Japanese Journal of Applied Physics. 2012;51(2):3002. [Google Scholar]
- 12.Janosek M, Ripka P, Platil A. Magnetic markers detection using PCB fluxgate array. Journal of Applied Physics. 2009;105(7):07E717. [Google Scholar]
- 13.Ludwig F, et al. Magnetorelaxometry of magnetic nanoparticles with fluxgate magnetometers for the analysis of biological targets. Journal of Magnetism and Magnetic Materials. 2005;293(1):690–695. [Google Scholar]
- 14.Richter H, et al. Magnetorelaxometry for localization and quantification of magnetic nanoparticles for thermal ablation studies. Physics in Medicine and Biology. 2010;55(3):623–633. doi: 10.1088/0031-9155/55/3/005. [DOI] [PubMed] [Google Scholar]
- 15.Romanus E, et al. Magnetic nanoparticle relaxation measurement as a novel tool for in vivo diagnostics. Journal of Magnetism and Magnetic Materials. 2002;252(1–3):387–389. [Google Scholar]
- 16.Sarangi S, I, Tan C, Brazdeikis A. Brownian relaxation of interacting magnetic nanoparticles in a colloid subjected to a pulsatile magnetic field. Journal of Nanoscience and Nanotechnology. 2011;11(5):4136–4141. doi: 10.1166/jnn.2011.4112. [DOI] [PubMed] [Google Scholar]
- 17.Yoshida T, et al. AC susceptibility of magnetic fluid in nonlinear brownian relaxation region: experiment and comparison with numerical simulation. Japanese Journal of Applied Physics. 2010;49(5):053001. [Google Scholar]
- 18.Chieh JJ, Hong CY. Non-invasive and high-sensitivity scanning detection of magnetic nanoparticles in animals using high-T-c scanning superconducting-quantum-interference-device biosusceptometry. Review of Scientific Instruments. 2011;82(8):084301. doi: 10.1063/1.3623795. [DOI] [PubMed] [Google Scholar]
- 19.Dieckhoff JH, et al. Homogeneous Bioassays Based on the Manipulation of Magnetic Nanoparticles by Rotating and Alternating Magnetic Fields-A Comparison. IEEE Transactions on Magnetics. 2012;48(11):3792–3795. [Google Scholar]
- 20.Enpuku K, et al. AC susceptibility measurement of magnetic markers in suspension for liquid phase immunoassay. Journal of Applied Physics. 2010;108(3):4701. [Google Scholar]
- 21.Herrera AP, et al. Monitoring colloidal stability of polymer-coated magnetic nanoparticles using AC susceptibility measurements. Journal of Colloid and Interface Science. 2010;342(2):540–549. doi: 10.1016/j.jcis.2009.10.041. [DOI] [PubMed] [Google Scholar]
- 22.Oisjoen F, et al. A new approach for bioassays based on frequency- and time-domain measurements of magnetic nanoparticles. Biosensors & bioelectronics. 2010;25(5):1008–1013. doi: 10.1016/j.bios.2009.09.013. [DOI] [PubMed] [Google Scholar]
- 23.Yang TQ, et al. Detection of magnetic nanoparticles with ac susceptibility measurement. Physica C-Superconductivity and Its Applications. 2004;412:1496–1500. [Google Scholar]
- 24.Anninga B, et al. Magnetic sentinel lymph node biopsy and localization properties of a magnetic tracer in an in vivo porcine model. Breast Cancer Research and Treatment. 2013;141(1):33–42. doi: 10.1007/s10549-013-2657-0. [DOI] [PubMed] [Google Scholar]
- 25.Ficko BW, et al. Development of a magnetic nanoparticle susceptibility magnitude imaging array. Physics in Medicine and Biology. 2014;59(4):1047. doi: 10.1088/0031-9155/59/4/1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chung SH, et al. Biological sensors based on Brownian relaxation of magnetic nanoparticles. Applied Physics Letters. 2004;85(14):2971–2973. [Google Scholar]
- 27.Rauwerdink AM, Weaver JB. Concurrent quantification of multiple nanoparticle bound states. Medical Physics. 2011;38(3):1136–1140. doi: 10.1118/1.3549762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Glockl G, et al. The effect of field parameters, nanoparticle properties and immobilization on the specific heating power in magnetic particle hyperthermia. Journal of Physics-Condensed Matter. 2006;18(38):S2935–S2949. [Google Scholar]
- 29.Rauwerdink AM, Weaver JB. Measurement of molecular binding using the Brownian motion of magnetic nanoparticle probes. Applied Physics Letters. 2010;96(3):3702. [Google Scholar]
- 30.Park K, et al. Multiplexed sensing based on Brownian relaxation of magnetic nanoparticles using a compact AC susceptometer. Nanotechnology. 2011;22(8):5501. doi: 10.1088/0957-4484/22/8/085501. [DOI] [PubMed] [Google Scholar]
- 31.Hong CY, et al. Magnetic susceptibility reduction method for magnetically labeled immunoassay. Applied Physics Letters. 2006;88(21):212512. [Google Scholar]
- 32.Nutting J, et al. The effect of particle size distribution on the usage of the ac susceptibility in biosensors. Journal of Applied Physics. 2006;99(8):B319. [Google Scholar]
- 33.Ludwig F. Characterization of Magnetic Core-Shell Nanoparticle Suspensions Using AC Susceptibility for Frequencies up to 1 MHz. 8th International Conference on the Scientific and Clinical Applications of Magnetic Carriers; 2010. pp. 249–254. [Google Scholar]
- 34.Astalan AP, et al. Magnetic response of thermally blocked magnetic nanoparticles in a pulsed magnetic field. Journal of Magnetism and Magnetic Materials. 2007;311(1):166–170. [Google Scholar]
- 35.Yoshida T, et al. Magnetic fluid dynamics in a rotating magnetic field. Journal of Applied Physics. 2012;111(5):053901. [Google Scholar]
- 36.Dieckhoff J, Schilling M, Ludwig F. Fluxgate based detection of magnetic nanoparticle dynamics in a rotating magnetic field. Applied Physics Letters. 2011;99(11):2501. [Google Scholar]
- 37.Rauwerdink AM, Giustini AJ, Weaver JB. Simultaneous quantification of multiple magnetic nanoparticles. Nanotechnology. 2010;21(45) doi: 10.1088/0957-4484/21/45/455101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.de Montferrand C, et al. An innovative nanoprobe for magnetic immunoassay: Individual gamma-Fe2O3 nanoparticles; towards high sensitive and multiparametric detection. IRBM. 2011;32(5):302–305. [Google Scholar]
- 39.Lenglet L. Multiparametric magnetic immunoassays utilizing non-linear signatures of magnetic labels. Journal of Magnetism and Magnetic Materials. 2009;321(10):1639–1643. [Google Scholar]
- 40.Lima EA, Irimia A, Wikswo JP. The SQUID Handbook. Wiley-VCH Verlag GmbH & Co. KGaA; 2006. The Magnetic Inverse Problem; pp. 139–267. [Google Scholar]
- 41.Thomas IM, et al. Spatial-Resolution and Sensitivity of Magnetic-Susceptibility Imaging. Ieee Transactions on Applied Superconductivity. 1993 Mar;3(1):1937–1940. Pts 2–4, 1993. [Google Scholar]
- 42.Wikswo JP. Noninvasive magnetic detection of cardiac mechanical activity: Theory. Medical Physics. 1980;7(4):297–306. doi: 10.1118/1.594710. [DOI] [PubMed] [Google Scholar]
- 43.Wikswo JP, Opfer JE, Fairbank WM. Noninvasive magnetic detection of cardiac mechanical activity: Experiments. Medical Physics. 1980;7(4):307–314. doi: 10.1118/1.594711. [DOI] [PubMed] [Google Scholar]
- 44.Thomas IM, Sepulveda NG, Wikswo JP., Jr Magnetic susceptibility tomography: a new modality for three-dimensional biomedical imaging. Engineering in Medicine and Biology Society, 1993. Proceedings of the 15th Annual International Conference of the IEEE; 1993. [Google Scholar]
- 45.Wikswo JP, Jr, et al. Magnetic susceptibility imaging for nondestructive evaluation (using SQUID magnetometer) Applied Superconductivity, IEEE Transactions on, 1993. 3(1):1995–2002. [Google Scholar]
- 46.Sepulveda NG, I, Thomas M, Wikswo JP. Magnetic-Susceptibility Tomography for 3-Dimensional Imaging of Diamagnetic and Paramagnetic Objects. Ieee Transactions on Magnetics. 1994;30(6):5062–5069. [Google Scholar]
- 47.Parente Ribeiro E, et al. Magnetic Susceptibility Tomography with Nonuniform Field. In: Aine C, et al., editors. Biomag 96. Springer; New York: 2000. pp. 671–674. [Google Scholar]
- 48.Crevecoeur G, et al. Advancements in Magnetic Nanoparticle Reconstruction Using Sequential Activation of Excitation Coil Arrays Using Magnetorelaxometry. IEEE Transactions on Magnetics. 2012;48(4):1313–1316. [Google Scholar]
- 49.Burke BA, Diamond SG. Measuring cerebral hemodynamics with a modified magnetoencephalography system. Physiological Measurement. 2012;33(12):2079–2098. doi: 10.1088/0967-3334/33/12/2079. [DOI] [PubMed] [Google Scholar]
- 50.Adolphi NL, et al. Characterization of single-core magnetite nanoparticles for magnetic imaging by SQUID relaxometry. Physics in Medicine and Biology. 2010;55(19):5985–6003. doi: 10.1088/0031-9155/55/19/023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gruttner C, et al. Synthesis and antibody conjugation of magnetic nanoparticles with improved specific power absorption rates for alternating magnetic field cancer therapy. Journal of Magnetism and Magnetic Materials. 2007;311(1):181–186. [Google Scholar]
- 52.Nakamura K, et al. Self-Heating Temperature and AC Hysteresis of Magnetic Iron Oxide Nanoparticles and Their Dependence on Secondary Particle Size. IEEE Transactions on Magnetics. 2013;49(1):240–243. [Google Scholar]
- 53.Johannsen M, et al. Magnetic nanoparticle hyperthermia for prostate cancer. International Journal of Hyperthermia. 2010;26(8):790–795. doi: 10.3109/02656731003745740. [DOI] [PubMed] [Google Scholar]