Development of a Population Pharmacokinetic Model Characterizing the Tissue Distribution of Azithromycin in Healthy Subjects

Abstract

Recent clinical trials indicate that the use of azithromycin is associated with the emergence of macrolide resistance. The objective of our study was to simultaneously characterize free target site concentrations and correlate them with the MIC₉₀s of clinically relevant pathogens. Azithromycin (500 mg once daily [QD]) was administered orally to 6 healthy male volunteers for 3 days. The free concentrations in the interstitial space fluid (ISF) of muscle and subcutaneous fat tissue as well as the total concentrations in plasma and polymorphonuclear leukocytes (PMLs) were determined on days 1, 3, 5, and 10. All concentrations were modeled simultaneously in NONMEM 7.2 using a tissue distribution model that accounts for nonlinear protein binding and ionization state at physiological pH. The model performance and parameter estimates were evaluated via goodness-of-fit plots and nonparametric bootstrap analysis. The model we developed described the concentrations at all sampling sites reasonably well and showed that the overall pharmacokinetics of azithromycin is driven by the release of the drug from acidic cell/tissue compartments. The model-predicted unionized azithromycin (AZM) concentrations in the cytosol of PMLs (6.0 ± 1.2 ng/ml) were comparable to the measured ISF concentrations in the muscle (8.7 ± 2.9 ng/ml) and subcutis (4.1 ± 2.4 ng/ml) on day 10, whereas the total PML concentrations were >1,000-fold higher (14,217 ± 2,810 ng/ml). The total plasma and free ISF concentrations were insufficient to exceed the MIC₉₀s of the skin pathogens at all times. Our results indicate that the slow release of azithromycin from low pH tissue/cell compartments is responsible for the long terminal half-life of the drug and thus the extended period of time during which free concentrations reside at subinhibitory concentrations.

INTRODUCTION

Azithromycin (AZM) is a semisynthetic macrolide antibiotic with a broad range of activity against Gram-positive bacteria and some community-acquired Gram-negative pathogens, including Haemophilus influenzae and Moraxella catarrhalis, and it is extensively used in the clinic setting for the treatment of respiratory tract infections (1, 2). Compared to the older macrolides, AZM is thought to have advantageous pharmacokinetic (PK) and pharmacodynamic (PD) properties, particularly due to its large distribution volume (∼23 liter/kg of body weight) and long half-life of 68 to 79 h (3), which allows for a convenient once-daily dosing regimen and a short overall duration of treatment of 3 to 5 days (4). However, emerging evidence suggests that the use of AZM also triggers the emergence of macrolide resistance (5), but the underlying mechanisms are currently unclear. Particularly alarming data originated from a WHO-recommended mass distribution study conducted in 1,015 Tanzanian children, where the proportion of the total macrolide-resistant Streptococcus pneumoniae isolates increased 2- to 3-fold, whereas that of the highly resistant isolates (MIC ≥ 16 μg/ml) was found to be up to 17-fold increased 6 months after a single dose of oral AZM treatment (6).

A closer evaluation of the PK properties of AZM shows that although its large distribution volume suggests extensive tissue distribution, the majority of the drug is confined to intracellular compartments and thus is unavailable for extracellular antimicrobial activity. This is due to the fact that AZM is a diprotic base (pK_a1, 8.1; pK_a2, 8.8) (7). Once it enters the acidic compartments, such as the acidic lysosomes of white blood cells, the drug is protonated and trapped inside the cells. This mechanism is widely known as ion trapping and is responsible for the presence of AZM in the tissue long after the administration of the last dose, as reflected by its long elimination half-life of 68 to 79 h (3, 4, 8). While the long presence of AZM in the body is certainly advantageous for exerting its time-dependent bacteriostatic or bactericidal activity at concentrations exceeding the MIC of the pathogen, concerns have been expressed about the long presence of the drug at subinhibitory levels, as they may trigger the development of resistance (9, 10).

It should further be noted that the primary infection site of most bacterial infections is in the extracellular tissue space, i.e., the interstitial space fluid (ISF) (4, 11). Many publications, however, refer to tissue concentrations as drug concentrations obtained from tissue homogenates. This approach is highly misleading, as the concentrations obtained from tissue homogenates represent a mixture of free and total and intra- and extracellular concentrations, making a distinction of how much free drug is in fact available at the infection site difficult. The high AZM concentrations found in white blood cells, different tissue-specific phagocytes, or tissue homogenates from the lung, lymph nodes, prostate, tonsils, and gastric tissue are consequently not representative of the actual target site concentrations (8, 12–17). In order to comprehensively evaluate the potential causes of resistance development against AZM, it is important to assess drug levels not only at the primary infection site, i.e., the lung (especially the epithelial lining fluid [ELF]), but also in other tissues, such as the skin, where microorganisms are available for interaction with AZM and resistance development. To this end, Matzneller et al. (4) determined the free pharmacologically active concentrations in the ISF of muscle and subcutaneous adipose tissue (subcutis) in a clinical microdialysis study, as well as the total plasma concentrations and total concentrations in polymorphonuclear leukocytes (PMLs) in six healthy male volunteers receiving 500 mg once daily (QD) AZM for 3 days.

The objective of this study was to develop a tissue distribution model for AZM that allows the simultaneous characterization of free drug concentrations in the ISF of muscle and subcutaneous adipose tissue, taking the ionization state at different tissue sites and plasma protein binding into account.

MATERIALS AND METHODS

Subjects and pharmacokinetic study.

AZM (500 mg once daily) was administered to 6 healthy male volunteers for 3 days. The total AZM concentrations in plasma were determined at baseline and 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 6, and 8 h after dosing on days 1 and 3, as well as at three defined time points on days 5 and 10 (4). The total concentrations in white blood cells were determined at baseline and 2, 6, and 10 h after dosing on days 1 and 3, as well as at a single time point on days 5 and 10. Free unbound concentrations in the ISF of muscle and subcutaneous adipose tissue were determined via clinical microdialysis at prespecified time points, and the details can be found elsewhere (4).

Pharmacokinetic model.

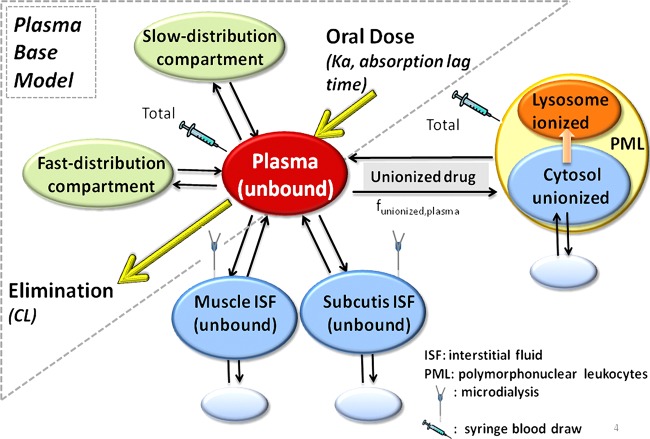
A tissue distribution model for AZM (Fig. 1) was developed in a stepwise approach: first, assuming that only free drug is available in the absence of a pH gradient between plasma and tissue fluids (18, 19), the free plasma concentrations were computed by multiplying the total plasma concentrations (C_p) by the fraction unbound in plasma (f_u,p). Given that plasma protein binding is saturable for AZM at therapeutic doses, a concentration-dependent function (cf. equation 1) for f_u,p was derived from digitized data (GetData Pty Ltd., Kogarah, Australia) from Bouvier d'Yvoire, Dresco, and Tulkens (20) using GraphPad Prism 5 (GraphPad Software, La Jolla, CA, USA).

$$f_{u,\text{p}}=0.4984+\frac{0.5339\times c_{\text{p}}}{230.9+c_{\text{p}}}$$ (1)

FIG 1.

Model structure of the proposed tissue distribution model for azithromycin.

Second, a three-compartment model with 1st-order absorption, lag time, and 1st-order elimination was set up to characterize the changes in unbound plasma concentrations over time (Fig. 1). This base model was then expanded in a third step to link changes in the free plasma concentrations over time to the corresponding free tissue concentrations (cf. equation 2), with the concentrations calculated as the ratio of the amount and the respective tissue volume:

$$\frac{dAmoun{t}_{(\text{tissue})}}{dt}=k_{\text{in}}\times Amoun{t}_{(\text{plasma})}-k_{\text{out}}\times Amoun{t}_{(\text{tissue})}+k_{\text{off}}\times Amoun{t}_{(\text{tissue},\text{deep})}-k_{\text{on}}\times Amoun{t}_{(\text{tissue})}$$ (2)

where k_in and k_out are the first-order rate constants describing the distribution of AZM in and out of the tissue, respectively. Given the affinity of protonated AZM to negatively charged phospholipids (21, 22), we compared the model performances with or without the inclusion of unspecific binding in PMLs and tissues [amount represented by Amount_{(tissue,deep)}], where drugs bind with a first-order rate constant, k_on, and become available again for distribution with a first-order rate constant, k_off. At steady state, the amount of drug going into the tissue is equal to the amount of drug coming out of the tissue, as shown in equation 3.

$$k_{\text{in}}\times Amoun{t}_{(\text{plasma})}=k_{\text{out}}\times Amoun{t}_{(\text{tissue})}$$ (3)

Converting amounts into the corresponding concentrations by accounting for the respective distribution volumes and rearranging for concentrations in tissue (C_tissue) yields the following expression:

$$C_{\text{tissue}}=\frac{Amoun{t}_{(\text{tissue})}}{V_{\text{tissue}}}=\frac{Amoun{t}_{(\text{tissue})}\times k_{\text{out}}\times C_{\text{tissue}}}{k_{\text{in}}\times C_{\text{plasma}}\times V_{\text{plasma}}}=\frac{Amoun{t}_{(\text{tissue})}\times k_{(\text{out})}\times D{F}_{\text{tissue}}}{k_{\text{in}}\times V_{\text{plasma}}}$$ (4)

where DF_tissue is a tissue distribution factor accounting for tissue-specific differences in the drug concentrations available for distribution with respect to plasma (cf. equation 5).

$$D{F}_{\text{tissue}}=\frac{C_{\text{tissue}}}{C_{\text{plasma}}}$$ (5)

For this analysis, three tissue distribution factors were defined, one for muscle (DF_muscle), one for subcutis (DF_subcutis), and one for the cytosol of PMLs [DF_PML(cytosol)]. In the absence of a pH gradient, e.g., between plasma and the ISF of muscle and subcutaneous adipose tissue under noninflammatory conditions, this tissue distribution factor approximates the ratio of free unbound drug concentrations between tissue and plasma, whereas the ionization state of AZM needs to be considered in the presence of a pH gradient. The respective unionized fraction (f_unionized), which takes the two pK_a values of AZM into consideration (pK_a1, 8.1; pK_a2, 8.8), can be computed according to equation 6 (23).

$$f_{\text{unionized}}=\frac{1}{1+{10}^{(\text{p}{\text{K}}_{\text{a}1}-\text{pH})}+{10}^{(\text{p}{\text{K}}_{\text{a}1}-\text{pH})+(\text{p}{\text{K}}_{\text{a}2}-\text{pH})}}$$ (6)

DF_PML(cytosol) can consequently be computed as in equation 7:

$$D{F}_{(\text{PML}(\text{cytosol}))}=\frac{c_{\text{PML}(\text{cytosol},\text{unionized})}}{c_{\text{plasma}(\text{uniomized})}}=\frac{c_{\text{PML}(\text{cytosol},\text{total})}\times f_{\text{unionized},\text{PML cytosol}}}{c_{\text{plasma}(\text{unbound})}\times f_{\text{unionized},\text{plasma}}}$$ (7)

where C_{PML(cytosol,unionized)} is the unionized concentration in the cytosol of PMLs, C_{plasma(unionized)} is the unionized concentration in plasma, C_{PML(cytosol,total)} is the total concentration in PMLs, C_{plasma(unbound)} is the free concentration in plasma, f_{unionized,PML(cytosol)} is the fraction unionized in the cytosol of PMLs, and f_{unionized,plasma} is the unionized fraction in plasma. Equation 6 can also be used to compute the differences in f_unionized in different cell compartments, e.g., between the cytosol of PMLs (pH ∼7 [23, 24]) and the lysosomes located within PMLs (pH ∼5 [23, 25]). Given that f_unionized in the lysosomes is very low (0.000013), we assumed that once AZM is protonated in the acidic environment of lysosomes, it is trapped and thus no longer available for direct exchange with the plasma compartment.

The total AZM concentrations in PMLs (C_PML,total) are the sum of the total amounts in the cytosol and lysosomes of PMLs divided by the total PML volume. Provided that approximately one-third of the drug resides in the cytosol of PMLs (26) and that the respective volume ratio between the lysosomes [V_{PML(lysosome)}] and cytosol [V_PML(cytosol)] is 5:95 for macrophages (27) and fibroblasts (28), the ratio between the total AZM concentrations in the cytosol of PMLs [C_{PML(cytosol,total)}] and total AZM concentrations in PML(C_PML,total) is computed according to equation 8.

$$\frac{c_{\text{PML}(\text{cytosol},\text{total})}}{C_{\text{PML},\text{total}}}=\frac{C_{\text{PML}(\text{cytosol},\text{total})}}{\left(\frac{{Amount}_{(\text{PML})}}{V_{\text{PML}(\text{lysosome})}+V_{\text{PML}(\text{cytosol})}}\right)=\frac{C_{\text{PML}(\text{cystol},\text{total})}}{\left(\frac{3\times C_{\text{PML}(\text{cytosol},\text{total})}\times V_{\text{PML}(\text{cytosol})}}{V_{\text{PML}(\text{lysosome})}+V_{PML(\text{cytosol})}}\right)=\frac{1}{3}\times \left(1+\frac{V_{\text{PML}(\text{lysosome})}}{V_{\text{PML}(\text{cytosol})}}\right)}}$$ (8)

C_{PML(cytosol,total)} is computed according to equation 9.

$$c_{\text{PML}(\text{cytosol},\text{total})}=\frac{1}{3}\times \left(1+\frac{V_{\text{PML}(\text{lysosome})}}{V_{\text{PML}(\text{cytosol})}}\right)\times C_{\text{PML},\text{total}}=\frac{1}{3}\times \left(1+\frac{5}{95}\right)\times C_{\text{PML},\text{total}}\approx 0.351\times C_{\text{PML},\text{total}}$$ (9)

The free unionized concentrations in the cytosol of PMLs [C_{PML(cytosol,unionized)}] is computed according to equation 10.

$$C_{\text{MPL}(\text{cytosol},\text{unionized})}=C_{\text{PML}(\text{cytosol},\text{total})}\times f_{\text{unionized},\text{PML cytosol}}$$ (10)

Similar relationships can be used to compute the total concentrations in the lysosomes of PMLs [C_{PML(lysosome,total)} (cf. equation 11)].

$$C_{\text{PML}(\text{lysosome},\text{total})}=\frac{2}{3}\times \left(1+\frac{V_{\text{PML}(\text{cytosol})}}{V_{\text{PML}(\text{lysosome})}}\right)\times C_{\text{PML},\text{total}}\approx 13.33\times C_{\text{PML},\text{total}}=38\times C_{\text{PML}(\text{cytosol},\text{total})}$$ (11)

We also tested a volume ratio of 1:200 between the lysosome and cytosol, as reported for liver cells (29), but a sensitivity analysis suggested that the resulting changes in the C_PML(cytosol)-to-C_PML,total ratio were marginal (0.351 for the 5:95 ratio versus 0.335 for the 1:200 ratio) and did not significantly improve the overall model fit. However, a volume ratio of 1:200 will affect the concentration ratio between C_{PML(lysosome,total)} and C_PML,total.

The population pharmacokinetic (pop-PK) model was built in NONMEM version 7.2.0 (Icon, Dublin, Ireland) using the ADVAN13 subroutine and the first-order conditional estimation with interaction (FOCEI) method. The objective function value computed by NONMEM was used in a log-likelihood ratio test for the comparison of hierarchical models. The addition of a structural or variance parameter was considered statistically significant when the objective function value dropped by ≥3.84 (P < 0.05 for 1 degree of freedom). Interindividual variability was modeled by an exponential error model, found in equation 12, which assumes a log-normal distribution:

$$P_i=P_{\text{p}}\times e^{\eta \text{i}}$$ (12)

where P_p is the population value for the parameter P, P_i is the value for this parameter for the ith individual, and η_i is the interindividual random variability, which is assumed to be normally distributed, with a mean of 0 and variance ω². The difference between the observed and model-predicted concentrations was modeled as an additive (ε_add,ij) and proportional (ε_prop,ij) error, as in equation 13:

$$y_{\text{obs}}=y_{\text{pred}}(1+{\epsilon }_{\text{prop},\text{ij}})+{\epsilon }_{\text{add},\text{ij}}$$ (13)

where ε_ij is the residual error, with mean 0 and variance ω², between the jth observation in the ith individual (y_obs) and its model-based prediction (y_pred). Due to the limited number of subjects (n = 6) and the relatively homogeneous study population (all healthy males; age, 29.0 ± 9.63 years; weight, 77.68 ± 8.56 kg; height, 184.17 ± 6.74 cm; body mass index, 22.83 ± 1.39 kg/m² [all values mean ± SD] [4]), a rigorous covariate analysis was deemed meaningless for this study. In addition to the statistical and graphical evaluations, physiological meaningfulness was considered imperative in the assessment of the model structure and the goodness-of-fit. The robustness of the final model and its parameter estimates were evaluated using a nonparametric bootstrap with 1,000 runs in PLT Tools (version 2.6; PLTsoft, San Francisco, CA) for NONMEM. The graphics were created by ggplot2 libraries for R (version 3.0.1) and GraphPad Prism 5.

RESULTS

The total AZM concentrations during and after treatment were highest in white blood cells due to intracellular accumulation, whereas the respective total concentrations in plasma and the free concentrations in the ISF of muscle and subcutis were markedly lower. In comparison, the calculated free and unionized AZM concentrations in the cytosol of PMLs (6.0 ± 1.2 ng/ml) were similar to the measured unbound concentrations in the ISF of muscle (8.7 ± 2.9 ng/ml) and subcutis (4.1 ± 2.4 ng/ml) on day 10. When taking pH differences between plasma and cell compartments into consideration, we showed that AZM is almost completely protonated in the acidic environment of the lysosomes of the PMLs (f_unionized, 0.000013), whereas it is less protonated in the cytosol of the PMLs (f_unionized, 0.0012). In plasma and the ISF of soft tissues, the f_unionized was calculated as 0.0076 due to the absence of significant pH differences between both tissues. These differences in f_unionized values reflect the pH gradients between the extracellular milieu (plasma) and the cytosol (about 0.4 pH units) or the lysosomes (about 2 to 2.4 pH units). Our calculations further indicate that the unionized concentrations in the lysosome and cytosol of PMLs appeared to be in the same range (6.0 ± 1.2 versus 2.5 ± 0.5 ng/ml) on day 10.

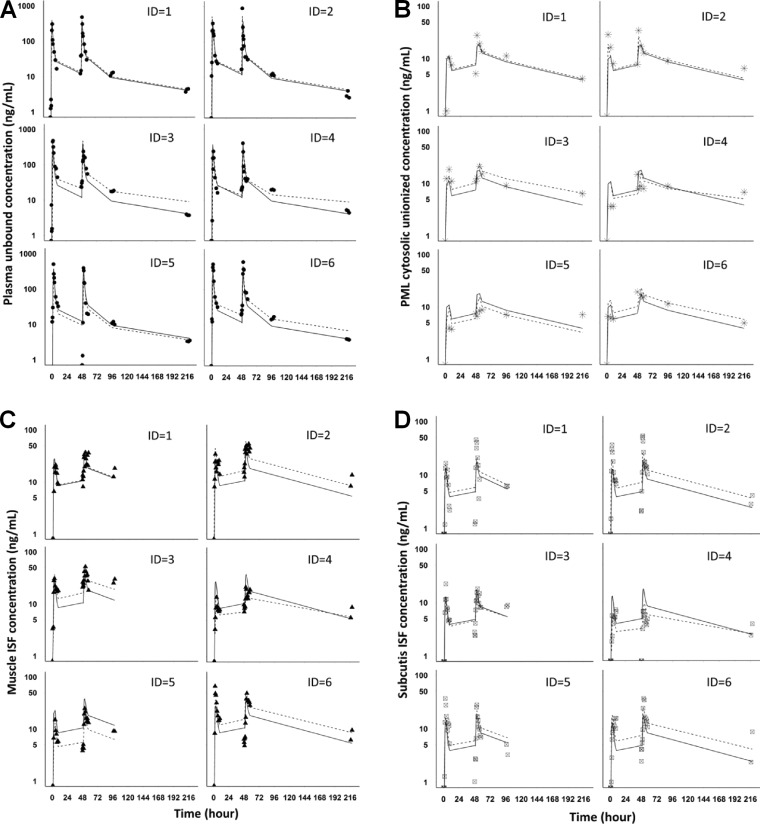
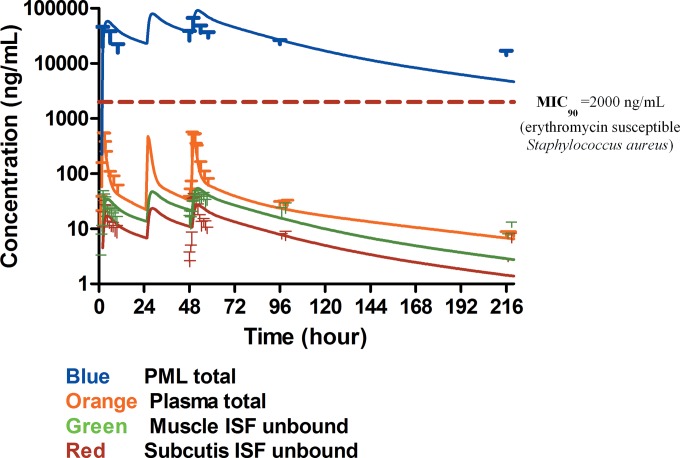
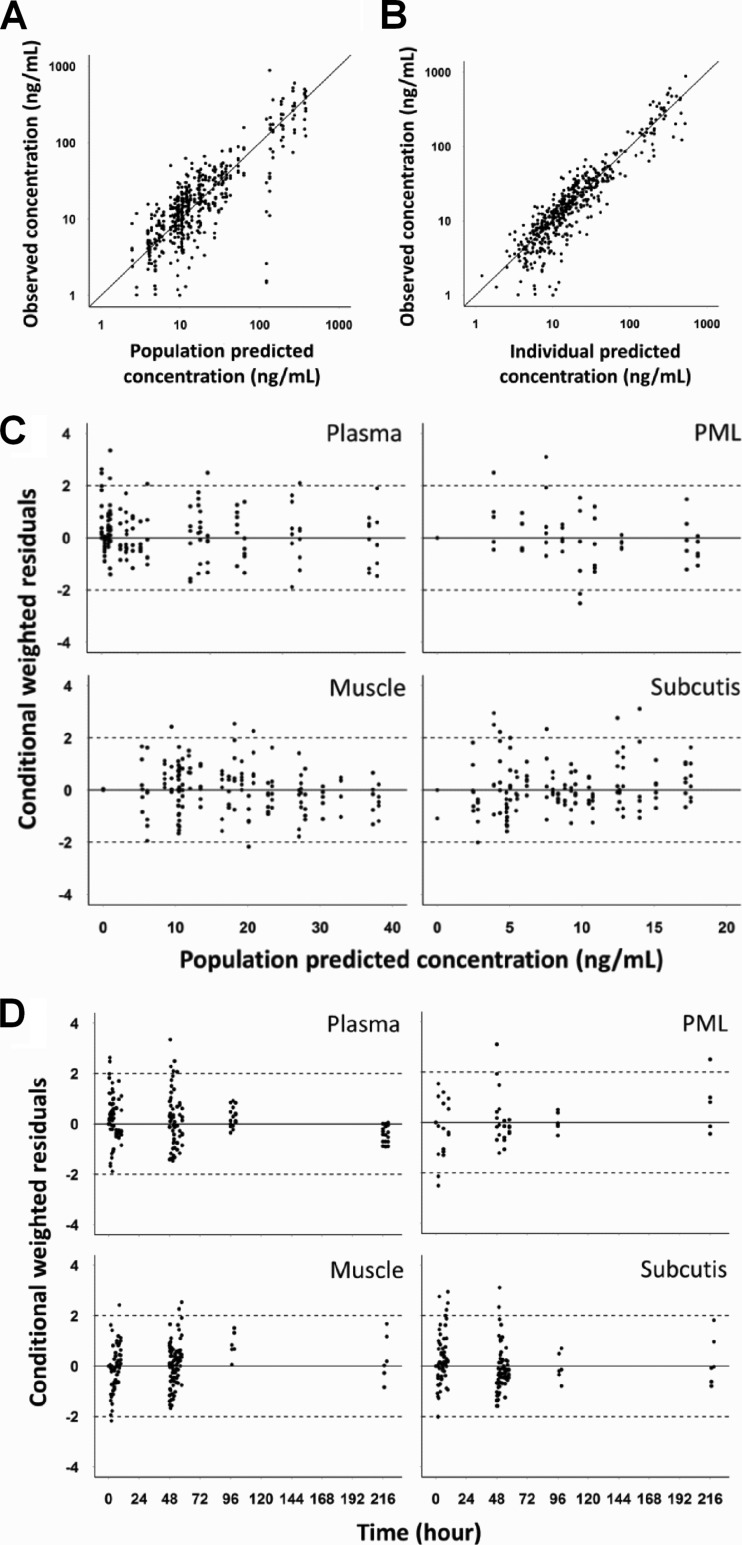
A model consisting of sampling and distribution compartments in the plasma and soft tissues, as well as a pH-driven distribution compartment in PMLs (Fig. 1), fit the experimentally determined AZM concentrations in plasma, PMLs, and the ISF of muscle and subcutaneous adipose tissue on the individual subject level (Fig. 2), as well as the population level (Fig. 3) reasonably well. Visual inspection of the goodness-of-fit plots also did not reveal any model misspecification (Fig. 4). The model parameter estimates obtained from a single estimation run are overall in good agreement with the respective bootstrap values, except for the peripheral distribution volume (Table 1), which is likely due to the small sample size and the relatively high variability in the data. Nevertheless, our model-predicted parameter values for plasma are consistent overall with those previously reported in the literature for healthy subjects (30, 31). Our findings further show that the tissue distribution factor for PMLs (DF_PML(cytosol), 52) is significantly higher than the corresponding values for muscle (DF_muscle, 0.55) and subcutis (DF_subcutis, 0.25), as would be expected, reflecting the differences in the extent of distribution into these tissues. The computed differences in the distribution factors are also reflective of the differences in the pH-mediated ionization state, which plays a major role in the distribution and accumulation of AZM in tissues. Our findings further indicate that there is significant nonspecific binding to tissues, as the inclusion of the additional distribution compartment with the same k_on (0.56 h⁻¹) and k_off (0.05 h⁻¹) values for the different tissue sites significantly improved the fit of the model to the data.

FIG 2.

Observed data and simultaneous model fitting for azithromycin in plasma (unbound) (A), PML (cytosolic unionized) (B), muscle (C), and subcutis ISF (unbound) (D) for assessment of the goodness of model fit. The symbols represent clinically measured concentrations, the solid lines represent model-predicted concentrations on a population level, and the dashed lines represent model-predicted concentrations on an individual level. ID, identification no.

FIG 3.

Model predicted time-mean concentration profile of azithromycin (solid lines) versus observed mean values (symbols) in plasma (total), PMLs (total), and the interstitial space fluid of muscle and subcutis (both unbound).

FIG 4.

Goodness-of-fit plots for the pharmacokinetic model of azithromycin observed versus population predicted concentration (A), observed versus individual predicted concentration (B), conditional weighted residuals versus population predicted concentration (C), and conditional weighted residuals versus time (D).

TABLE 1.

Parameter estimates and bootstrap values^a

Parameterb	Single run	Bootstrap (median)c	SEd	95% CIe
Fixed-effects parameters
Tlag (h)	1.45 (fixed)	1.50	0.34	(1.07, 2.45)
ka (h−1)	0.88 (fixed)	0.88	0.60	(0.61, 1.72)
CL/F (liters/h)	258 (fixed)	227	115	(71, 517)
Vc/F (liters)	160	240	561	(4.1, 1,790)
VP1/F (liters)	1,190	1,737	38,783	(262, 4,643)
QP1/F (liters/h)	207	208	82	(76, 389)
VP2/F (liters)	9,721	4,899	16,396	(84, 20,359)
QP2/F (liters/h)	101	100	55	(1.2, 214)
kin (h−1)	0.16	0.14	0.29	(9 × 10−8, 0.8)
kout (h−1)	0.15	0.10	0.05	(0.02, 0.21)
kon (h−1)	0.56	0.43	0.19	(0.18, 0.99)
koff (h−1)	0.05	0.04	0.03	(0.01, 0.10)
DFmuscle	0.55	0.67	0.70	(0.35, 3.10)
DFsubcutis	0.25	0.37	0.42	(0.14, 1.64)
DFPML(cytosol)	52	63	93	(39, 423)
Interindividual variability (%)
Tlag	17.6	18.6	8.6	(2.8, 31.1)
CL/F	29.3	22.4	45.8	(1.1, 64)
Vcentral/F	168.3	79.6	1,017	(1.6, 1,804)
kin	0.22	22.4	3,473	(0.2, 184)
DFmuscle	26.9	26.8	27.0	(8.0, 139)
DFsubcutis	31.5	31.5	69.8	(1.8, 235)
DFPML(cytosol)	0.22	9.0	35.6	(0.2, 174)
Residual variability
Plasma (proportional)	0.14	0.13	0.74	(0.08, 0.22)
Plasma (additive)	35.2	30.4	22.7	(7.2, 94.9)
Muscle ISF (proportional)	0.14	0.14	0.05	(0.05, 0.24)
Muscle ISF (additive)	0.51	0.38	0.49	(1 × 10−6, 1.37)
Subcutis ISF (proportional)	0.34	0.34	0.09	(0.21, 0.54)
Subcutis ISF (additive)	1 × 10−6	1 × 10−6	0.002	(1 × 10−6, 0.008)
PML cytosol (proportional)	0.23	0.23	0.09	(0.12, 0.48)
PML cytosol (additive)	1 × 10−6	1 × 10−6	0.003	(1 × 10−6, 0.009)

^an = 1,000.

^bSince the unbound concentrations in plasma did not equal the measured unbound concentrations in tissue ISF, a parameter termed the distribution factor for the tissue (DF_muscle, DF_subcutis, or DF_PML(cytosol)) was introduced. k_a, first-order absorption rate constant; T_lag, lag time for absorption; CL/F, apparent clearance; V_c/F, apparent volume of the central compartment; V_P1/F, apparent volume of the fast equilibrating peripheral compartment; Q_P1/F, intercompartmental distributional clearance of fast equilibrating compartment; V_P2/F, apparent volume of the slow equilibrating peripheral compartment; Q_P2/F, intercompartmental distributional clearance of slow equilibrating compartment; k_in, rate constant for unbound AZM uptake into tissue ISF or for unionized AZM in plasma uptake into PML; k_out, rate constant for the reverse process described for k_in; k_on and k_off, on and off rate constants, respectively, for nonspecific tissue binding in the tissue/PML.

^cThe bootstrap results for the T_lag, k_a, and CL/F fixed parameter estimates were based on bootstrap (n = 1,000) for unbound plasma only.

^dSE, standard error determined as the standard deviation (SD) of the bootstrap parameter distribution.

^e95% CI, 95% confidence interval computed as the 2.5th and 97.5th percentiles of the bootstrap parameter distribution.

When linking the model-predicted mean area under the concentration-time curve (AUC) values to the MIC₉₀ of clinically relevant skin pathogens (e.g., erythromycin-susceptible Staphylococcus aureus, with MIC₉₀, 2 μg/ml [32]), the total AUC_0–24/MIC₉₀ (AUC_0–24, area under the concentration-time curve from 0 to 24 h) ratios in plasma and in the ISF of muscle and subcutis were <2, while the ratios in PMLs were >50 throughout the sampling period (Fig. 3). On day 10, the AUC_0–24/MIC₉₀ ratios fell to <0.1, based on predicted plasma and tissue ISF concentrations.

DISCUSSION

Resistance to antibiotics is a major public health problem, as it leaves physicians with few or no drug choices to effectively treat patients (5, 33). A number of studies have shown that the primary reason for the development of drug resistance is the use of antimicrobials (34), even when an antibiotic is used at the recommended dose for the approved therapeutic indication(s). In recent years, this has become particularly evident for macrolide antibiotics (6, 35–37), where, for example, Malhotra-Kumar et al. (5) clearly demonstrated in a randomized, double-blind, and placebo-controlled study that following a single course of AZM, macrolide resistance increased by up to 60% and remained 14% higher even at 6 months after the end of drug therapy compared to that with the placebo. In order to better understand the pharmacokinetic/pharmacodynamic reasons behind this drug-induced increase in antimicrobial resistance, Matzneller et al. (4) determined the concentration-time course of AZM plasma (total), PMLs (total), and in the ISF of potential infection sites (muscle and subcutaneous adipose tissue) following three consecutive doses of 500 mg QD in healthy volunteers. Their findings confirmed that AZM accumulates in white blood cells, but they also showed that the respective free unbound soft tissue concentrations were markedly lower, resulting in subtherapeutic levels. The objective of our study was to develop a tissue distribution model that allows the simultaneous characterization and prediction of the concentration-time profiles of AZM in plasma, PMLs, and the ISF of muscle and subcutaneous adipose tissue by accounting for the differences in ionization at physiological pH values in the different tissues.

The findings of our study show that the dibasic nature of AZM plays a major role in its distribution into the tissues and explains its accumulation in acidic compartments of, for example, white blood cells, resulting in total cell concentrations that are >1,000-fold higher than the respective total concentrations in plasma. In particular, our calculation of AZM accumulation ratios in the subcellular compartments of PMLs are in agreement with the ratios predicted using another subcellular disposition model (23). In addition to the pH-dependent accumulation of AZM in acidic cell compartments, it has also been shown that the drug can bind in its protonated form to negatively charged phospholipids, which further increases its accumulation in tissues (22, 38). We accounted for this phenomenon by testing an additional distribution compartment for each of the tissues, i.e., muscle, subcutaneous adipose tissue, and PMLs, into which drug enters at a first-order rate, k_on, and from which it is released at a first-order rate, k_off. Significant improvement in the overall model fit for all tissues suggests that the inclusion of such a nonspecific tissue distribution compartment is necessary to appropriately account for the tissue distribution kinetics of AZM. The slow release of AZM from these tissue compartments, particularly from the acidic cell compartments, is responsible for its long terminal half-life of about 68 to 79 h (3) after multiple dosing and explains why it is still detectable 172 h after the last dose (4). Findings in the literature suggest that this long terminal half-life is associated with the turnover of neutrophils (half-life [t_1/2], ∼90 h in the uninfected state) (39), provided that ∼50 to 70% of the drug is trapped in the lysosomes at steady state, suggesting that it is almost completely unavailable for immediate back-distribution to the plasma. These findings are consistent with the results from in vitro assays, which show that cell-associated drug is released only slowly (7, 26). AZM, which is trapped within acidic cell compartments, consequently becomes available for clearance once the cell structural area is broken down during the natural turnover of white blood cells. In other words, the rate at which the drug is released from these cell compartments drives the kinetics of AZM in the terminal phase of the concentration-time profile. The fact that our calculated unionized concentrations in the lysosome and cytosol of PMLs are in the same range on day 10, i.e., the terminal elimination phase, further suggests that equilibrium exists between different subcellular compartments within the PMLs, as was discussed for the distribution of AZM between different tissue compartments (7, 26).

While the long terminal half-life of AZM certainly helps to maintain drug concentrations above the MIC of the infecting pathogen following drug administration in certain compartments, it is also responsible for exposing pathogens to subinhibitory concentrations for a very long time once concentrations drop below the respective susceptibility breakpoints. The data from Matzneller et al. (4) suggest that the total concentrations in plasma are sufficient to exceed the previously proposed AUC _0–24/MIC₉₀ value of 25 (40–42) for highly susceptible (MIC₉₀ ≤ 0.125 μg/ml) lung pathogens, such as erythromycin-susceptible S. pneumoniae. However, the concentrations in both the plasma and ISF of muscle and subcutaneous adipose tissue are insufficient to prevent infections with skin pathogens, such as S. aureus, at any point in time. These findings suggest that treatment with 500 mg QD oral AZM is insufficient to treat many skin and skin structure infections. Insufficient AZM concentrations in other tissues, such as the pharynx, where lung pathogens are located, may also contribute to off-target site emergence of resistance and/or to resistance development in bystander organisms.

It should be noted, however, that the concentration-time profiles of this study were obtained from healthy volunteers and are unlikely to accurately reflect disease conditions. This is due to the fact that chemotactic drug delivery is an important determinant for drug exposure in infected tissues, as phagocytes migrate to the infection site and increase local drug concentrations by releasing AZM from their lysosomes (43). In spite of being trapped inside the lysosomal compartments of white blood cells (WBCs) or fibroblasts (44–47), AZM retains its antimicrobial properties and, once released, is available for antimicrobial activity at the infection site (48, 49). It has also been shown that the local pH values in the ISF can be reduced, due to the metabolic activities of infiltrating neutrophils (anaerobic glycolysis) and infecting pathogens (e.g., production of short-chain fatty acids [50, 51]), which result in a further increase in local ISF concentrations. The relevance of this mechanism was demonstrated in several animal and clinical studies by showing that free AZM exposure in infected tissues was significantly higher than that in noninfected tissues (52). Ballow et al. (30) reported that the median PML count in the cantharidin-induced inflammatory blisters was about 10 times higher than that in the suction-induced noninflammatory blisters in healthy subjects. As a consequence, the mean AZM AUC in the inflammatory blisters was 2.2 times higher than that in the noninflammatory blisters, while the respective AUCs in serum were not significantly different (30). In addition, Freeman et al. (53) reported a gradual increase in the differences in AUC values obtained from inflammatory and noninflammatory blisters in healthy subjects, from ∼3-fold on day 1 to ∼30-fold on days 7 to 14. However, the impact of this phagocyte-mediated drug delivery primarily increases the antimicrobial exposure during infection. Once the infection is cleared and tissue homeostasis has been reestablished, the healthy volunteer kinetics outlined in the current paper should hold and may allow a determination of the impact of the terminal elimination kinetics of AZM on resistance development.

It should further be noted that routinely employed pharmacokinetic/pharmacodynamic (PK/PD) indices, such as the AUC_0–24/MIC ratio, are typically based on a 24-h dosing interval and do not fully account for the consequences that a very long elimination half-life may have on the emergence of resistance. While it is generally accepted that the selective pressure on a given pathogen due to the use of antimicrobial agents changes with increasing drug exposure (cf. inverted-U graphs [54, 55]), the time course of changes in the AUC is typically not taken into consideration. When plotting the number of resistant mutants per ml of growth medium (CFU/ml) versus the AUC_0–24/MIC ratio, pathogens do not undergo drug-induced selective pressure in the absence of the chemotherapeutic, i.e., at an AUC_0–24/MIC ratio of zero. As drug exposure (i.e., the AUC_0–24/MIC ratio) increases, the number of drug-resistant pathogens will also increase. At high AUC_0–24/MIC ratios, the number of resistant pathogens decreases due to the fact that enough drug is present to kill the pathogen. Once drug treatment is discontinued, AUC values and thus the AUC_0–24/MIC values decrease to a range in which drug-resistant mutants can survive. The longer the half-life of the drug, the slower the decrease in the AUC_0–24/MIC ratio, the more time the pathogen will have to adapt to drug-induced selective pressure. This rationale is in line with the finding that the emergence of macrolide-resistant streptococci was more pronounced in healthy volunteers following AZM treatment (t_1/2, ∼68 h) than following treatment with clarithromycin (t_1/2, ∼5 to 7 h) (5). In addition, it is important to realize that the actual shape of the inverted U relies, among other factors, on the following aspects: (i) the presence of resistant mutants at the start of therapy, (ii) the resistance mechanism employed, (iii) the bacterial burden, and (iv) the natural mutation frequency; also, the change in the AUC_0–24/MIC ratio can be the result of changes in both the AUC_0–24 and MIC (due to resistant clones), all of which are typically highly interlinked. It has been demonstrated that the probability of selecting preexisting antimicrobial-resistant subpopulations increases with increasing duration of antimicrobial therapy (56). It is consequently important to maximize bacterial kill as early as possible during therapy (“hit hard, hit early” [57]) and to have an antimicrobial agent cleared quickly from the body once treatment is discontinued in order to minimize the probability of creating drug-induced antimicrobial resistance, not only at the primary infection site, but throughout the body. The results of our study indicate that this goal is hard to achieve for AZM due to insufficient early drug exposure in soft tissues and its long residence time at subtherapeutic levels once treatment is discontinued; this leaves three options: (i) increase the dose, at the risk of reaching cytotoxic levels, to achieve maximum initial kill, (ii) give AZM in combination therapy in order to ensure sufficient antimicrobial activity during its long elimination phase, or (iii) do not use the drug, as AZM in and by itself is a resistance generator. Given that AZM has successfully been used for many years for the treatment of respiratory infections, it also showcases the dichotomy between clinical outcome and the emergence of resistance.

In summary, a population PK model was developed for AZM that was able to simultaneously characterize concentrations in plasma, PMLs, and the ISF of muscle and subcutaneous adipose tissue by accounting for differences in ionization at physiological pH values, nonlinear plasma protein binding, and nonspecific tissue binding. The slow release of AZM from the tissues, particularly from PMLs, is responsible for the long terminal half-life of the drug. It is also responsible for maintaining AZM concentrations at subinhibitory levels for a long period of time once drug treatment is discontinued, and it may explain the high rate at which pathogens become macrolide resistant.