Abstract
While numerous computational methods have been developed that use genome-scale models to propose mutants for the purpose of metabolic engineering, they generally compare mutants based on a single criteria (e.g., production rate at a mutant׳s maximum growth rate). As such, these approaches remain limited in their ability to include multiple complex engineering constraints. To address this shortcoming, we have developed feasible space and shadow price constraint (FaceCon and ShadowCon) modules that can be added to existing mixed integer linear adaptive evolution metabolic engineering algorithms, such as OptKnock and OptORF. These modules allow strain designs to be identified amongst a set of multiple metabolic engineering algorithm solutions that are capable of high chemical production while also satisfying additional design criteria. We describe the various module implementations and their potential applications to the field of metabolic engineering. We then incorporated these modules into the OptORF metabolic engineering algorithm. Using an Escherichia coli genome-scale model (iJO1366), we generated different strain designs for the anaerobic production of ethanol from glucose, thus demonstrating the tractability and potential utility of these modules in metabolic engineering algorithms.
Keywords: Flux balance analysis, Constraint-based model, Strain design, OptKnock
Highlights
-
•
Added modules to impose multiple design criteria for engineering algorithms.
-
•
Examples are provided to eliminate by-product secretion.
-
•
Examples are provided to control coupling between product and biomass formation.
-
•
Modules are tractable for genome-scale design.
1. Background
Genome-scale models (GEMS) are powerful tools allowing for the prediction of cellular growth, flux profiles, and mutant strain phenotypes (Orth et al., 2010). Over the last decade, with the development of new computational algorithms, GEMS have been used to guide the design of strains for biochemical production, such as biofuels and commodity chemicals (reviewed in Curran and Alper, 2012, Zomorrodi et al., 2012, Lee et al., 2012). While GEMs are valuable tools, new computational algorithms are still needed to evaluate them and apply them in new ways.
Many strain design algorithms exist that identify which network modifications are needed to improve chemical production. These modifications can involve reaction deletions (OptKnock), metabolic or regulatory gene deletions (OptGene and OptORF), reaction additions (OptStrain and SimOptStrain), or flux increases/decreases (OptReg, OptForce, CosMos, FSEOF) (Zomorrodi et al., 2012, Kim and Reed, 2010, Burgard et al., 2003, Pharkya et al., 2004, Ranganathan et al., 2010, Patil et al., 2005, Pharkya and Maranas, 2006, Cotten and Reed, 2013, Choi et al., 2010, Kim et al., 2011). The bi-level optimization approaches used to identify these modifications can be computationally expensive and recent efforts have improved their run-time performances (Patil et al., 2005, Kim et al., 2011, Ohno et al., 2013, Lun et al., 2009, Yang et al., 2011). Many of these metabolic engineering algorithms focus on improving the desired chemical production when the proposed mutant is operating at its maximal growth rate. By coupling chemical production to growth, selection for growth rate using a chemostat or sequential batch cultures can enrich for strains with increased chemical production (Fong et al., 2005). One such algorithm, OptORF, is used extensively in this work (Kim and Reed, 2010). The OptORF algorithm extends upon OptKnock by using gene rather than reaction deletions as potential modifications. By accounting for gene and transcriptional regulatory network information, OptORF proposes deleting or overexpressing metabolic or regulatory genes (as opposed to reaction level deletions proposed by OptKnock) to increase chemical production. By doing this, OptORF avoids designs that would be impossible to implement, due to genetic interactions between reactions or regulatory effects.
While metabolic engineering methods have been successful (Curran and Alper, 2012, Ranganathan et al., 2010, Fong et al., 2005, Yim et al., 2011), most of these approaches cannot consider the ramifications of undesirable suboptimal flux distributions (e.g. production with low productivity) (Patil et al., 2005, Feist et al., 2010, Lin et al., 2005, Sánchez et al., 2005, Vadali et al., 2005), or production phenotypes at or near stationary phase in batch cultures. Additionally, these algorithms are limited in their ability to tailor a strain׳s behavior to address more complex problems (e.g., the co-utilization of multiple substrates (Gawand et al., 2013, Lian et al., 2014, Trinh et al., 2008) or elimination of undesirable by-products (Aristidou et al., 1994; Eiteman and Altman, 2006; Jantama et al., 2008; Zha et al., 2009)). Consequently, while these approaches are valuable in designing adaptive evolutionary strains based on single criteria (e.g., high production at maximal growth rates), they often lack the ability to efficiently propose strains meeting multiple design criteria that are of interest to investigators. To address these problems in small networks, techniques such as constrained minimal cut sets (Hädicke and Klamt, 2011) can be used to allow researchers to meet additional design criteria (e.g., elimination of undesired by-products) without affecting the desired chemical production phenotype. Recent advances allow enumeration of the smallest minimal cut sets in genome-scale networks, from which constrained minimal cut sets can be identified (von Kamp and Klamt, 2014). However, all minimal cut sets can still not be enumerated for genome-scale networks, and the smallest minimal cut sets identified first might not correspond to constrained minimal cut sets meeting additional design criteria. Additionally, strategies for finding constrained minimal cut sets that consider transcriptional regulation, media selection or degree of coupling between biomass and chemical production have not been developed.
Previously, we developed the forced coupling algorithm (FOCAL) to identify conditions (e.g., gene deletions or media conditions) that ensure directional coupling between two fluxes (flux through vx implies flux through vy) (Tervo and Reed, 2012). By changing media conditions or deleting genes, FOCAL affects the shape of the resulting feasible solution space. We also showed how FOCAL can be modified to design a mutant strain that must co-utilize xylose and glucose simultaneously in order to grow. While these modifications were interesting, they did not work to increase the overall productivity of the organism since no metabolic engineering objective was included. Moreover, this approach could only enforce directional coupling between fluxes which is often an overly stringent condition for metabolic engineering strain designs.
Recently, Ohno et al. (2013) used shadow prices from flux balance analysis (FBA) solutions to guide a greedy algorithm for increasing chemical productivity as reaction deletions are added. Double deletion mutants with the top desired shadow prices (which indicate the rate of change in growth divided by the rate of change in chemical production) were used as “parent” strains to find triple deletion knockouts with the best shadow prices. This greedy search process, called FastPros, was repeated for up to 25 knockouts, and for each iterative screening step, any sets of deletions which resulted in a non-negative shadow prices (indicating coupling between growth and chemical production) were stored as candidates for further analysis and excluded from further screening. The authors then used OptKnock to maximize chemical production using only the stored reaction knockouts found by their FastPros process. Because they use a greedy algorithm, their method does not guarantee that the set of knockouts with the highest shadow prices are discovered. Additionally, since the authors use OptKnock to propose strain designs, their approach does not control or optimize the degree of coupling between chemical production and cellular growth when mutants are proposed.
Here, we have developed modules Feasible Space Constraint (FaceCon) and Shadow Constraint (ShadowCon) modules for controlling the shape an organism׳s feasible space. These modules allow many additional types of design criteria to be considered besides directional coupling. These modules can be easily added to mixed integer linear adaptive evolution metabolic engineering algorithms to incorporate additional design criteria, while retaining the original objective of the method (e.g., coupling growth and chemical production). Since there are often many possible solutions to these strain design algorithms, embedding these modules allows only the subset of those mutants to be found if the criteria associated with these modules is met. Such filtering is needed as models become larger and the computational cost (i.e., CPU time) of generating numerous strain designs increases, due to the combinatorial explosion associated with increasing numbers of integer variables and integer cuts needed to find alternate solutions. To date, the only type of filtering that can be done works to prevent finding solutions that have large ranges of chemical production at the maximum growth rate (Feist et al., 2010, Tepper and Shlomi, 2010).
FaceCon modules are included as additional inner optimization problems and ensure that any proposed mutant cannot operate within a user-defined region (i.e., no feasible flux distribution can exist within a user-defined region). By defining this excluded region, various feasible space characteristics can be enforced. Below we describe three FaceCon modules:
-
1.
Coupling module: This module allows a researcher to enforce different types of coupling (directional or weak) between a flux of interest (vy) and another flux (vx) depending on the formulation and parameter selection. This module can be used to find mutants with directional coupling (i.e., flux through vx implies flux through vy for all values of vx (Burgard et al., 2004)) or weak coupling (where flux through vx implies flux for vy only for some positive values of vx). Depending on how the coupling module is implemented one can require mutants having directional coupling, weak coupling, or either directional or weak coupling. The result of any of these implementations is that a defined portion of the vx axis is excluded from the solution space of a proposed mutant.
-
2.
Chemical level module: The chemical level module ensures proposed mutants meet criteria associated with the production level of a chemical of interest, vy (e.g., a desired product or undesired by-product). This module finds mutants whose solution space excludes solutions with vy below (or above) a user-defined threshold (β) within a defined region (e.g., vy must be greater than β when vx is greater than vmin).
-
3.
Direct constraint module: This module is the most comprehensive and with proper parameter selection can encompass the functions of the two previous FaceCon modules. This module allows the user to define a particular region that must be excluded from the solution space of any proposed mutant; thus, the researcher is able to directly influence the solution space of any mutant proposed by a metabolic engineering algorithm.
In the following sections, we detail the application, function and relevant parameters for each of these FaceCon modules. We then introduce the concept of shadow constraint (ShadowCon) modules, which can be used to control the degree of coupling once coupling between two fluxes occurs. To illustrate each module׳s functionality and potential use, we have included the FaceCon and ShadowCon modules as additional inner problems within the OptORF algorithm, to find metabolic gene deletions that couple growth and chemical production and that satisfy additional module criteria. Additionally, to demonstrate the methods are applicable on genome-scale networks we have applied them to identify mutants for ethanol production using the Escherichia coli model, iJO1366 (Orth et al., 2011). We demonstrate that when there are multiple solutions to metabolic engineering algorithms, the addition of FaceCon and ShadowCon modules allows only those mutants that meet additional criteria to be identified.
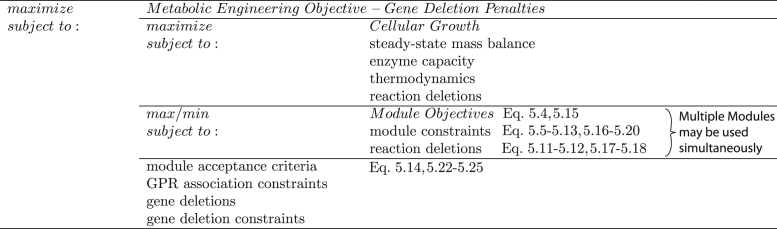
2. Methods
Most algorithms developed for metabolic engineering focus on maximizing chemical production assuming maximum cellular growth. We have developed FaceCon and ShadowCon modules that can be integrated into existing mixed integer linear adaptive evolution metabolic engineering algorithms which focus on deletions (e.g., OptKnock, OptORF, and their tilted variants, as well as RobustKnock) to allow for greater control over strain designs (Fig. 1) and to filter out designs with undesirable suboptimal behaviors. The resulting bi-level optimization problem is converted into a mixed integer linear programming problem (MILP) using duality theory. It is important to note that the modules and the metabolic engineering algorithm are completely independent subproblems (see Supplementary materials Fig. S5), which only share the same feasible space (altered by deletions in the outer problem) and integer variables. All continuous variables (e.g., fluxes) are unique to each subproblem. Interestingly, many of these bi-level algorithms include a maximum growth subproblem that determines chemical production capabilities at the maximum growth rate. This subproblem itself can be considered a module of the outer problem that selects gene deletions or reaction knockouts that constrain the maximum growth subproblem. Consequently, the FaceCon modules could be run in isolation of the maximum growth subproblem if chemical production is not of concern. Additionally, because these modules and the metabolic engineering algorithm share integer variables the combinatorial complexity of the problem does not substantially increase with addition of FaceCon or ShadowCon modules. Instead only additional linear constraints are added which should result in polynomial time scaling as the problem size increases.
Fig. 1.
Modules added as inner problems to extend existing metabolic engineering algorithms. Figure demonstrates how FaceCon and ShadowCon modules are implemented within a metabolic engineering algorithm, in this example OptORF. All module variables (including fluxes) are completely independent of the metabolic engineering variables, with the exception of reaction deletions which are shared across all subproblems. By being modular, these constraints can be added to most FBA-centric approaches and can be mixed and matched to include additional strain design criteria.
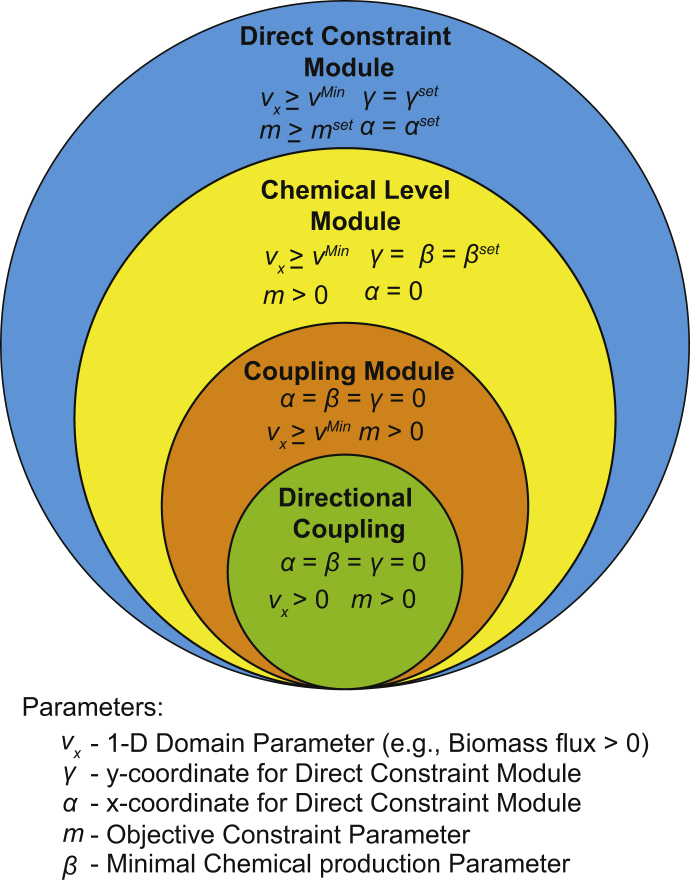
For simplicity, we describe only the direct constraint module since the coupling and chemical level modules can be implemented using the same equations with different parameter values (Fig. 2). Nonetheless, alternative formulations of the other FaceCon modules are provided in Supplementary materials. While all FaceCon modules are written as minimization problems, they can easily be modified to maximization problems (e.g., if one wishes to prevent by-product formation). Additionally, while all modules are included with acceptance criteria written as constraints – thus, not meeting the acceptance criteria forces the problem to be infeasible – such constraints can be reformulated as penalties within the outer metabolic engineering objective, which can be especially useful if finding a feasible solution is particularly challenging.
Fig. 2.
Hierarchy of FaceCon modules. The above Venn diagram depicts the set of constraints and parameter values that are used in a given FaceCon module. As can be seen, many modules are subsets of the more comprehensive direct constraint module. The necessary direct constraint parameter values are provided to reproduce the functionality of each of the other FaceCon modules.
2.1. Metabolic engineering algorithm
All modules were incorporated into a gene-deletion focused OptORF (Kim and Reed, 2010) (i.e., no regulatory information was considered) and the resulting MILP was written in the General Algebraic Modeling System (GAMS) and solved using CPLEX. A gene deletion penalty of one was used in the OptORF objective and a maximum of 20 gene deletions was used. The standard untilted inner objective function (maximize growth) was used, unless noted otherwise. In cases where a tilted objective function was used in OptORF (presented in Supplementary materials), the inner objective function was maximize growth rate minus 0.001 times the chemical production rate. Each problem was run for ten thousand seconds (except for the ShadowCon problems which were allowed to run for up to twenty thousand seconds) or until a global optimum was found, whichever occurred first. For the small illustrative network global solutions were found immediately. Using the iJO1366 model, the solver used all the time allotted when the objective for OptORF was tilted (with and without) FaceCon or ShadowCon modules. Similarly, the untilted OptORF required all the time permitted when FaceCon or ShadowCon modules were included. For untilted OptORF without additional modules (stand-alone OptORF), the first six solutions found were each found in ~20–25 min; however the next four solutions all took the time allotted. To improve computational performance, all subunits except one were retained (i.e., they cannot be deleted) and all isozymes but one were removed by fixing the relevant binary variables to one and zero, respectively prior to solving (as described previously (Hamilton and Reed, 2012)).
2.2. FaceCon modules
The direct constraint module is the most comprehensive of the FaceCon modules, since with proper parameter selection it can be used to formulate the coupling and direct chemical modules. In the direct constraint module the ratio of is minimized (or maximized). As a result, to ensure the objective remains positive, all fluxes, vj, are broken into their forward and reverse components (Eq. (1)) and normalized by the variable t (Eqs. (2), (3)).
| (1) |
| (2) |
| (3) |
Using these transformations, the direct constraint module has the following form:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
where α and γ are parameters corresponding to the coordinates on a vx–vy plane through which a line with the smallest (or largest) calculable slope (m) is found that also goes through the feasible space within a user-defined region (Eq. (7)). Eq. (5) enforces the steady-state material balances in the transformed flux space. Here Sij is the stoichiometric matrix where i and j refer to metabolites and reactions, respectively. M and R are the set of all metabolites and reactions within a model. Eq. (6) is a linear rearrangement of Eqs. (2), (3). Eq. (7) allows the user to define the region where the feasible space constraints will be enforced (e.g., where vx is greater than vmin). Thus, for the module to be feasible there must be at least one non-trivial flux distribution within the user-defined region. Additional optional transformed constraints Eq. (8) can be included that specify the user-defined region (or domain) over which the feasible space constraints apply (e.g., , such a constraint can be useful to define multiple excluded regions with varying slopes, m). Eqs. (9), (10), (11), (12) limit the flux of any reaction to its bound or to zero if the reaction has been deleted by the metabolic engineering algorithm (indicated by the binary variable aj being zero). In order to prevent the module from being infeasible or unbounded, t must be finite and positive and so vx must be greater than α (Eq. (11)).
The direct constraint module is included in the metabolic engineering algorithm as an inner problem (Fig. 1). The variables in the direct constraint module are independent of the variables in other inner problems (i.e., the optimal flux distributions for the different inner problems are not necessarily the same). To ensure the module satisfies additional design criteria, the minimum slope, m, needs to be greater (or less than in the case of maximization) than, mset, defined by the user. This criterion is enforced by either including a constraint (Eq. (14)) in the outer problem of the metabolic engineering algorithm or by modifying the outer objective to favor mutants that satisfy this acceptance criterion. To convert the resulting bi-level problem to a single level MILP, the inner optimization problem(s) can be replaced by the set of their primal and dual constraints and equating the primal and dual objectives.
| (14) |
2.3. ShadowCon module
In addition to feasible space constraints on the allowed feasible region, constraints can also be applied to the initial slope where coupling begins along the vx axis using the following formulation:
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
Here, vx is maximized while satisfying steady-state mass balances (Eq. (16)), flux lower and upper limits (Eqs. (17), (18)), and an additional constraint fixing vy (Eq. (20)) such that the optimal solution to Eqs. (15), (16), (17), (18), (19), (20) is positioned near the point where the degree of coupling between vy and vx (i.e., how a change in vy will affect the maximum value of vx) should be calculated.
While developed independently, the above optimization problem is similar to that used in FastPros (Ohno et al., 2013). However, in contrast to FastPros the ShadowCon module is included directly as an inner subproblem in the metabolic engineering algorithm (Fig. 1). Using this inner subproblem, the degree (or slope) of coupling for an OptORF proposed mutant can be controlled. Moreover, because ShadowCon uses a mixed integer formulation instead of a greedy algorithm, our approach will not get stuck in local maxima or minima if strains with a large or small shadow price are desired.
The bi-level problem, created by including a ShadowCon module into a metabolic engineering algorithm (like OptORF or OptKnock), is converted to a single level MILP, by replacing the inner optimization problem(s) with their set of primal and dual constraints and equating the primal and dual objectives. The dual variable (or shadow price) corresponding to Eq. (20) is the partial derivative representing how the maximum value for vx would change if the value for ε (or vy) changed. Using this relation, we can relate the slope (m) for the line of coupling between vy and vx as follows:
| (21) |
Thus, ushadow can be used as a proxy for the potential change in the vy with respect to a change in vx. In order to ensure that the optimal value for ushadow is unique (i.e., ushadow takes the value of the inverse slope of the line of interest), it is critical to select a value of ε such that the optimal solution ensures that Eq. (20) is binding, which is guaranteed for any feasible solution, and that vy is a basis variable. To accomplish this, it is sufficient to pick an ε such that the new optimum does not fall upon a preexisting pivot (i.e., if the solution is not degenerate, the dual solution is unique (Sierksma, 2002)). See Supplementary materials for extended explanation and example problem. For example, when both ε and vyLowerLimit are zero, ushadow becomes unbounded from above and thus may underestimate the slope, m. This occurs because Eqs. (18), (20) are simultaneously binding for vy. Consequently, their two shadow prices can both be increased in conjunction, counteracting one another such that there is no net increase in the objective. To avoid this problem we set the value for ε equal to 0.001.
Once the primal and dual for the ShadowCon module have been included in the metabolic engineering algorithm, acceptance criteria constraints (limiting the value for m) can be included in the outer problem (Eqs. Hädicke and Klamt, 2011, (23)):
| (22) |
| (23) |
where mmin and mmax are the minimum and maximum allowable slopes, respectively. Additional optional constraints for the ShadowCon module can be added to the outer problem to mimic simple coupling conditions and further filter possible solutions:
| (24) |
| (25) |
Here Eq. (24), makes use of user-defined parameters, and , to define a region where coupling between vx and vy must occur. Alternatively, Eq. (25), can be added to require a minimum distance between the optimal OptORF solution and where coupling actually begins.
3. Results and discussion
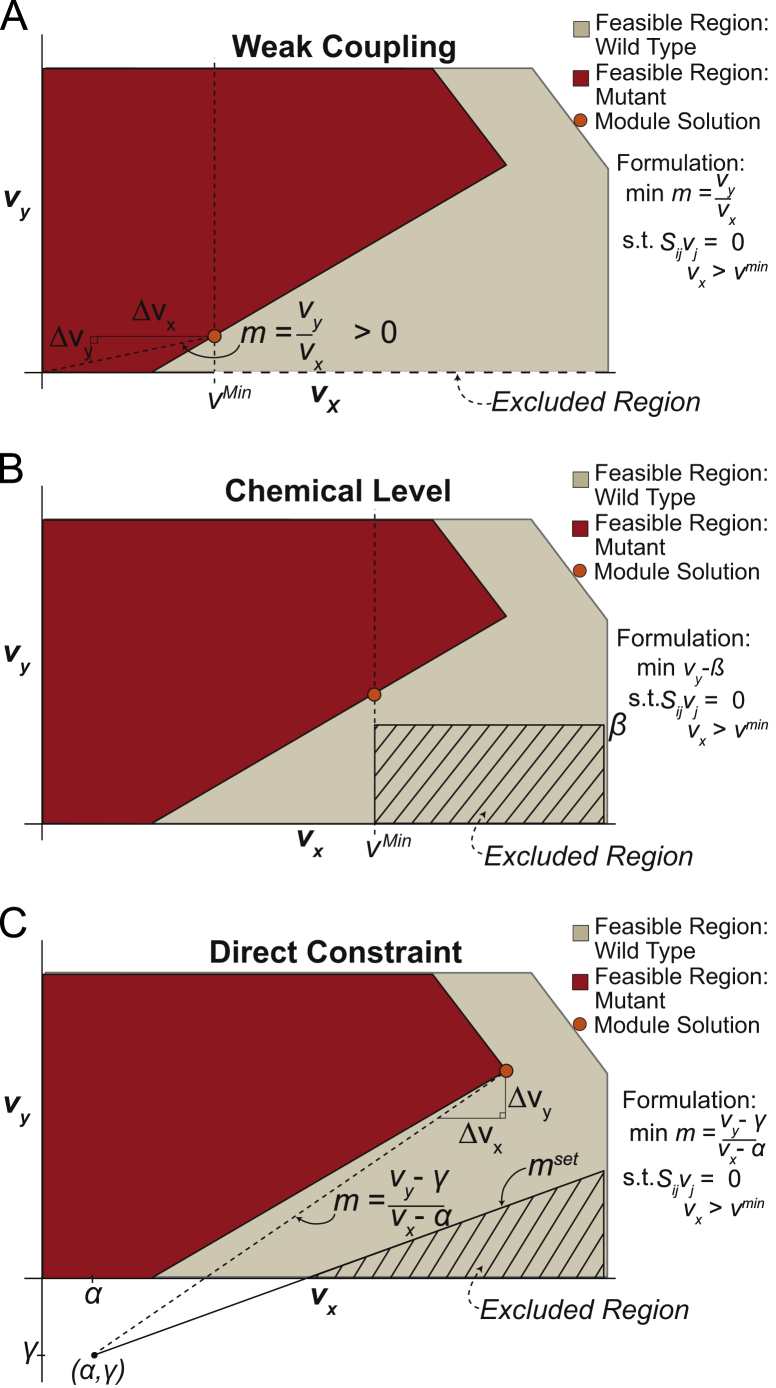
FaceCon modules are sub-problems, formulated such that their resulting inner objective values can be used to test acceptance criteria of mutants being evaluated by the strain design algorithm (see Fig. 3). While the formulations for each module are distinct they all share certain features. Firstly, all FaceCon modules check that no feasible solution exists within a user-defined region (e.g., region where flux vx is greater than vmin). Consequently, FaceCon modules create a mandatory feasible region (i.e., a region within which a non-trivial feasible solution must exist for any mutants proposed by the strain design algorithms). By evaluating these regions, FaceCon modules allow researchers to find mutants that meet additional criteria, which would not be possible using existing metabolic engineering algorithms alone. Below we describe the parameters and unique features of each FaceCon module. A summary of all modules included in this paper and their usage is provided in Table 1.
Fig. 3.
Examples of FaceCon modules and their effects on a strain׳s feasible region. The effects of the coupling (A), chemical level (B) and direct topology (C) modules are shown to illustrate each module׳s intent and capabilities. Here the orange dot indicates the optimal solution that would be found from including each module in OptORF. The dashed lines and hatched regions indicate the excluded regions imposed by the FaceCon modules.
Table 1.
Summary of modules and their usage.
| Module name | Description | Parameters | Potential usage |
|---|---|---|---|
| FaceCon | |||
| Coupling module | Module allows researcher to enforce weak or directional coupling. To enforce only weak coupling a second sub-problem is added | vmin, δa, σa | Can be used to define the nature of coupling proposed by metabolic engineering algorithms. Can be useful when proposals tend to generate sickly mutants |
| Chemical level module | Module allows researchers to define minimal or maximal chemical production limits, β, beyond a user defined point vmin | vmin, β | Can be used to eliminate undesired by-products or to define minimal chemical production criteria |
| Direct constraint module | Module allows researchers to create an exclusion region of their own design, defined by the line going through the point (α,γ) with the slope mset | vmin, α, γ, mset | Can be used to propose co-production or co-utilization of metabolites. All FaceCon modules are special cases of the direct constraint module |
| Other | |||
| ShadowCon module | Module allows greater control over the degree of coupling once it has initiated | mmin, mmax | Can be used to vary the intensity of selective pressure on a reaction when coupled to growth rate |
Parameters are only used when additional module sub-problems are required (e.g., when only weakly coupled mutants are desired).
3.1. Coupling module
The coupling module (Fig. 3A) works to enforce directional or weak coupling between two fluxes (vx and vy, where a non-zero vx implies a non-zero vy). By altering the formulation and parameters, the coupling module can be used to identify mutants with directional coupling (i.e., vx implies vy for all values of vx – effectively FOCAL sans media selection constraints), weak coupling (i.e., vx implies vy if vx is greater than a positive, user-defined value, vmin, and vx does not imply vy for some non-zero value of vx less than vmin), or either directional or weak coupling. Inclusion of such modules results in mutants having an infeasible region containing the vx-axis above vmin (for the directional coupling case vmin is zero). A coupling module adds a mixed-integer linear program (MILP) sub-problem to the strain design algorithm, and finds the minimum ratio (m) of vy/vx within the user-defined region (vx>vmin). To meet the acceptance criterion of this module, m must be non-trivial. In addition, to only find mutants with weak coupling (i.e., there also exists some vx>0 where vy can be 0 and thus the fluxes are not directionally coupled) another sub-problem is added to ensure that vy can be zero for some values of vx less than vmin. A coupling module determines the line going through the origin with the smallest slope that lives in the feasible space where vx>vmin for a given mutant.
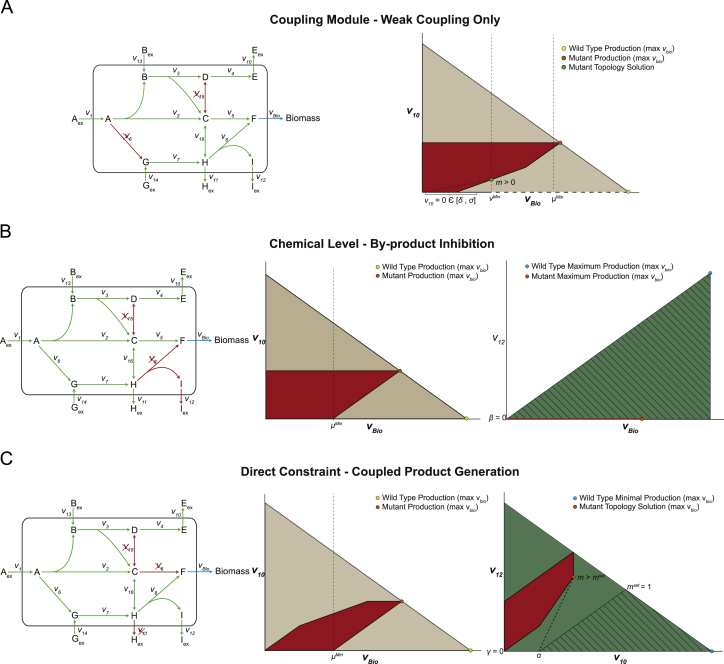
An illustrative example (Fig. 4A) is provided to demonstrate the functionality of the coupling module to only find mutants with weak coupling (we have previously shown examples of directional coupling involving substrate co-utilization (Tervo and Reed, 2012)). In this example, OptORF is used to design a strain that maximizes the production of Eex (v10) while maintaining a minimum biomass production rate (vbio>μmin). In addition, two sub-problems were added such that a proposed mutant found by OptORF must have a weak coupling phenotype (coupling between v10 and vbio occurs only for certain values of vbio). An optimization sub-problem is added which minimizes the ratio of v10/vbio, when vbio>vmin. (Note that by setting lower values for vmin a stronger selection pressure for chemical production can be achieved since more values of vbio must result in chemical production.) Then another sub-problem is added to ensure that directional coupling does not occur for some value of vbio within a defined range (i.e., v10=0 for δ<vbio<σ, where δ and σ are user-selected values greater than 0 and less than vmin, respectively. Adding these constraints guarantees that coupling will not occur for values of vbio≤δ). The inclusion of this second sub-problem guarantees that there is at least one solution where v10 is 0 and cellular growth is still possible, thus ensuring the weak coupling criteria is met. Such solutions may be of value when coupling is desired but directional coupling solutions are thought to be too deleterious to the cell׳s fitness. The solution proposed when these two sub-problems are included in OptORF involves knocking out fluxes v6 and v15, which works to couple both Aex and Bex consumption to the production of Eex while allowing Gex to be directed entirely to biomass production. With these fluxes eliminated, simultaneous consumption of Aex, Bex, and Gex will result in Eex production at the maximum growth rate; however, consumption of Gex alone can still proceed without any Eex production. The feasible region for this mutant growing in the presence of Aex, Bex, and Gex is shown in Fig. 4A.
Fig. 4.
Illustrative examples of FaceCon modules. OptORF was used in conjunction with the FaceCon modules to create unique phenotypes that would be difficult to produce by OptORF alone. (A) A coupling module was added to guarantee that weak coupling would occur but not directional coupling. The dashed line on the x-axis indicates where the excluded region begins. (B) The chemical level module was added to prevent any production of the undesired compound Iex. The hatched region indicates the excluded region imposed by the module. (C) The direct constraint module was added to force the co-production of Eex and Iex for large growth rates. For all panels, red arrows and x׳s on the network map indicate a reaction knockout. Dotted vertical lines show the μmin and vmin values used in OptORF and FaceCon modules, respectively. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)
3.2. Chemical level module
The chemical level module works to find the minimum (or maximum) flux value through a reaction of interest (vy, e.g., chemical production) when flux through another reaction (vx, e.g., growth) exceeds some threshold (vmin). When this module is embedded in a strain design algorithm the resulting strain proposed must have a value of vy greater (or less) than a user-defined requirement, β, when vx is greater than vmin (Fig. 3B). This type of module results in a rectangular excluded region of height, β. Such a module can, for example, be useful in guaranteeing a minimum amount of production at certain growth rates (and hence a minimum productivity) or limiting the production of undesired by-products. In the illustrative example, the chemical level module was used in conjunction with OptORF to maximize the production of Eex while guaranteeing that no undesired by-product Iex was produced (Fig. 4B). To ensure a mutant with this phenotype was proposed, the chemical level module was used to calculate the maximal amount of flux through reaction, v12. Since no by-product formation was desired, both vmin and β were set to zero resulting in an excluded region across the entire vbio−v12 sub-space. With these additional criteria, OptORF proposed knocking out fluxes v15 and v8, which prevents production of Iex and also results in weak coupling between v10 and vbio. The feasible region for the mutant is shown in Fig. 4B.
3.3. Direct constraint
The direct constraint module (Fig. 3C) is the most multifunctional of the FaceCon modules described. This module creates a line through the point (α,γ) with slope mset; all points below (or above) the line must be excluded from the feasible region of any proposed mutant. The module works by determining the line with the smallest (or largest) slope (m) going through a point within the user-defined region of the feasible vx−vy sub-space and the point, (vx,vy)=(α,γ) where α and γ are defined by the user. Once this slope has been calculated, a proposal is accepted on the condition that m is greater (or less) than a user-defined slope, mset.
To demonstrate how the direct constraint module works, an illustrative example is provided in Fig. 4C. In this example, the direct constraint module is applied to ensure that beyond a given production of Eex there will be equivalent or greater production of Iex, effectively forcing co-production of two compounds. This type of module could be used when the proposed strain needs to generate two products or co-utilize two substrates. To force such a mutant to be proposed by OptORF, we defined a point on the x-axis of the v10−v12 sub-space, (α,0), and used a slope acceptance criterion of mset=1. The resulting strain design is an interesting triple knockout mutant (missing fluxes v5, v11, and v15) where maximal cellular growth requires both Eex and Iex production. In this case, deletion of v15 ensures that production of Eex generates one or two molecules of C from Bex or Aex, respectively. The C molecules produced can only be converted into biomass with Iex as a by-product when v5 and v11 are deleted. Thus, an ideal strain is created such that the cell׳s biological imperative is coupled to the co-production of two chemicals. The feasible region for the mutant is shown in Fig. 4C.
3.4. Application of FaceCon modules to a genome-scale E. coli model
To demonstrate the scalability of FaceCon modules to genome-scale problems, we applied OptORF in conjunction with FaceCon modules to design strains for anaerobic ethanol production from glucose in E. coli using the iJO1366 model (Orth et al., 2011). A maximum glucose uptake rate (GUR) of 10 mmol/gDW/h was used. Fig. 5 shows the different strain designs and solution space topologies that can be generated using FaceCon modules without needing to exhaustively query the set of stand-alone OptORF (OptORF without any FaceCon modules) solutions using integer cuts. As a baseline, we first show a stand-alone OptORF strain design׳s feasible region (Fig. 5A). While we did not use a tilted objective function (Feist et al., 2010) for the solutions provided in Fig. 5, Fig. 6, this can easily be incorporated into OptORF with a FaceCon module (see Figs. S6 and S7 in supplemental materials for tilted solutions).
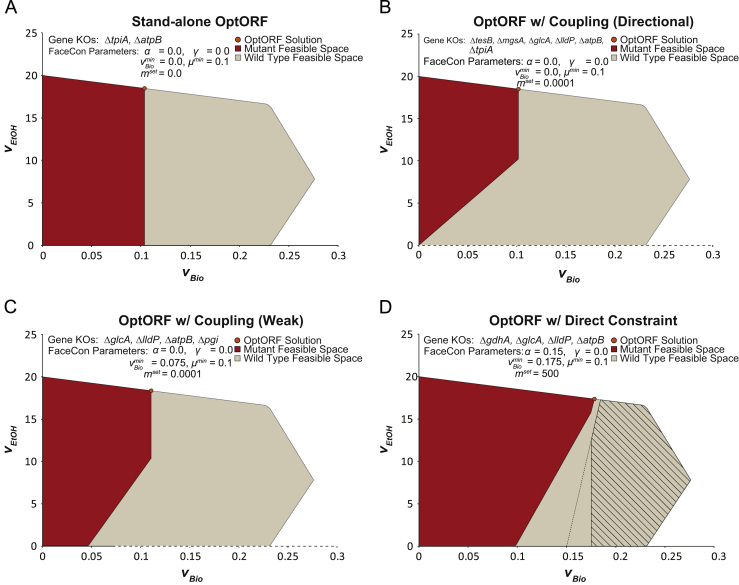
Fig. 5.
Application of FaceCon to iJO1366. Parameters used in FaceCon modules for each case are provided above the mutant feasible regions. Dashed lines and hatched regions indicate excluded regions imposed by the FaceCon modules. The module included in OptORF for each case was (A) no FaceCon modules, (B) coupling module (only directional coupling), (C) coupling module (only weak coupling), and (D) direct topology module. OptORF without any modules (A) finds a lower chemical production phenotype compared to (B) and (C) due to gene deletion penalties used in OptORF. Additionally, no tilt was applied to the OptORF algorithm resulting in a strain design where there is no coupling between biomass and ethanol production. Alternate solutions exist, and replacing the glcA and lldP deletions with dld and ldhA deletions has a negligible effect on the feasible regions shown in panels (B), (C), and (D).
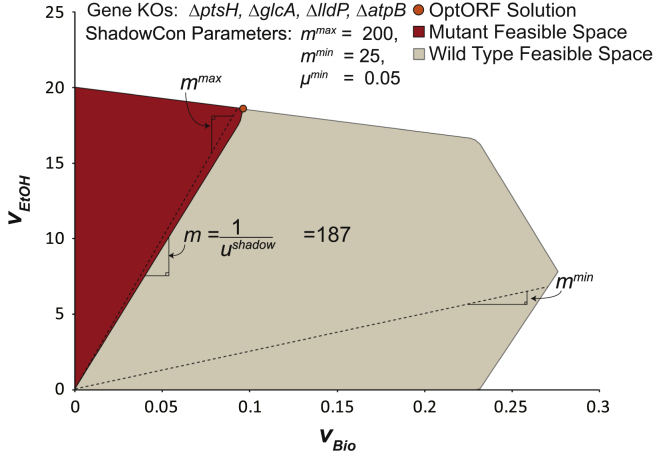
Fig. 6.
Application of ShadowCon module to iJO1366. The ShadowCon module works to limit the slope of the line at the onset of coupling between ethanol and biomass production. Using the dual variable, ushadow, associated with this line it is possible to constrain the slope, m, between a user-specified upper (mmax) and lower (mmin) bound (dashed lines).
Since no tilt or maximin modification was added to OptORF (Feist et al., 2010, Tepper and Shlomi, 2010), the double knockout mutant (ΔtpiA ΔatpB) proposed by OptORF can have different amounts of ethanol production at the maximum growth rate (including no production), resulting in no coupling between biomass and ethanol production (ethanol production ranges between 0 and ~18.5 mmol/gDW/h at the maximum growth rate). This lack of coupling is because lactate can be produced as an alternative to ethanol during maximum growth. All the knockouts that are shown in Fig. 5 secrete ethanol as a way to recycle NADH and NADPH anaerobically. Under fermentation conditions too many protons are generated internally and so ATP synthase operates in reverse, translocating protons from inside to outside the cell. Consequently, deleting ATP synthase (atpB), which appears in all solutions in Fig. 5, Fig. 6, forces the model to find alternate ways of dissipating intracellular protons. Converting pyruvate into ethanol or lactate consumes one cytoplasmic proton per NADH recycled, while an alternative path for consuming NADPH converts carbon dioxide into formate (using pyruvate formate lyase, pyruvate synthase, and flavodoxin reductase) and does not consume any cytoplasmic protons in the process. Consequently, the atpB deletion blocks this formate production pathway at the maximum growth rate and increases ethanol or lactate production so that more intracellular protons are incorporated into secreted products (ethanol or lactate). Deleting triose-phosphate isomerase (tpi) pushes flux through the Entner–Doudoroff pathway (instead of glycolysis), reducing ATP yields from glucose and thereby enhancing ethanol production by reducing maximum growth rates.
We next used a coupling module to generate a strain where there is always directional coupling between ethanol and biomass production (i.e., coupling module set strictly for directional coupling). To accomplish this, the minimal slope of a line in the feasible region going through the origin is calculated and a positive slope is required for acceptance. The feasible region for the resulting six gene deletion mutant is provided in Fig. 5B. This mutant also includes the tpiA and atpB knockouts, but also has deletions to remove alternative pathways for recycling NAD(P)H. The glcA and lldP knockouts prevents lactate production (which can also be accomplished by deleting the lactate dehydrogenases, dld and ldhA – an alternative solution), while the mgsA knockout, which codes for methylglyoxal synthase, prevents dihydroxyacetone from being converted to and secreted as (R)-1,2-propanediol. The final knockout of tesB, a fatty-acid CoA thioesterase, prevents flux through 3-hydroxyacyl-CoA dehydrogenase and acyl-CoA dehydrogenase, and secretion of fatty acids (e.g., hexanoate) which consumes reductant. At maximum growth, the model predicts that some l-valine can be produced instead of ethanol and thus there remains a range for ethanol production (between ~10.2 and ~18.5 mmol/gDW/h).
While the fully coupled phenotype may be ideal (since any growth requires ethanol production), the mutant requires numerous deletions and may initially be sickly. To relax the design criteria, we found a weakly coupled strain where growth and ethanol production are coupled when vBio is greater than 0.075 h−1. The four gene knockout mutant proposed (Fig. 5C) would be genetically simpler to construct and, while the selective pressure is not as strong as for the directionally coupled mutant, the ethanol production rates after adaptive evolution should be nearly equivalent (between ~10.4 and ~18.4 mmol/gDW/h). While this mutant also includes the atpB, glcA and lldP knockouts from the directionally coupled case, interestingly, this mutant uses the pgi (phosphoglucose isomerase) deletion (instead of tpi) to favor the Entner–Duodoroff pathway over glycolysis.
To demonstrate use of a direct constraint module, we created an excluded region where ethanol produced per unit additional biomass must be greater than 500 mmol ethanol/gDW (calculated from the point α=0.15 h−1) for cells growing above 0.175 h−1. Note, these parameters would ensure the designed mutant would have a minimum substrate-specific productivity (Patil et al., 2005) (calculated as ), of at least ~0.22 mmol ethanol/mmol glucose/h for growth rates above 0.175 h−1. Using this module, the four gene knockouts proposed (Fig. 5D) by OptORF achieved weak coupling between ethanol and biomass production and met the stated criteria. Unlike the previous solutions, this mutant would use glycolysis to achieve maximum growth. In this case, deleting gdhA (encoding glutamate dehydrogenase) forces glutamate to be produced using a less energy efficient pathway (involving glutamine synthetase and glutamate synthase, which consumes one additional ATP per glutamate synthesized). This reduces the maximum growth rate, such that the design criteria is satisfied. At the maximum growth rate, ethanol production is predicted to be ~17.4 mmol/gDW/h for this mutant.
In the previous examples, we selected feasible space constraints that restrict the ethanol production-cellular growth subspace; however, feasible space constraints can be used on other subspaces. We investigated the use of FaceCon modules for eliminating undesirable by-products, such as, succinate, acetate, and formate. A preliminary analysis indicated that under anaerobic conditions some baseline level of succinate secretion is required for cellular growth. Acetate secretion is not essential for growth but one or more acetate producing enzymes are essential for growth. Since there is no gene assigned to the acetate transport reaction there is no genetic way to eliminate acetate secretion. Consequently, we focused on finding a solution that could eliminate formate production at all growth rates and maximize ethanol production at the maximum growth rate (see Supplemental materials Fig. S7). This five gene deletion strategy knocks out transporters for lactate (glcA and lldP – an alternate solution could instead delete the lactate dehydrogenases, ldhA and dld) and formate (focA and focB). In addition, deleting ppc (which encodes for phosphoenolpyruvate carboxylase) increases flux through malate synthase and malate dehydrogenase – generating more NADH to produce oxaloacetate – and decreases the maximum growth rate. As a result, the ppc deletion requires additional ethanol production to balance the newly generated reductant. The predicted ethanol production for this mutant at the maximum growth rate is ~17.8 mmol/gDW/h.
These examples show that FaceCon modules are both tractable at the genome-scale and can aid OptORF in proposing interesting mutants which meet multiple design criteria, with minimal impacts on production of the chemical of interest. These solutions would not be easily obtained using stand-alone OptORF. To find the mutants that satisfy these additional design criteria (Fig. 5B–D) using stand-alone OptORF would require numerous integer cuts due to the large number of gene deletions required to produce these phenotypes and the gene deletion penalty used by OptORF. For example, using stand-alone OptORF with integer cuts took ~13.4 h to generate 10 alternate solutions (the last four solutions alone took 11.1 h). None of the 10 proposed solutions satisfy the design criteria of the FaceCon solutions shown in Fig. 5. In contrast, using OptORF in conjunction with FaceCon modules, desired solutions could be found directly, in a short amount of time (~2.8 h). In addition, all of the OptORF with FaceCon strategies have very similar levels of maximum ethanol production (at the maximum growth rate) as the best solution found by stand-alone OptORF.
Previous computational studies have identified strategies for improving ethanol production in E. coli using constraint-based models. Trinh et al. (2008) previously used elementary mode analysis to design an eight gene deletion strain of E. coli (Δndh Δzwf ΔfrdA ΔsfcA ΔmaeB ΔldhA ΔpoxB Δpta) with high ethanol yields. The OptORF with FaceCon strategies suggested in Fig. 5B–D required fewer mutations and are predicted to achieve higher ethanol yields at maximum cell growth; however, the Trinh et al. strains do guarantee a minimum yield 0.36 g ethanol/g glucose for all growth rates. Previously, OptORF was applied to an earlier metabolic model (iJR904) and eleven mutations were frequently suggested to improve ethanol production (appearing in at least 10% of 200 suggested strategies): ptsH, pgi, pflAB, pflCD, tdcE, tpi, pta, eutD, gdhA, gnd and nuoN (Kim and Reed, 2010). These genes differ from those commonly found in OptORF with FaceCon strategies, which include atpB, glcA, and lldP (or equivalently atpB, dld, and ldhA). While differences in strain designs could be due to differences in the metabolic networks, this work suggests new strategies for improving ethanol production.
3.5. Shadow price constraint (ShadowCon) module
While various methods such as ‘tilting’ the objective function, using a maximin problem, or adding FaceCon modules can ensure that growth and chemical production are coupled, none of these methods allow direct control over the ratio of Δvy/Δvx at the onset of coupling between two fluxes, vx and vy, thus defining the degree to which two fluxes are coupled. However, such a module can be designed by taking advantage of shadow prices in the dual of a flux balance analysis (FBA) problem. The FBA problem is formulated by adding an equality constraint for vy equal to ε (e.g., chemical production rate) to the standard set of FBA constraints and then maximizing vx (e.g., biomass production). In this case, the shadow price for the added equality constraint (ushadow) indicates how vx changes for small changes in vy and is the inverse of the coupling line׳s slope since the shadow price is calculated near where coupling initially occurs on the x-axis (within some user-defined ε). By setting criteria for the shadow price associated with the added equality constraint, one can effectively control the degree of coupling between the two fluxes of interest (see Methods and Supplementary File 1 for additional details). The shadow price constraints module (ShadowCon) includes the FBA problem (described above), its dual formulation and additional constraints on the equality constraint׳s dual variable. Addition of ShadowCon to a strain design algorithm, especially in conjunction with other FaceCon modules, allows for greater control over the strength of the selective pressure for producing a given chemical.
As a demonstration of how such a module works, we have applied ShadowCon to iJO1366 (Fig. 6) requiring that the slope of the initial coupling line, m, fall between 25 and 200 mmol/gDW. This range was chosen to create a strong coupling between ethanol and biomass production while also preventing strategies from being proposed where no coupling exists. The resulting mutant includes a new knockout, ptsH that encodes a component of the PTS transport system. Deletion of ptsH, forces glucose to be transported using either a proton symporter or ABC transporter, both of which produce a cytoplasmic proton. The additional proton reduces the growth rate and increases the maximum amount of ethanol produced (a ΔatpBΔglcAΔlldP mutant also satisfies the slope criteria but has a lower maximum ethanol production). In order to evaluate the sensitivity of ethanol production (at the maximum growth rate) to the coupling line׳s slope, we ran OptORF with the ShadowCon module using increasingly more stringent slope requirements. In this case, a tilted objective was used (see methods for details) and the lower bound on the slope was increased from 25 until the ShadowCon module prevented finding an OptORF solution (see Table S1 in Supplementary materials). As can be seen, the OptORF chemical production objective is eventually sensitive to increasing slope requirements; however, the predicted production is still sufficiently high for a wide range of slopes.
4. Conclusions
We have developed FaceCon and ShadowCon modules to extend upon the capabilities of existing mixed integer linear adaptive evolution metabolic engineering algorithms. Future work, could involve incorporating these methods into other types of metabolic engineering algorithms. Nonetheless, we show such modules are applicable to genome-scale models as shown using the E. coli model iJO1366. Using these modules will allow greater control over the knockout strategies proposed and allow for more efficient generation of phenotypes of interest, including complex phenotypes that would be difficult, if not impossible, to find using existing metabolic engineering algorithms alone. Moreover, using these approaches could allow for parallelization of metabolic engineering algorithms by starting multiple runs simultaneously with different FaceCon or ShadowCon parameters. Such an approach would result in more diverse and interesting solutions and could save additional time over sequential approaches for multiple solutions which rely on integer cuts. Using FaceCon and ShadowCon modules in conjunction with one another will allow researchers to define multiple engineering design criteria that should be met by any strain proposed. Through our illustrative and genome-scale examples, we have touched upon a number of possible applications for FaceCon modules such as by-product inhibition, coupling constraints, and co-production of metabolites. Another possible use may include constraining chemical production with increasing carbon uptake. Using these modular approaches, we hope to provide algorithm flexibility so that researchers have fewer limitations when using their strain design algorithm.
Author contributions
CJT developed the algorithms, and processing scripts, performed all the simulations, and composed all figures. CJT and JLR conceived of and designed the algorithm, analyzed results and wrote the paper. All authors read and approved the final manuscript.
Acknowledgments
This work was funded by the NSF (NSF 1053712) and by an NHGRI training grant to the Genomic Sciences Training Program (T32HG002760 to CT). We would also like to thank Joonhoon Kim for his contributions editing this manuscript prior to publication.
Footnotes
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.meteno.2014.06.001.
Appendix A. Supplementary materials
Supplementary materials
References
- Aristidou A.A., San K.-Y., Bennett G.N. Modification of central metabolic pathway in Escherichia coli to reduce acetate accumulation by heterologous expression of the bacillus subtilis acetolactate synthase gene. Biotechnol. Bioeng. 1994;44:944–951. doi: 10.1002/bit.260440810. [DOI] [PubMed] [Google Scholar]
- Burgard A.P., Pharkya P., Maranas C.D. Optknock: a bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol. Bioeng. 2003;84:647–657. doi: 10.1002/bit.10803. [DOI] [PubMed] [Google Scholar]
- Burgard A.P., Nikolaev E.V., Schilling C.H., Maranas C.D. Flux coupling analysis of genome-scale metabolic network reconstructions. Genome Res. 2004;14:301–312. doi: 10.1101/gr.1926504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi H.S., Lee S.Y., Kim T.Y., Woo H.M. In silico identification of gene amplification targets for improvement of lycopene production. Appl. Environ. Microbiol. 2010;76:3097–3105. doi: 10.1128/AEM.00115-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotten C., Reed J.L. Constraint-based strain design using continuous modifications (CosMos) of flux bounds finds new strategies for metabolic engineering. Biotechnol. J. 2013;8:595–604. doi: 10.1002/biot.201200316. [DOI] [PubMed] [Google Scholar]
- Curran K.A., Alper H.S. Expanding the chemical palate of cells by combining systems biology and metabolic engineering. Metab. Eng. 2012;14:289–297. doi: 10.1016/j.ymben.2012.04.006. [DOI] [PubMed] [Google Scholar]
- Eiteman M.A., Altman E. Overcoming acetate in Escherichia coli recombinant protein fermentations. Trends Biotechnol. 2006;24:530–536. doi: 10.1016/j.tibtech.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Feist A.M., Zielinski D.C., Orth J.D., Schellenberger J., Herrgard M.J. Model-driven evaluation of the production potential for growth-coupled products of Escherichia coli. Metab. Eng. 2010;12:173–186. doi: 10.1016/j.ymben.2009.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fong S.S., Burgard A.P., Herring C.D., Knight E.M., Blattner F.R. In silico design and adaptive evolution of Escherichia coli for production of lactic acid. Biotechnol. Bioeng. 2005;91:643–648. doi: 10.1002/bit.20542. [DOI] [PubMed] [Google Scholar]
- Gawand P., Hyland P., Ekins A., Martin V.J.J., Mahadevan R. Novel approach to engineer strains for simultaneous sugar utilization. Metab. Eng. 2013;20:63–72. doi: 10.1016/j.ymben.2013.08.003. [DOI] [PubMed] [Google Scholar]
- Hädicke O., Klamt S. Computing complex metabolic intervention strategies using constrained minimal cut sets. Metab. Eng. 2011;13:204–213. doi: 10.1016/j.ymben.2010.12.004. [DOI] [PubMed] [Google Scholar]
- Hamilton J.J., Reed J.L. Identification of functional differences in metabolic networks using comparative genomics and constraint-based models. PLoS ONE. 2012;7:e34670. doi: 10.1371/journal.pone.0034670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jantama K., Zhang X., Moore J.C., Shanmugam K.T., Svoronos S.A. Eliminating side products and increasing succinate yields in engineered strains of Escherichia coli C. Biotechnol. Bioeng. 2008;101:881–893. doi: 10.1002/bit.22005. [DOI] [PubMed] [Google Scholar]
- von Kamp A., Klamt S. Enumeration of smallest intervention strategies in genome-scale metabolic networks. PLoS Comput. Biol. 2014;10:e1003378. doi: 10.1371/journal.pcbi.1003378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J., Reed J. OptORF: optimal metabolic and regulatory perturbations for metabolic engineering of microbial strains. BMC Syst. Biol. 2010;4:53. doi: 10.1186/1752-0509-4-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J., Reed J.L., Maravelias C.T. Large-scale bi-level strain design approaches and mixed-integer programming solution techniques. PLoS ONE. 2011;6:e24162. doi: 10.1371/journal.pone.0024162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J.W., Na D., Park J.M., Lee J., Choi S. Systems metabolic engineering of microorganisms for natural and non-natural chemicals. Nat. Chem. Biol. 2012;8:536–546. doi: 10.1038/nchembio.970. [DOI] [PubMed] [Google Scholar]
- Lian J., Chao R., Zhao H. Metabolic engineering of a Saccharomyces cerevisiae strain capable of simultaneously utilizing glucose and galactose to produce enantiopure (2R,3R)-butanediol. Metab. Eng. 2014;23:92–99. doi: 10.1016/j.ymben.2014.02.003. [DOI] [PubMed] [Google Scholar]
- Lin H., Bennett G.N., San K.-Y. Metabolic engineering of aerobic succinate production systems in Escherichia coli to improve process productivity and achieve the maximum theoretical succinate yield. Metab. Eng. 2005;7:116–127. doi: 10.1016/j.ymben.2004.10.003. [DOI] [PubMed] [Google Scholar]
- Lun D.S., Rockwell G., Guido N.J., Baym M., Kelner J.A. Large-scale identification of genetic design strategies using local search. Mol. Syst. Biol. 2009;5:296. doi: 10.1038/msb.2009.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohno S., Shimizu H., Furusawa C. FastPros: screening of reaction knockout strategies for metabolic engineering. Bioinformatics. 2013;30:981–987. doi: 10.1093/bioinformatics/btt672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orth J.D., Thiele I., Palsson B.O. What is flux balance analysis? Nat. Biotechnol. 2010;28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orth J.D., Conrad T.M., Na J., Lerman J.A., Nam H. A comprehensive genome-scale reconstruction of Escherichia coli metabolism — 2011. Mol Syst Biol. 2011;7:535. doi: 10.1038/msb.2011.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patil K., Rocha I., Forster J., Nielsen J. Evolutionary programming as a platform for in silico metabolic engineering. BMC Bioinform. 2005;6:308. doi: 10.1186/1471-2105-6-308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pharkya P., Maranas C.D. An optimization framework for identifying reaction activation/inhibition or elimination candidates for overproduction in microbial systems. Metab. Eng. 2006;8:1–13. doi: 10.1016/j.ymben.2005.08.003. [DOI] [PubMed] [Google Scholar]
- Pharkya P., Burgard A.P., Maranas C.D. OptStrain: a computational framework for redesign of microbial production systems. Genome Res. 2004;14:2367–2376. doi: 10.1101/gr.2872004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranganathan S., Suthers P.F., Maranas C.D. OptForce: an optimization procedure for identifying all genetic manipulations leading to targeted overproductions. PLoS Comput. Biol. 2010;6:e1000744. doi: 10.1371/journal.pcbi.1000744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez A.M., Bennett G.N., San K.-Y. Novel pathway engineering design of the anaerobic central metabolic pathway in Escherichia coli to increase succinate yield and productivity. Metab. Eng. 2005;7:229–239. doi: 10.1016/j.ymben.2005.03.001. [DOI] [PubMed] [Google Scholar]
- Sierksma G. Marcel Dekker, Inc.; New York: 2002. Linear and Integer Programming: Theory and Practice. [Google Scholar]
- Tepper N., Shlomi T. Predicting metabolic engineering knockout strategies for chemical production: accounting for competing pathways. Bioinformatics. 2010;26:536–543. doi: 10.1093/bioinformatics/btp704. [DOI] [PubMed] [Google Scholar]
- Tervo C., Reed J. FOCAL: an experimental design tool for systematizing metabolic discoveries and model development. Genome Biol. 2012;13:R116. doi: 10.1186/gb-2012-13-12-r116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trinh C.T., Unrean P., Srienc F. Minimal Escherichia coli cell for the most efficient production of ethanol from hexoses and pentoses. Appl. Environ. Microbiol. 2008;74:3634–3643. doi: 10.1128/AEM.02708-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vadali R.V., Fu Y., Bennett G.N., San K.-Y. Enhanced lycopene productivity by manipulation of carbon flow to isopentenyl diphosphate in Escherichia coli. Biotechnol. Prog. 2005;21:1558–1561. doi: 10.1021/bp050124l. [DOI] [PubMed] [Google Scholar]
- Yang L., Cluett W.R., Mahadevan R. EMILiO: a fast algorithm for genome-scale strain design. Metab. Eng. 2011;13:272–281. doi: 10.1016/j.ymben.2011.03.002. [DOI] [PubMed] [Google Scholar]
- Yim H., Haselbeck R., Niu W., Pujol-Baxley C., Burgard A. Metabolic engineering of Escherichia coli for direct production of 1,4-butanediol. Nat. Chem. Biol. 2011;7:445–452. doi: 10.1038/nchembio.580. [DOI] [PubMed] [Google Scholar]
- Zha W, Rubin-Pitel SB, Shao Z, Zhao H. Improving cellular malonyl-CoA level in Escherichia coli via metabolic engineering. Metab. Eng. 2009;11:192–198. doi: 10.1016/j.ymben.2009.01.005. [DOI] [PubMed] [Google Scholar]
- Zomorrodi A.R., Suthers P.F., Ranganathan S., Maranas C.D. Mathematical optimization applications in metabolic networks. Metab. Eng. 2012;14:672–686. doi: 10.1016/j.ymben.2012.09.005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary materials