Abstract
Using genome-wide data from 253,288 individuals, we identified 697 variants at genome-wide significance that together explain one-fifth of heritability for adult height. By testing different numbers of variants in independent studies, we show that the most strongly associated ~2,000, ~3,700 and ~9,500 SNPs explained ~21%, ~24% and ~29% of phenotypic variance. Furthermore, all common variants together captured the majority (60%) of heritability. The 697 variants clustered in 423 loci enriched for genes, pathways, and tissue-types known to be involved in growth and together implicated genes and pathways not highlighted in earlier efforts, such as signaling by fibroblast growth factors, WNT/beta-catenin, and chondroitin sulfate-related genes. We identified several genes and pathways not previously connected with human skeletal growth, including mTOR, osteoglycin and binding of hyaluronic acid. Our results indicate a genetic architecture for human height that is characterized by a very large but finite number (thousands) of causal variants.
Height is a classical polygenic trait that has provided general insights into the genetic architecture of common human traits and diseases, and into the prospects and challenges of different methods used to identify genetic risk factors. Studies consistently estimate that the additive genetic contribution to normal variation in adult height (“narrow sense heritability”) is approximately 80% 1–3. Previous analysis of genome-wide association studies (GWAS) of adult height showed that common variants together account for 50% of this heritable contribution to height variation4,5. The most recent GWAS of adult height identified 180 loci, which together highlighted many genes relevant to human skeletal growth that had not been implicated in previous studies6. Common variants in these loci, however, only accounted for 10% of the phenotypic variation (~12% of heritability). Here, we report results from a GWAS meta-analysis of adult height in 253,288 individuals of European ancestry. We show that additive contributions of fewer than 10,000 SNPs (at P<5×10−3) can account for 36% of the heritability of adult height. Variants reaching genome-wide significance (P<5×10−8) in this larger study (697 SNPs) clustered in loci, were substantially enriched for regulatory variants, and implicated multiple known and previously unknown genes and pathways relevant to growth. More broadly, our results provide evidence that increasing GWAS sample sizes to the order of 100,000s, now plausible for many common traits, will likely continue to identify the variants and loci that close the “missing heritability” gap, whilst improving knowledge of the biology of those traits.
Results
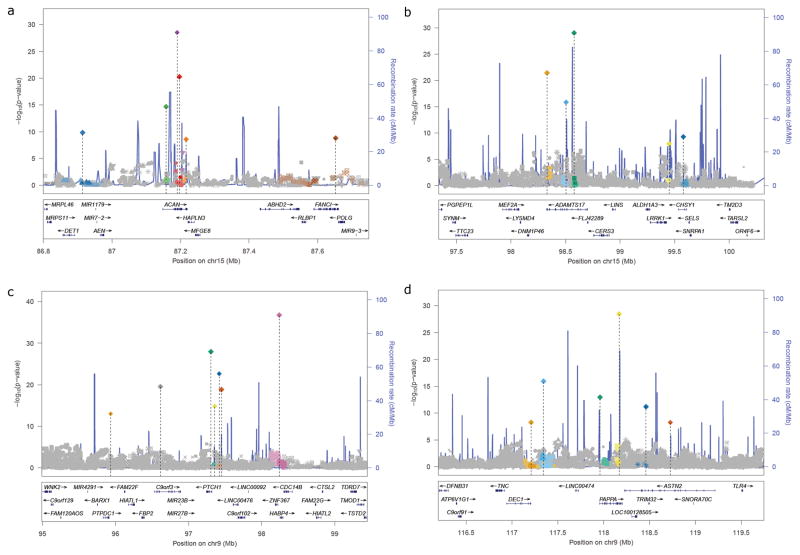
The overall analysis strategy is illustrated in Supplementary Figure 1. We first performed a GWAS meta-analysis of adult height using summary statistics from 79 studies consisting of 253,288 individuals of European ancestry (Online Methods). We identified 697 SNPs that reached genome-wide significance (P<5×10−8) using an approximate conditional and joint multiple-SNP (COJO) analysis7 in GCTA8 (Online Methods) which takes linkage disequilibrium (LD) between SNPs into account (Supplementary Table 1; Supplementary Figs. 2–3). The 697 SNPs clustered in 423 loci, with a locus defined as one or multiple jointly associated SNPs located within ±1Mb of each other. Most of these 697 SNPs are uncorrelated although those in close physical proximity (e.g. < 1Mb) may be in partial LD (see Supplementary Table 1 for LD between adjacent pairs of the 697 SNPs). The clustering of signals was non-random (empirical enrichment of 1.4 fold, P<1×10−4) with 90, 26 and 31 loci containing 2, 3 and ≥4 signals respectively, (Supplementary Note and Supplementary Tables 1 and 2). We observed strong evidence of clustering of association signals within loci across a range of locus sizes, from 100kb to 1.25Mb, but the clustering was almost entirely driven by variants within 250kb of index SNPs (Supplementary Note and Supplementary Table 2). As shown in Figure 1 and Supplementary Figure 4, in some loci, multiple signals cluster tightly around a single gene, whereas in other cases, the clustering of associated variants is likely due to multiple different height-related genes being in close proximity.
Figure 1. Regional association plots for loci with multiple association signals.
Panels a to d highlight examples of multiple signals after approximate conditional joint multiple-SNP analysis GCTA-COJO analysis. SNPs are shaded and shaped based on the index SNP with which they are in strongest LD (r2>0.4). Panels a–c show the majority of signals clustering in and around a single gene (ACAN, ADAMTS17, PTCH1, respectively) whereas panel d shows the multiple signals clustering through proximity.
Of the 697 SNPs, 403 were represented on the Metabochip array9. Using data from 80,067 individuals genotyped on the Metabochip array from 37 independent studies, we observed very strong evidence of concordance of effect sizes between the Metabochip and GWAS samples (P = 1.9×10−160); and >99% of variants were directionally consistent between Metabochip and GWAS (Online Methods, Supplementary Note, and Supplementary Table 3).
We observed a large genome-wide ‘inflation’ factor of the test statistic for association even after we corrected each study’s test statistics by its individual inflation factor (single λGC = 1.94). At least two phenomena could have contributed to this observation. First, as described previously10, highly polygenic models of inheritance are expected to increase the genomic inflation factor to levels comparable to what we observe. Second, height is particularly susceptible to confounding by population ancestry (stratification), which can also lead to inflation of the test statistics. We addressed these possibilities by comparing our results with those obtained using more stringent corrections for stratification (linear mixed models), and with results obtained in subsets of studies in which a purely family-based analysis was feasible, and by performing a within-family prediction analysis which partitioned the variance in the genetic predictor into the contributions of true associations and population stratification.
Our linear mixed model (LMM) analyses, performed in a subset of 15 individual studies comprising 59,380 individuals, provided strong evidence that the inflated statistics were driven predominantly by the highly polygenic nature of the trait. This approach utilizes a genomic relationship matrix (GRM) calculated through genome-wide SNP data to correct for distant relatedness between all pairs of individuals within a study. This resulted in a single λGC of 1.20. This value was entirely consistent with the single λGC of 1.20 obtained from the standard GWAS analysis of the same individuals and a single λGC of 1.94 obtained from the full 253,288 individuals (Supplementary Table 4). Because this approach may be overly conservative for a strongly genetic and highly polygenic trait, each study additionally repeated the analyses for each chromosome using a GRM generated from the remaining 21 chromosomes, or in the case of the largest study (WGHS) repeating the analysis for all odd numbered chromosomes using a GRM generated from the even numbered chromosomes and vice versa. The single λGC inflation factor for this analysis, 1.23, was also entirely consistent with the standard GWAS results (Online Methods, Supplementary Note, and Supplementary Table 4).
Our family based analyses also provided strong evidence that the inflated statistics are driven predominantly by the highly polygenic nature of height. We assessed whether variants that reached genome-wide significance after single GC correction replicated in family-based analyses of up to 25,849 samples (effective sample size 14,963, using methods that are immune to stratification (Online Methods, Supplementary Note, and Supplementary Tables 5 and 6). We identified genome-wide significant associations from a meta-analysis that excluded the family-based samples, and tested these associations for replication in the family-based samples; a lower rate of replication than expected could be due to inflation of effect sizes in the discovery sample from the “winner’s curse” and/or stratification. Of 416 genome-wide significant SNPs representing multiple signals selected after exclusion of family-based studies, 371 SNPs had a consistent direction of effect (compared with 208 expected by chance, and 400 expected in the absence of any inflation of estimated effect sizes), and 142 replicated with P<0.05 (compared with 21 expected by chance, and 210 expected in the absence of effect size inflation; Supplementary Table 5). These analyses (particularly the directional consistency) shows that most of the loci represent true associations, but also shows that there is a modest inflation in the effect size estimates, due to stratification and/or the winner’s curse. To distinguish between these possibilities, we repeated this analysis, substituting for the family-based samples a random set of studies with similar total effective sample size. The number of replicating loci was only slightly lower in the family-based cohorts than in the random samples (Supplementary Table 5, 12–17 fewer replications attributable to stratification at different P-value thresholds). This indicates that most of the modest inflation in effect estimates is due to the winner’s curse, that a small amount of inflation is due to residual stratification, and that few (upper limit ~15–25; Supplementary Note and Supplementary Table 5) if any of the loci that reach genome-wide significance after single GC correction are likely to be complete false positives due to stratification (that is, no real association whatsoever with height).
Variance explained by SNPs at different significance levels
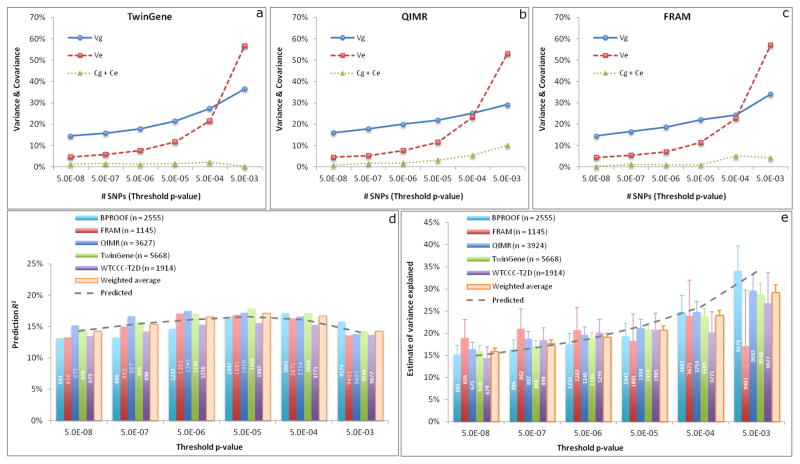
Having established that single GC correction is sufficient to identify SNPs that are likely to be truly associated with height, we next performed a series of analyses using GWAS data from five independent validation studies to quantify the fraction of phenotypic variance explained by SNPs selected from the GCTA-COJO analyses7 of the meta-analysis data, which excluded data from the validation studies, at a range of statistical thresholds, and to quantify the accuracy of predicting height using these selected SNPs (Online Methods). We first developed a new method that uses within-family prediction to partition the variance of the SNP-based predictor into components due to real SNP effects, errors in estimating SNP effects, and population stratification (Online Methods), and applied the method to data on full-sib pairs from three of the five validation studies (Online Methods). Consistently across the three studies, all the partitioned variance components increased as a less stringent significance level was used for SNP selection in the discovery sample and the error variance increased more dramatically than the genetic variance when more SNPs selected at a less significance level were included in the predictor (Fig. 2a–c). We demonstrated the partitioning of variance due to population stratification by the within-family prediction analyses with and without adjusting for principal components (PCs) (Supplementary Fig. 5). The results again confirmed that the impact of population stratification on the top associated SNPs was minor and demonstrated that the variation in the predictor due to true SNP effect, estimation error and population stratification was quantifiable. We next inferred, using these partitioned variance components from the within-family prediction analysis, how well different selected sets of SNPs would predict height in independent samples. We showed that the observed prediction accuracy (squared correlation between phenotype and predictor, R2) in five different population-based cohorts was highly consistent with the values inferred from the within-family based analyses, with prediction accuracy peaking at ~17% using the ~1,900 SNPs reaching P<5×10−5 (Fig. 2d). Finally we estimated variance explained by the selected SNPs in population-based studies using the GCTA-GREML method4,8 (Fig. 2e). The results showed that ~670 SNPs at P<5×10−8 and ~9,500 SNPs at P<5×10−3 captured ~16% and ~29% of phenotypic variance respectively (Table 1), which was also consistent with the estimates inferred from the within-family prediction analysis. As shown in equation [19], prediction R2 is not equal to the variance explained but a function of the variance of true SNP effects and the error variance in estimating SNP effects, in the absence of population structure. This is demonstrated in Figure 2, where at thresholds below genome-wide significance, variance explained is higher than the prediction accuracy, because the latter is deflated both by imprecise estimates of effect sizes (estimation errors) and by inclusion of SNPs that are not associated with height. The estimate of variance explained by all the HapMap3 (ref. 11) SNPs without SNP selection was ~50% (Table 1), consistent with previous estimates4,5. Thus, a group of ~9,500 SNPs (representing <1% of common SNPs) selected at P<5×10−3, explained ~29% of phenotypic variance. Since ~50% of phenotypic variance is explained by all common SNPs, the selected set of SNPs, despite being limited to <1% of common SNPs, accounts for the majority of variance attributable to all common SNPs (29/50 ~ 60%). This set of ~9,500 SNPs strongly clustered with the newly established height loci: 1,704 (19%) variants were located within 250kb of one of the 697 genome-wide associated SNPs, suggesting that a substantial fraction of “missing heritability” is within already identified loci. This clustering of additional variants within identified loci was confirmed in a parallel analysis based on two left-out studies where we observed that SNPs in closer physical proximity with the top associated SNPs explained disproportionally more variance (Online Methods and Supplementary Fig. 6).
Figure 2. Quantifying the variance explained by height associated SNPs at different levels of significance.
The SNPs were selected from the approximate conditional and joint multiple SNPs association analysis using GCTA-COJO analysis with the target cohort being excluded from the meta-analysis. a, b, c, Partitioning the variance in the SNP-derived genetic predictor using a within-family analysis. The SNP-based predictor was adjusted by the first 20 PCs. The four variance-covariance components Vg, Ve, Cg and Ce are defined in Online Methods. d, Accuracy of predicting phenotype by the genetic predictor in unrelated individuals. The prediction R2 shown on the y-axis is the squared correlation between phenotype and predictor. The SNP-based predictor was adjusted by the first 20 PCs. The solid line is the average prediction R2 weighted by sample size over the five cohorts. The dashed line is the prediction accuracy inferred from the within-family prediction analysis (Equation 19 in Online Methods). e, The variance explained by the SNPs was estimated by the whole-genome estimation method in GCTA. The phenotype was adjusted by the first 20 PCs. Each error bar represents the standard error of the estimate. The estimates from all the five cohorts (B-PROOF, FRAM, QIMR, TwinGene and WTCCC-T2D) were averaged by the inverse-variance approach. The dashed line is the variance explained inferred from the within-family prediction analysis. In panels d and e, the number shown in each column is the number of SNPs used in the analysis.
Table 1. Estimates of variance explained by SNPs selected at different significance levels.
The SNPs were selected by an approximate conditional and joint multiple-SNP analysis (GCTA-COJO) of the summary statistics from the meta-analysis. The target cohort for variance estimation was excluded from the meta-analysis.
| Threshold | QIMR (n = 3,924) | FRAM (n = 1,145) | TwinGene (n = 5,668) | WTCCC-T2D (n = 1,914) | B-PROOF(n = 2,555) | a Weighted average | b Pred. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||
| #SNP | h2g | SE | #SNP | h2g | SE | #SNP | h2g | SE | #SNP | h2g | SE | #SNP | h2g | SE | h2g | SE | h2g | |
| 5E-8 | 675 | 0.164 | 0.016 | 656 | 0.190 | 0.040 | 670 | 0.159 | 0.013 | 679 | 0.143 | 0.025 | 691 | 0.152 | 0.021 | 0.159 | 0.008 | 0.149 |
| 5E-7 | 887 | 0.187 | 0.017 | 862 | 0.210 | 0.045 | 866 | 0.170 | 0.013 | 890 | 0.184 | 0.028 | 886 | 0.162 | 0.022 | 0.176 | 0.009 | 0.166 |
| 5E-6 | 1245 | 0.196 | 0.018 | 1202 | 0.207 | 0.050 | 1186 | 0.188 | 0.014 | 1256 | 0.201 | 0.030 | 1232 | 0.175 | 0.024 | 0.190 | 0.009 | 0.186 |
| 5E-5 | 1950 | 0.212 | 0.020 | 1891 | 0.183 | 0.060 | 1918 | 0.208 | 0.015 | 1985 | 0.208 | 0.037 | 1947 | 0.194 | 0.029 | 0.206 | 0.010 | 0.218 |
| 5E-4 | 3754 | 0.248 | 0.024 | 3671 | 0.239 | 0.080 | 3689 | 0.239 | 0.017 | 3771 | 0.201 | 0.047 | 3661 | 0.248 | 0.037 | 0.240 | 0.013 | 0.259 |
| 5E-3 | 9693 | 0.297 | 0.035 | 9403 | 0.171 | 0.126 | 9548 | 0.287 | 0.025 | 9677 | 0.267 | 0.070 | 9174 | 0.341 | 0.055 | 0.292 | 0.018 | 0.339 |
| cHM3 | 1.08M | 0.473 | 0.086 | 1.06M | 0.313 | 0.291 | 1.12M | 0.522 | 0.060 | 0.97M | 0.534 | 0.170 | 1.09M | 0.463 | 0.126 | 0.498 | 0.044 | |
The estimates from all the five cohorts were averaged by the inverse-variance approach i.e. Σi (h2g(i)/SE2i)/Σi (1/SE2i);
the predicted variance explained by the selected SNPs (Vg) from the within-family prediction analysis;
SNPs from HapMap3 project11.
Larger GWAS identifies new biologically relevant genes and pathways
Having shown that ~1% of variants can account for the majority of heritability attributable to common variation, we next considered whether the expanded set of height-associated variants could be used to identify the genomic features and biological pathways of most relevance to normal variation in adult height. To test whether our GWAS could implicate new biology, we used established and novel approaches to test whether the height-associated loci were enriched for functionally relevant variants, genes, pathways, and tissues.
As with the 180 variants identified in our previous analysis, the 697 variants were non-randomly distributed with respect to functional and putatively functional regions of the genome (Online Methods). We observed that height associated variants were enriched for non-synonymous SNPs (nsSNPs) (empirical enrichment of 1.2 fold, P=0.02), cis-regulatory effects in blood (empirical enrichment of 1.5 fold, P=0.03), a curated list of genes that underlie monogenic syndromes of abnormal skeletal growth12 (empirical enrichment 1.4 fold, P=0.013), associations with apparently unrelated complex traits in the NHGRI GWAS catalog (empirical enrichment 2.6 fold, P<1×10−4) and functional chromatin annotations in multiple tissues and cell types (empirical enrichment 1.8 fold, P<1×10−3) (Supplementary Note and Supplementary Tables 7–11).
The greater resolution of height associated variants provided by increased sample size, combined with improved gene prioritization and gene set enrichment approaches, identified multiple new tissues, gene sets and specific genes that are highly likely to be involved in the biology of skeletal growth. Specifically, using a variety of established and novel pathway methods, we identified ~3 times as many enriched pathways and prioritized ~5 times as many genes (including genes newly prioritized in previously identified loci) compared to results derived from identical pathway methods to the previous GWAS of 133,000 individuals (Table 2).
Table 2.
Comparison of prioritized variants, loci, biology and variance explained from GWASs on human stature with 130,000 individuals (previously published in Lango Allen et al., 2010) and with 250,000 individuals (this paper).
| Height GWAS with 130,000 samples (Lango Allen et al., Yang et al)* | Height GWAS with 253,288 samples | |
|---|---|---|
| SNP based comparisons | ||
|
| ||
| GWAS significant SNPS | 199 | 697 |
| Genomic loci# (+/− 1Mb) | 180 | 423 |
| Loci# with multiple signals | 19 | 147 |
| Secondary associations in loci# | 19 | 273 |
|
| ||
| Biological annotation (DEPICT at FDR < 0.05) | ||
|
| ||
| Prioritized genes | 92 | 649 |
| Loci& with prioritized gene | 74 (43%) | 422 (75%) |
| Pruned gene sets and protein-protein complexes% | 813 | 2,330 |
| Tissues and cell-types | 5 | 43 |
|
| ||
| Variance explained | ||
|
| ||
| GWAS significant SNPs | 10% | 16% |
| Deep list of SNPs at 1×10−3 | 13% | 29% |
| All common SNPs | 45%** | 50% |
|
| ||
| Heritability explained | ||
|
| ||
| GWAS significant SNPs | 12.5% | 20% |
| Deep list of SNPs at 1×10−3 | 16% | 36% |
| All common SNPs | 56%** | 62.5% |
Counts, numbers and estimates for Lango Allen et al. are taken from respective publication.
Genomic loci defined by distance: +/− 1Mb from index height SNP
Genomic loci defined by LD: r2 > 0.5 from index height SNP
After clumping of similar gene sets and pathways
Yang et al. Nat Genet 42, 565–9 (2010).
We first focused on existing pathway and gene prioritization methods: (1) MAGENTA13, a method designed to identify gene sets enriched in GWAS data, and (2) GRAIL14, which uses published literature to highlight connections between likely relevant genes within GWAS loci. As expected, the GRAIL and MAGENTA analyses confirmed several previously identified gene sets and pathways clearly relevant to skeletal growth, but in the larger sample they also provided evidence for additional known and novel genes, gene sets and protein complexes not identified in our previous smaller study (for example, FGF signaling, WNT signaling, osteoglycin, and other genes related to bone or cartilage development) (Supplementary Tables 12–13 and Supplementary Fig. 7).
To obtain more detailed insight into height biology, we applied DEPICT, a novel data-driven integrative method that uses gene sets reconstituted based on large scale expression data to prioritize genes and gene sets, and also to identify tissues enriched in highly expressed genes from associated loci (Pers et al. in preparation; Online Methods and Supplementary Note). The DEPICT analysis highlighted 2,330 reconstituted gene sets (after pruning for high levels of redundancy). These gene sets both confirmed and extended the MAGENTA and GRAIL findings, and identified novel pathways not identified in our previous height GWAS (for example regulation of beta-catenin, biology related to glycosaminoglycans such as chondroitin sulfate and hyaluronic acid, and mTOR signaling) (Supplementary Table 14). Gene sets identified based on 327 strictly novel height variants (>1Mb from the 180 known variants loci) highly resembled gene sets highlighted by the already known 180 loci (Spearman’s rank correlation coefficient between gene set enrichment Z-scores r=0.91, P=2×10−16). Thus, the variants discovered through increased sample size continued to highlight specific and relevant growth-associated gene sets, while the combined analysis of both old and new loci provided the additional power needed to identify new gene sets (Table 3 and Supplementary Table 14).
Table 3. Significantly prioritized novel human growth associated genes.
The table lists 20 genes prioritized by DEPICT. Genes are ranked by the number of lines of supporting evidence and the DEPICT P-value (Supplementary Table 16). Because 20 of the 30 top-ranked genes were in a curated list of genes known to cause syndromes of skeletal12, these “OMIM genes” are not shown here. The top fifteen genes with prior literature support (based on GRAIL) are shown, followed by the top five novel genes. Each gene is accompanied by the significantly enriched reconstituted gene sets in which it appears in (DEPICT gene set enrichment analysis). Abbreviations; (GO – Gene Ontology; MP– Mice Phenotypes from Mouse Genome Informatics database; InWeb – protein-protein interaction complexes; KEGG and REACTOME databases).
| Locus (height SNP) | Gene symbol | New locus | Prioritization P-value | Levels of biological annotation | Top ranking reconstituted gene sets |
|---|---|---|---|---|---|
| Genes with prior literature support (GRAIL) | |||||
| rs10748128 | FRS2 | N | 1.0×10−16 | 7 | PI 3K cascade (REACTOME, P=6.2×10−13); Chronic Myeloid Leukemia (KEGG, P=1.6×10− 12); Response To Fibroblast Growth Factor Stimulus (GO, P=5.4×10−11); |
| rs2166898 | GLI2 | Y | 4.4×10−16 | 7 | Growth Factor Binding (GO, P=2.6×10−14); Regulation Of Osteoblast Differentiation (GO, P=2.3×10−11); WNT-Protein Binding (GO, P=1.9×10−12) |
| rs526896-rs9327705 | TBX4 | N | 9.9×10−9 | 7 | Short Mandible (MP, P=3.3×10−19); Respiratory System Development (GO, P=3.1×10−17); Abnormal Ulna Morphology (MP, P=1.9×10−15) |
| rs16860216 | SOX8 | N | 0.016 | 7 | Small Thoracic Cage (MP, P=6.9×10−14); Short Ribs (MP, P=2.7×10−8); Short Sternum (MP, P=6.5×10−7) |
| rs1199734 | LATS2 | Y | 1.0×10−16 | 6 | Partial Lethality Throughout Fetal Growth And Development (MP, P=1.2×10−18); Growth Factor Binding (GO, P=2.6×10−14); TGFB1 protein complex (InWeb, P=6.3×10−12) |
| rs12323101 | PDS5B | N | 1.0×10−16 | 6 | Chromatin Binding (GO, P=6.4×10−17); Nuclear Hormone Receptor Binding (GO, P=2.4×10−12); RBBP4 protein complex (InWeb, P=1.3×10−11); WNT16 protein complex (InWeb, P=1.9×10−8) |
| rs6746356 | SP3 | Y | 1.0×10−16 | 6 | BCOR protein complex (InWeb, P=2.7×10−17); AFF2 protein complex (InWeb, P=4.5×10−7); Intracellular Steroid Hormone Receptor Signaling Pathway (GO, P=9.0×10−6) |
| rs3923086 | AXIN2 | Y | 2.2×10−16 | 6 | Signaling By Transforming Growth Factor Beta (KEGG, P=3.8×10−15); WNT Receptor Signaling Pathway (GO, P=6.9×10−14); Polydactyly (MP, P=1.5×10−10) |
| rs3790086 | LTBP1 | N | 1.3×10−13 | 6 | Abnormal Skeleton Morphology (MP, P=1.1×10−15); TGF Beta Signaling Pathway (KEGG, P=3.8×10−15); Growth Factor Binding (GO, P=2.6×10−14) |
| rs2034172 | WNT5A | Y | 4.3×10−13 | 6 | Partial Lethality Throughout Fetal Growth And Development (MP, P=1.2×10−18); Tissue Morphogenesis (GO, P=4.1×10−20); Abnormal Skeleton Morphology (MP, P=1.1×10−15) |
| rs3915129 | CTNNB1 | Y | 3.5×10−12 | 6 | AR protein complex (InWeb, P=8.9×10−17); TCEB1 protein complex (InWeb, P=1.5×10− 11); GTF2I protein complex (InWeb, P=4.6×10−11) |
| rs12330322 | BMP2 | N | 5.6×10−10 | 6 | Transcription Factor Binding (GO, P=4.7×10− 26); Complete Embryonic Lethality During Organogenesis (MP, P=4.9×10−21); Short Mandible (MP, P=3.3×10−19) |
| rs10958476-rs6999671 | BMP6 | N | 2.9×10−8 | 6 | Small Basisphenoid Bone (MP, P=8.9×10−17); TGF Beta Signaling Pathway (KEGG, P=3.8×10−15); Growth Factor Binding (GO, P=2.6×10−14) |
| rs564914 | SOX5 | Y | 4.6×10−7 | 6 | Disproportionate Dwarf (MP, P=1.8×10−13); Abnormal Cartilage Morphology (MP, P=1.9×10−13); Short Limbs (MP, P=2.8×10−13) |
| rs17807185 | WNT4 | Y | 4.6×10−7 | 6 | Morphogenesis Of An Epithelium (GO, P=2.3×10−17); Gland Development (GO, P=5.4×10−16); Basal Cell Carcinoma (KEGG, P=1.5×10−12) |
| Novel genes without prior evidence | |||||
| rs8042424 | CHSY1 | N | 1.0×10−16 | 7 | Abnormal Cartilage Morphology (MP, P=1.9×10−13); Abnormal Bone Ossification (MP, P=2.1×10−12); Signaling by Transforming Growth Factor Beta (REACTOME, P=5.9×10−9) |
| rs7652177 | FNDC3B | N | 1.0×10−16 | 5 | Abnormal Spongiotrophoblast Layer Morphology (MP, P=3.2×10−16); Decreased Length Of Long Bones (MP, P=2.7×10−12); ITGB1 protein complex (InWeb, P=5.2×10−8) |
| rs7284476 | TRIOBP | Y | 1.0×10−16 | 5 | Negative Regulation Of Cell Proliferation (GO, P=4.3×10−17); Abnormal Vitelline Vasculature Morphology (MP, P=1.7×10−15); Beta-Catenin Binding (GO, P=3.0×10−5) |
| rs2149163-rs3927536 | BNC2 | N | 1.0×10−16 | 5 | Short Ulna (MP, P=4.7×10−13); Abnormal Joint Morphology (MP, P=8.6×10−11); Regulation Of Chondrocyte Differentiation (GO, P=2.9×10−9) |
| rs3790086 | WWP2 | Y | 1.0×10−16 | 5 | Cartilage Development (GO, P=2.0×10−19); Chondrocyte Differentiation (GO, P=3.0×10−15); Signaling By Platelet-Derived Growth Factor (REACTOME, P=4.8×10−10) |
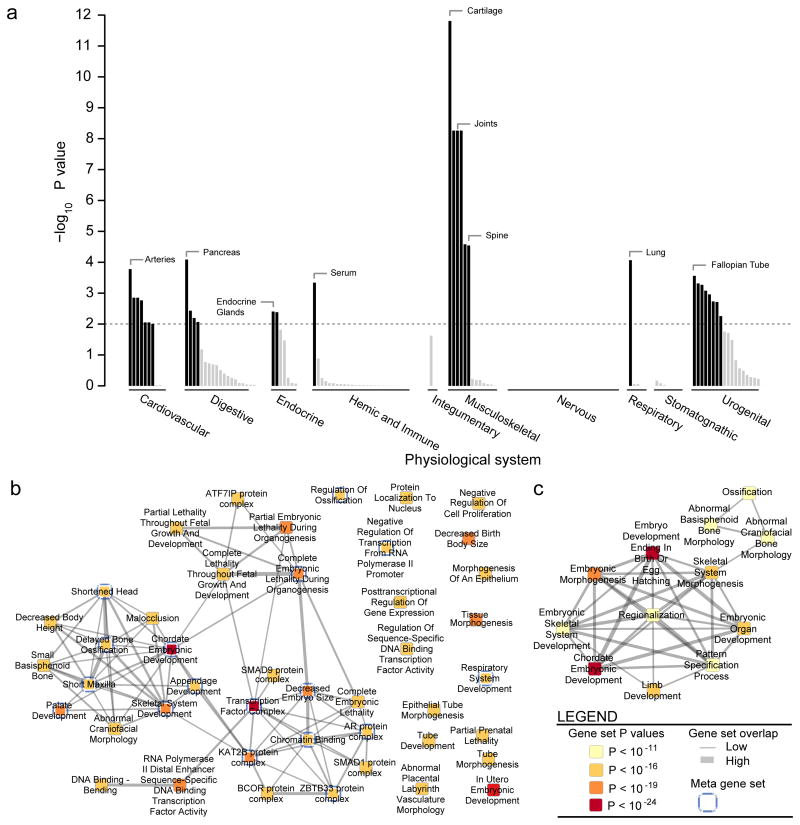
The DEPICT analysis also prioritized tissues and individual genes. We found that genes within associated height loci were enriched for expression in tissues related to chondrocytes (cartilage, joint capsule, synovial membrane, and joints; P<5.5×10−9, FDR<0.001), and other musculoskeletal, cardiovascular, and endocrine tissue-types (FDR<0.05) (Fig. 3; Supplementary Fig. 8; Supplementary Table 15). We also showed that a subset of the 697 height associated SNPs that represented lead cis-eQTLs in blood defined 75 genes that were collectively enriched for expression in cartilage (P=0.008) (Supplementary Note and Supplementary Table 8).
Figure 3. Tissue enrichment combined with pruned gene set network.
Genes within genome-wide significant height associated loci enriched for several relevant tissue annotations as well as gene sets. a, Genes in associated loci tended to be highly expressed in tissues related to chondrocytes and osteoblasts (cartilage, joints, and spine), and other musculoskeletal, cardiovascular and endocrine tissue-types. The analysis was conducted based on the DEPICT method and 37,427 human microarray samples. Tissue annotations are sorted by physiological system and significance. Significantly enriched (FDR<0.05) tissues are color-coded in black. b, Significantly enriched reconstituted gene sets (P-value<1×10−11, FDR<1×10−5) identified by DEPICT. Nodes represent reconstituted gene sets and are color-coded by statistical significance. Edge thickness between nodes is proportional to degree of gene overlap as measured by the Jaccard index. Nodes with gene overlap greater than 25% were collapsed into single meta nodes and marked by blue borders. c, reconstituted gene sets comprised by the Chordate Embryonic Development meta node, which represented several gene sets relevant to human height (e.g. ossification, embryonic skeletal system development, and limb development).
We used DEPICT to prioritize 649 genes (at FDR<0.05) within height-associated loci (Table 3 and Supplementary Table 16). Of these 649 genes, 202 genes (31%) were either significant in the GRAIL analysis (Supplementary Tables 13 and 16) and/or overlapped with a list of abnormal skeletal growth syndromes that we assembled from the OMIM database12 (n=40; Supplementary Tables 9 and 16). Many other newly prioritized genes had additional supporting evidence (Supplementary Table 16), including specific expression in the growth plate12, and/or connections to relevant pathways (for example: GLI2 and LAMA5 [hedgehog signaling]; FRS2 [FGF signaling]; AXIN2, NFATC1, CTNNB1, FBXW11, WNT4, WNT5A and VANGL2 [WNT/beta-catenin signaling]; SMAD3 and MTOR [TGF-beta and/or mTOR signaling]; WWP2/miR140, IBSP, SHOX2 and SP3 [required in mice for proper bone and cartilage formation]; CHYS1, DSE and PCOLCE2 [glycosaminoglycan/collagen metabolism]; SCARA3, COPZ2, TBX18, CRISPLD1 and SLIT3 [differential expression in growth plate and predicted to be in highly relevant pathways]).
DEPICT also prioritizes genes that are new candidates for playing a role in skeletal growth. The genes newly and strongly implicated in this study included not only genes with obvious relationships to skeletal biology, such as SOX5 and collagen genes, but also genes that have no clear published connection to skeletal growth, and likely represent as yet unknown biology (Table 3 and Supplementary Table 16). DEPICT strongly prioritized genes that do not have published annotations related to growth-related pathways but are predicted to be in gene sets that are both enriched in the associated loci and clearly connected to growth. These include genes newly predicted to be in pathways related to cartilage or bone development (FAM101A, CRISPLD1 and the noncoding RNA LINC00476), collagen or extracellular matrix (GLT8D2, CCDC3, and ZCCHC24), histone demethylation (ATAD2B and TSTD2) and other genes predicted to have skeletal phenotypes but not currently annotated as belonging to relevant pathways (ARSJ, PSKH1, COPZ2, ADAMTS17 and the microRNA cluster MIR17HG). Of note, mutations in both ADAMTS17 and MIR17HG have been identified as causes of syndromic short stature in humans15,16.
As suggested by the prioritization of ADAMTS17 and MIR17HG, it is possible that some of the newly highlighted genes may also underlie new syndromes of abnormal skeletal growth. As a further proof of principle, the second entry on our list of prioritized genes (Table 3 and Supplementary Table 16), CHSY1, was not a known monogenic gene in the OMIM database12 when we assembled our list, but mutations in this gene have since been shown to cause a syndrome including brachydactyly and short stature17,18. Thus, the novel DEPICT method, applied to the larger GWAS data set, not only identified similar biology to GRAIL and MAGENTA but also implicated a large number of additional genes, gene sets and pathways that that are likely important in skeletal biology and human growth.
Discussion
By performing a large GWAS study on adult height, a highly heritable polygenic trait, we have provided answers to several current questions of relevance to the genetic study of polygenic diseases and traits. First, we showed that by conducting larger GWAS, we can identify SNPs that explain a substantial proportion of the heritability attributable to common variants. As hypothesized by Yang et al. (2010), the heritability directly accounted for by variants identified by GWAS and inferred by whole-genome estimation approaches are converging with increasing sample size. The variance explained by genome-wide significant SNPs has increased from 3–5% with discovery samples of ~25,000 (ref. 19) to 10% with a discovery sample size of ~130,000 (ref. 6) to 16% with a discovery sample size of 250,000 (this study), and the variance explained from all captured common SNPs is ~50%4,5. The variance explained by genome-wide significant SNPs on a chromosome is also proportional to its length, consistent with the conclusion made by Yang et al.5 using all SNPs (Supplementary Fig. 9). Our new results show that ~21%, ~24% and ~29% of phenotypic variance in independent validation samples is captured by the best ~2,000, ~3,700 and ~9,500 SNPs respectively selected in the discovery samples (Table 1), and that the correlation between actual and predicted height in independent samples from the same population has increased to 0.41 (maximum prediction R2 = 0.412 = 0.17, Fig. 2d). The results are consistent with a genetic architecture for human height that is characterized by a very large but finite number (thousands) of causal variants, located throughout the genome but clustered in both a biological and genomic manner. Such a genetic architecture may be described as pseudo-infinitesimal, and may characterize many other polygenic traits and diseases. There is also strong evidence of multiple alleles at the same locus segregating in the population and for associated loci to overlap with Mendelian forms, suggesting a large but finite genomic mutational target for height, and effect sizes ranging from minute (<1mm; ~0.01 SDs) to gigantic (>300mm; >3 SDs, in the case of monogenic mutations).
It has been argued that the biological information emerging from GWA studies will become less relevant as sample sizes increase, because as thousands of associated variants are discovered, the range of implicated genes and pathways will lose specificity and cover essentially the entire genome20. If this were the case, then increasing sample sizes would not help to prioritize follow up studies aimed at identifying and understanding new biology, and the associated loci would blanket the entire genome. Our study provides strong evidence to the contrary: the identification of many 100’s and even 1000’s of associated variants can continue to provide biologically relevant information. In other words, the variants identified in larger sample sizes both display a stronger enrichment of pathways clearly relevant to skeletal growth and prioritize many additional new and relevant genes. Furthermore, the associated variants are often non-randomly and tightly clustered (typically separated by <250 kb), resulting in the frequent presence of multiple associated variants in a locus. The observations that genes and especially pathways are now beginning to be implicated by multiple variants suggests that the larger set of results retain biological specificity but that at some point, a new set of associated variants will largely highlight the same genes, pathways and biological mechanisms as have already been seen. This endpoint (which we have not clearly reached for height) could be considered analogous to reaching “saturation” in model organism mutagenesis screens, where new alleles typically map to previously identified genes21.
We have identified a large number of gene sets and pathways that are enriched for associations with height. Although the number of gene sets and pathways is large, many are overlapping and likely represent multiple annotations of a much smaller set of core biological mechanisms. We also highlight individual genes within associated loci as being relevant to skeletal growth, including candidates for contributing to syndromes of abnormal skeletal growth; for example, we strongly implicated CHSY1, recently identified as an underlying cause of a monogenic syndrome with short stature and brachydactyly17,18. The lists of prioritized genes and pathways should therefore provide a rich trove of data for future studies of skeletal growth; to facilitate such studies, we have made our results (including genome-wide association results and complete list of highlighted genes and pathways) publicly available. Based on the results of large genetic studies of height, we anticipate that increasing the number of associated loci for other traits and diseases could yield similarly rich lists that would generate new biological hypotheses and motivate future research into the basis of human biology and disease.
URLs
The Genetic Investigation of Anthropometric Traits (GIANT) Consortium, http://www.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium; The Mouse Genetics Initiative, www.informatics.jax.org
ONLINE METHODS
Genome-wide association study meta-analysis
We combined height summary association statistics from 79 genome-wide association (GWA) studies in a meta-analysis of 253,288 individuals using the same methods and studies as previously described6 and additional studies as described in Supplementary Tables 17–19. A total of 2,550,858 autosomal SNPs were meta-analyzed using inverse-variance fixed effects method using METAL22.
GCTA-COJO: conditional and joint multiple SNPs analysis
We used GCTA-COJO analysis7,8 to select the top associated SNPs. This method uses the summary statistics from the meta-analysis and LD correlations between SNPs estimated from a reference sample to perform a conditional association analysis7. The method starts with an initial model of the SNP that shows the strongest evidence of association across the whole genome. It then implements the association analysis conditioning on the selected SNP(s) to search for the top SNPs one-by-one iteratively via a stepwise model selection procedure until no SNP has a conditional P-value that passes the significance level. Finally, all the selected SNPs are fitted jointly in the model for effect size estimation. We used 6,654 unrelated individuals from the ARIC cohort as the reference sample for LD estimation. There were ~3.0M SNPs included in the original meta-analysis. We included in this analysis only the SNPs (~2.48M) on HapMap2 and with sample size > 50,000. We used the genome-wide significance level P<5×10−8 (as reported in Supplementary Table 1).
Metabochip replication
We combined height summary association statistics from 37 independent studies genotyped using Illumina’s Metabochip array9 in a meta-analysis of 80,067 individuals of European ancestry (Supplementary Tables 20–22). Each study tested association between each genotyped SNP and the same QC procedures, height transformations, adjustment, and inheritance model as described for the GWA analysis. Genomic control correction was applied to results for each study prior to meta-analysis, using a set of 4,427 SNPs associated with QT interval to control study-specific inflation factors. We used the inverse-variance fixed effects meta-analysis method.
Validation – linear mixed model (LMM) based association analysis
Each of 15 studies (59,380 individuals) used genome-wide SNP information to calculate a genomic relationship matrix (GRM) for all pairs of individuals and used this to correct association statistics for cryptic relatedness and population stratification. Each study used a linear mixed model as implemented in the software EMMAX23. Meta-analysis was performed as described for the standard GWAS and using a single GC correction. Each study additionally repeated the analyses for each chromosome using a GRM generated from the remaining 21 chromosomes, or in the case of the largest study (WGHS) repeating the analysis for all odd numbered chromosomes using a GRM generated from the even numbered chromosomes and vice versa. Each study then combined association results from the 22 or 2 parts of the genome into one set of data and we repeated the single GC meta-analysis.
Validation – within family (transmission) association analyses
A pure transmission based analysis was performed in seven cohorts for SNPs representing 416 signals of association (Supplementary Note), selected after repeating meta-analysis excluding these studies, with single GC correction. Filtering of low imputation quality SNPs in the studies was followed by inverse variance method of meta-analysis of the family based results. Because of the presence of related individuals, family based studies have lower power at a given sample size. For each study, we calculated the effective sample size (the size of a sample of unrelated individuals that would have the equivalent power; see Supplementary Note and Winkler et al. 24). Estimation of winner’s curse in our data set was performed by repeating the meta-analysis excluding either the family-based studies or excluding random sets of studies from GIANT matched by effective sample size to the family based studies. Independent genome-wide significant loci were selected from each meta-analysis. Power for replication in the excluded samples was estimated at different P-value thresholds and the deficit in replications (number of replications expected minus number observed) was calculated. The contribution of the winner’s curse to the deficit in replications was estimated as the average deficit across the three sets of random non-family-based cohorts. By subtracting this from the deficit observed for the family-based cohorts, we estimated the lack of replication that could be attributed to stratification (either inflation of effect size for true associations, or false positive associations).
Variance and heritability explained
We used GCTA-COJO analysis (Online Methods) to select the top associated SNPs at a range of stringent significance levels (5×10−3, 5×10−4, 5×10−5, …, 5×10−8) for estimation and prediction analyses. We then quantified the variance explained by those selected SNPs using a three-stage analysis, i.e. within-family prediction, GCTA-GREML analysis and population based prediction, in five validation studies (B-PROOF, FRAM, QIMR, TwinGene and WTCCC-T2D). To avoid sample overlap, we repeated the main GWAS meta-analysis and the multiple-SNP analysis five times, each time excluding one of the five validation studies. This approach ensured complete independence between data used to discover SNPs, and data used to estimate how much variance in height these SNPs explained and how well they predicted height. For the within-family prediction analyses, we selected 1,622, 2,758 and 1,597 pairs of full sibs from the QIMR, TwinGene and FRAM cohorts, respectively, with one sib pair per family. For the whole-genome estimation and prediction analyses, we used GCTA-GRM8 to estimate the genetic relatedness between individuals and selected unrelated individuals with pairwise genetic relatedness <0.025 in each of the five studies, i.e. B-PROOF (n = 2,555), FRAM (n = 1,145), QIMR (n = 3,627), TwinGene (n = 5,668) and WTCCC-T2D (n = 1,914).
Within-family prediction analysis
We used the SNPs selected from GCTA-COJO analysis to create a genetic predictor (also called “genetic profile score”) for each of all the full sibs using PLINK25. We then adjusted the genetic predictor by the first 20 principal components (PCs) generated from the principal component analysis (PCA)26. By comparing the predictors within and between families, we partitioned the variance in the predictor analysis into components due to real SNP effects (Vg), errors in estimating SNP effects (Ve), and population structure (Cg + Ce), as described in the Online Methods below.
We calculated the weighted average of each of the four (co)variance components over the three cohorts by their sample size, i.e. Σi (Vg(i) ni)/Σi (ni) with the subscript i indicating the cohort and n being the sample size. From the results of these partitioning analyses within families we can infer what the prediction R2 (Equation 19 in Online Methods below) and what the proportion of variance explained by SNPs (i.e. Vg/VP with VP being the phenotypic variance) would be in a sample of unrelated individuals when using the same set of SNPs. We then tested these inferred values in unrelated samples.
GCTA-GREML analysis
We performed the GREML analysis4 in GCTA8 to estimate the variance explained by the selected SNPs (h2g) in each of the five validation studies. This method fits the effects of a set of SNPs simultaneously in a model as random effects and estimates the genetic variance captured by all the fitted SNPs without testing the significance of association of any single SNPs. We combined the estimates of h2g from the five studies by the inverse-variance approach, i.e. Σi (h2g(i)/SE2i)/Σi (1/SE2i).
Population-based prediction analysis
We created a genetic predictor using the selected SNPs for the unrelated individuals in each of the five validation studies. We then calculated the squared correlation (R2) between phenotype and predictor in each validation study, and calculated the weighted average of the prediction R2 by the sample size across the five studies, i.e. Σi (R2i ni)/Σi (ni).
Theory and method to partition the variance in a genetic predictor
Under the assumption of an additive genetic model, the phenotype of a quantitative trait can be written as
| [1] |
where y is the trait phenotype, g is the total genetic effect of all SNPs, x is an indicator variable for SNP genotypes, b is the SNP effect, and ε is the residual.
From this model, the additive genetic variance is
| [2] |
with the first component being the expected value of additive genetic variance under linkage equilibrium (LE) and second component being the deviation from the expected value could be caused by linkage disequilibrium (LD), population structure or selection27.
Considering a pair of full siblings in a family, the additive genetic covariance between the sibs is
| [3] |
For full sibs,
cov(x1i, x2i ) = ½var(xi ),
cov(x1i, x2j) = ½cov(xi, xj) for SNPs that are in LD, and for SNPs that are not in LD (as shown by both empirical and simulation results).
Let | (SNPs are in LD), and | (SNPs are not in LD but correlated due to population structure)
Therefore, the genetic variance is
| [4] |
The genetic covariance between a pair of full-sibs is
| [5] |
If we take a set of SNPs with their effects estimated from GCTA-COJO analysis (Online Methods), and create a predictor using these SNPs in an independent validation sample, we can write the predictor as
| [6] |
where b̂ is the estimate of b with b̂ =b + e with e being the error in estimating b.
If we assume b and e are independent and denote and , the variance of the predictor is
| [7] |
The covariance between the predictors of a pair of full-sibs is
| [8] |
The covariance between the true phenotype and the predictor of a same individual is
| [9] |
The covariance between the true phenotype of one sib and the predictor of the other sib is
| [10] |
If we define Δĝ = ĝ1 − ĝ2 and Δy = y1 − y2,
| [11] |
| [12] |
We therefore can calculate these four parameters as
| [13] |
| [14] |
| [15] |
| [16] |
where Vg can be interpreted as the variance explained by real SNP effects, Cg is the covariance between predictors attributed to the real effects of SNPs that are not in LD but correlated due to population stratification, Ve is the accumulated variance due to the errors in estimating SNP effects, and Ce is the covariance between predictors attributed to errors in estimating the effects of SNPs that are correlated due to population stratification.
To assess the prediction accuracy, we usually perform a regression analysis of the real phenotype against the predictor, i.e.
| [17] |
so that the regression slope is actually
| [18] |
with the regression R2 being
| [19] |
In the absence of population structure,
| [20] |
Variance explained by SNPs in proximity to the top associated SNPs
We performed analyses to quantify the variance explained by SNPs in close physical proximity to the top associated SNPs in 9,500 unrelated individuals (pairwise genetic relatedness < 0.025) from a combined dataset of the QIMR and TwinGene cohorts. As in previous analyses, to avoid sample overlap between discovery and validation studies, we repeated the discovery meta-analysis excluding the QIMR and TwinGene cohorts, and identified 643 genome-wide significant SNPs from the GCTA-COJO analysis of the summary statistics using ARIC data for LD estimation. We used GCTA-GREML analysis4,8 to quantify the phenotypic variance explained by all the common SNPs (MAF > 0.01) within 100Kb, 500Kb or 1Mb of the 643 genome-wide significant SNPs. We show in Supplementary Figure 6a that there are 104K, 423K and 745K SNPs within 100Kb, 500Kb and 1Mb of the top associated SNPs, which explain 20.8% (s.e. = 1.3%), 25.7% (s.e. = 1.8%) and 29.5% (s.e. = 2.2%) of phenotypic variance, respectively. We then applied a regression-based approach28 to adjust for LD between SNPs. The estimates of variance explained after LD-adjustment were slightly higher than those without adjustment, and the ratio of between the estimates with and without LD-adjustment was consistently ~1.05 regardless of the window size (Supplementary Fig. 6a). However, the difference is small.
We then sought to investigate whether or not there is an enrichment of additional association signals at the top associated loci. We varied the window size from 20Kb to 50Kb, 100Kb, 150Kb, 200Kb, 300Kb, 400Kb, 500Kb, 750Kb and 1Mb, and fitted a two-component model in GCTA-GREML analysis, with the first component being the top associated SNPs and the second component being the rest of SNPs within the window. We found that the per-SNP variance explained excluding the top SNPs (variance explained by the second component divided by the number of SNPs included in this component) decreased with the size of window (Supplementary Fig. 6b), implying that SNPs in closer physical proximity to the top associated SNPs tend to explain disproportionally more variance.
Enrichment of associated SNPs in ENCODE regions, loci containing OMIM genes, eQTLs and nsSNPs
To identify putative causal variants among the height-associated markers, we explored whether the height-associated SNPs were in strong LD (r2>0.8) with non-synonymous coding variants in 1000 Genomes Project CEU Phase 1 data, showed an effect on whole blood gene expression levels, were located within ENCODE-annotated regions, were within loci harboring monogenic growth genes, or had previously been associated with other complex traits in NHGRI GWAS catalog (P<5×10−8) (Supplementary Tables 7–11). To estimate the empirical assessment of enrichment for listed features we used 10,000 permutations of random sets of SNPs matched to the pruned (LD r2>0.1) 628 height-associated SNPs by the number of nearby genes (within a distance of LD r2>0.5), physical distance to nearest gene, and minor allele frequency.
Enrichment of genes in associated loci in known and novel pathways
Data-Driven Expression-Prioritized Integration for Complex Traits (DEPICT) analysis
The DEPICT method (T.H.P. et al., unpublished data; see Geller et al.29 for an earlier application of DEPICT) relies on pre-computed predictions of gene function based on a heterogeneous panel of 77,840 expression arrays (Fehrmann et al., manuscript in review; ref. 30), 5,984 molecular pathways (based on 169,810 high-confidence experimentally derived protein-protein interactions31), 2,473 phenotypic gene sets (based on 211,882 gene-phenotype pairs from the Mouse Genetics Initiative (see URLs)), 737 Reactome pathways32, 5,083 Gene Ontology terms14, and 184 KEGG pathways33. The method leverages these predictions to extend the functional annotations of genes, including genes that previously had only a few or no functional annotations. DEPICT facilitates the analysis of GWAS data by (1) assessing whether genes in associated loci are enriched in tissue-specific expression, (2) identifying reconstituted gene sets that are enriched in genes from associated loci, and (3) systematically identifying the most likely causal gene(s) at a given locus (see Supplementary Note for a more detailed description of DEPICT). In order to run DEPICT, we first clumped the summary statistics from the meta-analysis using 500kb flanking regions, r2>0.1, and excluded SNPs with P≥5×10−8, which resulted in 628 SNPs. We then mapped genes to each of the 628 best-associated SNPs. For a given SNP, this was accomplished by including all genes that resided within LD r2>0.5 boundaries of that SNP, and always including the nearest gene, to its locus gene set. We used a locus definition that was calibrated using the GWAS data for height levels presented in this paper and optimized capture of known monogenic genes for those traits. We merged overlapping loci, and excluded loci that mapped near or within the major histocompatibility complex locus (chromosome 6, location: 20 to 40 Mb), which resulted in a list of 566 non-overlapping loci that were used as input to DEPICT. HapMap Project Phase II CEU genotype data was used for all LD calculations.
GRAIL and MAGENTA analysis
The GRAIL14 algorithm was run using the LD pruned (r2>0.1) 628 SNPs without correcting for gene size, and using text-mining data up to December 2006 (default setting). MAGENTA13 was run with the single genomic control adjusted summary statistics as input using default settings and excluding the HLA region.
Supplementary Material
Acknowledgments
A full list of acknowledgments appears in the Supplementary Note.
AUTHOR CONTRIBUTIONS
Steering Committee Overseeing the Consortium
G.R.A., T.L.A., I.B., S.I.B., M. Boehnke, I.B.B., P.D., C.S.F., T.M.F, L.C.G., I.M.H., J.N.H., D.J.H., E.I., R.C.K., R.J.F.L., M.I.M., K.L. Mohlke, K.E.N., J.R.O., D. Schlessinger, D.P.S., U.T., C.M.v.D.
Writing Group (wrote, edited and commented on manuscript)
S.I.B., D.I.C., A.Y.C., T.E., T.M.F., J.N.H., E.I., T.H.P., S.V., P.M.V., M.N.W., A.R.W., J.Y.
Data preparation group (checked and prepared data from contributing cohorts for meta-analyses)
D. C. Croteau-Chonka, F.R.D., T.E., T. Fall, T. Ferreira, S.G., I.M.H., Z.K., C.M.L., A.E.L., R.J.F.L., J. Luan, R.M., J.C.R., A. Scherag, E.K.S., S.V., T.W.W., A.R.W., T. Workalemahu.
Height meta-analyses group (GWAS and Metabochip) (analyses specific to the manuscript)
T.E., T.M.F. (chair), S.V., P. M. V., A.R.W. (lead - meta-analyses), J.Y. (lead - joint effects and approximate conditional analyses).
Mixed linear model analyses
J.S.B., M. Boehnke, D.I.C., A.Y.C., K.E., T.M.F. (chair), S.G., J.N.H., J.H.Z., E.I., A.U.J., Z.K., R.J.F.L., J. Luan, A. Metspalu, E.M., J.R.O., A.L.P., A.G.U., S.V., P.M.V., M.N.W., A.R.W. (lead), J.Y.
Large lambda group
T.M.F., J.N.H., P.M.V., M.E. Goddard, A.L.P, M.N.W., J.Y., G.R.A., H.M.K.
Family transmission analyses
G.R.A., N.A., I.B.B., Y.D., C.M.v.D., J.N.H. (chair), E.I., J.R.O., E.P., S.V. (lead), P.M.V., J.Y.
Variance, heritability, and prediction analyses
K.E., M.E.G., M.I.M., A.A.E.V., P.M.V. (chair), M.N.W., A.R.W., J.Y. (lead)
Biological Enrichment and Pathway analyses
T.E. (lead - biological enrichment analyses), J.N.H. (chair), T.H.P. (lead - pathway analyses).
ENCODE working group
M.L.B., G.L. (chair), K.S.L.
Gene expression (eQTL) working group
T.E. (chair), L. Franke, J. Karjalainen, J.C.L., A. Metspalu, E.R., J.E.P., H. Westra (lead)
Other Contributions
(DEPICT) R.F., L. Franke, J. Karjalainen, T.H.P.
Project Design, Management and Coordination of Contributing Studies
Previous GWAS studies
(AGES) V. Gudnason, T.B.H.; (AMISH) A.R.S., (ARIC) K.E.N.; (B58C T1D CONTROLS) D.P.S.; (B58C WTCCC) D.P.S.; (BRIGHT) M.J.B., N.J.S.; (CAPS) E.I.; (CHS) J.I.R.; (COLAUS) J.S.B. S. Bergmann; (CROATIA-Vis) I.R.; (deCODE) K. Stefansson, U.T.; (DGI) L.C.G.; (EGCUT) A. Metspalu; (EPIC-Norfolk) N.J.W.; (FENLAND) N.J.W.; (Finnish Twin Cohort) J. Kaprio, K. Silventoinen; (FRAM) L.A.C.; (FUSION) R.N.B., M. Boehnke; (GerMIFS I) J.E., C. Hengstenberg; (GerMIFS II) H. Schunkert; (H2000) S. Koskinen; (HFPS) D.J.H.; (KORA S4) C.G., A.P.; (MICROS) A.A.H., P.P.P.; (NFBC66) M.J., S. Sebert; (NHS) D.J.H.; (NSPHS) U.G.; (NTRNESDA) D.I.B.; (ORCADES) H.C.; (PLCO) S.I.B., S.J.C.; (RSI) C.M.v.D., A. Hofman, M. Kayser, F. Rivadeneira, A.G.U.; (RUNMC) L.A.K.; (SardiNIA) G.R.A.; (SASBAC) E.I.; (SHIP) R.B., H.V.; (WGHS) P.M.R.; (WTCCC-CAD) A.S.H., N.J.S.; (WTCCC-T2D) C.M.L., M.I.M., (Young Finns Study (YFS)) T.L., O.T.R.
New GWAS studies
(ASCOT) M.J.C., P.S.; (ATCG) P.I.W.d.B., D.W.H.; (Athero-Express Biobank Studies) F.W.A., H.M.d.R., F.L.M., G.P.; (B-PROOF) R.D., L.C.P.G.M.d.G., N.M.v.S., N.v.d.V; (BLSA) L. Ferrucci; (CLHNS) K.L. Mohlke, (COROGENE) M.P., J. Sinisalo; (DESIR) S. Cauchi, P.F., (DNBS) M. Melbye, J.C.M. (EGCUT) A.Metspalu, (EMERGE) M.G.H., (ERF) B.A.O., C.M.v.D.; (FamHS) I.B.B., (FINGESTURE) J. Tardif; (GOOD) C.O.; (HBCS) J.G.E.; (Health ABC) T.B.H., Y. Liu; (HERITAGE Family Study) C. Bouchard, D.C.R., M. A. Sarzynski, (InCHIANTI) L. Ferrucci, T.M.F.; (IPM) E.P.B., R.J.F.L., (LLS) P.E. Slagboom; (LOLIPOP) J.C.C., J.S.K.; (MGS) P.V.G.; (NELSON) P.I.W.d.B., P.Z., (PLCO2) S.I.B., S.J.C., (PREVEND) P.v.d.H., (PROCARDIS) H. Watkins, (PROSPER/PHASE) I.F., J.W.J.; (QFS) C. Bouchard, A. Marette, L.P., M.V., (QIMR) A.C.H., N.G.M., G.W.M., (RISC) E.F., T.M.F, A. Golay, M. Walker; (RS II) A. Hofman, M. Kayser, F. Rivadeneira, A.G.U.; (RS III) A. Hofman, M. Kayser, F. Rivadeneira, A.G.U.; (SHIP-TREND) R.B., H.V.; (SORBS) A. Tönjes; (TRAILS) A.J.O., H. Snieder; (TWINGENE) E.I.; (TwinsUK) T.D.S.;
Metabochip studies
(ADVANCE) T.L.A., T.Q.; (AMC-PAS) G.K.H., P.D.; (ARIC) E.B., K.E.N., (B1958C) E.H., C.P.; (BHS) J. Beilby, J. Hui; (CARDIOGENICS) P.D., W.H.O., H. Schunkert; (DESIR) S. Cauchi, P.F.; (DGE DietGeneExpression) B.J.; (DIAGEN) S.R.B., P.E.H.S., (DILGOM) P.J., A.M.J., S. Männistö, M.P., S. Salomaa; (DPS) M.U.; (DR’s EXTRA) T.A.L., R. Rauramaa; (DUNDEE – GoDARTS) C.N.A.P.; (EAS) J.F.P.; (EGCUT) A. Metspalu; (EMIL (SWABIA)) B.O.B., (FBPP) A.C., R.S.C., S.C.H.; (FIN-D2D 2007) S.M.K., T.E.S.; (FUSION 2) F.S.C., J. Saramies, J. Tuomilehto, (GLACIER) P.W.F., (GxE) R.S.C., J.N.H., C.A.M.; (HNR) R.E., P. Hoffmann, S. Moebus, (HUNT 2) K.H.; (IMPROVE) U.d.F., A. Hamsten, S.E.H., E.T.; (KORA S3) T.M., H. Wichmann; (KORA S4) K. Strauch; (Leipzig) M.S.; (LURIC) W.M.; (MEC) C.A. Haiman, L.L.M; (METSIM) J. Kuusisto, M. Laakso; (MORGAM) P.A., D. Arveiler, P. Brambilla; J.F., F.K., J.V.; (NSHD) D.K.; (PIVUS) E.I.; (PROMIS) J. Danesh, P.D., D. Saleheen; (ScarfSheep) A. Hamsten; (SPT) R.S.C., J.N.H., C.A.M. (STR) E.I., (Tandem) M. Bochud, P. Bovet; (THISEAS) G. Dedoussis, P.D.; (Tromsø) I.N.; (ULSAM) E.I., (WHI) C.K., U.P.; (Whitehall) A.D.H., M. Kivimaki, N.J.W; (WTCCC-T2D) C.M.L., M.I.M.
Genotyping of Contributing Studies
Previous GWAS studies
(AGES) A.V. Smith; (B58C T1D CONTROLS) W.L.M.; (B58C WTCCC) W.L.M.; (CAPS) H. Grönberg; (CROATIA-Vis) C. Hayward; (EGCUT) M. Nelis; (EPIC-Norfolk) N.J.W.; (FENLAND) N.J.W.; (Finnish Twin Cohort) J. Kaprio; (KORA S3) T.I., M. Müller-Nurasyid; (MICROS) A.A.H; (NFBC66) M.J; (ORCADES) A.F.W.; (PLCO) S.J.C.; (RSI) K.E., C. Medina-Gomez, F. Rivadeneira, A.G.U.; (SASBAC) P. Hall; (SHIP) A. Hannemann, M. Nauck; (WGHS) D.I.C., L.M.R.; (WTCCC-CAD) A.S.H. N.J.S.; (WTCCC-T2D) A.T.H, M.I.M.; (Young Finns Study (YFS)) T.L., O.T.R.
New GWAS studies
(ASCOT) P.B.M.; (ATCG) P.I.W.d.B., D.W.H., P.J.M.; (Athero-Express Biobank Study) S.W.v.d.L.; (CLHNS) D. C. Croteau-Chonka; (DESIR) E.E., S. Lobbens; (EGCUT) T.E., L.M.; (EMERGE) D. C. Crawford, M.G.H.; (ERF) A.I., B.A.O., C.M.v.D.; (FamHS) I.B.B., M.F.F., A.T.K., M.K.W, Q.Z; (GOOD) C.O., M. Lorentzon; (Health ABC) Y. Liu; (HERITAGE Family Study) M. A. Sarzynski; (HYPERGENES) S. Lupoli.; (IPM) E.P.B.; (LifeLines) M.A. Swertz; (LLS) J. Deelen, Q.H.; (LOLIPOP) J.C.C., J.S.K; (NELSON) J. Smolonska; (PLCO2) S.J.C., K.B.J., Z.W.; (PREVEND) P.v.d.H., I.M.L., (PROCARDIS) M.F., A. Goel; (PROSPER/PHASE) J.W.J., D.J.S., S.T.; (QFS) C. Bellis, J. Blangero; (QIMR) A.K.H.; (SHIP-TREND) A. Hannemann, M. Nauck; (RSII) K.E., C. Medina-Gomez, F. Rivadeneira, A.G.U.; (RSIII) K.E., C. Medina-Gomez, F. Rivadeneira, A.G.U.; (TRAILS) M. Bruinenberg, C.A. Hartman; (TWINGENE) A. Hamsten, N.L.P.; (TwinsUK) M. Mangino, A. Moayyeri; (WGHS) D.I.C., L.M.R.
Metabochip studies
(ADVANCE) D. Absher, T.L.A., T.Q.; (AMCPAS) K. Stirrups; (ARIC) E.B., K.E.N.; (B1958C) N.R.R., C.J.G. T.J.; (BHS) G.M.A., J. Hui; (CARDIOGENICS) K. Stirrups; (DESIR) E.E., S. Lobbens; (DGE DietGeneExpression) B.J.; (DIAGEN) M.A.M.; (DUNDEE - GoDARTS) A.J.B., C.N.A.P., N.W.R.; (EAS)
J.F.W.; (EGCUT) T.E., L.M.; (ELY) N.G.F., C.L., R.J.F.L., K.K.O, R.A.S, N.J.W; (EMIL (SWABIA)) B.O.B.; (EPIC-Norfolk) N.G.F, C.L., R.J.F.L., K.K.O, R.A.S, N.J.W; (FBPP) A.C.; (FENLAND) N.G.F, C.L., R.J.F.L., K.K.O, R.A.S, N.J.W; (FIN-D2D 2007) P.S.C.; (FUSION 2) L.K.; (GLACIER) I.B., (HNR) M.M.N.; (HUNT 2) N.N.; (KORA S3) N.K., M. Waldenberger; (KORA S4) H. Grallert, P.L.; (Leipzig) Y.B., P.K.; (LURIC) M.E.K.; (MEC) C.A. Haiman, L.A.H.; (NSHD) D.K., K.K.O., A.W.; (PIVUS) E.I., C. Berne, L.L., J. Sundström, (PROMIS) K. Stirrups; (STR) N.L.P., (Tandem) G.B.E., M. Maillard, (THISEAS) K. Stirrups; (Tromsø) P.S.C.; (ULSAM) J.Ä., E.I., A. Syvänen; (WHI) C.K., U.P.; (Whitehall) C.L.; (WTCCC-T2D) A.T.H, M.I.M.
Phenotype Coordination of Contributing Studies
Previous GWAS studies
(AMISH) A.R.S. (B58C T1D CONTROLS) D.P.S.; (B58C WTCCC) D.P.S.; (BRIGHT) M.J.B., N.J.S.; (CAPS) H. Grönberg; (CHS) R.C.K.; (CROATIA-Vis) I.R.; (DGI) V. Lyssenko; (EGCUT) A. Metspalu; (EPIC-Norfolk) N.J.W.; (FENLAND) N.J.W.; (Finnish Twin Cohort) J. Kaprio, (KORA S4) A.P.; (NFBC66) M.J.; (NTRNESDA) J.H.S.; (ORCADES) A.F.W.; (PLCO) S.I.B.; (RSI) A. Hofman, F. Rivadeneira, A.G.U.; (SASBAC) P. Hall; (SHIP) M. Dörr, W.H., T.K.; (UKBS-CC) J. Jolley; (WGHS) D.I.C., L.M.R, A.Y.C.; (WTCCC-CAD) A.S.H., N.J.S.; (WTCCC-T2D) A.B., A.T.H.; (Young Finns Study (YFS)) T.L., O.T.R.
New GWAS studies
(ASCOT) M.J.C., P.S., A.V. Stanton; (ATCG) D.W.H.; (Athero-Express Biobank Study) F.L.M., J.E.P.V.; (BLSA) S. Bandinelli; (DESIR) R. Roussel; (DNBC) H.A.B., B.F., F.G., (EGCUT) T.E., A. Metspalu; (eMERGE) J.C.D., A.N.K., (ERF) B.A.O., C.M.v.D.; (FamHS) I.B.B., M.F.F.; (FINGESTURE) J. Junttila; (GOOD) C.O., M. Lorentzon; (HBCS) J.G.E.; (Health ABC) M.E. Garcia, T.B.H., M.A.N.; (HERITAGE Family Study) C. Bouchard; (HYPERGENES) P.M.; (InCHIANTI) S. Bandinelli, L. Ferrucci; (IPM) O.G., (LifeLines) S. Scholtens, M.A. Swertz, J.M.V.; (LLS) D.v.H; (LOLIPOP) J.C.C., J.S.K., U.A., L.O., J. Sehmi; (NELSON) P.A.D.J.; (PLCO2) S.I.B.; (PREVEND) S.J.L.B., R.T.G., H.L.H; (PROCARDIS) R. Clarke, R. Collins, M.F., A. Hamsten; (PROSPER/PHASE) J.W.J., I.F., B.M.B.; (QFS) A. Tremblay; (QIMR) A.K.H., A.C.H., P.A.F.M., N.G.M., G.W.M.; (RSII) A. Hofman, Rivadeneira, A.G.U.; (RSIII) A. Hofman, Rivadeneira, A.G.U.; (SORBS) A. Tönjes; (SHIP-TREND) M. Dörr, W.H., T.K.; (TRAILS) C.A. Hartman, R.P.S., F.V.v.O.; (TWINGENE) P.K.E.M., N.L.P.,; (TwinsUK) M. Mangino, C. Menni; (WGHS) D.I.C., L.M.R.
Metabochip studies
(ADVANCE) A.S.G., M.A.H., (AMCPAS) J.J.P.K.; (ARIC) E.B.; (B1958C) E.H., C.P.; (BHS) A.L.J., A.W.M.; (DESIR) R. Roussel; (DGE DietGeneExpression) B.J.; I.H.C.; (DIAGEN) J. Gräßler, G.M.; (DPS) J. Lindström; (DR’s EXTRA) M.H., (DUNDEE - GoDARTS) A.S.F.D., A.D.M. C.N.A.P.; (EAS) S. McLachlan; (EGCUT) T.E., A. Metspalu; (EMIL (SWABIA)) B.O.B., S. Claudi-Boehm, W. Kratzer, S. Merger, T.S., R.W.; (FBPP) R.S.C., S.C.H.; (GLACIER) G. Hallmans; (GxE) T. Forrester, B.O.T.; (HNR) R.E., S. Moebus; (HUNT 2) O.H., (KORA S3) H. Wichmann; (Leipzig) M. Blüher; (MEC) L.R.W.; (METSIM) H.M.S.; (NSHD) D.K.; (PIVUS) C. Berne, E.I., L.L., J. Sundström, (PROMIS) D. Saleheen; (SPT) T. Forrester, B.O.T.; (STR) N.L.P.; (Tandem) M. Bochud, P. Bovet; (THISEAS) S. Kanoni; (Tromsø) T. Wilsgaard; (ULSAM) J.Ä., V. Giedraitis, E.I.; (WHI) C.K., U.P.; (Whitehall) M. Kumari; (WTCCC-T2D) A.B., A.T.H.
Data Analysis
Previous GWAS studies
(AGES) A.V. Smith; (ARIC) K.L. Monda, K.E.N.; (B58C T1D CONTROLS) D.P.S.; (B58C WTCCC) D.P.S.; (CAPS) E.I.; (CHS) R.C.K., B.M.; (COLAUS) S. Bergmann, Z.K.; (CROATIA-Vis) C. Hayward; (deCODE) V. Steinthorsdottir, G.T.; (EGCUT) M. Nelis; (EPIC-Norfolk) J.H.Z.; (FENLAND) J. Luan; (FRAM) L.A.C., N.L.H.; (FUSION) C.J.W.; (GerMIFS II) C.W.; (H2000) N.E.; (HPFS) L.Q.; (NHS) L.Q. (NSPHS) A. Johansson; (PLCO) S.I.B.; (RSI) K.E., C. Medina-Gomez, F. Rivadeneira, A.G.U.; (RUNMC) S.H.V.; (SardiNIA) S. Sanna; (SASBAC) E.I.; (SEARCH) J.P.T.; (SHIP) A. Teumer; (WGHS) D.I.C., L.M.R, A.Y.C; (WTCCC-T2D) A.P.M., T. Ferreira; A. Mahajan, R.M.
New GWAS studies
(ATCG) P.I.W.d.B., P.J.M., S.R.; (Athero-Express Biobank Studies) S.W.v.d.L.; (B-PROOF) S.v.D.; (BHS) M.C.; (BLSA) T.T.; (CLHNS) D. C. Croteau-Chonka, (DESIR) S. Cauchi, L.Y., (DNBC) B.F., F.G.; (EGCUT) T.E., K.F., T.H., R.M.; (eMERGE) M.G.H.; (ERF) N.A., A.D.; (FamHS) M.F.F.; (GOOD) C.O., M. Lorentzon; (HBCS) N.E.; (Health ABC) M.A.N.; (HERITAGE Family Study) C. Bouchard, M. A. Sarzynski, D.C.R., T.R., T.K.R, Y.J.S., (HYPERGENES) S. Lupoli; (InCHIANTI) D.P., T.T., A.R.W.; (IPM) J. Jeff, V. Lotay, Y. Lu; (LifeLines) I.M.N., J.V.V.V.; (LLS) M. Beekman, J.J.H.; (LOLIPOP) W.Z; (MGS) J. Shi, (NELSON) S.R., J.v.S; (PLCO2) S.I.B., Z.W.; (PREVEND) P.v.d.H., I.M.L., N.V.; (PROCARDIS) A. Goel; (PROSPER/PHASE) I.F., B.M.B., S.T.; (QFS) J. Blangero, L.P.; (QIMR) G. Hemani, D.R.N., J.E.P.; (RISC) D.P., A.R.W.; (RSII) K.E., C. Medina-Gomez, F. Rivadeneira, A.G.U.; (RSIII) K.E., C. Medina-Gomez, F. Rivadeneira, A.G.U.; (SHIP-TREND) A. Teumer; (SORBS) R.M., (TRAILS) H. Snieder; (TWINGENE) E.I., S.G.; (TwinsUK) M. Mangino; (WGHS) D.I.C., L.M.R.
Metabochip Studies
(ADVANCE) D. Absher, T.L.A, L.L.W.; (AMCPAS) S. Kanoni; (ARIC) S. Buyske, A.E.J., K.E.N.; (B1958C) T. Ferreira; (BHS) D. Anderson; (CARDIOGENICS) S. Kanoni; (DESIR) S. Cauchi, L.Y.; (DGE DietGeneExpression) I.H.C.; (DIAGEN) A.U.J., G.M.; (DILGOM) K.K.; (DUNDEE) T. Ferreira; (EAS) J.L.B., R.M.F.; (EGCUT) T.E., K.F., E.M.; (ELY) J. Luan; (EMIL (SWABIA)) B.O.B.; (EPIC-Norfolk) J. Luan, (FBPP) A.C., G.B.E.; (FENLAND) J. Luan; (GLACIER) F. Renstrom, D. Shungin; (GxE) C.D.P., (HNR) S. Pechlivanis, A. Scherag; (IMPROVE) L. Folkersen, R.J.S.; (KORA S3) J.S.R.; (KORA S4) E.A.; (Leipzig) A. Mahajan, I.P.; (LURIC) G. Delgado, T.B.G., M.E.K., S. Pilz, H. Scharnag; (MEC) U.L., F.R.S.; (METSIM) A. Stancáková; (NSHD) A.W., J. Luan; (PIVUS) S.G., E.I.; (PROMIS) S. Kanoni; (ScarfSheep) R.J.S.; (SPT) C.D.P. (STR) E.I., S.G.; (TANDEM) G.B.E.; (THISEAS) M. Dimitriou; (ULSAM) S.G., E.I.; (WHI) J. Gong, J. Haessler, M.R.; (Whitehall) J. Luan; (WTCCC-T2D) A.P.M., T. Ferreira; A. Mahajan, R.M.
References
- 1.Fisher RA. The correlation between relatives on the supposition of Mendelian inheritance. Trans R Soc. 1918;52:399–433. [Google Scholar]
- 2.Silventoinen K, et al. Heritability of adult body height: a comparative study of twin cohorts in eight countries. Twin Res. 2003;6:399–408. doi: 10.1375/136905203770326402. [DOI] [PubMed] [Google Scholar]
- 3.Visscher PM, et al. Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. PLoS Genet. 2006;2:e41. doi: 10.1371/journal.pgen.0020041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yang J, et al. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42:565–9. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yang J, et al. Genome partitioning of genetic variation for complex traits using common SNPs. Nat Genet. 2011;43:519–25. doi: 10.1038/ng.823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lango Allen H, et al. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 2010;467:832–8. doi: 10.1038/nature09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yang J, et al. Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat Genet. 2012;44:369–75. S1–3. doi: 10.1038/ng.2213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Voight BF, et al. The metabochip, a custom genotyping array for genetic studies of metabolic, cardiovascular, and anthropometric traits. PLoS Genet. 2012;8:e1002793. doi: 10.1371/journal.pgen.1002793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang J, et al. Genomic inflation factors under polygenic inheritance. Eur J Hum Genet. 2011;19:807–12. doi: 10.1038/ejhg.2011.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Altshuler DM, et al. Integrating common and rare genetic variation in diverse human populations. Nature. 2010;467:52–8. doi: 10.1038/nature09298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lui JC, et al. Synthesizing genome-wide association studies and expression microarray reveals novel genes that act in the human growth plate to modulate height. Hum Mol Genet. 2012;21:5193–201. doi: 10.1093/hmg/dds347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Segre AV, Groop L, Mootha VK, Daly MJ, Altshuler D. Common inherited variation in mitochondrial genes is not enriched for associations with type 2 diabetes or related glycemic traits. PLoS Genet. 2010;6 doi: 10.1371/journal.pgen.1001058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Raychaudhuri S, et al. Identifying relationships among genomic disease regions: predicting genes at pathogenic SNP associations and rare deletions. PLoS Genet. 2009;5:e1000534. doi: 10.1371/journal.pgen.1000534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.de Pontual L, et al. Germline deletion of the miR-17 approximately 92 cluster causes skeletal and growth defects in humans. Nat Genet. 2011;43:1026–30. doi: 10.1038/ng.915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Morales J, et al. Homozygous mutations in ADAMTS10 and ADAMTS17 cause lenticular myopia, ectopia lentis, glaucoma, spherophakia, and short stature. Am J Hum Genet. 2009;85:558–68. doi: 10.1016/j.ajhg.2009.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li Y, et al. Temtamy preaxial brachydactyly syndrome is caused by loss-of-function mutations in chondroitin synthase 1, a potential target of BMP signaling. Am J Hum Genet. 2010;87:757–67. doi: 10.1016/j.ajhg.2010.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tian J, et al. Loss of CHSY1, a secreted FRINGE enzyme, causes syndromic brachydactyly in humans via increased NOTCH signaling. Am J Hum Genet. 2010;87:768–78. doi: 10.1016/j.ajhg.2010.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Visscher PM. Sizing up human height variation. Nat Genet. 2008;40:489–90. doi: 10.1038/ng0508-489. [DOI] [PubMed] [Google Scholar]
- 20.Goldstein DB. Common genetic variation and human traits. N Engl J Med. 2009;360:1696–8. doi: 10.1056/NEJMp0806284. [DOI] [PubMed] [Google Scholar]
- 21.Nüsslein-Volhard C, Wieschaus E, Kluding H. Mutations affecting the pattern of the larval cuticle in Drosophila melanogaster: zygotic loci on the second chromosome. Roux’s Arch Dev Biol. 1984;193:267–282. doi: 10.1007/BF00848156. [DOI] [PubMed] [Google Scholar]
- 22.Willer CJ, Li Y, Abecasis GR. METAL: fast and efficient meta-analysis of genomewide association scans. Bioinformatics. 2010;26:2190–1. doi: 10.1093/bioinformatics/btq340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kang HM, et al. Variance component model to account for sample structure in genome-wide association studies. Nat Genet. 2010;42:348–54. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Winkler TW, et al. Quality control and conduct of genome-wide association meta-analyses. Nat Protoc. 2014;9:1192–212. doi: 10.1038/nprot.2014.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Purcell S, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–75. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Price AL, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–9. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 27.Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Incorporated; 1998. [Google Scholar]
- 28.Gusev A, et al. Quantifying missing heritability at known GWAS loci. PLoS Genet. 2013;9:e1003993. doi: 10.1371/journal.pgen.1003993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Geller F, et al. Genome-wide association analyses identify variants in developmental genes associated with hypospadias. Nat Genet. 2014 doi: 10.1038/ng.3063. [DOI] [PubMed] [Google Scholar]
- 30.Cvejic A, et al. SMIM1 underlies the Vel blood group and influences red blood cell traits. Nat Genet. 2013;45:542–5. doi: 10.1038/ng.2603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lage K, et al. A human phenome-interactome network of protein complexes implicated in genetic disorders. Nat Biotechnol. 2007;25:309–16. doi: 10.1038/nbt1295. [DOI] [PubMed] [Google Scholar]
- 32.Croft D, et al. Reactome: a database of reactions, pathways and biological processes. Nucleic Acids Res. 2011;39:D691–7. doi: 10.1093/nar/gkq1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kanehisa M, Goto S, Sato Y, Furumichi M, Tanabe M. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res. 2012;40:D109–14. doi: 10.1093/nar/gkr988. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.