Methane emissions from Alaska in 2012 from CARVE airborne observations

Significance

Alaska emitted 2.1 ± 0.5 Tg CH₄ during the 2012 growing season, an unexceptional amount despite widespread permafrost thaw and other evidence of climate change in the region. Our results are based on more than 30 airborne measurement flights conducted by CARVE from May to September 2012 over Alaska. Methane emissions peaked in summer and remained high in to the fall. Emissions from boreal regions were notably larger than from North Slope tundra. To our knowledge, this is the first regional study of methane emissions from Arctic and boreal regions over a growing season. Our estimates reinforce and refine global models, and they provide an important baseline against which to measure future changes associated with climate change.

Abstract

We determined methane (CH₄) emissions from Alaska using airborne measurements from the Carbon Arctic Reservoirs Vulnerability Experiment (CARVE). Atmospheric sampling was conducted between May and September 2012 and analyzed using a customized version of the polar weather research and forecast model linked to a Lagrangian particle dispersion model (stochastic time-inverted Lagrangian transport model). We estimated growing season CH₄ fluxes of 8 ± 2 mg CH₄⋅m⁻²⋅d⁻¹ averaged over all of Alaska, corresponding to fluxes from wetlands of ${56}_{-13}^{+22}$ mg CH₄⋅m⁻²⋅d⁻¹ if we assumed that wetlands are the only source from the land surface (all uncertainties are 95% confidence intervals from a bootstrapping analysis). Fluxes roughly doubled from May to July, then decreased gradually in August and September. Integrated emissions totaled 2.1 ± 0.5 Tg CH₄ for Alaska from May to September 2012, close to the average (2.3; a range of 0.7 to 6 Tg CH₄) predicted by various land surface models and inversion analyses for the growing season. Methane emissions from boreal Alaska were larger than from the North Slope; the monthly regional flux estimates showed no evidence of enhanced emissions during early spring or late fall, although these bursts may be more localized in time and space than can be detected by our analysis. These results provide an important baseline to which future studies can be compared.

Recent studies have raised concerns about an increase in methane (CH₄) emissions from Arctic regions as temperatures warm (1–3). Carbon stocks in polar regions are estimated to be as large as 1,700 Pg of soil organic carbon (4), preserved by cold, wet conditions that inhibit decomposition. Over the last 20 y, temperatures have increased more rapidly at these latitudes than the rest of the world (5); continuation of this trend will lead to permafrost warming and thawing (6), potentially releasing vast quantities of carbon dioxide (CO₂) and CH₄ into the atmosphere (7–10). A recent synthesis of carbon emissions predicted by permafrost models reported releases in the range of 120 ± 85 Pg C by 2100 (11). Large uncertainties are likewise associated with estimates of CH₄ emissions (12–90 Tg CH₄⋅y⁻¹) (12). The potential for large increases in CH₄ emissions are a particular concern because CH₄ strongly impacts both atmospheric chemistry and climate (13). Estimates of the impact of permafrost carbon emissions on future global temperatures range from ∼0.1–0.2 °C (14) to $0.3\pm 0.2$ °C (11) by 2100, with increased carbon emissions expected to continue after 2100 (11).

Recent global inversion studies find no evidence for increasing CH₄ emissions from these regions in the last 10 y (15, 16), despite warming, similar to earlier studies (17–19) and some biogeochemical models (14). Surface CH₄ flux observations across the pan-Arctic from 1990–2006 have ranged widely and measurement locations have changed, making it difficult to detect any trend over those years (ref. 20; cf. ref. 21).

The present paper derives estimates of CH₄ surface fluxes in Alaska from May to September 2012, based on an extensive program of regional-scale airborne measurements of atmospheric CH₄, the Carbon in Arctic Reservoirs Vulnerability Experiment (CARVE). We quantify the monthly mean CH₄ emissions from Alaska during the growing season, providing a snapshot of the interactions between climate and the vast reservoir of preserved soil organic matter in the Arctic.

Methods

Measurements.

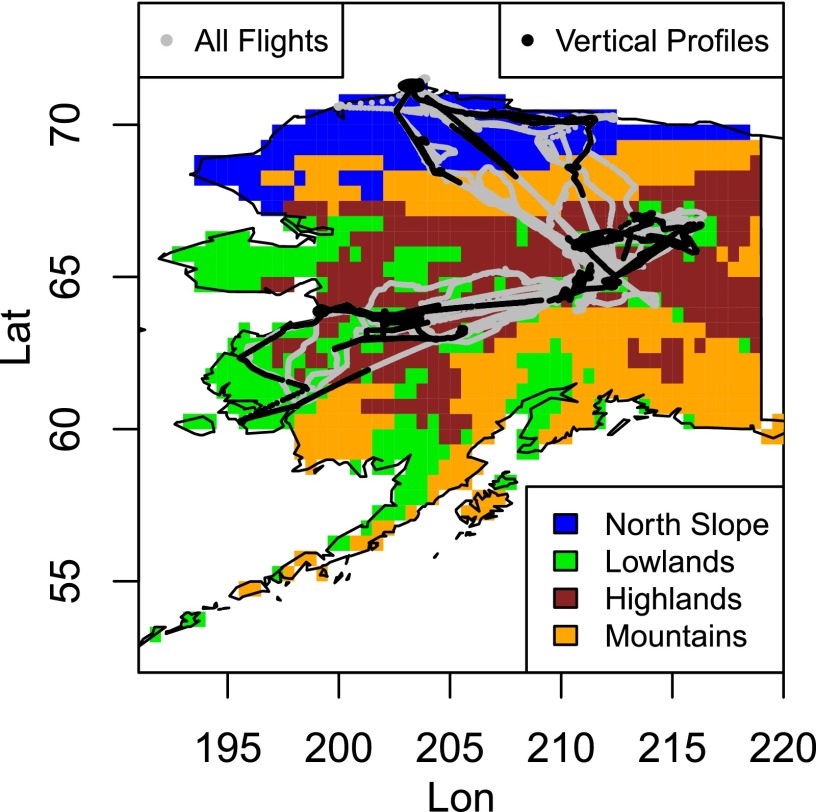
Measurements were made aboard a NASA C-23B aircraft (N430NA) during the last 2 wk of each month between May and September 2012. Flights were based in Fairbanks, AK, and ranged from 60.21° to 71.56° N and 164.5° to 143.6° W, covering three major regions: (i) the North Slope, which included transits to Barrow and Deadhorse on the northern coast; (ii) the Lower Yukon region following the course of the Yukon river south and west of Fairbanks, including the Yukon Delta National Wildlife Refuge (which includes the Yukon and Kuskokwim deltas) and the Innoko National Wildlife Refuge; and (iii) the Upper Yukon region which included the Yukon Flats National Wildlife Refuge (gray points in Fig. 1). Each flight lasted 4–10 h, with the majority of sampling occurring below 200 m above ground level (agl). One or more vertical profiles reaching a maximum of 5,500 m above sea level (asl) were flown during each flight, with the maximum height determined by weather conditions. In total, 200 flight hours were flown over 31 flight days.

Fig. 1.

Location of flight tracks (gray) and vertical profiles (black) during CARVE 2012. Background colors are elevation categories based on US EPA level III ecoregions (31).

Two independent cavity ringdown spectrometers measured in situ greenhouse gas mole fractions every ∼2.5 s with two separate on-board calibration standards for each unit. The first spectrometer measured CO₂, CH₄, and H₂O (Picarro; G1301-m) directly from the inlet. This sensor sampled one of two calibration gas cylinders every 30 min and is similar to the instrument described by Karion et al. (22). For the second instrument, ambient air first passed through a Nafion dryer followed by a dry ice trap which effectively lowered the dewpoint to ∼195 K, before being sampled by the spectrometer. This sensor reported CO₂, CH₄, and carbon monoxide (CO) mixing ratios (Picarro; G2401-m) and sampled both its calibration cylinders every 30 min. The time series used in our analysis merge the CH₄ data from these two instruments, enabling us to fill in gaps when an instrument was calibrating or malfunctioning. Further discussion on the comparison of these two instruments can be found in Supporting Information. Other relevant measurements made on board include ozone (O₃) mixing ratios (2B Technologies; model 205), dewpoint temperature (Edgetech; Vigilant), outside air temperature (Harco; 100366–18), pressure (Paroscientific; 745–15A) and location using a global positioning unit (Crossbow; NAV420).

Model Description.

Aircraft measurements were aggregated horizontally every 5 km and vertically in 50-m intervals below 1 km asl and 100-m intervals for measurements above 1 km, giving ∼23,000 data points. Each of these points at (x, y, z, t) was treated as a receptor for the stochastic time-inverted Lagrangian transport (STILT) model (23), which traces the trajectory of the air parcel at each receptor location backward in time over the preceding 10 d and quantifies in space and time where upstream surface fluxes influenced the measured concentrations. Particles are advected by the large-scale (i.e., explicitly resolved) wind field, as simulated by the Advanced Research version of the weather research and forecasting (WRF) model (Version 3.4.1) (24) on a 3.3-km grid in the innermost domain over Alaska, plus stochastic motions to simulate turbulence. To improve prediction of the meteorological fields in the Arctic, basic options from the Polar variant of WRF (25–27) were implemented. A 2D influence field (i.e., footprint) is available for each particle every 3 h over its 10-d travel period, representing the response of the receptor to a unit emission of tracer at each grid square [converted unit of parts per billion (ppb)/(mg⋅m⁻²⋅d⁻¹)]. The footprints used in this analysis were on a 0.5° × 0.5° grid. Further details of both the WRF and STILT models can be found in Henderson et al. (28). Fig. S1 shows the sum of all footprints for the vertical profiles (see CH₄ Fluxes Derived from Column Analysis) used in the analysis.

CH₄ Fluxes Derived from Column Analysis.

Our primary analysis focuses on applying the WRF-STILT framework to the partial column integrals of CH₄ mole fractions measured during vertical profiles, subtracting the background value for air flowing in from outside the study region (the state of Alaska). This column enhancement represents the mass loading of the atmosphere from the ground to the top of the residual layer (the maximum height influenced by surface emissions during transit from the boundary layer) due to emissions in the region. The advantage of this approach is that results only depend on the large-scale simulation of the vertical structure of the atmosphere, reducing our reliance on the detailed structure of the boundary and residual layers, fine-scale variations of emissions at the surface, and turbulent transport elements in the lower atmosphere.

Atmospheric column enhancements have been used in previous studies of CO₂ in the Amazon (29, 30), based on the concept that this quantity measures the total amount of trace gas added to the atmosphere during the transit of an air mass over the land. Similar to Chou et al. (29), we used the CH₄ mole fraction measured at the top of the residual layer height as our background value. The top of the residual layer is effectively equivalent to the bottom of the free troposphere and was identified by comparing the vertical profiles of CH₄, CO₂, CO, O₃, and water vapor ($P_{{\text{H}}_2\text{O}}$). For each vertical profile, the height at which the slope changes sign for each chemical compound was compared and used to determine the residual layer height for that profile. The height at which Alaskan land ceased to influence the column was also assessed using WRF-STILT and contributed to the identification of the residual layer height when there were discrepancies between different chemical compounds. The dashed purple line in Fig. 2 shows the top of the residual layer for a sample profile. Vertical profiles over Alaska from the National Oceanic and Atmospheric Administration measurements on board the Alaska Coast Guard flights (22) during this same period were consistent with the inferred background concentrations.

Fig. 2.

Sample CH₄ vertical profile (A) used for column analysis and corresponding O₃ profile (B) from September 22, 2012. The dashed purple line represents the identified top of the residual layer, and the hatched areas are used to determine the column enhancement.

Column enhancements below the residual layer height ($E_{{\text{CH}}_4,\text{obs}}$) were calculated by block averaging the observed CH₄ mole fraction ([CH₄]) from each vertical profile into 250-m altitude bins, subtracting the concentration at the top of the residual layer ([CH₄](h)) and then integrating the density-weighted concentration enhancements:

$$E_{{\text{CH}}_4,\text{obs}}={\displaystyle \underset{0}{\overset{h}{\int }}\left(\left[C{H}_4\right]\left(z\right)-\left[C{H}_4\right]\left(h\right)\right)\times \frac{P_{\text{air}}\left(z\right)-P_{{\text{H}}_2\text{O}}\left(z\right)}{RT\left(z\right)}dz},$$

where $P_{\text{air}}$, T, and R are the ambient pressure, temperature, and universal gas constant, respectively. The column enhancement is illustrated by the black hatch in Fig. 2A. A similar calculation is used to determine the column enhancement from WRF-STILT assuming a unit flux from land $E_{{\text{CH}}_4,\text{unit}}$. The mean surface flux associated with each profile ($\overline{F_{{\text{CH}}_4,{\text{VP}}_{\text{i}}}}$) is then calculated as $\overline{F_{{\text{CH}}_4,{\text{VP}}_{\text{i}}}}=E_{{\text{CH}}_4,\text{obs}}/E_{{\text{CH}}_4,\text{unit}}$. The overall mean was calculated by averaging the $\overline{F_{{\text{CH}}_4,{\text{VP}}_{\text{i}}}}$ for all vertical profiles weighted by their corresponding footprints. Monthly means were calculated in a similar manner but using only profiles from that month. Surface influences used to weight profiles can be seen in Fig. S2. The red hatch in Fig. 2A shows the modeled column enhancement calculated from the mean September surface flux. The mean emission for a given region ($\overline{F_{{\text{CH}}_4,\text{A}}}$, where A is the region of interest) is determined by weighing $\overline{F_{{\text{CH}}_4,{\text{VP}}_{\text{i}}}}$ for every vertical profile by the portion of the corresponding footprint influence in that region ($I_{{\text{A},\text{VP}}_{\text{i}}}$), such that

$$\overline{F_{{\text{CH}}_4,\text{A}}}=\frac{{\displaystyle {\sum }_i\overline{F_{{\text{CH}}_4,{\text{VP}}_{\text{i}}}}\times I_{\text{A},{\text{VP}}_{\text{i}}}}}{{\displaystyle {\sum }_i{I}_{{\text{A},\text{VP}}_{\text{i}}}}}.$$

To determine the uncertainties in the derived fluxes, observed parameters used in the calculation (measured mole fraction, pressure, temperature, and water vapor) were bootstrapped by randomly sampling 1,000 times with replacement at each 250-m altitude bin. The residual layer height, which also determines the background concentration, was also sampled 1,000 times assuming a uniform probability of the true residual layer height being ±500 m of the determined height. A second method of determining the uncertainty compared the calculated mean flux with $\overline{F_{{\text{CH}}_4,{\text{VP}}_{\text{i}}}}$ for each vertical profile. Fig. S2 shows this comparison with the mean monthly fluxes. Results are similar for the overall mean. The average uncertainty from this method lies within the uncertainty determined from our bootstrapping analysis.

Of the 50 vertical profiles from the 2012 campaign, 30 were well-suited for deriving CH₄ flux from the land surface in Alaska (locations shown as black points in Fig. 1; the sum of footprints for all vertical profiles is shown in Fig. S1; times are given in Table S1). Profiles were rejected due to (i) influences by biomass burning (increase in CO of at least 40 ppb within the residual layer) (four profiles); (ii) significant land influences (>30%) from outside the CARVE study region, usually from Siberia (10 profiles); or (iii) undefined residual layer, either because the maximum height of the aircraft was too low or the atmospheric structure was too complex for this simple analysis (six profiles).

Land Elevation Categories Derived from Ecoregions.

The US Geological Survey and Environmental Protection Agency (EPA) identify 20 level III ecoregions in Alaska (31). For the purposes of our CH₄ surface–atmosphere flux calculations, these 20 ecoregions were grouped into four categories based on elevation: Highlands (plateaus and uplands); Lowlands (plains, lowlands, and flats); the North Slope (Arctic coastal plain and Arctic foothills); and Mountains (ranges and mountains) (colored regions in Fig. 1, complete list in Elevation Categories Based on Ecoregions). This grouping was used because CH₄ fluxes depend on water table depth and elevation (32, 33) and the atmospheric data in this study cannot resolve all 20 ecoregions. The ecoregions were gridded to 0.5° × 0.5° to match the resolution of the STILT footprints.

Results and Discussion

Results of the Column Analysis.

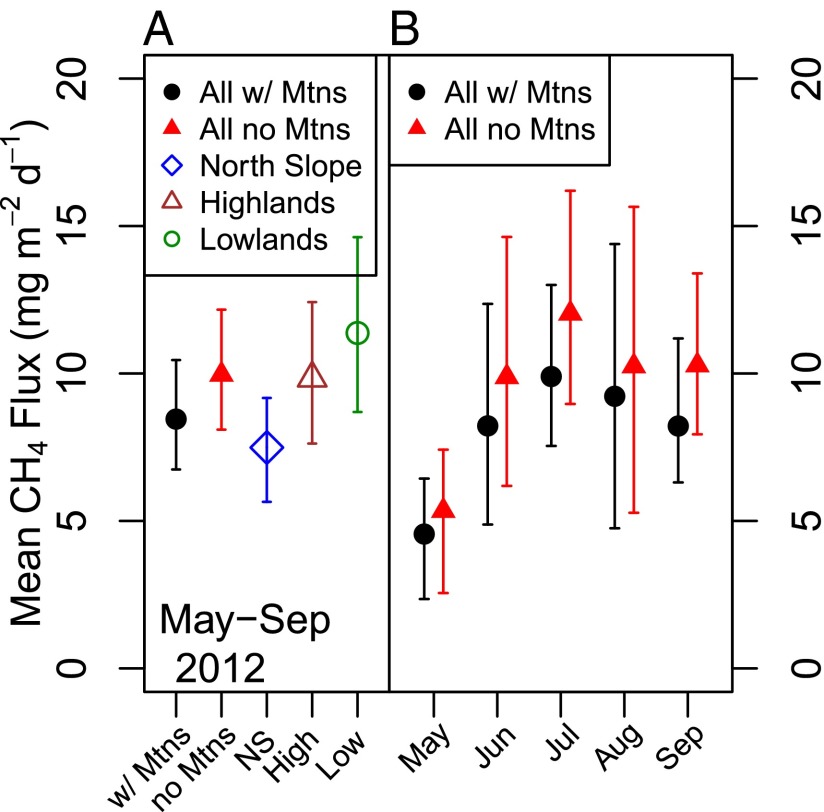
The black circle in Fig. 3A shows the overall mean CH₄ flux estimates from Alaska if we adopt a uniform emission rate for all land surfaces during all months: $8\pm 2$ mg CH₄⋅m⁻²⋅d⁻¹, where the uncertainty is the 95% confidence interval from the bootstrapping analysis described above. This baseline assessment does not reflect actual emissions at the surface, but it is determined independent of any assumed surface map and is the most robust number derived from our calculations. Flux estimates were also determined if the Mountains category was assumed to not contribute to CH₄ emissions, which increases the estimated mean flux from remaining land types ∼25% to 10 ± 2 mg CH₄⋅m⁻²⋅d⁻¹ (red triangle in Fig. 3A). Uncertainties in Fig. 3 show the 95% confidence interval derived from the bootstrapping analysis. These flux estimates represent all land emission processes: biogenic, anthropogenic, and geologic/thermogenic (including possible thermogenic seeps arising from thawing permafrost) (3), but exclude emissions from biomass fires and any ocean processes. These fluxes correspond to an overall emission of $2.1\pm 0.5$ Tg CH₄ from May to September 2012.

Fig. 3.

Estimated mean CH₄ fluxes from the column analysis for (A) the entire study period (May to September 2012) and (B) by month. Error bars are the 95th percentile determined from the bootstrapping analysis described in the text.

Mean fluxes for the entire study period were derived for the three broad land categories (Highlands, North Slope, and Lowlands) as shown in Fig. 3A. The CH₄ flux from the Lowlands (11 ± 3 mg CH₄⋅m⁻²⋅d⁻¹) is consistently greater than from the Highlands (10 ± 2 mg CH₄⋅m⁻²⋅d⁻¹), and both of these regions emit significantly more CH₄ than the North Slope (7 ± 2 mg CH₄⋅m⁻²⋅d⁻¹) ($P<0.001$ in a paired t test). This result is consistent with the Lowlands being wetter than the Highlands and the North Slope being cooler, with a thinner active soil layer, than the other regions.

The seasonality of CH₄ fluxes derived over the entire state is shown in Fig. 3B and exhibits an increase in emissions from May to July followed by a gradual decrease until September. The overall range is only 5 mg CH₄⋅m⁻²⋅d⁻¹, which is weaker than the 14–80 mg CH₄⋅m⁻²⋅d⁻¹ difference that can be observed over a season at ground sites (7, 34). The CH₄ column enhancements sampled by the CARVE aircraft are influenced by emissions from land types heterogeneous in elevation, soil moisture, and organic substrate, as well as diverse seasonal characteristics. (Even at altitudes below 200 m agl, footprints can span a distance of >500 km.) The large sampling area for each profile tends to dampen seasonal signals that may be observed at individual ground sites with more coherent seasonality.

The seasonal variation observed in our study is generally consistent with other regions in North America (7, 34) and with northern wetland emissions diagnosed from global inversion studies (15–17). We observe neither the pattern observed at Zackenberg, Greenland, with high spikes in CH₄ fluxes during the spring thaw and fall freeze up (35), nor as predicted for the Yukon River Valley (36). Sampling began before the spring thaw, so widespread bursts at that time should have been seen, but it is possible that we did not sample late enough in the season to capture CH₄ bursts in the fall, or that these bursts are more localized in time and space than can be detected by our flight program.

CH₄ Fluxes Estimated from CH₄:O₃ Covariance.

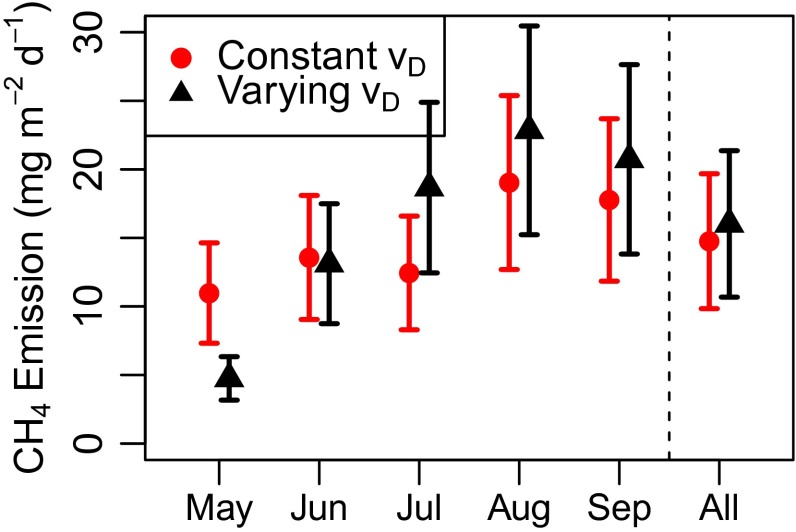
We developed a second independent method to estimate CH₄ fluxes using the observed covariance of CH₄ and O₃ in the lowest 1,500 m of the atmosphere. These flux estimates are independent of the WRF-STILT footprints and use the collected data merged at 5 s, resulting in ∼40,000 data points rather than just the vertical profiles. This method heavily weights the particular flight tracks and involves many simplifying assumptions; it is included to check the order of magnitude of the estimates calculated from the vertical profile analysis. Altitudes closest to the surface can be treated as a constant flux layer, where concentration changes of a chemical compound are dominated by surface exchange with little influence from atmospheric flux divergence. Near the surface in the Arctic, O₃ loss is dominated by dry deposition and in situ chemistry can be neglected (37, 38). Similar to the column analysis, influences from biomass burning were removed by excluding data when absolute CO mole fractions exceeded 150 ppb (39). At the scale of our measurements, we can assume that O₃ is effectively lost through dry deposition from the same surfaces that emit CH₄, and we can use similarity theory to independently determine CH₄ flux: $F_{{\text{CH}}_4}=F_{{\text{O}}_3}\times \left(\mathrm{\Delta }{\text{CH}}_4/\mathrm{\Delta }{\text{O}}_3\right)$, where $F_x$ is the flux of compound x. O₃ flux is computed from the deposition velocity ($v_{\text{D}}$) as $F_{{\text{O}}_3}=-v_{\text{D}}\times {\left[{\text{O}}_3\right]}_{500}$, where ${\left[{\text{O}}_3\right]}_{500}$ is the average O₃ mole fraction in the lowest 500 m agl. Fig. 4 shows O₃ and CH₄ mole fraction deviations from 10-min means in the lowest 1,500 m agl for June (see Fig. S3 for other months). The slope of the line $\left(\mathrm{\Delta }{\text{O}}_3/\mathrm{\Delta }{\text{CH}}_4\right)$ is determined using standard major axis regression (40) and used to calculate $F_{{\text{CH}}_4}$, shown in the red circles of Fig. 5. We used a constant O₃ $v_{\text{D}}=-0.3\pm 0.1$ cm⋅s⁻¹, as determined by Henderson et al. (28) which is consistent with measurements reported over fens, Scots pine forests, and tundra (41–43). Using this $v_{\text{D}}$ with WRF-STILT footprints results in the modeled O₃ shown in the red triangles in Fig. 2B, reasonably consistent with observations.

Fig. 4.

Covariance of O₃ and CH₄ below 1,500 m agl for June. See Fig. S3 for other months.

Fig. 5.

Estimated CH₄ fluxes from the O₃:CH₄ analysis assuming a constant and seasonally varying O₃ $v_{\text{D}}$, red and black points, respectively. Error bars reflect the uncertainty in the O₃ $v_{\text{D}}$ (∼33%).

The domain-wide average $F_{{\text{CH}}_4}$ from this method is estimated to be 15 ± 5 mg CH₄⋅m⁻²⋅d⁻¹ for May to September 2012, where the uncertainty reflects the range of O₃ $v_{\text{D}}$ in the literature and the calculated $v_{\text{D}}$ ($-0.3\pm 0.1$ cm⋅s⁻¹) (28). O₃ $v_{\text{D}}$ is expected to vary seasonally (43) because it is dependent on the reactivity of O₃ with leaves. Applying the seasonally varying $v_{\text{D}}$ determined by Henderson et al. (28) (0.13, 0.28, 0.44, 0.35, and 0.34 cm⋅s⁻¹ for May to September 2012, respectively, with ∼33% uncertainty) results in the estimated $F_{{\text{CH}}_4}$ shown in the black triangles of Fig. 5 (mean = 16 ± 5 mg CH₄⋅m⁻²⋅d⁻¹). The resulting seasonal cycle is not dissimilar to that calculated using the column analysis in Fig. 3, although the peak of the emissions is later. Overall, the CH₄ flux estimated from its covariance with O₃ is remarkably close to the mean value determined from all of Alaska if mountains were excluded ($10\pm 2$ mg CH₄⋅m⁻²⋅d⁻¹), which is most comparable because we seldom flew near the surface in mountainous terrain. The general agreement between these two independent estimates of CH₄ fluxes increases our confidence in the overall analysis.

Comparison with Other Flux Observations.

Our regional flux estimates integrate over wet and dry areas uniformly, giving a more objective regional flux than upscaling from chambers or towers which are typically deployed in areas expected to be significant CH₄ sources. To compare our estimates with these other studies that are sensitive to smaller spatial scales, a distribution map (44) was used to infer the emission rate for wetlands, effectively restricting the areal extent from which CH₄ was emitted and assuming that other CH₄ sources are negligibly small. Resulting emissions are seven times higher than the overall regional mean (${56}_{-13}^{+22}$ mg CH₄⋅m⁻²⋅d⁻¹) and follow a similar seasonal pattern. This value is similar to CH₄ fluxes measured via airborne eddy covariance during the Arctic Boundary Layer Experiment which took place over the Yukon–Kuskokwim River Delta in southwest Alaska July 28 to August 9, 1988 (${51}_{-26}^{+34}$ mg CH₄⋅m⁻²⋅d⁻¹) (45).

Flux measurements determined from static chambers in Alaska range from 0 to 300 mg CH₄⋅m⁻²⋅d⁻¹ (compiled by Olefeldt et al. in ref. 46), with a median over 90 studies of 49 mg CH₄⋅m⁻²⋅d⁻¹, and eddy covariance and gradient tower measurements in tundra regions range from 3 to 80 mg CH₄⋅m⁻²⋅d⁻¹, with a median over 13 studies of 34 mg CH₄⋅m⁻²⋅d⁻¹ (Table S2). A recent aircraft study over northern Sweden determined CH₄ fluxes equivalent to 29 ± 12 mg CH₄⋅m⁻²⋅d⁻¹ for a flight in July 2012 over extensive wetland areas (47). Our values are consistent with these previous measurements once the sampling differences are taken into account.

Comparison with Models and Inversion Studies.

Our integrated CH₄ emission estimate of 2.1 ± 0.5 Tg CH₄ over May to September 2012 falls within the 0.7–6 Tg CH₄ range of emissions estimated from an ensemble of 10 different global bottom–up models for the same region and months (Table 1). Our findings are also consistent with the 1.5 ± 0.2 Tg CH₄ estimated by Carbon Tracker-CH₄ (16) and the 1.3 ± 0.3 Tg CH₄ estimated by TM5-4DVAR when biomass burning is excluded (15) for May to September. Our mean is very close to the mean of all of the comparable values in Table 1 (2.1 vs. 2.3 Tg CH₄). Uncertainties in Table 1 are 2σ of the emissions from the averaging period. The global inversion study by Chen and Prinn (17) estimates an annual emission of 2 ± 1 Tg CH₄ from Alaska if 17% of North American wetlands are assumed to be in Alaska, as stated in their source map (48). Our value can be used as a lower bound for total emissions in 2012, and if we assume that 50% of annual CH₄ emissions occurs between October and April, as reported for a site in Greenland (35), then the upper bound for emissions in 2012 would be 4 ± 1 Tg CH₄. A reasonable annual estimate for 2012 is the mean of these two bounds, 3 ± 1 Tg CH₄, and is consistent with assuming that emissions for the months of October and November are similar to August and September and that emissions in the remaining months are near zero.

Table 1.

CH₄ emissions from various models

Lead author	Model	Emissions, Tg	Averaging period	Ref(s).
Land surface models
Melton	DLEM	0.8 ± 0.2	1993–2004	(49)
Melton	LPJ-Bern	1.2 ± 0.3	1993–2004	(49)
Melton	LPJ-WHyMe	6 ± 1	1993–2004	(49)
Melton	LPJ-WSL	0.9 ± 0.2	1993–2004	(49)
Melton	ORCHIDEE	1.0 ± 0.4	1993–2004	(49)
Melton	SDGVM	0.7 ± 0.2	1993–2004	(49)
Riley	CLM4Me	5 ± 2	2001–2010	(50)
Zhu		2.6 ± 0.1	2000–2009	(51)
Zhuang	TEM	3 (annual)	1980–1996	(32)
Matthews		4.34		(52)
Inverse models
Bergamaschi	TM5-4DVAR	1.3 ± 0.3	2001–2010	(15)
Bruhwiler	CT-CH4	1.5 ± 0.2	2000–2009	(16)
Chen	MATCH	2 ± 1	1996–2001	(17)
This study		2.1 ± 0.5	2012

Emissions were calculated for the region 55–75° N, 141–169° W for May to September of the given years, except TEM, where the given value is the annual emission for all of Alaska. CLM4Me, community land model with CH₄ biogeochemistry; CT-CH₄, CarbonTracker-CH₄; DLEM, dynamic land surface ecosystem model; LPJ, Lund–Potsdam–Jena dynamic global vegetation model; MATCH, model for atmospheric transport and chemistry; ORCHIDEE, organizing carbon and hydrology in dynamic ecosystems; SDGVM, Sheffield dynamic global vegetation model; TEM, terrestrial ecosystem model; TM5-4DVAR, tracer model V5-4-dimensional variational inverse modeling system; WHyMe, wetland hydrology and methane; WSL, Swiss Federal Institute for Forest, Snow and Landscape Research.

Our results are lower than emissions reported in a recent study of the Yukon River Valley (36), which gave an annual emission of 4.01 Tg CH₄⋅y⁻¹ for this region alone, which comprises 30% of Alaska. Likewise, the annual emissions from Alaskan thermogenic seeps have been reported to be 1.5–2 Tg CH₄⋅y⁻¹ (3). This value would comprise at least 50–67% of the total annual Alaskan emissions. Both of these estimates seem to be higher than can be accommodated by our observations.

Summary and Conclusions

To our knowledge, CARVE is the first study to make frequent and sustained airborne measurements of CH₄ over large areas of Arctic and boreal Alaska throughout the growing season. We derived emissions of $2.1\pm 0.5$ Tg CH₄ from Alaska during May to September 2012, and we found that the Lowland and Highland regions consistently emitted CH₄ at higher rates than the North Slope. A modest seasonal cycle was observed over all regions, with fluxes roughly doubling from May to July, then decreasing gradually in August and September. Stronger seasonality was likely not observed because the atmosphere integrates over heterogeneous land types with asynchronous seasonal cycles. Additional measurements made under different environmental forcings could allow factors affecting emissions at a regional scale to be determined.

The total estimated CH₄ emitted from the region ($2.1\pm 0.5$ Tg CH₄ over May to September 2012) is quite small compared with the global emissions of 550 Tg CH₄⋅y⁻¹ (21) (<0.5%), despite the recent warming of permafrost areas in Alaska. Because this is, to our knowledge, the first top–down regional study of Alaska based on observations, we cannot directly assess whether emissions have increased in response to climatic shifts. However, our results are consistent with fluxes obtained in global top–down inversion studies, which reported a lack of recent trends in CH₄ emission in the Arctic (15, 16, 18, 19). Our work and these studies together indicate that CH₄ emissions from Arctic regions have not contributed significantly to increasing levels of global CH₄ observed during the last decade. Our work during the growing season of 2012 in Alaska provides the baseline against which possible future increases in Arctic boreal and tundra CH₄ emissions can be assessed.