Hard sphere-like glass transition in eye lens α-crystallin solutions

Significance

Normal vision and accommodation rely on the clarity and softness of the eye lens. Hardening of the lens has been linked with presbyopia, the loss of accommodative capability with age, and lens clarity is disrupted in cataract, a leading cause of blindness worldwide. Here, realistically concentrated solutions of a prevalent eye lens structural protein, α-crystallin, which exhibits short-range order needed for lens transparency, are found in addition to show high-concentration dynamical slowing down similar to that of hard-sphere glass transitions. This suggests that analogous investigation of concentrated crystallin mixtures, like those in the living lens, may help to advance understanding of the molecular basis of both presbyopia and cataract.

Abstract

We study the equilibrium liquid structure and dynamics of dilute and concentrated bovine eye lens α-crystallin solutions, using small-angle X-ray scattering, static and dynamic light scattering, viscometry, molecular dynamics simulations, and mode-coupling theory. We find that a polydisperse Percus–Yevick hard-sphere liquid-structure model accurately reproduces both static light scattering data and small-angle X-ray scattering liquid structure data from α-crystallin solutions over an extended range of protein concentrations up to 290 mg/mL or 49% vol fraction and up to ca. 330 mg/mL for static light scattering. The measured dynamic light scattering and viscosity properties are also consistent with those of hard-sphere colloids and show power laws characteristic of an approach toward a glass transition at α-crystallin volume fractions near 58%. Dynamic light scattering at a volume fraction beyond the glass transition indicates formation of an arrested state. We further perform event-driven molecular dynamics simulations of polydisperse hard-sphere systems and use mode-coupling theory to compare the measured dynamic power laws with those of hard-sphere models. The static and dynamic data, simulations, and analysis show that aqueous eye lens α-crystallin solutions exhibit a glass transition at high concentrations that is similar to those found in hard-sphere colloidal systems. The α-crystallin glass transition could have implications for the molecular basis of presbyopia and the kinetics of molecular change during cataractogenesis.

The cytoplasm of the tightly packed fiber cells of the eye lens contains concentrated aqueous protein mixtures that have high refractive indexes, while normally remaining clear enough for vision. Lens clarity depends on short-range order between lens proteins (1, 2) and can be disrupted by both protein aggregation and liquid–liquid phase separation in cataract, a leading cause of blindness. At the high protein concentrations of lens cytoplasm, 25–60% by weight in mammals, small changes in interprotein interactions can disrupt transparency. For human lens proteins with cataractogenic point mutations, and for high-concentration lens protein mixtures, protein interaction changes as small as a fraction of thermal energy, $k_{B}T$, can induce phase separation and thus lead to opacification (3–7).

In addition to equilibrium phase transitions, dynamical transitions including glass formation and gelation can also occur at high protein concentrations like those of the eye lens (8, 9). Relatively abrupt viscoelastic changes associated with glass formation or gelation could harden the lens and contribute to presbyopia and could alter cataract formation rates by affecting aggregation and phase separation kinetics.

Here we study the equilibrium liquid structure and dynamics of concentrated solutions of eye-lens α-crystallin protein solutions, using small-angle X-ray scattering (SAXS), static light scattering (SLS) and dynamic light scattering (DLS), viscometry, liquid-state theory, event-driven molecular dynamics (MD) simulations, and mode-coupling theory (MCT). α-Crystallin is a polydisperse protein with about 40 subunits of two types, αA and αB, and accounts for up to 50% of lens protein mass. The forward scattering intensity from SAXS and light scattering experiments with concentrated α-crystallin solutions can be well represented by monodisperse hard-sphere liquid-structure models that have been key for understanding short-range order needed for lens transparency (1, 2). However, in physiological conditions α-crystallin ranges in molecular weight from 3 × 10⁵ to 2 × 10⁶, with an average near 8 × 10⁵ (10). There have indeed been reports that structure factors obtained from SAXS and small-angle neutron scattering data deviate from predictions for monodisperse hard spheres (11, 12).

Accordingly, we first show that a polydisperse hard-sphere liquid-structure model (PHSM) based on the Percus–Yevick (PY) approximation (13) can accurately model SAXS data obtained from the present bovine α-crystallin preparations for volume fractions up to 49%, using a polydispersity of 20%. In contrast, polydispersity did not strongly influence model predictions for the observed SLS, which unlike SAXS probes length scales much larger than molecular sizes.

We then test for glassy dynamics of α-crystallin solutions, using DLS and viscometry, and find glass transition features like those previously found for hard spheres. In particular, with increasing α-crystallin concentration, DLS intermediate scattering functions show expected progressively slower relaxations along with fast decays, and the viscosity diverges, both when approaching volume fractions in the vicinity of 58%. Using MCT (14), we obtain semiquantitative models of DLS data and corresponding data from MD simulations of high-concentration polydisperse sphere systems, in which MD polydispersity values were obtained from fits of the PHSM to the SAXS data. We note that for MCT we have used the theory for monodisperse systems, because the majority of the MCT work to date has focused on such systems. Recent results for polydisperse systems (15) support a similar overall picture.

In brief, the data show that the present α-crystallin solutions have liquid structure and glassy dynamics similar to those of polydisperse hard-sphere solutions. Thus, eye lens protein solutions show analogs to ordinary glass in linking short-range order, transparency, and arrested dynamics.

Experimental Results

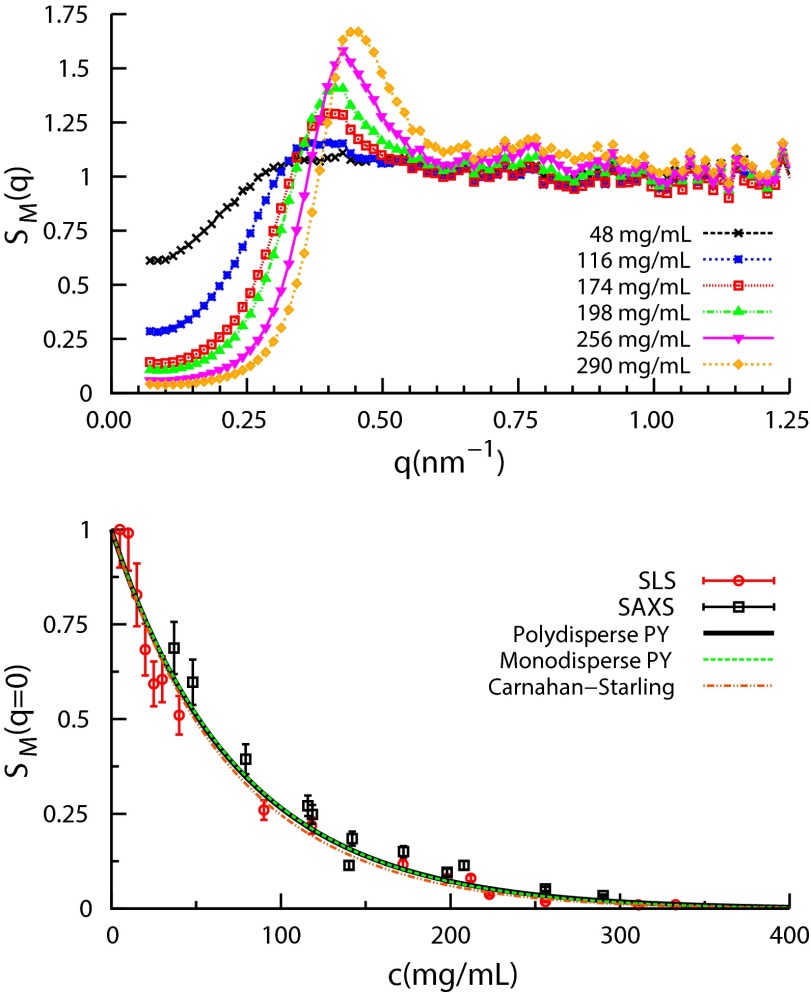
We first investigate structural properties of α-crystallin solutions with SAXS. Fig. 1 (Top) shows the measured structure factors $S_M\left(q\right)=\left(I\left(q\right)/c\right)/\left(I_0\left(q\right)/c_0\right)$ vs. scattering vector magnitude, q, for concentrations $c>c_0$, in which $I\left(q\right)$ denotes scattered intensity, c is the weight per volume protein concentration, and $I_0$ is the intensity from the form factor sample at concentration $c_0=5$ mg/mL. As c increases, there is a dramatic reduction of $S_M\left(0\right)$ and a growing first peak of $S_M\left(q\right)$, both characteristics of monodisperse and somewhat polydisperse hard-sphere solutions. Scattering intensities $I\left(q\right)$ vs. q are shown in Fig. S1. The term measured is used because α-crystallin is polydisperse.

Fig. 1.

(Top) Structure factors $S_M\left(q\right)$ deduced from the SAXS $I\left(q\right)$ data, using the 5-mg/mL data for the measured form factor $P_M\left(q\right)$. (Bottom) $S_M\left(q\to 0\right)$ vs. ϕ from both SLS and SAXS agree with hard-sphere models, but do not distinguish the polydisperse PY, Schulz-distributed mixture model with $p=0.20$ (black) from either the monodisperse PY (green) or the Carnahan–Starling (red) models.

Hard-sphere models have been used to interpret scattering data from α-crystallin solutions (4, 11, 16). Fig. 1 (Bottom) compares the measured reduction of SLS and SAXS $S_M\left(0\right)$ with c to that of the Carnahan–Starling (CS) equation of state for monodisperse hard spheres (HS) (17), $S_{\text{CS}}\left(0\right)$ (red dashed curve),

$$S_{\text{CS}}\left(0\right)=\frac{{\left(1-\varphi \right)}^4}{{\left(1+2\varphi \right)}^2+{\varphi }^3\left(\varphi -4\right)},$$ [1]

where ϕ is the α-crystallin packing fraction. To relate ϕ to c we used α-crystallin packing volume per unit weight (voluminosity) $v=\varphi /c=1.7\hspace{0.17em}\text{mL}/\text{g}$ (4, 11, 16). This packing volume, larger than that of a typical globular protein, $v=0.7\hspace{0.17em}\text{mL}/\text{g}$, reflects α’s open, multisubunit structure (11). We find that Eq. 1 reproduces $S_M\left(0\right)$ over the entire concentration range.

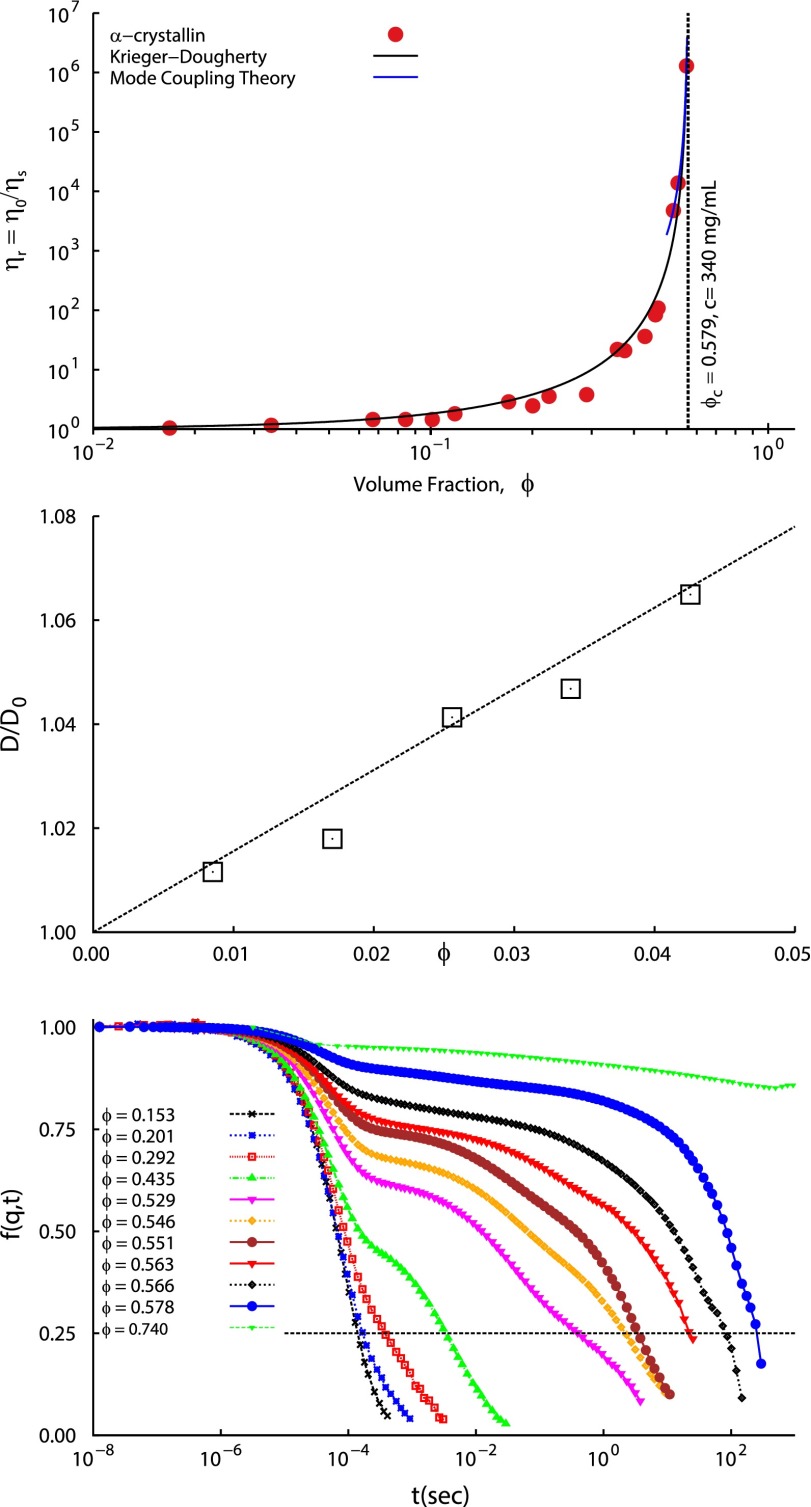
We next measure the zero shear viscosity ${\eta }_0$ and collective diffusion coefficient D of α-crystallin solutions and compare them to those of hard-sphere solutions, again using $v=1.7\hspace{0.17em}\text{mL}/\text{g}$. Fig. 2 (Top) shows that the relative zero-shear viscosity ${\eta }_r={\eta }_0/{\eta }_s$, measured using cone and plate viscometry, increases by six orders of magnitude as ϕ approaches $0.55-0.6$; here ${\eta }_s$ is the solvent viscosity, $7.93\times {10}^{-4}$ Pa⋅s. The dramatic increase of α-crystallin ${\eta }_r$ is similar to that found for hard-sphere colloid glass formation (18) and glass formation of the proteins BSA (19) and β-lactoglobulin (20). Fig. 2 (Top) shows that the α-crystallin ${\eta }_r\left(\varphi \right)$ data are well fitted by the Krieger–Dougherty (KD) form, often used to model hard-sphere ${\eta }_r\left(\varphi \right)$,

$${\eta }_r={\left(1-\frac{\varphi }{{\varphi }_m}\right)}^{-\left[\eta \right]{\varphi }_m},$$ [2]

where $\left[\eta \right]$ is the intrinsic viscosity and ${\varphi }_m$ is the volume fraction at which ${\eta }_r$ diverges, as discussed below.

Fig. 2.

(Top) α-Crystallin solution low shear rate relative viscosity ${\eta }_r={\eta }_0/{\eta }_s$ vs. α-crystallin volume fraction ϕ, using $v=1.7\hspace{0.17em}\text{mL}/\text{g}$ consistent with SAXS and SLS (see text). (Middle) Normalized diffusivities $\left(D/D_0\right)\left(\varphi \right)$, from second-order cumulant fits to the DLS-measured ISF $f\left(q,t\right)$. $D_0=2.2\times {10}^{-11}$ m²/s is the free-particle diffusion coefficient as ϕ approaches 0. Dashed line: the HS theory $D/D_0=1+1.45\varphi$. (Bottom) DLS $f\left(q,t\right)$ vs. delay time t; q = 0.023 nm⁻¹. Progressively slower $f\left(q,t\right)$ decays with increasing ϕ are qualitatively similar to those from MD simulations (Fig. S4, Top). Slow relaxation times ${\tau }_q$ for which $f\left(q,\tau \right)=0.25$ (dashed line) are shown in Fig. 5 (Left).

Fig. 2 (Middle) shows $D/D_0$ vs. ϕ; $D_0=2.2\times {10}^{-11}$ m²/s is the free-particle diffusion coefficient from extrapolation to $\varphi =0$. The solid line is the theoretical prediction for hard spheres, $D/D_0=1+1.45\varphi$ (21, 22). Thus, the low-concentration $D/D_0$ is consistent with the hard-sphere picture.

Fig. 2 (Bottom) shows the intermediate scattering function (ISF) or normalized field autocorrelation function $f\left(q,t\right)$ measured by DLS as a function of ϕ. For $\varphi \ge 0.435$ (256 mg/mL), $f\left(q,t\right)$ shows bimodal decay, and the slower component grows in amplitude and relaxation time with increasing ϕ. At $\varphi =0.58$, a characteristic slow decay time τ, gauged here as that to reach $f\left(q,t\right)=0.25$, as illustrated, is six orders of magnitude slower than the corresponding low-concentration relaxations of ${10}^{-4}$ s. At the highest-volume fraction, $\varphi =0.74$, the ISF shows characteristics of an arrested or nonergodic sample. Therefore, $f\left(q,t\right)$ was also measured using a slowly rotating sample, as described in SI Text, and shows a very slowly decaying plateau indicative of dynamical arrest.

The ${\eta }_r$, $D/D_0$, and ISF data suggest that the HS model used for static scattering can also represent dynamic properties. We now analyze the statics and dynamics in more detail.

Analysis and Discussion

Structural Properties and Polydispersity.

The structural analysis above did not consider polydispersity, an α-crystallin feature that we wish to incorporate quantitatively into MD. We found that $S_M\left(0\right)$ vs. c does not usefully distinguish polydisperse from monodisperse α-crystallin equation of state models. Fig. 1 (Bottom) shows close agreement between $S_{\text{CS}}\left(0\right)$ (red), the monodisperse PY model (green), and the PY $S_M\left(0\right)$ (black) for a Schulz HS diameter distribution (13) with variance ${\sigma }^2=p^2$ and $p=0.20$, using

$$\begin{array}{c}{S}_M\left(0\right)=\frac{{\left(1-\varphi \right)}^4}{{\left(1+2\varphi \right)}^2}[1+\frac{6\varphi \left(1+2\varphi \right)}{{\left(1-\varphi \right)}^2}\cdot \frac{\left(1+3{\sigma }^2\right)}{\left(1+5{\sigma }^2\right)}\\ -\frac{9{\varphi }^2}{{\left(1-\varphi \right)}^2}\cdot \frac{{\left(1+3{\sigma }^2\right)}^2}{\left(1+5{\sigma }^2\right)\left(1+4{\sigma }^2\right)}].\end{array}$$ [3]

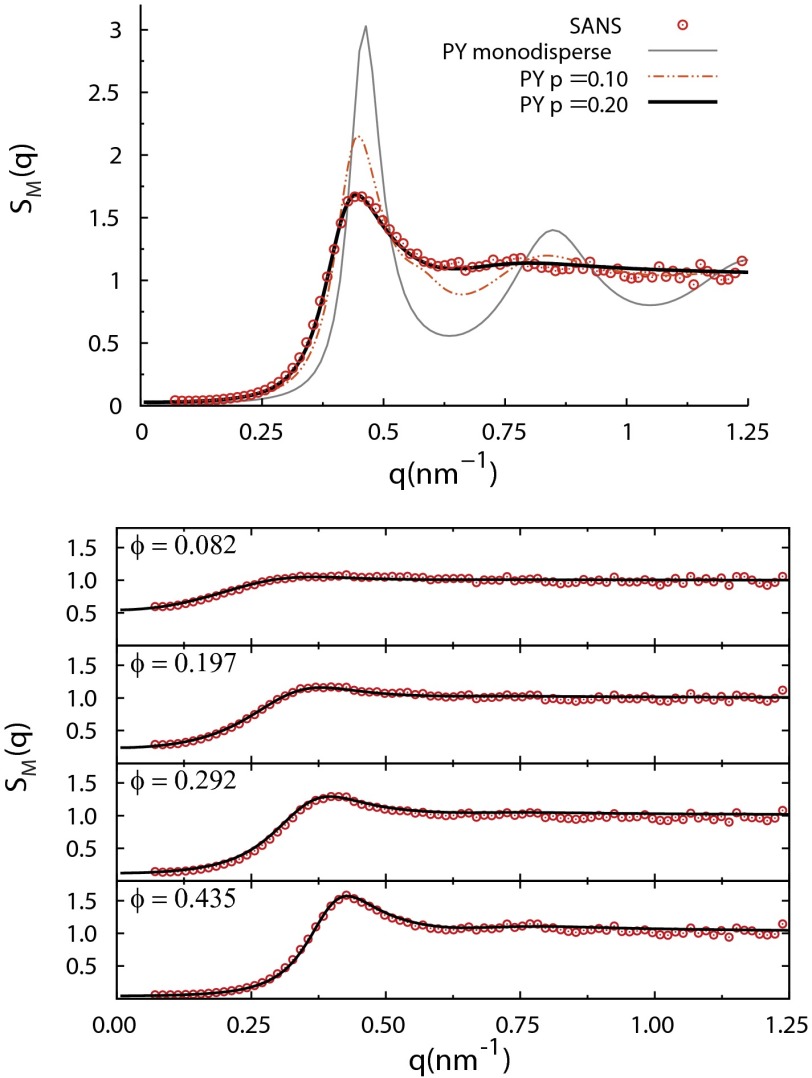
Instead, to estimate σ for input to MD, we compared SAXS $S_M\left(q\right)$ with the polydisperse Schulz PY model (13), as shown in Fig. 3 (Top) for $c=290$ mg/mL ($\varphi =0.49$), using $p=0$ (monodisperse, gray line), $p=0.1$ (dotted-dashed red line), and $p=0.20$ (black line). $p=0.20$ closely reproduces the measured $S_M\left(q\right)$, whereas the monodisperse model that fits $S_M\left(0\right)$ fails for intermediate and large q. Fig. 3 (Bottom) shows that $p=0.20$ fits the entire range (48 mg/mL $\le c\le 290$ mg/mL) of $S_M\left(q\right)$. Fig. S2 shows $1-R^2$ goodness-of-fit values vs. p and $\overline{d}$, the number-average diameter; $p=0.20$ and $\overline{d}=15$ nm are close to $1-R^2$ minima over the entire concentration range. $\overline{d}=15\hspace{0.5em}\text{nm}$ is consistent with previous analyses of small-angle neutron scattering (SANS) data (4). This analysis illustrates that the first peak of $S_M\left(q\right)$ can help quantify polydispersity.

Fig. 3.

Comparison of experimental structure factors $S_M\left(q\right)$ for α-crystallin solutions with polydisperse hard-sphere Percus–Yevick liquid-structure models, showing the basis for the parameter values $p=0.20$ and $d=15$ nm used in the present work. (Top) SAXS $S_M\left(q\right)$ for $c=290$ mg/mL, corresponding to a deduced $\varphi =0.49$. Percus–Yevick predictions are shown for three polydispersity parameters: $p=0$ (monodisperse, thin gray line), $p=0.1$ (dotted-dashed red line), and $p=0.20$ (thick black line). $p=0.20$ closely reproduces the measured $S_M\left(q\right)$, whereas the less polydisperse and monodisperse models do not match the data. (Bottom) Over the entire range of lower α-crystallin concentrations measured, the same polydisperse Percus–Yevick $S_M\left(q\right)$ with $p=0.20$ (solid lines) closely reproduces the experimental $S_M\left(q\right)$.

Having fixed $v=\varphi /c=1.7\hspace{0.17em}\text{mL}/\text{g}$, $p=0.20$, and $\overline{d}=15\hspace{0.5em}\text{nm}$, the calculated weight-average molecular mass of the α-crystallin is $M_W^{\alpha }=700\pm 125\hspace{0.5em}\text{kDa}$, in the range typically obtained by SLS (11). With $p=0.20$ the intensity-weighted dilute solution hydrodynamic radius $R_h=\langle R^6\rangle /\langle R^5\rangle$ = 9 nm agrees well with $R_h=9.6$ nm obtained from the DLS-measured free-particle diffusion coefficient, $D_0=2.2\times {10}^{-11}$ m²/s (Fig. 2), via the Stokes–Einstein relation. We note that whereas the predominant α-crystallin fractions used here are well modeled by spheres, higher molecular weight fractions show rod-like growth (23); thus a more general model for α scattering will call for shape and size polydispersity.

The present SAXS model differs from that in ref. 11; there, polydispersity was not included and SAXS data were modeled with $v\left(\varphi \right)$ ranging from $1.951\hspace{0.17em}\text{mL}/\text{g}$ at low concentration to $1.4\hspace{0.17em}\text{mL}/\text{g}$ at $0.35\hspace{0.17em}\text{g}/\text{mL}$. The present SAXS data alone do not rule out nonconstant $v\left(\varphi \right)$. However, with $v=1.7\hspace{0.17em}\text{mL}/\text{g}$, the experimental weight per volume glass concentration $c_g$ estimated from dynamics gives ${\varphi }_m=0.58$, consistent with hard spheres. If v were $1.4\hspace{0.17em}\text{mL}/\text{g}$ at high concentrations, $c_g$ would give ${\varphi }_m=0.4$, incompatible with hard spheres without attractions, whereas the $S\left(q=0\right)$ data (Fig. 1, Bottom) are well fitted by hard-sphere models and do not show evidence of attractions.

Dynamic Properties.

We now compare dynamic and glassy properties of α-crystallin solutions with HS models. The KD model fit (Fig. 2) to ${\eta }_r$ vs. ϕ gives intrinsic viscosity $\left[\eta \right]=5.5\pm 0.5$ and transition packing fraction ${\varphi }_m=0.579\pm 0.004$. The same $\left[\eta \right]$ results from a low-ϕ fit to ${\eta }_r=1+\left[\eta \right]\varphi$ (Fig. S3, Top). Whereas $\left[\eta \right]=5.5$ exceeds the theoretical value of 2.5 for monodisperse hard spheres, it is in the range of experimental and theoretical values for the globular proteins lysozyme, chymotrypsinogen-A, human serum albumin, and β-lactoglobulin (24–26), for which data in ref. 26 were available to convert weight per volume concentrations in refs. 24 and 25 to ϕ; for these proteins $3.4\le \left[\eta \right]\le 6.4$. At the high concentrations, Fig. S3 (Bottom) suggests that ${\eta }_r$ is compatible with a power law of the form

$${\eta }_r\sim {\left|\varphi -{\varphi }_c\right|}^{-\gamma },$$ [4]

with uncertainty in the value of γ. The high-concentration part of the KD model fit [Fig. S3, Bottom (black line)] would yield $\gamma =3.2$. However, the KD fit misses the three very high-concentration points we were able to obtain for $\left|{\varphi }_c-\varphi \right|<{10}^{-1}$ [Fig. S3, Bottom (blue line)], close to ${\varphi }_c$ where MCT predictions are expected to be most applicable; the latter give $\gamma =2.8$ and would yield ${\varphi }_c=0.58\pm 0.02$. In comparison, experiments on hard-sphere glass transitions in colloids report $\gamma \approx 2.5$ and ${\varphi }_c=0.58\pm 0.02$ (27–29). Experiments including polydispersity indicate a 5% increase in ${\varphi }_c$ for $p=0.3$, compatible with ${\varphi }_c=0.58\pm 0.02$ for $p=0.2$ as found here, and ${\eta }_r\left(\varphi \right)$ is still well described by the KD model when polydispersity is included (30). Thus, both the dramatic increase of α-crystallin ${\eta }_r\left(\varphi \right)$ and its near power-law dependence are consistent with previous work on hard-sphere glass transitions. The maximum ${\eta }_r\approx {10}^6$ is larger than previously measured values for colloidal hard spheres by about two orders of magnitude (29). We hypothesize that because the shear rate $\dot{\gamma }$ needed to reach the zero shear limit vanishes near the glass transition as $\dot{\gamma }\approx kT/6\pi R^3{\eta }_0\left(\varphi \right)\to 0$, the relatively small diameter of α-crystallin, $\overline{d}=15\text{nm}$, allows measurements of the zero shear viscosity closer to the glass transition. In comparison, for synthetic colloids true hard-sphere behavior is difficult to retain for $2R<200\hspace{0.5em}\text{nm}$.

To introduce the DLS analysis we briefly review relevant features of concentrated hard-sphere dynamics. Pusey and van Megen (31) found that colloidal hard spheres show dynamical slowing down that results in arrested, amorphous states at high packing fractions. The arrested states have very high macroscopic viscosities with relaxation times comparable to or larger than typical experimental times. Microscopically, relaxation of spontaneous number density fluctuations of spatial wavelength $2\pi /q$, ${\rho }_q$, can be measured by the ISF, $f\left(q,t\right)$, which for monodisperse systems is

$$f\left(q,t\right)=\frac{1}{N}\frac{\langle {\rho }_q\left(0\right){\rho }_{-q}\left(t\right)\rangle }{S\left(q\right)},$$ [5]

where $f\left(q,t=0\right)=1$ for the chosen normalization. In a normal fluid, the ISF relaxes exponentially, as shown schematically in Fig. 4 (Top, Inset). Approaching a glassy state, dynamical slowing down, which can eventually lead to dynamical arrest, creates additional slow ISF components that become more prominent at high concentration, as observed for α-crystallin (Fig. 2, Bottom). Fig. 4 (Top) schematically illustrates the origins of the principal relaxation processes, termed β- and α-relaxations. The increasing separation of ISF characteristic decay times with increasing concentration results from a so-called cage effect. At short times, particles diffuse within their surrounding cages, and the ISF shows a short time drop called the β-relaxation. Collective, coordinated rearrangement of caging particles is needed for escape of a central particle, and particles can be trapped for long times. This results in a very slow ISF drop called the α-relaxation. As liquids approach glassy states, the separation between β- and α-relaxation times grows, and a plateau region can occur in between, as in Fig. 4 (Top, Inset).

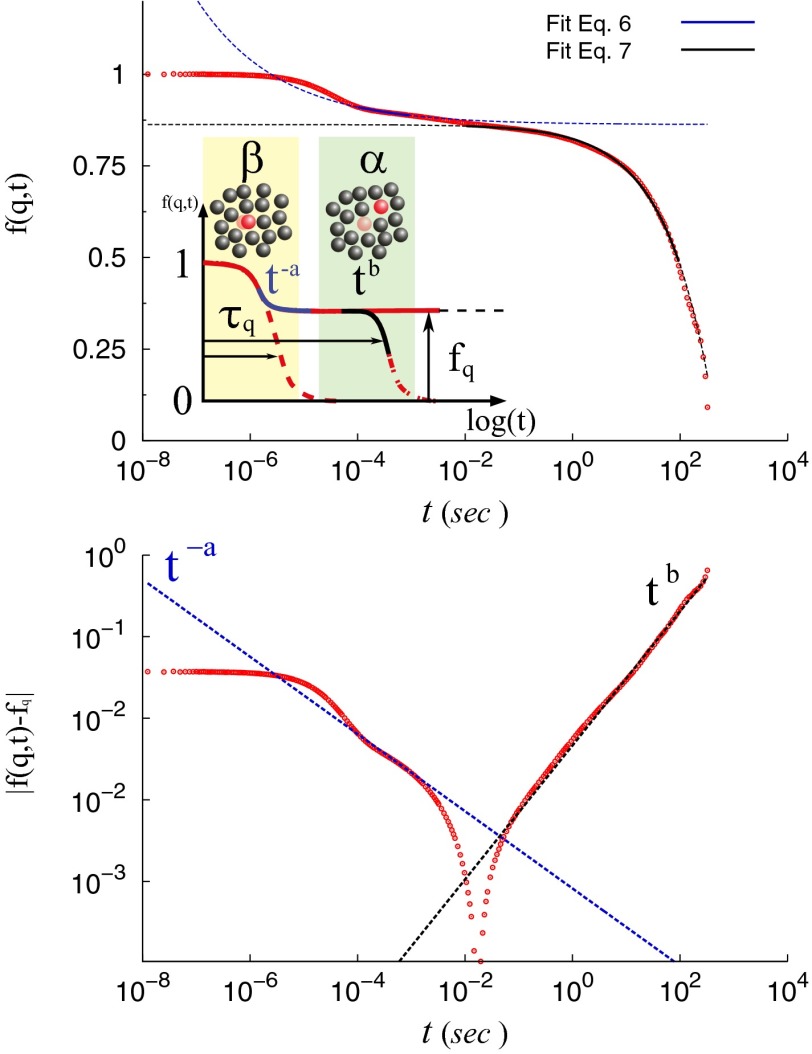
Fig. 4.

(Top, Inset) Schematic of idealized hard-sphere relaxation modes near dynamical arrest: fast motion within cages of caged neighbors (β-relaxation) and slow exchange between cages (α-relaxation). The plateau value, $f_q$, and approach and departure power-law exponents a and b (Eqs. 6 and 7) are shown. ${\tau }_q$ is the slow relaxation time, defined as in Fig. 2. (Top plot) Comparison of the experimentally determined ISF $f\left(q,t\right)$ at c = 340 mg/mL $\left(\varphi =0.58\right)$ with the theoretical predictions for the approach to and from the plateau value $f_q$. (Bottom) Rectification plot (32) of power-law fits to find a and b from ISF plateau approach and departure (text). $f_c=0.863$.

Although the α-crystallin DLS data (Fig. 2) show more than two relaxations, they do show fast and slow relaxations with rates that separate as concentration increases. At $q=0.023\hspace{0.5em}{\text{nm}}^{-1}$, the β-relaxation decay times are close to ${10}^{-4}$ s. Fig. 4 (Top) shows the DLS $f\left(q,t\right)$ at the highest fluid concentration assayed, 340 mg/mL, for analysis below.

As indicated in Fig. 4 (Top, Inset), MCT predicts a glassy-state ISF that remains finite, at a value $f_q$ called the nonergodicity parameter; at concentrations above an ideal glass transition point ${\varphi }_c$, ${\text{lim}}_{t\to \infty }f\left(q,t\right)=f_q$. For fluids near a glass transition, MCT predicts leading-order scaling laws for approach and departure of the ISF to and from such a plateau, respectively,

$$\left|f\left(q,t\right)-f_q\right|\propto t^{-a}$$ [6]

$$\left|f\left(q,t\right)-f_q\right|\propto t^b,$$ [7]

where a and b are related by Γ functions,

$$\frac{{\left[\mathrm{\Gamma }\left(1+b\right)\right]}^2}{\mathrm{\Gamma }\left(1+2b\right)}=\frac{{\left[\mathrm{\Gamma }\left(1-a\right)\right]}^2}{\mathrm{\Gamma }\left(1-2a\right)}.$$ [8]

MCT also predicts a power-law divergence of the slow relaxation time ${\tau }_q$ near $\varphi ={\varphi }_c$ and a decrease in the slow diffusivity D. All involve the a- and b-dependent exponent γ:

$$\gamma =\left(\frac{1}{2a}\right)+\left(\frac{1}{2b}\right)$$ [9]

$${\tau }_q\sim {\left|\varphi -{\varphi }_c\right|}^{-\gamma }$$ [10]

$$D\sim {\left|\varphi -{\varphi }_c\right|}^{\gamma }.$$ [11]

Polydispersity may also affect dynamics near the glass transition, as smaller spheres may require less cage rearrangement to escape, whereas larger spheres contribute more to the measured ISF. Therefore, we performed MD of polydisperse HS systems, using $p=0.20$ obtained above. MD mean-square displacements (MSD) and intermediate scattering functions (ISF) are shown in Fig. S4. The MD MSD and ISF show caging features as described, and MD ISF are qualitatively similar to DLS ISF, including the sloping “plateau” region.

Dynamic Light Scattering: Two-Step Relaxation.

We analyze the DLS-measured ISF at the highest fluid concentration, 340 mg/mL or $\varphi =0.58$ (Fig. 4, Top), in terms of MCT predictions, as done for colloidal glassy dynamics by Bartsch et al. (32). Because the measured ISF has substantial slope between the fast and slow decays, consistent also with MD results, a tightly constrained range of values of $f_q$ is not at first clear, but results from the fits. Using Eqs. 6 and 7, we can fit a and b directly, or fit a (or b), cross-check the MCT prediction by using Eq. 8 to determine b (or a), and finally compare with the b (or a) from a direct fit. Upon fitting b first, we obtain $b=0.495\pm 0.010$ (mean ± SD) and $f_q=0.863\pm 0.002$, from which $a=0.285\pm 0.010$. First fitting a, we find $a=0.27\pm 0.05$ and $f_q=0.854\pm 0.007$, from which $b=0.45\pm 0.14$. Thus, the two routes give similar results; we use those from first fitting b, which have smaller error because the ISF decay from the plateau is well described with b for three decades of delay time, whereas the power-law portion of the approach applies only over one decade. To test the fitted value of $f_q$, in Fig. 4 (Bottom) we plot $\left|f\left(q,t\right)-f_q\right|$, as for colloidal systems (32). Power laws for approach and departure from the plateau are evident. The fitted values of a and b, when used in Eq. 9, now give $\gamma =2.8\pm 0.2$, consistent with the ${\eta }_r$ results. The values of a, b, and γ agree well with the ranges of hard-sphere colloid values from full MCT theory (33, 34), simulations (35), and experiments (32, 36): $0.226<a<0.301$, $0.339<b<0.545$, and $2.57<\gamma <3.6$. Fig. S5 shows MD results that correspond to the experimental plots from Fig. 4. It shows $f_q$ and the power-law plot, using $\gamma =2.8$ from MD simulations at $\varphi =0.5925$ and $q=0.110\hspace{0.5em}{\text{nm}}^{-1}$; a comparable plot is noisy for the MD simulations at $q=0.037\hspace{0.5em}{\text{nm}}^{-1}$. Suitably reducing the MD simulation noise at the DLS q-vector magnitude 0.023 nm⁻¹ would at present be prohibitive in computation time.

The MCT theory used is not restricted to monodisperse systems; MCT glass transition tests have used polydisperse colloids to prevent crystallization at ${\varphi }_X=0.494$ (31). Although polydispersity slightly affects a, b, and γ, the overall picture is essentially unchanged (15). MCT validity has been debated for hard spheres above the MCT glass transition, in particular the form of Eqs. 6–11 (37–41), but this debate applies to higher concentrations than those studied here.

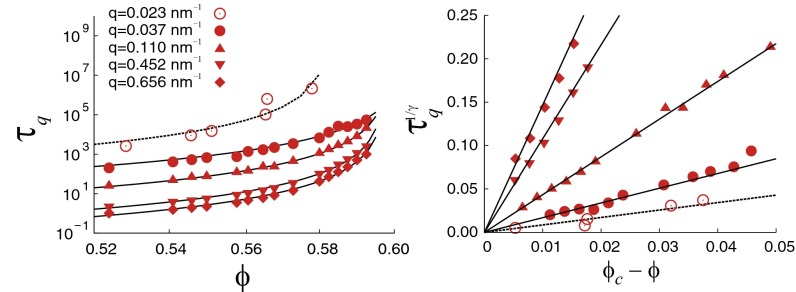
Finally, we use MD and DLS to test predicted MCT power laws in Eqs. 10 and 11, using $\gamma =2.8\pm 0.2$. MD number-average self-diffusion coefficients $D_{s,\text{na}}$ show power-law dependence and yield ${\varphi }_c=0.6074\pm 0.0003$, as described in SI Text and shown in Fig. S6. We tested Eq. 10, using the DLS and MD ${\tau }_q$ values that satisfy $f\left(q,{\tau }_q\right)=0.25$. For DLS data, $q=0.023\hspace{0.5em}{\text{nm}}^{-1}$, whereas for MD, $q=0.0366\hspace{0.5em}{\text{nm}}^{-1}$ is the smallest number achievable with the present simulation box. MD q values 0.1093, 0.4516, and 0.6559 nm⁻¹ are before, at, and after the first $S_M\left(q\right)$ peak, respectively. Fig. 5 (Left) shows the resulting DLS and MD ${\tau }_q$ values. Fits of Eq. 10, with $\gamma =2.8\pm 0.2$, agree well with MD and DLS for ϕ near ${\varphi }_c$. Specifically, DLS yields ${\varphi }_c^{\exp }=0.585\pm 0.01$, and MD yields ${\varphi }_c^{\mathrm{sim}}=0.603\pm 0.002$ for $q=0.0366\hspace{0.5em}{\text{nm}}^{-1}$, ${\varphi }_c^{\mathrm{sim}}=0.5990\pm 0.0003$ for $q=0.1093\hspace{0.5em}{\text{nm}}^{-1}$, ${\varphi }_c^{\mathrm{sim}}=0.5977\pm 0.0004$ for $q=0.4516\hspace{0.5em}{\text{nm}}^{-1}$, and ${\varphi }_c^{\mathrm{sim}}=0.5978\pm 0.00005$ for $q=0.6559\hspace{0.5em}{\text{nm}}^{-1}$. Fig. 5 (Right) exhibits the q-dependent power laws describing ${\tau }_q$ vs. ${\varphi }_c-\varphi$ with $\gamma =2.8$. These DLS and MD ${\varphi }_c$ estimates are consistent with ${\varphi }_c=0.58\pm 0.02$ obtained from the relative viscosity.

Fig. 5.

(Left) The slow relaxation time ${\tau }_q$ at which $f\left(q,{\tau }_q\right)=0.25$, defined as in Fig. 2, for the MD-simulated ISF (solid circles) and the DLS ISF (Fig. 2, Bottom) (open circles). (Right) Replotted data from Left, showing power-law dependence of ${\tau }_q$ on ${\varphi }_c-\varphi$, using $\gamma =2.8$ and the ${\varphi }_c^{\text{sim}}$ (MD) and ${\varphi }_c^{\text{exp}}$ (DLS) values reported in the text.

Conclusions

We have used a polydisperse hard-sphere liquid-structure model to accurately reproduce small-angle X-ray scattering data on α-crystallin solutions over a range of protein concentrations from 48 mg/mL to 290 mg/mL and static light scattering data from dilute concentrations up to 330 mg/mL. Dynamic light scattering, viscometry, polydisperse hard-sphere molecular dynamics simulations, and mode-coupling theory scaling relations indicate that high-concentration aqueous α-crystallin solutions behave like glassy materials and approach a glass transition volume fraction ${\varphi }_c$ near 58%. Measured and simulated dynamic properties of concentrated α-crystallin solutions show power-law dependences on the volume fraction difference ${\varphi }_c-\varphi$ that are compatible with previous work on glass-forming hard-sphere colloids and with predictions of mode-coupling theory. At high concentrations, the measured and simulated intermediate scattering functions show a prominent two-step decay that is also characteristic of a glass transition.

Whereas α-crystallin is a major lens protein and shows repulsive, hard-core interactions as modeled here, it accounts for about 40% of the lens crystallins in the human lens (42). Thus, although the high concentrations of α-crystallin studied here are comparable to the overall crystallin concentrations in the human lens (42), studies of the dynamics of realistic high-concentration lens protein mixtures will also need to include the phase-separating γ-crystallin, which shows attractive interactions with itself and with α-crystallin (4–7), as well as mixtures that include β-crystallins (43), oligomeric proteins that show repulsive interactions with each other (44).

We note that in our work on the equilibrium light scattering, phase separation, and liquid structure of high-concentration mixtures of γ- and α-crystallins (3–7), contrasted with the present studies of α-crystallin statics and dynamics by itself, we have not yet incorporated α-crystallin polydispersity, a topic that bears further study.

The present, polydisperse hard-sphere model for high-concentration α-crystallin solutions is a useful starting point for studying dynamics of lens protein mixtures at high concentration, together with related equilibrium properties (3). High-concentration lens protein dynamics may have implications for the development of presbyopia and cataract. First, it is tempting to speculate that age-related changes in lens protein interactions may induce an arrest transition in the lens nucleus, changing the protein mixture from a fluid-like to an arrested glassy state, with a dramatic increase in stiffness (45, 46). Because presbyopia is believed to involve age-related stiffness increase in the lens core, our finding that the major lens protein component α-crystallin undergoes a hard sphere-like glass transition calls for additional investigation of lens protein mixture dynamics, at the high concentrations present in vivo. Second, proximity to an arrest transition could also affect the kinetics of lens protein aggregation and could thereby influence the rate of cataract formation.

Methods

Sample Preparation.

Stock solutions of α-crystallin were prepared following Tardieu et al. (47), with use of size-exclusion chromatography of cortical homogenates from 4-mo-old calf lenses. Ultrafiltration was used for concentration. Further details are given in SI Text.

Small-Angle X-Ray Scattering.

SAXS measurements were carried out in a 1-mm quartz capillary at T = 20 °C, using a pinhole camera (NanoSTAR; Bruker AXS), equipped with a sealed Cu-K_α tube, a thermostatically regulated sample chamber, and a 2D gas detector. The scattering vector range was $0.1\hspace{0.5em}{\text{nm}}^{-1}\le q\le 2\hspace{0.5em}{\text{nm}}^{-1}$.

Light Scattering.

Light scattering experiments were performed with a commercial ALV/DLS/SLS-5000F monomode fiber compact goniometer system equipped with an ALV5000/E fast correlator and a solid-state laser (COMPASS 315M-150; Coherent, Inc.; $\lambda =532$ nm, 150 mW). The temperature was regulated by a circulating water bath at 20 °C. Ten-millimeter diameter quartz cuvettes were used for samples with concentrations 5 mg/mL < c < 100 mg/mL. High-quality NMR tubes with a diameter of 5 mm (Armar AG) were used at higher concentrations, to suppress possible multiple-scattering effects. Measurements of the arrested sample at c = 435 mg/mL were performed with a modulated 3D cross-correlation light-scattering instrument (LS Instruments) at a scattering angle of 140° and a wavelength of 632 nm. Further details are given in SI Text.

Rheology.

Rheological measurements were carried out on a Paar Physica 300 stress-controlled rheometer, using a cone-and-plate geometry (25 mm cone diameter, 2° cone angle). The experiments were done at 20 °C, using a temperature control unit TEK 150P. A standard solvent trap was used to protect the samples against drying. Viscosity measurements at a constant shear rate were performed at shear rates between 0.1 s⁻¹ and 1,000 s⁻¹, and the viscosity was monitored over extended periods of time to verify steady-state conditions. The zero-shear viscosity was then obtained from the low shear rate limit of these flow curves.

Simulations.

We performed event-driven molecular dynamics simulations (48) of 5,000 polydisperse hard spheres, having diameters typically in 20 binned categories, to represent a Schulz distribution for which a PY liquid-structure model has been detailed (13). The average diameter was $\langle d\rangle =1$. Because the simulation system is athermal, temperature was fixed to $T=1$. Further details are given in SI Text.