Interference-mediated synaptonemal complex formation with embedded crossover designation

Significance

Spatial patterns occur in biological and nonbiological systems. A paradigmatic example occurs during meiosis. As shown a century ago, crossover recombination events occur at different positions in different meiotic nuclei; nonetheless, occurrence of a cross-over at one position decreases the probability that another will occur nearby. As a result, crossovers tend to be evenly spaced. This study suggests that this classical cross-over interference is part of a broader program that concomitantly specifies even spacing of nucleation sites for formation of synaptonemal complex, a prominent meiotic chromosome structure. A model emerges for how the observed patterns could occur. This model provides an explanation for the formation of complex, multilayered patterns that is generally applicable to biological and nonbiological systems.

Abstract

Biological systems exhibit complex patterns at length scales ranging from the molecular to the organismic. Along chromosomes, events often occur stochastically at different positions in different nuclei but nonetheless tend to be relatively evenly spaced. Examples include replication origin firings, formation of chromatin loops along chromosome axes and, during meiosis, localization of crossover recombination sites (“crossover interference”). We present evidence in the fungus Sordaria macrospora that crossover interference is part of a broader pattern that includes synaptonemal complex (SC) nucleation. This pattern comprises relatively evenly spaced SC nucleation sites, among which a subset are crossover sites that show a classical interference distribution. This pattern ensures that SC forms regularly along the entire length of the chromosome as required for the maintenance of homolog pairing while concomitantly having crossover interactions locally embedded within the SC structure as required for both DNA recombination and structural events of chiasma formation. This pattern can be explained by a threshold-based designation and spreading interference process. This model can be generalized to give diverse types of related and/or partially overlapping patterns, in two or more dimensions, for any type of object.

Meiosis is the specialized cellular cycle that yields haploid gametes for sexual reproduction. A central feature of the meiotic program is recombination (1, 2). DNA/DNA recombination interactions, initiated by programmed double-strand breaks (DSBs), mediate the recognition and juxtaposition (pairing) of homologous chromosomes. A minority subset of these interactions matures into reciprocal crossover recombination products (COs); the remaining majority matures primarily into interhomolog non–crossover products (NCOs). COs promote genetic diversity but also are required for the segregation of homologous chromosomes (homologs) via their role in creating chiasmata (3).

A nearly universal feature of meiosis is that COs occur along a particular chromosome at different positions in different meiotic nuclei. Nonetheless, along any given chromosome, COs tend to be evenly spaced. This pattern results from the reduced possibility that a second cross-over will occur if a crossover has occurred nearby. The existence of such a pattern was identified more than a century ago as the genetic phenomenon of CO interference (4, 5). In this phenomenon, occurrence of a CO in one genetic interval is accompanied by a reduced probability that another CO will occur along the same chromosome in a nearby interval. This effect implies the existence of communication along chromosomes, with an event at one position triggering occurrence of an “interference signal” that spreads outward, inhibiting occurrence of subsequent events nearby.

A second central feature of the meiotic program is the synaptonemal complex (SC). This prominent structure links the axes of paired homologs along the lengths of the chromosome at midprophase, the “pachytene” stage (3, 6, 7). In the canonical meiotic program, as shown in several organisms, CO patterns and SC formation arise concomitantly at zygotene (Discussion and ref. 8). Also, in budding yeast, the SC is not required for CO patterning (9, 10). Intriguingly, however, in two organisms, Schizosaccharomyces pombe and Aspergillus nidulans, SC and CO interference are concomitantly absent (3), indicating some type of relationship between the two processes.

The present study began by investigating the possibility that interference is not confined specifically to COs but instead pertains more broadly to include SC nucleations. Such integration could concomitantly ensure regular SC formation along the chromosomes and the embedding of CO recombinational interactions in a specialized local relationship to the SC.

Here we analyze chromosomal events in the filamentous fungus Sordaria macrospora. Sordaria exhibits the canonical meiotic program and provides uniquely detailed readouts for recombination and SC formation including both ultrastructural data from 3D serial section reconstructions and whole-cell analysis of fluorescent signals for recombination complexes and the SC as they evolve through prophase (8, 11–13). Our findings support the existence of regularly-spaced SC nucleation sites, a subset of which comprise CO sites that exhibit classical interference.

We next investigated the possible scenarios by which such a pattern might arise. The entire pattern, with all its component features, appears to emerge during a single stage, zygotene. Correspondingly, the notion that the entire array arises in a single patterning process is attractive. Detailed analysis supports a scenario in which SC nucleations, with embedded CO designation, emerge via a single interference-mediated process, i.e., a process that involves a spreading interference signal. The basic principles that emerge could generate diverse complex interrelated patterns.

Results

Background.

In S. macrospora, cytological studies define a multistep recombination process (Fig. 1A) (8, 11). Throughout the process, recombination complexes are associated with chromosome structural axes and/or the SC, as in a variety of organisms (2, 14, 15).

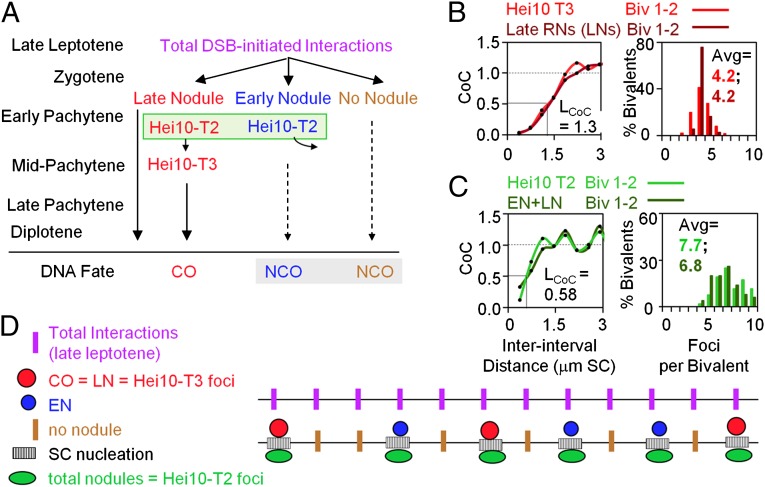
Fig. 1.

Recombinosome and SC morphogenesis in S. macrospora. (A) Progression of total recombinational interactions as manifested in RNs (ENs, LNs, and non–nodule-marked interactions) and two types of Hei10 foci (T2 and T3) in relation to final DNA outcome. (B) CoC relationships and the number and distribution of events along bivalents (Biv) 1 and 2 for Hei10-T3 foci and LNs, both of which mark the sites of COs/chiasmata. (C) CoC relationships and the number and distribution of events for Hei10-T2 foci and total RNs (ENs + LNs), both of which correspond to the sites of SC nucleation events (Results). (D) Hypothesis for integrated arrays of SC nucleation sites (stripes), LN/CO sites (red circles), EN sites (blue circles), and non–nodule-marked sites (brown bars). B and C reprinted with permission from ref. 8.

Recombination is initiated by programmed DSBs. By late leptotene, the ∼57 ± 6 DSBs, marked by foci of RecA homolog Rad51 (radiation sensitive 51), have evolved into a total of 75–80 interhomolog recombinational interactions marked by meiotic helicase Mer3 (meiotic recombination 3) and the MutS-homolog Msh4 foci (8, 11). These ensembles span closely aligned late-leptotene homolog axes marked by opposing pairs of foci of Mer3 (11) and a linking DNA segment. Turnover of Rad51 foci cannot be assessed, but this numerology suggests that, as in other organisms, most DSBs ultimately yield inter-homolog recombination rather than inter-sister recombination.

During zygotene, when SC is forming along the homologs, all recombinational interactions lose their Mer3 foci and develop foci of Msh4. Concomitantly, these total interactions differentiate into three types, as revealed by integrating these patterns with findings from ultrastructural studies (Fig. 1A) (8, 13).

• i)Approximately 22 interactions are designated for eventual maturation into COs. These interactions are marked by the presence of large SC-associated nodules (so-called “late nodules,” LNs), which emerge at zygotene. By early pachytene, when SC has formed all along the chromosomes, LNs occur in the same number and distribution as mid/late pachytene Hei10-T3 foci, diplotene chiasmata, and COs assayed genetically (see discussion in ref. 8). Thus, CO interference has arisen no later than zygotene. [We note that the above also suggests that, in Sordaria, the great majority of COs are “interfering CO”s, with relatively few arising in other ways, e.g., as so-called “noninterfering COs” (16).]
• ii)A similar number of interactions are marked by a second, smaller type of SC-associated nodule, early nodules (ENs). ENs also emerge at zygotene, concomitantly with LNs (13). LNs and ENs together are referred to as “recombination nodules” (RNs).
• iii)The remaining ∼30 interactions are not marked by any nodule. Their existence is inferred because the total number of LNs and ENs is less than the number of Mer3/Msh4 foci at leptotene/zygotene and because an appropriate corresponding subset of Msh4 foci exhibits a unique temporal pattern, unique absence of colocalization with Hei10 T2 foci, and unique functional dependence on Hei10 (8).

These three types of interactions then evolve further (Fig. 1A). At early pachytene, the subset of RN-marked interactions (ENs plus LNs) also is marked by ∼40 medium-sized foci of Hei10-T2 foci. The number of T2 foci and the sum of ENs plus LNs are identical, indicating that interactions not marked by a nodule do not develop such foci. At midpachytene, the two types of RN-marked interactions exhibit different maturation fates. ENs and their corresponding Hei10-T2 foci disappear. LNs, in contrast, persist to a later stage (diplotene), and their Hei10-T2 foci evolve into even larger Hei10-T3 foci. Interactions not marked with a nodule or a Hei10 focus also progress and do so more rapidly than the nodule/Hei10-marked interactions, as suggested by earlier loss of Msh4 foci (8).

Ultimately, both EN-marked and non–nodule-marked interactions progress, likely primarily to NCO products, as implied by genetic analysis (see the discussion in ref. 8 and see ref. 13) and probably not to intersister or noninterfering COs, as discussed above. Thus, according to these patterns, ENs and LNs develop T2 foci but have different DNA fates; in contrast, ENs and non–nodule-marked interactions are, by definition, morphologically noncongruent; nonetheless, both give NCO products (Fig. 1A).

Hypothesis.

Sordaria CO recombination sites exhibit classic CO interference (8, 13). Interference can be defined accurately by coefficient of coincidence (CoC) analysis (17). In brief, chromosomes are divided into intervals; for each pair of intervals, the frequency of chromosomes exhibiting a CO in each interval (“double CO”) is determined and compared with the frequency predicted for the independent occurrence of COs in the two intervals. The CoC is the ratio of the observed to the expected values. For intervals that are close together, the observed frequency is less than predicted, reflecting interference. The magnitude of this effect decreases with increasing inter-interval distance, reflecting interference. For closely spaced intervals, double COs are essentially absent. In Sordaria, CO interference is exhibited by the distributions of both LNs and Hei10-T3 foci (Fig. 1B). A convenient metric for the apparent strength of interference is the inter-interval distance at which CoC = 0.5 (L_COC). For both LNs and Hei10-T3 foci, L_COC = ∼1.3 μm as judged by CoC curves that include all regions of the genome.

LNs appear during zygotene and exhibit their final interference distribution by early pachytene, implying that CO patterning in Sordaria must occur no later than zygotene (above and ref. 8). Because a full array of total Mer3-marked recombinational interactions is observed at late leptotene (8, 11), CO site designation and interference likely arise during zygotene and thus are concomitant with SC formation.

In Sordaria, as in other organisms, SC formation is nucleated specifically at sites of recombinational interactions (10). Functional studies further show that nucleations occur at only a subset of total interactions (18, 19). Moreover, ultrastructural studies show that short segments of SCs often have an associated LN and/or EN (13). This feature suggests that SC formation might nucleate specifically at sites of interactions that are being designated to develop LNs and ENs, concomitant with LN/CO patterning. Recent analysis has further revealed that the array of total RNs and their correlated Hei10-T2 foci also exhibit interference, with L_COC = ∼0.6 μm (Fig. 1C) (8). Thus, if total RNs indeed mark the sites of SC nucleations, then SC nucleations also would exhibit interference and a tendency for even spacing. Moreover, the sites of CO-fated recombinational interactions would be embedded within this array, at a subset of nucleation sites, and exhibiting a classical CO interference distribution (Fig. 1D).

A 1:1 Relationship Between SC Nucleations and RNs (ENs + LNs)/T2 Foci.

To test this hypothesis, we analyzed in detail the relationship between SC segments and RNs (LNs and ENs) using data from 3D EM reconstructions (Fig. 2 A and B) (13). Analysis was performed on all bivalents 1 and 2 from 60 serially sectioned zygotene nuclei. Bivalents 1 and 2 are the longest and most easily identified of Sordaria's seven bivalents; moreover, bivalent 2 is distinguished by having one end embedded within the nucleolus.

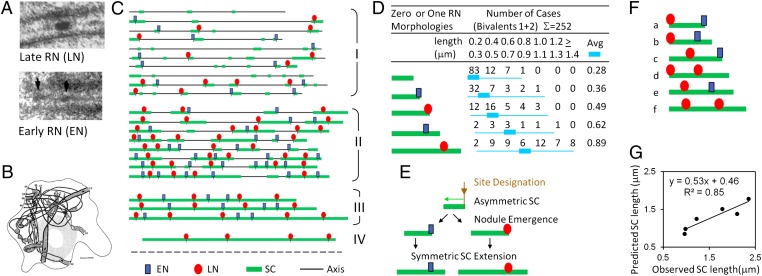
Fig. 2.

Evidence for a 1:1 relationship between SC nucleation sites and RN sites (ENs + LNs). (A) EM pictures of LN (Upper) nodules. Reprinted with permission from ref. 8. EM pictures of EN (arrow, Lower) nodules. Reprinted with permission from ref. 13. (B) Three-dimensional ultrastructural reconstruction of a whole midzygotene nucleus showing that most bivalents are synapsed at their ends. Reprinted from ref. 18 with kind permission of Springer Science+Business Media. (C) Examples of SC (green) and RN (ENs in blue, LNs in red) patterns along bivalent 1 in reconstructed nuclei. Each line corresponds to bivalent 1 in one nucleus. (I and II) Early and mid/late zygotene with progressive formation of SCs plus RNs. (III) Early pachytene with full complement of RNs. (IV) Mid/late pachytene nuclei exhibit only LNs because of the loss of ENs at early/midpachytene. (D) Numbers and lengths of all SC segments along bivalents 1 and 2 that exhibit one of five described morphologies reveal differences in the average and distribution of length: Length is shortest and distribution tightest for SC segments lacking a nodule; both are longer for segments with a terminal nodule (and among these are longer if the nodule is an LN rather than an EN) and are longest for segments with a single nonterminal nodule (again, length and distribution are longer if the nodule is an LN rather than an EN). (E) Progression of SC nucleation, nodule emergence, and SC extension (asymmetric and then symmetric) inferred from length patterns in D. (F) All SC segments from bivalents 1 and 2 that exhibit two RNs were sorted into classes a–f according to nodule type and position (terminal and/or internal). (G) The average lengths observed for members of each class were compared with the average lengths predicted on the assumption that each nodule exhibited the SC length associated with its corresponding type in D. The observed and predicted lengths are directly proportional.

Traced chromosomes can be divided into categories on the basis of SC and RN patterns (Fig. 2C). (I) Early zygotene bivalents exhibit short SC segments. Most segments exhibit a single associated LN or EN, which in many cases is located at the end of the associated SC segment. Some SC segments, known as “solo SCs,” have no associated RNs. (II) As zygotene progresses, short segments tend to exhibit a single RN located internally rather than at one end; some segments exhibit more than one nodule; and solo SCs also occur but are rarer than at early zygotene. (III) Early pachytene nuclei exhibit a full complement of LNs and ENs (8, 13 and text below). (IV) Mid/late pachytene nuclei exhibit only LNs, present in full complement, reflecting the precipitous loss of ENs at the early/midpachytene transition (8, 13).

For the present analysis, we concentrated on the relationship between SC segments and RNs as they emerge coordinately during zygotene. To characterize potential nucleation segments, we analyzed short SC segments containing zero, one, or two RNs. A clear progression emerges (Fig. 2D). Solo SCs lacking any RN are uniform in length and are very short, 0.2–0.3 μm. Segments with a terminal nodule are longer than solo segments, and segments with internal nodules are longer than segments with terminal nodules. Moreover, LN-associated SC segments are significantly longer than EN-associated segments in both categories. These patterns suggest a specific sequence of events (Fig. 2E): (i) an “event designation” occurs at the site of a recombinational interaction, triggering the emergence of a short SC segment which extends in one direction from the designation position; (ii) a nodule soon emerges at the designation site, preceded/accompanied by continued SC elongation; (iii) finally, SC elongates symmetrically in both directions.

The regularity of this pattern is confirmed by consideration of SC segments that exhibit two associated nodules, which occur in several configurations according to the types and positions of their nodules (Fig. 2F). The lengths of these different configurations are proportional to the lengths predicted from the sums of their two component nodule/SC segments, with the addition of a modest increase in SC length relative to the reference values (Fig. 2G). These results strongly support a 1:1 relationship between SC nucleations and RN (EN + LN) formation and thus, by extension, the coordinate patterning proposed above.

These results also provide two additional pieces of information.

• i)SC initially forms asymmetrically, in one direction away from its designation/nucleation site, as previously suggested (13). Asymmetry may be dictated by the recombination complex at the initiation site, where one DSB end has invaded a D-loop to give an asymmetric disposition of component features (1). SC formation is concomitant with D-loop extension (1). Perhaps the SC initially spreads in the same direction as the growing D-loop to ensure that the developing recombination complex is well-associated with the forming SC. Alternatively, the SC might spread specifically in the opposite direction so that the structure can maintain a robust interhomolog axis connection at developing CO sites despite the presence of an active recombination complex.
• ii)LN-associated SC stretches are longer than EN-associated SC stretches. This distinction confirms the notion that both of the corresponding types of interactions play nucleating roles and further demonstrates that the two types of nucleations are qualitatively distinct. It remains to be determined whether longer LN-associated SC stretches reflect earlier SC nucleation at those positions or an intrinsic difference in underlying molecular events. A difference in initial SC lengths could relate to a requirement that CO sites (and thus LNs) be integrally embedded within the SC, whereas ENs are less robustly associated and are lost from the SC at early pachytene, e.g., as part of a program to dissociate nucleation-associated recombinational interactions from the structure (Discussion).

A Threshold-Designation Model for Complex Interference Patterning.

Since the array of SC nucleations and the embedded array of CO-designated sites arise contemporaneously, it is simplest to suppose that both features arise as part of a single patterning process. How could such a process occur?

A general outline of a possible scenario is as follows (Fig. 3A). Event designation occurs progressively, operating on an array of undifferentiated precursor interactions and driven by some particular molecular change. Regardless of the underlying basis for this change, a critical feature will pertain: Each designation is accompanied by a spreading inhibitory interference signal which, by its intrinsic nature, tends to reduce the “reactivity” of affected remaining precursors. Consequently, as the process progresses, the local reactivity of the particular precursor that happens to undergo designation at a given moment will be highest for the first designations and will tend to become lower and lower as the process progresses. Finally, the reactivity is sufficiently low that no more designation events occur (Fig. 3A, Upper). This scenario opens the possibility that, as the designation process progresses, the molecular outcome of an event might change in relation to the decreasing local reactivity of the available precursors (Fig. 3A, Upper). Initially, when local reactivities are higher, designation would give one type of outcome. When reactivity falls below a certain threshold, another type of outcome might occur. In principle, any number of such thresholds could come into play sequentially during the designation process. Given multiple thresholds, diverse combinatorial patterns could be generated (Discussion).

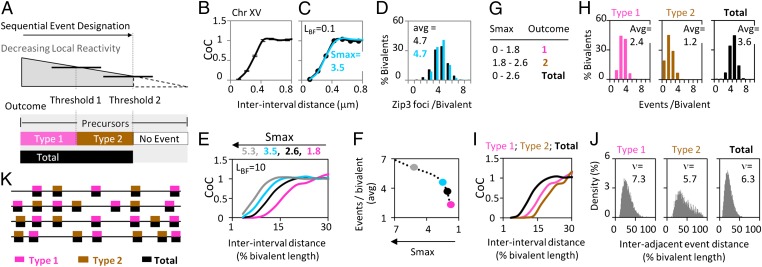
Fig. 3.

Complex patterning can be achieved by reactivity thresholding in a single round of patterning. (A) By the logic of the BF model, progressive event designation results in a progressive decrease in the reactivity of remaining precursors. If the outcome of event designation is different at different levels of reactivity, complex patterns can result. Pictured is a case involving two reactivity thresholds that specify two sequential types of designation outcomes. Below the lower threshold, no event designation occurs. Patterns can result from the two individual outcomes (types 1 and 2; pink and brown), which also may include a common component (total; black). (B–D) CoC relationships and the number plus distribution of events for CO-correlated Zip3 foci in budding yeast. The black trace shows observed results, and the turquoise trace shows the BF best-fit simulation (data from ref. 9). The parameters L and Smax are used in simulations to define the total number of event designations (Materials and Methods). (E and F) Under a given set of conditions, including a single specified progressive event designations will result in more and more events that are more and more closely spaced. This outcome is illustrated by BF simulations using the basic best-fit parameters for yeast chromosomes (B–D) except that the value of Smax is increased progressively. The effects include a shift of CoC relationships to smaller interinterval distances (E) plus an increase in total events (F). (G–J) BF modeling of the two-threshold scenario described in A. (G) Outcomes of BF simulations are based on yeast parameter values as in B–F, including a fixed value of L but with two thresholds defined by appropriate values of Smax. The number and distribution of events (H), corresponding CoC relationships (I), and corresponding distributions of distances between adjacent events (J) are shown in pink for the first and in brown for the second type of events and in black for total events. (K) Examples of the patterning outcome from the two-threshold scenario in G–J. An array of relatively evenly spaced total events (black) includes embedded arrays of events specified by the first (pink) and second (brown) thresholds.

Given only two thresholds, three types of patterns will be produced: the two types arising in the two phases and the total of all designation events (Fig. 3A Lower, pink, brown, and black, respectively). Event patterns in Sordaria could be described in this way: Both types of designation would yield SC nucleations; however, only the first type would concomitantly yield CO designation (and an LN); the second type would not be CO designated and would yield an EN, as discussed below.

This idea emerged from, and can be further described and evaluated in the context of, the beam-film (BF) model for interference (9, 17, 20, 21). By this model, patterning begins with an array of precursors [e.g., late leptotene total DSB-mediated interhomolog interactions, as seen for Mer3 foci in Sordaria (11)]. This array of precursors undergoes a sequential designation process. All interactions come under mechanical stress until a first (more stress-sensitive) interaction goes critical, undergoing a stress-promoted change in state that commits it to the CO fate (CO designation). That event, by its nature, alleviates stress locally at the site of the change. Because of the mechanical nature of the system, this local reduction in stress then redistributes outward in both directions, dissipating with distance. The resultant reduction in stress automatically reduces the probability of subsequent stress-promoted events in the affected region, most strongly near the nucleation site and to a lesser extent with increasing distance away from that site. A next designation event then may occur. If it does, it will occur preferentially in unaffected regions. If further events then occur, each of these events will tend to occur away from the positions of prior events, thus generating a tendency for even spacing. Designation events continue to occur until none of the remaining precursors remains sensitive to the level of global stress.

The outcome of such a process can be simulated mathematically as a function of key parameters relating to the nature of the precursor array, the patterning process per se, and the efficiency with which a designated event actually matures into a detectable signal. The most important patterning parameters are the level of stress (S) and the distance over which the spreading interference signal acts (L) (17; Materials and Methods). Simulations of experimental data by this model can describe CO patterns very accurately in wild-type and mutant budding yeast (Fig. 3 B–D), Drosophila, tomato, grasshopper (9, 17), and (as discussed below) Sordaria.

In such simulations, progressive event designation is achieved by a particular computational device: All parameter values are held constant, and the level of global stress is increased, step by step, after each designation event, with the final number of events specified by the maximum global stress level (Smax). In reality, the same effect could be achieved in other ways. In the context of the stress model, the same outcome would be achieved by a progressive global increase in the sensitivity of precursors to a fixed level of stress. Alternatively, the global stress level could be constant, with designation events occurring sequentially in time as a function of their local stress level at that moment.

Importantly, the predictions of the BF model will apply equivalently to any patterning process that exhibits the same basic logic: sequential event designation with each designation event triggering an inhibitory effect that dissipates exponentially in both directions away from its nucleation site.

The effects of progressive event designation are illustrated by BF simulations using basic parameter values derived from budding yeast (Fig. 3 B and C) and convenient increasing values of Smax. As the process progresses, more and more designation events are forced into a given length of chromosome, resulting in more and more closely spaced events. Correspondingly, the CoC curve shifts to the left (Fig. 3E), and the number of designated sites concomitantly increases (Fig. 3F). Notably, this progression phenomenologically gives apparently reduced CO interference. However, in fact, the spreading inhibitory interference signal, given by the parameter L_BF, is the same throughout (L_BF = 0.3 μm; Fig. 3B). The only change is a progressive increase in the fraction of precursor sites that have undergone event designation (discussed in ref. 17). We further note that, as more and more designation events occur, the distribution of distances between adjacent events also changes. The value of the gamma shape parameter ν, sometimes used as a metric of the tendency for even spacing (and thus interference), decreases (17).

The consequences of a thresholded designation process and also be illustrated in this context. We consider two particular threshold values of Smax (Fig. 3G). Up to a first threshold, one type of designation outcome occurs (type 1; pink in Fig. 3), and a further increase to a second threshold gives a second type of outcome (type 2; brown in Fig. 3), giving a final array of events comprising the sum of the two (total; black in Fig. 3). The three sets of events are characterized by different average numbers and distributions of events (Fig. 3H), different CoC relationships (Fig. 3I), and different distributions of distances between adjacent events with correspondingly different values of the gamma distribution evenness parameter ν (Fig. 3J).

The overall result of these events is a partially overlapping pattern of event designations in which a total array of relatively evenly spaced events (black) contains two embedded individual arrays (pink and brown), each of which also exhibits an interference distribution (Fig. 3K). This theoretical example demonstrates that, qualitatively, such a two-threshold scenario could explain the pattern of events seen along Sordaria chromosomes. A first set of event designations would concomitantly give both SC nucleation and CO designation (pink/black in Fig. 3K). Then, beyond a particular threshold of reactivity, further designations would still give SC nucleation but no longer would give CO designation concomitantly (brown/black in Fig. 3K). The result would be a larger array of relatively evenly spaced SC nucleations within which is embedded a smaller array of CO-designation events that exhibit a classical interference distribution.

Experimental Event Patterns Match Those Predicted for a Single Interference-Mediated Patterning Process.

In the model described above, the pattern of events observed along Sordaria chromosomes would arise in a single interference-mediated process that operates on an original starting array of precursor events, with a single set of basic patterning parameters operating throughout. In an obvious alternative model, the observed pattern of events could arise in two independent sequential processes: a first round of patterning with one set of parameters would operate on the original starting precursor array; then a second round characterized by a second set of patterning parameters would operate on the array of events produced by the first round. This scenario is not attractive a priori, because LNs, ENs, and SC nucleations all arise concomitantly during zygotene. However, a unique feature of Sordaria recombination patterns makes it possible to distinguish between these two scenarios.

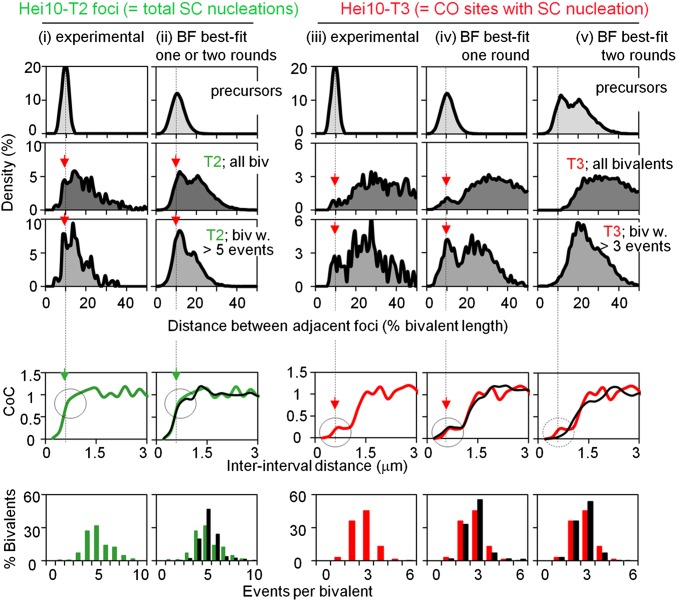
In Sordaria, the pattern of total recombinational interactions present at late leptotene is very well defined by the patterns of Mer3 and Msh4 foci (8, 11). These total interactions are spaced quite regularly, at an average distance of 0.6 μm, with a value of the gamma evenness parameter of >200 (Fig. 4 Top, First Row, i) (11). During any interference process that operates on this total array of interactions, those events will tend to be closer and closer together as more and more designation events occur and thus ultimately will tend to occur at adjacent precursor sites. Because, as discussed above, these precursor sites are very evenly spaced, the array of distances between adjacent events should tend to exhibit a peak specifically at the interprecursor distance (0.6 μm). Moreover, that peak should be more prominent for bivalents that have acquired more events relative to total bivalents. Exactly such a peak, which is more prominent in bivalents with more events, is observed in the experimental datasets for T2 foci, which represent total event designations/SC nucleations (Fig. 4 Top, Second Row, i). This result is expected for both scenarios (i.e., one round or two rounds of patterning), which give the same final total array of events that all arise from the original total array of precursor sites. Remarkably, however, exactly the same peak also is seen for T3 foci, which represent only the sites that have undergone both CO designation and SC nucleation (Fig. 4 Middle, iii). This result strongly suggests that T3 foci arise from the array of total precursor interactions, as predicted by the one-round scenario. If instead, as discussed further below, T3 foci had arisen from the array of T2 foci, there would have been a tendency for closely spaced double T3 foci to be separated by the distance between adjacent T2 foci.

Fig. 4.

Comparison of one-round and two-round scenarios for patterning of SC nucleations and CO sites in Sordaria. (Left) Patterns of Hei10-T2 foci whose sites represent the sites of SC nucleations. (Right) Patterns of Hei10-T3 foci that mark CO sites. (Top, First Row) Experimental data (Mer3 foci) define a tight distribution of interevent distances for total recombinational interactions (i and iii) (11). An analogous distribution of relatively evenly spaced events was used as the array of total starting precursors for BF simulations for T2 foci (ii) and for T3 foci in the one-round scenario (iv). The distribution of precursors for the two-round scenario (v) is the distribution of T2 foci (Top, Second Row, ii). (Top, Second and Third Rows) Experimental or predicted distributions of interfocus distances for T2 or T3 foci for all bivalents (Top, Second Row) and for the subset of bivalents exhibiting higher numbers of events (Top, Third Row). Experimentally observed patterns are compared with patterns resulting from BF best-fit simulations that model different patterning scenarios (compare i vs. ii and iii vs. iv and v). Two scenarios were examined. The first is a one-round scenario. A single patterning process, characterized by a single value for the distance over which interference spreads L, gives rise to both T2 and T3 foci, all from the same set of initial precursors. This scenario is qualitatively analogous to the two-threshold case described in Fig. 3 A and G–K. T3 foci correspond to events designated up to the first threshold (type 1, pink in Fig. 3), and T2 foci correspond to total events that occur up to the second threshold (black in Fig. 3). For RNs and SCs, LN-marked sites correspond to type 1 events, EN-marked sites correspond to type 2 events, and SC nucleations correspond to total events. The second is a two-rounds scenario in which T2 foci are defined in a first round, and T3 foci are defined in a second round for which T2 foci were the precursors. The best-fit simulation of T2 foci is the same in the two cases (ii). The best-fit simulations for T3 foci give significantly different patterns (iv and v) with a close match between the one-round scenario and the experimental data (compare iii vs. iv). Parameter values for best-fit simulations are given in Materials and Methods. (Middle and Bottom) Experimental or predicted CoC relationships (Middle) and number and distribution of events (Bottom). Experimental data are shown in green for T2 foci and red for T3 foci. BF best-fit simulation data are shown in black. A peak in T2 or T3 interfocus distances or a shoulder or hump in CoC relationships at the position of the average interfocus distance for total precursors (vertical black dashed line) is a diagnostic indicator that the corresponding events arose directly from total precursors (Results). This feature should be present for T2 foci in both scenarios. It will be true for T3 foci only in the one-round scenario (Middle). For T2 foci, this feature is apparent in both experimental and best-fit simulation data (green arrows). For T3 foci, this feature is apparent in experimental data, thus supporting the one-round scenario. Correspondingly, this feature also is apparent in data for the best-fit simulation of the one-round scenario (red arrows; black circles) and is absent in the best-fit simulation of the two-round scenario (dashed black circle). Furthermore, the occurrence of this diagnostic feature in the best-fit simulation of the one-round scenario is dependent upon a tendency for even spacing of precursors: The diagnostic hump is absent in the best-fit CoC curve when precursors are assumed to be randomly spaced (Fig. S1).

The effects of these tendencies also are apparent in CoC curves. Double-event bivalents, in which two events have occurred in different intervals along the same chromosome, are very rare at small inter-interval distances. Correspondingly, for events that arise directly from the original precursor array of total interactions, closely spaced double events will tend to occur specifically at the inter-interval distance corresponding to the distance between adjacent interactions (∼0.6 μm). This tendency is predicted to appear as a “hump” in the CoC curve at the appropriate position. Such a hump is discernible as a shoulder in the CoC curve for T2 foci; more tellingly, it also is a prominent discrete feature of the CoC curve for T3 foci (Fig. 4 Middle, i and iii).

BF best-fit simulation analysis confirms and extends these conclusions.

• i)We first defined the best-fit simulation match for the T2 focus pattern (total events) as they arise from the initial precursor array of total recombinational interactions. As described in the example above (Fig. 3G, Total), this match defines all BF parameter values, most notably the value of L (L_BF = 1 μm) and the value of Smax for total events (Smax_total = 4.5). The best-fit simulation for T2 foci accurately describes both CoC relationships and the average number and distribution of events (Fig. 4 Middle and Bottom, ii). It also recapitulates the tendency for adjacent T2 events to occur preferentially at the average interprecursor distance by all the above criteria, with a peak at the appropriate position in the distribution of interevent distances and a corresponding shoulder in the CoC curve (Fig. 4 Top, Second Row, and Middle, ii). Additionally, recapitulation of this tendency requires that precursors tend be evenly spaced; no such tendency is observed if precursors are assumed to occur randomly along the chromosomes (Fig. S1).
• ii)If the one-round threshold scenario pertains, it should now be possible, without changing the values of any other parameters including L_BF, to identify a value of Smax that is lower than Smax_total at which the number and distribution of designation events matches those of T3 foci (as illustrated by Fig. 3G, type 1). In fact, such a value can be obtained at Smax_T3 = 1.8 (Fig. 4 Middle and Bottom, iv). Importantly, this simulation also recapitulates the tendency for adjacent T3 events to occur preferentially at the average interprecursor distance by all the above criteria as seen in both the distribution of interevent distances and the CoC curve (Fig. 4 Top, Second Row, and Middle, iv). For T2 foci, recapitulation of this tendency requires that precursors tend to be evenly spaced (Fig. S1).
• iii)In contrast, if the two-round scenario pertains, it should be possible to use the array of T2 foci as the precursors for a second, independent round of interference, which yields appropriate T3 focus patterns. The best-fit simulation of this scenario does, in fact, provide reasonable matches between experimental and predicted data with respect to CoC curves and the number and distribution of designated events (Fig. 4 Middle and Bottom, v). However, there is no tendency for adjacent events to be separated by the distance corresponding to the distance between total starting recombinational interactions, nor is there any indication of a hump at the corresponding position (Fig. 4 Top, Second and Third Rows, and Middle, v). This simulation confirms that the two-round scenario does not adequately explain the experimental data, in a particular way that specifically distinguishes between the one- and two-round cases.

To understand further the nature of the closely spaced double events seen for T2 and T3 foci, we inspected the patterns along each analyzed chromosome in the experimental datasets. Interestingly, for both T2 foci and T3 foci, the majority of closely spaced double events tend to occur near the chromosome ends (70/117 pairs of T2 foci; 18/28 pairs of T3 foci). This tendency likely is related to the tendency for SC initiations, ENs, and LNs all to occur first near chromosome ends (Fig. S2) (13). The BF best-fit simulation of the one-round scenario also captures this feature of the data. In the stress hypothesis, the status assigned to the chromosome ends will influence the probability of event designations in nearby (subtelomeric) regions. If a chromosome end is free (“unclamped”), it will not support stress and will behave as a preexisting designation event, thus disfavoring near-end events. On the other hand, a clamped end will support stress and favor near-end events because the spreading inhibitory interference signal will emanate across subterminal positions only from internal regions and not from beyond the end of the chromosome (17, 20). [In vivo, clamping could correspond to the association of a chromosome end with the nuclear envelope; however, outside of the stress hypothesis, the clamping parameter simply provides a convenient way to modulate the probability of events occurring near ends.] In best-fit BF simulations of T2 and T3 foci by the one-round scenario, the occurrence of closely spaced double events near chromosome ends requires that both ends be clamped (in accord with nuclear envelope association of ends at this stage as defined by EM) (Fig. S2) (13). We also find that longer bivalents exhibit very few double events at any position, for reasons that presently are unclear. Correspondingly, the above analysis considers only the shorter bivalents 3–7, which are evaluated as a single group.

In summary, the considerations presented above suggest that the observed pattern of SC nucleations with embedded CO interference is well explained by a single round of interference-mediated patterning with thresholded designation first of SC nucleations and accompanying CO designations (and LNs) and then of more SC nucleations without accompanying CO designations (and ENs). Of course, in real chromosomes, these are probabilistic tendencies that need not comprise an absolute temporal sequence. However, we find experimentally that SC segments with an associated LN tend to be longer than SC segments with an associated EN. Although other explanations are not excluded, this pattern is the one that would be expected if the LN-associated segments tend to be nucleated earlier in zygotene than the EN-associated segments, i.e., if SC nucleations with associated CO designation tend to precede SC nucleations without CO designation. It also is true that LNs and ENs themselves appear concomitantly during zygotene, rather than sequentially. However, this timing reflects not only the time of designation of the corresponding sites but also the time required for the appearance of a visible nodule. Thus, LN site designation could occur earlier, as suggested by SC length comparisons, but with a longer time required for development of a visible LN than for a visible EN.

Alternative Models.

We have attempted to identify other models that could explain the observed event patterns. Experimental data do not appear compatible with the two-round scenario described above in which all SC nucleation sites are designated in one round of interference-mediated patterning, with CO/LN/T3 sites then designated from among those interactions in a second round. A related two-round model would suggest that total SC nucleations (T2 foci) first would occur at a random subset of total recombination sites, with CO designation then occurring at a subset of those sites by an interference process. This model is also not possible: By this scenario, the distribution of T2 foci would match the distribution of total recombination sites, which is not the case (Fig. S3).

Other types of two-round models could be envisioned in which LN- and EN-correlated designations occur sequentially, by two independent interference processes, but with both types of nodules arising from the set of total recombinational interactions. SC nucleations with CO designation might occur first, by one interference process, followed by SC nucleation without CO designation acting on remaining “unreacted” precursors by another process. Alternatively, SC nucleation without CO designation might occur first, followed by SC nucleation with CO designation acting on remaining precursors.

Another scenario would suppose that SC nucleations accompanied by CO designation, and SC nucleations that are not accompanied by CO designation, occur simultaneously by two independent interference processes. Such a mechanism would require rules for what happens if both processes encounter the same precursor site. None of these three models has the same economy and simplicity as the threshold mode. However, they cannot be excluded at present.

Discussion

Interference-Mediated SC Nucleation with Embedded CO Designation.

The presented analysis of RN and SC patterns in 3D-reconstructed nuclei points strongly to a 1:1 relationship between total RNs (ENs + LNs) and SC nucleation sites. We previously showed that total RNs (and corresponding Hei10-T2 foci) are spaced relatively evenly in an interference pattern, whereas LNs (and corresponding Hei10-T3 foci) mark the sites of CO-fated recombinational interactions (8). Taken together these findings suggest that zygotene chromosomes exhibit a relatively evenly spaced array of SC nucleations with embedded CO sites that exhibit classical CO interference. Consideration of events in other organisms suggests that this pattern is likely to be quite general, as discussed in detail below.

This observed pattern is biologically quite attractive because it concomitantly satisfies the distinct requirements of the SC for its global roles along the chromosomes and for its local roles at the sites of CO recombination.

• i)Continuous SC along the lengths of the chromosomes is a nearly ubiquitous feature of the meiotic program. Total recombinational interactions link homologs along their lengths through late leptotene, via their associations with axial structure (11). However, as discussed below, by early/midpachytene, only CO-fated interactions remain axis/SC associated (8, 13, and discussion in ref. 22). Thus, full-length SC is required to keep homologs together at and after this point. This requirement is particularly stringent in organisms with very few COs, especially when those few COs are always near the ends of the chromosomes and, most dramatically, in some higher plants in which the chromosomes are extremely long (e.g., refs. 23 and 24). The tendency for SC nucleations to be evenly spaced ensures that SC forms efficiently and regularly along the chromosome lengths, as this role requires. Additionally, SC formation per se appears to mediate the sensing of chromosome interlocks (11), a role that also requires multiple, well-spaced initiations along the chromosomes.
• ii)CO recombination and the SC undergo local functional interplay in both directions. The structural constraints of the SC may stabilize the recombination ensemble against biochemical turbulence. Recombinosome/SC relationships also could provide the geometric constraint required to direct the resolution of double Holliday junctions specifically to CO products, rather than to NCO products or to a mixture of the two (1, 25). Additionally, CO sites ultimately mature into chiasmata, and this maturation involves local structural changes (e.g., crossing-over at the level of chromosome axes). Cytological studies implicate local SC and associated recombination complexes in these processes as well (26, 27).

The current findings also are of interest because they bring the meiotic crossover interference process, previously considered to apply only to the patterning of recombination sites, into a general chromosomal context. Crossover interference is thereby linked to basic chromosomal phenomena in which a tendency for even spacing is known or suspected, e.g., DNA replication initiation, chromatin loop formation, or formation of intersister linkages (20, 28). The natures of these processes, in turn, encourage interference mechanisms in which transmission of information occurs via chromosome structural features, as suggested by recent studies in budding yeast (9), rather than solely involving effects targeted to recombination complexes.

Sordaria Zygotene Chromosomal Patterns Appear to Arise Via a Single Interference Process.

As detailed above, available evidence suggests that SC nucleation and CO designation occur contemporaneously during zygotene. Detailed analysis of these events, as reflected in the patterns of Hei10 T2 and T3 foci, provide evidence that both features arise via a single process. (i) SC nucleations (T2 foci) and CO designations (T3 foci) both arise from the array of total recombinational interactions defined for late-leptotene chromosomes. (ii) BF best-fit simulations of a single process can describe the observed experimental outcome very accurately. (iii) BF best-fit simulations argue strongly against the emergence of the observed patterns via two sequential rounds of interference, both occurring during zygotene, with one process acting on total interactions to yield SC nucleations and a second process acting on the array of SC nucleations to give a final pattern of CO-designated sites. (iv) Other models that we have been able to envision are incompatible with the data in principle, cannot give an appropriate outcome in BF simulations, and/or involve multiple ad hoc assumptions.

Complex Spatial Patterns Can Arise in a Single Interference-Mediated Process Via Event-Designation Thresholding.

The basic logic underlying CO interference is very well described by the logic of the BF model, whether a mechanical mechanism is involved or not (9, 17). By this logic, interference is intrinsically characterized by a basic progression. Every designation event triggers a spreading inhibitory interference signal, which reduces the reactivity of all affected precursor interactions. As a result, as more and more precursor events undergo event designation, the remaining precursors become less and less reactive to the designation process. The current study has shown that this feature may have previously unappreciated implications: If the molecular outcome of designation is sensitive to the reactivity of the precursor involved, then that outcome can change progressively as the process proceeds.

Many types of patterns can be envisioned a priori. In the case at hand, the process is defined by only two thresholds for event designation, with an overlapping effect. Zygotene chromosome patterns are explained if early designations give SC nucleation plus CO designation, with attendant intimate linkage of recombination and structure, and later designations give only SC nucleation. Morphologically, as seen at early pachytene, the first set of events also gives LNs; the second set of events also gives ENs; and all events give T2 foci. In principle, a patterning process could involve any number of different thresholds with diverse, combinatorial overlapping. Thus, this simple basic premise might underlie and explain very complex patterns.

We note that the predictions of the thresholding scenario for SC nucleation and CO designation can be integrated very smoothly with our previous proposal of how CO interference might occur (9, 20, 21). In fact, we now can appreciate that our model directly predicts the observed graded effect.

• i)We have proposed that global chromatin expansion places the structural axis meshwork of late leptotene chromosomes under mechanical stress. As a result, all local interaxis recombination complexes are under stress. That stress provokes changes that cause certain complexes to change into a CO-designated form. That change, in turn, alleviates local stress, implying local chromatin compaction. That local compaction, in turn, licenses local SC installation, giving nucleation at CO sites. Global compaction at the end of zygotene then permits SC to fill in between nucleation sites. The need for such an effect is shown directly in Sordaria, in which each SC nucleation spreads for only a limited distance along the chromosomes (19). This overall pattern also fits with the fact that leptotene is characterized specifically by chromatin expansion, whereas zygotene is characterized specifically by chromosome compaction (20). Indeed, even in Caenorhabditis elegans, in which CO interference occurs after SC formation, recent findings indicate that the chromosomes are under chromatin expansion stress caused by the constraints of the SC, in accord with a role for expansion stress in CO designation (29).
• ii)In the context of this proposed model, it is easy to envision that, as the designation/interference process progresses, local precursor reactivity will be insufficient to give CO designation; however, if passage of the interference signal implies decreased chromatin expansion, SC nucleation will be progressively favored as the process progresses, thus permitting/promoting a continued designation process that gives SC nucleations without accompanying CO designation, exactly as suggested by the current analysis.

Generality of Interference-Mediated SC Formation with Embedded CO Designation.

The pattern described here for Sordaria could be very general among organisms that exhibit the canonical meiotic program.

Plants and mammals.

In tomato, a large population of ENs emerges during zygotene, specifically at sites of SC nucleation (30): They are seen specifically at convergences (which are known to be sites of SC nucleation in this and other plants; e.g., refs. 3 and 31) as well as at synaptic forks. Moreover, they do not emerge on already-formed SC (30). These ENs tend to be evenly spaced, as shown by gamma distribution analysis of inter-EN distances (31), indicating that SC nucleation sites also exhibit such a distribution and thus are subject to interference. Importantly, this tendency for even spacing is seen not only in tomato (31) but also, analogously, in many higher plants, implying broad generality. It has been suggested that for tomato these ENs are precursors to LNs (32), with the further implication that one round of interference occurs to give the EN distribution and that CO designation then occurs during pachytene in a second round of interference that operates on the EN-marked complexes (e.g., ref. 31). This suggestion is based on the observation that ENs are present at zygotene and early pachytene; then, at early/midpachytene most of these nodules disappear precipitously, and a few CO-correlated larger nodules (LNs) emerge (e.g., ref. 32). However, MutL homolog Mlh1 foci, which are specifically diagnostic of interfering COs, are seen already at zygotene in tomato (31). Moreover, biochemical studies of ENs in tomato show that a subset of the many early pachytene nodules is physically more strongly associated with the SC than are the others (33), with the number and distribution of that subset of stably associated nodules matching the number and distribution of later large CO-correlated LNs. Both these findings suggest that, in fact, CO designation occurs at zygotene, as in Sordaria. Moreover, precipitous loss of ENs at early pachytene is not diagnostic of a second round of interference: As discussed above, this loss also is seen in Sordaria, well after CO designation has occurred.

It also has been proposed that interference arises in two rounds in mice (34). Again, one round of interference would operate during leptotene/zygotene on total recombinational interactions to yield a number of recombination complexes intermediate between the number of DSBs and the number of COs. A second round of interference during early/midpachytene would operate on the events generated in the first round to give the final array of COs. For this organism, the two-round proposition emerges from the finding that an intermediate number of Msh4 foci occur on early/midpachytene chromosomes and that Mlh1 foci, which specifically mark the sites of interfering COs, emerge at mid/late pachytene. However, as discussed above (also see ref. 8), exactly these same patterns are seen for Msh4/Hei10-T2 foci and Mlh1/Hei10-T3 foci in Sordaria, in which CO designation is completed before early pachytene. Specifically, (i) in Sordaria, an intermediate number of recombinational interactions are marked at early/midpachytene by Hei10-T2 foci, and these interactions already include CO-designated sites that show interference as a result of the events of zygotene. (ii) These early/midpachytene T2 foci also are marked by a corresponding specific, intermediate number of Msh4 foci corresponding exactly to the intermediate number of Msh4 foci seen in other organisms. (iii) Hei10-T3 foci emerge at mid/late pachytene when, by all available criteria, they correspond to the Mlh1 foci that emerge at this stage in all organisms tested so far. Thus, the basic findings upon which the two-round scenario is based can be explained just as easily by the one-round zygotene scenario seen in Sordaria. Notably, also, in mouse, Msh4 foci and SC nucleations strongly colocalize at zygotene, as is consistent with earlier specification of Msh4 focus patterns in local coordination with SC nucleation (35, 36).

Analogously, in human, interhomolog bridges of RPA occur in a number that is intermediate between the number of total DSBs and COs (37). However, in this organism, just as in Sordaria, CO-correlated LNs are morphologically visible at zygotene (38).

Furthermore, an intermediate number of Msh4 foci are seen also in Arabidopsis, with the same potential Sordaria-analogous interpretation as in mouse.

In summary, all available evidence is consistent with the existence of a single round of interference that gives rise to evenly spaced SC nucleations with concomitant embedded CO designation, not only in Sordaria but also in plants and mammals. By this view, different organisms differ only with respect to (i) the extent to which and/or timing with which CO-fated interactions develop morphologically distinct features at zygotene (rather than later) and (ii) the proportion of SC nucleations that are CO-fated, which is highest in Sordaria, intermediate in mammals, and lowest in plants.

Budding yeast.

Budding yeast provides an interesting exception that may prove the rule. In this organism, interference is imposed prior to and independently of SC formation, which then is nucleated as a downstream consequence at CO-designated sites. These conclusions emerge from the following findings: (i) CO-correlated Zip2/3 foci exhibit an interference pattern that arises independently of the SC central region component Zip1 (9, 10). (ii) CO-specific DNA intermediates arise at leptotene/zygotene and are dependent on Zip1, implying that CO designation precedes or is concomitant with SC nucleation (21). (iii) Zip2/3 sites mark not only sites of COs but also sites of SC nucleation (10). This relationship has two important implications. First, CO designation and SC nucleation are directly linked. Second, there is a 1:1 relationship between the two events: Every SC nucleation is a CO designation, and every CO designation is an SC nucleation. Thus, in this case, the more general pattern pertains, but in an extreme form in which there are no extra SC nucleations beyond those corresponding to sites of CO designation. Correspondingly, ENs (which mark the positions of extra SC nucleations in Sordaria) have not been observed in budding yeast. Moreover, as discussed above, in Sordaria and other organisms, Msh4 foci occur at midpachytene in an intermediate number corresponding to total SC nucleations; in contrast, in budding yeast, the number of Msh4 foci at this stage correspond to the number of specifically designated COs (∼65) (ref. 9 and figure 6 in ref. 39). This situation makes perfect sense given that yeast chromosomes not only are very short but also exhibit a much higher density of COs per SC length than other organisms. Thus, there is no need for extra nucleations to ensure full SC formation.

Noncanonical programs.

In S. pombe and A. nidulans, CO interference and SC are both absent. This absence was long cited as evidence that the SC mediates interference, which is not true in budding yeast as discussed above. The present observations provide a sensible possible rationale: If CO interference exists primarily to promote regular SC formation, then in the absence of SC, there will be no need for interference.

Different considerations pertain in the noncanonical meiotic programs of C. elegans and Drosophila. In these organisms, SC formation is independent of recombination and CO designation; moreover, both recombination initiation and interference is or can be implemented after SC formation (40–43). In these cases, the interference process seems limited to patterning of COs, and not SC nucleation, suggesting that an important functional rationale for interference may relate to CO/chiasma formation (27). Notably, however, in C. elegans, recombination-dependent SC formation can be observed in certain circumstances (44).

Why ENs?

The patterns of SC nucleations, ENs, and LNs in Sordaria and other organisms discussed above raise an interesting conundrum. LNs are robust, ultrastructurally visible features, and their prominence can be attributed to the need for robust association of CO-fated recombination complexes with the SC. However, why do ENs exist? They are not involved in CO-specific events. Moreover, genetic evidence in Sordaria suggests that all non–CO-designation interactions, including both EN-marked and non–nodule-marked interactions, are matured to NCO products. Thus, ENs apparently are not required to give an NCO outcome. The same could well be true in many organisms, because ENs always occur in an intermediate number, greater than the number of COs but fewer than the number of DSBs. The sole distinguishing feature of ENs appears to be that they mark the sites of SC nucleations that will not progress to a CO outcome. SC nucleation involves an intimate association of the recombination complex with SC components. For example, in Sordaria, Mer3 and Msh4 foci go from on-axis to between-axis positions exactly concomitantly with SC nucleation (11, 12). However, once nucleation is achieved, persistence of this association at nucleation sites that are not fated to become COs is unnecessary and/or deleterious. We propose that ENs (and T2 foci) are required to mediate the surgical dissociation of the corresponding (NCO-fated) recombination complex from the SC. Further, we suggest that this dissociation is triggered by Msh4-mediated progression of the associated recombination complexes. This possibility is suggested by the observation that in Sordaria (8) ENs and the corresponding subsets of Hei10-T2 and Msh4 foci disappear from the chromosomes concomitantly and abruptly at the early/midpachytene transition. Similarly, this role would rationalize the precipitous loss of ENs and/or Msh4 foci at early/midpachytene in plants, human, mouse, and Sordaria; the existence of intermediate numbers of Msh4-containing recombination complexes in Sordaria, mouse, and Arabidopsis; and the absence of ENs and intermediate numbers of Msh4 foci in budding yeast, where all SC nucleations appear to involve an accompanying CO designation, as discussed above (3, 6, 21, 34, 36, 45). Finally, the fact that ENs are less permanently and less strongly associated with the SC could be related to the fact that EN-nucleated SC segments are shorter than LN-nucleated segments.

Materials and Methods

Ultrastructural and Hei10 Focus Data.

Analysis of SC and RN patterns (Fig. 2) was performed on previously described 3D reconstructions (13). Pictures were taken at a magnification of 8,000×. Three-dimensional reconstructions were performed as follows. The SC elements and nuclear structures from five consecutive sections were traced onto acetate sheets, and when the nucleus was completed, each bivalent was redrawn on a new sheet with its relevant section numbers, centromere, synapsis regions, and nodule sites. The projected lengths were measured, and the chromosome lengths were calculated using the Pythagorean theorem (with a mean section thickness of 80 nm). Hei10 T2 and T3 data are from ref. 8.

BF Analysis.

BF simulations were performed as described previously (17). Three types of parameters must be specified. (i) The array of precursors is characterized by the average number per bivalent (N), the extent to which those precursors are spaced evenly or randomly along the bivalent (E), the extent to which the number precursors along the bivalent in different nuclei is constant or corresponds to a random distribution (B), and the distribution of intrinsic precursor sensitivities to stress (A). (ii) Patterning parameters include L, the distance over which the inhibitory interference signal spreads; Smax, the maximum level of global stress; and the degree of clamping at right (cR) and left (cL) ends. (iii) Maturation efficiency, M, describes the probability that an event designated to have a particular fate will then mature to the point that it is detected as such by the assay in use. For best-fit simulations of yeast and Sordaria data, the value of N is known from experiments (11, 17); precursors are known to be very evenly spaced in Sordaria (11) and also, by several criteria, to be relatively evenly spaced in yeast (17). Maturation efficiencies for yeast and Sordaria are both assumed to be 100% (M = 1). For best-fit simulations, approximate values of L and Smax are defined; then the values of these and other parameters are adjusted to give the optimal match to CoC and event distribution relationships as judged by visual inspection. Parameter values for best-fit simulations shown here are as follows:

• i)For CO-correlated Zip3 foci along yeast chromosome XV (Fig. 3B): L = 0.1 (0.3 μm); Smax = 3.5; N = 13; A = 1; B = 1; E = 0.6; cL = 0.85; cR = 0.85.
• ii)For Sordaria T2 foci (Fig. 4, ii): L = 0.15 (1 μm); Smax = 4.5 (corresponding to 1.8 for T3); N = 9; A = 2; B = 0.9; E = 0.8; cL = 1; cR = 1.
• iii)For Sordaria T3 foci, one-round scenario (Fig. 4, iv): Parameters are the same as for T2 foci except that Smax = 1.8.
• iv)For Sordaria T3 foci, two-round scenario: Precursors are the simulated T2 foci shown in ii (which can also be mimicked with N = 5, B = 0.9, E = 0.8). Based on these precursors, the best-fit simulation of T3 foci uses L = 0.205; Smax = 2.8; A = 2; cL = 1; cR = 1.