Abstract
One of the major challenges impeding advancement in image-guided surgical (IGS) systems is the soft-tissue deformation during surgical procedures. These deformations reduce the utility of the patient’s preoperative images and may produce inaccuracies in the application of preoperative surgical plans. Solutions to compensate for the tissue deformations include the acquisition of intraoperative tomographic images of the whole organ for direct displacement measurement and techniques that combines intraoperative organ surface measurements with computational biomechanical models to predict subsurface displacements. The later solution has the advantage of being less expensive and amenable to surgical workflow. Several modalities such as textured laser scanners, conoscopic holography, and stereo-pair cameras have been proposed for the intraoperative 3D estimation of organ surfaces to drive patient-specific biomechanical models for the intraoperative update of preoperative images. Though each modality has its respective advantages and disadvantages, stereo-pair camera approaches used within a standard operating microscope is the focus of this article. A new method that permits the automatic and near real-time estimation of 3D surfaces (at 1Hz) under varying magnifications of the operating microscope is proposed. This method has been evaluated on a CAD phantom object and on full-length neurosurgery video sequences (~1 hour) acquired intraoperatively by the proposed stereovision system. To the best of our knowledge, this type of validation study on full-length brain tumor surgery videos has not been done before. The method for estimating the unknown magnification factor of the operating microscope achieves accuracy within 0.02 of the theoretical value on a CAD phantom and within 0.06 on 4 clinical videos of the entire brain tumor surgery. When compared to a laser range scanner, the proposed method for reconstructing 3D surfaces intraoperatively achieves root mean square errors (surface-to-surface distance) in the 0.28-0.81mm range on the phantom object and in the 0.54-1.35mm range on 4 clinical cases. The digitization accuracy of the presented stereovision methods indicate that the operating microscope can be used to deliver the persistent intraoperative input required by computational biomechanical models to update the patient’s preoperative images and facilitate active surgical guidance.
Keywords: operating microscope, magnification, zoom lens, stereovision, intraoperative digitization, surface reconstruction, intraoperative imaging, image-guided surgery
1. Introduction
Intraoperative soft tissue deformations or shift can produce inaccuracies in the preoperative plan within image-guided surgical (IGS) systems. For instance, in brain tumor surgery, brain shift can produce inaccuracies of 1-2.5cm in the preoperative plan (Roberts et al., 1998a; Nimsky et al., 2000; Hartkens et al., 2003). Furthermore, such inaccuracies are compounded by surgical manipulation of the soft tissue. These real-time intraoperative issues make realizing accurate correspondence between the physical state of the patient and their preoperative images challenging in IGS systems. To address these intraoperative issues, several forms of intraoperative imaging modalities have been used as data to characterize soft tissue compensation methods can be categorized as: (1) partial or complete volume tomographic intraoperative imaging of the organ undergoing deformation and (2) intraoperative 3D digitization of points on the organ surface, the primary focus of this article. Tomographic imaging modalities such as intraoperative computed tomography (iCT) (King et al., 2013), intraoperative MR (iMR), and intraoperative ultrasound (iUS) have been used to compensate for tissue deformation and shift in hepatectomies (Lange et al., 2004; Bathe et al., 2006; Nakamoto et al., 2007) and neurosurgeries (Butler et al., 1998; Nabavi et al., 2001; Comeau et al., 2000; Letteboer et al., 2005). These types of volumetric imaging modalities provide direct access to the deformed 3D anatomy. However, these modalities are affected by surgical workflow disruption, engendered cost, or poor image contrast.
Employing 3D organ surface data to drive biomechanical models to compute 3D anatomical deformation is an alternative to the compensating for anatomical deformation using the above mentioned volumetric imaging based methods. Recent research has demonstrated that volumetric tissue deformation can be characterized and predicted with reasonable accuracy using organ surface data only (Dumpuri et al., 2010a; Chen et al., 2011; DeLorenzo et al., 2012; Rucker et al., 2013). These types of computational models rely on accurate correspondences between digitized 3D surfaces of the soft-tissue organ taken at various time points in the surgery. Certainly, persistent delivery of 3D organ surface measurements to this type of model-update framework can realize an active IGS system capable of delivering guidance in close to real time. Organ surface data and measurements to drive these computational models can be obtained using textured laser range scanners (tLRS), conoscopic holography (Simpson et al., 2012), and stereovision systems. All of these modalities deliver geometric measurements of the organ stereovision, the point clouds carry color information making them textured. These modalities allow for an inexpensive alternative to 3D tomographic imaging modalities and provide an immediate non-contact method of digitizing 3D points in a FOV. With these types of 3D organ surface digitization and measurement techniques, the required input can be supplied to the patient-specific biomechanical computational framework to compensate for soft tissue deformations in IGS systems with minimal surgical workflow disruption. In this paper, we compare the point clouds obtained by the tLRS and the developed stereovision system capable of digitizing points under varying magnifications and movements of the operating microscope.
Optically tracked tLRS have been used to reliably digitize surfaces or point clouds to drive biomechanical models for compensation of intraoperative brain shift and intraoperative liver tissue deformation (Cash et al., 2007; Dumpuri et al., 2010a, 2010b; Chen et al., 2011; Rucker et al., 2013). The tLRS can digitize points with sub-millimetric accuracy within a root mean square (RMS) error of 0.47mm (Pheiffer et al., 2012). While the tLRS provides valuable intraoperative information for brain tumor surgery, establishing correspondences between temporally sparse digitized organ surfaces is challenging and makes computing intermediate updates for brain tumor surgery even more challenging (Ding et al., 2011).
Stereovision systems of operating microscopes can remedy the deficiencies of the tLRS by providing temporally dense 3D digitization of organ surfaces to drive the patient-specific biomechanical soft-tissue compensation models. Initial work in a similar vein has been done with respect to using an operating microscope for visualizing critical anatomy virtually in the surgical FOV for neurosurgery and otolaryngology surgery (King et al., 1999; Edwards et al. 2000). In this augmented reality microscope-assisted guided intervention platform, bivariate polynomials establishing the correct 3D position of critical anatomies overlays. Figl et al. (2005) developed a fully automatic calibration method for an optical see-through head-mounted operating microscope for the full range of zoom and focal length settings, where a special calibration pattern is used. In this presented work, we use standard camera calibration techniques (Zhang, 2000) with a content-based approach and do not separate the zoom and focal length settings of the microscope’s optics as done in Willson (1994) and Figl et al. (2005). Our method is based on estimating the magnification being used by neurosurgeons. This magnification is the result of a combination of using the zoom and/or focal length adjustment functions on the operating microscope.
Although stereovision techniques are often used for surface reconstruction in computer-assisted laparoscopic surgeries (Maier-Hein et al., 2013, 2014), in this paper, we focus on three stereovision systems that have been used for brain shift correction using biomechanical models. These stereovision systems are housed externally or internally within the operating microscope, which is used routinely in neurosurgeries. The 3D digitization of the organ surface present in the operating microscope’s FOV can be accomplished using stereovision theory. The first system uses stereo-pair cameras attached externally to the operating microscope optics (Sun et al., 2005a, 2005b; Ji et al., 2010). This setup renders the assistant ocular arm unusable when the cameras are powered on. Often, the assistant ocular arm of the microscope is used as a teaching tool. This limits the acquisition of temporally dense cortical surface measurements. The second stereovision system also uses an external stereo-pair camera system attached to the operating microscope. This system relies on a game-theoretic approach for combining intensity information in the operating microscope’s FOV to digitize 3D points (DeLorenzo et al., 2007, computing 3D surfaces or point clouds using the developed game-theoretic framework. Similar to the disadvantages shouldered by the tLRS, the temporally sparse data from these two stereovision systems make establishing correspondence for driving the model-update framework challenging. Paul et al. (2005) developed the third stereovision system. This system uses external cameras and is capable of displaying 3D reconstructed cortical surfaces registered to the patient’s preoperative images for surgical visualization. In Paul et al. (2009), the stereovision aspect of this system has been extended for registering 3D cortical surfaces acquired by the stereo-pair cameras for computing cortical deformations. One of the major unaddressed issues in these three stereovision systems is the acquisition of reliable and accurate point clouds from the microscope under varying magnifications and microscope movements for the duration of a typical brain tumor surgery, approximately 1 hour.
During neurosurgery, the surgeon frequently moves the head of the operating microscope and zooms in and out of the surgical site to effectively manipulate the organ surface to perform the surgery. The magnification function of the operating microscope is a combination of changes in zooms and focal lengths of the complex optical system housed inside the head of the operating microscope. The unknown head movements and magnification changes alter the determined camera calibration parameters at the pixel level, cause calibration drift, and consequently, result in inaccurate point clouds. Several popular methods for self-calibration of cameras have been developed (Hemayed, 2003), where an initial camera calibration is not performed.
In published methods, the stereo-pair cameras are either recalibrated or the operating microscope’s optics are readjusted to the initial calibration state for the stereo-pair cameras when a point cloud needs to be obtained during the surgery. Overall, the inability to persistently and been one of the considerable barriers to widespread adoption of the operating microscope as a temporally dense intraoperative digitization platform. As a result, the development of an active IGS system capable of soft tissue surgical guidance to the clinical armamentarium has been slowed.
In this article, we develop a practical microscope-based digitization platform capable of near real-time intraoperative digitization of 3D points in the FOV under varying magnification settings and physical movements of the microscope. Our stereovision camera system is internal to the operating microscope and this keeps modifications and disruptions to the surgical workflow at a minimum. With this intraoperative microscope-based stereovision system, the surgeon can perform the surgery uninterrupted while the video streams from the left and right cameras get acquired. Furthermore, the assistant ocular arm of the operating microscope is still usable. Preliminary work comparing the accuracy of point clouds obtained from such a microscope-based stereovision system against the point clouds obtained from the tLRS on CAD phantom objects has been presented in our previous work (Kumar et al., 2013).
In this paper, we (1) build on the real-time stereovision system of Kumar et al. (2013) to robustly handle varying magnifications and physical movements of the microscope’s head based on a content-based approach. We (2) compare the theoretical magnification of the microscope’s optical system to the magnification computed from our near real-time algorithm; and (3) evaluate the accuracy of the digitization of 3D points using this intraoperative microscope-based digitization platform against the gold standard tLRS on a CAD designed cortical surface phantom object and cortical surfaces from 4 full-length clinical brain tumor surgery cases conducted at Vanderbilt University Medical Center (VUMC). To the best of our knowledge, microscope subject to unknown magnification settings has not been previously reported. Our fully automatic intraoperative microscope-based digitization platform does not require any manual intervention after a one-time initial stereo-pair calibration stage and can robustly perform under realistic neurosurgical conditions of large magnification changes and microscope head movements during the surgery. Additionally, we validate our methods on full-length highly dynamic neurosurgical videos that last over an hour, the typical duration of a brain tumor surgery. This type of extensive validation of an automatic digitization method has not been done before to the best of our knowledge. Validations on earlier digitization methods (Sun et al., 2005; DeLorenzo et al., 2007; Paul et al., 2009; Ding et al., 2011) have dealt with short video sequences (~3-5 minutes) acquired at sparse time points and rely on manual initializations. Furthermore, we perform a study comparing the surface digitization accuracy of the stereo-pair in the operating microscope against the gold standard tLRS on 4 clinical cases. Overall, we demonstrate a clinical microscope-based digitization platform capable of reliably providing temporally dense 3D textured point clouds in near real-time of the FOV for the entire duration and under realistic conditions of neurosurgery.
2. Materials and Methods
Section 2.1 describes the equipment and CAD models used for acquiring and evaluating stereovision data. Section 2.2 and 2.3 explain the digitization of 3D points using the operating microscope under fixed and varying magnification settings respectively.
2.1 Data acquisition and phantom objects
The proposed video-based method for 3D digitization under varying magnifications is an all-purpose method not limited to the use of an operating microscope and is independent of any hardware interfaces such as the StealthLink® (Medtronic, Minneapolis, MN, USA). To clarify, the magnification function on the operating microscope changes the zoom and focal length values of the microscope’s optical system, housed in the head of the microscope. Furthermore, the head of the microscope can be moved in physical space and this does not necessarily change the values of zoom and focal lengths in the optical system, but such movements changes the range of the operating microscope to the surgical field, i.e. the brain surface. This physical change in the range of microscope to the organ surface is reflected in the FOV of cameras and needs to be accounted for when sizing the point clouds correctly. Such movements and zoom and focal length changes can be recovered using our algorithm as a single value, which can then be used to digitize the FOV correctly. We call this single value the magnification factor affecting the FOV. This all-purpose method can also be used for surgeries that do not require an operating microscope. For instance, in breast tumor surgery, a stereo-pair camera system capable of magnification can be located afar from the surgical field in the operating room. The proposed algorithm can recover the magnification factor, which signifies the changes of the FOV captured in the cameras due to physical movement of the camera system with respect to the breast surface and the magnification (zoom and focal length) changes. Our method is more amenable to the surgical workflow as an all-purpose fully automatic 3D digitization method for different types of soft-tissue surgeries. It should be clarified, however, that optical tracking would be needed to transform the correctly sized digitized 3D organ surfaces to the stereo-camera system’s coordinate system for driving a model-based deformation compensation framework.
In this paper, we use the OPMI® Pentero™ (Carl Zeiss, Inc., Oberkochen, Germany) operating microscope with an internal stereo-pair camera system. This is the current microscope used in neurosurgery cases at VUMC. The internal stereo cameras of this operating microscope is comprised of two CCD cameras, Zeiss’ MediLive® Trio™, and have NTSC (720x540) resolution with an acquisition video frame rate of 29.5 frames per second (fps). The stereo-pair cameras are setup with a vergence angle of 4° to assist stereoscopic viewing. FireWire® Video cards at the back of the Pentero microscope are connected via cables to a desktop, which acquires video image frames from both cameras. Figure 1 shows the stereo video acquisition system of the Pentero microscope. This microscope was used at VUMC to obtain patient video data with Institution Board Review (IRB) approval. We test our methods on stereo-pair videos of 4 full-length clinical brain tumor surgery cases acquired by the Pentero microscope. The stereo-pair videos were acquired uninterrupted for the entire duration of clinical cases #2-4. Clinical cases #2-4 are approximately of duration 77 minutes, 115 minutes, and 78 minutes respectively. Clinical case #1’s stereo-pair video acquisition was not as seamless because of hard drive storage limitations on the acquisition computer and these stereo-pair videos were acquired periodically until the end of brain tumor surgery, the post-resection stage. The duration of clinical case #1 was approximately 99 minutes but the stereovision acquisition computer was able to capture a total of approximately 24 minutes of video interspersed throughout this clinical case.
Figure 1.

The Zeiss Pentero microscope as a test-bed, (a) the microscope, (b) the two FireWire® videocards for acquisition (indicated by red arrows), and (c) the OPMI head of the microscope.
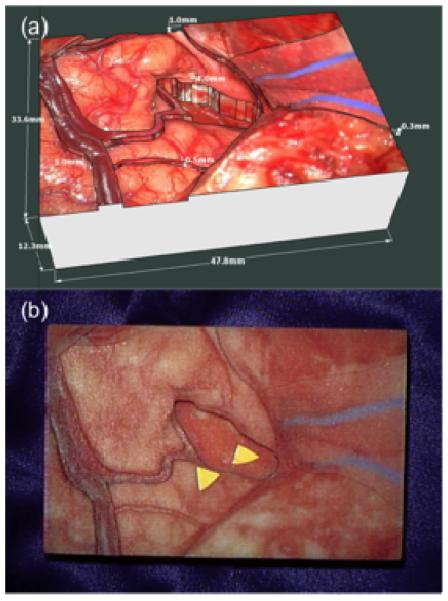
To test our stereovision approach and verify the accuracy of the digitized 3D points in the FOV of the microscope under varying magnifications, a phantom object of known dimensions was designed using CAD software. The phantom object, shown in Figure 2, was rapid prototyped within a tolerance of 0.1mm vertically (EMS, Inc., Tampa, Florida, USA). The bitmap texture on this phantom object is a cortical surface from a real brain tumor surgery case performed at VUMC. This is the kind of RGB texture expected in the FOV of the operating microscope during neurosurgery.
Figure 2.
CAD model of a cortical surface, where the texture is from a real brain tumor surgery case performed at VUMC is shown in (a), and (b) shows the phantom object in the FOV of the Pentero microscope.
2.2 Point clouds under a fixed focal length
Stereovision is a standard computer vision technique for converting left and right image pixels to 3D points in physical space. Trucco & Verri (1998), Hartley & Zisserman (2004) and Bradski & Kaehler (2008) describe this stereovision methodology in detail. In Kumar et al. (2013), we use the stereovision technique composed of stereo calibration (Zhang, 2000), stereo rectification (Bouguet, 1999, 2006), and stereo reconstruction based on Block Matching (BM) (Konolige, 1997) steps to digitize 3D points in the FOV of the Pentero operating microscope. Using Zhang’s calibration technique, a chessboard of known square size is shown in various poses to the stereovision system of the operating microscope. We use a chessboard square size of 3mm to provide metric scale to the point clouds acquired by the microscope. We perform Zhang’s calibration technique once prior to the start of the surgery and make sure the initial calibration is accurate. We achieve a calibration accuracy of approximately 0.67-0.81 pixel2 using Zhang’s method (Kumar et al., 2013). The main result from the stereovision methodology is the reprojection matrix, Q, shown in Equation 1(a). The elements of Q are image “focal lengths” or scale factors in the image axes, (fx, fy), the location of image-center in pixel coordinates, (cx, cy), and Tx is the translation between left and right cameras. It should be clarified that the intrinsic parameters (fx, fy, cx, cy) of the cameras are not the microscope optics’ focal length and zoom. The process of stereo calibration (Zhang, 2000) establishes the relationship between the microscope’s optics and the camera’s intrinsic parameters at the pixel level. Q is used for reprojecting a 2D homologous point (x, y) in the stereo-pair image and its associated disparity d to 3D by applying Equation 1(b). When the zoom and focal length of the operating microscope change, the intrinsic elements of the reprojection matrix, Q, changes as well.
| (1a) |
| (1b) |
In Kumar et al. (2013), we show that the accuracy of the 3D digitized points using BM (Konolige, 1997) and Semi-Global Block Matching (Hirschmuller, 2008) methods are in the 0.46-1.5mm range for different phantom objects. For the purpose of developing a real-time stereovision system, we picked BM for stereo reconstruction because of its simplicity and because the method can compute disparities in 0.03 seconds. Though other real-time techniques for the stereo reconstruction stage have been used for IGS (Chang et al., 2013), we have shown herein that BM provides sufficient accuracy and has no major drawbacks of its use in the acquisition of point clouds of the brain surface in clinical cases. An example of the stereovision point cloud acquired by the Pentero operating microscope on the phantom object using the BM method is shown in Figure 3.
Figure 3.
Block Matching (BM) stereo reconstruction results on the cortical surface phantom. The point cloud is shown at the bottom. The green rectangles indicate the FOV common to the left and right cameras, and BM uses this FOV to compute the point cloud.
It should be clarified that the captured stereo-pair videos’ image frames remain the same dimension, 720 x 480, regardless of the use of magnification function on the microscope or physical movements of the microscope. This means that if magnification were changed on the microscope, all reconstructed point clouds would be of the same dimensions (length, width, and depth). This is incorrect because the physical dimensions of the object did not change and the computed point clouds will be larger/smaller than it should be. If the magnification factor were estimated, the computed point clouds would be sized correctly and be reflective of the physical dimensions of the object.
2.3 Point clouds under varying magnifications
This section develops a method to automatically compute the change in magnification factor of the microscope’s FOV without any prior knowledge. This magnification factor is used for the digitization of 3D points using the stereovision framework of Section 2.2. Our method keeps the metric scale used in Section 2.2 valid for the digitization of points under varying magnification settings. Since initial calibration (Zhang, 2000) has been performed once at the start of the surgery, at the metric scale (in our case, 3mm), the problem of estimating the change in focal length resulting from the magnification function of the microscope becomes constrained and does not require self-calibration camera procedures devised by Hartley (1999), Pollefeys et al. (1999, 2007). Snavely et al. (2006) proposed methods for the automatic recovery of unknown camera parameters and viewpoint from large collections of images of scenic locations. Similar work involving the calibration of focal lengths for miniaturized stereo-pair cameras for laparoscopy has been proposed by Stoyanov et al. (2005), where a constrained parameterization scheme for the computation of focal lengths is developed. Though these techniques have been successfully used in various applications, estimation of the magnification factor of the operating microscope is less complex and we present a simple approach herein to compute this value. The proposed procedure of estimating the magnification factor of the stereovision system assumes that the extrinsic relationship between left and right cameras remain unchanged inside the operating microscope. In this section, we first explain the theoretical basis of the magnification of operating microscopes and then delve into the near real-time algorithm.
2.3.1 Magnification of operating microscopes
Magnification describes the size of an object seen with the unaided eye in comparison to the size seen through an optical system. The optical system of a microscope consists of a primary objective, a tube lens, and an eyepiece with focal lengths, fO, fT, and fE respectively (Born & Wolf, 1999; Lang & Muchel, 2011). The operating microscope’s optical system is equipped with a magnification changer or a zoom system with different telescope or Galilean magnifications, γ, which can be arranged between the primary objective and the tube lens. Including all these elements of the microscope, the total magnification of the operating microscope, VM, can be of the eyepiece (Lang & Muchel, 2011). The operating microscope’s magnification function changes the objective focal length fO and γ values while keeping fT and fE unchanged. Note that VM combines both the zoom parameter and focal length parameters of the operating microscope’s magnification function. On the Pentero microscope, the zoom and focal length can be adjusted separately but they can be combined to form Equation 2. In this paper we are concerned with changes in VM during neurosurgery. Figure 4 illustrates the optical system housed inside the head of the Pentero operating microscope. We expect other commercial optical systems of microscopes to be similar in construction. Our proposed algorithm is agnostic to various types of optical systems. The Pentero microscope shows radial distortion in its captured images (Lang & Muchel, 2011) and the stereo calibration algorithm by Zhang (2000) corrects for this radial distortion. We use Zhang’s method (2000) for performing stereo calibration once. changers. The autofocus function optimizes the values of γ and fO for which the organ surface is in focus and is sharp.
Figure 4.
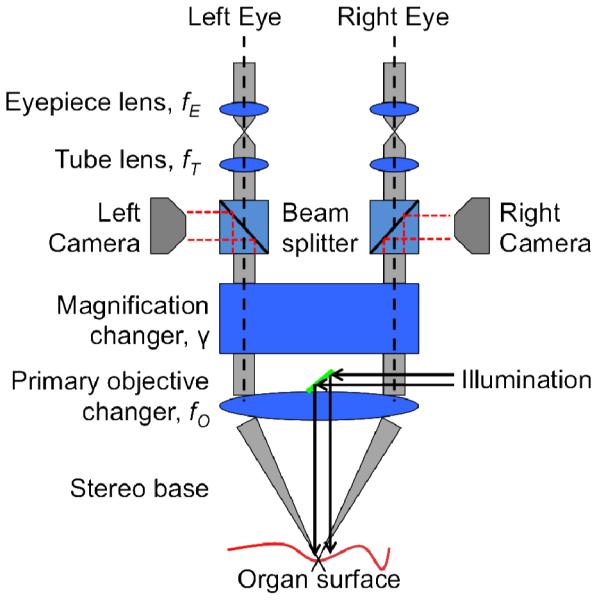
The optical system housed inside of the Pentero operating microscope is shown. The magnification function on the microscope uses the magnification and primary objective
| (2) |
Let denote the magnification of the operating microscope at any given time t. For instance, the microscope’s total magnification used during the initial stereo calibration stage, discussed in Section 2.2, is . When the surgeon uses the zoom function of the microscope at successive time points ti and tj, where ti < tj, the primary objective’s focal length, fO, and Galilean magnifications, γ, are changed. Furthermore, the use of the zoom function magnifies the FOV at ti by α to the zoomed version of the FOV at tj. This signifies that the change in total magnification of the microscope at time ti and tj are proportionally related by α, as shown in Equation 3. We denote the magnification from time ti to tj. We derive Equation 4 using Equations 2-3. Using Equation 4, we can now compute the change in magnification at different time points, ti and tj. Since Zeiss’ Pentero microscope’s screen displays the fO and γ values, we can compute the theoretical from Equation 4. It should be clarified that the running magnification from time ti to tk, where ti < tj < tk, denoted by can be derived as a serial relationship as shown in Equation 5. The manual entering of fO and γ for the calculation of α leads to an inelegant solution for a seamless and persistent microscope-based digitizer.
| (3) |
| (4) |
| (5) |
The physical range between the organ surface and the stereo-pair’s image planes is changed when the microscope’s head is moved by the neurosurgeon. These movements may not affect the theoretical magnification, α, but changes the reprojection matrix, Q, in Equation 1a. It should be clarified that our proposed algorithm computes a magnification factor, , which is a scale change of the FOV of the camera resulting from the use of the magnification function on the microscope and/or physical movements of the microscope’s head. The magnification function on the microscope can change the zoom or focal length of the microscope’s optics, as shown in Equation 2. In the projective geometry case for the pinhole camera model, this magnification factor, , gets multiplied with the camera “focal lengths” or image axes scale factors, (fx, fy), and the location of image-center in pixel coordinates, (cx, cy), for each camera of the stereo-pair. It should be noted that knowing the exact reason for the change in the microscope’s optics – the focal length or zoom changes of the optics – is not needed to compute the scaling of the intrinsic camera parameters (fx, fy, cx, cy), which characterize the size of the camera’s FOV. The radial and tangential distortions of the camera lenses, and the extrinsic parameters of the stereo-pair remain constant when the cameras are zoomed in and out of the FOV. Our goal in this paper is to use the temporally dense videos acquired by the stereovision system to automatically estimate the magnification factor from time ti to tj, which is denoted by We assume that for , the magnification factor during the initial calibration stage. This estimation of the magnification factor, , will enable the reliable 3D digitization of points using the stereovision system of the operating microscope under different magnifications and movements.
2.3.2 Algorithm
The method for computing the magnification factor of the operating microscope, , is comprised of the following parts: (1) feature detection, (2) matching and homography computation, (3) estimation of magnification factor, and (4) analysis of divergence. Steps (1) and points-based tracking in endoscopic surgery videos has been a challenging problem in minimally invasive surgery (MIS) technology. Recent works tackling this problem for lengthy video sequences have been presented by Yip et al. (2012), where a combination of feature detectors are used to persistently track the organ surface in animal surgery and human nephrectomy endoscopic videos. These tracked points are then used with the stereovision methodology to find 3D depth. In Giannarou et al. (2013), anisotropic regions are tracked using Extended Kalman Filters and tested on in vivo robotic-assisted MIS procedures. Puerto et al. (2012) compared several feature matching algorithms over a large annotated surgical data set of 100 MIS image-pairs. In this paper, we perform salient feature point matching between two consecutive image frames of the video to compute the magnification factor. This means that the set of homologous salient feature points detected between any two pairs of consecutive image frames can be different. In this paper, we do not aim to track feature points for the course of the neurosurgery video and we leave that for future work.
2.3.2.1 Feature Detection
We take a content-based approach for computing the magnification factor of the microscope. This requires the detection of features in the FOV of the operating microscope, which is captured by the cameras. The image location, in pixels, of these distinct features is called a keypoint. The FOV under the microscope is subject to scale changes from the magnification function and possible rotational changes from the physical movements of the microscope’s head. To detect keypoints subject to these realistic conditions of neurosurgery, we opt for a robust scale- and rotational-invariant feature detector. Feature detection is a well-Transform or SIFT by Lowe (2004) and Speeded Up Robust Features or SURF by Bay et al. (2006) are two popular scale-invariant and rotation-invariant detectors. We use the SURF detector because of its fast computation time (Bay et al., 2006) to detect keypoints in the stereo-pair video streams. This feature detector yields a 128-float feature descriptor per keypoint in the image. Let φi be the set of keypoints detected at magnification, , at time ti and φj be the set of keypoints detected at magnification, , at time t, where ti < tj and are within a temporal range of approximately 1 second. Typically, 1200-1800 SURF keypoints are detected per image frame for clinical cases.
2.3.2.2 Matching and Homography
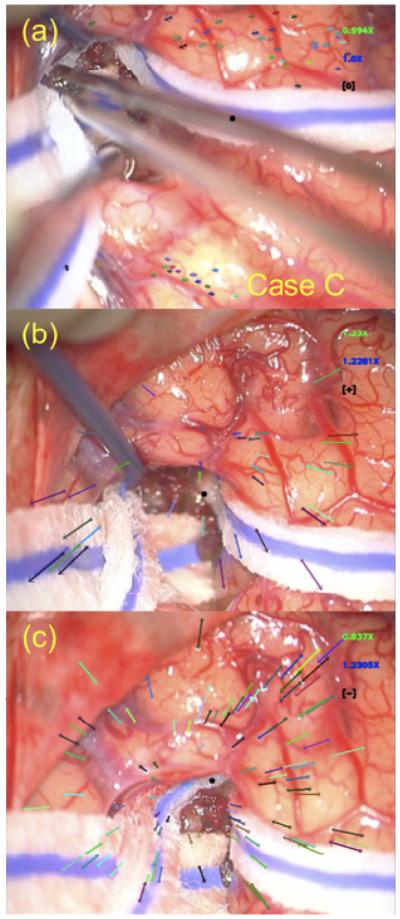
Once the φi and φj sets of SURF keypoints are computed, a matching stage will establish homologous points. The putative matching between the sets of keypoints of φi to those of φj are determined using an approximate nearest neighbor approach on the 128-float SURF feature descriptors of the keypoints. The computationally fast implementation of k-d trees from the FLANN library is used for establishing these putative matches (Muja & Lowe, 2009). Figure 5(a) shows the computed nearest neighbor matches between the keypoints on brain tumor surgery cases performed at VUMC using the Pentero operating microscope. The nearest neighbor approach estimates the correspondences between φi and φj with several mismatches or outliers.
Figure 5.
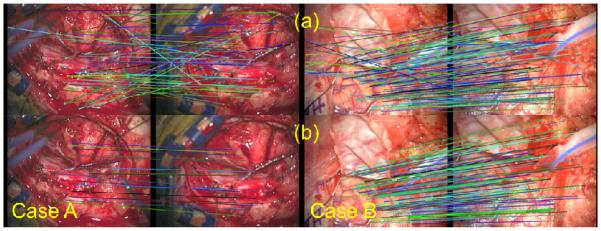
The left and right columns are of different brain tumor surgery cases. Row (a) of both cases shows the results of the nearest-neighbor matching between SURF keypoints between ti and tj time points. Row (b) shows the results of the homography procedure for cleaning up mismatches to find the homologous points between ti and tj. Note that the matching and homography procedures are robust to movements of the microscope as shown by the clinical case in the right column.
Estimating a homography or affine transformation between a pair of images taken from different viewpoints is a standard technique for finding homologous points in panoramic stitching (Hartley & Zisserman, 2004; Bradski & Kaehler, 2008; Szeliski, 2011). The these keypoints will be collinear in the other image as well. In Yip et al. (2012), a homography estimation was used to determine homologous keypoints, reject mismatches, and drive the registration stage for endoscopic surgical videos. We take a similar approach for finding homologous keypoints in brain tumor surgery video.
In this paper, images acquired at ti and tj form the different viewpoints for the purpose of eliminating mismatches between correspondences. The soft-tissue deformation from ti and tj is small in magnitude and local when compared to global rigid changes caused by the use of the microscope’s magnification or physical movements of the microscope. Video 1 demonstrates this notion for clinical brain tumor surgery cases #3-4 performed at Vanderbilt University Medical Center. In Video 1, one can see that when the magnification is changed on the operating microscope, the feature keypoints in the field of view expand or contract everywhere or globally. Such a global change makes the divergence field, computed between the homologous keypoints at ti and tj, to show an expansion or contraction. The computation of the divergence field is described later in Section 2.3.2.4.
From our experimental results and previously acquired tLRS point clouds, we observe that the frame-to-frame (1 second apart) soft-tissue deformation in neurosurgery is smoothly varying and small in magnitude. Computing a homography between times ti and tj is thus a reasonable assumption for finding homologous points. However, in MIS applications this may not be the case (Puerto et al., 2012). Homography estimation finds the homologous points that are at the intersection of the organ surface and of its tangent plane. In brain tumor surgery, the tangent plane will roughly capture the brain surface and bone areas, but may not capture the tumor resection. Computing a homography enables the localization of keypoints on the brain surface and bone areas and not in the highly dynamic areas of tumor resection. Indeed, using highly dynamic areas of the FOV to estimate a global change such as movements and magnification will lead to erroneous estimations of magnification factors.
In Equation 6, the homography matrix, H, relates the keypoint pi on an image plane to the keypoint qj on another image plane, where keypoints pi ∊ φi and qj ∊ <pj. The putative correspondences from the nearest neighbor matching stage and the estimated homography matrix between them help eliminate spurious matches. We use RANSAC to estimate H that maximizes the number of inliers of all the putative correspondences between keypoints in φi and φj, subject to the reprojection error threshold of Equation 7, εH. The RANSAC-estimated homography matrix, , is further refined from all the correspondences classified as inliers using the Levenberg-Marquardt algorithm (Hartley & Zisserman, 2004; Bradski & Kaehler, 2008). The resulting inliers are the sets of homologous keypoint matches, and , and an example is shown in Figure 5(b). Typically, 300-1000 homologous points can be determined between ti and tj on clinical cases.
| (6) |
| (7) |
2.3.2.3 Estimation of Magnification Factor ()
The set of keypoints, , detected at the microscope magnification , is visible as , detected at the microscope magnification . Using the relation in Equation 4, the estimation of the magnification factor, , is achieved by the notion of spatial coherence between and . Spatial coherence ensures that two adjacent keypoints in remain adjacent in . This idea is shown in Figure 5(b), where adjacent keypoints on the left image remain adjacent on the right image. When the magnification function is used on the operating microscope or if the microscope’s head is physically moved, pairwise distances between any two keypoints in and are scaled by a factor of . Let and be the pairwise Euclidean distances for all the keypoints in and respectively. Then, the magnification factor can be written as Equation 8 and computed by the linear least squares method. With for , the magnification factor of the microscope at any time point, tk, can be computed as using Equation 5.
| (8) |
2.3.2.4 Analysis of Divergence
When the microscope is in use during neurosurgery, the content-based approach for estimating the unknown magnification factor at any time point may be prone to small drift in values. This drift in values can be attributed to the manipulation and the non-rigid motion of the soft-tissue, which are captured in the videos as motions of small magnitudes. This dynamic content of the FOV causes the resulting to hover around 1.000 when the magnification function of the operating microscope has not been used or if the microscope’s head has not been moved. To account for this magnification factor drift, the divergence of the vector field generated by the homologous keypoints in and is used. Specifically, the vectors are computed between the pixel locations of the homologous points in and . When the magnification function of the microscope is used or if the microscope’s head is physically moved, the global scaling change in the FOV will produce a large divergence value, whereas soft-tissue deformation produces a small divergence value. A user-defined threshold, ε∇, for the divergence determines if the magnification factor should be accepted versus rejected for digitizing the FOV as a point cloud. If the FOV has been zoomed-in, the divergence should be positive and the vector field between the homologous points will be characterized by an expansion. The divergence is negative and the vector field shows compression if the FOV has been zoomed-out. This is illustrated in Figure 6. Experimentally, we have determined that the absolute value of divergence tends to be around 0.1-0.3 when the microscope’s magnification has been used or if the microscope has been physically moved, otherwise the value is below 0.02. A ε∇ value of 0.02 works well for the 4 full-length clinical cases (~ 1 hour) we have presented in this paper.
Figure 6.
The divergence sign is indicated in the top-right corner in black, the is indicated in green and is indicated in blue. The divergence is computed at the centroid of all keypoints, indicated by the filled black circle. The divergence in (a) is small and the computed magnification factor, , can be rejected. In (b) and (c) the divergence has large magnitude and the sign of divergence indicates whether the microscope’s zoom-in or the zoom-out function was used. Based on the magnitude of the divergence, the current magnification factor, , is accepted for reliably changing the overall magnification factor, .
2.3.2.5 Microscope-based 3D Point Clouds
The estimated magnification factor, , is used for finding using Equation 5, which scales the left and right camera intrinsic matrices and the reprojection matrix, Q, described in Section 2.2. The BM stereo reconstruction method computes the disparity map of the stereo-pair images acquired at tj. Using the scaled reprojection matrix, Qj, the disparity map produces a point cloud of the microscope’s FOV via Equation 1b.
3. Results
3.1 Magnification Factor Evaluation
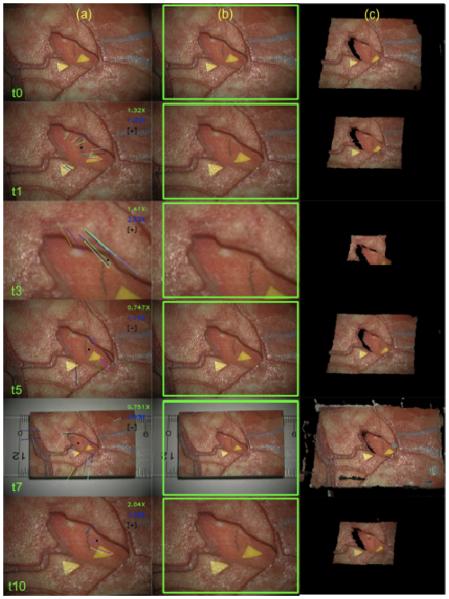
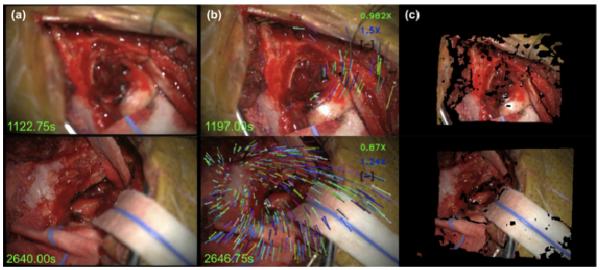
In this section, we present the estimation of the magnification factors using the presented algorithm and compare it to the theoretical magnification factor. The magnification factor used on the phantom object and the VUMC clinical cases is computed using the Pentero microscope’s left camera video stream. The Pentero microscope displays the primary objective’s focal length, fo, and the Galilean magnification, γ, and the theoretical values of and can be computed from Equations 4-5. Table 1 compares the theoretical values of magnification factors against our algorithm’s estimations, and , for two datasets of the cortical surface phantom. With tube focal length fT=170mm and eyepiece magnification VE=10, the theoretical total microscope magnification VM (see Equation 2) can be computed for every time point reported in Table 1 as well. Examples of magnification factors of Dataset 1 are shown in Figure 7. Figure 7(c) shows the point clouds of Dataset 1 at various magnifications of the Pentero microscope. The BM method with a block-size of nBM=21 was used for reconstructing the point clouds and is used for quantitative error analysis in Section 3.3 of this paper.
Table 1.
Comparison of theoretical and estimated magnification factors. Each row is a successive time point, in 2.25s increments. The start of video acquisition is indicated by t=0.
|
Theoretical
|
Algorithm
|
|||||
|---|---|---|---|---|---|---|
| t | ||||||
| Dataset 1 | ||||||
|
| ||||||
| 0 | - | 1.00 | 1.00 | - | - | |
| 1 | 1.30 | 1.30 | 1.32 | 1.32 | 0.02 | 0.02 |
| 2 | 1.35 | 1.76 | 1.35 | 1.79 | 0.00 | 0.03 |
| 3 | 1.42 | 2.49 | 1.41 | 2.52 | 0.01 | 0.03 |
| 4 | 0.609 | 1.51 | 0.610 | 1.54 | 0.01 | 0.03 |
| 5 | 0.768 | 1.16 | 0.747 | 1.15 | 0.021 | 0.01 |
| 6 | 0.720 | 0.838 | 0.731 | 0.839 | 0.011 | 0.001 |
| 7 | 0.742 | 0.622 | 0.751 | 0.630 | 0.009 | 0.008 |
| 8 | 1.52 | 0.946 | 1.52 | 0.956 | 0.00 | 0.01 |
| 9 | 0.829 | 0.784 | 0.818 | 0.782 | 0.011 | 0.002 |
| 10 | 2.03 | 1.59 | 2.04 | 1.59 | 0.01 | 0.00 |
| 11 | 0.695 | 1.11 | 0.688 | 1.10 | 0.007 | 0.01 |
|
| ||||||
| Dataset 2 | ||||||
|
| ||||||
| 0 | - | 1.00 | - | 1.00 | - | |
| 1 | 0.580 | 0.580 | 0.598 | 0.598 | 0.018 | 0.018 |
| 2 | 0.393 | 0.228 | 0.425 | 0.254 | 0.032 | 0.026 |
| 3 | 4.39 | 1.00 | 3.95 | 1.00 | 0.44 | 0.00 |
|
| ||||||
| Root Mean Square Error | 0.118 | 0.018 | ||||
Figure 7.
The cortical surface phantom is used for estimating different magnification settings at various time points is shown in (a). The FOV of the left camera for these time points is shown in (b). The point clouds computed using the estimated magnification factor and the BM method is shown in (c). Note the point clouds of the phantom object are sized correctly and reflect the physical dimensions of the phantom object.
For the results shown in Table 1, a minimum of 5 homologous points were required for computing the homography, εH = 10.0, ε∇ = 0.02, and each time point is 2.25s apart. The root mean square error is computed between all the estimated and theoretical values of the magnification factor for both datasets. Our algorithm is able to estimate the magnification factor for successive time points, ti and tj, within 0.12 of the theoretical value. Furthermore, the algorithm is able to estimate the current magnification factor of the microscope from the initial start time point of the video acquisition, t0, within 0.02 of the theoretical value.
3.2 Phantom Object Data Evaluation
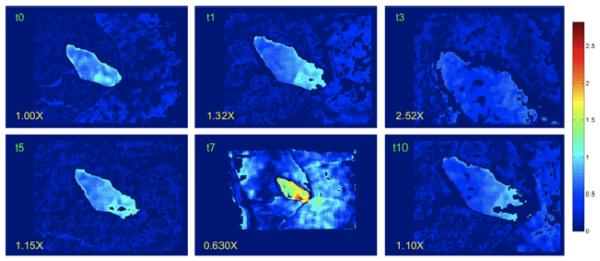
The computed stereovision point clouds at different magnifications are compared to the ground truth relative depths of the cortical surface phantom object. The known relative depths, z, of the phantom object are annotated for each pixel (x, y) in the reference left camera image, which is used in stereo reconstruction. The stereovision point cloud intrinsically keeps the mapping from a pixel to its 3D point. Arithmetic mean and root mean square error (RMS) is computed between all the points in the point cloud to its respective ground truth z values. From Kumar et al. (2013), the tLRS’ RMS error on the cortical surface phantom was determined to be 0.69mm and the mean error was 0.227 ± 0.308mm. Table 2 shows the arithmetic mean and RMS errors for all the magnification settings for Dataset 1. We are able to achieve accuracy in the 0.28-0.81mm range using our stereovision system and the presented automatic algorithm for estimation of the magnification factor of the microscope. The mean error for this dataset is 0.289 ± 0.283mm. The accuracy of our proposed stereovision system is on par with the accuracy of the tLRS. Absolute-deviation-based error maps of the cortical surface phantom object are computed for the point clouds of Dataset 1 at various magnifications. These are presented in Figure 8. These error maps help contrast the microscope’s stereovision system’s ability to digitize 3D points in its FOV at different magnification settings.
Table 2.
Arithmetic mean and RMS errors for point clouds of Dataset 1 obtained at different magnification settings of the microscope.
| t | Mean (mm) | RMS (mm) | |
|---|---|---|---|
| 0 | 1.00 | 0.203 ± 0.265 | 0.354 |
| 1 | 1.32 | 0.288 ± 0.274 | 0.364 |
| 2 | 1.79 | 0.288 ± 0.272 | 0.359 |
| 3 | 2.52 | 0.282 ± 0.173 | 0.276 |
| 4 | 1.54 | 0.270 ± 0.276 | 0.406 |
| 5 | 1.15 | 0.229 ± 0.295 | 0.358 |
| 6 | 0.839 | 0.290 ± 0.303 | 0.480 |
| 7 | 0.630 | 0.600 ± 0.418 | 0.810 |
| 8 | 0.956 | 0.231 ± 0.267 | 0.416 |
| 9 | 0.782 | 0.295 ± 0.312 | 0.486 |
| 10 | 1.59 | 0.265 ± 0.234 | 0.320 |
| 11 | 1.10 | 0.226 ± 0.308 | 0.357 |
|
| |||
| Average | 0.289 ± 0.283 | 0.415 | |
Figure 8.
Absolute deviation error maps for the cortical surface phantom at various time points acquired at different magnification settings of the microscope is shown. The limitations of the stereovision system and the BM method can be especially seen at time point t=7.
It is apparent from Figure 7(c) and Figure 8 that time point t=7’s point cloud has artifacts. These artifacts occur at abrupt transitions or boundaries as the window for BM catches the abrupt transition leading to the artifact. Boundaries of objects in the left camera may be occluded in the right camera and this causes the BM stereo reconstruction to be inaccurate around boundaries. Other stereo reconstruction algorithms, which are typically non-real-time, have addressed these artifacts (Scharstein & Szeliski, 2002). This issue is not a critical limitation for neurosurgical applications because the organ surfaces are relatively smooth when compared to the abrupt edges in and around the cortical surface phantom object for example. Additionally, the stereovision system lacks accuracy in estimating surfaces that are far away from the cameras’ image planes. This is attributed to the nonlinear relationship between disparity and depth mapping (Trucco & Verri, 1998). The precision of determining the disparity of surfaces that is farther away from the cameras is lower because a small number of pixels capture this distant surface. The size of a typical craniotomy for brain tumor surgery is the size of the cortical phantom object, 4.78cm x 3.36cm, and this is reflected in the microscope’s FOV, shown as t=0 in Figure 7-8. This is the FOV used during stereo-pair camera calibration and is the working distance of the stereovision system. Zooming out of the surgical field to the extent of t=7 will seldom occur as that particular magnification scale of the operating microscope is not practical for performing neurosurgery effectively.
3.3 Clinical Data Evaluation
In this section we evaluate our presented algorithm for computing magnifications of the microscope being used in clinical cases and we also compare the computed stereovision point clouds with the acquired tLRS point clouds of the pre- and post-resection cortical surfaces of 4 brain tumor surgery cases performed at VUMC. The correct magnification factor is needed to size the stereovision point cloud for evaluation against the tLRS, especially, for the post-resection evaluation. As a result, the magnification factors are computed for the entire duration of the 4 clinical cases.
Table 3 shows computed magnification errors from our fully automatic algorithm and the theoretical magnification values for the magnifications used during these clinical cases. The ti and tj columns in Table 3 show the discrete time points when the magnification factor has been changed. To keep Table 3 succinct, we present the magnification factors used for the full-length of clinical cases 1-2 and partially for clinical cases 3-4. As mentioned earlier, the stereo-pair consequently, the time points in ti and tj columns of Table 3 are not 1 second apart for clinical case #1. For this error analysis study, the neurosurgeon changed the magnification of the Pentero microscope and moved the microscope head towards/away from the FOV several times in a short time interval for clinical cases 3-4 and we present these results in Table 3. The autofocus function of the operating microscope was enabled during this short time interval for clinical cases 3-4, which changed the theoretical magnification values of the optical system automatically during physical movements of the microscope’s head. This allowed for the correct manual noting of theoretical magnification values regardless of whether the magnification function was used or if the microscope’s head was moved physically. It should be clarified that the autofocus function on the Pentero microscope may not be enabled to perform the brain tumor resection surgery as per the preference of the neurosurgeon. Furthermore, the neurosurgeon may take more than 2-6 seconds to use the magnification function of the microscope but only one theoretical magnification value was manually noted down. The ti and tj columns in Table 3 reflect this scenario, especially, for clinical cases 2-4.
Table 3.
Comparison of theoretical magnification and estimated magnification factors for 4 clinical cases. The value of ti,j=0 indicates the start of video acquisition. The units for ti,j is seconds. (εH = 10.0, ε∇ = 0.02)
| Theoretical |
Algorithm |
||||||
|---|---|---|---|---|---|---|---|
| ti | tj | ||||||
| Full-length Clinical Case 1 | |||||||
|
| |||||||
| 0 | 0 | - | 1.00 | - | 1.00 | - | - |
| 4.50 | 6.75 | 1.28 | 1.28 | 1.28 | 1.28 | 0.00 | 0.00 |
| 290.25 | 412.25 | 1.19 | 1.52 | 1.21 | 1.55 | 0.02 | 0.03 |
| 1122.75 | 1197.00 | 0.933 | 1.42 | 0.980 | 1.50 | 0.047 | 0.08 |
| 2002.00 | 2139.00 | 1.07 | 1.52 | 1.02 | 1.51 | 0.05 | 0.01 |
| 2633.25 | 2637.75 | 0.954 | 1.45 | 0.911 | 1.40 | 0.043 | 0.05 |
| 2640.00 | 2646.75 | 0.925 | 1.34 | 0.870 | 1.24 | 0.055 | 0.10 |
| 2646.75 | 2655.75 | 1.33 | 1.78 | 1.35 | 1.68 | 0.02 | 0.10 |
|
| |||||||
| Full-length Clinical Case 2 | |||||||
|
| |||||||
| 0 | 0 | - | 1.00 | - | 1.00 | - | - |
| 893.90 | 894.92 | 0.988 | 0.988 | 1.02 | 1.02 | 0.027 | 0.027 |
| 928.47 | 929.49 | 1.24 | 1.23 | 1.24 | 1.18 | 0.0004 | 0.046 |
| 935.59 | 936.61 | 1.12 | 1.38 | 1.11 | 1.32 | 0.008 | 0.061 |
| 2862.71 | 2863.73 | 1.13 | 1.55 | 1.19 | 1.52 | 0.069 | 0.024 |
| 2881.02 | 2882.03 | 1.02 | 1.58 | 1.05 | 1.60 | 0.028 | 0.018 |
| 3702.71 | 3703.73 | 1.15 | 1.82 | 1.11 | 1.78 | 0.04 | 0.037 |
| 3703.73 | 3704.75 | 1.39 | 2.53 | 1.32 | 2.35 | 0.07 | 0.184 |
| 3722.03 | 3724.07 | 0.630 | 1.60 | 0.633 | 1.49 | 0.003 | 0.108 |
| 3735.25 | 3737.29 | 0.856 | 1.37 | 0.871 | 1.30 | 0.015 | 0.070 |
| 3751.53 | 3753.56 | 1.65 | 2.25 | 1.69 | 2.19 | 0.04 | 0.067 |
| 3769.83 | 3771.86 | 0.800 | 1.80 | 0.798 | 1.75 | 0.002 | 0.057 |
|
| |||||||
| Clinical Case 3 | |||||||
|
| |||||||
| 0 | 0 | - | 1.00 | - | 1.00 | - | - |
| 6809.49 | 6810.51 | 0.613 | 0.613 | 0.580 | 0.580 | 0.033 | 0.033 |
| 6856.27 | 6859.32 | 1.72 | 1.06 | 1.74 | 1.01 | 0.02 | 0.05 |
| 6865.42 | 6866.44 | 1.23 | 1.29 | 1.17 | 1.18 | 0.06 | 0.11 |
| 6871.53 | 6873.56 | 0.711 | 0.920 | 0.718 | 0.850 | 0.007 | 0.07 |
| 6878.64 | 6879.66 | 0.722 | 0.664 | 0.710 | 0.603 | 0.012 | 0.061 |
|
| |||||||
| Clinical Case 4 | |||||||
|
| |||||||
| 0 | 0 | - | 1.00 | - | 1.00 | - | - |
| 3917.97 | 3923.39 | 0.903 | 0.903 | 0.912 | 0.912 | 0.008 | 0.008 |
| 3923.39 | 3924.75 | 0.612 | 0.553 | 0.631 | 0.575 | 0.019 | 0.022 |
| 3936.27 | 3939.66 | 1.50 | 0.829 | 1.43 | 0.826 | 0.065 | 0.003 |
| 3950.51 | 3951.19 | 1.12 | 0.926 | 1.12 | 0.921 | 0.001 | 0.005 |
| 3960.00 | 3968.14 | 1.29 | 1.20 | 1.30 | 1.19 | 0.002 | 0.005 |
| 3979.66 | 3982.37 | 1.23 | 1.48 | 1.17 | 1.40 | 0.055 | 0.072 |
| 3990.51 | 3992.54 | 0.465 | 0.687 | 0.462 | 0.648 | 0.003 | 0.038 |
| 4007.46 | 4008.81 | 1.35 | 0.927 | 1.32 | 0.853 | 0.033 | 0.073 |
|
| |||||||
| Root Mean Square Error | 0.044 | 0.062 | |||||
Experimentally, we determined that a minimum of 10 homologous points computed the magnification factors consistently for the full-length clinical cases. Figure 9 shows the stereovision point clouds for a clinical case at a few magnification settings. For time points where the magnification of the microscope has changed, our algorithm is able to estimate the magnification factor of successive time points, ti and tj, within 0.044 of the theoretical value in 4 clinical brain tumor surgery cases. Furthermore, our algorithm is able to estimate the current or running magnification factor of the microscope for these clinical cases from the initial start time point of the video acquisition, t0, within 0.062 of the theoretical value.
Figure 9.
(a) Rectified left camera at time ti, and (b) time tj, is used for estimating the magnification factor of the microscope, which yields the correct size of the point cloud, shown in (c). This data is from clinical case #1.
Video 2 shows point clouds acquired by the operating microscope at different magnifications for clinical case #4. On the left side of the Video 2 is the "view selector" of the field of view (FOV) acquired at a different magnification. The point clouds for each view are shown on the right. Video 2 first shows the point clouds for each of the 3 views. Then, Video 2 shows the point clouds between the views 1-2 and views 2-3. Based on the presented magnification factor estimation algorithm, the point clouds have been sized correctly and reflect the physical dimensions of the brain surface. It should be clarified that the point clouds are not registered to each other because the operating microscope is not optically tracked.
To compare the stereovision point clouds obtained from our presented method to the gold standard tLRS, the tLRS and stereovision point clouds were obtained as close in time as possible without disrupting the surgical workflow. This also minimized the effect of any occurring brain shift. The acquisition perspective of the tLRS and stereovision systems are different and thus, different parts of the craniotomy are viewable from both modalities. As a result, the tLRS point clouds were manually cropped to contain the cortical surface area that is common to the FOV of the stereovision system. These tLRS point clouds and the stereovision point clouds for each brain tumor surgery case were manually aligned. We expect minimal alignment error if the operating microscope were optically tracked.
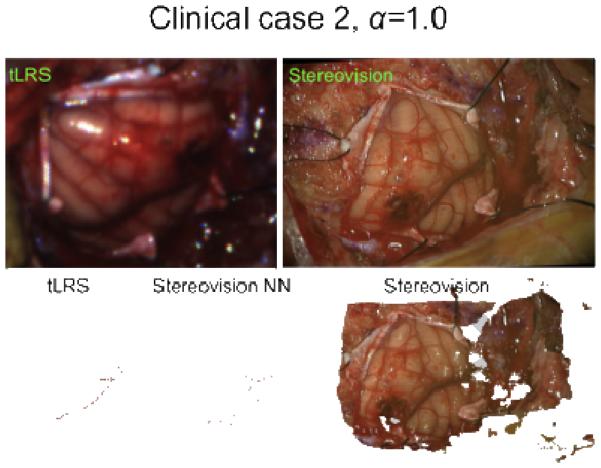
The stereovision point cloud is much denser than the tLRS’ point cloud because of different acquisition distances. For each 3D point in the tLRS, a point in the stereovision point cloud is determined using nearest-neighbors, and these stereovision-tLRS nearest-neighbor points are used for evaluation. An example is shown in Figure 10 for a clinical case. The RMS errors computed between the tLRS point clouds and the nearest-neighbor stereovision-tLRS point clouds for the clinical cases are presented in Table 4. Figure 11 shows the tLRS point clouds and the stereovision point clouds acquired at different magnifications (pre- and post-resection) for a clinical case performed at VUMC. It should be clarified that the magnification factor is computed continuously throughout the duration of the surgery for the stereovision point cloud to have the correct size (length, width, and depth) for post-resection analysis. Using our intraoperative microscope-based stereovision system, we achieve accuracy in the 0.535-1.35mm range. This accuracy is comparable to the tLRS used in digitizing the cortical surface, which as an intraoperative digitization modality has an accuracy of 0.47mm (Pheiffer et al., 2012). It should be noted the accuracy values presented in Table 4 is essentially a surface-to-surface measure between the tLRS and stereovision point clouds. If the operating microscope were optically tracked, then a point-based measure between the tLRS and the stereovision point clouds could be performed. We aim to perform such a study once the optical tracking for the Pentero microscope has been developed. This could possibly lead to lower RMS errors computed between the tLRS point clouds and the nearest-neighbor stereovision-tLRS point clouds for the clinical cases. The manual alignment makes the errors presented in Table 4 an upper bound for digitization error of the presented method. In Table 4, the post-resection tLRS point cloud for clinical case #3 was unavailable due to tLRS data acquisition issues.
Figure 10.
Pre-resection clinical case #2 is shown. The nearest-neighbor (NN) stereovision point cloud to the tLRS point cloud is shown. This is used for error evaluation. The original stereovision point cloud is shown as well.
Table 4.
RMS errors (surface-to-surface distance) computed between tLRS and the nearest-neighbor stereovision-tLRS point clouds at different magnifications for 4 clinical cases performed at VUMC. RMS values are in millimeters
| Clinical Case | Surgery Stage | RMS (mm) | Timestamp (minutes) | |
|---|---|---|---|---|
| 1 | Pre-resection | 0.887 | 1.28 | 0.077 |
| 1 | Post-resection | 1.35 | 1.67 | 99.65 |
| 2 | Pre-resection | 0.536 | 1.0 | 0.034 |
| 2 | Post-resection | 1.12 | 1.73 | 77.03 |
| 3 | Pre-resection | 1.06 | 1.0 | 0.017 |
| 4 | Pre-resection | 0.945 | 1.0 | 0.147 |
| 4 | Post-resection | 0.850 | 0.578 | 78.09 |
|
| ||||
| RMS Range | 0.536 − 1.35mm | |||
Figure 11.
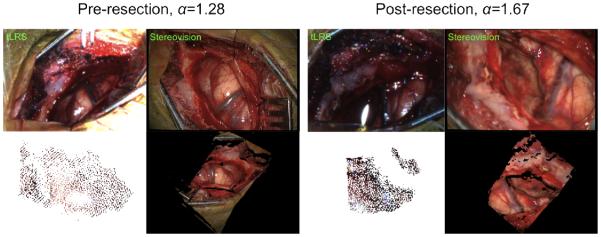
Clinical case #1 tLRS point clouds taken at different time points (pre-resection (, post-resection ) and from our stereovision system is shown. The tLRS’ point cloud is acquired at a specific working distance and at a different angle from the operating microscope, this is apparent in the tLRS bitmap. The tLRS point cloud has been made larger for visualization purposes. The stereovision point clouds and the tLRS point clouds were manually aligned for the error analysis shown in Table 4. Note, the presented algorithm for magnification factor estimation runs for the duration of the surgery to size the post-resection point cloud correctly.
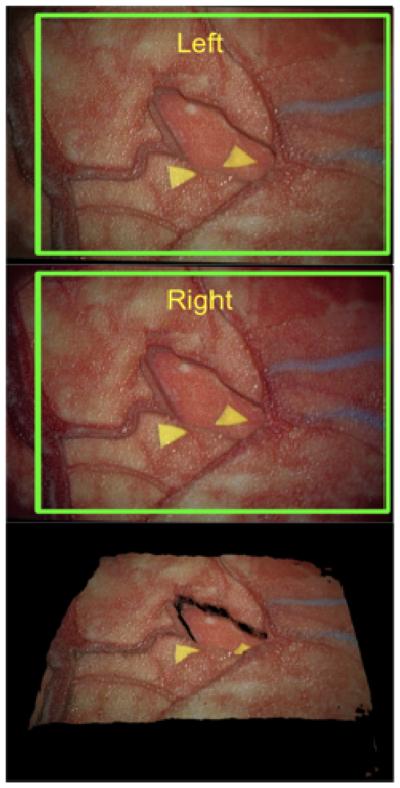
Our presented algorithm is also robust to physical movements of the microscope, which usually occurs when the neurosurgeon and their resident are performing the brain surgery together. Figure 11 is of clinical case #1 performed at VUMC and shows that the correspondences extracted for computing the magnification of the microscope automatically is tracked well through the rotation of the microscope from the neurosurgeon to the resident. Video 3 shows the robust tracking of homologous points and estimation of magnification factors under realistic movements of the microscope for clinical case #2 performed at VUMC. Both Figure 11 and Video 3 show realistic and typical movements of the microscope during neurosurgery.
From Figures 9-11, it is clear that the stereovision point clouds have missing points or holes. This limitation is attributed to outliers or undetermined disparities in the disparity map computed from the stereo reconstruction stage. It is well recognized in computer vision literature that disparities between left and right cameras’ images cannot be computed for scenes that are out of focus or without texture (Bradski & Kaehler, 2008). In surgery, the areas with no texture typically consist of bloody regions, drapes, surgical instruments, and out of focus regions. Determining disparities for texture-less regions of the FOV and filling the missing points in the point cloud is beyond the scope of this article, and several robust techniques for doing so are discussed in Scharstein & Szeliski (2002). Recently, Hu et al. (2012) proposed an interesting method, based on evolutionary agents, for reconstructing organ surface data robustly in endoscopic stereo video subject to missing disparities and outliers in the disparity map. Maier-Hein et al. (2013, 2014) also presented a review of 3D surface reconstruction methods for laparoscopic surgeries, where stereo-pair cameras are used. For the purpose of model-updated surgical guidance, having holes in the point cloud is not a critical limitation. This is because the model-update framework relies on deformation measurements of the organ surface based on established correspondences for registration. Registration methods such as thin plate splines (Goshtasby, 1988) provide smooth deformation fields, which have been used as input into model-update framework (Ding et al., 2009, 2011).
3.4 Perturbation of keypoints
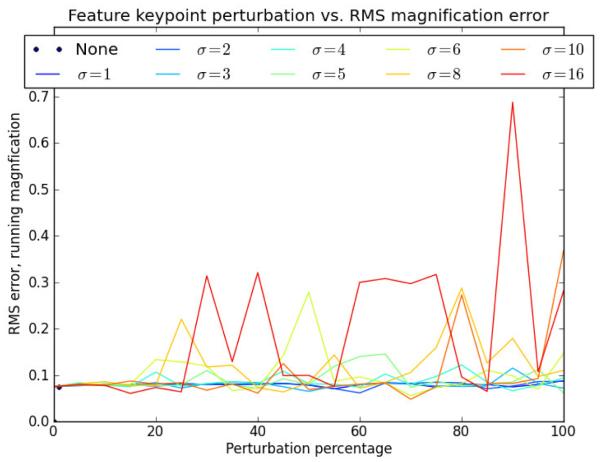
At its core, the presented algorithm is dependent on the matching and homography estimation of SURF keypoint pixel locations. We perturb the keypoints at ti and tj on a portion of clinical case #2 to test the robustness of our magnification factor estimation algorithm. The duration of the portion of clinical case #2 used in this section is approximately 77 seconds. This portion of clinical case #2 is where we asked the neurosurgeon to change the magnification of the autofocus-enabled microscope and physically move the microscope’s head towards/away from the FOV repeatedly at several time points and manually noted down the theoretical magnification values. We perturb a percentage of the detected keypoint locations at ti and tj, in increments of 5 from 5% to 100%, by Gaussian noise of standard deviation, σ. In essence, we are adding pixel-level localization error, of σ magnitude, to a percentage of detected SURF keypoints. The standard deviations of Gaussian noise have been increased from 1 pixel to 16 pixels. Then, we execute our algorithm to estimate the running magnification factor, , on the portion of clinical case #2. We compute Δ (shown in Table 3) and report the RMS error per percentage of perturbation per σ. Depending on the value of σ, approximately 1200 keypoints were detected and around 20-500 homologous keypoints were determined from the matching stage of this paper. Figure 13 shows the plots of the RMS error as a function of percentages of perturbed keypoint pixel locations with a specified σ. The graph in Figure 13 shows that as slowly. Without any perturbation of the SURF keypoints, the RMS error for the portion of the clinical case #2 is 0.07. The RMS error is the highest, 0.7, for the severe keypoint localization noise of σ = 16 pixels, which is not expected of a typical brain tumor surgery video sequence. From Figure 13, our presented method for estimating the magnification factor gives a reasonable RMS error when 40% of SURF keypoints can be localized within an error of 6-8 pixels. Our algorithm also performs with a low RMS error in magnification factor estimation when 20% of SURF keypoints can be localized with an error of 1-16 pixels. This indicates that the proposed algorithm can robustly estimate the magnification factor to correctly size the point clouds obtained from the microscope. The presented algorithm’s robustness to perturbations of keypoints can be attributed to the robust RANSAC step of finding homologous points by estimating a homography. The RANSAC-based homography estimation method is able to mark some of the perturbed keypoints as outliers and then magnification factor is estimated using the determined homologous points. As the perturbations become greater, less homologous points are found by the RANSAC-estimated homography leading to poorer estimation of magnification factor.
Figure 13.
Plots showing the RMS running magnification errors when a percentage of SURF keypoint pixel locations are perturbed by Gaussian noise of different standard deviations, σ. The RMS error value with no perturbation (0%), indicated by the black dot, is 0.07. As the noise increases, the RMS error increases slowly as well.
3.6 Digitization Time
For the developed microscope-based digitization system to be a viable intraoperative data source, the execution time for all involved steps needs to be considered. Table 5 lists the execution time for all the steps of the stereovision framework, and the presented algorithm for the automatic estimation of the microscope’s magnification factor for a Windows 7 Dell Precision Desktop T1500 with Intel Core i7 2.80GHz Processor and 12GB RAM. The listed execution times can be made faster through code optimizations and by using GPUs. The initial stereo calibration stage is performed once prior to the start of the surgery, while the rest of the steps for obtaining point clouds from the operating microscope’s FOV subject to unknown magnification changes takes 0.9 seconds per stereo-pair image frame. This translates to processing the microscope’s stereo-pair video streams at approximately 1 Hz for active near real-time 3D digitization. Moreover, this quick 3D digitization does not require any manual action and is actively performed while the neurosurgery is in progress. In addition, it is also important to realize that the current use of image-guidance within the surgical theatre involves periodic intraoperative data acquisition of the surgical field at distinct time points, for example, intraoperative data may be obtained 4-5 times over the course of a 3-4 hour surgery. Table 5 suggests the possibility of a near real-time minimally cumbersome solution for providing relatively continuous intraoperative data of the surgical field compared to the very sparse data acquisitions that occur routinely today.
Table 5.
Average runtimes for all the tasks involved in the presented operating microscope-based digitization of 3D points. The tasks are executed per stereo image pair unless otherwise noted.
| Task | Average Time |
|---|---|
| Acquisition of stereo video | 0.03s, 29.5 fps |
| Initial stereo calibration (done once) | 30s |
| Stereo rectification | 0.06s |
| BM stereo reconstruction | 0.3s |
| SURF keypoints | 0.2s |
| Matching & Homography | 0.2s |
| Estimation of & Divergence | 0.1s |
|
| |
| Total Digitization Time | 0.9s |
4. Discussion
The presented algorithm for automatically estimating the magnification factor of the operating microscope is built on a content-based approach. This approach relies on the temporal persistence of features in the FOV of the microscope, which is a reasonable assumption in neurosurgery. The organ surface is very rich in features for determining SURF keypoints and stereo video acquisition can seamlessly provide the temporal persistence needed to estimate the unknown magnification settings and movements of the microscope. Digitizing points on distant regions in the FOV of the stereo-pair cameras, beyond its working plane, is a limitation of stereovision theory. The working distance of the stereo-pair cameras is determined by the calibration pattern’s initial poses during the stereo calibration stage. The tLRS is also limited by its working distance for digitization of points and thus, the tLRS cannot digitize regions closer than its working distance. For stereovision systems, closer regions are digitized with better accuracy and fine-grain depth measurements can be estimated (Bradski & Kaehler, 2008). Digitizing distant surfaces, beyond the working plane, is not a critical limitation for the use of the proposed intraoperative microscope-based digitization system. The size of the calibration pattern can be made similar to the size of the surgical site in neurosurgery. This allows for the stereovision’s working plane for the accurate estimation of disparity to be the area of the organ surface. Furthermore, computing the unknown magnification factor of the operating microscope keeps the stereovision’s working plane intact for disparity estimation and 3D digitization.
The limitations of the block matching stereo correspondence algorithm have been previously discussed in this paper and the disparities can be computed robustly using newer techniques such as Maier-Hein et al. (2013). The computation of magnification factors depends on the SURF keypoints being homologous between ti and tj. Drastic changes such as when the neurosurgeon’s gloves are suddenly blocking the entire FOV can hamper the matching process for finding homologous keypoints. For large abrupt movements of the microscope’s head, increasing the sampling rate for finding homologous points from 1 second to analyzing every frame helps find homologous points. This is because movements appear smooth at every frame, but taking every 30th frame (every 1 second) for analysis makes these movements appear abrupt.
It should be noted that if the presented algorithm miscalculates the magnification factor with a large error between ti and tj, then the error does accumulate. This will lead to incorrectly sized stereovision point clouds at the post-resection stage yielding a larger error when compared to the post-resection tLRS. However, from our results in Table 4, the presented algorithm is able to estimate the magnification factor for the entire duration of the brain tumor surgery and the post-resection digitization error between the presented method and the gold standard tLRS is quite reasonable, in the RMS error range of 0.84-1.35mm. To clarify this further, the tLRS and stereovision point clouds were manually aligned for the error computation and the error evaluation can be driven by any misalignment. Table 4 presents the upper bound of digitization error between the presented stereovision system and the tLRS.
Another limitation of the presented method occurs when the FOV remains out of focus for long periods of time because the neurosurgeon has adjusted the surgical microscope’s focal point to view the resection cavity better. Though it does not adversely affect the performance of keypoint matching to a great extent, it does severely affect the block matching disparity estimation algorithm and a better stereo correspondence method can solve this issue. To counter these effects, the autofocus function on the operating microscope may be used to make the entire FOV sharp and the presented method performs well. Recall that the autofocus function of the Pentero microscope adjusts its optics every time the magnification function is used or if the microscope’s head is moved.
It should be noted that the goal of this paper is to correctly size the digitized point clouds acquired from an operating microscope that is reflective of the physical dimensions of the organ of these correctly sized clinical point clouds to the microscope’s coordinate system is not achieved. These coordinate transformations are needed to compute organ surface displacements for driving a model-based deformation compensation framework. Overall, the vital information contained in the feature-rich regions of the cortical surface digitized accurately with an optically tracked microscope can facilitate the delivery of continuous intraoperative measurements required for driving a deformation compensation framework. To satisfy a major part of this requirement, our stereovision system is designed to reliably and accurately digitize the organ surface in near real-time. The optical tracking aspect of the operating microscope is currently under development. Lastly, the presented stereovision digitization platform is not limited to operating microscopes used in neurosurgeries and related research is underway for extending this kind of stereovision platform for other soft tissue surgeries.
5. Conclusion
The proposed non-contact intraoperative microscope-based 3D digitization system has an error in the range of 0.28-0.81mm on the cortical surface phantom object and 0.54-1.35mm on clinical brain tumor surgery cases. These errors were computed based on surface-to-surface distance measures between point clouds obtained from the tLRS and the operating microscope’s stereovision system. These ranges of accuracy are acceptable for neurosurgical guidance applications. Our system is able to automatically estimate the magnification factor used by the surgeon in full-length clinical cases without any prior knowledge within 0.06 of the theoretical value. The operating microscope-based intraoperative digitization system is able to acquire video reliable point clouds at approximately 1 Hz. This reliable digitization of 3D points in the FOV using the operating microscope provides the impetus to pursue novel methods for surgical instrument tracking for additional guidance and microscope-based image to physical registration in IGS systems sans optical trackers. Using the proposed microscope-based digitization system as a foundation, a functional intraoperative IGS platform within the operating microscope capable of real-time surgical guidance is quite achievable in the future. When this novel digitization platform is combined with biomechanical model-based updating of IGS systems, a particular powerful and workflow-friendly solution to the problem of soft-tissue surgical guidance is realized and would be an attractive addition to the clinical armamentarium for neurosurgery.
Supplementary Material
Highlights.
- 3D stereovision digitization delivers persistent input for brain shift compensation
- Feature-based algorithm recovers microscope zoom factors used by neurosurgeon
- Zoom factors estimated within 0.06 on 4 full-length clinical brain tumor surgery videos
- 3D cortical surfaces digitized in near real-time with accuracy in 0.54-1.35mm range
Figure 12.
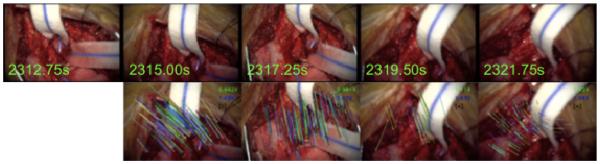
The tracking of corresponding keypoints frame-to-frame is robust to movements and rotations of the microscope. The top row shows the left camera sequence of clinical case #1 and the bottom row shows the movement of keypoints from the previous frame to the current frame.
Acknowledgements
National Institute for Neurological Disorders and Stroke Grant R01-NS049251 funded this research. We acknowledge Vanderbilt University Medical Center, Department of Neurosurgery, EMS Prototyping, Stefan Saur of Carl Zeiss Meditec Inc., and The Armamentarium, Inc. (Houston TX, USA) for providing the needed equipment and resources.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bathe OF, Mahallati H, Sutherland F, Dixon E, Pasieka J, Sutherland G. Complex hepatic surgery aided by a 1.5-tesla moveable magnetic resonance imaging system. American Journal of Surgery. 2006;191:598–603. doi: 10.1016/j.amjsurg.2006.02.008. [DOI] [PubMed] [Google Scholar]
- Bay H, Ess A, Tuytelaars T, Gool LV. SURF: Speeded up robust features. Computer Vision and Image Understanding 110. 2008;3:346–359. [Google Scholar]
- Born M, Wolf E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Cambridge University Press; 1999. Chapter 6. [Google Scholar]
- Bouguet J-Y. Visual methods for three-dimensional modeling. California Institute of Technology; 1999. Ph.D. Thesis. [Google Scholar]
- Bouguet J-Y. Camera calibration toolbox for Matlab. 2006 http://www.vision.caltech.edu/bouguetj/calib_doc/
- Bradski G, Kaehler A. In: Learning OpenCV: Computer Vision with the OpenCV Library. Loukides M, Monaghan R, editors. O'Reilly Media: 2008. [Google Scholar]
- Butler WE, Piaggio CM, Constantinou C, Niklason L, Gonzalez RG, Cosgrove GR, Zervas NT. A mobile computed tomographic scanner with intraoperative and intensive care unit applications. Neurosurgery. 1998;42:1304–1310. doi: 10.1097/00006123-199806000-00064. [DOI] [PubMed] [Google Scholar]
- Cash DM, Miga MI, Sinha TK, Galloway RL, Chapman WC. Compensating for intraoperative soft-tissue deformations using incomplete surface data and finite elements. IEEE Transactions on Medical Imaging. 2005;24:1479–1491. doi: 10.1109/TMI.2005.855434. [DOI] [PubMed] [Google Scholar]
- Cash DM, Miga MI, Glasgow SC, Dawant BM, Clements LW, Cao Z, Galloway RL, Chapman WC. Concepts and preliminary data toward the realization of image-guided liver surgery. Journal of Gastrointestinal Surgery. 2007;11:844–859. doi: 10.1007/s11605-007-0090-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang P-L, Stoyanov D, Davison AJ, Edwards PE. Real-time dense stereo reconstruction using convex optimization with a cost-volume for image-guided robotic surgery. Medical Image Computing and Computer-Assisted Intervention. 2013:42–49. doi: 10.1007/978-3-642-40811-3_6. (MICCAI 2013) [DOI] [PubMed] [Google Scholar]
- Chen I, Coffey AM, Ding S, Dumpuri P, Dawant BM, Thompson RC, Miga MI. Intraoperative brain shift compensation: accounting for dural septa. IEEE Transactions on Biomedical Engineering. 2011;58:499–508. doi: 10.1109/TBME.2010.2093896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clatz O, Delingette H, Talos I-F, Golby AJ, Kikinis R, Jolesz FA, Ayache N, Warfield SK. Robust nonrigid registration to capture brain shift from intraoperative MRI. IEEE Transactions on Medical Imaging. 2005;24:1417–1427. doi: 10.1109/TMI.2005.856734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeau RM, Sadikot AF, Fenster A, Peters TM. Intraoperative ultrasound for guidance and tissue shift correction in image-guided neurosurgery. Medical Physics. 2000;27:787–800. doi: 10.1118/1.598942. [DOI] [PubMed] [Google Scholar]
- DeLorenzo C, Papademetris X, Staib LH, Vives KP, Spencer DD, Duncan JS. Nonrigid intraoperative cortical surface tracking using game theory. IEEE 11th International Conference on Computer Vision. 2007:1–8. (ICCV 2007) [Google Scholar]
- DeLorenzo C, Papademetris X, Staib LH, Vives KP, Spencer DD, Duncan JS. Image-guided intraoperative cortical deformation recovery using game theory: Application to neocortical epilepsy surgery. IEEE Transactions on Medical Imaging. 2010;29:322–338. doi: 10.1109/TMI.2009.2027993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorenzo C, Papademetris X, Staib LH, Vives KP, Spencer DD, Duncan JS. Volumetric Intraoperative Brain Deformation Compensation: Model Development and Phantom Validation. IEEE Transactions on Medical Imaging. 2012;31:1607–1619. doi: 10.1109/TMI.2012.2197407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding S, Miga MI, Noble JH, Cao A, Dumpuri P, Thompson RC, Dawant BM. Semiautomatic registration of pre- and postbrain tumor resection laser range data: method and validation. IEEE Transactions on Biomedical Engineering. 2009;56:770–780. doi: 10.1109/TBME.2008.2006758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding S, Miga MI, Pheiffer TS, Simpson AL, Thompson RC, Dawant BM. Tracking of vessels in intra-operative microscope video sequences for cortical displacement estimation. IEEE Transactions on Biomedical Engineering. 2011;58:1985–1993. doi: 10.1109/TBME.2011.2112656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumpuri P, Thompson RC, Dawant BM, Cao A, Miga MI. An atlas-based method to compensate for brain shift: preliminary results. Medical Image Analysis. 2007;11:128–145. doi: 10.1016/j.media.2006.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumpuri P, Thompson RC, Cao A, Ding S, Garg I, Dawant BM, Miga MI. A Fast and Efficient Method to Compensate for Brain Shift for Tumor Resection Therapies Measured Between Preoperative and Postoperative Tomograms. IEEE Transactions on Biomedical Engineering. 2010;57:1285–1296. doi: 10.1109/TBME.2009.2039643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumpuri P, Clements LW, Dawant BM, Miga MI. Model-updated image-guided liver surgery: preliminary results using surface characterization. Progress in Biophysics and Molecular Biology. 2010;103:197–207. doi: 10.1016/j.pbiomolbio.2010.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards P, King A, Maurer C, Jr., de Cunha DA, Hawkes DJ, Hill DL, Gaston RP, Fenlon MR, Jusczyck A, Strong AJ, Chandler CL, Gleeson MJ. Design and evaluation of a system for microscope-assisted guided interventions (MAGI) IEEE Transactions on Medical Imaging. 2000;19:1082–93. doi: 10.1109/42.896784. [DOI] [PubMed] [Google Scholar]
- Figl M, Ede C, Hummel J, Wanschitz F, Ewers R, Bergmann H, Birkfellner W. A fully automated calibration method for an optical see-through head-mounted operating microscope with variable zoom and focus. IEEE Transactions on Medical Imaging. 2005;24:1492–1499. doi: 10.1109/TMI.2005.856746. [DOI] [PubMed] [Google Scholar]
- Ferrant M, Nabavi A, Macq B, Jolesz FA, Kikinis R, Warfield SK. Registration of 3- D intraoperative MR images of the brain using a finite-element biomechanical model. IEEE Transactions on Medical Imaging. 2001;20:1384–1397. doi: 10.1109/42.974933. [DOI] [PubMed] [Google Scholar]
- Giannarou S, Visentini-Scarzanella M, Yang G-Z. Probabilistic tracking of affine-invariant anisotropic regions. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2012;35:130–143. doi: 10.1109/TPAMI.2012.81. [DOI] [PubMed] [Google Scholar]
- Goshtasby A. Registration of images with geometric distortions. IEEE Transactions on Geoscience and Remote Sensing. 1988;26:60–64. [Google Scholar]
- Hartkens T, Hill DLG, Castellano-Smith AD, Hawkes DJ, Maurer CR, Martin AJ, Hall WA, Liu H, Truwit CL. Measurement and analysis of brain deformation during neurosurgery. IEEE Transactions on Medical Imaging. 2003;22:82–92. doi: 10.1109/TMI.2002.806596. [DOI] [PubMed] [Google Scholar]
- Hartley RI. Theory and Practice of Projective Rectification. International Journal of Computer Vision. 1999;35:115–127. [Google Scholar]
- Hartley R, Zisserman A. Multiple View Geometry in Computer Vision. Cambridge University Press; 2004. [Google Scholar]
- Heikkila J, Silven O. A four-step camera calibration procedure with implicit image correction. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 1997;0:1106–1112. (CVPR 1997) [Google Scholar]
- Hemayed EE. A survey of camera self-calibration. Proceedings of the IEEE Conference on Advanced Video and Signal Based Surveillance. 2003:351–357. [Google Scholar]
- Hill D, Maurer C, Jr., Maciunas RJ, Barwise JA, Fitzpatrick JM, Wang M,Y. Measurement of intraoperative brain surface deformation under a craniotomy. Neurosurgery. 1998;43:514–526. doi: 10.1097/00006123-199809000-00066. [DOI] [PubMed] [Google Scholar]
- Hirschmuller H. Stereo processing by semiglobal matching and mutual information. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2008;30:328–41. doi: 10.1109/TPAMI.2007.1166. [DOI] [PubMed] [Google Scholar]
- Hu M, Penney G, Figl M, Edwards P, Bello F, Casula R, Rueckert D, Hawkes D. Reconstruction of a 3D surface from video that is robust to missing data and outliers: Application to minimally invasive surgery using stereo and mono endoscopes. Medical Image Analysis. 2010;16:597–611. doi: 10.1016/j.media.2010.11.002. [DOI] [PubMed] [Google Scholar]
- Ji S, Fan X, Roberts DW, Hartov A, Paulsen KD. An integrated model-based neurosurgical guidance system. Proceedings of SPIE Medical Imaging 2010: Visualization, Image-Guided Procedures, and Modeling. 2010;7625:762535. [Google Scholar]
- King A, Edwards P, Maurer C, Jr., de Cunha DA, Hawkes DJ, Hill DL, Gaston RP, Fenlon MR, Strong AJ, Chandler CJ, Richards A, Gleeson MJ. A system for microscope-assisted guided interventions. Stereotactic And Functional Neurosurgery. 1999;72:107–111. doi: 10.1159/000029708. [DOI] [PubMed] [Google Scholar]
- King E, Daly MJ, Chan H, Bachar G, Dixon BJ, Siewerdsen JH, Irish JC. Intraoperative cone-beam CT for head and neck surgery: Feasibility of clinical implementation using a prototype mobile C-arm. Head and Neck. 2013;35:959–67. doi: 10.1002/hed.23060. [DOI] [PubMed] [Google Scholar]
- Konolige K. Small vision system: hardware and implementation. Proceedings of Eighth International Symposium on Robotics Research. 1997:111–116. [Google Scholar]
- Kumar AN, Pheiffer TS, Simpson AL, Thompson RC, Miga MI, Dawant BM. Phantom-based comparison of the accuracy of point clouds extracted from stereo cameras and laser range scanner. Proceedings of SPIE Medical Imaging 2013: Image-Guided Procedures, Robotic Interventions, and Modeling. 2013;8671:867125. [Google Scholar]
- Lang WH, Muchel F. Zeiss Microscopes for Microsurgery. Springer-Verlag; 2011. Section 10.1. [Google Scholar]
- Lange T, Eulenstein S, Hünerbein M, Lamecker H, Schlag P-M. Medical Image Computing and Computer-Assisted Intervention. 2004. Augmenting intraoperative 3D ultrasound with preoperative models for navigation in liver surgery; pp. 534–541. (MICCAI 2004) [Google Scholar]
- Lathrop RA, Hackworth DM, Webster RJ. Minimally invasive holographic surface scanning for soft-tissue image registration. IEEE Transactions on Biomedical Engineering. 2010;57:1497–1506. doi: 10.1109/TBME.2010.2040736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letteboer MMJ, Willems PWA, Viergever MA, Niessen WJ. Brain shift estimation in image-guided neurosurgery using 3-D ultrasound. IEEE Transactions on Biomedical Engineering. 2005;52:268–276. doi: 10.1109/TBME.2004.840186. [DOI] [PubMed] [Google Scholar]
- Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision. 2004;60:91–110. [Google Scholar]
- Lunsford LD, Martinez AJ. Stereotactic exploration of the brain in the era of computed tomography. Surgical Neurology. 1984;22:222–30. doi: 10.1016/0090-3019(84)90003-x. [DOI] [PubMed] [Google Scholar]
- Maier-Hein L, Mountney P, Bartoli A, Elhawary H, Elson D, Groch A, Kolb A, Rodrigues M, Sorger J, Speidel S, Stoyanov D. Optical techniques for 3D surface reconstruction in computer-aided laparoscopic surgery. Medical Image Analysis. 2013;17:974–996. doi: 10.1016/j.media.2013.04.003. [DOI] [PubMed] [Google Scholar]
- Maier-Hein L, Groch A, Bartoli A, Bodenstedt S, Guillaume B, Chang PL, Clancy N, Elson D, Haase S, Stoyanov D. Comparative validation of single-shot optical techniques for laparoscopic 3D surface reconstruction. IEEE Transactions on Medical Imaging. 2014 doi: 10.1109/TMI.2014.2325607. (in print) [DOI] [PubMed] [Google Scholar]
- Miga MI, Paulsen KD, Lemery JM, Eisner SD, Hartov A, Kennedy FE, Roberts DW. Model-updated image guidance: initial clinical experiences with gravity-induced brain deformation. IEEE Transactions on Medical Imaging. 1999;18:866–874. doi: 10.1109/42.811265. [DOI] [PubMed] [Google Scholar]
- Muja M, Lowe DG. Fast approximate nearest neighbors with automatic algorithm configuration. International Conference of Computer Vision Theory and Applications. 2009:331–340. (VISAPP’09) [Google Scholar]
- Nabavi A, Black PM, Gering DT, Westin CF, Mehta V, Pergolizzi RS, Ferrant M, Warfield SK, Hata N, Schwartz RB, et al. Serial intraoperative magnetic resonance imaging of brain shift. Neurosurgery. 2001;48:787–797. doi: 10.1097/00006123-200104000-00019. [DOI] [PubMed] [Google Scholar]
- Nakamoto M, Hirayama H, Sato Y, Konishi K, Kakeji Y, Hashizume M, Tamura S. Recovery of respiratory motion and deformation of the liver using laparoscopic freehand 3D ultrasound system. Medical Image Analysis. 2007;11:429–442. doi: 10.1016/j.media.2007.07.009. [DOI] [PubMed] [Google Scholar]
- Nimsky C, Ganslandt O, Cerny S, Hastreiter P, Greiner G, Fahlbusch R. Quantification of, visualization of, and compensation for brain shift using intraoperative magnetic resonance imaging. Neurosurgery. 2000;47:1070–9. doi: 10.1097/00006123-200011000-00008. [DOI] [PubMed] [Google Scholar]
- Nimsky C, Ganslandt O, Kober H, Buchfelder M, Fahlbusch R. Intraoperative magnetic resonance imaging combined with neuronavigation: a new concept. Neurosurgery. 2001;48:1082–1089. doi: 10.1097/00006123-200105000-00023. [DOI] [PubMed] [Google Scholar]
- Paul P, Fleig O, Jannin P. Augmented virtuality based on stereoscopic reconstruction in multimodal image-guided neurosurgery: methods and performance evaluation. IEEE Transactions on Medical Imaging. 2005;24:1500–1511. doi: 10.1109/TMI.2005.857029. [DOI] [PubMed] [Google Scholar]
- Paul P, Morandi X, Jannin P. A surface registration method for quantification of intraoperative brain deformations in image-guided neurosurgery. IEEE Transactions on Information Technology in Biomedicine. 2009;13:976–983. doi: 10.1109/TITB.2009.2025373. [DOI] [PubMed] [Google Scholar]
- Pheiffer TS, Simpson AL, Lennon B, Thompson RC, Miga MI. Design and evaluation of an optically-tracked single-CCD laser range scanner. Medical Physics 39. 2012;2:636–642. doi: 10.1118/1.3675397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollefeys M, Koch R, Gool LV. Self-Calibration and Metric Reconstruction Inspite of Varying and Unknown Intrinsic Camera Parameters. International Journal of Computer Vision. 1999;32:7–25. [Google Scholar]
- Pollefeys M, Sinha SN, Yan j. Calibration and shape recovery from videos of dynamic scenes. In: Harris L, Jenkins M, editors. Computational Vision in Neural and Machine Systems. Cambridge University Press; 2007. [Google Scholar]
- Puerto G, Mariottini G-L. A comparative study of correspondence-search algorithms in MIS images. Medical Image Computing and Computer-Assisted Intervention. 2012;15:625–633. doi: 10.1007/978-3-642-33418-4_77. (MICCAI 2012) [DOI] [PubMed] [Google Scholar]
- Roberts DW, Hartov A, Kennedy FE, Miga MI, Paulsen KD. Intraoperative brain shift and deformation: a quantitative analysis of cortical displacement in 28 cases. Neurosurgery. 1998;43:749–758. doi: 10.1097/00006123-199810000-00010. [DOI] [PubMed] [Google Scholar]
- Roberts DW, Miga MI, Hartov A, Eisner S, Lemery JM, Kennedy FE, Paulsen KD. Intraoperatively updated neuroimaging using brain modeling and sparse data. Neurosurgery. 1998;45:1199–1206. [PubMed] [Google Scholar]
- Rucker DC, Wu Y, Ondrake JE, Pheiffer TS, Simpson AL, Miga MI. Nonrigid liver registration for image-guided surgery using partial surface data: A novel iterative approach. Proceedings of SPIE Medical Imaging 2013: Image-Guided Procedures, Robotic Interventions, and Modeling. 2013;8671:86710B. [Google Scholar]
- Scharstein D, Szeliski R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. International Journal of Computer Vision. 2002;47:7–42. [Google Scholar]
- Siciliano B, Khatib O. Handbook of Robotics. Springer; 2008. [Google Scholar]
- Simpson AL, Burgner J, Chen I, Pheiffer TS, Sun K, Thompson RC, Webster RJ, Miga MI. Intraoperative bran resection cavity characterization with conoscopic holography. Proceedings of SPIE Medical Imaging 2012: Image-Guided Procedures, Robotic Interventions, and Modeling. 2012;8316:831631. [Google Scholar]
- Simpson AL, Burgner J, Glisson CL, Herrell SD, Ma B, Webster RJ, Miga MI. Comparison study of intraoperative surface acquisition methods for surgical navigation. IEEE Transactions on Biomedical Engineering. 2013;60:1090–1099. doi: 10.1109/TBME.2012.2215033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha TK, Dawant BM, Duay V, Cash DM, Weil RJ, Thompson RC, Weaver KD, Miga MI. A method to track cortical surface deformations using a laser range scanner. IEEE Transactions on Medical Imaging. 2005;24:767–781. doi: 10.1109/TMI.2005.848373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha TK, Miga MI, Cash DM, Weil RJ. Intraoperative cortical surface characterization using laser range scanning: preliminary results. Neurosurgery. 2006;59:368–376. doi: 10.1227/01.NEU.0000222665.40301.D2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skrinjar O, Nabavi A, Duncan J. Model-driven brain shift compensation. Medical Image Analysis. 2002;6:361–373. doi: 10.1016/s1361-8415(02)00062-2. [DOI] [PubMed] [Google Scholar]
- Snavely N, Seitz SM, Szeliski R. Photo tourism: Exploring photo collections in 3D. ACM Transactions on Graphics. 2006;25:835–846. [Google Scholar]
- Stoyanov D, Darzi A, Yang G-Z. Laparoscope self-calibration for robotic assisted minimally invasive surgery. Medical Image Computing and Computer-Assisted Intervention. 2005;8:114–121. doi: 10.1007/11566489_15. (MICCAI 2005) [DOI] [PubMed] [Google Scholar]
- Sun H, Lunn KE, Farid H, Wu Z, Roberts DW, Hartov A, Paulsen KD. Stereopsis-guided brain shift compensation. IEEE Transactions on Medical Imaging. 2005;24:1039–1052. doi: 10.1109/TMI.2005.852075. [DOI] [PubMed] [Google Scholar]
- Sun H, Roberts DW, Farid H, Wu Z, Hartov A, Paulsen KD. Cortical surface tracking using a stereoscopic operating microscope. Neurosurgery. 2005;56:86–97. doi: 10.1227/01.neu.0000146263.98583.cc. [DOI] [PubMed] [Google Scholar]
- Szeliski R. Computer Vision: Algorithms and Applications. Springer; 2011. [Google Scholar]
- Trucco E, Verri A. Introductory techniques for 3-D computer vision. Prentice Hall; 1998. [Google Scholar]
- Tuytelaars T, Mikolajczyk K. Local invariant feature detectors: A Survey. Foundations and Trends® in Computer Graphics and Vision. 2007;3:177–280. [Google Scholar]
- Willson RG. Modeling and calibration of automated zoom lenses. Proceedings of SPIE 1994 2350: Videometrics III. 1994;2350:170. [Google Scholar]
- Wittek A, Miller K, Kikinis R, Warfield SK. Patient-specific model of brain deformation: application to medical image registration. Journal of Biomechanics. 2007;40:919–929. doi: 10.1016/j.jbiomech.2006.02.021. [DOI] [PubMed] [Google Scholar]
- Yip MC, Lowe DG, Salcudean SE, Rohling RN, Nguan CY. Tissue tracking and registration for image-guided surgery. IEEE Transactions on Medical Imaging. 2012;31:2169–2182. doi: 10.1109/TMI.2012.2212718. [DOI] [PubMed] [Google Scholar]
- Zhang Z. A flexible new technique for camera calibration. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000;22:1330–1334. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.