Advanced colorectal neoplasia risk stratification by penalized logistic regression

Abstract

Colorectal cancer is the second leading cause of death from cancer in the United States. To facilitate the efficiency of colorectal cancer screening, there is a need to stratify risk for colorectal cancer among the 90% of US residents who are considered “average risk.” In this article, we investigate such risk stratification rules for advanced colorectal neoplasia (colorectal cancer and advanced, precancerous polyps). We use a recently completed large cohort study of subjects who underwent a first screening colonoscopy. Logistic regression models have been used in the literature to estimate the risk of advanced colorectal neoplasia based on quantifiable risk factors. However, logistic regression may be prone to overfitting and instability in variable selection. Since most of the risk factors in our study have several categories, it was tempting to collapse these categories into fewer risk groups. We propose a penalized logistic regression method that automatically and simultaneously selects variables, groups categories, and estimates their coefficients by penalizing the L1-norm of both the coefficients and their differences. Hence, it encourages sparsity in the categories, i.e. grouping of the categories, and sparsity in the variables, i.e. variable selection. We apply the penalized logistic regression method to our data. The important variables are selected, with close categories simultaneously grouped, by penalized regression models with and without the interactions terms. The models are validated with 10-fold cross-validation. The receiver operating characteristic curves of the penalized regression models dominate the receiver operating characteristic curve of naive logistic regressions, indicating a superior discriminative performance.

1 Introduction

Prognostic models are useful tools in medicine to support tasks such as benchmarking, identification of patients at risk, and individual clinical decision making. A number of techniques have been suggested for the development of clinical prediction, including a variety of statistical methods (e.g. logistic and linear regression, discriminant analysis, and recursive partitioning), and the clinical judgment of experts.^1,2 For predicting binary outcomes, such as mortality or the presence of disease, logistic regression has emerged as the statistical technique of choice.³

Logistic regression is widely used to model medical problems because the methodology is well established and coefficients may have intuitive clinical interpretations. However, when a number of risk factors are presented, logistic regression may be inadequate to handle these variables including their interactions; such highly parameterized models may overfit the data and could perform poorly for prediction. Moreover, the logistic model breaks down in the face of sparse outcomes for the different categories determined by these risk factors. To identify the “important” variables in predicting the outcome, model selection methods such as stepwise deletion and subset selection are often adopted. These techniques, though practically useful, are prone to problems such as a lack of stability as analyzed, for example, by Breiman.⁴ Another disadvantage of logistic regression is that, unlike classification methods such as decision trees,² it cannot be easily converted to a set of rules, a limitation that may reduce its clinical utility.

In this paper, we focus on scenarios where the risk factors are categorical, and maybe ordered, which is common in clinical settings. In cases where there is no a priori ordering expected between the categories and the outcome, a categorical covariate is modeled by the use of dummy variables. In many cases, however, we might expect the effect of category on the outcome to follow some natural ordering. For instance, the odds ratio for the light smoker category is expected to be smaller than that for the heavy smoker category. When the coefficients of two neighboring categories are close in risk magnitude, it is tempting to collapse them into one risk group for easier clinical use. This, along with the above-mentioned concerns, motivates us to propose a penalized logistic regression method that automatically and simultaneously selects variables, groups categories, and estimates their coefficients.

Tibshirani et al.⁵ first proposed the fused lasso method, which penalizes the L1-norm of both the coefficients and their successive differences, for problems with features that can be ordered in some meaningful way. Lin et al.⁶ proposed to develop cancer staging systems by using a Cox proportional hazards model with penalties on the differences between neighboring coefficients. Following the same line of thought, we attempt the double tasks of selection and grouping by using a lasso-type penalty in the usual logistic regression. Specifically, we pose constraints on neighboring coefficients such that

$$\sum _j\mid {\beta }_{j,1}\mid +\sum _j\sum _k\mid {\beta }_{j,k}-{\beta }_{j,k-1}\mid \le s$$ (1)

where β_j,k is the coefficient for the kth level of the jth covariate, and s > 0 is a pre-specified tuning parameter. These penalty terms together encourage sparsity in both variable selection and the grouping of the categories. The constraints can also be modified to handle interaction terms.

An attractive feature of this penalized regression method is that, by including fewer variables into the model and at the same time aggregating their categories, it produces a relatively small number of unique predicted values. These predicted values can then be directly used in decision rules for risk stratification or treatment selection. The well-known tree-based methods, being self-explanatory and easily converted to a set of rules, are theoretically applicable.² However, since a decision tree does not assign estimated coefficient values to the variables deemed important, the magnitude of the covariate effects could be somewhat unclear. Moreover, as decision trees use a “divide and conquer” method, they tend to perform well if a few highly relevant attributes exist, but less so if many complex interactions are present.

The penalized regression method can be easily adapted to handle two-way interactions of interest. This represents another strength of the proposed approach. For instance, for colorectal cancer (CRC), used as a motivating example in Section 3, no existing epidemiology studies of this disease have systematically explored interactions.

The structure of this paper is as follows. In Section 2, we describe the motivating data example of advanced colorectal neoplasia. The proposed penalized logistic regression method is described in Section 3 along with the computational approach and estimation of the tuning parameter. The method is then illustrated using the example of advanced colorectal neoplasia in Section 4. Discussion and conclusions are presented in Section 5.

2 The advanced colorectal neoplasia data

CRC is the second leading cause of death from cancer in the United States. This year, it is estimated that there will be 147,000 newly diagnosed cases of CRC and nearly 50,000 deaths associated with this disease.⁷ Screening is an effective way to reduce cause-specific mortality. Colonoscopy is the most commonly used screening test in the US, promoted in cancer prevention guidelines for people starting at age 50 because of its higher sensitivity than other less costly procedures such as stool-sample tests.^8–10 Colonoscopy allows doctors to examine the entire colon and remove abnormal tissue growths called adenomatous polyps that may progress to cancer. However, high non-adherence to colonoscopy is observed because of its risks, cost, feasibility (availability and insurance coverage), and uncertain incremental benefit over other screening tests for meaningful patient outcomes such as cancer-related morbidity and mortality.^11,12

One reason for support of widespread colonoscopic screening is that there is no accurate and precise way to stratify risk for advanced colorectal neoplasia (CRC and advanced, adenomatous polyps) among the 90% of US residents who are considered “average risk.” If such stratification could be established, then a tailored screening recommendation would be both highly effective and cost-effective. For example, people in the subgroup at very low risk for advanced neoplasia could have screening deferred or performed with methods less invasive than colonoscopy; for people at high risk, colonoscopy would be considered the preferred strategy. Tailoring according to risk of advanced neoplasia could also be useful for allocating CRC screening resources.

In this paper, we investigate such risk stratification rules for advanced neoplasia among people considered to be average risk. We use a recently completed large cohort study funded by the National Cancer Institute of subjects undergoing first time screening colonoscopy in a variety of clinical outpatient settings. The targeted risk factors are derived from the NCI’s CRC Risk Assessment tool (http://www.cancer.gov/colorectalcancerrisk) and include a previous cancer-negative sigmoidoscopy/colonoscopy in the last 10 years, polyp history in the last 10 years, history of CRC in first-degree relatives, aspirin and non-steroidal anti-inflammatory drug (NSAID) use, cigarette smoking, body mass index (BMI), leisure-time vigorous activity, vegetable consumption, and for women, post-menopausal estrogen use. All risk factors are categorical variables, with two to four levels. The derived rules are expected to facilitate decisions about initial CRC screening.

Logistic regression models have been used in the literature to estimate the risks of CRC based on quantifiable risk factors. For instance, with a similar group of variables, Freedman et al.¹³ developed models for men and women that use logistic regression to estimate future risk for CRC. In this paper, we will illustrate that the proposed penalized logistic regression can be a better choice for developing such risk stratification tools than the usual logistic regression.

3 Penalized logistic regression

3.1 A Lasso-type modeling procedure

We consider a prediction problem with N cases having binary outcomes y₁, y₂, …, y_N and covariates x_ij, i = 1, 2, …, N, j = 1, 2, …, p. In logistic regression, the outcome y_i follows a Bernoulli probability function that takes on the value 1 with probability π_i and 0 with probability 1 − π_i, where π_i varies over the observations as an inverse logistic function of the vector x_i:

$${\pi }_i=\frac{1}{1+exp(-{\beta }^T{x}_i)}.$$

To estimate β, we can maximize the conditional log-likelihood

$$\ell (\beta )=\sum _{i=1}^N[y_i\text{log}{\pi }_i+(1-y_i)\text{log}(1-{\pi }_i)]=\sum _{i=1}^N[y_i{\beta }^T{x}_i-log(1+exp({\beta }^T{x}_i))]$$ (2)

with respect to the regression coefficients β = {β_j}, j = 1, 2, …, p. The usual iteratively reweighted least squares (IRLS) procedure is used to obtain maximum likelihood estimates of the parameters.¹⁴

We focus on situations where the covariates are categorical, which corresponds to the advanced colorectal neoplasia study and is very common in clinical settings. We rewrite β as {β_j,k}, j = 1, 2, …, q, k = 1, 2, …, n_j, where q is the number of covariates and n_j is the number of categories or levels (excluding the reference level) for covariate j. Suppose that all covariates have an a priori ordering. Then, without loss of generality, β is ordered such that 0 ≤ β_j,1 ≤ ··· ≤ β_{j nj}, j = 1, …, q, with 0 being the coefficient of the reference level. The double tasks of selection and grouping can be attempted by using a lasso-type model selection technique. We propose to estimate β such that it minimizes the penalized negative log-likelihood:

$$\begin{array}{c}\widehat{\beta }=\text{argmin}\left\{-\ell (\beta )+\lambda \sum _{j=1}^q\mid {\beta }_{j,1}\mid +\lambda \sum _{j=1}^q\sum _{k=2}^{n_i}\mid {\beta }_{j,k}-{\beta }_{j,k-1}\mid \right\}\\ \text{subject}\text{to}0\le {\beta }_{j,1}\le \cdots \le {\beta }_{j,n_j},j=1,\dots ,q\end{array}$$ (3)

where λ is a tuning parameter. The two penalty terms together encourage sparsity in the variables, i.e. variable selection, and sparsity in the categories, i.e. grouping of the categories. This penalty is similar to the fused lasso penalty,⁵ yet different in that it enforces a natural ordering.

The sparsity-enforcing property of the penalty results in fewer variables as well as fewer categories in the final model, leading to a relatively small number of unique predicted values. These predicted values can then be directly used as decision rules for risk stratification or for guiding a management strategy. The penalty provides a continuous model that ensures the stability of model selection. It also facilitates model stability in the presence of sparse outcome data for different categories determined by these risk factors.

Our method naturally deals with ordinal and categorical risk factors by imposing constraints. In fact, with the ordering constraint, the absolute values in equation (3) can be dropped and the objective function can be simplified as min

$$\underset{\beta }{min}\left\{-\ell (\beta )+\lambda \sum _{j=1}^q{\beta }_{j,n_j}\right\}\text{subject}\text{to}0\le {\beta }_{j,1}\le \cdots \le {\beta }_{j,n_j},j=1,\dots ,q.$$ (4)

Note that only the coefficient for the highest level category of each covariate is taken into account in equation (4). Yet this is mathematically equivalent to equation (3) and will give the same estimates as the original formulation. Normally, different weights are given to covariates with different numbers of levels in order to avoid excess penalty on covariates with large number of categories. This is not needed here since the penalty only involves one coefficient for each covariate.

The penalty can be easily adapted for covariates without a priori ordering or that are partially ordered. For covariates without a priori ordering, the penalty is the summation of all pairwise absolute differences (including the differences with the reference level):

$$\lambda \sum _{k=1}^{n_j}\mid {\beta }_{j,k}\mid +\lambda \sum _{k=2}^{n_j}\sum _{l=1}^{k-1}\mid {\beta }_{j,k}-{\beta }_{j,l}\mid .$$ (5)

Now with all pairwise absolute differences included, a smaller weight can be given to the penalty term in order to avoid excess penalty on this covariate. This is similar for covariates that are partially ordered.

3.2 Computational approach

Because it does not feature absolute values, the penalized logistic regression in equation (4) can be solved by the usual IRLS procedure with the weighted least squares step replaced by a constrained weighted least squares procedure. Let X denote the design matrix with x_i as the ith row and π = (π₁, …, π_n)^T, where π_i = 1/(1 + e^−βTx_i). Denote A = diag(π_i(1 − π_i)), z = Xβ + A⁻¹(y − π), and $P_{\lambda }(\beta )=\lambda {\sum }_{j=1}^q{\beta }_{j,n_j}$. Then at the kth iteration, β̂^(k) is the solution of

$${\text{argmin}}_{\beta }\{{(z-X\beta )}^{T}A(z-X\beta )+P_{\lambda }(\beta )\},$$ (6)

where z and A are based on β̂^(k−1). The iterative procedure is as follows:

1. Fix λ and initialize β̂ = 0.

2. Compute π, A and z based on the current value of β̂.

3. Minimize (z − Xβ)^T A(z − Xβ) + P_λ(β) subject to 0 ≤ β_j,1 ≤ ··· ≤ β_j,nj, J = 1, …, q.

4. Repeat steps 2 and 3 until convergence of β̂.

The minimization in step 3 can be done through a quadratic programming procedure. When “warm starts” are used for computing the path of solutions over a grid of λ’s, the initial β̂ in step 1 is set to be the solution for the previous λ.

When covariates without a priori ordering are present, their contribution to the penalty as in equation (5) can be added into P_λ(β) with proper weights. The same iterative procedure is then applied. The computation can become more difficult when the absolute values remain in the penalty. In this case, the computational approach introduced by Tibshirani et al.⁵ for the fused lasso can be applied as an alternative.

3.3 Estimation of the tuning parameter

Estimates from equation (4) depend on the tuning parameter λ. When λ = 0, the solution is the usual logistic regression estimate. As λ increases, the absolute differences between neighboring coefficients go to 0 successively, corresponding to the successive grouping and dropping of the coefficients, until all coefficients are dropped. The estimated coefficients from the penalized logistic regression fit can be displayed as a function of the tuning parameter λ; an example is given in Section 4. “Warm starts” are used to efficiently compute the path of solutions over a grid of values for λ.

A method is needed to select the optimal tuning parameter λ. Following Lin et al.,⁶ we propose to use the Bayesian Information Criterion (BIC)

$$\text{BIC}(\lambda )=-2\ell ({\widehat{\beta }}_{\lambda })+k_{\lambda }ln(n)$$ (7)

to select the tuning parameter λ, where ℓ(β̂_λ) is the log-likelihood with β̂_λ, and k_λ is the model’s degrees of freedom. In this paper, we estimate k_λ by the number of unique parameters. Intuitively, the BIC inflates the negative log-likelihood by a penalty term proportional to the effective number of parameters.¹⁵ The BIC is calculated over a grid of values of λ which are uniformly distributed on the log scale from 0 to some big number, and the value λ̂ yielding the lowest estimated BIC is selected.

3.4 Two-way interactions

The penalized regression method can be adapted to handle two-way interactions of interest. For simplicity, we consider a model with two categorical covariates with p and q levels (excluding the reference levels), respectively, and their interaction terms. With some abuse of notation, we denote θ = (α₁, …, α_p, β₁, …, β_q, ν_1,1, …, ν_p,q)^T as the model parameters, where α’s and β’s are regression coefficients for the two main effects and ν’s are coefficients for the two-way interaction. Let X denote the design matrix with the interaction and x_i the ith row of X. The log-likelihood is

$$\ell (\theta )=\sum _{i=1}^N[y_i{\theta }^T{x}_i-log(1-exp({\theta }^T{x}_i))].$$

To develop the penalty, we consider the interaction terms {ν_j,k}, j = 1, …, p, k = 1, …, q, as features arranged on a two-way grid. Like the main effects, we expect to shrink and group the interaction terms. An intuitive way is to constrain the differences between neighboring coefficients in both directions in the two-way grid, as well as the difference with the reference, such that

$$\mid {\nu }_{1,1}\mid +\sum \mid {\nu }_{j,k}-{\nu }_{j,k-1}\mid +\sum \mid {\nu }_{j,k}-{\nu }_{j-1,k}\mid \le s.$$ (8)

Hence when both main effects are a priori ordered, the penalized logistic regression can be written as

$$\begin{array}{l}\widehat{\theta }=\text{argmin}\left\{-\ell (\theta )+\lambda ({\alpha }_p+{\beta }_q+\mid {\nu }_{1,1}\mid +\sum _{j=1}^p\sum _{k=2}^q\mid {\nu }_{j,k}-{\nu }_{j,k-1}\mid +\sum _{j=2}^p\sum _{k=1}^q\mid {\nu }_{j,k}-{\nu }_{j-1,k}\mid )\right\}\\ \text{subject}\text{to}0\le {\alpha }_1\le \cdots \le {\alpha }_p\text{and}0\le {\beta }_1\le \cdots \le {\beta }_q.\end{array}$$ (9)

We do not assume here the interactions are ordered whenever the main effects are ordered. In many cases it might be safe to assume this, and the interactions will satisfy a partial ordering constraint, i.e. 0 ≤ ν_j,1 ≤ ··· ≤ ν_j,q and 0 ≤ ν_1,k ≤ ··· ≤ ν_p,k, j = 1, …, p, k = 1, …, q. The above penalty can be further simplified given these constraints.

4 Data analysis and results

Study subjects were aged 50 to 80 years and underwent first-time screening colonoscopy between 12/2004 and 9/2011. Advanced neoplasia, the outcome of interest, is defined as a tubular adenoma greater than 1 cm, a polyp with villous histology or high-grade dysplasia, or CRC. Among 4,526 subjects (mean age 57.30 ± 6.78 years; 51.8% women), the prevalence of advanced neoplasia was 7.96%. Among the 4,464 (98.6%) with complete data (mean age 57.25 ± 6.70 years; 51.6% women), the prevalence of advanced neoplasia was 8.36%, including 46 subjects with CRC.

4.1 Fitted models

Data from men and women are analyzed separately. Table 1 presents a summary of the variables included in the analysis. There are eight risk factors for men and nine for women. Among the nine variables, eight are a priori ordered with greater index associated with higher risk, and one (screening and polyp history) is partially ordered – patients in category 3 are expected to have higher risk than those in category 1. BMI is divided into three categories for men and two categories for women. Some categories have very few cases in them (e.g. categories 1 and 3 of screening and polyp history), which might be problematic under a naive logistic regression.

Table 1.

Summary of variables in the advanced colorectal neoplasia data set.

Variable	Categories	Male (n = 2160)	Female (n = 2304)
Age group	0 = younger than 65	1910	2019
	1 = older than 65	250	285
Sigmoidoscopy/colonoscopy and polyp history	0 = Unknown screen or polyps	301	314
	1 = Screened and NO polyps	24	14
	2 = No screening	1793	1938
	3 = Screened and polyps	39	38
Number of relatives with CRC	0 = 0 relatives w/CRC	1554	1430
	1 = 1 relative w/CRC	432	575
	2 = 2 or more relatives w/CRC	174	299
Cigarette smoking, pack-years	0 = 0 pack-year	1172	1537
	1 = greater than 0 and <20	460	437
	2 = 20 or more pack-years	528	330
Leisure-time vigorous activity	0 = greater than 4 h/week	1341	1127
	1 = 2–4 h/week	161	203
	2 = 0–2 h/week	114	134
	3 = 0 h/week	544	840
Vegetable consumption	0 = 5 or more servings/day	73	141
	1 = less than 5 servings/day	2087	2163
BMI	0 = less than or equal to 24.9	410
	1 = greater than 24.9 and ≤ 29.9	974	1581
	2 = greater than 29.9	776	723
NSAID use	0 = Regular user of Aspirin/NSAID	1148	1089
	1 = Nonuser of Aspirin/NSAID	1012	1215
Estrogen use (female)	0 = estrogen use in the past 2 years	–	953
	1 = no estrogen use in the past 2 years	–	1351

NSAID: non-steroidal anti-inflammatory drug; BMI: body mass index.

We fit a naive logistic regression, a penalized logistic regression with only main effects (PLR-1), and a penalized logistic regression with main effects and their two-way interactions (PLR-2). A naive logistic regression with interactions cannot be fit because of its singular design matrix. Table 2 presents the model estimates for men. Because of the natural ordering, all coefficients are expected to be positive. The penalized regression models are able to preserve these orders by dropping unimportant variables and by merging the categories that violate the ordering constraints. This is not guaranteed by the naive logistic regression, where the coefficients for vegetable consumption and BMI are negative, contradictory to common knowledge. These variables are found to be not significant for predicting advanced neoplasia under all models.

Table 2.

Estimated coefficients for men.

Variable	Categories		LR	PLR-1	PLR-2
Age group	0 = younger than 65
	1 = older than 65	Age1	0.996	0.798	0.611
Sigmoidoscopy/colonoscopy and polyp history	0 = Unknown screen or polyps
	1 = Screened and NO polyps	SigCol1	0.610	0.167	0
	2 = No screening	SigCol2	0.739	0.383	0
	3 = Screened and polyps	SigCol3	2.006	0.734	0.317
Number of relatives with CRC	0 = 0 relatives w/CRC
	1 = 1 relative w/CRC	Rel1	0.196
	2 = 2 or more relatives w/CRC	Rel2	0.346	0.090	0.023
Cigarette smoking, pack-years	0 = 0 pack-year
	1 = greater than 0 and <20	Packyear1	0.855	0.766	0.197
	2 = 20 or more pack-years	Packyear2	0.971	0.826	0.302
Leisure-time vigorous activity	0 = greater than 4 h/week
	1 = 2–4 h/week	Act1	−0.276	0	0
	2 = 0–2 h/week	Act2	0.113	0.022	0
	3 = 0 h/week	Act3	0.469	0.412	0.379
Vegetable consumption	0 = 5 or more servings/day
	1 = less than 5 servings/day	Veg1	−0.047	0	0
BMI	0 = less than or equal to 24.9
	1 = greater than 24.9 and ≤ 29.9	BMI1	−0.229	0	0
	2 = greater than 29.9	BMI2	−0.121	0	0
NSAID use	0 = Regular user of Aspirin/NSAID
	1 = Nonuser of Aspirin/NSAID	NSAID1	0.217	0.167	0
Interactions	Packyear1&2: SigCol2&3		–	–	0.245
	Packyear1&2: NSAID1		–	–	0.271
	Packyear1&2: Rel1&2		–	–	0.159
	Age1: SigCol2&3		–	–	0.168
	Age1: NSAID1		–	–	0.067
	SigCol2&3: NSAID1		–	–	0.142

LR: logistic regression; PLR-1: penalized logistic regression with only main effects; PLR-2: penalized logistic regression with main effects and their two-way interactions; NSAID: non-steroidal anti-inflammatory drug; BMI: body mass index.

Six and five variables are selected, respectively, by the main effect penalized model and the penalized model with interactions. Vegetable consumption and BMI are deemed unimportant variables under both models. The estimated coefficients are shrunk to reach a more stable model. The coefficients for polyp history are shrunk the most since this risk factor is most likely to be correlated with other risk factors. Close categories are grouped simultaneously under both models. For instance, the four-level variable of leisure-time activity can be simplified into two groups, nonactive and active, under the penalized model with interactions.

In addition to five main effects, the interaction model selects six interaction terms (of possibly grouped categories). At the same time, some main effect coefficients become much smaller in the interaction model, especially cigarette smoking and polyp history. It appears that these variables, as well as NSAID/aspirin use, which is dropped under the interaction model, exhibit risk that is modified by other factors. For example, cigarette smoking does more harm when other risk factors (i.e. polyp positive, non-user of NSAID/aspirin, and relatives with CRC) are presented. Hence this model sheds more light on how the variables interact and better explains the risk of advanced neoplasia than the main effect model.

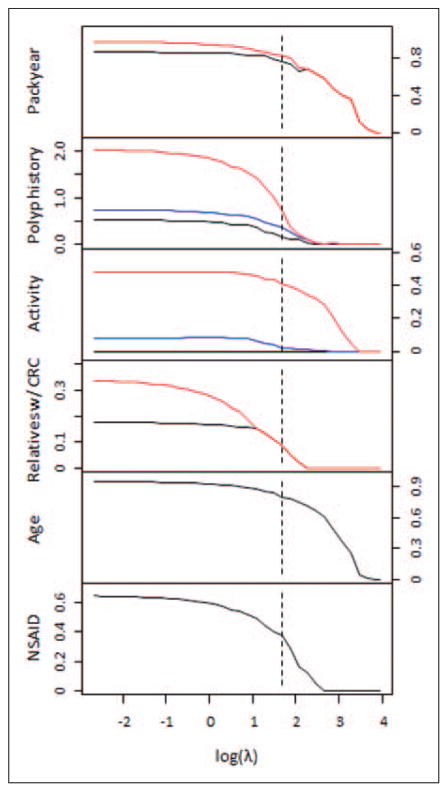
Figure 1 shows the estimated coefficients for men for the six selected variables under the main effect penalized model as a function of the log tuning parameter log(λ). The dotted line is where the BIC is minimized. From this figure, we gain a glimpse of the relative importance of the risk factors. For instance, cigarette smoking, non-activity, and older age all retain large coefficients for most values of λ, reflecting the significance of their effects on the risk for advanced neoplasia.

Figure 1.

Coefficient estimates for men for the six selected variables under the main effect penalized logistic regression model as a function of log(λ). The dotted line represents the value of log(λ) that minimized the BIC.

Table 3 displays the model estimates for female subjects. For women, seven of nine variables are selected by the main effect penalized model. The findings and interpretations are similar to those for men. One thing worth mentioning is that the main effect coefficient of estrogen use is zero under the interaction model because of its significant interactions with many other risk factors. Again, the penalized regression is considered superior and provides more information than the simple logistic regression.

Table 3.

Estimated coefficients for women.

Variable	Categories		LR	PLR-1	PLR-2
Age group	0 = younger than 65
	1 = older than 65	Age1	0.815	0.692	0.530
Sigmoidoscopy/colonoscopy and polyp history	0 = Unknown screen or polyps
	1 = Screened and NO polyps	SigCol1	1.152	0.364	0
	2 = No screening	SigCol2	0.937	0.364	0
	3 = Screened and polyps	SigCol3	2.827	1.624	0.617
Number of Relatives with CRC	0 = 0 relatives w/CRC
	1 = 1 relative w/CRC	Rel1	0.330	0.247
	2 = 2 or more relatives w/CRC	Rel2	0.567	0.318	0.062
Cigarette smoking, pack-years	0 = 0 pack-year
	1 = greater than 0 and <20	Packyear1	0.680	0.562	0.063
	2 = 20 or more pack-years	Packyear2	1.150	0.972	0.482
Leisure-time vigorous activity	0 = greater than 4 h/week
	1 = 2–4 h/week	Act1	−0.188	0	0
	2 = 0–2 h/week	Act2	−0.205	0	0
	3 = 0 h/week	Act3	0.308	0.265	0.041
Vegetable consumption	0 = 5 or more servings/day
	1 = less than 5 servings/day	Veg1	−0.314	0	0
BMI	0 = less than or equal to 29.9
	1 = greater than 29.9	BMI1	0.521	0.389	0.130
NSAID use	0 = Regular user of Aspirin/NSAID
	1 = Nonuser of Aspirin/NSAID	NSAID1	0.140	0	0
Estrogen use	0 = estrogen use in the past 2 years
	1 = no estrogen use in the past 2 years	Estrogen1	0.708	0.558	0
Interactions	Packyear1&2: SigCol3		–	–	0.073
	Packyear1&2: BMI1		–	–	0.087
	Packyear1&2: Estrogen1		–	–	0.437
	Age1: SigCol2&3		–	–	0.123
	SigCol2&3: Estrogen1		–	–	0.093
	Act3: Estrogen1		–	–	0.321
	BMI1: Rel1&2		–	–	0.088
	BMI1: Estrogen1		–	–	0.151
	Rel1&2: Estrogen1		–	–	0.248

LR: logistic regression; PLR-1: penalized logistic regression with only main effects; PLR-2: penalized logistic regression with main effects and their two-way interactions: NSAID: non-steroidal anti-inflammatory drug; BMI: body mass index.

In summary, the penalized logistic regression simultaneously selects important risk factors and provides models with fewer categories. The penalized model with interactions is more desirable since it offers more detailed risk stratification. As the penalized interaction models have only 12 and 16 distinct estimated coefficients for men and women, respectively (compared to a full interaction model which would have 83), these models can be conveniently developed into risk stratification rules for guiding treatment strategy.

4.2 Model validation

We validate and compare the discriminatory performance of the logistic regression models using receiver operating characteristic (ROC) curves. The area under an ROC curve (AUC) indicates how well a prediction model discriminates between healthy patients and patients with disease. ROC curves are generated by means of 10-fold cross-validation for the three models. The increase in the AUC was evaluated and tested for significance using the test proposed by DeLong et al.¹⁶

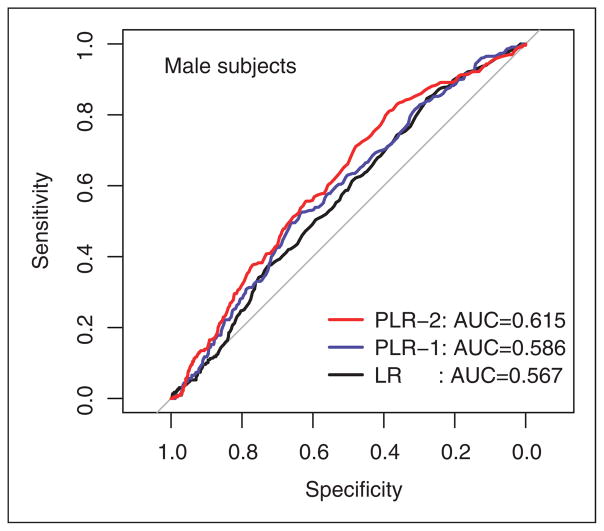
The ROC curves of the penalized regression models dominate that of naive logistic regression at most cutoff thresholds for men (Figure 2). The naive logistic regression achieves an AUC of 0.567 (95% CI, 0.531–0.604). The penalized regression models achieve AUCs of 0.586 (95% CI, 0.549–0.623) and 0.615 (95% CI, 0.578–0.651) without and with interactions, respectively. The penalized model with interactions performs significantly better (p-value = 0.026) than the naive logistic regression, while the difference between the main effect penalized model and the naive logistic regression is not significant (p-value = 0.322). No statistically significant difference is found between the AUCs of the two penalized models (p-value = 0.394). These findings suggest that the proposed penalized logistic regression models, in particular the model with interactions, have a favorable performance compared to naive logistic regression.

Figure 2.

Receiver-operating characteristic (ROC) curves for the risk prediction models: male subjects.

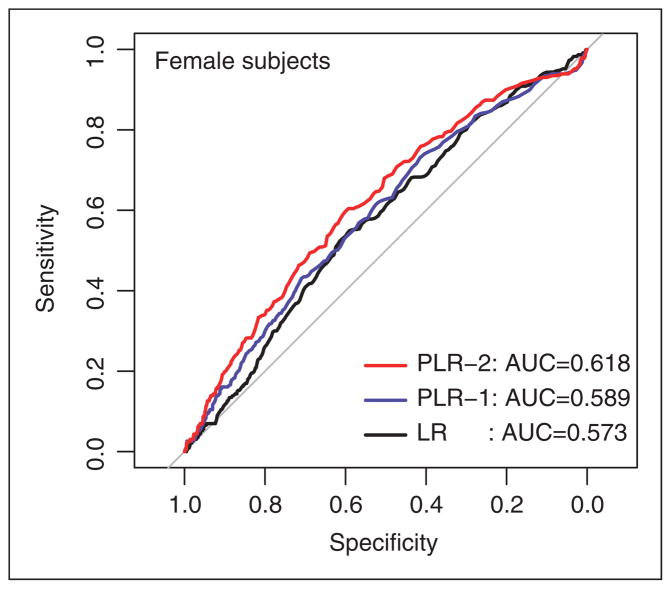
Validation is also performed for women and similar improvement in performance is observed (Table 4). The ROC curves are shown in Figure 3. Again, the penalized model with interactions performs significantly better (p-value = 0.009) than the naive logistic regression. No statistically significant difference is found between the AUCs of the two penalized models (p-value = 0.155).

Table 4.

Areas under ROC curves for the risk prediction models.

	Male			Female
	AUC	95% CI	p	AUC	95% CI	p
LR	0.567	(0.531, 0.604)	–	0.573	(0.535, 0.611)	–
PLR-1	0.586	(0.549, 0.623)	0.322	0.589	(0.551, 0.629)	0.339
PLR-2	0.615	(0.578, 0.651)	0.026	0.618	(0.580, 0.657)	0.009

The p values are for comparing the penalized models to the naive logistic regression. ROC: receiver operating characteristic; AUC: area under an ROC curve.

Figure 3.

Receiver-operating characteristic (ROC) curves for the risk prediction models: female subjects.

Note that in this example, all models examined show modest discriminatory power (AUC = 0.57–0.62). This suggests the need to find additional strong risk predictors. Nonetheless, the proposed model is able to improve discriminatory power without using extra covariates. It is well documented that improvement on AUC is extremely difficult.^17–20 Often “extremely” strong association improvement is needed for meaningful improvement in AUC.¹⁷ To gauge the improvement based on AUC, Gail¹⁹ and Raji et al.²⁰ showed that adding many newly discovered biomarkers to existing risk models only improved AUC by around 0.03. The benefit we see here is hence substantial in terms of improvement in AUC. Moreover, holding sensitivity at 80%, the improvement in specificity is 10%. This is significant considering we are looking at a screening program with millions of subjects.

5 Discussion and conclusions

In this paper, we have considered a penalized logistic regression method that automatically selects variables, groups categories, and estimates their coefficients. The model penalizes the L1-norm of both the coefficients and their differences. Thus it encourages sparsity in the categories via grouping of the categories and also sparsity in the variables via variable selection. The method can investigate many variables including their interactions in logistic regression where the traditional maximum likelihood based method can break down due to the high number of parameters and insufficient outcome data for certain categories. The order and partial order constraints we put on risk factors in the model incorporates existing scientific findings so that the probability of disease does not decrease at a higher level of risk. The penalty we put on odds ratio coefficients for adjacent categories encourage grouping and lead to parsimonious models. We have applied our method to a recently completed colon cancer screening data. Advantages of our method are seen in terms of both the ROC curves and fitted coefficients for risk factors over naive logistic regression. The capability for investigating various interactions among numerous risk factors should make our method a powerful tool for cancer risk modeling because currently very few, if any, scientific publications systematically consider interaction terms when there are many risk factors.

Risk stratification models in our example, as well as in some other CRC literature.^13,21 were developed gender-specifically because the risk factor of estrogen use is only relevant for women. Yet a model including both sexes by ignoring estrogen use is likely as useful given that fact that estrogen use shows limited effect in the resulting models. Risk stratification is not and does not have to be gender-specific in many other disease areas, and including both sexes is very easy to do statistically.

In our example, we consider the final penalized models “minimally parsimonious models” based on BIC alone. They are not necessarily the best in terms of parsimony since the BIC might not choose the most parsimonious model but the one meets the mathematical criterion. In order to meet the requirements of simplicity, the users of this method can always get further reductions by posing heavier penalty on the number of variables, or by directly choosing the number of variables to have at the end.

Low discriminatory power (Figures 2 and 3) seen in this, as well as other studies,²¹ has been a common issue with CRC risk stratification/prediction. This limitation is largely due to the current limited scientific knowledge on CRC risk stratification and presents a broader scientific issue that is out of the scope of our paper. There will be more favorable examples in other medical areas than colorectal screening, and perhaps our readers will know of such and try our method on them. Nevertheless this paper offers an improvement, and with continuing clinical advances it will be even more useful.

Our models estimate the probability of developing advanced neoplasia over a prespecified time interval from data collected from a recently completed large cohort study. The data are reasonably representative of the US population. Yet an external validation is still desirable to support further evaluation of the prognostic models across increasingly diverse settings. Among the fitted models, the ones with interactions are particularly interesting. These models will also need to be further evaluated.

Although we used colon cancer as illustration, our methodology has general appeal. The penalized model is flexible enough to accommodate practical variations. In particular, if no prior knowledge supports the order constraint of a variable, such a constraint can be easily dropped from our method. The method also can incorporate more than two way interactions although computation will be much more involved. The variables in the colon cancer screening example are entirely categorical, but the penalized regression model can be applied to continuous variables with no extra difficulty. In addition to binary outcomes, our method can generalize to other types of outcomes such as continuous or time to event outcomes.

One limitation of the logistic regression model is that it models additive effects of covariates on the logs odds ratio (in contrast to regression trees, for instance). Such models may or may not be biologically plausible. The penalized model might address this limitation with proper modification. The flexibility allowed by the proposed model’s relaxation of strict additivity could make the limitations less onerous (for example, in the ultimate relaxation, a saturated model, the link is irrelevant). Our model can also easily be extended to other links/scales, and to guide we have a variety of diagnostic methods.

A possible limitation of our method is speed of computation. Our penalty shares the property with fused lasso of requiring extensive computation. When high-dimensional data are involved, the procedure in Section 3.2 might not be adequate for computing the estimates. The least angle regression (LAR) algorithm of Efron et al.²² efficiently solves a wide spectrum of lasso problems by exploiting the fact that the solution profiles are piecewise linear functions of the L1-bound. However, an LAR-style algorithm for quickly solving the fused lasso type problem can be much more complex because of the many possible ways that the active sets of constraints can change. This would present interesting challenges for future work.

The main purpose of this study and the analysis is to develop a sparse prognostic model rather than formal testing. Therefore, we have not developed a significance testing procedure for the model estimates. One option is to get confidence intervals by bootstrapping but this might be computationally intensive. On the other hand, for the penalized model, the final variables can be considered “significant” given their being selected by the penalized regression model.

We have not shown asymptotic properties of the resulting estimators. Fan and Li^23,24 have shown oracle properties for lasso-type estimates under various models. Rinaldo²⁵ investigated the asymptotic properties for the fused lasso under the least squares settings. Establishing such properties for our estimators may also be possible and will be a topic of future research.