Worth the Weight: Using Inverse Probability Weighted Cox Models in AIDS Research

Abstract

In an observational study with a time-to-event outcome, the standard analytical approach is the Cox proportional hazards regression model. As an alternative to the standard Cox model, in this article we present a method that uses inverse probability (IP) weights to estimate the effect of a baseline exposure on a time-to-event outcome. IP weighting can be used to adjust for multiple measured confounders of a baseline exposure in order to estimate marginal effects, which compare the distribution of outcomes when the entire population is exposed versus when the entire population is unexposed. For example, IP-weighted Cox models allow for estimation of the marginal hazard ratio and marginal survival curves. IP weights can also be employed to adjust for selection bias due to loss to follow-up. This approach is illustrated using an example that estimates the effect of injection drug use on time until AIDS or death among HIV-infected women.

Introduction

Survival analysis is often used in infectious disease research to compare the time to occurrence of clinical events between treatment or exposure groups.¹ Randomized trials are the gold standard to estimate exposure effects on survival time, but are not always ethical or feasible. Although observational studies may provide estimates of effects when trial data are unavailable, the estimates they yield are often riddled with confounding.² Informally, confounding occurs when the exposure and outcome share a common cause. The standard approach in survival analysis to account for multiple measured confounders is the Cox proportional hazards regression model.³

As an alternative to the standard Cox model, we present a method in this article that uses inverse probability (IP) weights to estimate the effect of a baseline exposure on survival time. Under certain assumptions, results from an IP-weighted Cox model of observational data can be interpreted in a manner similar to a randomized trial with no drop out (i.e., loss to follow-up). In particular, unlike the standard Cox model, this approach allows for the estimation of marginal effects that compare the distribution of outcomes when the entire population is exposed versus when the entire population is unexposed.⁴ For example, this IP-weighted approach yields marginal Kaplan–Meier⁵ type survival curve estimates that account for confounding by measured covariates.^6,7 Informally, each participant is weighted to create a pseudopopulation in which (1) exposure is not associated with covariates such that (measured) confounding is eliminated, and (2) drop out is not associated with exposure or covariates such that selection bias due to drop out is eliminated.⁸ This approach is akin to survey sampling weighting used to estimate a quantity in the population.^9,10 Herein, we refer to IP weighting as standardization, in which the standardization is to the entire population under two different exposures.^7,11 We illustrate this standardization method through an example that estimates the effect of injection drug use (IDU) on AIDS-free survival among HIV-infected women.

Motivating Example: AIDS-Free Survival Among Injection Drug Users

The Women's Interagency HIV Study (WIHS) is a prospective, observational, multicenter study of women living with HIV and women at risk for HIV infection in the United States.¹² A total of 4,129 women (1,065 HIV-uninfected women) were enrolled between October 1994 and December 2012 at six U.S. sites. An institutional review board at each site approved study procedures and all study participants provided written informed consent. We were interested in determining if AIDS-free survival among HIV-infected women differed by IDU, accounting for possible confounding by factors measured at baseline and selection bias due to drop out by factors measured during study follow-up. We estimated the hazard ratio and the absolute risk difference at 10 years to quantify this effect.

The study sample consisted of 1,164 women enrolled in WIHS who were alive, HIV infected, and free of AIDS on December 6, 1995.¹³ The endpoint was either death or a diagnosis of AIDS. Women who did not reach this endpoint by December 6, 2005 were censored at that time or at the last visit at which they were known to be alive and AIDS free, whichever came first. A history of IDU at WIHS enrollment is denoted as X=1 (X=0 otherwise). The baseline covariates African American race, age, and nadir CD4 count (in cells/μl) measured from WIHS enrollment to baseline (i.e., December 6, 1995) are denoted by the vector Z. The time-varying covariate antiretroviral therapy (ART) initiation during study follow-up is denoted by Z(t), where Z(t)=1 if an individual starts ART before time t since baseline and Z(t)=0 otherwise.

Inverse Probability Weighted Cox Models

Researchers are often interested in estimating effects of an exposure fixed at study entry. IP-weighted Cox models are a method to compare the timing of clinical events under two different exposures. An appealing feature of the IP-weighted Cox model is that the results from this method can be interpreted in a manner similar to results from randomized trials with no drop out. An IP-weighted Cox model is fit by maximizing a weighted partial likelihood, where participant i who died or was diagnosed with AIDS at time t from baseline contributes the term

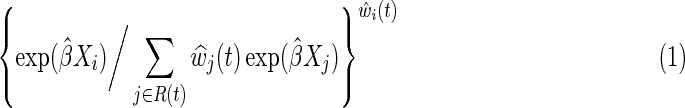where R(t) is the risk set at time t and exp(β) is the marginal hazard ratio for a unit difference in exposure X accounting for confounding and selection bias measured by covariates through the estimated IP weight 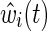(discussed below).¹⁴ When the estimated IP weight 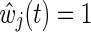for all 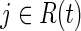, Eq. (1) is the usual contribution to the partial likelihood for the standard (i.e., unweighted) Cox model (see the Appendix). A slight modification of the likelihood is needed in the presence of tied survival times. The robust variance estimator¹⁵ can be employed to account for the fact that the IP weights are estimated.¹⁶ See the Appendix for a review of inference for the standard (i.e., unweighted) Cox proportional hazards model.

The estimated IP weight 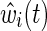is the product of an estimated time-fixed IP exposure weight 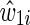and an estimated time-varying IP drop out weight for each participant i at each survival time t. The time-fixed IP exposure weights are constructed to account for confounding by covariates measured at baseline. The IP exposure weights essentially create a pseudopopulation in which exposure is not associated with covariates, thus eliminating (measured) confounding. For example, if non-African Americans are more likely to report IDU than African Americans, then an African American in the study who reports IDU will be upweighted because she is representing more participants. Different versions of these weights have been proposed. It is generally recommended to use the (estimated) stabilized IP exposure weight 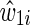defined as the ratio of the estimated marginal probability of having the exposure that participant i had, formally 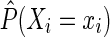, to the estimated covariate-conditional probability of having the exposure that participant i had, formally 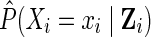, where Z_i are the measured covariates for participant i assumed sufficient to adjust for confounding. Details on estimating the IP exposure weights using the observed data are provided in the next section tailored to the example.

The time-varying IP drop out weights 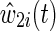are constructed to account for possible selection bias due to drop out.¹⁴ The IP drop out weights essentially create a pseudopopulation as if no participants had dropped out. Participants last observed alive and AIDS free for more than 1 year prior to December 6, 2005 were considered drop outs. Participants receive a time-varying weight that corresponds to their probability of remaining free from drop out. This stabilized IP weight 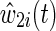is defined as the ratio of the estimated marginal probability of remaining free of drop out, formally 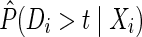, where D_i is the time from baseline to drop out for participant i, to the estimated covariate-conditional probability of remaining free of drop out, formally 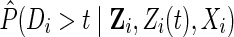, where Z_i and Z_i(t) are the measured common causes of drop out and the study outcome for participant i up to time t. (Note the covariates in the drop out model can be different from the covariates in the exposure weight model.) Details on estimating the IP drop out weights using the observed data are provided in the next section tailored to the example.

Standardized survival curve estimates can be obtained by fitting an IP-weighted Cox model stratified by exposure with no covariates and then nonparametrically estimating the baseline survival functions for the two strata.⁷ In the absence of weighting, these survival curve estimates will be (asymptotically) equivalent to Kaplan–Meier estimates obtained separately for each of the exposure stratum.¹⁷

For all Cox models presented below, we employed Efron's method to account for events that occurred on the same date.¹⁸ We obtained confidence intervals for the risk difference at 10 years using a nonparametric bootstrap with 200 random samples with replacement.¹⁹ The data analysis for this article was conducted using SAS software version 9.3 (SAS Institute Inc., Cary, NC). SAS code for analyses in the present article is provided in the Supplementary Material; Supplementary Data are available online at www.liebertpub.com/aid

Illustrative Example

The 1,164 women were 58% African American; the median age was 36 years and the median nadir CD4 count was 349 cells/μl at baseline (Table 1). At enrollment, 38% of women reported a history of IDU. During follow-up, 664 (57%) of women initiated ART. Women were followed for up to 10 years with a total of 7,090 person-years during which 579 (50%) developed AIDS or died and 117 (10%) dropped out of the study.

Table 1.

Characteristics of 1,164 HIV-Infected Women in the Women's Interagency HIV Study December 6, 1995 Through December 6, 2005

Characteristicsa	History of injection drug use (IDU) n=439	No history of injection drug use (IDU) n=725	Overall n=1,164
Age (years)	40 (35, 44)	33 (29, 39)	36 (31, 41)
African American race	273 (62%)	399 (55%)	672 (58%)
Nadir CD4+ count (cells/μl)	352 (208, 522)	348 (216, 505)	349 (213, 517)
Initiated antiretrovirals (ARTs)b	208 (47%)	456 (63%)	664 (57%)

^aMedian (interquartile range) or number (percent).

^bDuring follow-up.

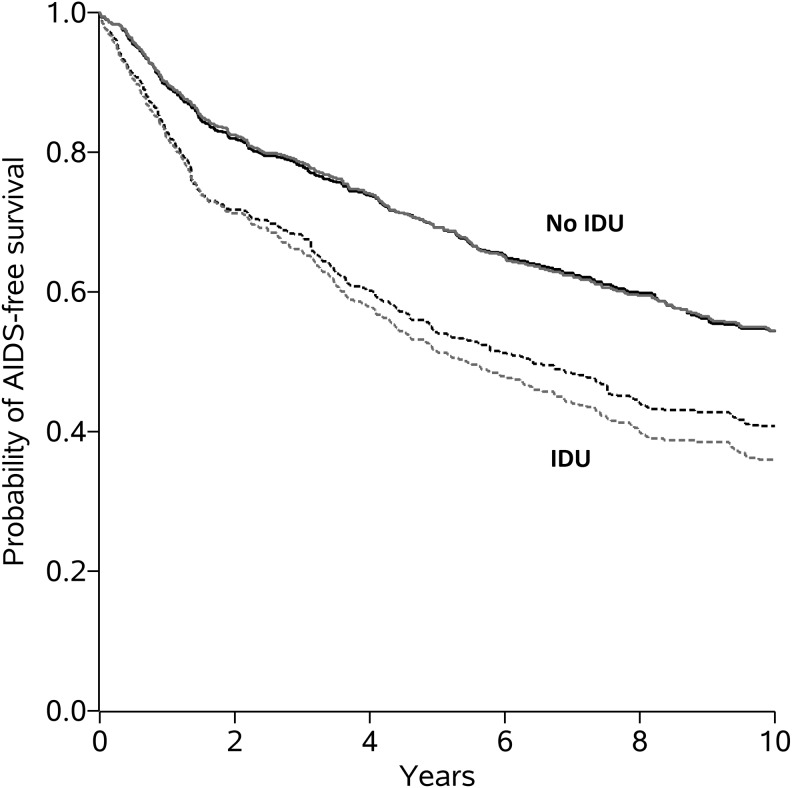
In analyses that did not account for covariates, women with a history of IDU had notably worse AIDS-free survival than women without a history of IDU (Fig. 1). The estimated hazard ratio from the unadjusted Cox model was 1.72 (95% confidence interval (CI): 1.46, 2.03; Wald p value<0.001), suggesting that the hazard of AIDS or death for those with a history of IDU was almost twice the hazard of those without a history of IDU (Table 2). We assessed the proportional hazards assumption graphically by examining whether the log cumulative hazard function estimates (see Supplementary Fig. S1) were approximately parallel. We also assessed this assumption statistically by inclusion of a product term between history of IDU and time in the Cox model, for which the Wald p value was 0.40. Neither graphical nor statistical assessment suggested a meaningful departure from proportional hazards.

FIG. 1.

Kaplan–Meier estimated AIDS-free survival curves without accounting for any covariates (gray curves) and standardized estimated AIDS-free survival curves [accounting for age, race, nadir CD4, and antiretroviral therapy (ART) initiation] (black curves) for 1,164 HIV-infected women with and without a history of injection drug use (IDU) in the Women's Interagency HIV Study December 6, 1995 through December 6, 2005

Table 2.

Association of History of Injection Drug Use with Time to AIDS or Death for 1,164 HIV-Infected Women in the Women's Interagency HIV Study December 6, 1995 Through December 6, 2005

	History of injection drug use (IDU) n=439	No history of injection drug use (IDU) n=725	Overall n=1,164
Unadjusted
AIDS cases and deaths	272 (62%)	307 (42%)	579 (50%)
Person-years	2,368	4,721	7,090
Hazard ratio (95% CI)	1.72 (1.46, 2.03)	1	—
10-year risk (95% CI)	0.64 (0.59, 0.68)	0.46 (0.42, 0.49)	0.53 (0.50, 0.56)
10-year risk difference (95% CI)	0.18 (0.13, 0.24)	0	—
Standardizeda
AIDS cases and deaths	248.49 (58%)	308.18 (43%)	556.67 (48%)
Person-years	3,730.97	7,582.69	11,313.66
Hazard ratio (95% CI)	1.53 (1.26, 1.85)	1	—
10-year risk (95% CI)	0.59 (0.54, 0.64)	0.46 (0.42, 0.49)	0.51 (0.47, 0.54)
10-year risk difference (95% CI)	0.14 (0.06, 0.22)	0	—

^aIP weighted to account for confounding of exposure due to baseline covariates [age (spline), race, and nadir CD4 (spline)] and selection bias due to loss to follow-up (covariates included exposure, time-varying ART initiation, and baseline covariates).

We then obtained a standardized hazard ratio estimate from the IP-weighted Cox model that involved two steps. In the first step, using separate logistic regression models, weights were estimated for the probability of exposure (i.e., history of IDU) and for the probability of not dropping out. For the exposure weights, we fit logistic regression models for both the numerator and denominator. The exposure model for the numerator had no covariates, whereas the exposure model for the denominator included age at baseline, race, and nadir CD4 count, as well as all pairwise interactions. Age and nadir CD4 were included as continuous variables using restricted quadratic splines with four knots placed at the 5th, 35th, 65th, and 95th percentiles.²⁰ For the drop out weights, time was coarsened into months since baseline.²¹ Then, using pooled logistic regression,²² the drop out model for the numerator included only exposure (i.e., history of IDU) and time (using restricted quadratic splines), whereas the drop out model for the denominator included exposure, time (spline), age (spline), race, nadir CD4 count (spline), and ART initiation (time varying), as well as all pairwise interactions. In the pooled logistic regression model, each person contributed up to 120 records and the weights were cumulatively multiplied for each person. The estimated weights 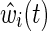had a mean of 1.01 (with a standard deviation of 0.76), and ranged from 0.43 to 12.43 (see Supplementary Table S1). In the second step, the IP-weighted Cox model was fit by weighting participants according to their estimated weights, with outcome time to AIDS or death, and history of IDU as the sole covariate.

We obtained the estimated survival functions from an IP-weighted Cox model with no covariates stratified by history of IDU. After standardization for confounding and drop out by IP weighting, survival curves showed an attenuated difference in AIDS-free survival compared to the survival curves without accounting for any covariates (Fig. 1). Under certain assumptions discussed below, the dashed black curve can be interpreted as an estimate of the AIDS-free survival if (contrary to fact) everyone had a history of IDU at enrollment and did not drop out, whereas the solid black curve can be interpreted as an estimate of the AIDS-free survival if (contrary to fact) no one had a history of IDU at enrollment and everyone did not drop out.^6,7 The standardized hazard ratio from the IP-weighted Cox model was 1.53 (95% CI: 1.26, 1.85; Wald p value<0.001) (Table 2). We again assessed the proportional hazards assumption graphically by examining whether the IP-weighted log cumulative hazard function estimates (see Supplementary Fig. S2) were approximately parallel. We also assessed this assumption statistically by inclusion of a product term between history of IDU and time, for which the Wald p value was 0.18. Neither graphical nor statistical assessment suggested a meaningful departure from proportional hazards. From the standardized survival curves, the 10-year risk of AIDS or death was 0.59 if (contrary to fact) everyone had a history of IDU at enrollment and 0.46 if (contrary to fact) no one had a history of IDU at enrollment. The 10-year risk difference was 0.14 (bootstrap 95% CI: 0.06, 0.22). For comparison, we also estimated a covariate-adjusted hazard ratio by including history of IDU, age (spline), race, and nadir CD4 count (spline) directly in an unweighted Cox model. The covariate-adjusted hazard ratio estimate was 1.62 (95% CI: 1.35, 1.95; Wald p value<0.001).

Discussion

IP-weighted Cox models and standardized survival curves were presented as methods to compare the timing of clinical events for two different exposure conditions under certain assumptions. We compare this method to the traditional Cox model and discuss assumptions and caveats below.

Although hazard ratio estimates from the IP-weighted and covariate-adjusted Cox model were comparable in the WIHS example above, the standardized (i.e., IP-weighted) method provides several potential benefits over the covariate-adjusted Cox model. First, the results from the standardized approach may be interpreted in a manner similar to results from a randomized trial with no drop out when only observational data are available (under certain assumptions discussed below). In particular, the estimated hazard ratio using the standardized approach can be interpreted in the same way as the (marginal) hazard ratio that would be obtained in a randomized experiment such as a clinical trial in which there is no confounding and no drop out. In contrast, a covariate-adjusted Cox model hazard ratio does not necessarily equal the marginal hazard ratio (even in the absence of unmeasured confounding) because the Cox model is not collapsible for the hazard ratio parameter.^7,23 A regression model is said to be collapsible for a parameter (in this case, the hazard ratio) if the covariate-adjusted parameter is the same as the unadjusted parameter.²⁴

Second, the IP weighting approach yields standardized survival curve estimates. Although the hazard ratio is a common summary parameter to compare survival distributions between exposure groups, there are drawbacks to focusing inference on hazard ratios. For instance, the hazard ratio can be difficult to interpret, especially when trying to summarize the effect of a treatment or exposure.²⁵ Presenting estimated survival curves is an alternative to reporting hazard ratios that may be more interpretable because survival curves summarize all information from baseline up to any time t. The IP-weighted approach leads to Kaplan–Meier type survival curve estimates that are standardized to the entire population under two different exposures at baseline while accounting for confounding by multiple covariates. A covariate-adjusted Cox model does not afford such survival curve estimates.^4,6–7

Third, the IP-weighted approach with drop out weights requires a weaker assumption about censoring than the covariate-adjusted Cox model.^8,26,27 The adjusted Cox model assumes that the censoring hazard is independent of survival time conditional on being at risk, exposure, and baseline covariates, whereas the IP-weighted Cox model makes the weaker assumption that censoring is independent conditional on being at risk, exposure, baseline covariates, and time-varying covariates.^27,28 Specifically, if there are measured time-varying covariates predictive of censoring and survival time, the IP-weighted approach will yield consistent estimates of the marginal hazard ratio, whereas the covariate-adjusted Cox model estimator will not be consistent for the marginal or conditional hazard ratio.^8,14,28

Results using standardization by IP weights also have, in general, a different interpretation than results from an unadjusted Cox model. In particular, when exposure is confounded, the parameter of an unadjusted Cox model is a measure of association and will generally differ from the parameter of an IP-weighted Cox model (i.e., the marginal hazard ratio), which is a measure of effect.¹⁴ On the other hand, when exposure is unconfounded (e.g., as in randomized trials), the target parameter of both models is the marginal effect. In this case, drop out weights might still be employed to account for selection bias due to loss to follow-up.²⁹ Moreover, the use of IP drop out weights yields estimators that are more efficient (i.e., less variable) than those from an unadjusted Cox model even when there is no selection bias.²⁸

The estimation of the hazard ratio and survival curves using standardization by IP weights requires certain assumptions to yield a valid inference about the exposure effect. In particular, this approach assumes positivity, well-defined exposures, correctly specified models, and no unmeasured confounding or selection bias. For each level defined by the covariates, positivity means that there is a positive probability of each level of exposure.¹⁶ For example, positivity assumes African American women could possibly have either a history of IDU or no history of IDU (and similarly for non-African American women). On the other hand, if African American women could never have a history of IDU, the positivity assumption would be violated. Well-defined exposures imply that there are not multiple versions of exposure, or if there are, that they are unimportant.^30–32 For instance, the duration of exposure to IDU in the example is assumed to be irrelevant in the sense that an individual's time until AIDS or death is assumed to be the same regardless of exposure duration. Alternatively, the marginal effects being estimated can be viewed as average effects over the distribution of IDU exposure. The standardized hazard ratio estimator and survival curves require correctly specified IP weights (i.e., correct covariate functional forms). It is also assumed that sufficient sets of covariates have been measured to effectively address confounding (i.e., no unmeasured confounding)^8,14 and selection bias due to drop out.²⁸ In the example, age, race, and nadir CD4 were assumed to be sufficient to account for confounding and these baseline covariates, time-varying ART initiation, and exposure were assumed to be sufficient to account for selection bias due to drop out.

Typically, when assessing the effect of a baseline exposure, one would not adjust for post-baseline covariates in order to avoid potential selection bias.^33,34 For example, post-baseline covariates might be on the causal pathway from the exposure to the outcome and adjusting for such covariates might lead to attenuated estimates of the total effect of the exposure.²⁷ In the example, the time-varying covariate ART initiation was not included in the covariate-adjusted Cox model. On the other hand, time-varying ART initiation may be predictive of both drop out and the survival time, so excluding that variable from the Cox model has the potential to introduce selection bias. In contrast, the use of IP drop out weights provides a valid approach to adjusting for a time-varying covariate associated with drop out and survival.^8,21

We discussed only exposure groups defined at baseline. When interest focuses on exposures that change over time, methods must be adapted accordingly. When a time-varying covariate is a risk factor for the outcome, predicts later exposure, and is affected by prior exposure, standard statistical methods (e.g., Cox models with time-varying covariates) are biased and fail to provide consistent estimators of effects.^21,35,36 IP weighting can be used to fit marginal structural Cox models of time-varying exposures in the presence of such time-varying confounders.¹⁴ For example, in HIV-infected individuals, CD4 count is a risk factor for death, predicts subsequent treatment with ART, and is affected by prior treatment; thus, the marginal structural Cox model is appropriate for assessing the effect of time-varying ART on overall survival while adjusting for time-varying CD4 count.

In the illustrative example, we estimated the total effect of IDU history on time to AIDS or death, which included the indirect effect mediated through ART and the direct effect not mediated through ART. Estimating the direct and indirect effects of IDU separately may be of interest and can be obtained by fitting marginal structural models using IP weights as long as all relevant data are available for these models.³⁷

We suggest using expert knowledge to determine which covariates to adjust for prior to model fitting. Many epidemiologists would retain a possible confounder if its inclusion changes the estimate of association by more than 10% or 20% and a great deal of precision is not sacrificed.³⁸ Other approaches for determining which covariates to adjust for in a model include conditioning on (i) all causes of the exposure or outcome³⁹ or (ii) a sufficient set of covariates based on a causal directed acyclic graph⁴⁰ informed by a priori beliefs or knowledge.⁴¹ For the weight models, inclusion of covariates that are unrelated to the exposure but related to the outcome may yield effect estimates with smaller variance and no increase in bias, so they should be included in the model; however, inclusion of covariates that are related to the exposure but not to the outcome may lead to effect estimates with larger variance and no reduction in bias, so they should be excluded from the model.⁴¹ Machine learning techniques^42,43 can be used as an alternative approach to logistic regression for estimating weights.

Although the IP-weighted method used to analyze the WIHS data attempts to adjust for confounding and selection bias, the conclusions from the analysis are still subject to the following considerations. Comparisons of groups from observational studies may be susceptible to unmeasured confounding bias, as the assumption of no unmeasured confounding is untestable. Similarly, the IP-weighted method assumes drop out is independent of the survival time conditional on being at risk, exposure, baseline covariates, and time-varying covariates. The absence of unmeasured covariates predictive of both censoring and survival times is also an untestable assumption. Even in the absence of unmeasured covariates, IP drop out weights could fail to correct for selection bias if there is not a sufficient number of participants during follow-up.²⁶ The models for the IP weights need to be correctly specified and sensitivity analysis should be performed to assess the robustness of the effect estimates to model misspecification.¹⁶ When there are longer follow-up periods (specifically, a large number of participant assessments) or near positivity violations, weights can become large, leading to imprecise effect estimates. Truncating estimated weights offers some solution to this problem, although results can be sensitive to the choice of truncation cut-off points.^16,44 Finally, as with all methods, error in the measurement of exposure, covariates, or the event status or times could bias the results.⁴⁵

In conclusion, we have presented an example of survival data pertinent to infectious disease research and illustrated how to compare groups of study participants using the IP-weighted Cox proportional hazards model. The methods presented here have broad applicability in infectious disease research. Careful use of this and other methods for survival analysis will continue to enrich the evidence base in the field of infectious diseases by providing answers to questions that are difficult or impossible to answer well without explicitly accounting for time. Inverse probability weighted Cox models provide a method to estimate covariate-standardized hazard ratios and survival curves in observational studies, and obtain information about effects of treatments or exposures to prevent infectious diseases or their sequela.

Appendix: Review of the Standard (Unweighted) Cox Proportional Hazards Model

Let uppercase letters denote random variables and lowercase letters denote possible realizations of random variables or constants. Let 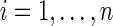index the study participants. Let T_i be the time from baseline to AIDS diagnosis or death, D_i be the time from baseline to study drop out, and C_i be the time from baseline to administrative censoring. In practice, only the minimum of T_i, D_i and C_i is observed, denoted by 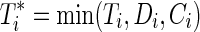. See Cole and Hudgens¹ for a review of univariate survival analysis methods.

The Cox proportional hazards regression model³ is one of the most widely used statistical methods in biomedical research. The univariate Cox model is defined as 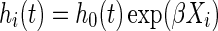, where h_i(t) is the hazard function for individuals with covariate X_i, h₀(t) is the reference hazard at time t for those with X_i = 0, and β is the log hazard ratio for a one unit change in X_i.

Heuristically, Cox regression may be understood as a series of logistic regression models, where at each ordered survival time, the log odds of the event are regressed on the exposure groups and any covariates.¹⁸ The Cox model is a semiparametric model because no assumption is placed on the probability distribution for the reference survival time distribution. Equivalently, the function h₀(t) is left arbitrary. The parameters of a Cox model are estimated using maximum partial likelihood.⁴⁶ For the case of a single covariate and assuming no tied survival times, participant i who had the event at time t contributes the term

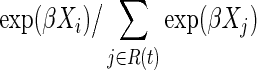to the partial likelihood function, where R(t) is the set of participants at risk at time t. The partial likelihood is defined as simply a product of these individual contributions for events, or

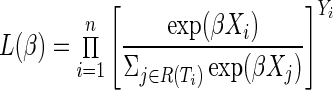where Y_i is an event indicator (i.e., 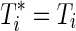). Only events contribute to the numerator of the likelihood due to the exponent Y_i. There are several ways to handle tied survival times, including methods ascribed to Peto and Peto,⁴⁷ Breslow,⁴⁸ Efron,¹⁸ and an exact approach,²⁷ which all return the same results if there are no ties. In the presence of moderate ties and if time is truly continuous, Efron's approximation performs well compared to the other approaches.⁴⁹

One of the central assumptions of the Cox model is that the ratios of the hazards defined by levels of the covariates are constant over time. This is the proportional hazards assumption. The proportional hazards assumption can be assessed by fitting the model 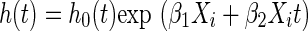and testing the null hypothesis that β₂ = 0, where X_it is a product of the covariate and time t.

In general, a 1−α Wald confidence interval (CI) for the hazard ratio is defined as 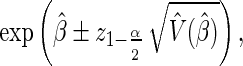where 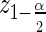is the 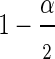percentile of a standard normal distribution and 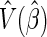is the estimated variance of 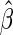. A Wald test statistic is defined as 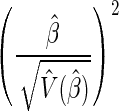and is chi-squared distributed with 1 degree of freedom under the null hypothesis β = 0.

Acknowledgments

These findings are presented on behalf of the Women's Interagency HIV Study (WIHS). We would like to thank all of the WIHS investigators, data management teams, and participants who contributed to this project. Funding for this study was provided by National Institutes of Health Grants R01AI100654, R01AI085073, U01AI069918, R56AI102622, 5 K24HD059358-04, 5 U01AI103390-02 (WIHS), and P30AI50410 (CFAR). Data in this manuscript were collected by the WIHS. The contents of this publication are solely the responsibility of the authors and do not represent the official views of the NIH. WIHS (Principal Investigators): UAB-MS WIHS (Michael Saag, Mirjam-Colette Kempf, and Deborah Konkle-Parker), U01-AI-103401; Atlanta WIHS (Ighovwerha Ofotokun and Gina Wingood), U01-AI-103408; Bronx WIHS (Kathryn Anastos), U01-AI-035004; Brooklyn WIHS (Howard Minkoff and Deborah Gustafson), U01-AI-031834; Chicago WIHS (Mardge Cohen), U01-AI-034993; Metropolitan Washington WIHS (Mary Young), U01-AI-034994; Miami WIHS (Margaret Fischl and Lisa Metsch), U01-AI-103397; UNC WIHS (Adaora Adimora), U01-AI-103390; Connie Wofsy Women's HIV Study, Northern California (Ruth Greenblatt, Bradley Aouizerat, and Phyllis Tien), U01-AI-034989; WIHS Data Management and Analysis Center (Stephen Gange and Elizabeth Golub), U01-AI-042590; Southern California WIHS (Joel Milam), U01-HD-032632 (WIHS I – WIHS IV). The WIHS is funded primarily by the National Institute of Allergy and Infectious Diseases (NIAID), with additional co-funding from the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD), the National Cancer Institute (NCI), the National Institute on Drug Abuse (NIDA), and the National Institute on Mental Health (NIMH). Targeted supplemental funding for specific projects is also provided by the National Institute of Dental and Craniofacial Research (NIDCR), the National Institute on Alcohol Abuse and Alcoholism (NIAAA), the National Institute on Deafness and other Communication Disorders (NIDCD), and the NIH Office of Research on Women's Health. WIHS data collection is also supported by UL1-TR000004 (UCSF CTSA) and UL1-TR000454 (Atlanta CTSA).

B.L. acquired the WIHS data used in the example. A.L.B., M.G.H., and S.R.C. wrote the initial draft of the manuscript. A.L.B. performed the analyses under the guidance of M.G.H. and S.R.C. A.L.B., M.G.H., S.R.C., B.L., and A.A.A. participated in discussions on technical points. A.A.A. provided guidance on the data example and ensured that the level of technicality was appropriate for the readership. All authors were involved in the review and editing process of the final manuscript. The authors gratefully acknowledge the comments of the two anonymous reviewers, which greatly improved the article.

Author Disclosure Statement

No competing financial interests exist.