Abstract
Objective
Estimates of prehospital transport times are an important part of emergency care system research and planning; however the accuracy of these estimates is unknown. We examined the accuracy of three estimation methods against observed transport times in a large cohort of prehospital patient transports.
Methods
We performed a validation study using prehospital records in King County, Washington and southwestern Pennsylvania from 2002 to 2006 and 2005 to 2011, respectively. We generated transport time estimates using three methods: linear arc distance, Google Maps and ArcGIS Network Analyst. We assessed estimation error, defined as the absolute difference between observed and estimated transport time, and the proportion of estimated times that were within specified error thresholds. Based on the primary results, we then tested whether a regression estimate that incorporated population density, time-of-day and season could improve accuracy. Finally, we compared hospital catchment areas using each method with a fixed drive time.
Results
We analyzed 29,935 prehospital transports to 44 hospitals. The mean absolute error was 4.8 minutes (± 7.3) using linear arc, 3.5 minutes (± 5.4) using Google Maps and 4.4 minutes (± 5.7) using ArcGIS. All pairwise comparisons were statistically significant (p<0.01). Estimation accuracy was lower for each method among transports more than twenty minutes (mean absolute error was 12.7 minutes (± 11.7) for linear arc, 9.8 minutes (± 10.5) for Google Maps and 11.6 minutes (± 10.9) for ArcGIS). Estimates were within five minutes of observed transport time for 79% of linear arc estimates, 86.6% of Google Maps estimates and 81.3% of ArcGIS estimates. The regression-based approach did not substantially improve estimation. There were large differences in hospital catchment areas estimated by each method.
Conclusion
We showed that route-based transport time estimates demonstrate moderate accuracy. These methods can be valuable for informing a host of decisions related to the system organization and patient access to emergency medical care; however, they should be employed with sensitivity to their limitations.
INTRODUCTION
Time to definitive therapy is a benchmark in the management of many emergency conditions, including acute ischemic stroke,1 acute myocardial infarction, 2,3 sepsis4 and trauma.5 Accordingly, accurate measurement of transport times between the scene of an emergency and the hospital is an important part of emergency care system planning. For example, transport times6 are frequently used to define population access to emergency hospital care, 7,8 dictate how and where patients are brought by prehospital providers, and inform efforts to reorganize emergency care at the regional level.9 Several methods are available to estimate transport times, including stand-alone commercial software10 and publicly available internet-based search engine tools.11,12 However, these methods have not been validated against observed prehospital transport times, limiting their utility in research and planning.
Accurate prehospital transport time estimation is essential for efforts to assess hospital access for patients with time-sensitive conditions and public health planning surrounding allocation of emergency care resources. Actual transport times are not always available prospectively, and even well-developed emergency medical services (EMS) systems use estimates to predict EMS responsiveness and hospital access.13,14 Research into the accuracy of these estimates will qualify their usefulness in resource allocation decisions and predictions of population access to emergency hospital care.
We sought to determine the accuracy of three transport time estimation methods against observed prehospital transport times. Based on the primary results, we then assessed whether estimation could be improved by incorporating transport characteristics in a regression-based approach. Finally, we graphically compared the estimated population within a twenty-minute drive time to the hospital using each method to see how choice of estimation method affected estimates of access to emergency care.
METHODS
Study design and setting
We performed a validation study comparing the accuracy of three methods to estimate prehospital transport times against observed transport times in a cohort of EMS patient transports from two separate data sources.
We used prehospital records from King County, Washington and southwestern Pennsylvania from 2002 to 2006 and 2005 to 2011, respectively. We chose these two locations based on data availability, patient case-mix and EMS catchment geography.
We used records from the King County Emergency Medical Services database, an administrative record of 911 dispatches in King County, Washington.15-17 The King County Emergency Medical Services database does not include cardiac arrest or trauma patient transports. King County has a population of 1.9 million persons living in rural, suburban, and urban areas and is the 14th most populous county in the United States.
We used records from southwestern Pennsylvania from the Resuscitation Outcomes Consortium Epistry-Cardiac Arrest study, a large observational registry of out-of-hospital cardiac arrest cases.18 This catchment area includes an estimated 936,000 persons living in rural, suburban and urban areas.
Population
All adult patients enrolled in either prior study15,18 and transported by ground EMS were initially eligible. We excluded records if the patient was not transported to a hospital, or if the transport time, starting location or other transport characteristics were not recorded.
Methods and Measurements
From each prehospital record we abstracted departure time, departure street address, arrival time, arrival street address (i.e., the destination hospital) and transport date. To determine the departure and arrival location we geocoded the latitude and longitude of the departure and arrival street addresses using ArcGIS.
To simplify interpretation of transport characteristics, we created categories for each variable. We grouped transport date into four seasons: spring (March to May), summer (June to August), fall (September to November) and winter (December to February). We grouped departure time into four categories: morning (6:01AM to 10AM), mid-day (10:01AM to 3PM), afternoon (3:01PM to 8PM), and nighttime (8:01PM to 6AM), corresponding to typical traffic patterns.19 We used the population density for each starting location ZIP code using 2009 US Census data,20 which we categorized into deciles, based on the national distribution of ZIP code population densities.
Analysis
We analyzed records from both data sources as a combined cohort. We combined data sources to increase generalizability across a range of EMS system structures, including records from thirty-five EMS agencies in King County, Washington and six EMS agencies in southwestern Pennsylvania. We included region in our univariate analysis to verify that transport time estimates did not vary by cohort origin.
We defined observed transport time as the prehospital interval between departure from the starting location and arrival at the destination hospital. We then compared the observed transport time to transport times estimated using three different methods: linear arc distance, Google Maps and ArcGIS Network Analyst.
Linear arc distance transport time estimate
For this method we first calculated the linear arc distance between the departure and arrival location, defined as the straight path connecting the points that accounts for the curvature of the Earth. This distance is akin to “as the crow flies” between two locations and is referred to as the “geodesic line” in mathematics. The typical method for linear arc transport time estimation involves calculating the linear arc distance and then dividing this distance by assumed average speeds based on population density. We estimated transport time by dividing the linear arc distances by 20.1 miles per hour for transports starting in ZIP codes in the highest tertile of population density, 47.5 miles per hour for transports starting in ZIP codes in the middle tertile of population density and 56.4 miles per hour for transports starting in ZIP codes in the lowest tertile of population density, as previously performed.7
Google Maps transport time estimate
For this method we estimated transport time using traveltime,21 a Google plug-in for the Stata statistical software package (StataCorp, College Station, TX). Google Maps is a proprietary software program maintained on-line by Google (Mountain View, CA). Google Maps travel time estimates are produced using road network calculations and a crowd-sourced traffic adjustment. We accessed Google Maps at 9:00am EST on April 20, 2013.
ArcGIS Network Analyst transport time estimate
For this method we estimated transport time using Environmental Sciences Research Institute ArcGIS Network Analyst version 10.1 (Redlands, CA) with StreetMap USA Premium 2010. Travel time estimates in this version are produced using road network calculations, but do not automatically adjust for road traffic. ArcGIS allows the user to customize transport routing rules, and is used widely in geographic healthcare studies.8,22,23
Outcome
The primary outcome was the transport time estimate error, defined as the absolute value of the difference between the observed transport time and transport time estimate.24 A secondary outcome was the estimate percent error, defined as the median absolute percent difference between the observed transport time and transport time estimate. We evaluated both outcomes to address relative and absolute error difference for longer and shorter duration transports. We summarized errors using the mean, standard deviation and range. We compared errors between methods using paired t-tests and Wilcoxon signed-rank tests as appropriate. Consistent with guidelines for reporting reliability and agreement studies,25 we also calculated the proportion of agreement within one minute, five minutes and ten minutes of the observed time. Additionally we generated Bland-Altman plots for each estimation method, plotting mean transport time against the difference between estimated and observed transport time.
We performed analysis of variance or the F* test26 as appropriate to determine if the mean absolute errors varied across key subgroups based on transport characteristics. These included time-of-day category, season and starting location ZIP code population density. We selected these variables a priori as they are routinely available in prehospital records, and may plausibly modify transport times.
Regression-based transport time estimates
After determining the most accurate estimation method, we then explored whether a linear regression model that incorporated case-specific data could further improve transport time estimation. We decided a priori to initially include three variables in the model: season, time of day, and starting location population density. We did not include cohort location or patient physiology in the regression model in order to maximize generalizability of our results. Variables with coefficients that were not statistically significant at the alpha=0.05 level in the multivariable model were excluded to create a parsimonious final model. We assessed the assumptions of linear regression modeling in the usual fashion. We anticipated that the dependent variable would have a non-normal distribution; however, our goal was to create a predictive model,27 rather than perform hypothesis testing for model parameter estimates. We assessed fit of the model using the coefficient of determination. We compared the mean absolute error of the regression approach to the best performing non-regression method using a paired t-test.
Population estimates
We estimated geographic access to the hospital using each method and a twenty-minute drive time. We performed this analysis to illustrate the magnitude of differences in population access predicted with each method. The drivable area around a hospital, also known as a hospital service area, estimates the population reached by ground transportation within a specified time. We measured the population included within each method’s hospital service area by aggregating 2009 US Census block population data.28
Sensitivity analysis
Starting in 2007, Google incorporated real-time crowd-sourced traffic estimates into its Maps application.29 To determine how this may have affected our results, we compared Google Maps transport time estimates at three additional times on a weekday (11AM, 5PM and 11PM), and four times on a weekend (8AM, 11AM, 5PM, and 11PM) to determine whether estimates changed according to day-of-week or time-of-day.
Paired t-test and Wilcoxon signed-rank test results were considered statistically significant at the alpha=0.017 level, using a Bonferonni correction to account for multiple comparisons. All other results were considered statistically significant at the alpha=0.05 level. We did not perform a sample size calculation for planned comparisons as we expected to obtain a large analytic cohort from the combined data sources. Statistical analyses were performed using STATA version 12.1 (College Station, TX). The University of Pittsburgh Institutional Review Board determined that the study qualified for exempt status.
Results
Characteristics of study subjects
Among 72,931 EMS transports to 67 hospitals, we included 29,935 transports to 44 hospitals (Figure 1). Most transports occurred during daytime hours (n=20,974; 70.0%) and from ZIP codes in the 70th percentile or greater of population density (n=28,821; 96.2%; Table 1). Respiratory, neurological and cardiovascular diagnoses described more than half of all transports. Transports were reported equally across seasons.
Figure 1.
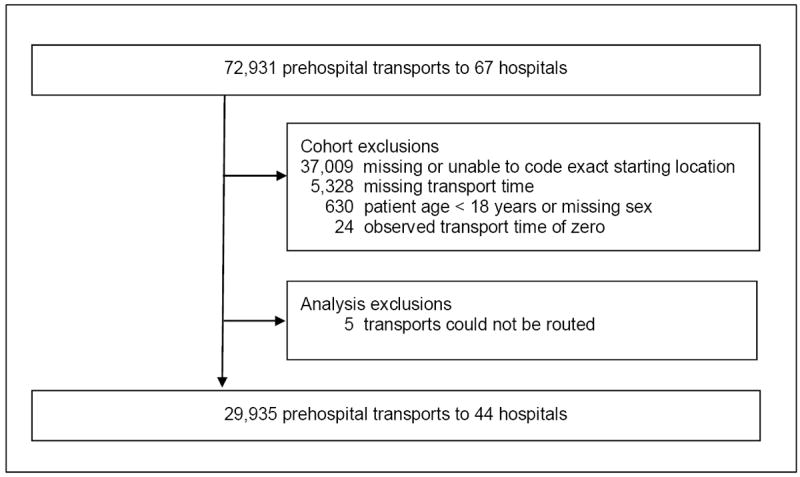
Cohort Accrual.
Table 1.
Prehospital cohort characteristics
| Characteristic | N=29,935 | |
|---|---|---|
| Demographic | ||
| Age, median (IQR) | 66 | (48-80) |
|
| ||
| Female sex, n (%) | 16,776 | (56.0) |
|
| ||
| Diagnostic category, n (%) | ||
| Respiratory | 3,285 | (11.0) |
| Neurological | 3,692 | (12.3) |
| Cardiovascular | 9,054 | (30.3) |
| Other | 11,070 | (37.0) |
| Unknown | 2,834 | (9.5) |
|
| ||
| Transport | ||
| Season, n (%) | ||
| Spring (March – May) | 7,671 | (25.6) |
| Summer (June – August) | 7,201 | (24.1) |
| Fall (September – November) | 7,432 | (24.8) |
| Winter (December – February) | 7,631 | (25.5) |
|
| ||
| Time of day, n (%) | ||
| Morning (6-10am) | 5,455 | (18.2) |
| Mid-day (10am-3pm) | 8,464 | (28.3) |
| Afternoon (3pm-8pm) | 7,055 | (23.6) |
| Nighttime (8pm-6am) | 8,961 | (29.9) |
|
| ||
| ZIP code population density, n (%) | ||
| 90 to 100th percentile | 19,511 | (65.2) |
| 80 to 89th percentile | 6,996 | (23.4) |
| 70 to 79th percentile | 2,314 | (7.7) |
| Less than 70th percentile | 1,114 | (3.7) |
| Region, n (%) | ||
| King County, Washington | 28,922 | (96.6) |
| Southwestern Pennsylvania | 1,013 | (3.4) |
IQR, interquartile range
The median observed transport time was 10 minutes (interquartile range (IQR): 6.7 to 15.0 minutes).
Accuracy of estimated transport times
The overall mean absolute error was 4.8 minutes (± 7.3) for linear arc, 3.5 minutes (± 5.4) for Google Maps and 4.4 minutes (± 5.7) for ArcGIS (all pairwise differences had p-values <0.01; Table 2). The overall median absolute percent error was 30.2 (IQR: 14.4 to 52.2) for linear arc, 21.4 (IQR: 10.0 to 40.0) for Google Maps and 32.7 (IQR: 17.0 to 49.8) for ArcGIS (all pairwise differences had p-values <0.01). All three methods were more accurate for observed transport durations less than ten minutes and less accurate for transports more than twenty minutes (all pairwise differences had p-values <0.01). All pairwise differences between percent errors were also significantly different, with the exception of the linear arc - ArcGIS pair for transports greater than twenty minutes (p=0.025). The percentage of estimates within five minutes of the observed time was 79.0% for linear arc, 86.6% for Google Maps and 81.3% for ArcGIS. Estimates were more accurate for all methods among nighttime transports and those originating from highest population density ZIP codes (Table 3). Accuracy was similar between data sources for linear arc and ArcGIS methods; however, Google Maps estimation accuracy was greater in King County, Washington compared to southwestern Pennsylvania (3.5 versus 4.2 mean absolute error, p<0.01.)
Table 2.
Comparison of estimation methods.
| Linear arc | Google Maps | ArcGIS | |
|---|---|---|---|
| Overall (N=29,935) | |||
| Mean absolute error in minutes* (SD) | 4.8 (7.3) | 3.5 (5.4) | 4.4 (5.7) |
| Median absolute percent error* (IQR) | 30.2 (14.4 to 52.2) | 21.4 (10.0 to 40.0) | 32.7 (17.0 to 49.8) |
| Range error in minutes | 0 to 396 | 0 to 157 | 0 to 188 |
| Percentage of estimates within one minute of observed time | 19.8 | 23.9 | 16.7 |
| Percentage of estimates within five minutes of observed time | 79.0 | 86.6 | 81.3 |
| Percentage of estimates within ten minutes of observed time | 89.9 | 94.5 | 93.4 |
|
| |||
| Transports < 10 minutes (n=14,321) | |||
| Mean absolute error in minutes* (SD) | 2.9 (5.0) | 2.4 (3.6) | 2.6 (3.4) |
| Median absolute percent error* (IQR) | 34.7 (16.7 to 58.1) | 27.7 (12.5 to 50.0) | 36.9 (19.2 to 54.7) |
| Range error in minutes | 0 to 83 | 0 to 66 | 0 to 75 |
| Percentage of estimates within one minute of observed time | 26.2 | 29.6 | 23.8 |
| Percentage of estimates within five minutes of observed time | 89.8 | 91.3 | 92.6 |
| Percentage of estimates within ten minutes of observed time | 96.9 | 97.4 | 98.1 |
|
| |||
| Transports > 20 minutes (n=3,610) | |||
| Mean absolute error in minutes* (SD) | 12.7 (11.7) | 9.8 (10.5) | 11.6 (10.9) |
| Median absolute percent error** (IQR) | 34.1 (15.2 to 59.1) | 23.1 (10.0 to 45.5) | 31.3 (15.0 to 55.3) |
| Range error in minutes | 0 to 114 | 0 to 114 | 0 to 116 |
| Percentage of estimates within one minute of observed time | 6.9 | 8.6 | 6.0 |
| Percentage of estimates within five minutes of observed time | 31.6 | 42.3 | 30.6 |
| Percentage of estimates within ten minutes of observed time | 52.5 | 66.1 | 58.0 |
SD, standard deviation; IQR, interquartile range
All pairwise differences between methods were statistically significant with p-value <0.01.
Pairwise differences between linear arc and Google Maps and between Google Maps and ArcGIS were statistically significant with p-value <0.01. The difference between linear arc and ArcGIS had a p-value of 0.025.
Table 3.
Absolute difference between observed transport time and estimates by subgroup.
| Linear arc | Google Maps | ArcGIS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean Absolute Error (minutes) | SD | p-value | Mean Absolute Error (minutes) | SD | p-value | Mean Absolute Error (minutes) | SD | p-value | |
| Season | |||||||||
| Spring (March – May) | 4.8 | (8.4) | 0.90 | 3.5 | (5.6) | 0.76 | 4.3 | (6.0) | 0.72 |
| Summer (June – August) | 4.8 | (7.2) | 3.4 | (5.5) | 4.4 | (5.8) | |||
| Fall (September – November) | 4.8 | (6.7) | 3.5 | (5.3) | 4.4 | (5.6) | |||
| Winter (December – February) | 4.8 | (6.8) | 3.5 | (5.2) | 4.3 | (5.5) | |||
|
| |||||||||
| Time of day | |||||||||
| Morning (6-10am) | 4.9 | (6.9) | <0.01 | 3.5 | (5.2) | <0.01 | 4.5 | (5.5) | <0.01 |
| Mid-day (10am-3pm) | 5.1 | (7.4) | 3.7 | (5.6) | 4.8 | (5.9) | |||
| Afternoon (3pm-8pm) | 5.0 | (7.1) | 3.7 | (5.6) | 4.8 | (5.9) | |||
| Nighttime (8pm-6am) | 4.4 | (7.7) | 3.1 | (5.1) | 3.5 | (5.5) | |||
|
| |||||||||
| ZIP Code Population density | |||||||||
| 90 to 100th percentile | 3.9 | (6.2) | <0.01 | 3.1 | (5.0) | <0.01 | 4.2 | (5.3) | <0.01 |
| 80 to 89th percentile | 4.9 | (7.8) | 3.5 | (5.0) | 4.0 | (5.4) | |||
| 70 to 79th percentile | 9.9 | (10.2) | 5.8 | (8.1) | 6.2 | (8.5) | |||
| Less than 70th percentile | 9.1 | (8.6) | 5.1 | (6.4) | 6.3 | (6.7) | |||
|
| |||||||||
| Region | |||||||||
| King County, Washington | 4.8 | (7.3) | 0.42 | 3.5 | (5.3) | <0.01 | 4.4 | (5.7) | 0.62 |
| Southwestern Pennsylvania | 4.6 | (8.6) | 4.2 | (6.7) | 4.3 | (7.3) | |||
SD, standard deviation
Bland-Altman plots showed that estimated transport times were biased to be lower than observed transport times (Figure 2a-c). Bias increased with longer transports for all three methods; however, the magnitude of bias was not consistent across transport times. Therefore, an overall correction cannot be applied to any of the methods.
Figure 2.
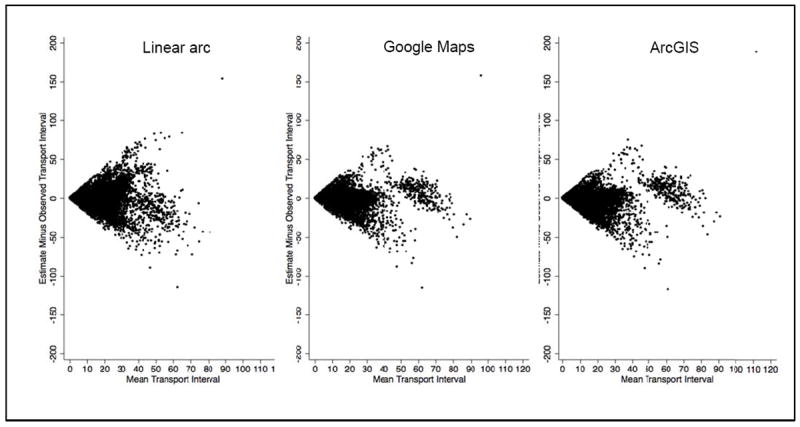
Bland-Altman plots for observed transport time and three estimation methods.
Regression-based transport time estimates
The final regression model included terms for Google Maps estimate, time-of-day, season and population density (eTable 1). The model produced low estimation error (mean absolute error: 3.4 minutes ± 5.1) and had the highest one-, five- and ten-minute agreement with observed transport times (25.7%, 88.6%, and 95.0% respectively; eTable 2). The adjusted R2 was 0.57, indicating moderate model fit. The difference in mean absolute error between Google Maps estimate and linear regression was statistically significant (p<0.01). Of note, the linear regression assumptions of residual normality and homoscedasticity were not satisfied in our data. However, our objective was not to test for individual parameter significance, rather we sought to build a multivariable model that produced more accurate transport time estimates.27,30
Population estimates
We created a twenty-minute driving perimeter around a group of five hospitals in Pittsburgh using each estimation method. The linear arc area included 698,049 persons (198 square miles), the Google Maps area included 883,615 persons (310 square miles) and the ArcGIS area included 960,844 persons (352 square miles) (Figure 3).
Figure 3.
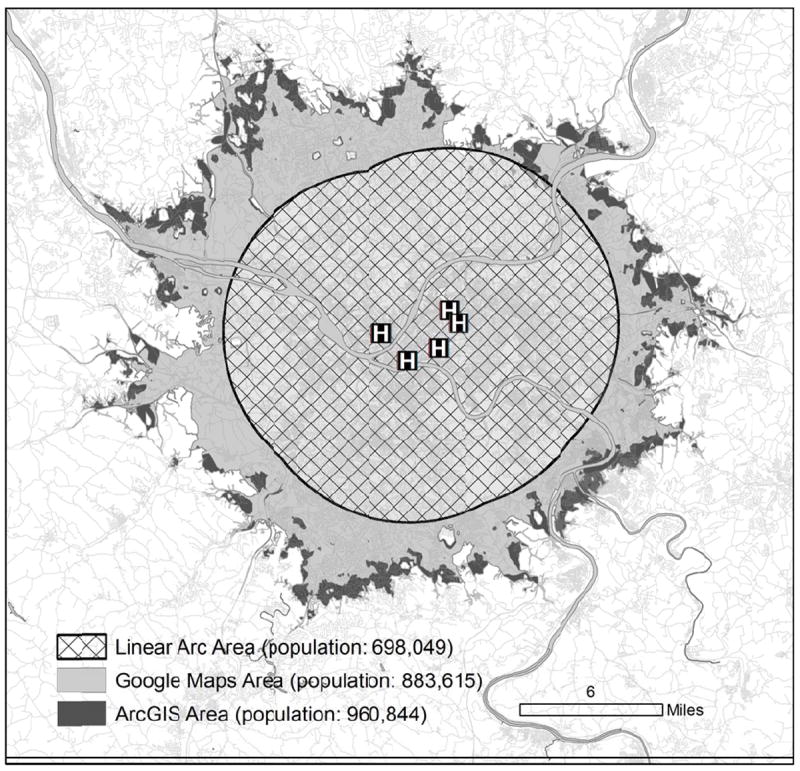
Estimated population living within a twenty-minute drive of hospitals in Pittsburgh, Pennsylvania.
Day of the week sensitivity analyses
We observed that Google Maps estimates varied to a small extent according to the day of the week of the analysis. The largest cumulative difference was found comparing weekday morning and weekend morning analyses (Eastern Standard Time). For this comparison there were 5,099 different estimates (17.0%), accumulating 405 differential minutes (i.e., absolute value of estimate difference between the two days) out of 354,998 total transport minutes. Median transport times were comparable on weekend versus weekend (10.0 minutes, IQR: 7 to 14 min for both).
Discussion
In a large prehospital cohort we demonstrated that route-based transport time estimation is most accurate using Google Maps and least accurate using a linear arc method. The three methods also produced large population differences when used to estimate time-based access to hospital care. A linear regression model that included selected transport characteristics improved estimation accuracy; however, the magnitude of improvement was small.
Both route-based methods were more accurate than the linear arc method of estimating the prehospital transport time. In the past, route-based estimation was limited to computationally intensive software, rendering it impractical for studying large regions or databases. Now, these analyses are feasible with readily available high-speed computing, software interfaces to Google Maps and a highly customizable set of analysis tools through ArcGIS. Linear arc methods no longer offer any advantages to route-based estimation of ground transport times and therefore should be avoided for research or public health planning.
We found that prediction errors for transport times were greater for longer transports. Future applications of transport time estimates should recognize that estimates lose fidelity with increasing trip distance. We also demonstrated that small differences in transport time estimates can translate into large population effects. In our Pittsburgh example, estimates of twenty-minute hospital access by Google Maps and ArcGIS differed by 77,229 persons. Hospital service area projections therefore run the risk of masking geographic “white spaces,” regions without timely access to definitive hospital management. Validation of predicted access with empiric data may therefore be advisable in some circumstances.
We noted a cluster of more accurate estimates in our Bland Altman plots for Google Maps and ArcGIS, when mean transport times were more than fifty minutes (n=330, Figure 2). It is possible that these longer trips had improved estimation accuracy from highway use, but we did not have information on the route traveled by the EMS provider to verify this explanation.
Google Maps generated transport time estimates were more accurate than ArcGIS. This suggests that publically available estimation methods for transport times may be suitable for specific applications. However, there are still compelling reasons to consider dedicated geographic software rather than publicly available internet-based applications such as Google Maps. For example, reproduction of results potentially limits research applications, as Google Maps estimates varied on the day of analysis, albeit to a small extent. Patient privacy and terms of use may also dissuade investigators from using internet-based routing programs. Finally, there are currently limited customization options through the Google Maps interface in STATA, preventing tailored analyses. Consequently, the inability to specify transit time-of-day, as opposed to using the current time, will result in further loss of estimation accuracy for regions with significant traffic variation during the day.
Public health access to definitive hospital care for trauma, acute myocardial infarction, stroke, burns and general emergency care is frequently projected using estimates of EMS response and transport. Route-based methods are generally accurate, although there is lower fidelity during longer trips. For that reason, we should acknowledge the uncertainty about true access for populations more than twenty minutes from acute care hospitals. Estimates may describe geographic access under best conditions, and therefore may underestimate a vulnerable population to time-sensitive medical events. Equally important, transport time overestimates may create duplication of services and system-level inefficiency.
Limitations
This study has several limitations. We focused on transport time, although other prehospital intervals play important roles in clinical care (e.g., notification interval, activation interval, response interval, and on-scene interval).31 Hospital service area calculations can incorporate these other parts of the prehospital timeline. However, we sought to evaluate the accuracy of the transport interval most closely related to population access.
We did not include information on lights and siren use in our regression model. Lights and siren use does not typically have a large impact on EMS transport time, but the effect is more pronounced for longer distances.32,33 It is possible the lights and sirens information would have additionally improved estimation accuracy. We also did not include information on patient severity-of-illness. Severity-of-illness, which is likely correlated with lights and siren use, may have similarly improved the accuracy of our regression model.31
ArcGIS Network Analyst estimates were generated using a software version that did not account for real-time or historical road traffic. These features are available on a subscription basis using a new version of their road atlas.34
Our results may not generalize to all regions. Although our sample included rural areas, the majority of the transports came from ZIP codes with high population density. Therefore, our transport error time estimates may not describe transports in primarily rural ZIP codes. Investigators modeling hospital access in primarily rural areas should consider collecting empiric transport times, in place of generating estimates, to improve accuracy.
We elected to aggregate EMS transports collected in two separate studies. The relative accuracy for each estimation method did not vary within cohorts; however, Google Maps was more accurate in the King County EMS cohort. We considered stratifying all analyses by cohort origin, but ultimately rejected this approach, as each regional cohort was served by multiple EMS agencies. As our objective was to evaluate the accuracy of estimation methods in a large heterogeneous group of prehospital transports, we analyzed both cohorts as a whole.
Finally, we noted significant missing data in certain components of the EMS incident. The majority of excluded records were due to our inability to geocode the exact starting location. Many records had ambiguous starting locations with multiple potential street addresses (e.g. airport or shopping mall), while others indicated a street name without either a number or a cross street. We erred on the side of creating high fidelity starting locations, and consequently, many transports were excluded from analysis. Excluded records were generally similar to the final analysis cohort with respect to patient age, gender, diagnostic category, season and transport time of day. As geographic information systems become more commonplace in prehospital care, future studies will benefit from accurate automated measures of location.
Conclusion
In this validation study, we showed that route-based transport time estimates demonstrate moderate accuracy. These methods can be valuable for informing a host of decisions related to the system organization and patient access to emergency medical care; however, they should be employed with sensitivity to their limitations.
Supplementary Material
Acknowledgments
Grant support: K12-HL109068, K23-GM104022
Footnotes
Financial disclosures: None
References
- 1.The National Institute of Neurological Disorders and Stroke rt-PA Stroke Study Group. Tissue plasminogen activator for acute ischemic stroke. The National Institute of Neurological Disorders and Stroke rt-PA Stroke Study Group. N Engl J Med. 1995;333(24):1581–7. doi: 10.1056/NEJM199512143332401. [DOI] [PubMed] [Google Scholar]
- 2.Berger PB, Ellis SG, Holmes DR, et al. Relationship Between Delay in Performing Direct Coronary Angioplasty and Early Clinical Outcome in Patients With Acute Myocardial Infarction : Results From the Global Use of Strategies to Open Occluded Arteries in Acute Coronary Syndromes (GUSTO-IIb) Trial. Circulation. 1999;100(1):14–20. doi: 10.1161/01.cir.100.1.14. [DOI] [PubMed] [Google Scholar]
- 3.Cannon CP, Gibson CM, Lambrew CT, et al. Relationship of symptom-onset-to-balloon time and door-to-balloon time with mortality in patients undergoing angioplasty for acute myocardial infarction. JAMA: The Journal of the American Medical Association. 2000;283(22):2941–7. doi: 10.1001/jama.283.22.2941. [DOI] [PubMed] [Google Scholar]
- 4.Rivers E, Nguyen B, Havstad S, et al. Early goal-directed therapy in the treatment of severe sepsis and septic shock. N Engl J Med. 2001;345(19):1368–77. doi: 10.1056/NEJMoa010307. [DOI] [PubMed] [Google Scholar]
- 5.MacKenzie EJ, Rivara FP, Jurkovich GJ, et al. A national evaluation of the effect of trauma-center care on mortality. N Engl J Med. 2006;354(4):366–78. doi: 10.1056/NEJMsa052049. [DOI] [PubMed] [Google Scholar]
- 6.Penchansky RR, Thomas JWJ. The concept of access: definition and relationship to consumer satisfaction. Med Care. 1981;19(2):127–40. doi: 10.1097/00005650-198102000-00001. [DOI] [PubMed] [Google Scholar]
- 7.Branas CC, MacKenzie EJ, Williams JC, et al. Access to trauma centers in the United States. JAMA: The Journal of the American Medical Association. 2005;293(21):2626–33. doi: 10.1001/jama.293.21.2626. [DOI] [PubMed] [Google Scholar]
- 8.Klein M, Kramer C, Nelson J, Rivara F, Gibran N, Concannon T. Geographic access to burn center hospitals. JAMA: The Journal of the American Medical Association. 2009;302(16):1774–81. doi: 10.1001/jama.2009.1548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Branas CC, MacKenzie EJ, ReVelle CS. A trauma resource allocation model for ambulances and hospitals. Health Serv Res. 2000;35(2):489–507. [PMC free article] [PubMed] [Google Scholar]
- 10. [2013 Mar 2];Esri Products ∣ A Complete GIS Mapping Software System [Internet] esri.com. Available from: http://www.esri.com/products.
- 11. [2013 Mar 2];Google Maps [Internet] maps.google.com. Available from: http://maps.google.com/
- 12. [2013 Mar 2];Yahoo! Maps, Driving Directions, and Traffic [Internet] maps.yahoo.com. Available from: http://maps.yahoo.com/
- 13. [2013 Jun 15];High-Tech Web Mapping Helps City of New York’s Fire Department Before Emergencies ∣ ArcNews Fall ∣ 2010 Issue [Internet] esri.com. Available from: http://www.esri.com/news/arcnews/fall10articles/new-york-fire-dept.html.
- 14. [2013 Jun 15];County of Los Angeles - Department of Health Services [Internet] ems.dhs.lacounty.gov. Available from: http://ems.dhs.lacounty.gov/GIS/GIS.htm.
- 15.Seymour CW, Kahn JM, Cooke CR, Watkins TR, Heckbert SR, Rea TD. Prediction of critical illness during out-of-hospital emergency care. JAMA: The Journal of the American Medical Association. 2010;304(7):747–54. doi: 10.1001/jama.2010.1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Seymour CW, Band RA, Cooke CR, et al. Out-of-hospital characteristics and care of patients with severe sepsis: A cohort study. J Crit Care. 2010;25(4):10. doi: 10.1016/j.jcrc.2010.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dumas F, Rea TD. Long-term prognosis following resuscitation from out-of-hospital cardiac arrest: Role of aetiology and presenting arrest rhythm. Resuscitation. 2012;83(8):1001–5. doi: 10.1016/j.resuscitation.2012.01.029. [DOI] [PubMed] [Google Scholar]
- 18.Nichol G, Thomas E, Callaway CW, et al. Regional Variation in Out-of-Hospital Cardiac Arrest Incidence and Outcome. JAMA: The Journal of the American Medical Association. 2008;300(12):1423–31. doi: 10.1001/jama.300.12.1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. [2013 Mar 3];Traffic Congestion and Reliability: Linking Solutions to Problems [Internet] ops.fhwa.dot.gov. Available from: http://www.ops.fhwa.dot.gov/congestion_report_04/chapter3.htm.
- 20.GeoLytics Inc. CensusCD 2005-2009 [Google Scholar]
- 21.Ozimek A, Miles D. Stata utilities for geocoding and generating travel time and travel distance information. Stata Journal. 2011;11(1):106. [Google Scholar]
- 22.Sasson C, Cudnik MT, Nassel A, et al. Identifying High-risk Geographic Areas for Cardiac Arrest Using Three Methods for Cluster Analysis. Academic Emergency Medicine. 2012;19(2):139–46. doi: 10.1111/j.1553-2712.2011.01284.x. [DOI] [PubMed] [Google Scholar]
- 23.Sasson C, Keirns CC, Smith D, et al. Small area variations in out-of-hospital cardiac arrest: does the neighborhood matter? Ann Intern Med. 2010;153(1):19–22. doi: 10.1059/0003-4819-153-1-201007060-00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hyndman RJ, Koehler AB. Another look at measures of forecast accuracy. Int J Forecast. 2006;22(4):679–88. [Google Scholar]
- 25.Kottner J, Audigé L, Brorson S, et al. Guidelines for Reporting Reliability and Agreement Studies (GRRAS) were proposed. J Clin Epidemiol. 2011;64(1):11–1. doi: 10.1016/j.jclinepi.2010.03.002. [DOI] [PubMed] [Google Scholar]
- 26.Wilcox RR, Char1in VL, Thompson KL. New monte carlo results on the robustness of the anova f, w and f statistics. Commun Stat Simul Comput. 1986;15(4):933–43. [Google Scholar]
- 27.Diehr P, Yanez D, Ash A, Hornbrook M, Lin DY. Methods for analyzing health care utilization and costs. Annu Rev Public Health. 1999;20:125–44. doi: 10.1146/annurev.publhealth.20.1.125. [DOI] [PubMed] [Google Scholar]
- 28. [2013 Mar 6];TIGER/Line® with Demographic Data - Geography - US Census Bureau [Internet] census.gov. Available from: http://www.census.gov/geo/maps-data/data/tiger-data.html.
- 29. [2013 Apr 9];Official Blog: The bright side of sitting in traffic: Crowdsourcing road congestion data [Internet] googleblog.blogspot.com. Available from: http://googleblog.blogspot.com/2009/08/bright-side-of-sitting-in-traffic.html.
- 30.Diehr P, Lumley T. The importance of the normality assumption in large public health data sets. Annu Rev Public Health. 2002;23:151–69. doi: 10.1146/annurev.publhealth.23.100901.140546. [DOI] [PubMed] [Google Scholar]
- 31.Spaite DW, Tse DJ, Valenzuela TD, et al. The impact of injury severity and prehospital procedures on scene time in victims of major trauma. Ann Emerg Med. 1991;20(12):1299–305. doi: 10.1016/s0196-0644(05)81070-4. [DOI] [PubMed] [Google Scholar]
- 32.Hunt RCR, Brown LHL, Cabinum ESE, et al. Is Ambulance Transport Time With Lights and Siren Faster Than That Without? Ann Emerg Med. 1995;25(4):5–5. doi: 10.1016/s0196-0644(95)70267-9. [DOI] [PubMed] [Google Scholar]
- 33.O’Brien DJ, Price TG, Adams P. The effectiveness of lights and siren use during ambulance transport by paramedics. Prehospital Emergency Care. 1999;3(2):127–30. doi: 10.1080/10903129908958920. [DOI] [PubMed] [Google Scholar]
- 34. [2013 Apr 29];StreetMap Premium for ArcGIS ∣ Street Dataset ∣ Geocoding Addresses [Internet] esri.com. Available from: http://www.esri.com/data/streetmap.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


