Digital Color in Cellulose Nanocrystal Films

Abstract

Cellulose nanocrystals (CNCs) form chiral nematic phases in aqueous suspensions that can be preserved upon evaporation of water. The resulting films show an intense directional coloration determined by their microstructure. Here, microreflection experiments correlated with analysis of the helicoidal nanostructure of the films reveal that the iridescent colors and the ordering of the individual nematic layers are strongly dependent on the polydispersity of the size distribution of the CNCs. We show how this affects the self-assembly process, and hence multidomain color formation in such bioinspired structural films.

Introduction

Cellulose nanocrystals (CNCs) are rodlike crystalline components with diameters ranging from 3 to 20 nm and lengths ranging from 50 nm to a few micrometers.¹ CNCs are obtained by subjecting pure cellulose to concentrated sulfuric acid, which selectively hydrolyses the amorphous domains of the cellulose nanofibrils. In this process, sulfonation of the CNC surface occurs which promotes dispersion of the CNCs in water. A striking feature of CNCs, discovered in 1992 by Revol et al.,² is an isotropic to chiral liquid-crystalline phase transition that is found above a critical concentration. The chiral nematic phase has a helicoidal structure, which consistently shows left-handed chirality. The chiral nematic self-assembly consists of pseudolayers in which the CNCs align along a vector (director), with the orientation of each director rotated slightly about the helicoidal axis from one layer to the next. The vertical distance required to complete a 180° rotation of the director is known as the pitch (p). Chiral nematic order can be retained upon complete drying of a thin film.³ The chiral nematic order gives rise to remarkable optical properties of these films. First, they cause a strong optical rotation of the light.⁴ Second, they selectively reflect light of wavelengths equal to the pitch length. Therefore, only circularly polarized light with the same handedness as the chiral nematic cellulose with the color corresponding to the pitch is reflected.⁵ The relation between the angular-dependent color (in terms of the wavelength λ_r) reflected by the helicoid structure can be approximated as

1

where n_av is the average refractive index of the film (∼1.56 for CNCs⁶) and θ is the angle of reflection with respect to the surface of the film.⁷

The conditions of hydrolysis in the precursor production changes the properties of the resulting nanocrystals by modifying the aspect ratio of the individual nanocrystals, their charge distribution and the defects within the crystalline structure of the cellulose. All these parameters lead to changes in the self-assembly of the rod-like cellulose nanocrystals and thus in the final properties of the CNC films.^8,9 Recently, several different methods have been proposed to tune the chiral nematic pitch and consequently the color¹⁰⁻¹⁵ in order to develop applications such as sensors,¹⁶ decorative coatings,¹⁴ and security encryption in banknotes.¹⁷ However, a complete and quantitative optical characterization of cellulose-based chiral nematic solid films correlated to their microstructure has not yet been performed.

In the present paper, we probe the optical response of CNC films on the microscale. The measured optical response and structural parameters of the structures can be used to extract the refractive index of condensed cellulose nanocrystals in our system. We demonstrate that within a single batch of chiral nematic films, there are distinct color transitions between different domains of different periodicities that can be correlated with the chiral nematic pitch and layering. We reveal a very unusual and unexpected digital layering of these cellulose twists, arising from size-selective assembly processes.

Experimental Section

Materials

The 92-Alpha eucalyptus sulphite pulp was used for the extraction of the CNCs. Sulfuric acid (95–98%) for hydrolysis was purchased from Sigma-Aldrich. All water used was purified (Millipore Milli-Q purification system).

Cellulose nanocrystals (CNCs) were prepared by hydrolysis of the commercial milled hardwood pulp (<0.5 mm). The pulp powder was hydrolyzed in sulfuric acid (10 mL of sulfuric acid solution/g pulp) at a concentration of 64 wt % at room temperature with vigorous stirring for 1 h. The cellulose suspension was then diluted by a factor of 10 with cold Millipore water to stop the hydrolysis reaction and allowed to settle overnight. The clear top layer was removed and the remaining white suspension was centrifuged. After centrifugation, the supernatant was removed and the resulting thick white suspension was diluted and reconcentrated 3 times with millipore water to remove all soluble cellulose materials. The white suspension obtained after the last centrifugation step was placed inside dialysis membrane tubes with a 12 000–14 000 molecular weight cutoff (Spectrumlabs/Spectra-por membranes) and dialyzed against slow running pure water for 2–4 weeks or until the pH of the nanocrystalline cellulose suspension reached 6. This final suspension was concentrated by centrifugation to reach a concentration of 5 wt %.

Optical Analysis

The optical imaging and spectroscopy were performed using a custom-modified BX-51 Olympus optical microscope equipped with a color digital CCD camera (Lumenera Infinity 2–1C). Unpolarised light from a halogen lamp was coupled into a 10× objective (Olympus, MPLFLN-BD 10) with a numerical aperture NA = 0.3. The reflected signal from the sample was filtered using a superachromatic quarter wave-plate (B. Halle) combined with a polarizer (Thorlabs). The polarizer and wave-plate were mounted onto independent motorized rotation stages that can be inserted and removed from the optical path.¹⁸ Part of the transmitted signal was coupled into a 50-μm core optical fiber (Ocean Optics) mounted in confocal configuration to achieve a spatial resolution of approximately 20 μm, smaller than the domain dimensions within which the samples showed homogeneous color. The remaining beam was focused into the camera for imaging.

Microstructure of the Films

The structure and morphology of the samples were characterized using a Leo Gemini 1530VP-Zeiss scanning electron microscope (SEM). The CNC films on polystyrene Petri dishes were flaked off and the flakes were placed on a sample holder so that the cross-section could be imaged. In order to prevent charging in the SEM, the samples were coated with a thin layer of metal alloy using a sputter-coater (Emitech K550) with a Pd/Au target at a current of 55 mA for 6 s.

CNC Analysis

Atomic force microscopy (AFM) images of the cellulose nanocrystals were acquired with a Pico Plus atomic force microscope (Molecular Imaging) operating in air. All samples were scanned in tapping mode with a Mikro Masch NSC36/NO AL probe (cantilever C, tip radius 8 nm, nominal resonance frequency 65 kHz, nominal spring constant 2 N/m). The samples were prepared by drop-casting 10 μL of a 0.001 wt % CNC suspension onto a freshly cleaved mica surface with an approximate area of 2 cm², and air-dried for approximately 30 min. Prior to the drop casting, the CNC suspensions were ultrasonicated for 5 min to reduce the number of aggregates.

Results and Discussion

To employ these films in advanced optical systems, the ability to distinguish pure chiral nematic order from related phases, which show only partial chiral nematic order, is of great importance. For this reason, accurate and quantitative optical characterization is essential.

To form iridescent solid films of cellulose nanocrystals, 1 mL of the 4 wt % CNC suspension was poured into a polystyrene Petri dish of 3 cm diameter and allowed to dry at ambient conditions. The slow evaporation process resulted in highly colorful dry films after approximately 12 h, shown in Figure 1a under white light illumination. During the evaporation process, a bright, rainbowlike ring developed at the edge of the Petri dish, with colors ranging from dark blue at the perimeter to red in the inner ring. Although the center of the film displays a weaker reflection, only this part exhibits pure chiral nematic order (see Figure S1 in the Supporting Information).

Figure 1.

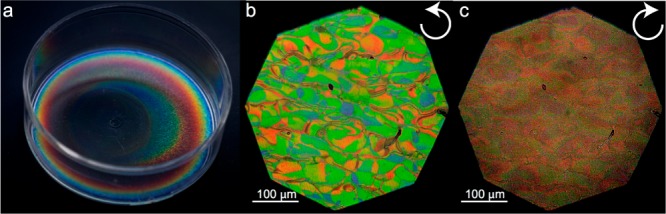
(a) Dry chiral nematic CNC films in a polystyrene Petri dish formed from a 4 wt % CNC suspension in water. Polarization optical micrographs at the center of the film showing reflected (b) left-handed circularly polarized light LCP and (c) right-handed circularly polarized light RCP light.

During drying, the CNC suspension adopted a radial concentration profile, which is a common phenomenon in particulate suspensions, often called the “coffee ring effect”.¹⁹ The annular pattern arises from capillary flow because of differential evaporation rates across the droplet. Because the evaporation flux at the edge of the droplet is faster than in the center, the liquid and particles flow to the drop perimeter, increasing the deposition of particles at the edge. This effect also plays a crucial role in the arrangement of the nanocrystals during water evaporation and is responsible for an additional linear dichroism at the edge of the solid film. Similarly, this gives rise to a CNC concentration gradient toward the edge, resulting in a thickness gradient in the dry film, which is the reason for the formation of the rainbowlike color gradient.

The remainder of our analysis focuses on the central area of the film. Vivid colors were detected only in the reflected left-hand circularly polarized (LCP) light, while the right-hand circularly polarized (RCP) reflection image is largely colorless (Figure 1b, c). The size distribution of the CNCs sensitively influences the domain morphology arising from the CNC self-assembly process. Therefore, the width and the length distribution of the cellulose nanocrystals were determined via a statistical analysis of AFM images containing about 100 individual nanocrystals (see Figure S2 in the Supporting Information). The average CNC width was 5.7 nm with a variation between 4 and 11 nm, which indicates side-by-side adhesion of a few cellulose nanocrystals, which is commonly seen in CNCs.²⁰ The average CNC length was 60 nm with a large length distribution of 30 to 160 nm.

Two main factors play a role in the self-assembly process: the first is water evaporation from the anisotropic phase and the second are interactions between the particles in the thin film. As the water evaporates, the interparticle forces increase and selectively transport CNCs with different aspect ratios to different regions within the suspension. Thus, the broad particle length distribution leads to formation of different domains⁸ while also contributing to the observed CNC concentration gradient toward the edge. Uniformly deposited monodisperse ellipsoidal particles experience increasing interparticle interactions with rising anisotropy in particle shape.²¹ The CNCs with the highest anisotropy are expected to assemble at the edge of the solution where the radial flow induces CNC alignment, which competes with helical layer formation. This is in agreement with the linear dichroism observation at the film edge.

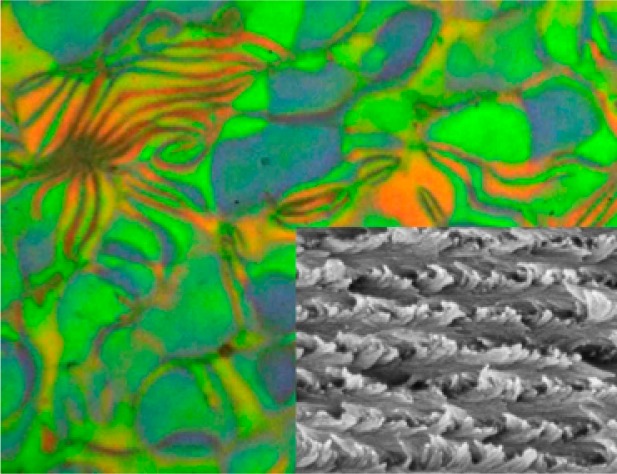
By observing the film in cross polarisation configuration and also using a circular polarization filter in different areas, we find that only the central region of the film (up to 12 mm from the center) exhibits pure chiral nematic behavior, where however the color is not uniform but “digital”. We clearly observe individual domains with dimensions that vary from 2 to 20 μm. The LCP image displays a mosaic of domains with different shapes and three dominating colors: green, blue and orange. To reveal the origin of this color formation and correlate it with the chiral nematic pitch, we studied the cross-section of the film by scanning electron microscopy (SEM). At selected locations near a fracture edge, the film was first investigated optically and the labeled domains were then examined using high magnification SEM. The reflection polarization optical microscopy (POM) and SEM images of three different domains along the fracture line (Figure 2) clearly show a pseudolayered helical structure. The left-handed twisting alignment of the nematic director is evident: going from the bottom to the top of the film, the long axes of the nanocrystals rotate clockwise around an vector perpendicular to the surface, indicating a left-handed helicoidal organization. In each SEM, the chiral nematic order is quite uniform and well-defined along the entire fracture edge. Interestingly, this film is also the thinnest chiral nematic CNC film reported to date, with a thickness that ranges from only 1 to 1.3 μm. This also explains the lower reflectivity at the center of the film under ambient light illumination but indicates that even in the presence of strong adhesion forces the chiral nematic phase can be maintained.

Figure 2.

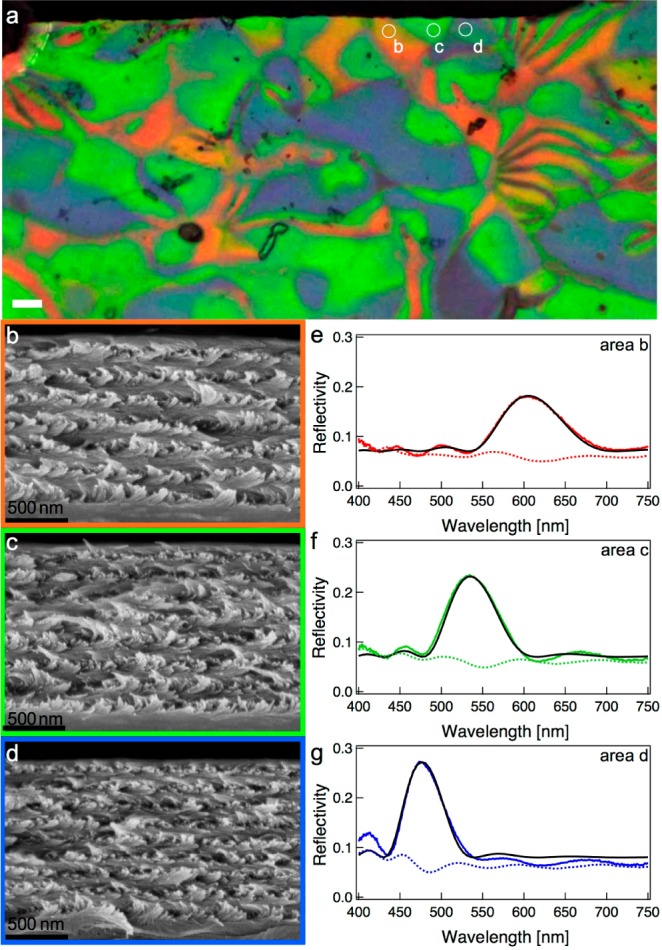
Correlation of optical and electron microscopy and the reflectance spectra of the different domains. (a) Reflected LCP image zoomed into Figure 1b. The white circles show areas b, c, d from which reflectance spectra and (b–d) cross-sectional SEMs were acquired. (e–g) Corresponding reflectance spectra; the black solid lines are curve fits to the spectra using Berreman’s 4 × 4 matrix method.

By correlating the POM images to SEM cross-sections, the origin of the different colors can be determined. According to eq 1, there are two possible explanations for the variation in color of the different domains: a difference in the tilt angle of the helicoidal axes or a difference in pitch. In the first case, the helicoidal structure would have a nematic vector axis which is slightly tilted with respect to the surface normal, and therefore the incident and reflected light are effectively oblique to the helicoidal axis. However, a tilt in the chiral nematic axis would be visible in the SEM images and would also influence the optical response in the RCP channel. In particular, the reflected light would then be elliptically polarized instead of perfectly LCP. Both from images b and c in Figure 1 and from the spectra in Figure 2 we observe that there is no color contribution in the RCP channel and we therefore conclude that the domains are not tilted.

Consequently the color variation has to be associated with the variation of pitch inside the layered structure, with a larger pitch resulting in a longer reflected wavelength. To investigate this effect, we measured the structural periodicities of domains in the different areas and compared these to the observed spectral peaks, as reported in Table 1. The values of λ_r predicted by eq 1 using the structural parameters from Table 1 and an average refractive index n_av ≈ 1.56 matches the peak wavelengths of Figure 2 very well, thus confirming that the variation in pitch lies at the origin of the color variation.

Table 1. Chiral Nematic Pitch of Different Domains in the CNC Film As Determined from the Cross-Sectional SEM Images.

	domain b	domain c	domain d
color of the domain	orange	green	blue
λr (nm) extracted from spectra	590	530	470
pitch (nm) from SEMs	190 ± 15	170 ± 10	150 ± 10
no. of periods	6.5 ± 0.5	7.5 ± 0.5	8.5 ± 0.5
predicted λr (nm) from SEMs	593	530	468
predicted thickness (μm)	1.235	1.275	1.275

We have performed a thorough analysis of the reflectance spectra using the Berreman method,²² which allows a full calculation of the reflectance spectra.²³ In this technique, helicoidal structures of optical anisotropic media are treated as finite stacks of birefringent plates. The method takes into account the effects of refraction and multiple reflections of the electromagnetic waves between plate interfaces and is capable of producing exact solutions.²⁴ The complete reflectance spectrum of a film under normal incidence can be calculated based on three parameters: the magnitude of the linear birefringence (Δn), the pitch p, and the number of periods (N). While fixing the average refractive index at n_av = 1.555, the value of n₀ is taken as 1.524 and n_e =1.586 (that is, Δn = n_e – n₀ = 0.062) in order to obtain best fits. The values of p and N were determined from the SEM images, incorporating also the uncertainty given in Table 1 in the calculation. The resulting best fits are shown as solid black lines in Figure 2e–g, with the fit parameters listed in Table 2. We find good agreement between the experimental and theoretical spectra, which confirms the excellent correlation between the SEM and POM data.

Table 2. Fit Parameters for LCP Reflectance Spectra of Different Domains in the CNC Films.

	Domain B	Domain C	Domain D
Pitch (nm)	196	172	154
No. Of Periods	6	7	8
Linear Birefringence (ΔN)	0.062	0.062	0.062

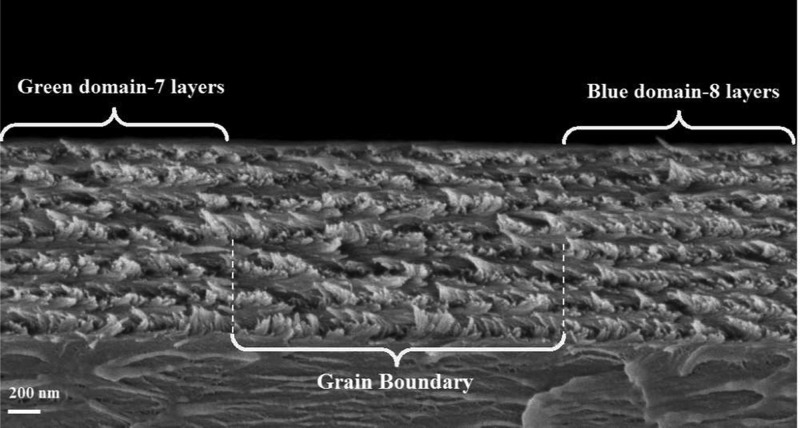
Both the POM images and the SEM analysis show that within each single color domain the chiral nematic order is quite homogeneous. Moreover, the chiral nematic order is preserved over a long lateral range of up to several tens of μm in the largest domains, 10–100 times greater than the length of individual nanocrystals. However, at boundaries between the domains, distinct defects are visible. One such defect is depicted in Figure 3. Grain boundaries appear dark in the LCP image, with a lateral width on the order of 1–2 μm, delimiting crystalline regions of different periodicities, where the symmetry of the chiral nematic order is broken. In Figure 3, the distinct transition between domains of different periodicities are clearly shown: upon going from left to right, which corresponds to a transition from a green to a blue domain, the number of layers increases from 7.5 to 8.5 via a disclination that is evident in the SEM image. Because the thickness of the film is the same across this field of view, this implies that the pitch of the blue domain is smaller. This is consistent with the reflected wavelengths measured by POM.

Figure 3.

SEM image of the transition between two differently colored domains in the CNC film.

Although the correlation between the pitch and the spectra is evident, the origin of a digital layering in the film is unexpected. Note that the total thickness of the film is highly conserved across the different domains (Figure 3 and Table 1), caused presumably by surface tension during film formation. Also, the nematic directors in the top and bottom layers of the film of neighboring domains must be strongly coaligned. These are two requirements for the formation of digital layering. Neighboring domains can only differ by an integer number of chiral layers (N), ensuring that only distinct sets of colors are observed across the film.

The number of observed layers depends on the favorable twist angle, which in turn depends on the individual morphology and dimensions of the nanocrystals as well as surface interactions between them.²⁵ For a given film thickness and a monodisperse assembly, a unique optimal pitch would be expected, giving rise to a uniform color. However, the strong nematic order implies that domains can form within different regions by adding or subtracting an entire layer, while retaining the director alignment at top and bottom of the film, producing the observed color effects. The director coalignment at top and bottom surface is likely caused by surface tension steric alignment of the highly anisotropic CNC surface, suggesting the importance of surface preparation in future work. Because a larger interlayer twist induces a reduced string for smaller nanocrystals, it is likely that self-sorting occurs within the films, driving the segregation of smaller nanocrystals to regions with a larger number of layers. Indeed, more monodisperse nanocrystals yield films with more uniform color appearance, but this effect require a more detailed study.

The lateral size of the domains is influenced by many factors including the initial concentration of the suspension, the evaporation rate and temperature, the CNC surface and the ionic strength of the medium. Critically, however, the digital layering observed here emphasizes the need for the careful of the CNC assembly process.

Conclusion

Multicolored chiral nematic cellulose films were produced by the slow evaporation of CNC suspensions on polystyrene substrates. Polarized optical microscopy reveals that these films selectively reflect left-hand circularly polarized light at a specific set of wavelengths. These films exhibit distinct differently colored domains with sizes ranging from a few micrometers to several tens of micrometers, depending on the preparation conditions. Scanning electron microscopy confirms that the films have a left-handed helicoidal structure and contain multilayers of specific pitch. Within domains of a single color, the pitch is very well-defined, with defects at grain boundaries separating the domains. These defects represent discontinuities in the orientational order as a result of a sudden change in the pitch. Rigorous quantitative microscopic optical analysis is essential to reveal the optical properties of such films. Combining this with fits to a model of the local reflection spectra allows noninvasive probing of the sample microstructure. These results show that the self-assembly of nanocrystals of cellulose is considerably more subtle than previously suspected, with surface and nematic energies competing to determine the final helicoidal structure. This work suggests that surface preparation and new approaches to film formation that control the surface director will be important to produce advanced optical materials from such a self-assembly process. In addition, the results clearly suggest new questions about the assembly of chiral cellulose stacks within plants, reflecting the importance of biomimetic approaches to both synthetic and natural systems.

Supporting Information Available

Photograph of a dry CNC film showing the color at the edge of the film and corresponding optical images of the left and right polarization channels; AFM image of the cellulose nanocrystals in the height-mode. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The research leading to these results has received funding from the BBSRC David Phillips fellowship (BBSRC David Phillips, BB/K014617/1) and Next Generation fellowship (to S.V.) and the Schlumberger Foundation (Faculty for Future fellowship to A.G.D.), the EPSRC Carreer Acceleration Fellowship (EP/H00338X/2) the Royal Society (E.R.), EPSRC grant EP/G060649/1 (to U.S. and J.J.B.), and ERC LINASS 320503 (to J.J.B.).

The authors declare no competing financial interest.