Abstract
We review a multiscale model of saliva secretion, describing in brief how the model is constructed and what we have so far learned from it. The model begins at the level of inositol trisphosphate receptors (IPR), and proceeds through the cellular level (with a model of acinar cell calcium dynamics) to the multicellular level (with a model of the acinus), finally to a model of a saliva production unit that includes an acinus and associated duct. The model at the level of the entire salivary gland is not yet completed. Particular results from the model so far include (i) the importance of modal behaviour of IPR, (ii) the relative unimportance of Ca2+ oscillation frequency as a controller of saliva secretion, (iii) the need for the periodic Ca2+ waves to be as fast as possible in order to maximise water transport, (iv) the presence of functional K+ channels in the apical membrane increases saliva secretion, (v) the relative unimportance of acinar spatial structure for isotonic water transport, (vi) the prediction that duct cells are highly depolarised, (vii) the prediction that the secondary saliva takes at least 1 mm (from the acinus) to reach ionic equilibrium. We end with a brief discussion of future directions for the model, both in construction and in the study of scientific questions.
Keywords: calcium oscillations, inositol trisphosphate, water transport, Sjögrens syndrome, aquaporins, salivary gland duct cells, salivary gland acinar cells
1. Introduction
The primary physiological role of salivary glands is the production of saliva; a hypotonic fluid containing electrolytes and a complex mixture of macromolecules [1,2,3]. Saliva begins the initial digestion of food, provides defence from microorganisms and protection from physical and chemical assault on the oral cavity. Saliva is therefore vital for oral health and general well being. The importance of saliva is most acutely appreciated in individuals with salivary gland hypo-function [4, 5]. “Dry mouth” most commonly occurs as a consequence of medication and radiotherapy for head and neck malignancies. Dry mouth also can result from organic disease such as duct obstruction in cystic fibrosis patients or frequently in Sjögrens syndrome [6, 7, 8], a relatively common autoimmune disease associated with significant morbidity. Patients with Sjögrens syndrome typically have a profound dry mouth resulting in altered perception of taste, difficulty in swallowing and speech, together with an increased susceptibility to dental caries and oral candidiasis.
A fundamental prerequisite for developing therapies for salivary gland dysfunction is a thorough understanding of the entire fluid secretion process, not just its isolated components. Experimental approaches to the study of salivary function and pathology are, of course, crucial. Nevertheless, theoretical methods can also play a vital complementary role. Although it is clear that the behavior of an organ is the result of the integrated sum of the behaviors of its constituent cells and molecules, it is extraordinarily difficult to make this connection explicit, and therefore to understand it in detail. In general, experiments measure the constituent properties, or the whole-organ behavior, but cannot easily make a direct link between the two. In addition, measurements of the isolated components of a complex system are not necessarily predictive of the overall behavior of that system.
Computational models have a vital role to play in helping to understand the relationship between cellular properties and whole-organ behaviour, but come with their own set of difficulties and limitations. It is not a trivial matter to understand, within the framework of a single unified model, the behaviour of cells and organs, from the level of cellular components (with space and time scales on the submicron and millisecond time scales) to the level of the organ (with typical space and time scales of centimetres and minutes). Such models, varying as they do over multiple time and space scales are called multiscale models, and are arguably the most important challenge presently facing computational modellers in physiology. The challenge arises not only because there are few available methods even for the construction, let alone the analysis, of such models. It also arises from the fact that each multiscale problem in physiology must be treated on its own merits, possibly in a way quite different to every other exisiting multiscale model – a multiscale model of the heart, for example, may be of quite limited use in the construction of multiscale models of the lung, or the liver, or the salivary gland – and thus, in a sense, different wheels need to be continually reinvented.
The multiscale model of saliva secretion that we present here is still a work in progress, and we can still only ask, not answer, many questions about the interaction of spatial structure and organ function. Nevertheless, it has already contributed a significant amount to our understanding of how parotid acinar cells work, and how they interact, and is the first step along the path towards a greater understanding of salivary gland function, from molecule to organ.
2. The physiology of saliva secretion
Reviews of the physiology of saliva secretion can be found in [9, 10, 11, 12, 1, 13, 14, 15]. Saliva is secreted by three major pairs of glands – the sublingual, submandibular and parotid glands – as well as from a large number of minor glands scattered through the oral cavity. In each of the major glands primary saliva is produced by acinar cells, which are grouped in grape-like clusters at the terminal branches of a tree-like branching system of ducts, which are lined by duct cells. The primary saliva then travels along the ducts, where its ionic composition is modified by duct cells, to produce secondary saliva which is secreted into the oral cavity. Acinar cells are either serous or mucus, with the proportion of each type determined by the gland and the species, while duct cells also come in a variety of types each with different ion transport functions.
Secondary saliva is typically about 99% water, although the secretion from some glands can be a lot more viscous, due to the presence of large amounts of mucus. The majority of saliva (humans typically produce about a litre a day) comes from the submandibular and parotid glands.
Here, we focus almost entirely on the parotid gland, although data from other glands is used if there are no other options.
2.1. Acinar cells
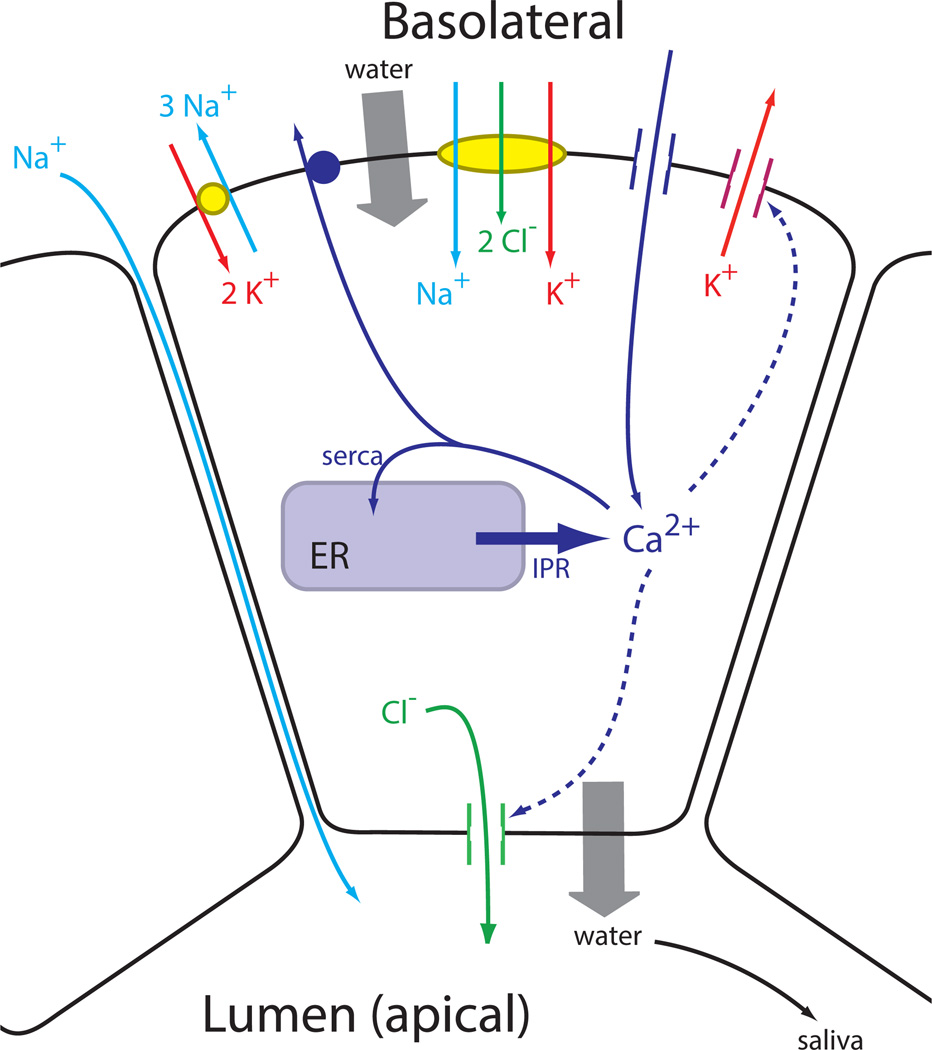
Parotid acinar cells are polarized epithelial cells (Fig. 1). The basolateral membrane faces to the extracellular space, while the apical membrane faces into the lumenal compartment, which is where the primary saliva is secreted. Multiple acinar cells secrete into the same lumen, a fact that will become important later when we consider the multicellular spatial structure.
Figure 1.
The major ion channels involved in the secretion of saliva, and their control by Ca2+. Although Ca2+-sensitve K+ channels are also situated on the apical membrane, they are omitted here for clarity.
The basolateral membrane has a variety of ion exchangers and channels (Fig. 1), including the Na+/K+ ATPase, a Na+/K+/Cl− cotransporter and a Ca2+-dependent K+ channel. On the apical membrane the most important ion channel is a Ca2+-dependent Cl− channel.
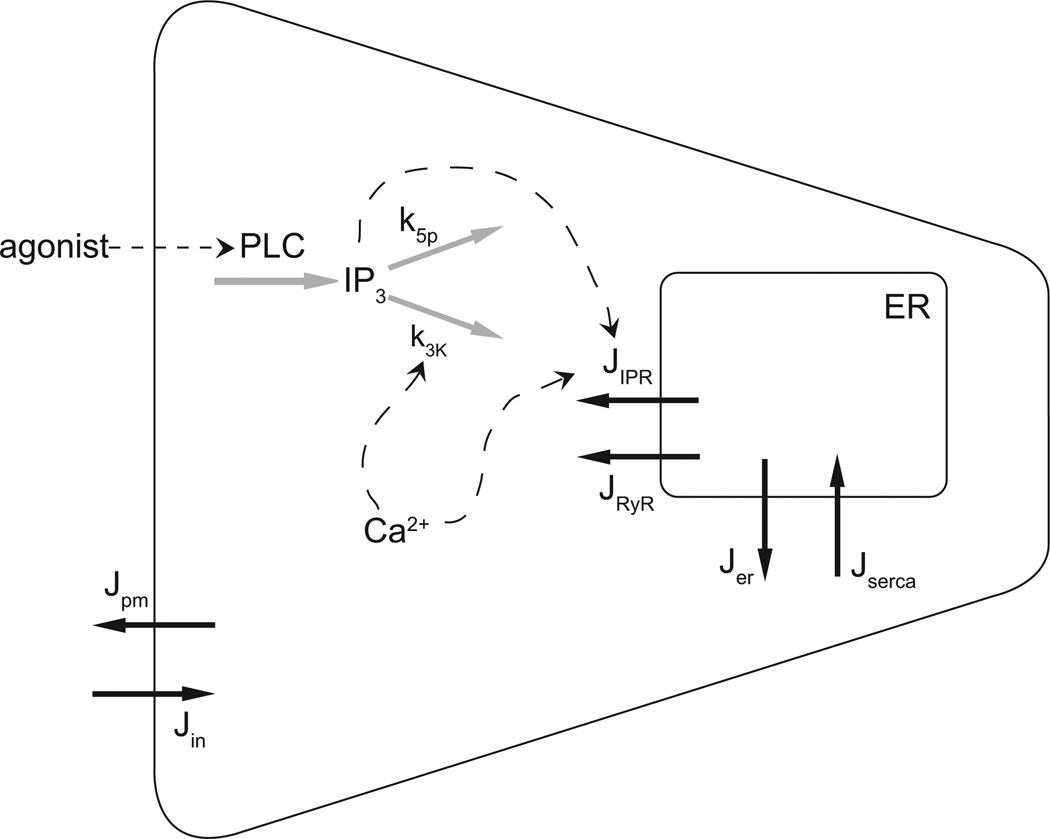
Control of Ca2+ is crucial (Fig. 2). Binding of an agonist to G-protein-coupled receptors (P2Y purinergic receptors, for example, or alpha-adrenergic receptors) results in the activation of phospholipase C (PLC) and thus production of inositol trisphosphate (IP3). This pathway is important for the control of Ca2+ dynamics in almost all cell types, and is described in much more detail in [16, 17, 18, 19, 20, 21]. IP3 binds to IP3 receptors (IPR), which are Ca2+ channels situated on the membrane of the endoplasmic reticulum (ER), resulting in the release of Ca2+ from the ER. Ca2+ can also be released from the ER through ryanodine receptors (RyR) or through a generic small background leak (Jer), and is taken up into the ER by SERCA pumps. Finally, Ca2+ is removed from the cell by ATPase pumps on the plasma membrane and enters the cell through a variety of channels (although we shall simplify the modeling of Ca2+ entry by presuming only a single channel type). The rate of degradation of IP3 is controlled by Ca2+ via its effect on the 3-kinase that converts IP3 to IP2. Thus, k3K is an increasing function of Ca2+.
Figure 2.
Summary of the important reactions involved in the control of Ca2+ in a salivary acinar cell. Agonist stimulation induces the formation of IP3, which releases Ca2+ from the endoplasmic reticulum (ER) via the opening of IP3 receptors (IPR). The rate of degradation of IP3 is Ca2+-dependent. Calcium is pumped into the ER, and out of the cell, by ATPase pumps, while it can also leave the ER through ryanodine receptors (RyR). Jpm represents the removal of Ca2+ from the call by plasma membrane ATPase pumps, while Jin represents a generic influx of Ca2+, most likely through receptor-operated or store-operated Ca2+ channels.
The basic mechanism of saliva secretion is thus as follows. Stimulation of the cell by agonist results in the release of Ca2+ from the ER, and the resultant increased [Ca2+] activates the Ca2+-dependent Cl− channel on the apical membrane. Cl− thus flows out of the cell, down its electrochemical potential gradient into the lumenal space, depolarising the cell. If there were no other ion currents, this Cl− current would quickly Cease as the membrane depolarises. However, simultaneous activation of the Ca2+-dependent K+ channels on the basolateral membrane maintains the membrane potential at a sufficiently negative voltage to allow for the continued flow of Cl− out of the cell. Na+ follows Cl− into the lumenal space, most likely via an extracellular pathway, and water follows via osmosis.
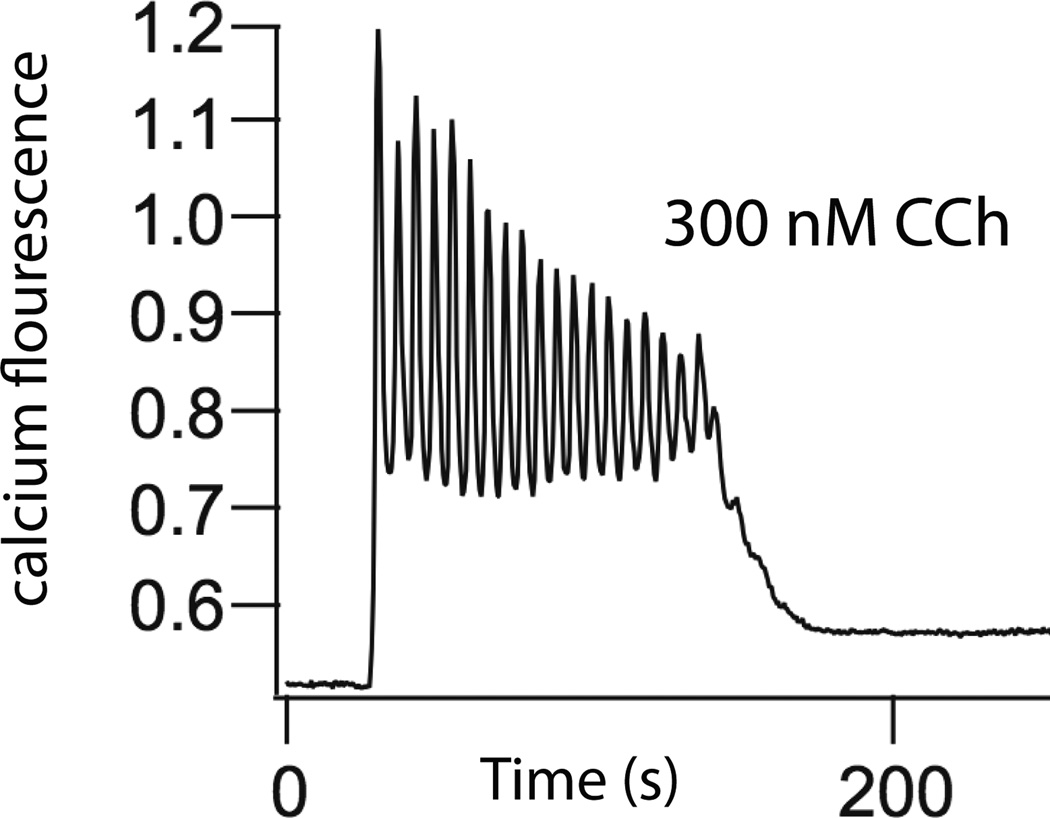
Upon agonist stimulation [Ca2+] does not simply rise to a new steady plateau. It is observed experimentally that [Ca2+] oscillates with a period of around 5–30 seconds (Fig. 3). Despite multiple quantitative models [16] the exact mechanisms underlying such oscillations remain unclear. However, since it is not the purpose of this paper to enter into such questions in detail we present only a single model here, although we urge the reader to keep in mind the associated uncertainties. In our model, an increased [Ca2+] increases the activity of the 3-kinase that degrades IP3 (Fig. 2), and thus there is a negative feedback loop controlling [Ca2+] [23]. It is this feedback loop that causes oscillations in [Ca2+].
Figure 3.
Oscillations of Ca2+ concentration in a parotid acinar cell, in response to carbachol (CCh) [22].
2.2. Duct cells
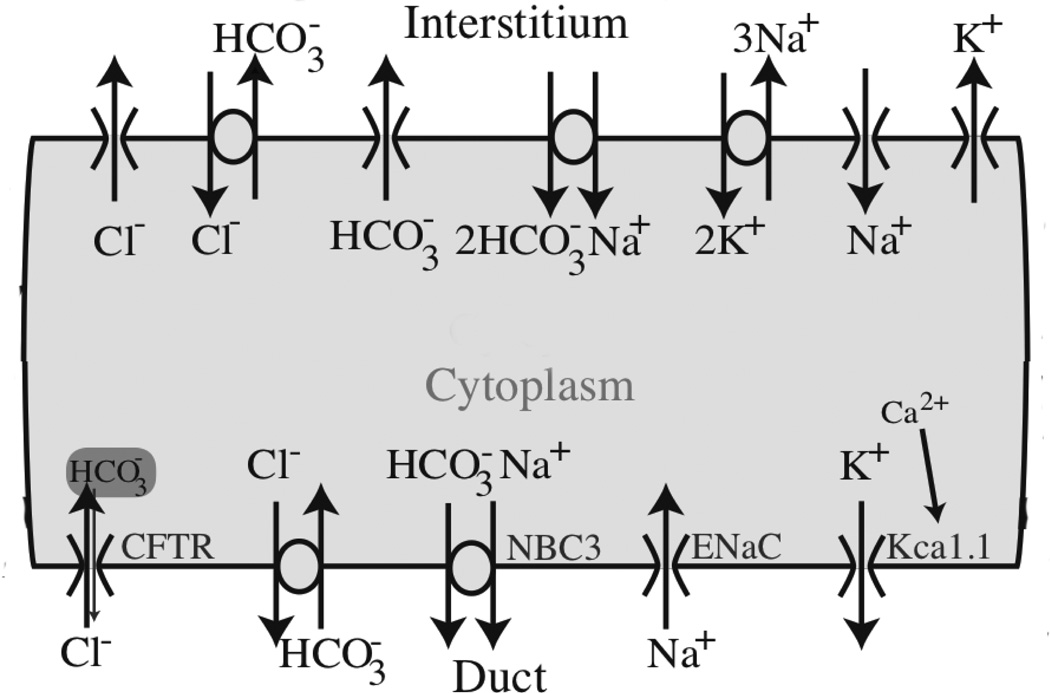
Considerably less is known about duct cells. Their principal function is to replace NaCl with KHCO3, and thus they come equipped with a variety of ion channels on their apical and basolateral membranes (Fig. 4) [24]. Furthermore, secondary saliva is hypotonic with respect to the cell. Thus, duct cells need to be impermeable to water, otherwise they would absorb water leading to a severe decrease in saliva production. In this respect salivary duct cells are quite different to pancreatic duct cells, which are permeable to water.
Figure 4.
Diagram of the major ionic currents in a salivary duct cell [24]
Calcium dynamics has been measured in detail in duct cell lines (HSY and HSG cells) [25, 26, 27, 28], but at present it is not known how accurately the behaviour of these cell lines reflects that of parotid duct cells in vivo.
2.3. Spatial structure
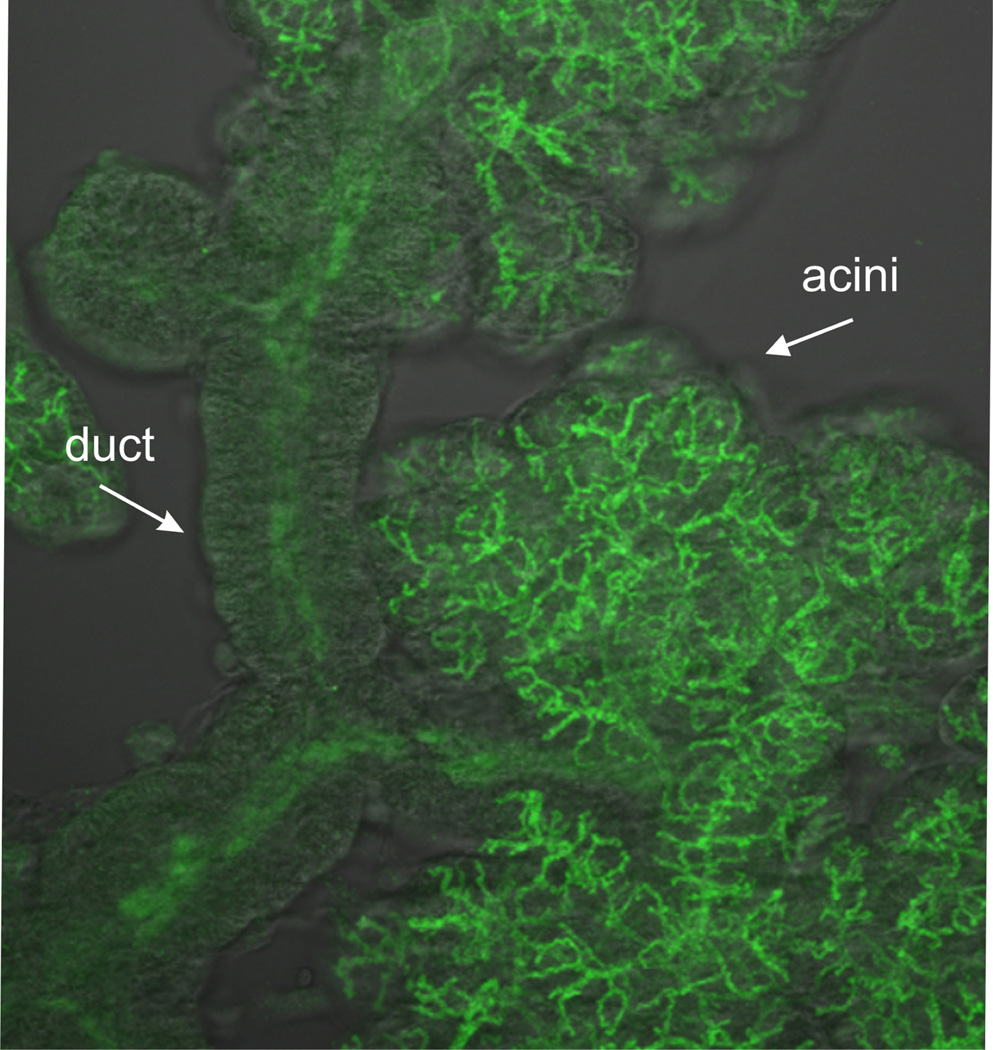
It is now possible to obtain detailed images of the structure of a parotid acinus and its associated ducts (Fig. 5). As has been known for a long time, the ducts form a tree-like branching structure [29], and the acinar cells are situated at the terminals of the tree branches. However, the acinar cells themselves are distributed around a lumen which is itself a branching structure [30]. Thus, each acinar cell secretes fluid into a small lumenal tube, and there is no common lumen into which all the acinar cells secrete. It is currently not known what role this lumenal spatial structure plays in determining the properties of the primary saliva, and this is one question (among many) which will be addressed, although not yet answered, by our multiscale model.
Figure 5.
The detailed spatial structure of the lumen and associated ducts of a salivary acinus, obtained by flourescent labelling of apical membrane markers (such as the TMEM16a Cl− channel) in a clump of acinar tissue.
3. The model
The multiscale model is built as a series of modules, from the molecular level through to the organ level (although the organ level is not yet completed), and these modules are then connected into an overall multiscale model. Much of the interaction between the modules is of a feed-forward type. For example, a typical chain of effect would go as follows,
without any apparent feedback from, say, the primary saliva to the level of agonist stimulation, or to the properties of the Ca2+ oscillations. This greatly simplifies the construction of the multiscale model; at each stage, the input to one level can just be taken to be the output from the previous level, and at the organ scale these outputs are summed to give the output of the entire gland. Within each module, of course, there are multiple feedback processes (otherwise one could never obtain Ca2+ oscillations, for example), but these are dealt with internally to each module.
In the following description of the model we do not list all the equations for each module. To do so would require more space than we have available. Instead, we try to give an overview of the model structure. The exact model equations can all be found in the literature, to which we refer the reader.
3.1. The molecular level: IPR
At the heart of the multiscale model sits the model for Ca2+ oscillations, and this in turn depends crucially on the properties of the inositol trisphosphate receptors (IPR). This is the Ca2+ channel that controls Ca2+ release from the ER, and is thus necessary for Ca2+ oscillations to occur. Many models of the IPR have been constructed [31, 32], but the latest generation of models is based on single-channel data measured from on-nuclei patch clamp experiments [33, 34, 35, 36]. These data have allowed the construction of IPR that are more closely based on in vivo behaviour. The IPR model we use is discussed in slightly more detail in the Results section, as it was derived specifically as part of the construction of our multiscale model.
It is not always a simple matter to use a detailed IPR model as the basis of a model for Ca2+ oscillations. The IPR model is stochastic, and is controlled by Ca2+ concentrations in very small microdomains around the mouth of the channel [37]. Thus, methods must be developed to allow for the simplification of the IPR into an approximate deterministic model, and the incorporation of Ca2+ microdomains in a way that is not too computationally intensive. Work on such model simplifications are ongoing.
3.2. The cellular level: acinar cells
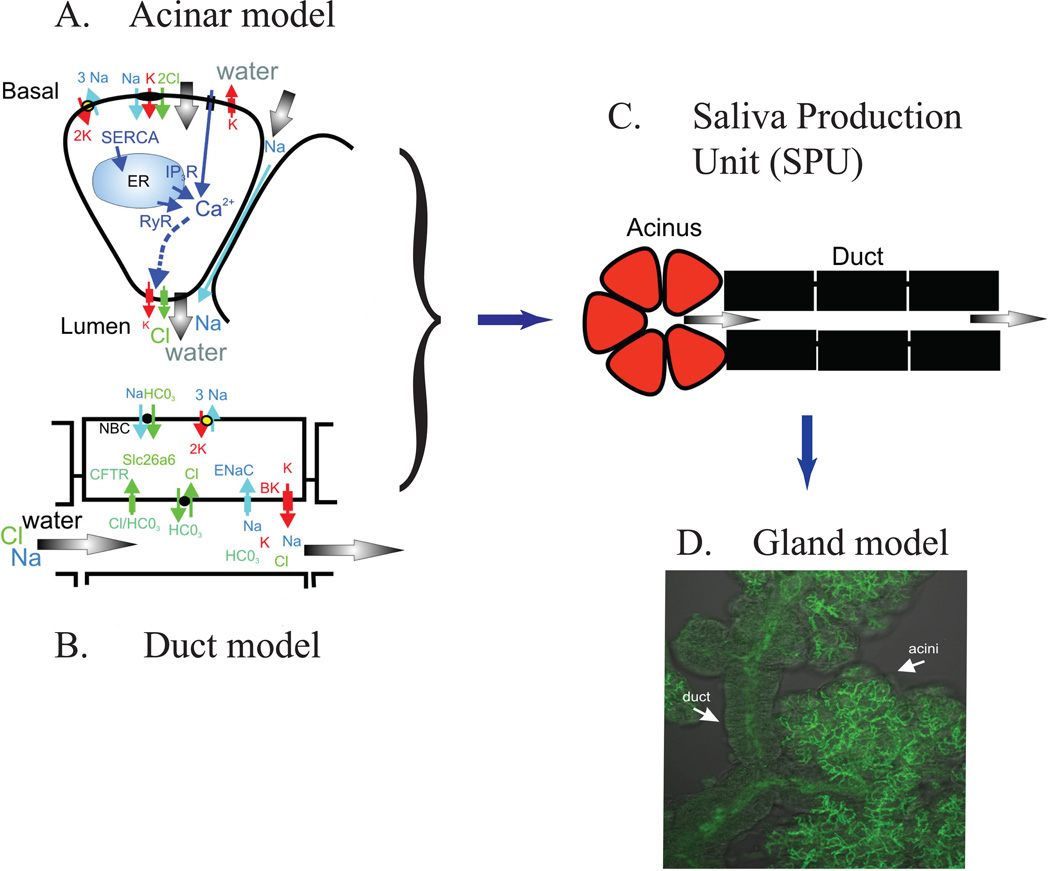
The acinar cell model is based on the schematic diagrams of Figs. 1 and 2.
3.2.1. The calcium and IP3 equations
The cell is initially assumed to be well-mixed, with no spatial gradients of [Ca2+]. This severe approximation will be relaxed subsequently, but is useful for the initial model construction. If we let c denote the concentration of Ca2+ in the cytoplasm (with volume w), and ce denote the concentration of Ca2+ in the ER (with volume we), then conservation of Ca2+ gives
| (1) |
| (2) |
Each J denotes a flux of Ca2+, in units of moles/second, and comes with its own model.
JIPR is the flux through the IPR and is modelled as described in the previous section and in [33]; it is a function of c and the IP3 concentration, p.
JRyR is the flux through the RyR and is modeled as in [38].
Jer is a background leak out of the ER, and modelled as a linear function of ce – c.
Jserca is the flux through SERCA pumps and is modelled as a Hill function with coefficient 2 [39].
Jpm is an analogous flux through plasma membrane ATPase Ca2+ pumps and is modelled as another Hill function, but with coefficient 3. There is no good reason for choosing a different Hill coefficient for the plasma membrane pump, and changes to this coefficient have little effect on behaviour.
Jin is a flux of Ca2+ into the cell and is assumed here to be through a receptor-operated channel (ROC) of unknown mechanism. We thus assume that this flux is a linearly increasing function of agonist stimulation.
The equation for [IP3] (p) is
| (3) |
where ν denotes the level of agonist stimulation, and the rate of IP3 degradation is an increasing function of c (see Fig. 2).
3.2.2. The current and voltage equations
There are similar conservation equations for the concentrations of Na+, Cl− and K+, based on the transport mechanisms shown in Fig. 1. Thus, for example,
| (4) |
where ICl is the current through the apical Cl− channels, zCl is the valence of Cl−, F is Faraday’s constant, and JNKCC is the flux (in moles per second) through the Na+/K+/Cl− exchanger (which transports 2 Cl− ions for each cycle). The conductance of the Cl− channel is an increasing function of Ca2+ [40], while the NKCC model is a simplified version of the model of [41].
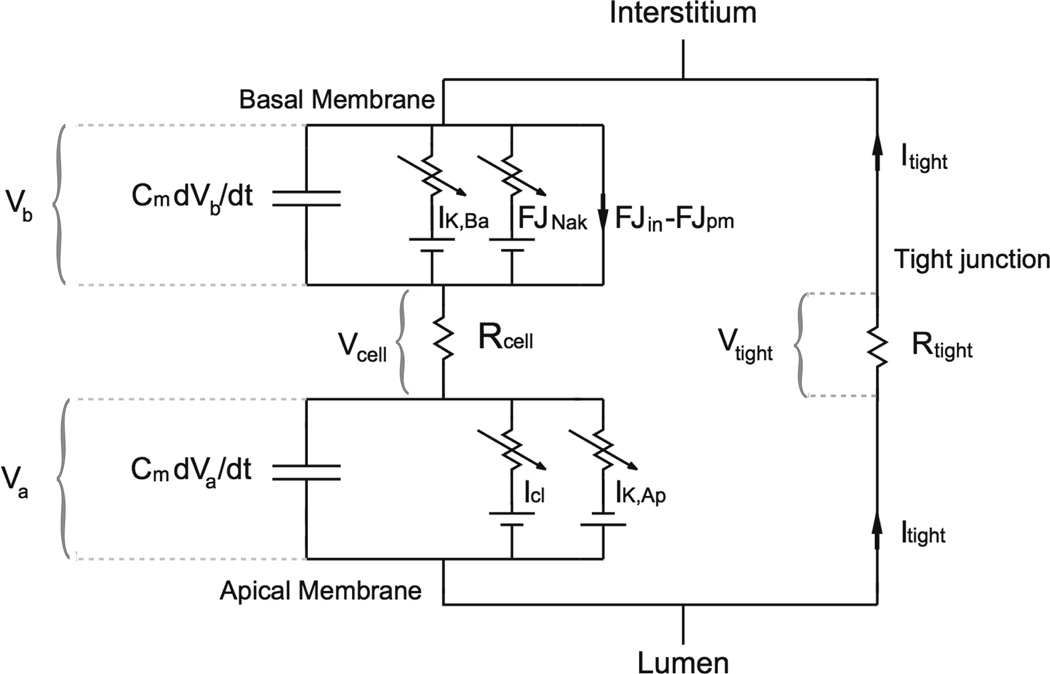
The equation for the membrane voltage is slightly more complicated, as the model assumes that there is a potential difference between the basolateral and apical regions. Thus, the cell is modelled by the circuit diagram shown in Fig. 6. Application of Kirchoff’s Laws to this circuit gives
| (5) |
| (6) |
where Jin and Jpm are the fluxes of Ca2+ in and out of the cell (assumed to occur only across the basolateral membrane). Note that the Na+/K+/Cl − transporter is electrically neutral and thus does not appear in the voltage equation. Also note that we have assumed the presence of a K+ current in the apical membrane, even though this does not appear in Fig. 1. This because we wish to investigate the effect on secretion of an apical K+ current.
Figure 6.
Circuit diagram of a salivary acinar cell where the apical membrane potential is different from the basal [22].
Since the sum of voltage drops around the circuit must be zero, it follows that
| (7) |
and since Vtight = RtightItight, and Vcell = ItightRcell, it follows that
| (8) |
This tight junctional current is assumed to consist of Na+ and K+ currrent, of relative fractions gt and 1 – gt, where gt is assumed to be constant. Thus, time-dependent changes in Na+ and K+ current across the cell membrane are not reflected by time-dependent changes through the tight junction.
3.2.3. Osmosis
Finally, we assume that water flow across each membrane is osmotically driven, and linearly proportional to the difference in ionic concentration across the membrane. Thus
| (9) |
where the flow across the basal membrane, qb (usually expressed in units of litres per second. Since this is a very small number, it is often normalised to cell volumes per second), is given by
| (10) |
and the flow across the apical membrane, qa, is given by
| (11) |
Here, X denotes the number of moles of other molecules (such as proteins, etc) inside the cell, R is the gas constant, T is absolute temperature, and La and Lb are permeabilities, with units of litres2 J−1s−1.
This completes the specification of the model of a single parotid cell.
3.3. The cellular level: duct cells
The duct cell model is similar to the parotid cell model, except that it has no Ca2+ dynamics and it has different ion transporters on the apical and basolateral membranes. Although it is not unlikely that dynamic changes in [Ca2+] are important in duct cells, as they are in acinar cells, as yet we have no experimental data about them. The only available data presently are from duct cell lines, HSY and HSG cells [25, 27, 26], and it is still unknown how accurately Ca2+ responses in these cell types reflect behaviour of duct cells in vivo. Hence, the duct cell model is based only on the ionic fluxes shown in Fig. 4, and the equations for each ion are based simply on conservation, as in the acinar model. The major difference is that the apical membrane of the duct cell is assumed to be impermeable to water.
3 4. The Saliva Production Unit (SPU)
At the next spatial level, we construct a model of an acinus and an associated length of duct, a structure that we call a Saliva Production Unit, or SPU, as illustrated in Fig. 7. The lumen collects the fluid output from a number of acinar cells (anywhere from 3 to 20 cells), and this total fluid output then flows along the duct, being modified in ionic composition as it does so. Mathematically, the construction of the SPU model partakes more of the brute force approach, the model being constructed essentially by solving multiple coupled cell models, with no underlying simplications to the spatial or model structures.
Figure 7.
The multiscale model is developed as a series of modules at the molecular, cellular and glandular level. A: The model is developed based on experimental data to represent the fluid secretion process of the acinar cells. B: The ionic modification by the duct. C. These models are integrated into a combined acinar and duct model of a salivary production unit (SPU). D. Finally, the model is developed to incorporate the morphology of the tissue to describe the entire salivary gland.
Fluid flow and ionic concentrations along the duct are modelled using a radially symmetric advection equation with a lumen of fixed radius, R (the model can be easily adapted to a varying lumenal radius if desired). Let C denote some ion (Na+ for instance, or K+), and let JC denote the flux, with units of moles per unit area per unit time, of ion C across the apical membrane of the duct cells. Also, let x denote distance along the duct, and let ν be the fluid velocity along the duct. Note that ν will be constant, as the duct radius is assumed to be constant, and the duct is assumed to be impermeable to water. Then, the concentration of C in the duct is modelled as
| (12) |
This equation is coupled to the duct cell equations via the expression for Jc, which also appears in the equation for the local duct cell concentration of ion C, and which depends on the duct cell concentration of ion C. The boundary conditions at x = 0 (i.e., where the duct abuts the acinar cells) are given by the composition and flow rate of the primary saliva produced by the acinar cells.
3.5. The multiscale structure
At the highest spatial level, multiple SPUs are connected in a branching structure similar to that seen experimentally. However, we have not yet developed a model at this highest spatial scale. This is a matter for current investigation; in the Discussion we shall briefly discuss some ideas for how this might be done.
The entire multiscale model, from the molecular to the organ level is summarised in Fig. 7.
Full details of the model equations and parameter values can be found in [42, 22, 40, 24, 34].
4. Results
The model has been used to develop hypotheses and predictions at the three lowest scales. At the molecular level, most of our work was focused on the properties of the most important Ca2+ release channel, the inositol trisphosphate receptor (IPR). At the cellular level our model considered mostly the dynamics of Ca2+ in the acinar cells, the interaction of cytosolic Ca2+ with the membrane ion channels, and the subsequent movement of water by osmosis. At the next highest spatial scale, the multicellular scale, we include consideration of the spatial structure of the acinus, and its influence on water transport. At the next highest scale the output of the acinus is used as the input to the duct model, which can then predict the composition of the secondary saliva. The model results and predictions associated with each of these scales are briefly discussed in turn in the following sections.
4.1. The inositol trisphophate receptor
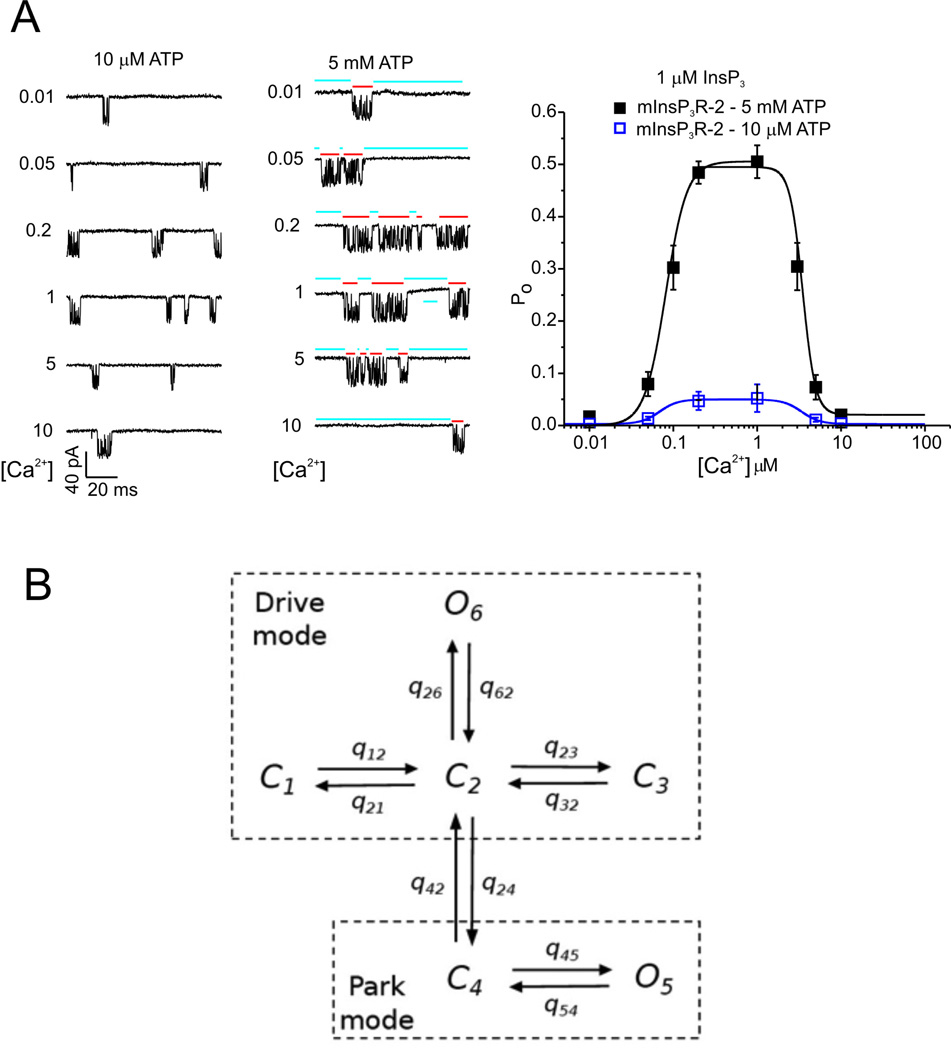
Our model of the IPR is illustrated in Fig. 8. The left side of Panel A shows some sample single-channel recordings, while the right side of panel A shows the steady-state open probability of the IPR as a function of [Ca2+] (for two different ATP concentrations). These data (and a great many more of similar type) were fitted using a Bayesian Markov Chain Monte Carlo method. Such a fitting method finds distributions for the unknown parameters (rather than finding so-called “best-fit” values), and thus can be used to determine whether or not a model is unambiguously determined by the data. More details can be found in [43, 34, 44]. The result is the Markov model shown in Fig. 8B. The IPR exists in two modes, Park and Drive. In Park mode the IPR is almost always closed (q45 ≈ 10−3 ms, q 54 ≈ 3.4 ms), while in the Drive mode it is open about 70% of the time (q26 ≈ 10 ms, q62 ≈ 3.3 ms). Transitions within each mode are independent of [Ca2+] or [IP3]; it is only the intermode transitions (with rates q42 and q24) that depend on those ligands. Full details of the model parameters, the fits to data, and the most recent modifications can be found in [37]. Similar work by [45] has suggested that the IPR can exist in three modes rather than just two, but it is yet unclear which is a more accurate and useful description of the IPR.
Figure 8.
A: activity from single type-2 IPR recorded from the isolated nuclear envelope, showing modulation by Ca2+ and ATP at submaximal IP3. Two modes of channel activity are evident; a long-lived Park mode that is mostly closed (blue bars), and a bursting mode refered to as Drive mode (red bars). The panel on the right shows the steady-state open probability as a function oc Ca2+ concentration, at a single fixed IP3 concentration and two different ATP concentrations. B: schematic diagram of the IPR model [34]. C and O denote, respectively, closed and open states. The only transitions that are dependent on [Ca2+] and [IP3] are q42 and q24, the transitions between the Park and Drive modes.
4.2. Calcium oscillations and waves
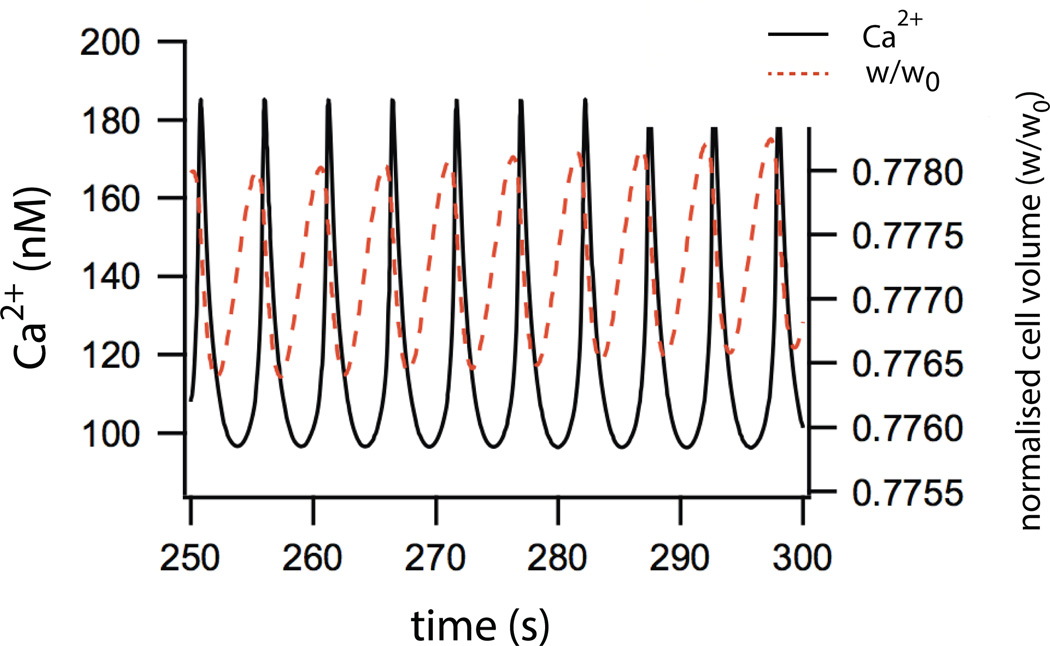
Upon stimulation by an agonist such as acetylcholine, the cytosolic Ca2+ concentration (in the model) oscillates in a way that is qualitatively similar to experimentally observed oscillations [22]. These oscillations occur in the absence of extracellular Ca2+,and are modified by flux through the RyR, both features that are observed experimentally. Oscillations in cell volume and water secretion occur in synchrony with the Ca2+ oscillations, with the cell volume decreasing to approximately 70% of the resting volume (Fig. 9). Fluid flow also oscillates, with an amplitude of around 0.006 cell volumes per second.
Figure 9.
Model simulations showing oscillations of [Ca2+] and cell volume in response to addition of agonist [22].
Most interestingly (and surprisingly) the total fluid flow does not depend sensitively on the Ca2+ oscillation frequency, with only a 4% change in secretion over a wide range of frequencies. As agonist increases saliva secretion does increase, but this is due almost entirely to the increase in average Ca2+ concentration. If the oscillations are scaled to have the same mean level, but a different frequency, almost no change in saliva secretion is observed [40].
In parotid cells, the Ca2+ oscillations do not occur as whole-cell oscillations, but are instead periodic Ca2+ waves that begin in the apical region (where there is a higher density of IPR) and travel across the cell to the basal region [46], with a wave speed of around 25 µm s−1. Model simulations [40] predict that saliva secretion is highest when [Ca2+] rises simultaneously in the apical and basal regions of the cell (i.e., when the Ca2+ rise takes the form of a whole-cell oscillation, not a wave). If the time-dependence of the Ca2+-dependent Cl− channels is taken into account this prediction is relaxed somewhat, but the model still predicts that the most efficient wave speed is on the order of 100–200 µm s−1, much faster than the observed waves.
4.3. K+ channels inapical membrane
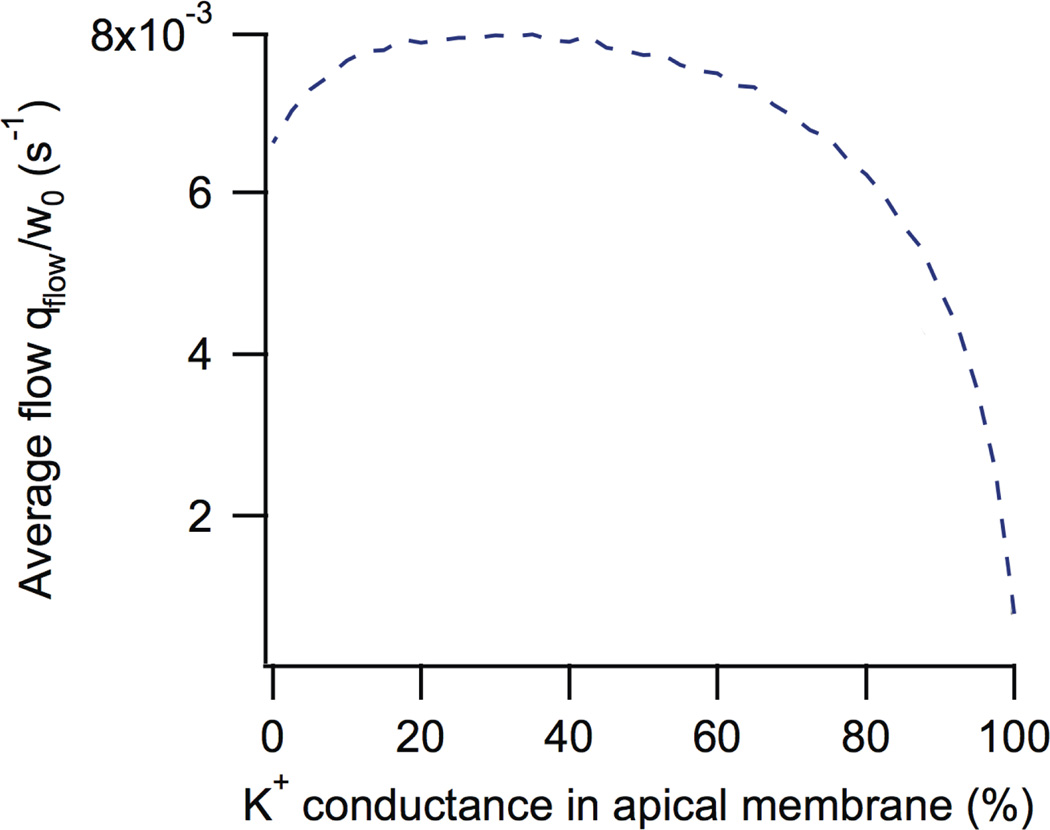
Although it used to be generally accepted that Ca2+-activated K+ channels were situated only on the basolateral membrane, while Ca2+-activated Cl− channels were situated only on the apical membrane, the model predicted that the greatest saliva secretion occurs when approximately 20% of the total K+ conductance is situated on the apical membrane (Fig. 10). Motivated by this model prediction we showed experimentally that the apical membrane of parotid acinar cells contains functional Ca2+-dependent K+ channels [47]. As yet it is not known what fraction of the total cellular Ca2+-dependent K+ current is across the apical membrane, so that detail of the model prediction has not yet been tested.
Figure 10.
Salivary flow as a function of the proportion of K+ conductance in the apical membrane. It can be seen that saliva flow is maximised if approximately 20% of the K+ conductance is in the apical membrane [22].
4.4. Efficiency of secretion
It is observed experimentally that the lumen is almost isotonic to the external medium, and that the cell is highly permeable to water. These observations can be understood by a relatively simple argument [48], that has important implications for the construction of the multiscale model.
Firstly, if we assume that the lumen has a constant volume, wl, the equation for the concentration of Cl− in the lumen is
| (13) |
Note that, since the lumen has constant volume, all the water that flows into it (at qa litres per second) must also flow out, taking with it Cl− at concentration [Cl−]l. It is shown in [48] that [Cl−]l can be assumed to be at quasi-steady state, in which case
| (14) |
It turns out to be useful to write this in terms of a slightly different variable
| (15) |
where [Cl−]e is the constant Cl− concentration in the external medium. In this new variable
| (16) |
Secondly, to a good approximation we can also assume that the volume of the cell is also at quasi-steady state, in which case qa = qb, from which it follows that
| (17) |
where C denotes the total concentration of osmolites in the relevant compartment. Hence,
| (18) |
Since
| (19) |
it thus follows that
| (20) |
where is the total cell permeability. We note in passing that this last equation is a useful one, as it essentially a cell-free equation; it uses only the total cell permeability to water, and does not involve any of the internal ionic concentrations. In this equation the cell can be thought of simply as a barrier, with permeability Lt, separating two solutions with total concentrations Cl and Ce.
Next, notice that, because both the lumenal and external solutions must be electroneutral (and, in this model at least, contain only Na+, K+ and Cl− ions), it follows that 2[Cl−]l = Cl and similarly for the external solution. Thus,
| (21) |
Finally, we eliminate [Cl−]d between (16) and (21) to get
| (22) |
where
| (23) |
| (24) |
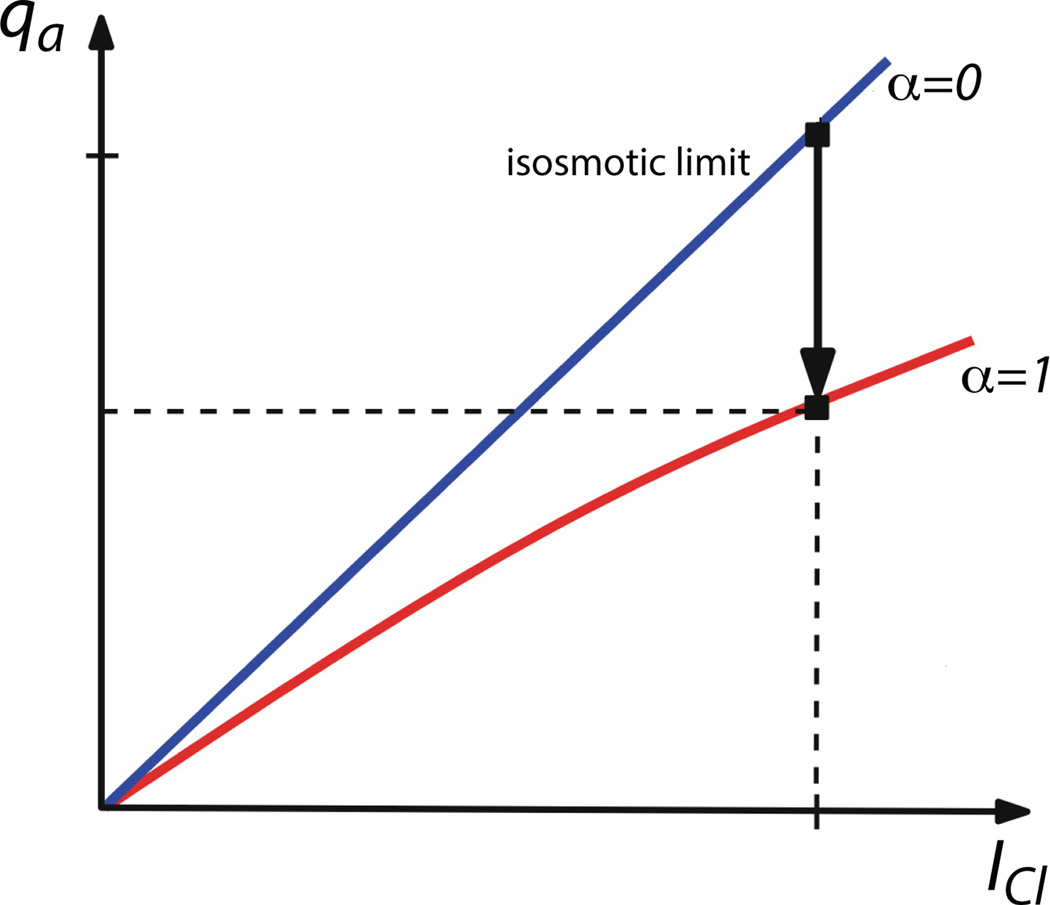
In Fig. 11 we sketch a plot of qa against ICl for two cases; α = 0 and α ≠ 0. Note that α = 0 corresponds to the case of infinite permeability, and thus isotonic transport. The curve for α = 0 always lies above the curve for α ≠ 0. Numerical simulations [48] show that for realistic values of the cell permeability, (22) gives an excellent approximation to the exact solutions.
Figure 11.
Salivary flow as a function of Cl− current for isotonic transport (blue line; α = 0) and non-isotonic transport (red line; α = 1). For a given Cl− current flow is always greater in the isotonic limit (in which case the permeability of the cell must go to infinity) [48].
This explains why a cell would wish to transport water in an isotonic manner. For a fixed Cl− current, and thus for a fixed expenditure of energy, fluid secretion is maximised as α → 0, i.e., as Lt → ∞. In this limit Cl – Ce → 0, i.e., the lumen becomes isotonic with the external medium.
4.5. Influence of acinar spatial structure
We now ask the question: what role is played by the spatial structure of the lumen? For example, if N cells all secrete into a common lumen, and thus all experience the same lumenal [Cl−], does this result in more water secretion than if the N cells were all secreting independently and the secretions were summed?
Let us consider first the case of the common lumen. From (20) we see immediately that cells (with the same permeability) that share a common lumen all secrete water at the same rate (at least to a first approximation). Since the rate of water secretion through a cell is dependent only on the difference between the lumenal and external concentrations, and since cells that share a common lumen all see the same lumenal and external concentration, the conclusion follows easily. Hence, from symmetry, the water flux through each cell is given by (22), where
| (25) |
Here, ICl,i is the Cl− current through the ith cell. The ICl,i need not all be the same, even though the fluid secretion through each cell is identical.
If the cells do not share a common lumen, the argument is almost the same, but with a crucial difference. Each cell again has its own ICl,i, different from all the other cells, but now we can no longer use the argument that each cell must have the same rate of secretion, and thus appeal to symmetry. In this case, each cell’s rate of secretion is calculated from
| (26) |
where
| (27) |
The total secretion is then Σqa,i.
In summary, when the cells ‘share a common lumen, the average rate of secretion is obtained by first averaging the Cl− current across all the cells, and then solving for the flux generated by that average current. When there is no common lumen, you first find the flux for each cellular Cl− current, and then average the fluxes. Of course, one must ensure that the total Cl− current is the same in both cases.
In the isotonic case, the equation for the flux is linear (as α = 0). In this case it matters not whether you average the Cl− current first and then solve, or whether you solve for the flux first and then average. The result is the same either way. Hence, for isotonic transport, a common lumen gives the same flux as N independent cells. However, when water transport is not isotonic, it is a relatively simple matter to show that the common lumen always gives slightly greater transport than does the case of independent cells [48], although it remains less than the isotonic case.
There are clear implications for a multiscale model; the closer water secretion is to isotonic, the less important is the detailed spatial structure of the lumen, and thus the simpler is the model that needs to be used. Although we have only shown this to be true for the case of a single common lumen, we predict that a similar result will be true for a lumen with the more complicated spatial structure shown in Fig. 5. However, this remains to be tested.
4.6. Production of secondary saliva
The output of the acinus, the primary saliva, is then transported along the duct, where its ionic composition is modified by the duct cells. Although there are multiple kinds of duct cells our model presently includes only a single type. Together, a single acinus and duct form the Saliva Production Unit (SPU).
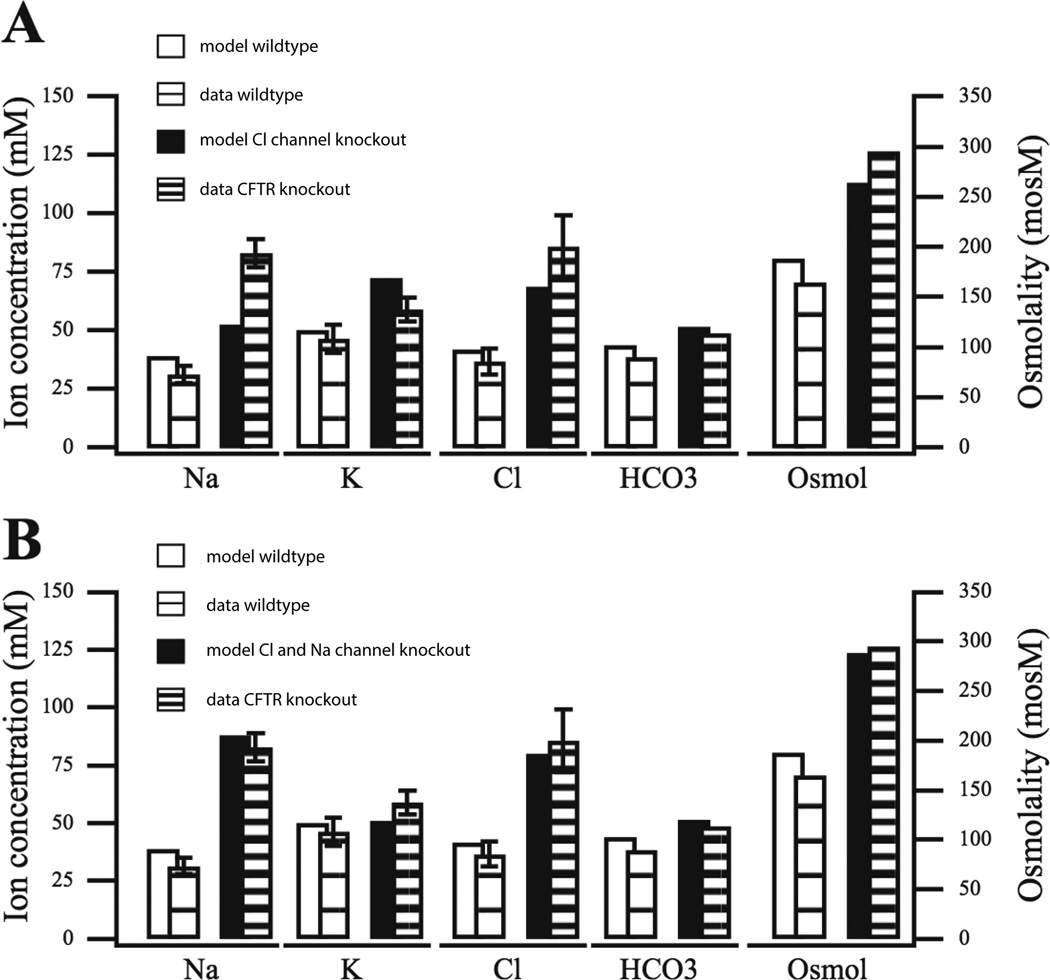
We compared the output of the model SPU to a variety of results from wild-type and knockout mice [49, 50]. Typical results are shown in Fig. 12, where we compared the model to results from mice submandibular glands with the CFTR channel knocked out. In this case, the data show a large increase in [Na+] and [Cl−], as well as a significant increase in osmolarity of the secondary saliva (the wild-type data, labelled data WT, are the same in panels A and B; they are given twice purely for ease of comparison with the model results).
Figure 12.
Model variations against data from the wild-type and CFTR knockout mouse secondary saliva [24]. The CFTR knockout mouse model has the CFTR channel deleted. A: CFTR channel conductance is reduced (to 0.15 of base value). Notice how the model [Na+] for the deletion is unable to capture behavior as measured in the CFTR knockout mouse. B: in addition to the CFTR channel reduction performed in A, the ENaC channel conductance is also reduced (to 0.4 of base value), in which case the model is able to reproduce the observed rise in [Na+].
Panel A shows the model results when CFTR knockout is assumed to affect only the CFTR channel. In this case the model is able to reproduce the increase in [Cl−], but is unable to reproduce the observed rise in [Na+]. If the Na+ conductance, ENaC, is also assumed to be downgraded in CFTR knockout mice (panel B) then the rise in [Na+] is obtained in the model. Thus the model is consistent with the observation that CFTR knockout also affects ENaC conductance [49]. Interestingly, a rise in [Na+] is not observed in mice for which the CFTR channel has been only blocked chemically, not knocked out entirely [49].
The SPU results predict that the apical membrane potential along the duct increases to as high as −11 mV, that the steady state is attained within 1 mm of the acinus, and that the tight junctions are highly impermeable to cations. However, it is not yet possible to test such model predictions with any ease or accuracy
5. Discussion
Although the multiscale model remains incomplete, much has been accomplished so far. Models at the molecular scale (the IPR) have been successfully integrated into models at the cellular scale (Ca2+ and voltage dynamics), which have in turn been incorporated into a multicellular acinus, and thence into a full saliva production unit, involving hundreds of cells. What remains is to combine thousands of SPUs into a model of the entire salivary gland, thus completing the multiscale model.
We have learned a lot from our model, incomplete though it is. At the molecular level our work fitting Markov models to single-channel data from the IPR have shown us that the IPR exists in two different modes, and that Ca2+ and IP3 control the open probability of the IPR by switching the channel between modes. This work is similar to complementary work of [51, 35, 45], although their model proposes three modes of the IPR, not two. Our IPR model has also been used to study Ca2+ dynamics in airway smooth muscle [37]. At the cellular level, our conclusion that the period of Ca2+ oscillations is almost entirely unimportant is unexpected, and contradicts the current dogma. Such a prediction is not easy to test, however, and experimental confirmation has yet to appear. Another model prediction, the presence of functional K+ channels in the apical membrane, has been confirmed experimentally, but other quantitative aspects of the model, such as the difference between the apical and basolateral membrane potentials, again have yet to be confirmed in detail.
One of the most surprising things to arise so far from the model is the prediction that the spatial structure of the lumen is unimportant. This is true (theoretically at least) in the limit of isotonic water transport, as long as the cell volume and the Cl− concentration in the lumen are in quasi-steady state. Although it is unlikely that such a prediction will be amenable to direct experimental testing, it is well-known that saliva secretion is close to isotonic, and that acinar cells are highly permeable to water, both of which observations strongly indicate that an acinus does indeed operate close to the isotonic limit. In this case the model strongly suggests that any spatial structures may be of little importance, and that the total output of the salivary gland is essentially just a sum of the outputs of the individual cells.
Much remains to be done, both in model construction, and in use of the model to address scientific questions. Firstly, the full multiscale model of the entire organ needs to be constructed. Although daunting at first sight due to the thousands of PMUs that need to be included, and their intricate spatial structure and arrangement, such complexity may well be a red herring. If secretion is close enough to isotonic (and assuming the necessary quasi-steady state conditions are satisfied), then all this intricate spatial structure might be doing almost nothing at all. In this case, the output from each acinus will be just the sum of the outputs from each cell in the acinus, and then the acini can be combined using a continuum approach in which each part of the domain contains both acinar and duct cells mixed together. However, such a model would have to be compared carefully to more accurate spatial representations to ensure that important behaviours are not lost.
Duct cells have been far less studied than acinar cells, and we still have only very limited knowledge of such things as their internal Ca2+ dynamics. Studies in HSY cells [28] suggest that duct cells may themselves exhibit complex Ca2+ and IP3 dynamics and that such responses might be important for controlling duct cell ion transport, but construction of detailed models awaits more experimental work. Duct cells are particularly important given the effectiveness of aquaporin transfection treatments [52, 53, 54], in which salivary function can be restored, even in the seeming absence of acinar cells, by transfecting aquaporins into duct cells. How this might work remains a mystery, but to answer this question a quantitative model of duct cell transport will be required. Our multiscale model will be ideally positioned for such studies.
Another major question our model is designed to study is how to understand pathological conditions associated with salivary hypofunction. To do this will require the construction of a model of an irradiated and malfunctioning salivary gland; this will not be merely a reparamaterisation of the healthy model, but will most likely require dramatic changes in prevalance and function of important cellular components. Any model changes must be done in close consultation with additional experimental data, but the model will then be able to predict the most efficient ways in which salivary function might be restored.
Although our model is the first to study saliva secretion across multiple scales, there are many previous models of fluid transport by epithelial cells [55, 56, 57, 58, 59, 60, 61]. Our model differs principally in the detailed inclusion of intracellular Ca2+ dynamics, and the specific application to salivary glands, but the fundamental mechanisms of water transport by osmosis are unchanged. Previous models of the pancreatic duct [62, 63, 64, 65], however, are significantly different from our duct cell model, as the pancreatic duct is permeable to water, necessitating a qualitatively different approach.
We review the construction of a multiscale model of saliva secretion.
We predict that calcium oscillation frequency is unimportant for saliva secretion.
We predict that Ca-sensitive K channels are situated in the apical membrane.
We predict that saliva secretion is most efficient in the isoosmotic regime.
Acinar spatial structure might be unimportant.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Melvin JE, Yule D, Shuttleworth T, Begenisich T. Regulation of fluid and electrolyte secretion in salivary gland acinar cells. Annual Review of Physiology. 2005;67(1):445–469. doi: 10.1146/annurev.physiol.67.041703.084745. [DOI] [PubMed] [Google Scholar]
- 2.Pedersen AM, Bardow A, Jensen SB, Nauntofte B. Saliva and gastrointestinal functions of taste, mastication, swallowing and digestion. Oral Dis. 2002;8(3):117–129. doi: 10.1034/j.1601-0825.2002.02851.x. [DOI] [PubMed] [Google Scholar]
- 3.Ship JA, Fox PC, Baum BJ. How much saliva is enough? “Normal” function defined. J Am Dent Assoc. 1991;122(3):63–69. doi: 10.14219/jada.archive.1991.0098. [DOI] [PubMed] [Google Scholar]
- 4.Fox PC, van der Ven PF, Sonies BC, Weiffenbach JM, Baum BJ. Xerostomia: evaluation of a symptom with increasing significance. J Am Dent Assoc. 1985;110(4):519–525. doi: 10.14219/jada.archive.1985.0384. [DOI] [PubMed] [Google Scholar]
- 5.Melvin JE. Saliva and dental diseases. Curr Opin Dent. 1991;1(6):795–801. [PubMed] [Google Scholar]
- 6.Daniels TE, Wu AJ. Xerostomia – clinical evaluation and treatment in general practice. J Calif Dent Assoc. 2000;28(12):933–941. [PubMed] [Google Scholar]
- 7.Fox PC, Speight PM. Current concepts of autoimmune exocrinopathy: immunologic mechanisms in the salivary pathology of Sjögren’s syndrome. Crit Rev Oral Biol Med. 1996;7(2):144–158. doi: 10.1177/10454411960070020301. [DOI] [PubMed] [Google Scholar]
- 8.Fox RI, Maruyama T. Pathogenesis and treatment of Sjögren’s syndrome. Curr Opin Rheumatol. 1997;9(5):393–399. doi: 10.1097/00002281-199709000-00004. [DOI] [PubMed] [Google Scholar]
- 9.Cook D, Van Lennep E, ML R, JA Y. Secretion by the major salivary glands. In: Johnson L, editor. Physiology of the Gastrointestinal Tract. 3rd Edition. Raven Press; 1994. pp. 1061–2017. [Google Scholar]
- 10.Nauntofte B. Regulation of electrolyte and fluid secretion in salivary acinar cells. Am J Physiol. 1992;263(6 Pt 1):G823–G837. doi: 10.1152/ajpgi.1992.263.6.G823. [DOI] [PubMed] [Google Scholar]
- 11.Turner RJ, Sugiya H. Understanding salivary fluid and protein secretion. Oral Dis. 2002;8(1):3–11. doi: 10.1034/j.1601-0825.2002.10815.x. [DOI] [PubMed] [Google Scholar]
- 12.Melvin JE. Chloride channels and salivary gland function. Crit Rev-Oral Biol Med. 1999;10(2):199–209. doi: 10.1177/10454411990100020601. [DOI] [PubMed] [Google Scholar]
- 13.Ambudkar IS. Polarization of calcium signaling and fluid secretion in salivary gland cells. Curr Med Chem. 2012;19(34):5774–5781. doi: 10.2174/092986712804143321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Putney JW. A model for receptor-regulated calcium entry. Cell Calcium. 1986;7(1):1–12. doi: 10.1016/0143-4160(86)90026-6. [DOI] [PubMed] [Google Scholar]
- 15.Martinez JR. Cellular mechanisms underlying the production of primary secretory fluid in salivary glands. Crit Rev Oral Biol Med. 1990;1(1):67–78. doi: 10.1177/10454411900010010601. [DOI] [PubMed] [Google Scholar]
- 16.Falcke M. Reading the patterns in living cells – the physics of Ca2+ signaling. Advances in Physics. 2004;53(3):255–440. [Google Scholar]
- 17.Keener J, Sneyd J. Mathematical Physiology. 2nd Edition. New York: Springer-Verlag; 2008. [Google Scholar]
- 18.Dupont G, Combettes L, Bird GS, Putney JW. Calcium oscillations. Cold Spring Harb Perspect Biol. 3(3) doi: 10.1101/cshperspect.a004226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Berridge MJ. Calcium signalling remodelling and disease. Biochem Soc Trans. 2012;40(2):297–309. doi: 10.1042/BST20110766. [DOI] [PubMed] [Google Scholar]
- 20.Berridge MJ, Bootman MD, Roderick HL. Calcium signalling: dynamics, homeostasis and remodelling, Nature Reviews. Molecular Cell Biology. 2003;4(7):517–529. doi: 10.1038/nrm1155. [DOI] [PubMed] [Google Scholar]
- 21.Thul R, Bellamy TC, Roderick HL, Bootman MD, Coombes S. Calcium oscillations. Adv Exp Med Biol. 2008;641:1–27. doi: 10.1007/978-0-387-09794-7_1. [DOI] [PubMed] [Google Scholar]
- 22.Palk L, Sneyd J, Shuttleworth TJ, Yule DI, Crampin EJ. A dynamic model of saliva secretion. J Theor Biol. 2010;266(4):625–640. doi: 10.1016/j.jtbi.2010.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dupont G, Erneux C. Simulations of the effects of inositol 1,4,5-trisphosphate 3-kinase and 5-phosphatase activities on Ca2+ oscillations. Cell Calcium. 1997;22(5):321–331. doi: 10.1016/s0143-4160(97)90017-8. [DOI] [PubMed] [Google Scholar]
- 24.Patterson K, Catalan MA, Melvin JE, Yule DI, Crampin EJ, Sneyd J. A quantitative analysis of electrolyte exchange in the salivary duct. Am J Physiol: Gastrointestinal and Liver Physiology. 2012;303(10):G1153–G1163. doi: 10.1152/ajpgi.00364.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liu X, Liao D, Ambudkar IS. Distinct mechanisms of [Ca2+]i oscillations in HSY and HSG cells: role of Ca2+ influx and internal Ca2+ store recycling. J Membr Biol. 2001;181(3):185–193. doi: 10.1007/s00232-001-0020-6. [DOI] [PubMed] [Google Scholar]
- 26.Tanimura A, Turner RJ. Calcium release in HSY cells conforms to a steady-state mechanism involving regulation of the inositol 1,4,5-trisphosphate receptor Ca2+ channel by luminal [Ca2+] J Cell Biol. 1996;132(4):607–616. doi: 10.1083/jcb.132.4.607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tanimura A, Turner RJ. Inositol 1,4,5-trisphosphate-dependent oscillations of luminal [Ca2+] in permeabilized HSY cells. J Biol Chem. 1996;271(48):30904–30908. doi: 10.1074/jbc.271.48.30904. [DOI] [PubMed] [Google Scholar]
- 28.Tanimura A, Morita T, Nezu A, Tojyo Y. Monitoring of IP3 dynamics during Ca2+ oscillations in HSY human parotid cell line with FRET-based IP3 biosensors. J Med Invest. 2009;(56 Suppl):357–361. doi: 10.2152/jmi.56.357. [DOI] [PubMed] [Google Scholar]
- 29.Flint JM. The ducts of the human submaxillary gland. Am J Anat. 1902;1(3):269–295. [Google Scholar]
- 30.Masedunskas A, Porat-Shliom N, Tora M, Milberg O, R Weigert. Intravital microscopy for imaging subcellular structures in live mice expressing fluorescent proteins. J Vis Exp. (79) doi: 10.3791/50558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sneyd J, Falcke M. Models of the inositol trisphosphate receptor. Prog Biophys Mol Biol. 2005;89(3):207–245. doi: 10.1016/j.pbiomolbio.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 32.Foskett JK, White C, Cheung K-H, Mak D-OD. Inositol trisphosphate receptor Ca2+ release channels. Physiol Rev. 2007;87(2):593–658. doi: 10.1152/physrev.00035.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gin E, Falcke M, Wagner LE, 2nd, Yule DI, Sneyd J. A kinetic model of the inositol trisphosphate receptor based on single-channel data. Biophys J. 2009;96(10):4053–4062. doi: 10.1016/j.bpj.2008.12.3964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Siekmann I, Wagner LE, Yule D, Crampin EJ, Sneyd J. A kinetic model for type I and II IP3R accounting for mode changes. Biophys J. 2012;103(4):658–668. doi: 10.1016/j.bpj.2012.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mak D-OD, Pearson JE, Loong KPC, Datta S, Fernandez-Mongil M, Foskett JK, Rapid ligand-regulated gating kinetics of single. inositol 1,4,5-trisphosphate receptor Ca2+ release channels. EMBO Rep. 2007;8(11):1044–1051. doi: 10.1038/sj.embor.7401087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wagner LE, Yule DI. Differential regulation of the InsP3 receptor type-1 and −2 single channel properties by InsP3, Ca2+ and ATP. J Physiol. 2012;590(14):3245–3259. doi: 10.1113/jphysiol.2012.228320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cao P, Donovan G, Falcke M, Sneyd J. A stochastic model of calcium puffs based on single-channel data. Biophys J. 2013;105(5):1133–1142. doi: 10.1016/j.bpj.2013.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Keizer J, Levine L. Ryanodine receptor adaptation and Ca2+-induced Ca2+ release-dependent Ca2+ oscillations. Biophys J. 1996;71(6):3477–3487. doi: 10.1016/S0006-3495(96)79543-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lytton J, Westlin M, Burk S, Shull G, MacLennan D. Functional comparisons between isoforms of the sarcoplasmic or endoplasmic reticulum family of calcium pumps. J Biol Chem. 1992;267:14483–14489. [PubMed] [Google Scholar]
- 40.Palk L, Sneyd J, Patterson K, Shuttleworth TJ, Yule DI, Ma-claren O, Crampin EJ. Modelling the effects of calcium waves and oscillations on saliva secretion. J Theor Biol. 2012;305:45–53. doi: 10.1016/j.jtbi.2012.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Benjamin BA, Johnson EA. A quantitative description of the Na-K-2Cl cotransporter and its conformity to experimental data. Am J Physiol. 1997;273(3 Pt 2):F473–F482. doi: 10.1152/ajprenal.1997.273.3.F473. [DOI] [PubMed] [Google Scholar]
- 42.Gin E, Crampin EJ, Brown DA, Shuttleworth TJ, Yule DI, Sneyd J. A mathematical model of fluid secretion from a parotid acinar cell. J Theor Biol. 2007;248(1):64–80. doi: 10.1016/j.jtbi.2007.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Siekmann I, Sneyd J, Crampin EJ. Statistical analysis of modal gating in ion channels, Proceedings of the Royal Society A: Mathematical. Physical and Engineering Science. 2014;470(2166):20140030. [Google Scholar]
- 44.Siekmann I, Sneyd J, Crampin EJ. Mcmc can detect nonidentifiable models. Biophysical journal. 2012;103(11):2275–2286. doi: 10.1016/j.bpj.2012.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ionescu L, White C, Cheung KH, Shuai J, Parker I, Pearson JE, Foskett JK, Mak DO. Mode switching is the major mechanism of ligand regulation of InsP3 receptor calcium release channels. J Gen Physiol. 2007;130(6):631–645. doi: 10.1085/jgp.200709859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Giovannucci DR, Bruce JIE, Straub SV, Arreola J, Sneyd J, Shuttleworth TJ, Yule DI. Cytosolic Ca2+ and Ca2+-activated Cl− current dynamics: insights from two functionally distinct mouse exocrine cells. J Physiol. 2002;540(Pt 2):469–484. doi: 10.1113/jphysiol.2001.013453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Almassy J, Won JH, Begenisich TB, Yule DI. Apical Ca2+-activated potassium channels in mouse parotid acinar cells. J Gen Physiol. 2012;139(2):121–133. doi: 10.1085/jgp.201110718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Maclaren OJ, Sneyd J, Crampin EJ. Efficiency of primary saliva secretion: an analysis of parameter dependence in dynamic single-cell and acinus models, with application to aquaporin knockout studies. J Membr Biol. 2012;245(1):29–50. doi: 10.1007/s00232-011-9413-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Catalan MA, Nakamoto T, Gonzalez-Begne M, Camden JM, Wall SM, Clarke LL, Melvin JE. CFTR and ENaC ion channels mediate NaCl absorption in the mouse submandibular gland. J Physiol. 2010;588(4):713–724. doi: 10.1113/jphysiol.2009.183541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Nakamoto T, Romanenko VG, Takahashi A, Begenisich T, Melvin JE. Apical maxi-K (KCa1.1) channels mediate K+ secretion by the mouse submandibular exocrine gland. Am J Physiol Cell Physiol. 2008;294:C810–C819. doi: 10.1152/ajpcell.00511.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ullah G, Daniel Mak DO, Pearson JE. A data-driven model of a modal gated ion channel: The inositol 1,4,5-trisphosphate receptor in insect Sf9 cells. J Gen Physiol. 2012;140(2):159–173. doi: 10.1085/jgp.201110753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Baum BJ, Zheng C, Cotrim AP, Goldsmith CM, Atkinson JC, Brahim JS, Chiorini JA, Voutetakis A, Leakan RA, Van Waes C, Mitchell JB, Delporte C, Wang S, Kaminsky SM, Illei GG. Transfer of the AQP1 cDNA for the correction of radiation-induced salivary hypofunction. Biochim Biophys Acta. 2006;1758(8):1071–1077. doi: 10.1016/j.bbamem.2005.11.006. [DOI] [PubMed] [Google Scholar]
- 53.Baum BJ, Zheng C, Cotrim AP, McCullagh L, Goldsmith CM, Brahim JS, Atkinson JC, Turner RJ, Liu S, Nikolov N, Illei GG. Aquaporin-1 gene transfer to correct radiation-induced salivary hy-pofunction. Handb Exp Pharmacol. 2009;190:403–418. doi: 10.1007/978-3-540-79885-9_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gao R, Yan X, Zheng C, Goldsmith CM, Afione S, Hai B, Xu J, Zhou J, Zhang C, Chiorini JA, Baum BJ, Wang S. AAV2-mediated transfer of the human aquaporin-1 cDNA restores fluid secretion from irradiated miniature pig parotid glands. Gene Therapy. 2010;18(1):38–42. doi: 10.1038/gt.2010.128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Diamond JM, Bossert WH. Standing-gradient osmotic flow. a mechanism for coupling of water and solute transport in epithelia. J Gen Physiol. 1967;50(8):2061–2083. doi: 10.1085/jgp.50.8.2061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Swanson CH. Isotonic water transport in secretory epithelia. Yale J Biol Med. 1977;50(2):153–163. [PMC free article] [PubMed] [Google Scholar]
- 57.Weinstein AM, Stephenson JL. Electrolyte transport across a simple epithelium. Steady-state and transient analysis. Biophys J. 1979;27(2):165–186. doi: 10.1016/S0006-3495(79)85209-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Weinstein AM, Stephenson JL. Models of coupled salt and water transport across leaky epithelia. J Membr Biol. 1981;60(1):1–20. doi: 10.1007/BF01870828. [DOI] [PubMed] [Google Scholar]
- 59.Weinstein A. Mathematical models of tubular transport. Ann Rev Physiol. 1994;56:691–709. doi: 10.1146/annurev.ph.56.030194.003355. [DOI] [PubMed] [Google Scholar]
- 60.Weinstein AM. Modeling epithelial cell homeostasis: steady-state analysis. Bull Math Biol. 1999;61(6):1065–1091. doi: 10.1006/bulm.1999.0127. [DOI] [PubMed] [Google Scholar]
- 61.Mathias RT, Wang H. Local osmosis and isotonic transport. J Membr Biol. 2005;208(1):39–53. doi: 10.1007/s00232-005-0817-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sohma Y, Gray MA, Imai Y, Argent BE. A mathematical model of the pancreatic ductal epithelium. J Membr Biol. 1996;154(1):53–67. doi: 10.1007/s002329900132. [DOI] [PubMed] [Google Scholar]
- 63.Sohma Y, Gray MA, Imai Y, Argent BE. transport in a mathematical model of the pancreatic ductal epithelium. J Membr Biol. 2000;176:77–100. doi: 10.1007/s00232001077. [DOI] [PubMed] [Google Scholar]
- 64.Sohma Y, Gray MA, Imai Y, Argent BE. 150 mM – how does the pancreas do it? Clues from computer modelling of the duct cell. JOP : Journal of the pancreas. 2001;2(4 Suppl):198–202. [PubMed] [Google Scholar]
- 65.Whitcomb DC, Ermentrout GB. A mathematical model of the pancreatic duct cell generating high bicarbonate concentrations in pancreatic juice. Pancreas. 2004;29(2):e30–e40. doi: 10.1097/00006676-200408000-00016. [DOI] [PubMed] [Google Scholar]