Uncertainty in Integrative Structural Modeling

Abstract

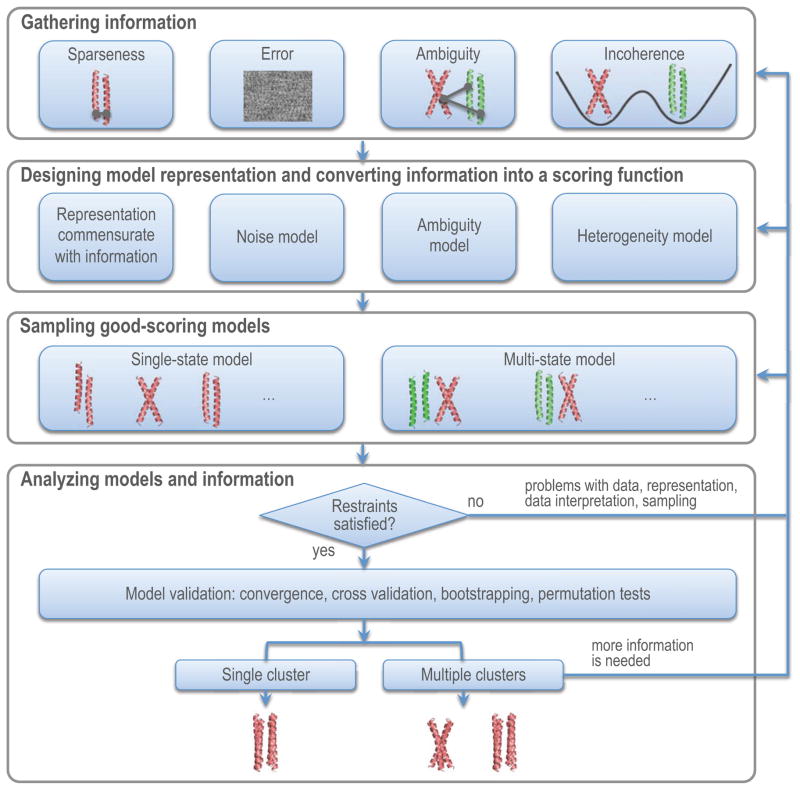
Integrative structural modelling uses multiple types of input information and proceeds in four stages: (i) gathering information, (ii) designing model representation and converting information into a scoring function, (iii) sampling good-scoring models, and (iv) analyzing models and information. In the first stage, uncertainty originates from data that are sparse, noisy, ambiguous, or derived from heterogeneous samples. In the second stage, uncertainty can originate from a representation that is too coarse for the available information or a scoring function that does not accurately capture the information. In the third stage, the major source of uncertainty is insufficient sampling. In the fourth stage, clustering, cross-validation, and other methods are used to estimate the precision and accuracy of the models and information.

Introduction

To understand and modulate biological processes, we need their spatiotemporal models. These models can be computed based on input information about the structure and dynamics of the system of interest, including physical theories, statistical inference from databases of known sequences and structures, as well as a large variety of experimental methods. A structural model of a molecule is defined by the relative positions and orientations of its components (eg, atoms, pseudo-atoms, residues, secondary structure elements, domains, and subunits). All structural characterization approaches correspond to finding models that best fit input information, as can be judged by a scoring function; when the scoring function includes experimental data, it quantifies the difference between the observed data and the data computed from the model. Therefore, structural characterization can be described as a four-stage process: (i) gathering input information, (ii) designing model representation and converting information into a scoring function, (iii) sampling good-scoring models, and (iv) analyzing models and information. For example, in X-ray crystallography a model consists of atomic positions, and the scoring function assesses the agreements (i) between the computed and observed structure factors via the R_free parameter [1] as well as (ii) between the model geometry and the ideal geometry implied by a molecular mechanics force field via the potential energy of the model.

To use a model well, we need to assess its accuracy (stage iv above). Assessment standards and corresponding tools have already been developed for X-ray crystallography [2] and Nuclear Magnetic Resonance (NMR) spectroscopy [3], while they are still evolving for electron microscopy (EM) [4], Small Angle X-ray Scattering [5,6], and comparative modeling [7]. Standard validation of the crystallographic and NMR entries in the Protein Data Bank (PDB) [8] includes assessing geometrical features such as stereochemistry and packing, fit of the model to the experimental data, and the quality of the data itself. In the EM field, Fourier Shell Correlation (FSC) is commonly used to estimate map resolution [4,9,10]. Recently, new validation methods for EM maps were suggested, including tilt pair analysis [11], gold-standard FSC curves [4], high-resolution noise substitution [12,13], and ResLog plots [14^•]. In SAXS data validation, the χ-free criterion was recently proposed [15^••], inspired by R_free in crystallography. Protein aggregation can be revealed in the Guinier plot, inter-particle interference can be detected by measuring SAXS profiles at multiple concentrations, and conformational heterogeneity is to some degree reflected in the Kratky or Porod-Debye plots [16]. Estimating the accuracy of comparative models is still challenging, but methods based on a variety of criteria do exist [7,17,18].

No single experimental method is guaranteed to produce a satisfactory structure for a given system. Nevertheless, structure determination can often benefit from an integrative (hybrid) approach, where information from multiple experimental datasets is used to compute all structural models that are consistent with the available data [19–22]. Data from X-ray crystallography, EM, NMR spectroscopy, SAXS, cross-linking combined with mass spectrometry (MS), Förster resonance energy transfer (FRET) spectroscopy, double electron-electron resonance (DEER), and hydrogen–deuterium exchange (HDX) is frequently used in integrative structure determination (Table 1). Sometimes integrative models are assessed based on clustering of models, modeling with simulated data, observation of non-random patterns in the models, and modeling with subsets of data [20]. However, a set of standards for validating integrative models has not yet been developed [22].

Table 1.

Some of the recent structures solved by an integrative approach.

Structure	Experimental information	Method
S. cerevisiae INO80 [56]	Cryo-EM map (17Å resolution), 212 intra-protein and 116 inter-protein cross-links	Manual modeling in Chimera
Polycomb Repressive Complex 2 [57]	Negative stain EM map (21Å resolution) and ~60 intra-protein and inter-protein cross-links	Manual modeling in Chimera
39S large subunit of the porcine mitochondrial ribosome [58]	Cryo-EM map (4.9Å resolution) and ~70 inter-protein cross-links	COOT, O, PHENIX
S. pombe 26S holocomplex [52••]	Cryo-EM map (8.4Å resolution) and 35 cross-links from S. pombe and 36 cross links from S. cerevisiae	IMP
S. cerevisiae RNA polymerase II transcription pre-initiation complex [54••]	Cryo-EM map (16Å resolution), 157 intra-protein and 109 inter-protein cross-links	Exhaustive enumeration
S. cerevisiae 40S•eIF1•eIF3 translation initiation complex [59••]	965 cross-links, including 126 unique eIF3-eIF3 and 40S•eIF1-eIF3 cross links, negative stain EM map (28Å resolution), crystallographic structures of 40S complex, eIF3 domains	IMP
S. typhimurium Type III secretion system needle [53]	solid-state NMR, cryo-EM (19.5Å resolution)	Rosetta
Methane monooxygenase hydroxylase (MMOH), toluene/o-xylene monooxygenase hydroxylase (ToMOH), and urease [60]	Composition and stoichiometry from native MS, collision cross section from ion mobility–MS and cross-links	IMP
ESCRT-I complex [61•]	SAXS, double electron-electron transfer (DEER), and FRET	EROS
Hsp90 substrate recognition [46]	31 cross-links and NMR spectroscopy	IMP
Splicing factor U2AF65 [62]	Paramagnetic relaxation enhancement (PRE), residue dipolar couplings (RDCs), and SAXS	ASTEROIDS
HIV-1 capsid protein [63]	RDCs and SAXS	Xplor-NIH
500-kilobase (kb) domain of human chromosome 16 [64,65]	Chromosome Conformation Capture Carbon Copy (5C) experiments and excluded volume	IMP
Human genome architecture [66••]	Tethered chromosome conformation capture (TCC) and population-based modeling	IMP

It is essential for appropriate use of a structural model to estimate errors in the model as well as the data used to compute it. Model error is defined as the difference between the model and true structure. It originates from several different sources. First, input data can be sparse, noisy, ambiguous, or incoherent (Glossary). Second, the system representation can be too coarse, resulting in some input information being ignored. Third, the scoring function may not accurately capture the input information or the input information is insufficient to identify the true structure. Fourth, sampling may not find the true structure due to many degrees of freedom used to represent the system. Because the true structure is unknown in real applications, model error is also unknown. However, the lower bound on the model error can often be estimated as the precision of the set of models consistent with the input information. Here, we describe the origins of uncertainty in each stage of integrative modeling, and suggest how to quantify and minimize it.

Stage 1: Gathering information

Spatial information about a given system can include data from experiments such as those listed above, statistical propensities such as atomic statistical potentials extracted from known protein structures, and physical laws, such as interatomic interactions approximated by a molecular mechanics force field. This information is used to represent the system as well as to sample and rank its possible configurations. There are four sources of uncertainty in the information, as follows.

Data sparseness

The data sparseness measures the amount of information in the data relative to the number of degrees of freedom in the model; the amount of information in the data depends on the number of data points and their precision as well as their interdependence. Data sparseness affects the precision of the model [23]. For example, for a protein-protein complex mapped by a single cross-link, if each protein is represented by a single sphere, the data sparseness is 1 data point per 1 degree of freedom; if the proteins are represented by their rigid atomic structures, the data sparseness is 1 data point per 6 degrees of freedom (3 rotations and 3 translations). In X-ray crystallography, the data sparseness can be quantified by the number of reflections divided by the number of atoms in the unit cell. In NMR spectroscopy, the data sparseness is usually quantified by the number of NOE restraints per residue. In SAXS, the data sparseness of a SAXS profile is defined using the Nyquist-Shannon sampling theorem: given the maximum dimension (d_max), the sampling theorem determines that the number of unique, evenly distributed observations for a maximum scattering vector (q_max) is given by (d_max q_max)/π. The problem with sparse data is that there are more free parameters than observations, which may lead to an over-interpretation of the data (over-fitting).

Data error

Error of the data is the sum of random and systematic measurement errors. The magnitude of random error can best be assessed by multiple repeated measurements; systematic errors for a given type of data can be estimated by benchmarks relying on known structures. For example, in X-ray crystallography the random error is caused by random variations among the crystals as well as noise in the X-ray flux, detector and electronics, while the systematic error can result from radiation damage, conformational heterogeneity of the sample, and crystal packing defects [24]. In SAXS, the random error sources are similar to those in crystallography, while the systematic error can result from sample aggregation and radiation damage [5].

Data ambiguity

Data ambiguity is the uncertainty in assigning data points to specific components of the system. For example, it is generally not possible to assign which of the three methyl protons gave rise to an observed NOE signal [25]. Another example is the ambiguity of assigning a cross-link to a specific instance of a protein when the complex contains multiple instances of it. In contrast, diffraction and scattering data are a function of all components of a system and thus not ambiguous.

Data incoherence

Data incoherence is a result of compositional or conformational heterogeneity of one or more samples used to generate one or more datasets for modeling; for example, a system may exist as a mixture of two states in an NMR solution experiment or it may exist in different states in X-ray (crystal) and SAXS (solution) experiments. As a result, the measured data will be a mixture of contributions from each state. The ability to disentangle different states depends on the precision and accuracy of the data; for example, conformational differences smaller than the precision of the data may be difficult to detect.

Stages 2 and 3: Converting input information into system representation, scoring function, and sampling

Input information about the structure of the system can be used (i) to select the set of variables that represent the system (system representation), (ii) to rank the different configurations (scoring function), and (iii) to search for good scoring solutions (sampling). It is often most computationally efficient, although not always possible, to encode information into the representation; in contrast it is generally most straightforward, but least efficient, to encode information into the scoring function. For example, in protein-protein docking, maximization of shape complementarity can be encoded into a scoring function that is then optimized by a generic optimization method. Alternatively, maximization of shape complementarity can also be encoded more efficiently through a representation consisting of shape descriptors, such as surface curvature, resulting in faster sampling by generating only configurations of subunits with complementary shape descriptors [26].

Representation

The representation of a system is defined by all the variables that need to be determined based on input information, including the assignment of the system components to geometric objects, such as points and spheres. A simple example is Cartesian coordinates for points corresponding to the individual atoms. More complex representations can assign a component to other geometric primitives (eg, spheres, ellipsoids, and 3D Gaussian density functions) and include additional degrees of freedom, such as the number of states in the system and their weights. For instance, in a high-resolution representation, a sphere can represent a single atom, while in a coarse-grained representation it may correspond to a residue. Coarse-graining can be used to encode the uncertainty arising from both static and dynamic variability. Moreover, in a “rigid body”, the relative positions of the primitives (eg, atoms in a domain) can be constrained, for example based on a crystallographic structure. In most applications, the representation is determined before any other computations and is not changed. The resolution of the representation should be commensurate with the input information. In some cases, it is beneficial to represent different parts of a structure with different representations or a part may be described with several different inter-linked representations simultaneously (ie, multi-scale representation); in such a case, information can be applied to restrain the model by using the most convenient representation [27].

When defining the representation, we usually have to balance between the requirements of scoring and sampling. We need a representation that is sufficiently detailed for accurately assessing a match between a model and the input information. For example, when using chemical cross-linking information, we need to choose between representing the cross-linker explicitly with all of its atoms [28] or implicitly as a function of the distance between the cross-linked residues. To minimize data sparseness, we also need a representation that is sufficiently coarse, given the invariably limited information content of the data. Finally, the representation should also be sufficiently coarse to allow for exhaustive sampling of good scoring models in a feasible timeframe. While it would be best to be able to compute an optimal representation based on the input information, this is not yet possible.

Scoring

Most generally, the scoring function ranks alternative models based on the evidence provided by the input information. The scoring function should take into account the uncertainty in the input information, including sparseness, error, ambiguity, and incoherence. For example, a scoring function could evaluate whether or not a given model fits the data within its error bars. Ambiguity in the data assignment should also be accounted for by the scoring function. For example, to address the ambiguity in methyl proton assignment for an observed NOE signal, the signal is often assigned to the center of mass of the three methyl protons [25]. For a complex with multiple copies of the same protein, a cross-link can be assigned to the copy of the protein that satisfies it best [20]. When a sample is heterogeneous (ie, data are incoherent), a scoring function should rank instances of a model, each one of which consists of multiple structures (multi-state model). For example, protein heterogeneity in a crystal can be modeled using snapshots of molecular dynamics simulations [29^••]. Protein dynamics in solution, as measured by SAXS and NMR spectroscopy, can be modeled by fitting multiple weighted conformations to the data [30–34]. In EM single particle reconstruction, heterogeneity can be addressed by multi-model reconstruction using multi-stage clustering [35].

The most objective ranking of models is in principle achieved by a Bayesian scoring function [36]. The Bayesian approach estimates the probability of a model, given information available about the system, including both prior knowledge and newly acquired experimental data. When modeling heterogeneous systems, model M includes a set of N modeled structures X = {X_i}, their population fractions in the sample {w_i}, and potentially additional parameters (eg, the unknown data errors). The posterior probability p(M|D, I) of model M given data D and prior knowledge I is

$$p(M\mid D,I)\propto p(D\mid M,I)·p(M\mid I)$$

where the likelihood function p(D|M, I) is the probability of observing data D given M and I; and the prior p(M|I) is the probability of model M given I. The likelihood function is based on the forward model f(X) that predicts the data point that would have been observed for structure(s) X in the absence of experimental error, and a noise model that specifies the distribution of the deviation between the experimentally observed and predicted data points. The Bayesian scoring function is defined as S(M) = − log[p(D|M, I)· p(M|I)] which ranks the models the same as the posterior probability. The most probable models are found by selecting the best scoring models sampled from the posterior distribution.

The Bayesian scoring function can account for most sources of uncertainty in data without over-fitting. It was successfully adopted for NMR spectroscopy data [36,37], and recently cryo-EM density maps [38,39^••]. Bayesian structure determination based on sparse NOE measurements produces more accurate structures and better estimates of precision than standard NMR structure determination methods [36,37,40]. In single particle EM reconstruction, the Bayesian approach results in density maps with higher resolution than those from standard reconstruction methods using the same input datasets [38,39]; moreover, high-resolution maps can be obtained from only a few thousand of particles [41–43]. Recently, the BioEM method for Bayesian analysis of individual EM images that can deal with conformational heterogeneity was developed [44]. Bayesian scoring functions have also been developed for cysteine cross-linking [45], chemical cross-linking [46], FRET spectroscopy [47], and atomic statistical potentials [48].

The Bayesian approach is more objective than traditional scoring functions in a number of respects: (i) inference of unknown quantities, such as data error and state weights, (ii) combination of different types of information, (iii) inference of multiple structures, (iv) estimate of model precision, and (v) “marginalization” of parameters that are difficult to determine. The main disadvantage is that the model is more elaborate (cf, noise model and priors) and a more exhaustive sampling of structural and parameter space is required.

Sampling

A variety of optimization methods (eg, conjugate gradients), sampling algorithms (eg, Monte Carlo), and even exhaustive enumeration (eg, Fast Fourier Transform) can be used to find models consistent with input information. The major source of uncertainty in this stage is insufficient sampling due to the ruggedness and high dimensionality of the scoring function landscape that needs to be sampled. As a result, it is almost never certain that the best scoring models were sampled. For stochastic sampling, such as the Monte Carlo algorithm, the thoroughness of sampling can be indicated by showing that new independent runs (eg, using random starting configurations and different random number generator seeds) do not result in significantly different good-scoring solutions (“convergence test”) [49]. Passing such a test is a necessary but not sufficient condition for thorough sampling; a positive outcome of the test may be misleading if, for example, the landscape contains only a narrow, and thus difficult to find, pathway to the pronounced minimum corresponding to the native state.

For multi-state models, the sampling is often performed in two steps, due to the relatively high number of degrees of freedom involved. First, a large set of possible single configurations is sampled. Second, the sets of configurations in a multi-state model are enumerated, for example by using a genetic algorithm [31,32], a maximum entropy approach [33], or a deterministic method [34].

Stage 4: Analyzing models and information

Input information and output models are analyzed in order to estimate model precision and accuracy, to detect inconsistent information and missing information, as well as to suggest most informative future experiments. There are three possible outcomes of modeling, based on the number of clusters of models and consistency between the models and information. The following discussion applies to single-state models, but similar considerations can also be extended to multi-state models. First, if only a single model (or a cluster of similar models) satisfies all restraints and thus all input information, there is probably sufficient information for determining the structure (with the precision corresponding to the variability within the cluster). Second, if two or more different models are consistent with the restraints, the information is insufficient to define the single state or there are multiple significantly populated states. If the number of distinct models is small, the structural differences between the models may suggest additional experiments to narrow down the possible solutions. Third, if no model satisfies all input information, the information or its interpretation in terms of the restraints are incorrect, the representation needs to include additional degrees of freedom, and/or sampling needs to be improved (regardless of the outcome of the convergence test above).

If multiple structural states are indicated, care must be taken that the scoring function explicitly allows for this possibility [31–34,45,46]. When a mixture of states is modeled, the number of states needs to be determined. Frequently, Occam’s razor suggests that the smallest number of states sufficient to explain the input information within some threshold is the optimal choice. An example of this approach is the “minimal ensemble” method in molecular modeling based on SAXS data [32]. However, sometimes Occam’s razor is not applicable. For example, even though a SAXS profile of an intrinsically disordered protein may be matched by a sum of profiles for the minimal ensemble structures, the system is likely to exist in a large ensemble of many widely different states; such cases are indicated by similarity between distributions of structural properties, such as the radius of gyration, of the minimal and large ensembles [31].

Once we obtain a model (single or multi-state) that satisfies the input data, we can analyze it to estimate precision and accuracy. It is impossible to know with certainty the accuracy of the proposed structure without knowing the real native structure. However, accuracy can be estimated based on rules derived from benchmark studies that involve modeling of known structures. For example, there is a strong correlation of the accuracy of an X-ray structure with the resolution of the X-ray dataset and R_free [1]. In addition to such broad rules, five types of analysis that are indicative of model precision and accuracy in specific cases have been proposed [20], as follows (the first three tests are examples of statistical resampling [50]).

Estimating model precision based on variability in the ensemble of good-scoring models

The model ensemble is analyzed in terms of the precision of its features, such as the protein positions and contacts [49,51–53]; the precision is defined by the variability in the ensemble and likely provides the lower bound on its accuracy. Of particular interest are the features that are present in most configurations in the ensemble and have a single maximum in their probability distribution. The spread around the maximum describes how precisely the feature was determined by the input information. A more thorough test is performed by estimation of structural variability in multiple random subsets of the ensemble [52^••,54^••].

Self-consistency of the experimental data

Inconsistencies in the experimental data or its interpretation are indicated by an ensemble of models containing only frustrated structures that do not satisfy the input data, although such an outcome can also arise from the failure of sampling. If there is a model that satisfies all data, the probability of such a model occurring by chance can be indicated by statistical significance tests; if this probability is low, the model is likely to be correct. In these tests, the labels on the data points are randomized or permuted, followed by re-computing the model; for example, one can assign cross-links to random residue pairs [55].

Validating models by using random subsets of experimental data

The structure can be directly validated against experimental data that was not included in the structure calculation [52^••]. This criterion is similar to the crystallographic R_free parameter and can be used to assess both the model accuracy and the input data [1]. Alternatively, modeling can be repeated with random subsets of the data. Common statistical techniques for this validation include cross validation and bootstrapping [50].

Reproducibility of the model with simulated data

In this approach, a native structure is assumed, the restraints to be tested are simulated from this structure, the structure is then reconstructed based only on these restraints, and finally the reconstruction is compared to the original assumed structure [49]. Using such simulations, the dependence of model accuracy on the amount, quality, and type of information can be mapped for future prediction of accuracy.

Patterns unlikely to occur by chance

Unlikely patterns emerging from mapping independent and unused data on the structure also increase our confidence in a model, similarly to validation by information not used in modeling. For example, the model of the nuclear pore complex (NPC) revealed an unexpected 16-fold pseudo-symmetry in the arrangement of fold types of the constituent proteins, in addition to the known 8-fold symmetry [49]. The 16-fold pseudo-symmetry validates the model because the fold types were not used in modeling and the 16-fold pseudo symmetry is unlikely to arise by chance (while it can be reasonably explained by gene duplications in the evolution of the NPC).

Conclusions

Integrative structure determination needs de facto standards and tools for assessing the input data and resulting models, following in the footsteps of X-ray crystallography and NMR spectroscopy with established structure validation criteria.

Figure 1.

Uncertainty in integrative structure modeling. The four-stage scheme of integrative structure modeling is used to describe how to approach uncertainty in the data and the models. The collected information is converted into a scoring function that accounts for data error, ambiguity, and incoherence. The model representation should reflect data sparseness. After sampling, if good-scoring models satisfy the restraints, they are further evaluated by structural clustering and data validation tests.

Box 1. Glossary.

Input data

experimental data used to compute a model

Input information

experimental data and any additional information

Data sparseness

a measure of the amount of data relative to the number of degrees of freedom in the model

Data error

the difference between the measured data and its true value, which can be computed given a forward model and the true structure; data error can be random and/or systematic, affecting the precision and the accuracy of the measured data

Data ambiguity

a data point is ambiguous when it cannot be assigned to the specific components of the model

Data incoherence

a dataset is incoherent when it is derived from a compositionally or configurationally heterogeneous sample

Single-state model

a model that specifies a single structural state and value for any other parameter

Multi-state model

a model that specifies two or more co-existing structural states and values for any other parameter

Ensemble of structural models

a set of structural models each one of which is consistent with the data

Ensemble precision

variability among structural models in the ensemble

Error or accuracy of a structural model

the difference between the structural model and the true structure(s)

Representation resolution

a descriptor of the detail in the representation of the structural model (eg, atomic models consist of atoms)

Highlights.

• Integrative modeling needs standards and tools for assessing models and input data

• Model uncertainty originates from sparse, noisy, ambiguous, or incoherent data

• Model uncertainty also originates from representation, scoring function and sampling

• Some methods for assessing data and models are listed