Simultaneous time-temperature-thickness superposition theoretical and statistical modelling of convective drying of guava

Abstract

Modelling studies of guava drying and quality are presented using theoretical and statistical models by varying temperature from 55 to 75 °C and slice thickness from 3 to 9 mm. The quality of dried fruit was measured for its water activity, colour, vitamin C, and texture. The superposition technique with Midilli-Kucuk model showed efficiency in modelling the drying process with R² = 0.9991. The second-order polynomial equations adequately described the quality of dried guava with regression coefficient, R² > 0.7. Drying time was a good function of temperature and thickness (P < 0.001); water activity, colour and vitamin C showed strong dependence on temperature (P < 0.1); while texture was mainly influenced by its thickness (P < 0.005). The optimum drying temperature of 70 °C at slice thickness of 6 mm was determined using the desirability function method. Simultaneous modelling using the theoretical and statistical drying models provides information on water diffusion and evaporation with the drying responses and factors.

Introduction

The aim of modelling is to establish a quantitative relationship between independent and dependent variables using mathematical and statistical methods in characterising how one variable affects the other (Huang et al. 2001). The disadvantage of a statistical model is that it derives relationship between variables based on conventional linear regression techniques e.g. the simple and multiple regressions. Although these models are useful in investigating the possible effects of certain variable (Rahman 2005), they lack in providing understanding on its process mechanisms. In theoretical models, mathematical models are established using laws, theorems, principles, and assumptions about the phenomena which provide more information about the process variables.

The thin-layer drying models proposed for evaluating drying behaviour are reported as theoretical (Fick’s second law of diffusion), semi-theoretical and empirical in fruit drying studies which include apple (Sacilik and Elicin 2006), strawberries (Akpinar and Bicer 2006), kiwifruits (Kaya et al. 2010) and a range of tropical fruits, like chempedak (Chong et al. 2008a), salak (Ong and Law 2009) and litchi (Janjai et al. 2010). The semi-theoretical model which is derived from Fick’s second law is the most commonly adapted to predict drying kinetics of food materials. They often give good estimation by incorporating lump sum values of other effects into the model parameters (Ong and Law 2009). They are simpler and do not need assumptions of sample geometry, mass diffusivity and conductivity. While the empirical models contain parameters that have no physical meaning as they neglect the fundamentals of the drying process (Akpinar and Bicer 2006), the semi-theoretical models have limitations of reporting drying time for specific drying conditions.

The superposition technique is applicable to model the complex drying data into a single master curve which incorporates a large number of variables for prediction of drying kinetics. This time-temperature superposition technique (TTST) is also known as the reduced parameters technique which is used in modelling of rheological behaviour of polymeric materials and fluid food (Steffe 1996; Chin et al. 2009). TTST was used to model the effect of air temperature and slice thickness on drying kinetics of tomato slices and Avishan leaves at different temperatures and velocities (Khazaei et al. 2008b; Khazaei et al. 2008a). The use of TTST in modelling could reduce model constants and enhance the fitted semi-theoretical model to be a single and general model which represents the overall drying kinetics of a dried fruit.

The objective of this research was to model guava fruit drying using both theoretical and statistical models to obtain a qualitative understanding of the drying process and quantitative evaluation of product evolution to desired quality attributes for ease of control in a food drying process and optimisation. The effect of temperature and slice thickness on the drying kinetics of dried guava was investigated through TTST modelling. The optimum drying condition to produce dehydrated products with low water activity, high vitamin C retention, attractive colour, and acceptable texture for minimum processing time was determined using response surface methodology (RSM) with aim of producing dried guava to be used as dried fruit ingredients (Myers et al. 2009).

Materials and methods

Materials

Fresh guava fruits (Psidium guajava; Kampuchea cultivar Vietnam, GU8) were obtained from Kampung Pelegong, Labu, Negeri Sembilan, Malaysia. Guava fruits are widely planted for fresh consumption and it is one of the top tropical fruits rich in vitamin C content. The initial moisture content of guava slices was determined by heating in a convection oven (UM500, Memmert GmbH, Schwabach, Germany) at 105 °C for 48 h following the AOAC method, 931.04 (AOAC 1990). Guava samples were kept in refrigerator at 10 °C to maintain its maturity before use and they were in the range of 8.0 ± 0.2 °Brix.

Drying process

Guava samples were cut vertically into quarters and its core with seeds removed. Each fruit slice was then cut horizontally to their axis into three different thicknesses of 3, 6, and 9 mm with top surface area of 20 mm × 20 mm, measured to ± 0.02 mm using a digital caliper (Mitutoyo, Japan) from the white fleshy part of guava fruit. The guava slices were placed in stainless steel petri dishes and dried at temperature of 55, 65, or 75 °C in a convection oven. Samples were removed at various intervals and weighed, before returning to the oven to continue drying. The weight loss of samples was determined using an electronic balance (Ross B204-S, Mettler Toledo, Swiss). Weighing interval of 15 min was used during the first hour drying, 30 min the following next 2 h, and a 60 min’ interval until the calculated final moisture content of the guava reached approximately 20 % (w.b.). Each run was performed in an identical manner and replicates of four were obtained from the same batch of fruits.

Determination of effective diffusivity and activation energy

The guava slices were assumed in the form of infinite slab and the analytical solution of the Fick’s second law is given as (Crank 1975):

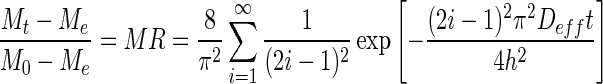1

where MR is the dimensionless moisture ratio, M_t is the moisture content at any time, t (g water/g dry solids), M_e is the equilibrium moisture content, M₀ is the initial moisture content, D_eff is the effective diffusivity, h is the thickness of the guava slice (mm) where drying occurs from only one side, and i is a positive integer.

Thus, for sufficiently long drying time, Fick’s second law is simplified and expressed in a logarithmic form as shown in Eq. (2) with its dimensionless moisture ratio (MR) simplified to M_t/M₀ due to relatively small M_e compared to M_t or M₀ (Doymaz 2009; Sacilik and Elicin 2006).

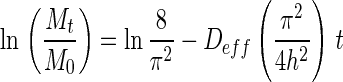2

The effective diffusivity of dried guava was calculated from the slope of the logarithm form of simple diffusion model from Eq. (2).

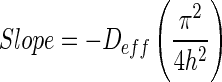3

The effective diffusivity, as a function of the drying temperature, was correlated by an Arrhenius-type equation where activation energy was determined.

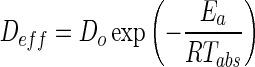4

D₀ is the Arrhenius diffusivity constant, E_a is the activation energy (kJ/mol), R is the universal gas constant (8.314 J/mol K), and T_abs is the absolute temperature in Kelvin.

The effective diffusivity was also reported as a function of the drying temperature and sample thickness in the Arrhenius-type equation using multiple regression analysis (Panchariya et al. 2002; Khazaei et al. 2008b).

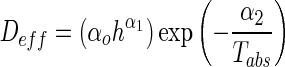5

where T_abs is the absolute temperature, h is the slice thickness (mm), α₀, α₁, and α₂ are constants.

Model development

Theoretical modelling

A 3² factorial design experiment with drying temperatures of 55, 65 and 75 °C and slice thickness of 3, 6 and 9 mm which gave a total of 9 runs was conducted for drying kinetics studies. The experimental data of drying curves, MR(t) was fitted to the selected semi-theoretical thin layer drying models shown in Table 1. In selecting the best suited model describing the drying process of guava, curve fitting was performed by computing the sum square errors (SSE) and minimising it with the least square method using Microsoft Excel SOLVER tool (Microsoft Office Professional 2007, USA). The generalised reduced gradient (GRG2) nonlinear optimisation code was adopted in determining the model constants, a, b, c, k and n.

Table 1.

Common semi-theoretical models applied to the drying curves of guava slices

No.	Model name	Model equation
1	Newton	MR = exp(−kt)
2	Page	MR = exp(−kt n )
3	Henderson and Pabis	MR = a exp(−kt)
4	Logarithmic	MR = a exp(−kt) + c
5	Two term	MR = a exp(−k 1 t) + b exp(−k 2 t)
6	Midilli-Kucuk	MR = a exp(−kt n ) + bt

The dependence of the drying rate constant, k selected from the best fitted model on drying temperature and slice thickness variables was then described in the Arrhenius-type model using multiple regression analysis (Panchariya et al. 2002; Khazaei et al. 2008b):

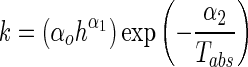6

where T_abs is the absolute temperature, h is the slice thickness (mm), α₀, α₁, and α₂ are constants.

Time-temperature-thickness superposition

A total of nine average drying curves sharing the same data for theoretical modelling were superposed by shifting along the abscissa to form a master curve in two steps of shifting. The drying curves, MR(t) of three slice thickness at common drying temperature were first shifted horizontally on the log(time) axis to a reference slice thickness of 6 mm to obtain the dimensionless time-thickness shift factors, a_h,i:

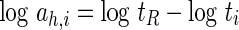7

where t_R = time at reference thickness and t_i = time at other thickness for each moisture ratio ranging between 0.1 and 0.8. At reference thickness, log a_h,R = 0, where a_h at reference is 1. When t_R = t·a_h, where the quantity t·a_h is known as the reduced or pseudo time, t′ (Khazaei et al. 2008b), the horizontal shifting with average a_h forms one master curve MR(t′) for each drying temperature.

Subsequently, the three developed temperature master curves were shifted to a reference temperature of 65 °C to construct a single master curve with the average temperature shift factor of a_T following Eq. (7). The final master curve MR(t′′) where t′′=t·a_h·a_T was used to estimate moisture ratio of guava slices at temperature of 55–75 °C and thickness of 3–9 mm. The final single master curve was fitted to all six semi-theoretical models (Table 1) to obtain the best fitted universal moisture ratio master curve as a function of time, temperature and thickness, MR(t,T,h).

Statistical modelling

Response surface methodology (RSM) was used to design the experiment and determine the adequate model for dried guava quality analysis using Minitab Statistical Software (Version 15, Minitab Inc., USA). A face-centred central composite design was chosen to evaluate the relationship of drying temperature and slice thickness as independent variables, X to the dependent responses, Y which included the drying time, water activity, colour, vitamin C, and texture of dried guava. The complete design consisted 13 sets of test conditions including five replicates of the centre point (Table 2) which shared the same data for 9 experimental runs conducted for theoretical modelling.

Table 2.

Face-centred central composite design matrix used to evaluate the effects of processing variables (uncoded) on quality properties of guava slices

Runs	Temperature (°C)	Thickness (mm)
1	75	3
2	65	9
3	55	6
4	55	3
5a	65	6
6a	65	6
7a	65	6
8	55	9
9a	65	6
10	65	3
11a	65	6
12	75	6
13	75	9

^acentre point

Second-order polynomial model equation (Eq. (8)) was defined and fitted for each response from the experimental data.

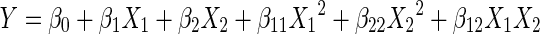8

Y indicates the estimated response, β₀, β₁, β₂, β₁₁, β₂₂, and β₁₂ are constant coefficients where β₀ is a constant, β₁ and β₂ are coefficients for linear terms, β₁₁ and β₂₂ are coefficients for quadratic terms, and β₁₂ is the coefficient for interaction terms. X₁ and X₂ are the uncoded values of the independent variables of drying temperature (°C) and slice thickness (mm), respectively.

Quality parameters

Water activity

The water activity of the dried samples was determined using a water activity meter (FA-st, GBX, Bourge de Peage, France). Each water activity measurement was based on the average values of three measurements.

Colour analysis

The colour of the samples was measured using UltraScan PRO Spectrophotometer (Hunter Associates Laboratory, Inc., VA, U.S.A.). The colour was expressed in terms of L (lightness), a (redness) and b (yellowness) according to the Hunter Lab colour scale. The total colour change (ΔE) is calculated from the L, a, and b values.

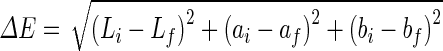9

where i and f indicates the initial colour values of fresh samples and final colour values of dried samples respectively.

Texture analysis

Texture Profile Analysis (TPA) was used to determine the texture of the samples by using a texture analyser (TA-XT_plus, Stable Micro Systems, Surrey, U.K.). Samples were placed horizontally at the centre of platform. Two compression cycles were performed on samples with a 2.0 mm diameter cylinder stainless steel probe at strain 50 % of sample height with 5 s between cycles. The pre-test speed was 1.0 mm/s, test speed was 5.0 mm/s, post-test speed was 5.0 mm/s, and the trigger force was 5 g. Hardness, springiness, cohesiveness, and chewiness of the samples were computed from each TPA curve using the texture analyser software macro (TEE 32 Stable Micro System, UK). The textural measurement was based on the average values from the four samples slices for each combination of drying temperature and slice thickness.

Vitamin C analysis

The vitamin C contents of samples were determined with a standard vitamin C measurement (Boyer 1986). Each sample was weighed and ground in a porcelain mortar with 25 ml of the metaphosphoric acid 4 % solution, HPO₃. The liquid extract was poured into 100 ml volumetric flask and the solid residual was again ground with 25 ml of the HPO₃ solution. Total volume of liquid extract was made up to 100 ml with HPO₃ solution. The solution was filtered and 10 ml of the filtrate was transferred into an Erlenmeyer flask. The filtrate was titrated with 2,6-Dichlorophenolindophenol solution until a distinct rose-pink colour persisted for 10 to 20 s. Each measurement was based on the average values of three determinations. 10 ml of HPO₃ solution was also titrated as blank.

Statistical analysis

The goodness of fit of the proposed semi-theoretical models was evaluated with the coefficient of determination (R²), reduced chi-squared (χ²), and root mean square error (RMSE) which was calculated as follow:

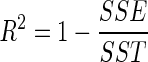10

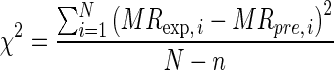11

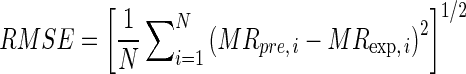12

where SSE is the sum of square error, SST is the total corrected sum of squares, MR_exp,i is the i^th experimentally observed moisture ratio, MR_pre,i is the i^th predicted moisture ratio, N is the number of observations and n is the number of constants. R² was the primary criterion for selecting best fitted model with minimum SSE (Walpole et al. 2002).

The statistical models were tested for their adequacy by performing analysis of variance (ANOVA) to test the significance of the model. The suitability of the second-order polynomial function was judged by the associating it with probability (P value) and R². The optimisation response variables were performed by using response optimiser option of MINITAB (Version 15) with the desirability function technique.

Verification of models

Experimental data for quality attributes and drying kinetics were obtained by conducting an independent set of experiment following the optimum conditions found. The experimental value was compared with the predicted from the optimised model by calculating the percentage error (Eq. (13)) to determine the adequacy of the drying kinetics and response surface models. The percentage error, PE which is lower than 10 % indicates a good fit (McLaughlin and Magee 1998).

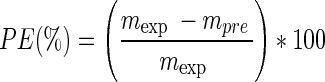13

where m_exp is experimental value and m_pre is predicted value.

Results and discussion

Drying characteristics of dried guava

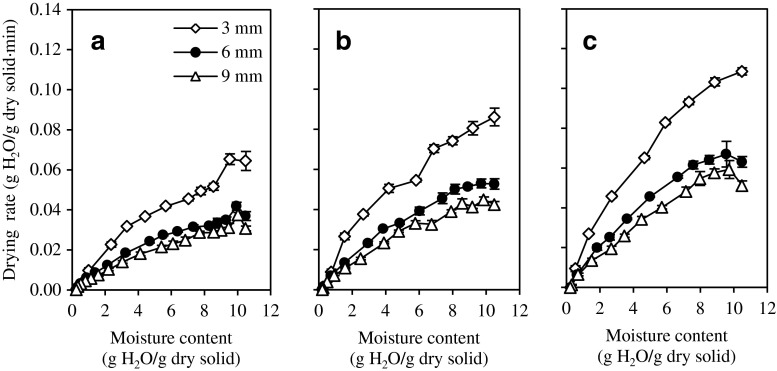
The initial moisture content of the fresh guava slices was 91.31 ± 0.59 % wet basis (w.b.) and it was dried until approximately 20.36 ± 1.05 % (w.b.) or about 0.2564 ± 0.0165 g water/g dry solids to achieve an edible form. Rapid drying to the range of 15–20 % moisture was suggested to minimise the time for Maillard browning (DeLong 1992; Sagar and Suresh 2010). Figure 1 shows the variation in drying rate as a function of moisture content. There was an initial transient state at the beginning of the drying process, where fresh guava slices at ambient needed some time to reach the set oven temperature before drying starts and the drying rate increased. It was also observed that the drying rate decreased continuously with decreasing moisture content or increasing drying time. Since fresh guava is high in moisture content, there was only the falling-rate period during the drying process (Bakshi and Singh 1980). The only falling-rate period proved that diffusion has pre-dominantly governed the moisture movement in the samples. This observation was in agreement with previous work on bananas (Nguyen and Price 2007), guava and papaya (Hawlader et al. 2006). Figure 1 illustrates that the higher the temperature and the thinner the material, the higher the drying rate due to high evaporation rate of moisture transfer from the surface to heated air and the reduced distance for the moisture travels in thinly slices. It was observed that the surface area to volume ratio is bigger for thin slices which increased the exposure of samples to heated air. The calculated surface area to volume ratio for the 3, 6 and 9 mm samples are 0.87:1, 0.53:1 and 0.42:1, respectively. This has resulted the highest drying rates and least drying time for guava slices with smallest thickness of 3 mm at drying temperature of 75 °C. A thinner sample slice and higher drying temperature give a greater drying rate and shorter drying period, as reported in drying of apple slices (Sacilik and Elicin 2006) and chempedak (Chong et al. 2008a). No significant difference of drying rates between slice thickness of 6 and 9 mm as the curves were closed to each other in this study.

Fig. 1.

Effects of different slice thickness of guava slices at a 55 °C, b 65 °C and c 75 °C on drying rates given as means ± standard error (n = 4)

Effective diffusivity and activation energy

The effective moisture diffusivity, D_eff is an important mass transport property that refers to the rate of moisture movement in solids where water diffuses from inner regions (where moisture content is higher) to surface regions (with lower moisture content). The process of water evaporating off at the surface with sufficient heat supplied is accounted as the drying rate (Derossi et al. 2011). Lee and Kim (2009) and Nguyen and Price (2007) are in agreement that D_eff increases with temperature for the radish and banana samples studied respectively due to a rapid initial rate of moisture evaporation. However, with sample thickness, Lee and Kim (2009) reported that D_eff increased with reducing sample thickness while Nguyen and Price (2007) found otherwise. From the values of effective diffusivity tabulated in Table 3 for guava slices, D_eff increased about two times greater with every 3 mm increase in slice thickness, similar trend to those reported in Nguyen and Price (2007). Side diffusion of moisture migration might present in thick slabs which enhanced the diffusion defying assumptions of one-directional diffusion from inside to the surface of the slabs known as the edge effect. For the thinner slabs, a high temperature could have resulted a fast surface hardening where it slows down the drying rates and lowers the effective diffusivity.

Table 3.

Effective diffusivity, D _eff and constant diffusivity, D _o for different thickness and temperatures

Thickness (mm)	Temperature (°C)	D eff (m2/s)	D o (m2/s)
3	55	5.139E-10	8.174E-05
	65	7.624E-10
	75	1.021E-09
6	55	1.312E-09	4.918E-05
	65	1.918E-09
	75	2.395E-09
9	55	2.357E-09	1.000E-04
	65	3.418E-09
	75	4.338E-09

The effective diffusivities of guava slices found were from 5.139 × 10⁻¹⁰ to 4.338 × 10⁻⁹ m²/s which is within the general range of 10⁻¹¹−10⁻⁸ m²/s for 82 % of food materials (Marinos-Kouris and Maroulis 1995; Erbay and Icier 2009). The effect of temperature and thickness on effective diffusivity was tested with two-way analysis of variance (ANOVA). The effective diffusivity increased significantly when both drying temperature (P = 0.04) and slice thickness (P = 0.003) increased and the diffusivity of guava slices was a strong function of temperature and thickness. A multiple linear regression analysis was used to express the effective diffusivity, D_eff as a function of temperature, T and thickness, h following Eq. (5). High correlations between effective diffusivity with temperature and thickness in Eq. (14) verify that water diffusion is affected by both these factors. This water diffusion coefficient model for guava slices provides useful information through the diffusion rate in explaining the drying kinetics upon the conditions within the material.

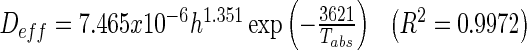14

The activation energy, E_a is important in describing the sensibility of D_eff with temperature (Erbay and Icier 2009). The calculated activation energy using Eq. (4) was 32.63, 28.67, and 29.02 kJ/mol for guava thickness 3, 6, and 9 mm, respectively. These activation energy values are in the range of 15–40 kJ/mol for various food (Rizvi 1986). The greater value of activation energy for thickness 3 mm means more sensibility of effective diffusivities to temperature (Erbay and Icier 2009).

Drying models

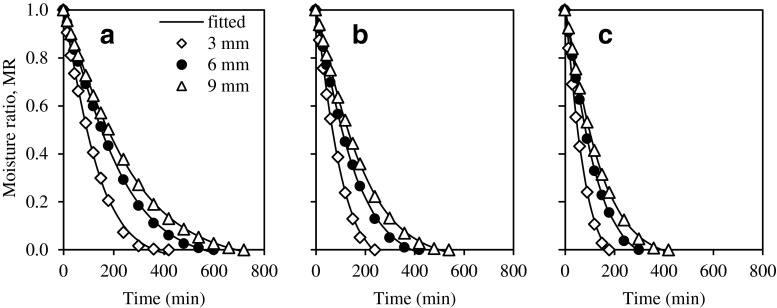
Table 4 shows the goodness of fit of six common drying models and the Midilli-Kucuk model was the best model to represent the thin layer drying behaviour of guava slices at different drying temperatures and slice thickness based on the criteria of the highest R², lowest χ² and RMSE. Generally, R², χ², and RMSE varied between 0.9982 and 0.9998, 3.048 × 10⁻⁵ and 2.726 × 10⁻⁴, and 0.00434 and 0.01453, respectively. Figure 2 shows that the experimental moisture ratio was excellently fitted with the Midilli-Kucuk model which describes the drying kinetics of guava adequately.

Table 4.

Statistical parameters and model constants of semi-theoretical models for modelling the drying kinetics of guava slices

Name of model	Statistical parameters and model constants	Various temperature-thickness combinations									Master-curve	Optimal condition
		55 °C			65 °C			75 °C			55–75 °C	70 °C
		3 mm	6 mm	9 mm	3 mm	6 mm	9 mm	3 mm	6 mm	9 mm	3–9 mm	6 mm
Newton	R 2	0.9902	0.9890	0.9932	0.9855	0.9891	0.9910	0.9850	0.9873	0.9925	0.9897	0.9927
	χ 2	1.228E-03	1.407E-03	8.603E-04	1.753E-03	1.360E-03	1.153E-03	1.895E-03	1.521E-03	9.245E-04	1.205E-03	8.978E-04
	RMSE	0.03366	0.03632	0.02851	0.03972	0.03543	0.03280	0.04104	0.03719	0.02921	0.03456	0.02869
Page	R 2	0.9977	0.9988	0.9994	0.9978	0.9989	0.9993	0.9988	0.9993	0.9997	0.9988	0.9995
	χ 2	3.095E-04	1.584E-04	7.789E-05	2.982E-04	1.497E-04	8.934E-05	1.767E-04	8.645E-05	3.618E-05	1.452E-04	6.237E-05
	RMSE	0.01618	0.01177	0.00832	0.01545	0.01126	0.00880	0.01172	0.00841	0.00553	0.01195	0.00721
Henderson and Pabis	R 2	0.9922	0.9921	0.9953	0.9887	0.9922	0.9938	0.9882	0.9914	0.9954	0.9925	0.9950
	χ 2	1.065E-03	1.087E-03	6.290E-04	1.534E-03	1.052E-03	8.469E-04	1.698E-03	1.147E-03	6.242E-04	8.798E-04	6.771E-04
	RMSE	0.03002	0.03084	0.02365	0.03503	0.02984	0.02709	0.03634	0.03064	0.02298	0.02941	0.02375
Logrithmic	R 2	0.9961	0.9976	0.9988	0.9976	0.9979	0.9981	0.9980	0.9979	0.9984	0.9974	0.9982
	χ 2	5.906E-04	3.568E-04	1.702E-04	3.778E-04	3.126E-04	2.821E-04	3.449E-04	3.066E-04	2.316E-04	3.062E-04	2.655E-04
	RMSE	0.02131	0.01703	0.01191	0.01626	0.01551	0.01502	0.01516	0.01493	0.01335	0.01720	0.01411
Two term	R 2	0.9922	0.9921	0.9953	0.9887	0.9922	0.9938	0.9882	0.9914	0.9954	0.9925	0.9950
	χ 2	1.302E-03	1.268E-03	7.189E-04	2.045E-03	1.286E-03	1.001E-03	2.377E-03	1.475E-03	7.629E-04	8.953E-04	8.463E-04
	RMSE	0.03002	0.03084	0.02365	0.03503	0.02984	0.02709	0.03634	0.03064	0.02298	0.02941	0.02375
Midilli-Kucuka	R 2	0.9982	0.9994	0.9997	0.9989	0.9995	0.9996	0.9996	0.9998	0.9998	0.9991	0.9997
	χ 2	3.048E-04	1.004E-04	4.090E-05	1.958E-04	9.103E-05	5.708E-05	9.054E-05	3.478E-05	2.726E-05	1.028E-04	4.844E-05
	RMSE	0.01453	0.00868	0.00564	0.01084	0.00794	0.00647	0.00709	0.00470	0.00434	0.009964	0.00568
	k (min-1)	2.592E-03	1.348E-03	1.579E-03	4.402E-03	2.493E-03	1.943E-03	5.779E-03	3.308E-03	3.206E-03	2.436E-03	3.861E-03
	n	1.217	1.230	1.163	1.185	1.195	1.197	1.201	1.198	1.164	1.200	1.165
	a	0.9821	0.9839	0.9899	0.9920	0.9911	0.9901	0.9952	0.9964	0.9987	0.9898	0.9949
	b (min-1)	−2.218E-05	−2.660E-05	−2.284E-05	−1.853E-04	−5.936E-05	−2.735E-05	−2.048E-04	−9.348E-05	−2.856E-05	−4.144E-05	−3.690E-05

^abest fitted model

Fig. 2.

Moisture ratio as a function of drying time for different slice thickness for temperatures at a 55 °C, b 65 °C and c 75 °C and fitted with the Midilli-Kucuk model

The values of the Midilli-Kucuk model constants, a, k, n, and b are listed in Table 4. The drying rate constant, k increases with the increase in drying temperature and decrease of slice thickness. This indicated that higher temperature and smaller thickness enhanced the driving force of heat and mass transfer. However, a, b and n values did not show any clear trends as they may have depended on additional processing conditions. Similar findings on the model constants are reported in Khazaei et al.’s (2008b) work on tomato drying. Hence, the drying rate constant, k (min⁻¹) is correlated by the Arrhenius-type equation model as given in Eq. (15):

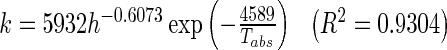15

By inserting function k (Eq. (15)) into the 4-term variables Midilli-Kucuk model, it allows the moisture ratio’s expression to be reduced to a 3-term variable model known as the single model which is expressed as a function of drying time, drying temperature, and slice thickness (Eq. (16)), with constants a = 0.9915, n = 1.198 and b = −1.930 × 10⁻⁵ fitted using data obtained from entire experimental data.

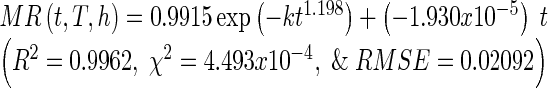16

In general, the drying rate, dM/dt, drying rate constant, k, and effective diffusivities, D_eff of this guava drying study increased with drying temperature. The effective diffusivities increased with sample thickness, which also seem to give a lower drying rate (Fig. 1) and drying rate constant (Table 4). Although the effective diffusivity increased in thick guava slices, it did not manage to increase the drying rate, and this may be due to the reasons of insufficient heat to evaporate off the moisture that gathered at the surface in shorter period and the effect of lower surface-volume ratio in thicker samples. This was found similar to reports by Falade and Solademi (2010) and Khazaei et al. (2008b) on drying of sweet potato and tomato with no explanations given. In addition, the drying rate and drying rate constant can also be expressed as a function of effective diffusivities and thickness. Following the liquid diffusion theory (Geankoplis 2003), by rearranging and differentiating Eq. (2), the drying rate can be written as 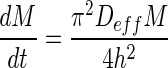. When the slope in Eq. (3) was compared with the slope of Henderson and Pabis’s Eq. in Table 1, the drying rate constant could be expressed as 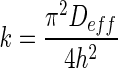(Erbay and Icier 2009). Both equations show that that the drying rate and drying rate constant are inversely proportional to the square of the thickness (Mittal 1999) which supported that thickness could give low drying rates and drying rate constants.

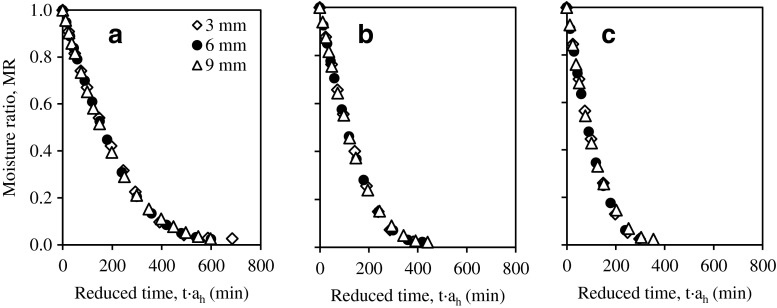
Master curve

Drying curves in Fig. 2 show a similar trend for the different thicknesses and temperatures. This suggests that the master-curve technique could be used to obtain a general drying kinetics model describing the drying behaviour of guava slices. With the reference of 6 mm slice thickness, the master curve for each temperature was obtained (Fig. 3) through the average time-thickness shifting factors, a_h (Table 5) which combines the effect of the drying time and slice thickness into a single value of reduced time t′. Time-thickness shift factor, a_h was regressed into the Arrhenius-type equation as a function of thickness, h (mm) and temperature, T_abs (K).

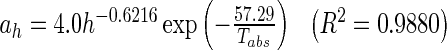17

Fig. 3.

Master-curves fitted with Midilli-Kucuk model showing moisture ratio versus reduced time with reference thickness of 6 mm at temperatures a 55 °C, b 65 °C and c 75 °C

Table 5.

Average thickness shift factors, a _h and temperature shift factors, a _T for guava slices of 3, 6, and 9 mm dried at temperatures of 55, 65, and 75 °C

Temperature (°C)	a h			a T
	Slice thickness (mm)
	3	6	9
55	1.63	1	0.83	0.70
65	1.59	1	0.82	1
75	1.66	1	0.84	1.28

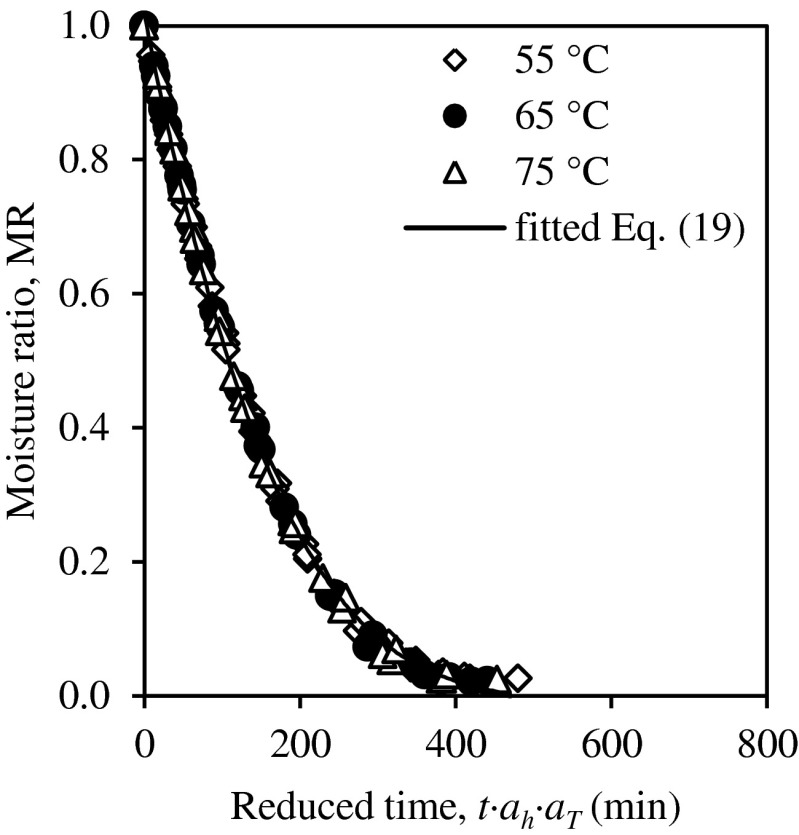
Master curves in terms of t · a_h in Fig. 3 were shifted again to drying temperature of 65 °C, acting as the reference to generate a single master curve (Fig. 4) of moisture ratio as a function of reduced time t′′. The relationship between temperature shift factor a_T and temperature, T (°C) was determined as follow:

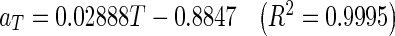18

Fig. 4.

Master curve fitted with Midilli-Kucuk model showing time-temperature-thickness superposition for guava slices

The final master curve was fitted with the selected semi-theoretical models in Table 1 in order to derive a relationship between moisture ratio, drying time, drying temperature, and slice thickness. The master curve that combines drying time, temperature, and thickness was best fitted with the Midilli-Kucuk model (Table 4).

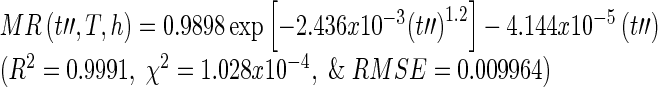19

where t′′ = t·a_h·a_T

A comparison between R² for the master curve fitted with Midilli-Kucuk model for Eq. (19) generated using the superposition technique and the single model in Eq. (16) shows that the superposition technique has higher accuracy in predicting the moisture ratio of guava slices. The results indicated that curve shifting based on the time-temperature-thickness superposition technique is applicable in the drying process to predict the moisture ratio.

Statistical model for product quality

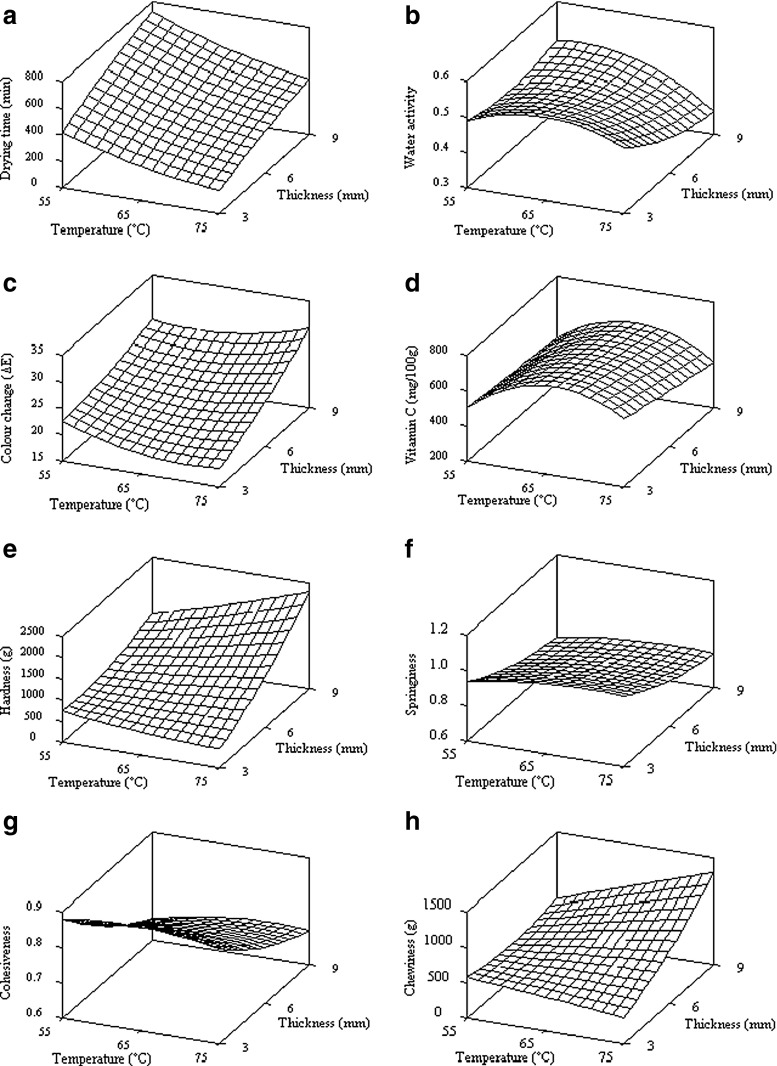
Table 6 lists the coefficients for the response surface equations in uncoded units with indication of significance through its P-value. All the response models were statistically significant at P < 0.1 with acceptable R² values (R² > 0.7) and non-significant lack-of-fit. The coefficient of determination, R² was used to validate each of the models and explained the overall predictive capability of the model. Granato et al. (2010) stated that the value of R² ≥ 70 % was considered good for sensory, colorimetric and physico-chemical results. The regression models for the quality attributes of dried guava were fitted adequately with the second-order polynomial model. A close observation on the effect of temperature and thickness on the quality attributes of dried guava showed that water activity, colour and vitamin C were significantly affected by the temperature (P < 0.1); while thickness had more influence on hardness and chewiness (P < 0.005). The combined effect of drying temperature and slice thickness on any response are visualised by the three dimensional surface plots for the fitted model as the function of these two independent variables in Fig. 5.

Table 6.

Coefficient of the regression model equations for drying time and quality properties of guava slices

Coefficient	Drying time (min)	Water activity	Colour change	Vitamin C (mg/100 g)	Hardness (g)	Springiness	Cohesiveness	Chewiness (g)
β 0	2335.34	−1.55145	117.518	−6300.13	5619.96	−0.090994	0.379917	2392.60
β 1	−59.41****	0.06449**	−2.692*	210.71****	−108.11	0.036426	0.022700	−24.12
β 2	109.51****	0.02418	−3.707	27.00	−798.81****	−0.075578	−0.088611	−541.18****
β 11	0.37****	−0.00047*	0.018	−1.57****	0.45	−0.000254	−0.000190	−0.08
β 22	−2.53***	0.00273	0.087	0.26	19.56**	0.004180	0.002333	9.31
β 12	−0.50**	−0.00103	0.061*	−0.68	11.67****	−0.000117	0.000433	7.80****
R 2	0.9969	0.7275	0.8534	0.8734	0.9691	0.8630	0.6862	0.9126
P (lack of fit)	–	0.927ns	0.787ns	0.258ns	0.747ns	0.863ns	0.606ns	0.681ns
P (overall model)	< 0.0005****	0.057*	0.008***	0.005***	< 0.0005****	0.006***	0.088*	0.001****

β ₀ the estimated constant regression coefficient

β ₁ and β ₂ the estimated linear regression coefficient of drying temperature and slice thickness, respectively

β ₁₁ and β ₂₂ the estimated quadratic regression coefficient of drying temperature and slice thickness, respectively

β ₁₂ the estimated interaction regression coefficient of drying temperature and slice thickness

*P < 0.10, **P < 0.05, ***P < 0.01, ****P < 0.005; ^ns not significant (P > 0.5)

Fig. 5.

Effects of drying temperature and slice thickness on a drying time, b water activity, c colour change, d vitamin C, e hardness, f springiness, g cohesiveness, and h chewiness

Drying time is an external condition that affects fruit quality directly and indirectly. Prolonged exposure to drying environment causes degradation of fruit properties. Apart from displaying moisture distribution through the drying curve plot, the statistical model fitting of drying time shows a strong function of drying temperature and slice thickness where it was significantly affected by all the model terms (P < 0.05) as shown in Table 6. Figure 5(a) shows that drying time increased with decreasing drying temperature from 75 °C to 55 °C, and increasing slice thickness. With a reference of drying time for thickness 3 mm as basis, the drying time increased by 42.9 %, 75.0 %, and 66.7 % for 6 mm thickness, 71.4 %, 125 %, and 133 % for 9 mm at drying temperatures of 55 °C, 65 °C, and 75 °C, respectively.

Water activity (a_w) is referred for food stability and safety control as it is very much linked to microbial growth, rates of deteriorative reactions and chemical/physical properties (Jangam and Mujumdar 2010). Water activity of fresh guava was as high as 0.954 ± 0.002 but after drying, it reduced significantly to a range of 0.45–0.55 (Fig. 5(b)). Despite these small variations of water activities was due to minor variances in the final moisture content of dried guava at the end of drying, these hot air-dried guava are safe for storage as they achieved the minimum level of below 0.62 for storage to prohibit microbial growth (Patkai 2006; Jangam and Mujumdar 2010). Beauchat (1981) and Fellows (1988) also reported that a_w = 0.60 was the lowest limit for growth of osmophilic or xerophilic yeast and fungi for dried fruit with 15 ~ 20 % water. Water activity of dried guava was significantly affected (P < 0.10) by temperature and the quadratic of temperature model terms (Table 6).

Colour is the key of attractiveness and directly affects consumers’ acceptance on foods. High colour change indicates the dried samples are far different from fresh fruit. Figure 5(c) shows that total colour change (ΔE) of guava slices decreased when temperature and thickness decreased. Higher temperature and longer drying times were observed to degrade colour much due to the natural fruit pigment losses and non-enzymatic browning reactions. Highest colour change occurred when drying at the highest temperature of 75 °C for the longest duration of 420 min. The colour change during drying is mainly caused by chemical and biochemical reactions of the surface characteristics of food (Perera 2005). Pott et al. (2005) also found noticeable colour change towards the red hue and caused by browning reaction when high air temperatures and excessive drying times were applied on dried mango slices.

Vitamin C is an essential nutrient for human. Being a water soluble and a most labile component among all vitamins contained in foods, it is highly sensitive to heat and can be degraded greatly when heat is applied for a given residual moisture content of fruit (Hawlader et al. 2006). Due to its perishable characteristics, removing moisture is desired to enable storage for a longer time with minimum loss of nutrients. Statistical analysis shows that vitamin C is strongly affected by temperature (P = 0.001). Figure 5(d) illustrates that maximum vitamin C content was retained at 65 °C. The lowest vitamin C retention (419.21 mg/100 g) occurred in samples dried at 75 °C with 9 mm thickness, lower than those dried at 55 °C.

Changes in texture of dried food are due to modification of microstructure or more generally due to case hardening or crust formation. Hardness is defined as the peak force on the first compression and is used to investigate case hardening in dried fruit; while, chewiness refers to the energy required to masticate a solid food product (Bourne 2002). Both attributes, the hardness and chewiness are desirable in dried fruit to obtain good mouth-feel. Hardness and chewiness have a similar trend where they increase with drying temperature and slice thickness (Fig. 5(e) & (h)). They are also significantly affected by thickness (Table 6). Increase of hardness at high temperature is due to the formation of a hard impermeable skin on the sample surface, which is known as case hardening or crust formation (Fellows 1988). Increase of hardness leads to increase of chewiness at high drying temperature as chewiness is also defined as a function of hardness. However, less hard and chewy product was found for the combination of 75 °C temperature and 3 mm thickness. It is noticeable that hardness of thin slices would only increase minimally due to thinner crust formation caused by a rapid drying rate even though it has been dried at high temperature (Achanta and Okos 1996). Perera (2005) reported that most air-dried products suffers collapse of structure, having firmer textures and increasing in chewiness, which can be undesirable to the customer. Chong et al. (2008b) explained that hardness in dried samples is due to depolymerisation of cell wall constituents such as occurrence of pectin after the exposure to heat during drying. Similar results was noted for hot-air dried chempedak where both hardness and chewiness values increased and springiness decreased with increase of drying temperatures (Chong et al. 2008a).

Table 6 shows that springiness and cohesiveness were not significantly affected by both process variables. Thinly dried guava was found to be more elastic due to its high springiness. Figure 5(f) and (g) show that springiness and cohesiveness have reduced slightly when the size of the dried fruit was thicker with small deviations when temperature increased. Hardening indicates a decrease of fruit elasticity (Sirisomboon et al. 2000) and a high value of hardness results in lower springiness.

Optimisation of dried guava attributes

Optimum conditions to hot air dried guava were determined by specifying the goal for each response. It was targeted to obtain minimum drying time, water activity, colour change and maximum vitamin C and to achieve 1,761 g of hardness and 407 g of chewiness by referring to the texture attributes of commercial dried guava with moisture content about 0.036 g water/g dry solid (Chong et al. 2009). Minimisation of drying time reflects the reduction of heat exposure and energy consumption of the drying operation whilst also minimising the degradation of product quality. The texture attributes of commercially dried guava samples reported in Chong et al. (2009) was used as reference because of its Malaysian variety and it was inappropriate to target the texture attributes as maximum or minimum where the desired mouth-feel of dried guava for product acceptance was important. Springiness and cohesiveness attributes were excluded in the optimisation since they are not significantly affected by temperature and thickness.

The composite desirability value of the optimum solution was 0.6192 for the optimised temperature 70 °C and thickness 6 mm. The values of responses at the optimum condition are given in Table 7. The desirability of hardness was much lower at 0.4715 and this could be resulted by the different moisture content between the commercial products (0.036 g water/g dry solid) and experimental samples (0.2564 ± 0.01654 g water/g dry solid). The commercial product is known to be added with accepted food additives that gives variances to hardness. However, it was acceptable to set 1,761 g of hardness and 407 g of chewiness as target in optimisation because they were in the range of texture for dried guava produced in this research.

Table 7.

Process variables, responses optimisation, desirability, and experimental value for the responses at optimum condition

Variables	Goal	Lower	Target	Upper	Predicted	Desirability	Experimental
Factors						0.6192
Temperature (°C)	in range	55	in range	75	70		70
Thickness (mm)	in range	3	in range	9	6		6
Responses
Drying time (min)	minimum	180	180	720	357	0.6718	360
Water activity	minimum	0.367	0.367	0.547	0.452	0.5259	0.481 ± 0.006
Colour change	minimum	17.51	17.51	30.16	22.18	0.6305	23.85 ± 3.76
Vitamin C (mg/100 g)	maximum	395.03	687.72	687.72	624.66	0.7652	704.72 ± 59.43
Hardness (g)	target	429.253	1761.000	2330.810	1057.189	0.4715	1501.406 ± 508.025
Chewiness (g)	target	396.636	407.000	1341.038	686.142	0.7011	756.944 ± 255.022

Verification of the optimised drying

The adequacy of the statistical model equations for predicting optimal response attributes were tested by drying guava of 6 mm thickness at 70 °C. Table 7 shows the model verification results. The final moisture content of dried guava was 19.99 ± 1.35 % (w.b.) after drying for 360 min. The percentage errors from Eq. (13) for water activity, colour change, vitamin C, hardness and chewiness are 6.03 %, 7 %, 11.36 %, 29.59 %, and 9.35 %. The predicted values were found mostly in the range of experimental value. Although the percentage error of hardness was 29.59 %, the experimental value of hardness of 1501.4 g at optimum drying temperature, 70 °C and slice thickness, 6 mm was comparable to the hardness of the commercially dried guava, which was 1,761 g reported by Chong et al. (2009).

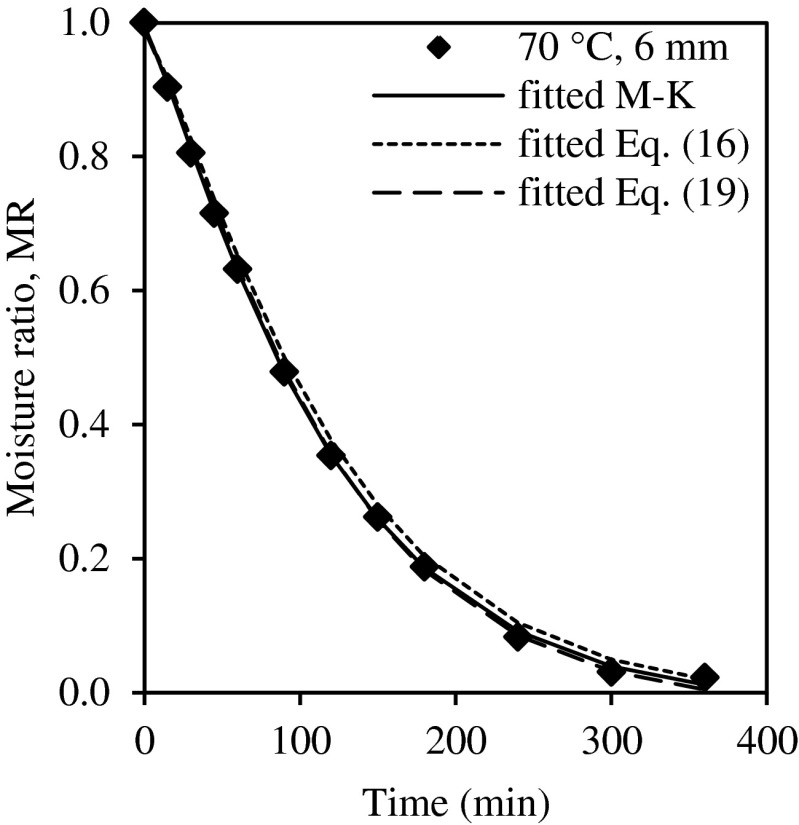
The drying curve for this optimum drying condition was also fitted with all the semi-theoretical models in Table 1 where the Midilli-Kucuk model was also best fitted model (Table 4) with R² = 0.9997. In fitting this data to the single model (Eq. (16)) and the master curve fitted Midilli-Kucuk model (Eq. (19)) as shown in Fig. 6, the master curve fitting was slightly better with R² = 0.9995, χ² = 9.138 × 10⁻⁵, RMSE = 0.007805, versus the single model R² = 0.9973, χ² = 4.106 × 10⁻⁴, RMSE = 0.01755. The predicted effective diffusivity calculated from Eq. (14) of 2.196 × 10⁻⁹ m²/s was very close to the experimentally found diffusion coefficient, 2.303 × 10⁻⁹ m²/s. The percentage error, PE for the effective diffusivity was 4.65 % with no significant difference between the predicted and experimental values.

Fig. 6.

Moisture ratio as a function of drying time for optimal condition at 70 °C with 6 mm guava slices and fitted with Midilli-Kucuk model (M-K), single model (Eq. (16)) and master curve fitted with Midilli-Kucuk model (Eq. (19))

Conclusions

Theoretical and statistical models have been established simultaneously in relating the drying kinetics and quality attributes of dried guava through the determination and comparison of drying rates, drying rate constants, effective diffusivity at different drying temperature, time and guava thickness. Elevated air temperature and thin slices resulted in higher drying kinetics. Effective diffusivity was enhanced by increasing drying temperature and thickness. The Midilli-Kucuk model has described the thin layer drying behaviour of guava slices where the superposition technique showed high accuracy in predicting the moisture ratio of guava slices conveniently. The statistical modelling is important in predicting drying responses including drying time, water activity, colour change, vitamin C content, and texture of sample and subsequently used for drying process optimisation. Drying time presented a strong dependence on both drying temperature and sample thickness; temperature had more significant effect on water activity, colour and vitamin C (P < 0.091) while increasing slice thickness caused an increase in hardness and chewiness (P < 0.004). The theoretical drying kinetics and constants of the optimised drying at 70 °C for 6 mm slices are useful in reflecting the drying mechanisms of a practical drying process.

Nomenclature

a, b, c, n

model constants

a_h

dimensionless time-thickness shift factor

a_T

dimensionless time-temperature shift factor

D_eff

effective diffusivities (m²/s)

D_o

constant in Arrhenius equation (m²/s)

E_a

activation energy (kJ/mol)

h

slice thickness (mm)

k

drying rate constant (min⁻¹)

M₀

initial moisture content (g water/g dry solids)

M_e

equilibrium moisture content (g water/g dry solids)

M_t

moisture content at any time (g water/g dry solids)

M = M_t-M_e

free moisture content at any time (g water/g dry solids)

MR

moisture ratio (dimensionless)

PE

percentage error (%)

R

universal gas constant 8.314 (J/mol K)

R²

coefficient of determination

RMSE

root mean square error

t

time (s or min)

t′, t′′

reduced or pseudo time (min)

T

temperature (°C)

T_abs

absolute temperature (K)

X₁, X₂

independent variables of temperature and thickness in RSM

Y

dependent responses in RSM

ΔE

colour change

Greek letters

α

constants

β

constant coefficients

χ²

reduced chi-squared

Subscripts

exp

experimental

pre

predicted