BOLD Subjective Value Signals Exhibit Robust Range Adaptation

Abstract

Many theories of decision making assume that choice options are assessed along a common subjective value (SV) scale. The neural correlates of SV are widespread and reliable, despite the wide variation in the range of values over which decisions are made (e.g., between goods worth a few dollars, in some cases, or hundreds of dollars, in others). According to adaptive coding theories (Barlow, 1961), an efficient value signal should exhibit range adaptation, such that neural activity maintains a fixed dynamic range, and the slope of the value response varies inversely with the range of values within the local context. Although monkey data have demonstrated range adaptation in single-unit correlates of value (Padoa-Schioppa, 2009; Kobayashi et al., 2010), whether BOLD value signals exhibit similar range adaptation is unknown. To test for this possibility, we presented human participants with choices between a fixed immediate and variable delayed payment options. Across two conditions, the delayed options' SVs spanned either a narrow or wide range. SV-tracking activity emerged in the posterior cingulate, ventral striatum, anterior cingulate, and ventromedial prefrontal cortex. Throughout this network, we observed evidence consistent with the predictions of range adaptation: the SV response slope increased in the narrow versus wide range, with statistically significant slope changes confirmed for the posterior cingulate and ventral striatum. No regions exhibited a reliably increased BOLD activity range in the wide versus narrow condition. Our observations of range adaptation present implications for the interpretation of BOLD SV responses that are measured across different contexts or individuals.

Introduction

Many theories of decision making assume that choice options are assessed along a common subjective value (SV) scale (Kable and Glimcher, 2009). In line with this assumption, neural evidence has shown that value modulates activity across several cortical and subcortical regions. In monkeys, value modulates single-unit spike rates in the orbitofrontal cortex (OFC), anterior cingulate cortex (ACC), and the striatum (for review, see Rushworth et al., 2011; Bissonette et al., 2014). In humans, value modulates BOLD signals in the likely anatomical homologues of these regions, and also in the ventromedial prefrontal cortex (VMPFC) and posterior cingulate cortex (PCC; Levy and Glimcher, 2012; Bartra et al., 2013; Clithero and Rangel, 2014).

Both monkey and human studies report an approximately linear relationship between value and neural activity (Padoa-Schioppa and Assad, 2006; Kable and Glimcher, 2007). This relationship is maintained across highly variable scales of value. In fMRI tasks, values may span a few cents (Valentin et al., 2007) or hundreds of dollars (Kable and Glimcher, 2007). Real-world settings exhibit even greater variability in the possible range of values.

How can a potentially infinite range of values be encoded within a finite range of neural activity? The efficient coding hypothesis states that the neural code should adapt to the present context, so that a neuron exploits its entire dynamic range within that context (Barlow, 1961; Wark et al., 2007). In the case of value, efficient coding implies that the neural code should adapt to fluctuations in the decision context, such that the range of possible spike rates precisely spans the anticipated range of values. Therefore, optimal range adaptation implies that the slope of the value response function should decrease in direct proportion to increases in value range (Padoa-Schioppa, 2009).

A limited number of monkey electrophysiological studies have investigated whether single-unit value signals exhibit range adaptation. These studies found the expected inverse relationship between value range and neural sensitivity in the OFC and ACC (Padoa-Schioppa, 2009; Kobayashi et al., 2010; Cai and Padoa-Schioppa, 2012), although nonadapting subpopulations of OFC neurons have also been reported (Kobayashi et al., 2010).

Whether human BOLD value correlates exhibit similar range adaptation is unknown. Although a recent fMRI study demonstrated adaptive coding of reward prediction errors (Park et al., 2012), no imaging studies have investigated range adaptation in the value signals evoked during decision making. fMRI evidence of range adaptation would confirm an additional dimension of correspondence between single-unit and BOLD value signals, and would indicate that possible changes in the range of values could figure importantly into the interpretation of changes in BOLD value sensitivity observed across different decision settings.

Here, we examine the range sensitivity of BOLD value signals in an intertemporal choice paradigm (Kable and Glimcher, 2007). Analyses compared the value signals evoked by delayed payment options that spanned either a narrow or wide value range. Throughout the valuation circuitry, we observed trends consistent with adaptive coding, and statistically significant range adaptation emerged in the ventral striatum (vStr) and PCC.

Materials and Methods

Healthy, right-handed young adults (18–30 years old) were recruited from the University of Pennsylvania and surrounding community. All participants provided written informed consent, and study procedures were approved by the Institutional Review Board of the University of Pennsylvania. Thirty-nine participants (13 males, 26 females) completed an initial prescan behavioral screening session. Eligible individuals (n = 27; see Screening session for eligibility criteria) were invited to participate in a subsequent fMRI session. Seven of these participants are not included in our reported dataset, due to either excessive in-scanner head movement (n = 2; see FMRI data preprocessing), fMRI task behavior that did not meet study criteria (n = 3; see Scan session), sleeping in the scanner (n = 1), or cancellation of the scheduled fMRI session (n = 1). The final dataset includes 20 participants (9 males, 11 females; mean age ± SD, 22.1 ± 2.69 years; range, 19–28 years). All analyses of fMRI BOLD data (see fMRI data analysis) and fMRI session behavioral data (see Behavioral analyses) were restricted to this reduced dataset.

Protocol overview

We examined the range sensitivity of value signals in the context of intertemporal decision making. Participants completed three intertemporal choice tasks over the course of one screening and one fMRI session. During the screening session, two tasks (1) allowed estimation of each individual's discount rate, (2) provided prescan exposure to a shifting range of delayed option SVs, and (3) confirmed choice stability in the presence of this shift. The fMRI task used a similar range manipulation as was used for the screening session. For the 20 reported participants, the intersession delay varied from 2 to 14 d (mean ± SD, 6.65 ± 3.91 d).

Screening session

At the outset, participants were instructed regarding the general nature of the screening tasks, the incentive scheme, and the methods of payment (see descriptions below). All participants completed the first screening task, with presentation of the second screening task contingent upon the behavior observed during the first. Both the screening and fMRI tasks were presented using E-Prime 2.0 software (Psychology Software Tools).

Screening Task #1 (stable range).

During the first screening task, each trial began with the display of a central fixation dot (500 ms), which was subsequently flanked by a pair of immediate and delayed payment options (e.g., “$40 now” vs “$62 in 15 days”; position of the immediate option randomized across trials). The participant could choose the left or right option by pressing the 1 or 0 key, respectively, within a response time (RT) limit of 6 s. A valid response triggered the feedback display (500 ms), which consisted of a single checkmark indicating the side of the chosen option. Following a missed trial (expired RT limit), feedback consisted of a centrally presented question mark. The feedback display was followed by a blank intertrial interval (ITI) screen of variable duration (6 s minus recorded RT). The adaptive ITI was intended to discourage participants from responding rapidly in an attempt to complete the task quickly. Before starting the task, participants answered a series of comprehension questions and completed three practice trials.

The screening task presented 57 unique option pairs. For each pair, one of three possible immediate amounts ($35, $40, $45) was coupled with a variable delayed amount (range, $44–$97) and delay (range, 1–359 d). Amounts and delays were selected so that each option pair approximated a point of indifference for a specific discount rate, with these rates evenly sampled across the range of study-eligible discount rates.

Discount rates were estimated through optimization routines implemented in Matlab (Mathworks). Temporal discounting was modeled according to the hyperbolic function, SV = A/(1 + kD), where SV denotes an option's estimated SV, A and D represent the option amount and delay, and k represents the individual's estimated discount rate (Mazur, 1987). Choices were predicted with the logistic function, p_(delayed) = 1/(1 + βe^{(now − SV)}), where SV denotes the delayed option's SV, “now” represents the immediate offer, β models the slope of the logistic curve, and p_(delayed) returns the probability of delayed option choice. The optimization process converged upon the pair of k and β values associated with the maximum log likelihood of observing the actual choices that the participant made. Since discount rates are not normally distributed, the estimated k values were log transformed before submission to statistical analysis.

An estimated log(k) value in the range of −2.7 to −0.9 (k of 0.002–0.136) was required for a participant to proceed to the second screening task. This requirement was necessary to ensure the practicality of presenting a wide SV range to all participants, since the wide range was designed to include delayed options with very high SVs (leading to impractically large delayed amounts for high discounters) and with very low SVs (leading to impractically long delays for low discounters). Eight participants' discount rates fell outside of the required range. These participants were dismissed and provided with both a $10 base compensation payment and an added incentive payment.

The incentive payment corresponded to the option chosen on a single trial, which was randomly selected through a series of participant-executed dice rolls. If a missed trial was selected, then the participant received no incentive payment. As in previous studies (Kable and Glimcher, 2007, 2010), all incentive payments were provided through debit cards to which the funds could be remotely loaded on the appropriate date.

Screening Task #2 (manipulated range).

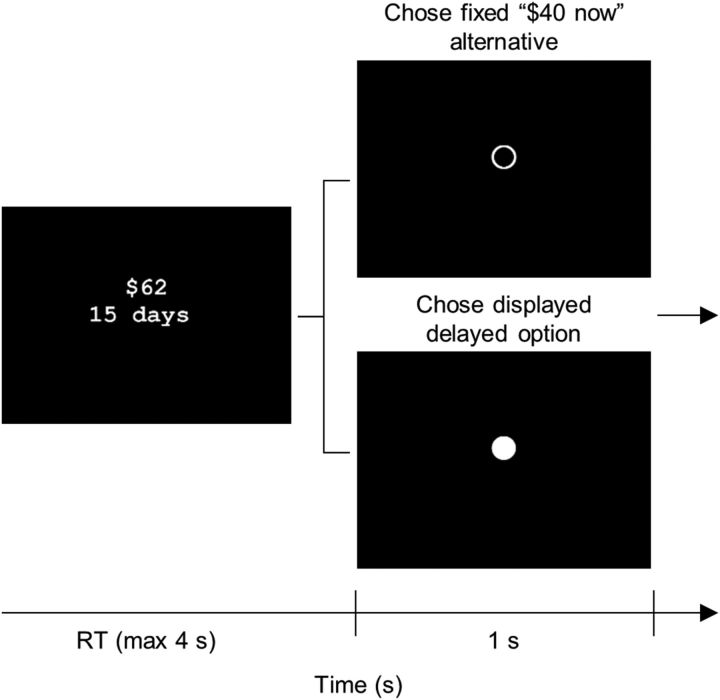
The second screening task presented 192 choices between an immediate option of $40 now and a delayed option that varied across trials. Trials began with the central display of the delayed option (with the immediate option not shown; Fig. 1). Within an RT limit of 4 s, participants could choose the delayed or immediate option by pressing the 1 or 0 key, with the key-option mapping alternating across the four task blocks. A valid response triggered the feedback display (1 s), which consisted of a filled circle (chose delayed option), an open circle (chose immediate option), or a question mark (missed trial). As in the first screening task, feedback was followed by a blank ITI display of variable duration (ITI, 4 s minus RT). Participants were informed of the change in task format and completed two practice trials before starting the task. Additionally, each block was preceded by instructions and a brief quiz regarding the upcoming key-option mapping.

Figure 1.

Sample intertemporal choice trial, as presented during the fMRI task and Screening Task #2. On each trial, participants chose either the displayed, delayed option, which varied from trial to trial, or the fixed, nondisplayed $40 now option. Responses were made with a left or right button press (fMRI) or the 1 or 0 key (screening) within an RT limit of 4 s. The response-option mapping alternated across task blocks. Responses prompted the transition to a feedback screen that confirmed choice of $40 now (open circle), choice of the delayed option (filled circle), or a missed trial (a question mark). The feedback screen was followed by a blank ITI screen, with the ITI set equal to the unused fraction of the RT window plus (in the fMRI task) a variable jittered duration (median jitter, 5 s).

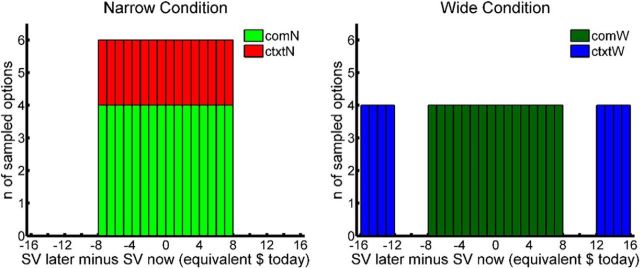
The delayed payment options were generated individually for each participant, and consisted of two 96-option sets that spanned either a narrow or wide range of SVs (Fig. 2). Identical option generation procedures were used for the second screening task and the fMRI task. Options were drawn from an initial pool that consisted of all amount–delay combinations falling within the bounds of $41–$100 and 1–365 d (integer values only). This initial pool was reduced in two steps.

Figure 2.

SV distributions constructed for the Narrow (N) and Wide (W) Range Conditions. A total of 192 delayed options (96 per Condition) were selected to be paired with the fixed $40 now option. Each Condition included 64 Common options (com), for which the SVs spanned an identical, near-indifference range, and 32 Contextual options (ctxt), which spanned differing ranges.

In the first step, we identified subpools of amount–delay pairs that corresponded to prespecified ranges of SV. SV (in units of equivalent “now” amount, in dollars) was calculated using the participant's estimated discount rate. For the second screening task, this discount rate was set equal to the log(k) estimate from the first task; for the fMRI task, we used the mean of the log(k) estimates from the two screening tasks. We retained only those amount–delay pairs for which the SV fell into one of four zones: (1) $24 ≤ SV < $28 (negative wide zone), (2) $32 ≤ SV < $40 (negative narrow zone), (3) $40 < SV ≤ $48 (positive narrow zone), or (4) $52 < SV ≤ $56 (positive wide zone). In the second step, we determined the ranges of amounts and delays present among all narrow zone options, and then eliminated any wide zone options for which the corresponding amount or delay fell outside of these ranges. This step ensured that the narrow and wide zone options spanned identical ranges of amounts and delays, and therefore decoupled our SV range manipulation from changes in the range of either individual attribute.

The final, reduced pool was sampled to create the Narrow and Wide Range Condition option sets. In preparation for this sampling process, the pool was divided into bins of $1 width (in SV units). Each Range Condition contained 64 “Common” options, which were generated by sampling four option pairs from each of the 16 narrow zone bins ($32 ≤ SV ≤ $48). Therefore, the two sets of Common options [Common Narrow (ComN) and Common Wide (ComW)] contained matching distributions of SVs. The two Range Conditions were distinguished by 32 “Contextual” options. For the Narrow Condition, Contextual options (CtxtN) were again sampled from the 16 narrow zone bins (two options per bin, $32 ≤ SV ≤ $48). For the Wide Condition, Contextual options (CtxtW) were sampled from the eight wide zone bins (four options per bin, $24 ≤ SV < $28 and $52 < SV ≤ $56). In our primary analyses (see descriptions below), we tested whether BOLD responses to the Common options, which spanned identical SV ranges, varied as a function of the Contextual options, which spanned different SV ranges.

For each Range Condition, the Common and Contextual options were evenly divided across two 48-trial blocks. Within each block, the first three trials presented Contextual options to ensure that this range-specific information was immediately available. The final trial presented a Common option, and the remaining 44 options were randomly assigned to the remaining trials.

During a session, the participant first viewed two blocks of one Range Condition, followed by the two blocks of the remaining Condition. Since the key-option mapping alternated from block to block, all possible combinations of Range Condition and key-option mapping were present. The Condition and key mapping sequences were counterbalanced across participants, and each participant experienced the same sequences across the screening and fMRI sessions (with the exception of one participant, due to a procedural error).

At the end of the screening session, the choice data from the second task were analyzed to determine the participant's eligibility for the fMRI session. Choices were evaluated against two criteria. First, due to the same practicality constraint described above, the participant was required to maintain a log-transformed discount rate within the −2.7 to −0.9 range. Second, choices were required to meet a stability criterion, which was satisfied if the participant accepted ≥50% of the delayed options in the positive wide zone, and rejected ≥50% of the delayed options in the negative wide zone. Failure to meet this requirement suggests that the discount rate estimated following the first screening task was not a reliable indicator of the participants' preferences in the second screening task, and that the delayed options did not actually span the SV ranges that they were designed to span.

Four participants were excluded from the fMRI session on the basis of their second screening task choices (out of range log(k) values for three of four participants, and stability criteria violation for three of four). For all participants who completed both screening tasks, compensation included the $10 base pay and an added incentive payment (trial drawn from the combined data from the two screening tasks).

Scan session

fMRI task.

The fMRI task stimuli were projected onto a screen behind the scanner bore and viewed on a mirror affixed to the head coil. Participants could respond using their left and right thumbs, which were positioned over the outermost buttons of a four-button respond pad. Instructions emphasized the general similarity between the fMRI task and the second screening task, but made no reference to the range manipulation.

During anatomical data acquisition, participants completed 12 practice trials, which were followed by the functional scans and the main task trials. Trials retained the same fundamental structure as was used in the second screening task, with the exception of an additional jitter period that followed each base adaptive ITI (as determined by the Freesurfer program optseq2; Dale, 1999; jitter range, 0–20 s; median, 5 s).

The fMRI task behavioral data were evaluated according the same eligibility criteria that were used for the second screening task. Three participants' data were excluded from subsequent analysis due to failure to meet these criteria [out-of-range log(k) estimates for three of three participants, and insufficient choice stability for two of three]. All fMRI participants received a base $20 payment plus the incentive payment indicated by a randomly selected fMRI task trial.

MRI data acquisition.

Imaging data were acquired using a 3T Siemens Trio scanner equipped with a 32-channel head coil. Each session began with the acquisition of a high-resolution T1-weighted anatomical image (MPRAGE sequence; TR = 1630 ms; TE = 3.11 ms; TI = 1100 ms; flip angle, 15°; 160 axial slices; voxel size, 0.9375 × 0.9375 × 1.000 mm; matrix, 192 × 256) and a T2-weighted anatomical image (TR = 7000 ms; TE = 90.0 ms; flip angle, 180°; 44 axial slices; voxel size, 0.75 × 0.75 × 3.0 mm; matrix, 256 × 256). The anatomical scans were followed by four T2*-weighted functional scans (EPI sequence; TR = 2.5 s; TE = 25 ms; flip angle, 75°; 44 axial slices; interleaved ascending acquisition sequence; voxel size, 3 × 3 × 3 mm; matrix, 64 × 64; total volumes, 200; duration, 8 min 25 s). For each functional run, the first two volumes were discarded to minimize T1 saturation effects. Following the functional scans, we acquired a B0 field map (TE 1 = 4.31 ms; TE 2 = 6.77 ms; 44 axial slices; voxel size, 3 × 3 × 3 mm; matrix, 64 × 64) to support off-line estimation of geometric distortion in the functional data.

To reduce signal dropout in the orbitofrontal cortex, functional scans (and the T2-weighted and B0 scans) were acquired at a 30° tilt relative to the anterior commissure-posterior commissure plane (Deichmann et al., 2003). The resulting slice prescription provided whole or near-whole brain coverage across participants.

fMRI data preprocessing

Functional data were preprocessed with a combination of the Analysis of Functional NeuroImages (AFNI; Cox, 2012) and FMRIB (Functional Magnetic Resonance Imaging of the Brain) Software Library (FSL; Jenkinson et al., 2012) software packages. Image data were interpolated in time to correct for staggered slice acquisition times and motion-corrected with six-parameter rigid body transformation to an EPI image acquired immediately before the first run. Two participants' data were discarded due to excessive motion, which was defined as the frequency of sudden large head displacements (i.e., the rate of single TR displacements >0.5, in units of the six parameter estimates' Euclidean norm; for discarded participants, rates were 4.8 and 7.0%, vs mean ± SD rates of 0.19 ± 0.38% in the 20 reported participants).

Motion-corrected functional data were coregistered to the participant's anatomy and to the MNI template. The single, complete functional-to-MNI warp consisted of (1) geometric distortion correction, (2) alignment to the T2 anatomical image, (3) alignment to the high-resolution MPRAGE image, (4) nonlinear warping to the MNI template, and (5) restoration of the original 64 × 64, 3 mm isotropic resolution. Warped images were spatially smoothed with a 6.0 FWHM Gaussian kernel.

The AFNI 3dAutomask program was used to identify the brain voxels that were common to all participants. In each participant, a mask was created to label the largest contiguous region of suprathreshold intensity found within the smoothed functional data. The intersection of the 20 single participant masks was applied to all reported voxelwise fMRI analyses.

fMRI data analysis.

Each participant's functional data were fit with four separate general linear models (GLMs) using the AFNI program 3dDeconvolve. Each GLM specified an identical baseline model, which included the six motion time-series estimates, first-order through fourth-order polynomial trend terms, and an intercept term. Regressors of interest were modeled as delta functions, which were time-locked to trial onset and convolved with a canonical gamma hemodynamic response function. Parametric modulator regressors were constructed using the mean-centered values of the corresponding parameter, and SV regressors were generated using the discount rates estimated for the fMRI task specifically. All GLMs included a regressor that indicated the occurrence of missed trials (one trial for each of four participants); these trials were omitted from all regressors of interest.

GLM #1: localization.

The first GLM localized regions that reliably tracked SV within each Range Condition, while remaining sensitive to the possibility that SV responses might vary across Conditions. For each Condition, regressors estimated the mean trial response (Trial_N, Trial_W) and the modulation of these responses by SV (SV_N, SV_W). In the group analysis, coefficient estimates were submitted to a voxelwise joint t test of the Narrow and Wide Range SV effects [i.e., β(SV_N) + β(SV_W)]. Clusters that survived a whole-brain corrected threshold of p < 0.05 (two-tailed) were identified using FSL randomize (cluster-forming threshold set at p < 0.0005, two-tailed, uncorrected). The localized clusters served as the regions-of-interest (ROIs) for all subsequent analyses, each of which entailed simple contrasts performed upon each ROI (via two-tailed t test, evaluated against a significance threshold of p < 0.05).

GLM #2: range adaptation.

The second GLM provided the most direct test of range adaptation. Range adaptation predicts that the slope of the SV effect (i.e., the β estimate) should be greater in the Narrow versus Wide Range Condition (Fig. 3). Our primary test of this prediction was restricted to the Common options. As such, the GLM #2 regressors were created by splitting the GLM #1 regressors according to the option type (Trial_ComN, Trial_ComW, Trial_CtxtN, and Trial_CtxtW; and SV_ComN, SV_ComW, SV_CtxtN, and SV_CtxtW). In the group analysis, we tested for range adaptation by comparing the Common Narrow and Common Wide SV effects [β(SV_ComN) − β(SV_ComW)].

Figure 3.

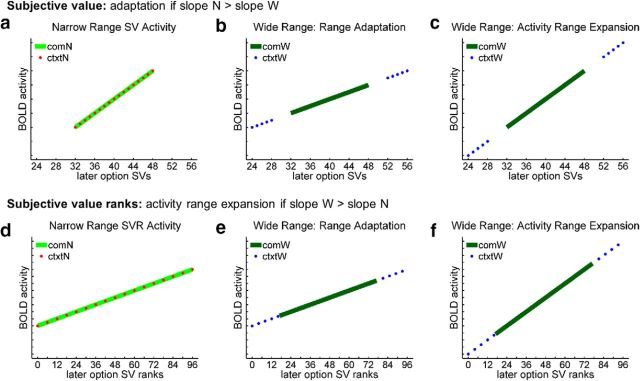
Predicted activity profiles for a signal that either completely adapts or completely expands in response to increasing SV range. Both models assume a positive, linear SV code. Predicted SV effects are constrained to pass through a constant mean magnitude (Kobayashi et al., 2010). a–c, When activity is plotted against SV, range adaptation predicts that the slope of the SV effect should decrease with increasing SV range. The alternative, range expansion model predicts a stable SV effect slope and, consequently, an increase in the spanned activity range. d–f, Different predictions hold when activity is plotted against SVR. Range adaptation predicts a stable SVR effect slope, and range expansion predicts a slope that increases in proportion to SVR range. Abbreviations follow the conventions from Figure 2.

In a parallel, less well controlled test, we compared the SV effects estimated over all stimuli within the Narrow and Wide Conditions [using the GLM #1 regressors, β(SV_N) − β(SV_W)]. Note that this contrast is orthogonal to that which was used to localize the ROIs [β(SV_N) + β(SV_W)]. Additional t tests contrasted the Trial effects estimated for the two Conditions [β(Trial_ComN) − β(Trial_ComW), and β(Trial_N) − β(Trial_W)] to determine whether SV range influenced general BOLD sensitivity to task events.

In addition to the tests of range adaptation, GLMs #1 and #2 supported a test of the alternative model of range expansion. Here, “expansion” refers the broadening of the activity range that results from suboptimal adaptation to a broadening value range. Optimal adaptation requires that the slope of the SV activity function must decrease in proportion to any increase in value range [formally, slope ∝ 1/range(V)]. A slope decrease that falls short of this numerical requirement should be detectable as an increase in the observed activity range [estimated as slope · range(V)].

Following this logic, we tested for range expansion by scaling the estimated Wide Condition slopes by the ratio of the Wide and Narrow value ranges, and comparing the result to the original Narrow Condition slopes (GLM #1: [β(SV_W) · range(V)_wide/range(V)_narrow] − β(SV_N); GLM #2: [β(SV_ComW) · range(V)_wide/range(V)_narrow] − β[SV_ComN]). Note that, although the range manipulation was designed to approximate a range(V) ratio of 2, there was some variability in the actual ratio that was presented to participants (median range(V)_wide/range(V)_narrow = 1.96; minimum-maximum, 1.34–2.08). This variability was largely attributable to slight shifts in the discount rates estimated for the screening and fMRI sessions.

Optimal range adaptation predicts that the scaled Wide and unscaled Narrow slopes should be identical. Adaptation that is suboptimal, and therefore associated with range expansion, predicts a greater scaled Wide versus Narrow Condition slope. Note that, in the event of partial range adaptation, a region could simultaneously show a significant range expansion effect [e.g., β(SV_ComW) · range(V)_wide/range(V)_narrow > β(SV_ComN)] and a significant range adaptation effect [e.g., β(SV_ComN) > β(SV_ComW)].

GLM #3: activity range over ranked SVs.

The third GLM supported an additional, alternative test of range expansion. GLM #3 was identical to GLM #1, with the exception that the SV regressors were converted to represent condition-specific SV ranks (SVRs). For each Range Condition, SVs were ranked using the Matlab “tiedrank” function, which assigns ascending ranks to ascending numerical values, and a mean rank to any repeating values (e.g., for [40 50 50], rank = [1 2.5 2.5]). Since the two Range Conditions span identical ranges of SVR (1–96), expansion of the activity range should be manifested as a steepening of the slope of the SVR effect within the Wide Condition [in other words, β(SVR_W) − β(SVR_N) > 0; Fig. 3f]. Note that this contrast was not restricted to the Common stimuli, since the unrestricted stimulus sets already span matching ranges of the predictor variable (SVR).

GLM #4: activity visualization.

The fourth GLM enabled visualization of the ROIs' activity profiles. For each Range Condition, the 96 trials were sorted by ascending SVR and split across 12 eight-trial bins. GLM #4 included 24 regressors (two Range Conditions × 12 Bins) that modeled the mean BOLD response to the trials corresponding to each bin. For each ROI, the resulting 24 coefficient estimates were plotted against both the median SVs and median SVRs for each bin.

GLM #4 also supported a test of range expansion. For each Range Condition, we estimated the activity range by contrasting the estimated coefficients for the two most extreme bins (12 and 1). Range expansion predicts that the contrast result should be greater for the Wide versus Narrow Range Condition [(β_(BinW12) − β_(BinW1)) − (β_(BinN12) − β_(BinN1)) > 0].

Behavioral analyses

Cross-range comparisons of choice behavior.

Our fMRI analyses assumed that discount rates remained stable across the two Range Conditions. To test for possible violation of this assumption, we estimated participants' discount rates for the two Range Conditions separately. Estimates were obtained using both the Common options in isolation (allowing for comparisons across similar value ranges) and the combined Common and Contextual options (allowing for the derivation of estimates over larger pools of choice data). In each case, the resulting log(k) estimates were compared with a paired t test.

The separate regression fits also informed analyses of choice consistency. These analyses asked whether the increased BOLD sensitivity to SV in the Narrow Range Condition corresponded to improved discrimination between SVs during the choice process. In an initial test, we compared the two logistic function slopes to determine whether the slope increased in the Narrow versus Wide Range Condition. Since logistic slope estimates are sensitive to the range of the predictor variable, we performed a single t test using the Common stimuli alone, and minor differences in the SV ranges (created by the minor differences in the Common Narrow and Common Wide k estimates) were included as a covariate. Second, using the same t test structure (Common-only restriction, range difference covariate), we compared the percentage of choices that were successfully predicted by the estimated discount rates, where a delayed choice is predicted if SV > 40. A greater percentage of choices predicted in the Narrow Range would be expected in the event of improved SV discrimination during decision making.

Range effects on RT.

In keeping with classical distance effects in perceptual and cognitive judgments (Festinger, 1943; Moyer and Landauer, 1967), RTs typically increase as choices become more “difficult,” where difficulty is defined in terms of decreasing distance between two options' SVs (Soltani et al., 2012; De Martino et al., 2013). A series of RT analyses asked whether the increased neural SV sensitivity of the Narrow Range condition was associated with an enhanced distance effect. Under the assumption of a fixed range of choice RTs, which is fully exploited in each context, one might anticipate that the relationship between distance and RT might become more pronounced within the Narrow Range Condition.

The RT analyses paralleled those that were used to seek range effects in the fMRI data. First, for each participant and Range Condition, we regressed RT against SV distance [SVD; abs(SV − $40)]. The reliability of the distance effect was confirmed through a joint t test of the separately estimated slope coefficients [β(SVD_N) + β(SVD_W)]. Identical analyses that substituted SVD with SV did not yield a significant contrast result [for β(SV_N) + β(SV_W), p = 0.45].

Second, to test for range effects, we conducted similar Condition-specific regressions using the Common options alone. Range adaptation predicts that RT should be more sensitive to SVD in the Narrow versus Wide Range Condition [i.e., β(SVD_ComN) − β(SVD_ComW) < 0]. This contrast was repeated using the coefficients estimated for the combined Common and Contextual stimuli [β(SVD_N) − β(SVD_W)]. As an initial test for range expansion, we scaled the Wide Condition slopes by the ratio of the Wide and Narrow SVD ranges (again ∼2 across participants: median, 1.77; minimum-maximum, 1.25–2.04). Range expansion predicts a steeper scaled Wide versus Narrow Condition slope [β(SVD_ComWscaled) − β(SVD_ComN) < 0; β(SVD_Wscaled) − β(SVD_N) < 0].

Range expansion was additionally tested by regressing RT against the Condition-specific SVD ranks (SVDRs). Again, range expansion predicts a steeper, more negative slope for the Wide versus Narrow Range Condition [i.e., β(SVDR_W) − β(SVDR_N) < 0].

Finally, the RT effects were visualized by grouping each Condition's trials into 12 uniformly sized bins (8 trials/bin; SVDR ascending across bins). Mean bin RTs were plotted against both the median SVs and SVRs for each bin. As a final test of range expansion, we estimated Condition-specific RT ranges by contrasting the most extreme bins (12 and 1); range expansion predicts a more extreme (i.e., more negative) contrast result for the Wide versus Narrow Condition [(mean_(BinW12) − mean_(BinW1)) − (mean_(BinN12) − mean_(BinN1)) < 0].

Results

During fMRI scanning, participants completed 192 unique choices between a fixed $40 now option and variable delayed alternatives (e.g., $62 in 15 d; Fig. 1). Individual participant discount rates, which had been estimated during a previous screening session, were used to construct separate conditions in which the delayed options spanned either a narrow or wide range of SVs (Fig. 2). Each Range Condition contained 64 Common options for which the SVs spanned a matching near-indifference range. The Conditions were distinguished by 32 Contextual options, which were drawn from either the same near-indifference range (in the Narrow Condition) or more extreme SV ranges (in the Wide Condition).

fMRI analyses

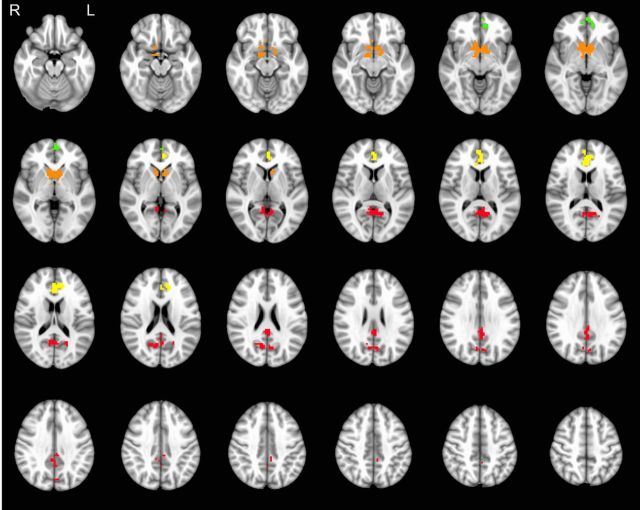
Activity that tracked the delayed options' SVs was localized to four regions: the PCC, the vStr, the ACC, and the VMPFC. Localization entailed the estimation, for each Range Condition, of the mean BOLD response to all choices, and the parametric modulation of that response by the delayed option's SV. A joint analysis of the two Conditions identified positive SV effects that were restricted to the PCC, vStr, ACC, and VMPFC (threshold at p < 0.05, corrected; Fig. 4; Table 1). These regions replicate the findings of previous intertemporal choice research (Kable and Glimcher, 2007; Peters and Büchel, 2009; Pine et al., 2009; Kable and Glimcher, 2010; Hare et al., 2014) and overlap with the typical valuation network that emerges across fMRI studies of diverse decision-making domains (for review, see Peters and Büchel, 2010; Levy and Glimcher, 2012; Bartra et al., 2013). Our localized clusters served as the ROIs in which we sought range effects.

Figure 4.

Regions exhibiting a positive effect of the delayed options' SV as assessed with a joint t test of the SV effects estimated for the two Range Conditions separately [β(SV_N) + β(SV_W), p < 0.05, corrected]. Analyses of range effects were performed upon the four localized ROIs: PCC (red; peak MNI coordinates, −6, −69, 27), vStr (orange; peak, −6, 9, −6), ACC (yellow; peak, 0, 36, 15), and the VMPFC (green; peak, −3, 60, 0). Note that no reliable negative SV effects were observed.

Table 1.

Regions exhibiting SV effects during Narrow and Wide Range choices^a

Region	Brodmann Area	n voxels	Peak t	Peak MNI coordinate
Posterior cingulate, cingulate, precuneus, cuneus (left, right)	7, 23, 29, 30, 31	277	6.40	−6, −69, 27
Striatum (caudate, nucleus accumbens), globus pallidus (left, right)	Not applicable	238	9.75	−6, 9, −6
Anterior cingulate, medial frontal gyrus (left, right)	9, 10, 24, 32	127	7.34	0, 36, 15
Medial frontal gyrus (VMPFC), anterior cingulate (left, right)	10, 32	37	5.24	−3, 60, 0

^ap < 0.05, corrected.

We evaluated two opposing models of range responsiveness (Fig. 3). The first model, range adaptation, predicts a greater slope of the SV effect in the Narrow Range Condition, and a consistent SVR effect across Conditions. The second model, range expansion, predicts a greater slope of the SVR effect in the Wide Condition, and a consistent SV effect across Conditions. Partial adaptation would predict a combination of these two models' effects.

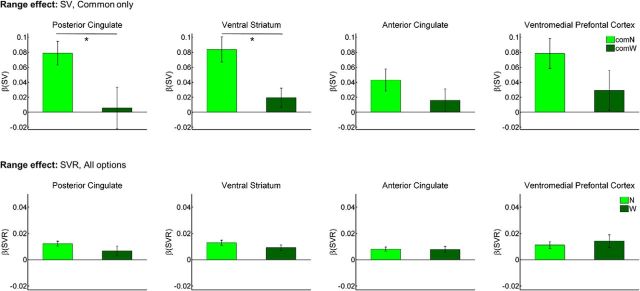
We found reliable range adaptation in two regions, vStr and PCC, and trends consistent with range adaptation in the ACC and VMPFC (Fig. 5). These results held across analyses performed on the Common options alone (ensuring identical analyzed SV ranges) and on all presented options. Narrow Range SV effects significantly exceeded Wide Range SV effects in the vStr (Com: t₍₁₉₎ = 3.04, p = 0.0067; All: t₍₁₉₎ = 3.07, p = 0.0063) and PCC (Com: t₍₁₉₎ = 2.15, p = 0.044; All: t₍₁₉₎ = 2.74, p = 0.013) and were numerically greater in the ACC (Com: t₍₁₉₎ = 1.38, p = 0.18; All: t₍₁₉₎ = 1.76, p = 0.093) and VMPFC (Com: t₍₁₉₎ = 1.71, p = 0.10; All: t₍₁₉₎ = 0.92, p = 0.37). None of the ROIs exhibited Condition-related differences in the mean trial responses evoked by either the Common options alone (p's > 0.58) or all options (p's > 0.35). Therefore, the observed range adaptation cannot be readily explained in terms of a general change in these regions' sensitivity to task events.

Figure 5.

Range-adapting BOLD activity throughout the valuation network. Bars present the mean effects of either SV (top row) or SVR (bottom row), as estimated for the two Range Conditions. Note that SV effects were estimated using the Common options alone, to ensure that comparisons were made across identical ranges of the predictor variable. In accordance with the predictions of range adaptation, SV effects generally decreased with widening SV range, and no reliable range differences emerged in the SVR effects. *p < 0.05. Error bars reflect SEM. All abbreviations follow the conventions from Figure 2.

Across multiple tests, we found no evidence of activity range expansion. In the first test, we scaled the Wide Condition SV effect by the ratio of the Wide and Narrow SV ranges (∼2), and contrasted the scaled result against the Narrow Condition effect. A larger scaled slope for the Wide Condition would suggest incomplete or nonexistent range adaptation, and accompanying activity range expansion. However, we found no reliable differences between the scaled Wide and Narrow slopes, either when restricting the comparison to the Common options (range t's = −1.69 to −0.44; p's = 0.11–0.66) or when including all stimuli (range t's = −1.27 to 0.51; p's = 0.22–0.89). In the second test, we compared the effects that had been estimated using SVR, rather than SV. Range expansion predicts a greater SVR effect in the Wide versus Narrow Condition. We observed no reliable Condition differences in the SVR effects for any of the four ROIs (Fig. 5; p's > 0.22).

To illustrate each ROI's activity profile, we sorted each Condition's 96 trials by ascending SV, grouped the trials into 12 bins, and plotted the mean activity for each bin against either SV or SVR (Fig. 6). Consistent with the predictions for range adaptation, these plots illustrate an increased SV effect slope in the Narrow Condition, and similar SVR effects across Conditions. The binned data also permitted a third test of range expansion. For each Condition, the activity range was estimated by taking the difference of the activation coefficients that had been obtained for the maximum-valued and minimum-valued bins. The difference results were no greater in the Wide versus Narrow Condition for any of the four ROIs (p's > 0.26 for vStr, PCC, and ACC; for VMPFC, p = 0.057).

Figure 6.

Illustration of BOLD SV sensitivity across the Narrow (N) and Wide (W) Range Conditions. Points mark the mean responses [β(Trial)] to binned trials of ascending SV, and are plotted against each bin's estimated median SV (top row) or SVR (bottom row). Linear fits are plotted for illustration purposes, and were derived by regressing the group means against the median SVs/SVRs. Error bars reflect SEM.

Behavioral analyses

Cross-range comparisons of discounting behavior

As our fMRI analyses assumed, discount rates did not significantly differ across the two Range Conditions. To test this assumption, we compared discount rates that had been estimated for the Narrow and Wide Range Conditions separately, using either the Common options alone, or all options. Neither analysis yielded reliable differences in discount rate across Conditions (Com: mean difference ± SE = 0.0028 ± 0.016; t₍₁₆₎ = 0.18, p = 0.86; All: mean difference ± SE = 0.013 ± 0.015; t₍₁₈₎ = 0.86, p = 0.40).

Similarly, using the same set of regression fits, we failed to find any reliable range effects on choice consistency. In theory, the greater neural sensitivity to SV in the Narrow Condition might support more reliable discrimination between SVs, and therefore more consistent decision making within the Narrow Condition. However, neither of two different consistency measures bore evidence in line with this possibility. The estimated slope of the logistic function (which relates the delayed option's relative SV to the probability of choosing this option) was no steeper for the Common Narrow versus Common Wide options (Com: p = 0.89; note no “All” tests were performed, due to the sensitivity of logistic slope estimates to the range of the predictor variable). Likewise, we found no Condition differences in the percentage of choices successfully predicted by the fitted functions (Com: p = 0.66).

Range effects on RT

A final set of analyses did reveal range effects on RT. Decision-making studies frequently report an RT distance effect, in which choice RTs decrease as two options' SVs grow increasingly distant (Soltani et al., 2012; De Martino et al., 2013). If this distance effect is range adapting, then a stable range of RTs should be maintained across contexts, and RT sensitivity to SV distance should decrease in response to increasing distance range. If the distance effect exhibits range expansion, then the RT range should expand, and RT sensitivity to SV distance should remain stable in the presence of increasing distance range.

Our data replicated the expected SV distance effect; however, in contrast to BOLD activity, choice RTs exhibited range expansion, rather than range adaptation. The linear relationship between SVD and RT was significantly negative, as demonstrated in a joint test of SVD effects that had been separately estimated for the two Conditions (t₍₁₉₎ = −6.08, p < 0.001). The SVD effect did not reliably vary across conditions, regardless of whether comparisons involved the Common options alone (t₍₁₉₎ = 0.3, p = 0.77) or all stimuli (t₍₁₉₎ = −1.35, p = 0.19). Instead, across multiple tests, we found that the RT range expanded as SVD range increased. After scaling the Wide Condition SVD slope by the ratio of the two Conditions' SVD ranges, we found a significantly stronger (i.e., more negative) scaled Wide versus Narrow SVD effect (using either the Common options or all stimuli; Com: t₍₁₉₎ = −2.38, p = 0.03; All: t₍₁₉₎ = −2.58, p = 0.02). Similarly, when slopes were estimated using SVDR, we found a steeper Wide versus Narrow Condition effect (All: t₍₁₉₎ = −3.07, p = 0.006).

For each Condition, we illustrate the distance effect by plotting the mean RTs estimated for each of 12 equally sized bins (sorted by ascending SVD; Fig. 7). Consistent with range expansion, these plots illustrate similar effects of SVD within the two Conditions, and the strongest (i.e., most negative) effect of SVDR within the Wide Condition. Again taking advantage of the binned data to perform a third test of range expansion, we confirmed that the RT range (difference in RTs for the maximum-distance and minimum-distance bins) was significantly greater in the Wide Condition (t₍₁₉₎ = −3.46, p = 0.0026).

Figure 7.

RT sensitivity to SVD [abs(SV − $40)] across the Narrow (N) and Wide (W) Range Conditions. Points mark the mean RTs recorded for binned trials of ascending SV distance, and are plotted against each bin's estimated median SVD (top row) or SVDR (bottom row). Linear fits are plotted for illustration purposes, and were derived by regressing the group means against the median SVDs/SVDRs. Error bars reflect SEM.

Discussion

Here we show that BOLD value signals exhibit range adaptation in a manner that is consistent with the predictions of the efficient coding hypothesis.

We studied range adaptation as choices were made between immediate and delayed monetary rewards. As in prior work (Kable and Glimcher, 2007, 2010), we used participants' preferences to estimate the idiosyncratic SV placed on delayed rewards. For each participant, we constructed two sets of choices, for which the SVs spanned a narrow or wide range. In our primary tests of range adaptation, we analyzed matching sets of choice trials, which were drawn from an overlapping region of the narrow and wide SV distributions.

Following from the efficient coding hypothesis, BOLD sensitivity to SV was predicted to increase as the range of SVs narrowed (Padoa-Schioppa, 2009; Kobayashi et al., 2010). The alternative, range expansion hypothesis predicted that the range of BOLD activity would expand as the range of SVs expanded.

Across both Range Conditions, SV reliably modulated activity in the anticipated network of regions: PCC, vStr, ACC, and VMPFC. This entire network exhibited trends consistent with the efficient coding predictions, and statistically significant range adaptation was found in the vStr and PCC. We found no evidence supporting the alternative, range expansion hypothesis. None of three different tests detected expansion of the BOLD activity range in response to expansion of the SV range.

These results leave open the possibility that the observed range adaptation was either complete or partial. Complete adaptation requires that the full activity range be used within a given context, and predicts that, in our design, value sensitivity in the narrow context should be approximately double that observed in the wide context. Because our statistical tests only reject the null hypothesis of no BOLD sensitivity change, we cannot conclusively speak to the issue of whether the observed sensitivity adjustment met this precise numerical requirement. At the same time, because we found no positive evidence of activity range expansion—and because the mean SV effects for the Common Narrow stimuli were greater than double those estimated for the Common Wide stimuli (Fig. 5)—the possibility of complete adaptation merits further study. Parametric variation of the SV range (Padoa-Schioppa, 2009; Cai and Padoa-Schioppa, 2012) could yield data that more definitively address this issue.

Our findings strengthen the parallel between the BOLD value correlates observed in humans and the single-unit value correlates observed in animal models (Padoa-Schioppa, 2009; Kobayashi et al., 2010). That said, further electrophysiological data are needed to determine the extent to which our vStr and PCC adaptation effects (and the consistent ACC and VMPFC trends) are attributable to adaptation in the spiking output of these regions. The BOLD signal is commonly assumed to reflect local field potentials, which are often correlated with spiking output, but are more tightly coupled to perisynaptic activity (Logothetis, 2008). Therefore, our adaptation results could reflect adaptive coding in upstream regions that provide inputs to the valuation circuitry.

This issue is particularly relevant when considering the vStr. Midbrain dopaminergic neurons, which send projections to the vStr (Haber and Knutson, 2010), have also been shown to exhibit adaptive coding (Tobler et al., 2005). As DA neurons typically track reward-prediction errors—the difference between actual and predicted rewards (Schultz, 2000)—DA neurons exhibit adaptive coding for this variable. In other words, greater ranges of reward prediction errors are associated with a decreased sensitivity of spike rates to prediction error magnitude.

Good arguments exist both for and against the speculation that the observed ventral striatal BOLD adaptation reflected adaptation in DA neuron spiking. On the one hand, it is possible that ventral striatal BOLD was tracking some form of prediction error information, since our SV parameter was correlated with any term that might contrast SV against a constant expectation (for a detailed treatment of the SV vs prediction-error debate, see Hare et al., 2008). Additionally, pharmacological manipulations of DA transmission have been shown to significantly modulate striatal BOLD activity (Pessiglione et al., 2006; van der Schaaf et al., 2014). On the other hand, ventral striatal BOLD may have indeed tracked SV, and the pharmacological evidence alone does not justify the reverse inference that striatal BOLD always provides a direct window onto DA neuron activity (Knutson and Gibbs, 2007). Therefore, the relationship between range-adapting midbrain spiking and ventral striatal BOLD adaptation remains uncertain. Future work should seek to clarify the relative contributions of range-adapting DA neurons, range-adapting ventral striatal neurons, and also range-adapting glutamatergic OFC neurons (which also project to the vStr and adapt to value range; Padoa-Schioppa, 2009; Haber and Knutson, 2010; Kobayashi et al., 2010).

In the ACC and VMPFC, we observed trends that were consistent with range adaptation but did not reach statistical significance. In comparison, reliable range adaptation has been reported for single neuron spike rates in monkey ACC (Cai and Padoa-Schioppa, 2012) and OFC (Padoa-Schioppa, 2009; Kobayashi et al., 2010; note monkey OFC is often assumed to share functional features with human VMPFC). A possible explanation for this discrepancy relates to the slightly different variables that were examined in our study and in the single-unit work. Cai and Padoa-Schioppa (2012) analyzed ACC spiking as a function of the value of the option that was chosen on each trial, and observed adaptive coding as a function of chosen value range. Likewise, Padoa-Schioppa (2009) found that for a subset of OFC neurons, firing rates were best explained as encoding chosen value, and also adapted to chosen value range. These findings raise the question of whether ACC and VMPFC BOLD signals would also exhibit reliable range adaptation if signals were analyzed as a function of the chosen option's SV. Although other fMRI studies have reported chosen value signals in the ACC and VMPFC (Gläscher et al., 2009; Wunderlich et al., 2009, 2010), our study was not optimized to examine adaptation using this alternative variable. In a set of secondary analyses, we found that chosen value elicited only weak responses in the ACC and VMPFC, perhaps due to this variable's restricted range, relative to that of SV.

Although we observed range adaptation of BOLD activity, similar adjustments were not found in the behavioral responses. The enhanced BOLD SV sensitivity seen in the Narrow Range condition was not associated with an enhancement in choice consistency. Likewise, we did not observe range adaptation in choice RTs. Although, as expected, responses speeded as the SVs of an option pair grew more distant, this sensitivity to difficulty did not change across contexts, such that a tighter range of RTs was observed in the Narrow versus Wide Range Condition.

The decoupling of our behavioral and BOLD effects might be interpreted in multiple ways. Our procedures may have hindered the detection of corresponding behavioral changes, especially within the consistency measure. The extensive prescan practice may have promoted choice consistency, and the stability criterion may have selected for participants with usually consistent behavior. Either of these factors could have resulted in a ceiling effect that prevented the emergence of reliably greater consistency for the Common Narrow choices. Alternatively, our results may indicate a fundamentally limited impact of neural range adaptation on the choice process, with implications for models that relate the dynamics of valuation to choice behavior (for the drift diffusion model, see Ratcliff and McKoon, 2008; Milosavljevic et al., 2010; for the divisive normalization model, see Louie et al., 2013; for the biophysical model, see Chau et al., 2014). In addition, nonadapting decision RTs would provide an interesting contrast to previous monkey data (Kobayashi et al., 2010) that demonstrated adaptation in the invigoration effect of anticipated reward magnitude: when subjects performed saccades to earn cued juice rewards, saccade RTs generally decreased with increasing prospective reward, and this inverse relationship strengthened as the range of potential cued rewards narrowed.

A final, broad implication of our fMRI results involves the constraints that range adaptation places upon the use of the BOLD signal to infer SVs. If value sensitivity varies with value range, then BOLD effects cannot be used as a proxy measure of SV that may be generalized beyond the measurement context. Most immediately, this limitation suggests that studies that train classifiers to predict values from BOLD activity (Kahnt et al., 2010; Smith et al., 2014) will be most successful when the training and test data are drawn from similar contexts. In the long term, range adaptation raises caution with respect to the prospect that BOLD measures might enable cross-individual comparisons of utility that cannot be derived through choice behavior alone (Glimcher, 2010).