The Flex Track: Flexible Partitioning between Low- and High-Acuity Areas of an Emergency Department

Abstract

Study Objective

EDs with both low- and high-acuity treatment areas often have fixed allocation of resources, regardless of demand. We demonstrate the utility of discrete-event simulation to evaluate flexible partitioning between low- and high-acuity ED areas to identify the best operational strategy for subsequent implementation.

Methods

A discrete-event simulation was used to model patient flow through a 50-bed, urban, teaching ED that handles 85,000 patient visits annually. The ED has historically allocated ten beds to a Fast Track for low-acuity patients. We estimated the effect of a Flex Track policy, which involved switching up to five of these Fast Track beds to serving both low- and high-acuity patients, on patient waiting times. When the high-acuity beds were not at capacity, low-acuity patients were given priority access to flexible beds. Otherwise, high-acuity patients were given priority access to flexible beds. Wait times were estimated for patients by disposition and emergency severity index (ESI) score.

Results

A Flex Track policy using three flexible beds produced the lowest mean patient waiting of 30.9 (95% CI 30.6–31.2) minutes. The typical Fast Track approach of rigidly separating high- and low–acuity beds produced a mean patient wait time of 40.6 (95% CI 40.2–50.0) minutes, 31% higher than the three-bed Flex Track. A completely flexible ED, where all beds can accommodate any patient, produced mean wait times of 35.1 (95% CI 34.8–35.4) minutes. The results from the three-bed Flex Track scenario were robust, performing well across a range of scenarios involving higher and lower patient volumes and care durations.

Conclusion

Using discrete-event simulation, we have shown that adding some flexibility into bed allocation between low- and high-acuity can provide substantial reductions in overall patient waiting and a more efficient ED.

INTRODUCTION

Background

As patient volumes continue to rise and EDs are expected to serve more patients with less funding,^{1 –2,14–15} the imbalance of capacity and demand for health care services has resulted in decreased quality of care and increased adverse events.^1–5 One approach that has been used to handle increased demand for services is implementing a Fast Track (Figure 1B). Fast Tracks, which often include the direct allocation of specific resources (e.g., beds, rooms, or staffing), have allowed EDs to be more responsive to less-acute patients.^6–9 But, in a dynamic environment – one facing highly variable rates of arrival and acuity at arrival – with constrained capacity, this rigid dedication of capacity to high- and low-acuity patients can lead to periods of mismatch between capacity (available beds) and demand (patients needing care). Other industries, such as manufacturing and hospitality services, have explored the benefits of flexibility when faced with the problems that arise from constrained capacity and variable demand. Research has shown that, in addition to capacity balancing and variability buffering, even a small amount of flexibility may achieve nearly all of the benefits of complete flexibility.^10–13 Whether this approach could increase efficiency and responsiveness in an ED requires evaluation.

Figure 1.

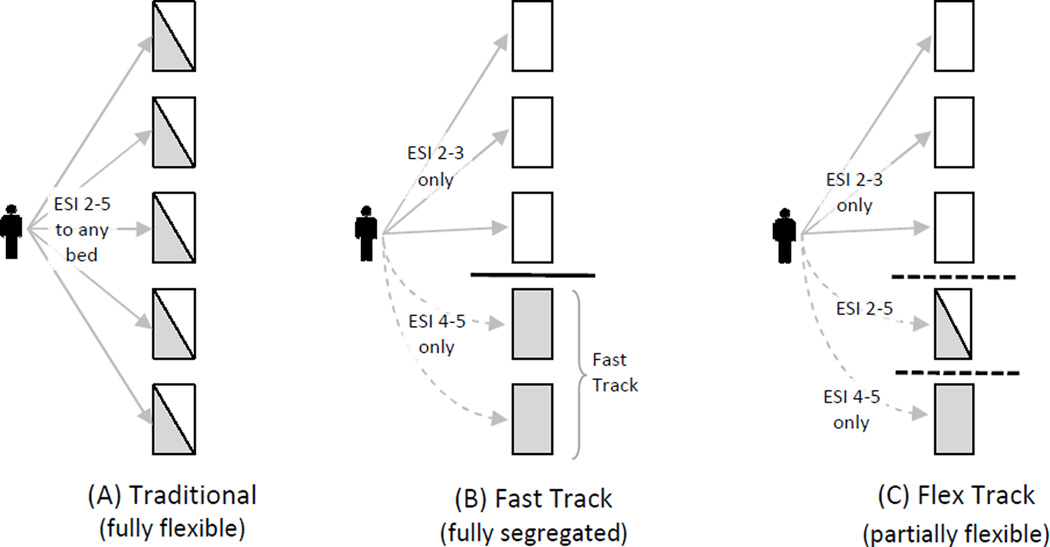
Assignment of patients under three simplified policies:

1. Traditional ED: complete flexibility; any bed may accommodate any patient ESI 2–5
2. ED with Fast Track: beds are dedicated to either higher- or lower-acuity patients
3. ED with Flex Track: some beds are dedicated to either higher- or lower-acuity patients, but some Flex Track beds may accommodate any patient ESI 2–5

Importance

In the financially constrained environment that exists for EDs today, it is imperative to identify methods for maximizing the use of existing resources, including the exploration of the possible benefits of flexible capacity. In medicine, the most common approach to operational change is to expend significant resources on implementation, with subsequent evaluation of whether benefits were realized. Whether the change to be implemented is the most likely to maximize benefit, or if it will even realize benefit, is unknown at the time of implementation. Discrete-event simulation (DES) can be used to estimate statistical performance measures of complex systems without disrupting actual care delivery environments.^17–27 As such, DES is a powerful tool that can be used to evaluate operational strategies without the costly step of implementing each possible solution. We demonstrate the value of DES to model flexible capacity strategies so as to select the optimal change to make in our ED.

Goals of This Investigation

Beyond demonstrating the potential for DES in improving healthcare delivery, the primary goal of this study was to predict the likely effect of flexible partitioning between low- and high-acuity ED areas on mean patient waiting time using DES. Supplemental analyses were employed to estimate the robustness of the simulated Flex Track policy, or the degree to which it is sensitive to variation in service times and patient volumes.

MATERIALS AND METHODS

Theoretical Model of the Problem

This study was based on the proposition that changing a portion of the Fast Track beds, which are strictly dedicated to low-acuity patients, to Flex Track beds, which are available for use by both low- and high-acuity patients, will enable the ED to better respond to demand variability than the traditional ED bed-allocation policies illustrated in Figure 1. Policy A features full flexibility, where no Fast Track exists and any patient can be placed in any bed, with higher-acuity patients generally receiving priority service. As a reaction to the extremely long waits that low-acuity patients can experience in these traditional arrangements, the Fast Track (policy B) has become commonplace. This policy features a strict separation of capacity, allocating a portion of beds to higher-acuity patients and the remaining beds to lower-acuity patients. The lack of flexibility can make Fast Track arrangements unresponsive to patient demand as it changes throughout the day. A proposed arrangement – the Flex Track (policy C) – which restores some of the flexibility from policy A back into policy B, is introduced and evaluated here.

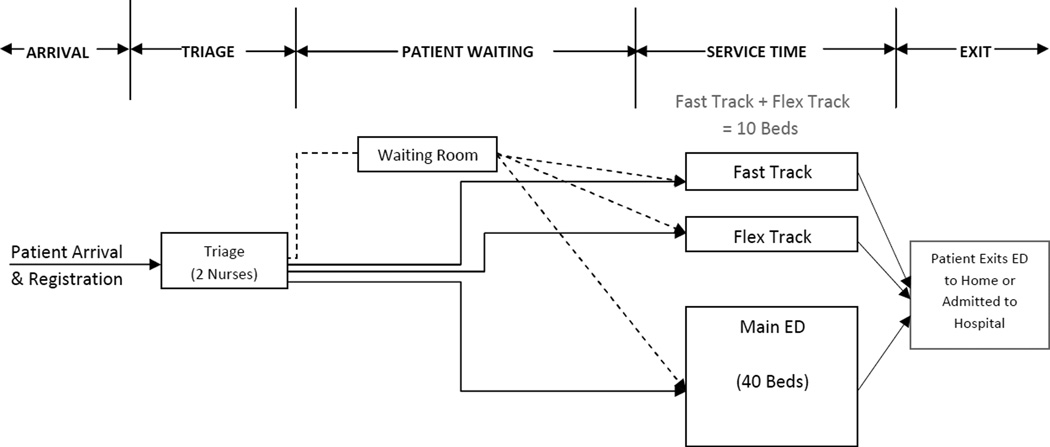
The symbolic model of patient flow through the ED is outlined in Figure 2. Using time stamps from ED operations data, the following stages of care were modeled: A) Arrival, B) Triage, C) Patient Waiting, D) Service Time and E) Exit. Patient arrival is defined as the time the patient is entered into the registration system. Patient waiting is defined as the duration of time starting when a patient ends triage until placed in a bed. Service time is defined as the duration of time starting when a patient is placed in a bed and including evaluation by a clinician, provided therapies, and a decision is made whether to admit or discharge the patient; service time ends when the patient exits the ED.

Figure 2.

Diagram of patient flow in the ED simulation model.

The following is a description of the ED care delivery process as modeled in the discrete-event simulation. First, upon arrival to the ED, patients enter registration and are then are seen on a first-in/first-out (FIFO) basis in the triage area. There are two nurses assigned 24 hours a day, 7 days a week to perform a brief, focused assessment of patient acuity. Patient acuity is assigned at triage and is based on the emergency severity index (ESI). The ESI, most commonly used in the United States,¹⁶ is an integer score that ranges from 1 to 5, inclusive, with the most urgent patients being assigned a score of 1 and least urgent patients being assigned a score of 5.¹⁷

The treatment area consists of two physically separated spaces: the main ED and the Fast Track. In this analysis, the number of beds in the main ED remains constant at 40 and they are available 24 hours a day, 7 days a week. The number of beds in the Fast Track area is always equal to ten. New patients are accepted in this area from 8:00 AM daily until 2:30 AM the next morning. Patients remain in the Fast Track area until they are appropriately discharged and Fast Track beds remain empty until they begin accepting new patients again at 8:00 AM.

When modeling the Flex Track, the Fast Track area is conceptualized as including both Fast Track and Flex Track beds. Fast Track beds are designated for use by low-acuity (ESI 4 and 5) patients only. Flex Track beds are available for use by both low- and high-acuity (ESI 2 and 3) patients based on the following prioritization policy: When the main ED beds are at full capacity, high-acuity patients are placed in main ED beds first and then in an open Flex Track bed with priority over low-acuity patients. Low-acuity patients are placed in Fast Track beds when they are available (during times that the area is open and a bed is open). If all Fast Track beds are full and Flex Track beds are available, low-acuity patients are placed in Flex Track beds with lower priority than high-acuity patients. When the Fast Track area is not accepting new patients (between 2:30 and 8:00 AM each day), low-acuity patients are placed in main ED beds with lower priority than high-acuity patients. Patients are always prioritized based on ESI score. For example, if an ESI 2 and an ESI 3 are both waiting for a bed, the ESI 2 is always placed in a bed before the ESI 3 even though they are both categorized here as high acuity. If two waiting patients have the same acuity score, consistent with FIFO, the patient waiting longer is placed in a bed first.

When constructing a DES, it is important to model all causes of variability. There are many interacting operational constraints that can be considered. However, complex models require a comprehensive understanding of the operational environment of interest, and sufficient empirical data to model each variable. Our objective here is to demonstrate the potential of DES for operational decision making using the Flex Track as an example. We recognize that there are many possible extensions to the model we present, but we have made the following simplifying assumptions to facilitate reporting and interpretation of our findings: (A) mode of patient arrivals is not considered in assigning acuity; (B) all patients follow the pattern of flow described in Figure 2; (C) a patient’s acuity stays the same throughout his or her stay; (D) once a patient enters a designated area within the ED, he or she remains in that area until service is complete; (E) overall patient waiting, by acuity, is volume-weighted; (F) patients leaving without being seen are not considered; (G) staffing allocation is fixed; (H) spatial parameters, such as precisely where the Flex Track beds are located, are not considered; and (I) ‘beds’ include all possible patient care spaces, including hallway beds.

Study Design

This study was a DES approved by the local Institutional Review Board. The simulation was built and validated using historical ED information system data spanning the period from 7/2010 to 6/2011. The study consisted of seven experiments using single- and multi-factorial designs with the aim of understanding how patient waiting is related to the following four factors: 1) number of Flex Track beds, 2) low-acuity patient volume, 3) high-acuity patient volume, and 4) service time (i.e., the time required to evaluate and disposition a patient).

First, we completed a single-factor experiment to evaluate the effect on patient wait times of switching between zero and five beds from Fast Track to Flex Track use. This initial scenario helped identify which configuration (what number of Flex Track beds) yielded the lowest mean patient waiting.

Second, we conducted three 2-factor experiments as sensitivity analyses. These sensitivity analyses separately tested the effects on mean patient waiting resulting from changes in 1) low-acuity volume, 2) high-acuity volume, and 3) service time. Low-acuity patient volume was evaluated at seven levels ranging from −10% up to +20% in 5% increments. High-acuity patient volume was evaluated at five levels ranging from −10% up to +10% in 5% increments. For the ED modeled, a 5% change is equivalent to about 4,000 to 4,500 patient visits per year. Service times were evaluated at four levels ranging from −10% up to +5% in 5% increments. A 5% change in service times represents an approximate change of 14 minutes.

Last, we conducted three 3-factor experiments that tested the effects on mean patient waiting times of the following combinations of factors: 1) number of Flex Track beds, low-acuity volume changes, and high-acuity volume changes; 2) number of Flex Track beds, low-acuity volume changes, and service time changes; and 3) number of Flex Track beds, high-acuity volume changes, and service time changes. All within-factor levels were retained from the second set of experiments.

Setting, Selection of Participants, Data Collection and Processing

The model was based on data from a single, adult, urban, tertiary–care, 50–bed, teaching ED with a Level I Trauma Center that sees about 85,000 patient visits annually. The facility currently has a forty-bed main ED that sees high-acuity patients and a ten-bed, dedicated Fast Track that sees low-acuity patients only.

The development of a DES includes the construction of two models: a structural model, which is a symbolic representation of the logic and tasks involved in the process, and a quantitative model. The structural model illustrated in Figure 2 describes the abstraction of the system being studied and the key input variables. The following patient-level variables were identified as key inputs: (1) day of the week, (2) time of arrival, (3) time placed in triage, (4) triage ESI score, (5) time placed in an ED bed, (6) time of discharge from the ED bed, and (7) disposition (admission or discharge).

The quantitative model specifies the numerical or distributional assumptions that represent the activities included in the structural model and drive the simulation. In development of the quantitative model, key patient-level data were obtained from ED information systems for every ED visit from 7/2010 to 6/2011 (n=82,523). Records were excluded for patients categorized as ESI 1 since only 0.16% of all patients were triaged as ESI 1 and those patients would never be placed in a Flex Track area and have their own designated resuscitation area that is separate from the main ED. A total of 9,849 records were excluded due to required time stamps being missing, and 1,387 records were excluded due to lack of disposition information. There were 70,625 patient records used in the final analysis. The model was built using the Arena v14.5 simulation software package (Rockwell Automation, Wisconsin).¹⁸

Outcome Measures

The main outcome measured was mean patient wait time. Patient waiting time was defined as the duration of time from completing triage until bed placement. First, mean wait time for patients, stratified by ESI score, was calculated from 225 simulation replications. Next, using simulated patient volume and ESI, a weighted overall patient mean wait time was calculated. The median and 90^th percentile wait times were also estimated and are reported as secondary outcomes.

Primary Data Analysis

The quantitative model was built and validated using patient-level data collected from the ED information system. The data were used to generate theoretical distributions for patient arrivals, time in triage, service time distributions, and disposition.

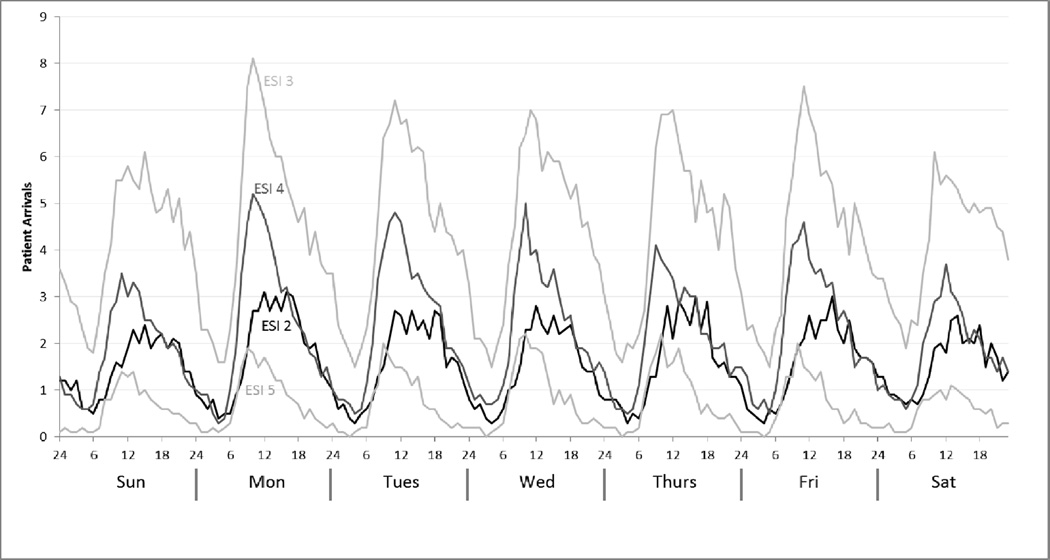
Patient arrivals (Figure 3) were found to be day-, time-, and acuity-dependent. Consistent with DES theory and previous ED simulation models, a nonstationary Poisson process was used to model ED arrivals for each ESI group.^19–23 Rate functions were estimated for intervals of time where the rate remained relatively constant. The number of patient arrivals generated by the DES were less than 0.5% different from the number of patient arrivals in the empirical data collected from the ED information systems, with no significant differences across categories.

Figure 3.

Mean patient arrivals to the ED by ESI, by day-of-week, by hour-of-day.

The theoretical distributions used to model time-in-triage were based on discussions with emergency physicians familiar with the system being modeled. Several distributions with varying parameter values were tested and it was determined that the model’s results were insensitive to changes in the distribution of time-in-triage. A lognormal distribution with the following parameters was selected: mean (µ) = 8.0 minutes, and standard deviation (σ) = 4.0 minutes (Table 1).

Table 1.

A lognormal distribution was used to model time-in-triage and service-times in the simulation model. This table provides the values used for the mean and standard deviation for each distribution. To illustrate the versimilitude of the model, the 10th and 90th percentiles for the each distribution is also included.

	**All Times are in Minutes**
	Triage	ESI 2 Admit	ESI 2 Discharge	ESI 3 Admit	ESI 3 Discharge	ESI 4 Admit	ESI 4 Discharge	ESI 5 Admit & Discharge
Mean	8	487	333	577	263	573	123	91
Standard Deviation	4	480	266	439	230	441	108	97
10th percentile	4	121	106	192	76	190	35	20
90th percentile	13	993	637	1,098	519	1,087	246	190

Parameters for the service-time distributions were estimated and validated using the results generated from two data-fitting software packages: Arena Input Analyzer¹⁸ and the Palisade @Risk (Palisade Corporation, Ithaca, NY) Excel add-in,²⁴ in combination with knowledge of the system being modeled. The simulation used separate distributions for each ESI category. Patients with an ESI of 2, 3, or 4 were further stratified by disposition (admit versus discharge); the service time durations for admitted versus discharged patients differed significantly. ESI 5 patients were only rarely admitted (< 1%) and so a single distribution was used to represent the service times for all ESI 5 patients. Service time distributions remained consistent throughout the simulation as they were not state-dependent (Table 1).

Several steps were taken to validate the service-time distributions used in the model. First, scatter diagrams confirmed the independence of the data points. Second, in hypothesizing the most appropriate families of distributions, a graphical estimate of the plot of the density functions corresponding to the distribution of the data showed the lognormal distribution to be a reasonable choice for all process-time distributions. Last, due to large sample sizes and the possibility of failing the Chi-Square test, graphical visualization and evaluation of the P-P and Q-Q plots were used to conclude goodness of fit.

Simulations are based upon the generation of random variates from theoretical distribution functions. To ensure analytic accuracy, it is important to control for variance in the simulation output. This was achieved by identifying the sources of variation in the model, applying a variance reduction technique (VRT), and synchronizing random number streams. Sources of randomness were from the exponential arrivals, service-time probability distributions, and admit-versus-discharge decisions. Common random numbers, one of the most widely employed VRTs,^20–21 were used in the model. To maintain synchronization of random numbers, separate random number streams were assigned to each source of randomness.

EDs operate 24 hours per day and 7 days a week and, therefore, have no natural starting or stopping point, so this model was run as a steady-state simulation. A warm-up period of 30 days was used to reduce initial condition bias. We used a replication period of 1 year (365 days) beyond the warm-up period. In order to obtain a 95% confidence interval of ±1 min for all pairwise comparisons of means, the initial model was run with 300 replications. With the application of the VRTs, the final model achieved the same confidence interval width with 225 replications.

RESULTS

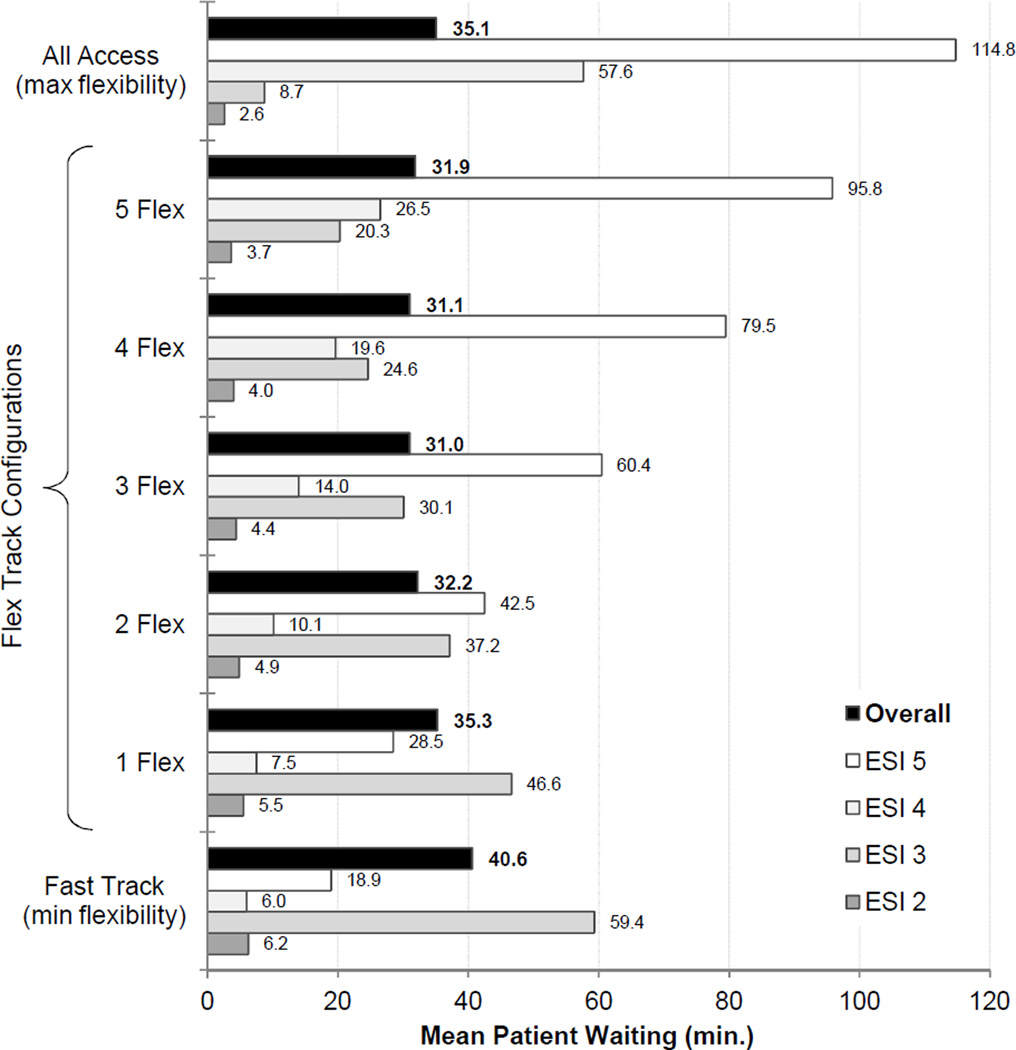
The baseline, single-factor experiment (which evaluated the effect of converting from zero to five beds from Fast Track to Flex Track on mean patient wait times) demonstrated that introducing flexibility was valuable. The optimal policy, where all waits were volume-weighted by ESI level and mean overall patient waiting time was minimized, was found to specify three Flex Track beds. These baseline results are shown in Figure 4 and Table 2a. Using a traditional Fast Track policy that rigidly separates high- and low-acuity patients (Figure 1B) – where all ten beds in the Fast Track are assigned to low-acuity patients only – the mean wait time over all patients presenting to the ED was 40.6 (95% CI 40.2–50.0) minutes. On the other end of the flexibility spectrum, an “all access” (fully flexible) bed allocation policy – where physicians prioritized patients solely based on acuity (Figure 1A) – produced a mean overall patient waiting time of 35.1 (95% CI 34.8–35.4) minutes. Using a partial flexibility arrangement (Figure 1C) of three Flex Track beds (and the remaining seven Fast Track beds dedicated to low-acuity patients) resulted in the lowest mean overall patient waiting time of 31.0 (95% CI 30.7–31.3) minutes. Either more or fewer than three flexible (Flex Track) beds resulted in an increase in mean overall patient waiting. Examination of the median and 90^th percentile wait times also supports these conclusions (Table 2b).

Figure 4.

Mean patient wait times resulting from switching zero to five beds from Fast Track to Flex Track beds and for the traditional All Access policy. The confidence intervals can be found in Table 1. The lowest overall mean wait time resulting from switching zero to five beds from Fast Track to Flex Track was achieved with 3-flexible beds. (N= 70,625).

Table 2.

a. This table illustrates the results of the base case scenario, the mean patient wait times resulting from switching zero to five beds from Fast Track to Flex Track beds and for the traditional All Access policy. The 95% confidence intervals can be found in the parentheses. The lowest overall mean wait time resulting from switching zero to five beds from Fast Track to Flex Track was achieved with 3-flexible beds. (N= 70,625).
	**All Times are in Minutes (95% CI)**
Triage	Fast Track (min flexibility)	1 Flex	2 Flex	3 Flex	4 Flex	5 Flex	All Access (max flexibility)
ESI 2	6.24 (6.20 to 6.28)	5.49 (5.46 to 5.52)	4.88 (4.85 to 4.91)	4.39 (4.36 to 4.42)	4.00 (3.97 to 4.03)	3.68 (3.66 to 3.7)	2.60 (2.58 to 2.62)
ESI 3	59.4 (58.7 to 60.0)	46.6 (46.1 to 47.1)	37.2 (36.8 to 37.6)	30.1 (29.8 to 30.4)	24.6 (24.3 to 24.9)	20.3 (20.1 to 20.6)	8.70 (8.60 to 8.80)
ESI 4	5.98 (5.80 to 6.16)	7.48 (7.29 to 7.67)	10.1 (9.9 to 10.4)	14.0 (13.7 to 14.4)	19.6 (19.2 to 20.0)	26.5 (26.0 to 27.1)	57.6 (56.7 to 58.5)
ESI 5	19.0 (18.6 to 19.3)	28.5 (28.0 to 29.0)	42.5 (41.8 to 43.3)	60.4 (59.4 to 61.5)	79.5 (78.2 to 80.9)	95.8 (94.4 to 97.3)	115 (114 to 116)
Overall	40.6 (40.3 to 41.0)	35.3 (35.0 to 35.6)	32.2 (32.0 to 32.5)	31.0 (30.7 to 31.3)	31.1 (30.8 to 31.3)	31.9 (31.6 to 32.2)	35.1 (34.8 to 35.4)

b. This table illustrates the results of the base case scenario, the median and 90th percentile of patient wait times resulting from switching zero to five beds from Fast Track to Flex Track beds and for the traditional All Access policy. The lowest overall mean wait time resulting from switching zero to five beds from Fast Track to Flex Track was achieved with 3-flexible beds, just as seen with the mean patient wait time results. (N= 70,625).
	**All Times are in Minutes**
Triage	Fast Track (min flexibility)		1 Flex		2 Flex		3 Flex		4 Flex		5 Flex		All Access (max flexibility)
	Median	90th percentile	Median	90th percentile	Median	90th percentile	Median	90th percentile	Median	90th percentile	Median	90th percentile	Median	90th percentile
ESI 2	6.2	6.6	5.5	5.8	4.9	5.2	4.4	4.7	4.0	4.3	3.7	3.9	2.6	2.8
ESI 3	59.3	65.3	46.4	51.2	37.0	40.9	29.9	33.1	24.5	27.1	20.2	22.6	16.9	18.2
ESI 4	6.0	7.3	7.6	8.9	10.1	11.9	14.0	16.6	19.5	23.0	26.3	31.0	66.9	75.5
ESI 5	18.8	22.3	28.3	33.0	42.5	49.4	59.5	71.4	78.0	92.2	94.3	110.6	114.0	126.9
Overall	40.1	44.1	35.1	38.1	32.1	34.9	30.8	33.7	30.9	34.0	31.8	35.0	35.1	38.4

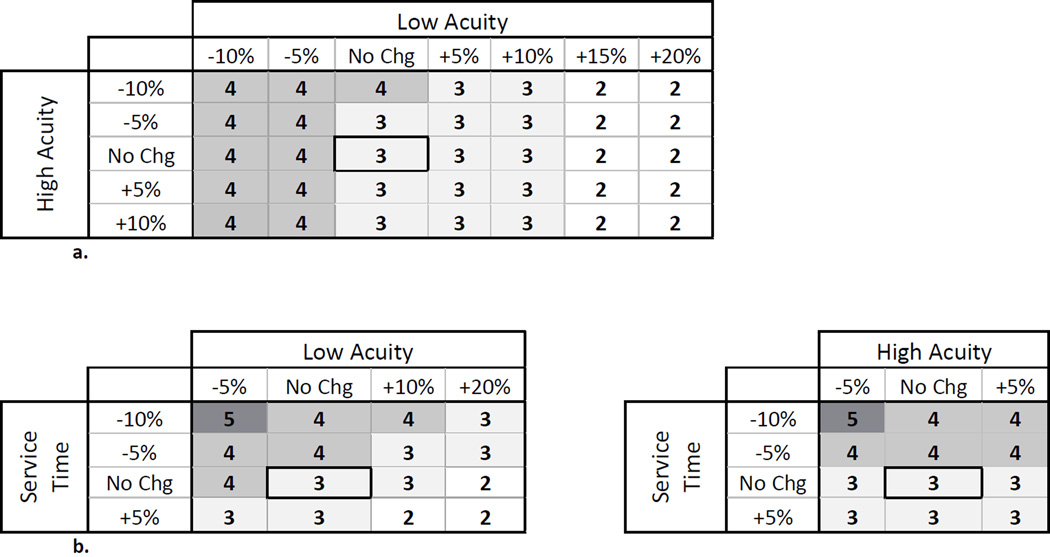
The second set of experiments considered scenarios beyond our initial baseline scenario by exploring the effects of variation in patient volume and patient care service times on patient waiting. Changes in patient volume resulted in the optimal number of Flex Track beds varying from two to four (Figure 5a), with higher low-acuity patient volume decreasing the recommended number of flexible beds (and vice versa) and high-acuity patient volume having a similar, but less pronounced, effect. However, the baseline result of three flexible beds was robust: for all scenarios examined, the mean overall waiting time for the optimal number of flexible beds for any scenario was never more than one minute better (lower) than the mean overall waiting time for the 3-bed Flex Track policy (Table 3a) subjected to the same patient volume conditions. Additionally, for all scenarios examined, the mean overall waiting time for the optimal number of beds was better (lower) than the mean overall waiting time for the standard Fast Track Policy (Table 3b) subjected to the same patient volume conditions.

Figure 5.

a. Preferred number of Flex Track beds given variations in low- and highacuity patient volumes.

b. Preferred number of Flex Track beds given variations in service time and patient volume.

Table 3.

a. This table illustrates the preferred number of flexible rooms given various combinations in changes to low- and high-acuity patient volumes. Additionally, this table shows the difference in mean wait times for the preferred number of flexible beds as compared to the optimal 3-bed Flex Track policy.
			**All Times are in Minutes (99% CI)**
Changes to High- Acuity Patient Volume	Changes to Low -Acuity Patient Volume	Preferred Number of Flex Beds	Mean Wait for Optimal Policy vs. 3-bed Flex Track Policy
			Overall	ESI 2	ESI 3	ESI 4	ESI 5
10% Decrease	No Change	4	0.02 (0.00 to 0.04)	−0.2 (−0.21 to −0.19)	−1.9 (−1.94 to −1.86)	1.8 (1.73 to 1.87)	5.5 (5.3 to 5.7)
5% Decrease		3	--	--	--	--	--
5% Increase		3	--	--	--	--	--
No Change	10% Decrease	4	−0.7 (−0.75 to −0.65)	−0.4 (−0.41 to −0.39)	−5.4 (−5.48 to −5.32)	4.3 (4.1 to 4.5)	16.3 (15.8 to 16.8)
	5% Decrease	4	−0.3 (−0.35 to −0.25)	−0.4 (−0.41 to −0.39)	−5.4 (−5.48 to −5.32)	5.0 (4.8 to 5.2)	18.0 (17.4 to 18.6)
	10% Increase	3	--	--	--	--	--
	15% Increase	2	−0.2 (−0.27 to −0.13)	0.5 (0.49 to 0.51)	7.1 (7.09 to 7.11)	−5.9 (−6.1 to −5.7)	−23.9 (−24.6 to −23.1)
10% Decrease	5% Increase	3	--	--	--	--	--
5% Decrease	5% Decrease	4	−0.2 (−0.23 to −0.17)	−0.3 (−0.31 to −0.29)	−3.3 (−3.35 to −3.25)	3.0 (2.9 to 3.1)	9.8 (9.5 to 10.1)
5% Decrease	15% Increase	2	−0.05 (−0.09 to −0.01)	0.4 (0.39 to 0.41)	4.3 (4.24 to 4.36)	−3.5 (−3.6 to −3.4)	−13.0 (−13.3 to −12.7)
5% Increase	5% Decrease	4	−0.4 (−0.48 to −0.32)	−0.5 (−0.51 to −0.49)	−8.9 (−9.0 to −8.8)	8.0 (7.8 to 8.2)	32.7 (31.6 to 33.8)

b. This table illustrates the preferred number of flexible rooms given various combinations in changes to low- and high-acuity patient volumes. Additionally, this table shows the difference in mean wait times for the preferred number of flexible beds as compared to a standard Fast Track policy.
			**All Times are in Minutes (99% CI)**
Changes to High- Acuity Patient Volume	Changes to Low- Acuity Patient Volume	Preferred Number of Flex Beds	Mean Wait for Optimal Policy vs. Fast Track Policy
			Overall	ESI 2	ESI 3	ESI 4	ESI 5
10% Decrease	No Change	4	−3.1 (−3.17 to −3.03)	−1.2 (−1.3 to −1.1)	−12.1 (−12.3 to −11.9)	5.1 (4.9 to 5.3)	13.5 (13.1 to 13.9)
5% Decrease		3	−5.4 (−5.5 to −5.3)	−1.5 (−1.52 to −1.48)	−17.3 (−17.6 to −17.0)	5.3 (5.1 to 5.5)	24.0 (23.4 to 24.6)
5% Increase		3	−18.7 (−19.2 to −18.2)	−2.2 (−2.0 to −2.4)	−52.4 (−53.5 to −51.3)	11.8 (11.5 to 12.1)	71.3 (69.2 to 73.4)
No Change	10% Decrease	4	−12.9 (−13.2 to −12.6)	−2.4 (−2.42 to −2.38)	−34.9 (−35.5 to −34.3)	9.7 (9.4 to 10.0)	44.0 (42.8 to 45.2)
	5% Decrease	4	−11.3 (−11.5 to −11.1)	−2.3 (−2.32 to −2.28)	−34.7 (−35.2 to −34.2)	11.6 (11.3 to 11.9)	33.8 (33.0 to 34.6)
	10% Increase	3	−6.7 (−6.9 to −6.5)	−1.8 (−1.82 to −1.78)	−29.1 (−29.6 to −28.6)	11.2 (10.9 to 11.5)	56.7 (55.2 to 58.2)
	15% Increase	2	−5.3 (−5.5 to −5.1)	−1.3 (−1.32 to −1.28)	−22.0 (−22.4 to −21.6)	7.0 (6.8 to 7.2)	40.8 (39.5 to 42.1)
10% Decrease	5% Increase	3	−2.6 (−2.67 to −2.53)	−1.1 (−1.11 to −1.09)	−10.2 (−10.4 to −10.0)	3.9 (3.8 to 4.0)	15.7 (15.3 to 16.1)
5% Decrease	5% Decrease	4	−6.4 (−6.5 to −6.3)	−1.8 (−1.82 to −1.78)	−20.6 (−20.9 to −20.3)	7.4 (7.2 to 7.6)	30.1 (29.3 to 30.9)
5% Decrease	15% Increase	2	−2.9 (−2.82 to −2.98)	−1.0 (−1.01 to −0.99)	−13.0 (−13.2 to −12.8)	4.6 (4.5 to 4.7)	22.8 (22.2 to 23.4)
5% Increase	5% Decrease	4	−21.6 (−22.1 to −21.1)	−2.8 (−2.82 to −2.78)	−61.8 (−63.1 to −60.5)	17.9 (17.4 to 18.4)	90.3 (88.0 to 92.6)

Note: If the value in the table is negative, the mean wait for the Optimal Policy is less than the 3-bed Flex Track Policy (by the amount listed), if the value is positive, the mean wait time for the Optimal Policy is greater than the 3-bed Flex Track Policy (by the amount listed).

Note: If the value in the table is negative, the mean wait for the Optimal Policy is less than the Fast Track Policy (by the amount listed), if the value is positive, the mean wait time for the Optimal Policy is greater than the Fast Track Policy (by the amount listed).

We also explored the effect of variation in service times on the optimal number of Flex Track beds (Tables 4a and 4b). As the amount of time a patient occupies a bed (service time) decreases, the optimal number of Flex Track beds increases. Also, as before, the baseline 3-bed Flex Track policy was found to be robust to changes in service time: for all scenarios examined, the mean overall waiting time for the optimal number of flexible beds for any scenario was never more than one minute better (lower) than the mean overall waiting time for the 3-bed Flex Track policy (Table 4a) subjected to the same service time conditions. Also, for all scenarios examined, the mean overall waiting time for the optimal number of flexible beds was better (lower) than the mean overall waiting time for the standard Fast Track Policy (Table 4b) subjected to the same service time conditions.

Table 4.

a. This table illustrates the preferred number of flexible rooms given various changes in service times. Additionally, this table shows the difference in mean wait times for the preferred number of flexible beds as compared to the optimal 3-bed Flex Track policy.
		**All Times are in Minutes (99% CI)**
Changes to Service Time	Preferred Number of Flex Beds	Mean Wait for Optimal Policy vs. 3-bed Flex Track Policy
		Overall	ESI 2	ESI 3	ESI 4	ESI 5
10% Decrease	4	−0.3 (−0.32 to −0.27)	−0.2 (−0.21 to −0.19)	−1.8 (−1.83 to −1.77)	1.3 (1.24 to 1.36)	4.3 (4.1 to 4.5)
5% Decrease	4	−0.2 (−0.23 to −0.17)	−0.3 (−0.31 to −0.29)	−3.2 (−3.25 to −3.15)	2.8 (2.71 to 2.89)	9.5 (9.2 to 9.8)
5% Increase	3	--	--	--	--	--

b. This table illustrates the preferred number of flexible rooms given various changes in service times. Additionally, this table shows the difference in mean wait times for the preferred number of flexible beds as compared to a standard Fast Track policy.
		**All Times are in Minutes (99% CI)**
Changes to Service Time	Preferred Number of Flex Beds	Mean Wait for Optimal Policy vs. Fast Track Policy
		Overall	ESI 2	ESI 3	ESI 4	ESI 5
10% Decrease	4	−4.3 (−4.38 to −4.22)	−1.3 (−1.31 to −1.29)	−11.8 (−12.0 to −11.6)	3.4 (3.3 to 3.5)	12.6 (12.2 to 13.0)
5% Decrease	4	−6.5 (−6.6 to −6.4.)	−1.8 (−1.82 to −1.79)	−20.4 (−20.7 to −20.1)	7.1 (6.9 to 7.3)	19.4 (18.9 to 19.9)
5% Increase	3	−16.5 (−16.9 to −16.1)	−2.3 (−2.33 to −2.27)	−53.6 (−54.7 to −52.5)	14.8 (14.4 to 15.2)	88.7 (85.9 to 91.5)

Note: If the value in the table is negative, the mean wait for the Optimal Policy is less than the 3-bed Flex Track Policy (by the amount listed), if the value is positive, the mean wait time for the Optimal Policy is greater than the 3-bed Flex Track Policy (by the amount listed).

Note: If the value in the table is negative, the mean wait for the Optimal Policy is less than the Fast Track Policy (by the amount listed), if the value is positive, the mean wait time for the Optimal Policy is greater than the Fast Track Policy (by the amount listed).

The last set of experiments tested the combined effects of patient volume, service time, and the number of Flex Track beds. The results showed that, as volume and service time decreased, the optimal number of Flex Track beds decreased. In addition, as the service time increased and the low-acuity patient volume increased, the optimal number of flexible beds decreased (Figure 5b). Consistent with other results from this study, the 3-bed Flex Track policy was robust and an improvement over a standard Fast Track Policy: using three flexible beds instead of the optimal number for that scenario would increase mean overall waiting time by no more than two minutes under any scenario considered (Table 5a) and the mean overall wait time for the optimal number of flex beds was lower than a standard fast track across all scenarios (Table 5b).

Table 5.

a. This table illustrates the preferred number of flexible rooms given various combinations in changes to low- and high-acuity patient volumes and service times. Additionally, this table shows the difference in mean wait times for the preferred number of flexible beds as compared to the optimal 3-bed Flex Track policy.
				**All Times are in Minutes (99% CI)**
Changes to Service Time	Changes to High- Acuity Patient Volume	Changes to Low- Acuity Patient Volume	Preferred Number of Flex Beds	Mean Wait for Optimal Policy vs. 3-bed Flex Track Policy
				Overall	ESI 2	ESI 3	ESI 4	ESI 5
10% Decrease	5% Decrease	No Change	5	−0.2 (−2.2 to −1.8)	−0.3 (−0.33 to −0.27)	−1.8 (−1.84 to −1.76)	1.5 (1.43 to 1.57)	4.3 (4.1 to 4.5)
	5% Increase		4	−0.4 (−4.3 to −3.7)	−0.3 (−0.31 to −0.29)	−3.0 (−3.04 to −2.96)	2.3 (2.22 to 2.38)	7.8 (7.5 to 8.1)
	No Change	5% Decrease	5	−0.4 (−4.3 to 3.7)	−0.4 (−0.41 to −0.39)	−3.2 (−3.25 to −3.15)	2.7 (2.6 to 2.8)	7.9 (7.6 to 8.2)
		10% Increase	4	−0.1 (−0.12 to −0.08)	−0.2 (−0.21 to −0.19)	−1.8 (−1.83 to −1.77)	1.6 (1.55 to 1.65)	5.1 (4.9 to 5.3)
		20% Increase	3	--	--	--	--	--
5% Decrease	5% Decrease	No Change	4	−0.2 (−2.2 to −1.8)	−0.2 (−0.21 to −0.19)	−1.9 (−1.93 to −1.87)	1.6 (1.53 to 1.67)	5.1 (4.9 to 5.3)
	5% Increase		4	−0.3 (−0.35 to −0.25)	−0.4 (−0.41 to −0.39)	−5.2 (−5.27 to −5.13)	4.7 (4.6 to 4.8)	17.1 (16.4 to 17.6)
	No Change	5% Decrease	4	−0.4 (−4.3 to −3.7)	−0.3 (−0.31 to −0.29)	−3.2 (−3.25 to −3.15)	2.5 (2.4 to 2.6)	8.7 (8.4 to 9.0)
		10% Increase	3	--	--	--	--	--
		20% Increase	3	--	--	--	--	--
5% Increase	5% Decrease	No Change	3	--	--	--	--	--
	No Change	5% Decrease	3	--	--	--	--	--
		10% Increase	2	−0.5 (−0.6 to −0.4)	0.6 (0.4 to 0.8)	12.1 (11.9 to 12.3)	−10.1 (−10.4 to −9.8)	−45.4 (−47.1 to −43.7)
		20% Increase	2	−2.0 (−2.2 to −1.8)	0.5 (0.48 to 0.52)	12.2 (12.0 to 12.4)	−13.2 (−13.6 to −12.8)	−47.2 (−49.1 to −45.3)

This table illustrates the preferred number of flexible rooms given various combinations in changes to low- and high-acuity patient volumes and service times. Additionally, this table shows the difference in mean wait times for the preferred number of flexible beds as compared to a standard Fast Track policy.
				**All Times are in Minutes (99% CI)**
Changes to Service Time	Changes to High- Acuity Patient Volume	Changes to Low- Acuity Patient Volume	Preferred Number of Flex Beds	Mean Wait for Optimal Policy vs. Fast Track Policy
				Overall	ESI 2	ESI 3	ESI 4	ESI 5
10% Decrease	5% Decrease	No Change	5	−2.5 (−2.55 to −2.45)	−1.1 (−1.11 to −1.09)	−7.7 (−7.8 to −7.6)	2.8 (2.7 to 2.9)	9.1 (8.8 to 9.4)
	5% Increase		4	−7.0 (−7.1 to −6.9)	−1.7 (−1.72 to −1.68)	−19.1 (−19.4 to −18.7)	5.4 (5.2 to 5.6)	21.7 (21.1 to 22.3)
	No Change	5% Decrease	5	−4.7 (−4.8 to −4.6)	−1.6 (−1.62 to −1.58)	−13.2 (−13.4 to −13.0)	4.5 (4.3 to 4.7)	15.0 (14.6 to 15.4)
		10% Increase	4	−3.4 (−3.5 to −3.3)	−1.3 (−1.32 to −1.28)	−11.8 (−12.0 to −11.6)	4.4 (4.3 to 4.5)	16.7 (16.3 to 17.1)
		20% Increase	3	−2.5 (−2.6 to −2.4)	−1.0 (−1.01 to −0.99)	−9.8 (−9.9 to −9.7)	3.5 (3.4 to 3.6)	14.5 (14.1 to 14.9)
5% Decrease	5% Decrease	No Change	4	−3.8 (−3.88 to −3.72)	−1.4 (−1.42 to −1.38)	−12.3 (−12.5 to −12.1)	4.3 (4.1 to 4.5)	16.3 (15.9 to 16.7)
	5% Increase		4	−10.9 (−11.1 to −10.7)	−2.2 (−2.22 to −2.18)	−33.2 (−33.7 to −32.7)	10.9 (10.6 to 11.2)	49.0 (47.9 to 50.1)
	No Change	5% Decrease	4	−7.3 (−7.4 to −7.2)	−1.8 (−1.82 to −1.78)	−20.4 (−20.7 to −20.1)	6.2 (6.0 to 6.4)	24.9 (24.3 to 25.5)
		10% Increase	3	−4.7 (−4.8 to −4.6)	−1.3 (−1.32 to −1.28)	−17.1 (−17.3 to −16.9)	5.8 (5.6 to 6.0)	33.2 (32.5 to 33.9)
		20% Increase	3	−3.2 (−3.3 to −3.1)	−1.9 (−1.92 to −1.88)	−16.9 (−17.1 to −16.7)	7.4 (7.2 to 7.6)	48.0 (46.8 to 49.2)
5% Increase	5% Decrease	No Change	3	−8.0 (−8.2 to −7.8)	−2.3 (−2.33 to −2.27)	−28.6 (−29.1 to −28.1)	9.6 (9.3 to 9.9)	72.3 (71.3 to 74.3)
	No Change	5% Decrease	3	−19.0 (−19.5 to −18.5)	−0.6 (−0.62 to −0.58)	−53.2 (−54.3 to −52.1)	12.2 (11.8 to 12.6)	45.4 (43.7 to 47.1)
		10% Increase	2	−10.5 (−10.9 to −10.1)	−1.6 (−1.62 to −1.58)	−41.2 (−42.1 to −40.9)	11.5 (11.2 to 11.8)	80.2 (77.1 to 83.3)
		20% Increase	2	−5.2 (−5.6 to −4.8)	−1.5 (−1.52 to −1.48)	−41.4 (−42.5 to −40.3)	16.4 (15.9 to 16.9)	114.0 (109.1 to 118.9)

Note: If the value in the table is negative, the mean wait for the Optimal Policy is less than the 3-bed Flex Track Policy (by the amount listed), if the value is positive, the mean wait time for the Optimal Policy is greater than the 3-bed Flex Track Policy (by the amount listed).

Note: If the value in the table is negative, the mean wait for the Optimal Policy is less than the Fast Track Policy (by the amount listed), if the value is positive, the mean wait time for the Optimal Policy is greater than the Fast Track Policy (by the amount listed).

Across all tested experiments, the optimal policy did not change when considering either median patient waiting or the 90^th percentile of patient waiting times. For example, in the baseline scenario described above, the 3-bed Flex Track policy resulted in the lowest overall median waiting time of 30.8 (95% CI 30.5–31.1) minutes and the 90^th percentile of waiting time was 33.7 (95% CI 33.4–34.0) minutes.

LIMITATIONS

Our results suggest that the proper use of exam room flexibility has the potential to reduce ED patient waiting times when compared with either rigid dedication (Fast Track) or complete flexibility (all access) policies. However, these findings should be considered in light of several limitations. Importantly, the simulation models were based on data from a single, urban, teaching hospital. It is not clear whether EDs with a different distribution of high- versus low-acuity patient volume and different allocations of beds between Fast Track and the main ED will benefit similarly.

Recent research has shown that the speed at which a provider works may be partly dependent on work load.^25–26 While we explored how service times affect the relationship between Flex Track beds and wait times, we did not incorporate load-dependent service rates. We also excluded all ESI 1 patients for reasons previously discussed. The use of a distribution with extreme values helps account, from a patient-waiting perspective, for situations such as the arrival of a resource-intensive trauma patient. But, the model does not adjust bed management policies. In our study, less than 0.16% of the n=82,523 patient records were listed as major resuscitations. Given the resource-intensive nature of this type of event, if an ED finds they routinely encounter disruptions, this should be accommodated for in an expanded analysis.

Many different care processes occur once a patient occupies a bed. We intentionally chose to simplify this aspect of the model since our analysis was concerned primarily with the amount of time a patient waits for a bed. The theoretical distributions used in the models accurately reflect the wide variety of process times without needing to model every step within that process. The use of these distributions also enabled testing the effect of changes in process times without specifying the source of change. For example, we were able to evaluate the preferred number of Flex Track beds when an increase in service time occurs without specifying whether it was due to events that could potentially prolong service times (e.g., new residents in July) or a result of provider variability. The validation of the model against the empirical ED data demonstrates that the model provides reasonable estimates of mean patient waiting for this environment.

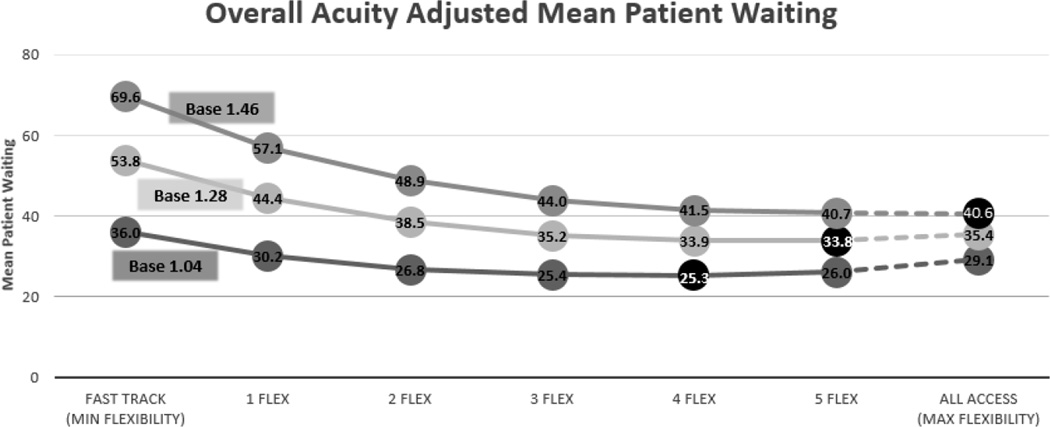
One of the limitations of our model is the underlying assumption that all waiting time is exchangeable. In a supplemental analysis, we sought to evaluate how relaxing that assumption (weighting sicker patients higher), would influence our operational policies. As can be seen in Figure 6, our analysis showed that the higher the value placed on the waiting time for sicker patients, the value of the flexibility becomes greater. Thus, when considering the implementation of a Flex Track, the organization needs to have a substantive discussion on the value of patient waiting. The relative importance of patient waiting by acuity will help an ED make the best choices regarding operational flexibility.

Figure 6.

This figure illustrates the acuity adjusted mean patient waiting. With a base adjusted value of 1.04, 4 flexible beds produces the lowest overall mean wait. As the acuity adjusted base approaches 1.46, the lowest overall mean wait can be found with the all access (max flexibility) policy.

Acuity Weights: ESI2 = (base)^3; ESI3 = (base)^2; ESI4 = (base;) ESI5 = 1.

DISCUSSION

According to the National Report Card on the State of Emergency Medicine Hospitals, “It is the inescapable conclusion of numerous studies: hospitals are crowded, emergency departments are backed up, ambulance diversions are common, and patients are facing longer waits.”²⁷ Adding complexity to this already challenging situation is the continual rise in ED patient volume and tightening operating budgets.^{1–2,14–15} It is critical to identify more efficient ways to respond to this increasing demand given existing or potentially even more limited resources.

Within the operations research discipline, a wide variety of methods exist to study the performance of a system of interest. Some of the more traditional analytical methods, such as dynamic programming, can be used to develop models with exact closed-form solutions for a problem being examined, but often at the expense of removing much of reality’s complexity. Complex systems, such as an ED, can seldom be validly represented by such simple analytical models. For analysis of complex systems, DES models are valuable for their capacity to handle a high level of detail, fewer restrictive assumptions than traditional analytical models, and their ability to handle nonstationarity in modeling. Our study highlights the value of discrete-event simulation modeling to inform decision making in a complex environment.

While many organizations are doing something similar to Flex Track, at least informally, our results add to the evidence suggesting that operational flexibility is a valuable tool for improving efficiency. The introduction of flexible capacity with Flex Track beds resulted in lower mean overall patient waiting time than incorporating either a rigid Fast Track or an all-access policy across all patient volume and service time scenarios considered. The first experiment, which evaluated the effect of converting Fast Track beds to Flex Track beds on mean overall waiting time demonstrated that a policy of three Flex Track beds resulted in the lowest overall mean wait time for patients. Building upon that result, our sensitivity analyses evaluated whether changes in volume or service times would significantly alter our initial conclusion. The three bed Flex Track policy was reasonably robust to changes in both patient volume and service time. As seen in Figures 5a and 5b, the optimal policies worked well across a wide range of possible scenarios. Additionally, as can be seen in Table 2–5, the differences between mean waiting for the optimal condition when compared to the three bed Flex Track, were small across all tested scenarios. These results give confidence to recommending the three bed Flex Track as the most suitable policy for this ED.

Our model was found to be fairly robust to the variables we considered. A distinct value of DES is that it can be expanded to include additional constraints and complexities. For example, it would be possible to consider staffing variability, to include disruptions, to model spatial constraints and to determine whether there is a threshold ED volume above or below which flexibility is no longer beneficial. While generalizing our results to other EDs is inappropriate without considering their specific patient volume, physical space, and service data, this methodological approach to identifying the optimal number of Flex Track beds should be applicable to a wide range of ED environments.

This study calls into question the belief that either traditional, open-access beds or a rigidly separated Fast Track approach is the best option for accommodating time-varying patient demand. We found that neither approach was optimal for reducing patient wait times if a Flex Track policy is considered. This seems reasonable because, when a system is faced with variable demand, complete dedication of resources can lead to periods of mismatched capacity and demand. Consistent with research in other industries,^10–13 flexible capacity can enable better responses to demand variability; we found that limited flexibility can satisfy nearly all of the benefits obtained from full flexibility.

As facilities consider implementation of a Flex Track, there are resource, personnel, architectural and cultural barriers. First, the implementation of assuming an ED’s physical plant can support the implementation of a Flex Track, and an upfront investment in equipment to ensure appropriate monitoring and capabilities may be required. Depending on the facility and potential nurse-patient ratios, there may be a difference between the Fast Track and main ED settings. Additionally, staff must have appropriate skills to see higher-acuity patients. Each facility will have to consider the costs of such investments as well as the operational challenges of incorporating flexibility into staff and clinician scheduling when weighing the potential benefits of a Flex Track policy.

Additionally, one of the underlying assumptions in our model is that all waiting time is exchangeable. In a supplemental analysis, we sought to evaluate how relaxing that assumption, (weighting sicker patients higher), would influence our operational policies. As can be seen in Figure 6, our analysis showed that the higher the value that is placed on the waiting time for sicker patients, the value of the flexibility becomes greater. Thus, when considering the implementation of a Flex Track, the organization needs to have a substantive discussion on the relative value of patient waiting. The relative importance of patient waiting by acuity will help an ED make the best choices regarding operational flexibility.

In summary, this research demonstrates that using DES, it is possible to identify likely solutions to operational problems prior to implementation. We showed that assigning some existing Fast Track resources to a Flex Track can decrease patient waiting times and is effective across a wide range of acuity, volume, and service times. Flexible resource allocation should be considered in order to help EDs respond more effectively to demand variability and to mitigate resource-based operational constraints.