Abstract
We develop a mathematical model of tumor growth in complex, dynamic microenvironments with active, deformable membranes. Using a diffuse domain approach, the complex domain is captured implicitly using an auxiliary function and the governing equations are appropriately modified, extended and solved in a larger, regular domain. The diffuse domain method enables us to develop an efficient numerical implementation that does not depend on the space dimension or the microenvironmental geometry. We model homotypic cell-cell adhesion and heterotypic cell-basement membrane (BM) adhesion with the latter being implemented via a membrane energy that models cell-BM interactions. We incorporate simple models of elastic forces and the degradation of the BM and ECM by tumor-secreted matrix degrading enzymes. We investigate tumor progression and BM response as a function of cell-BM adhesion and the stiffness of the BM. We find tumor sizes tend to be positively correlated with cell-BM adhesion since increasing cell-BM adhesion results in thinner, more elongated tumors. Prior to invasion of the tumor into the stroma, we find a negative correlation between tumor size and BM stiffness as the elastic restoring forces tend to inhibit tumor growth. In order to model tumor invasion of the stroma, we find it necessary to downregulate cell-BM adhesiveness, which is consistent with experimental observations. A stiff BM promotes invasiveness because at early stages the opening in the BM created by MDE degradation from tumor cells tends to be narrower when the BM is stiffer. This requires invading cells to squeeze through the narrow opening and thus promotes fragmentation that then leads to enhanced growth and invasion. In three dimensions, the opening in the BM was found to increase in size even when the BM is stiff because of pressure induced by growing tumor clusters. A larger opening in the BM can increase the potential for further invasiveness by increasing the possibility that additional tumor cells could invade the stroma.
Keywords: Tumor progression, Basement membrane, Dynamic geometry, Tumor invasiveness, Computer model
1. Introduction
The tumor microenvironment (TME) is a dynamic structure with varying composition and distribution. The TME is composed of extracellular matrix and stromal cells and plays a crucial role on tumor progression and suppression (e.g., Tlsty et al., 2006; Albini et al., 2007; Place et al., 2011; Pickup et al., 2013). Changing the tissue geometry alters tension gradients, sites of mechanotransduction and the location of the proliferating, migrating and differentiating cells within a tissue. Even small local changes in cell-cell or cell-ECM interaction can have dramatic consequences for global tissue structure and function (DuFort et al., 2011). The mechanisms of communication between tumor cells and the TME are complex but fall into two main categories: contact-dependent mechanisms that involve cell-cell and cell-ECM adhesion and contact-independent mechanisms in which soluble molecules such as growth factors, chemokines and cytokines, and soluble subcellular organelles including microvesicles and exosomes play an essential role (Fang and DeClerck, 2013). The interaction between cancer cells and their microenvironment can largely determine the phenotype of the tumor (Mueller and Fusenig, 2004). Recently it has been shown that not only can the microenvironment enhance growth of the primary cancer but also facilitate its metastatic dissemination to distant organs (Joyce and Pollard, 2009; Li et al.,2007).
Because tumor progression is difficult to approach by experimental methods alone, mathematical models and sophisticated computer simulations can help explain experimental and clinical observations and aid in assessing effective cancer treatment strategies. As a consequence, a keen interest in the mathematical modeling of cancer and numerical simulation of the tumor growth has persisted amongst mathematicians in recent years. A variety of modeling strategies are now available for investigating one or more aspects of cancer. For instance, in discrete cell-based approaches such as cellular automata and agent-based models the behavior of individual cells is simulated according to biological rules. Continuum models such as single-phase and multiphase mixture models treat tumors as a collection of cells at larger scales and principles from continuum mechanics such as mass and momentum conservation are used to construct partial differential equations and integro-differential equations governing the motion of cell densities, or volume fractions, stresses and cell velocities. See, for example, the recent reviews (Ribba et al., 2004; Quaranta et al., 2005; Hatzikirou et al., 2005; Nagy, 2005; Wodarz et al., 2005; Byrne et al., 2006; Fasano et al., 2006; van Leeuwen et al., 2007; Roose et al., 2007; Graziano et al., 2007; Harpold et al., 2007; Drasdo and Höhme, 2007; Friedman et al., 2007; Sanga et al., 2007; Anderson and Quaranta, 2008; Bellomo et al., 2008; Cristini et al., 2008; Deisboeck et al., 2009; Byrne, 2010; Rejniak and McCawley, 2010; Lowengrub et al., 2010; Deisboeck et al., 2011; Frieboes et al., 2011; Kim et al., 2011; Kam et al., 2012; Hatzikirou et al., 2012; Szabó et al., 2013; Baldock et al., 2013; Katira et al., 2013) for a collection of recent results.
There are a number of models that focus on different aspects of cell-cell and cell-ECM mechanical interactions on solid tumor progression. For example, the interaction of multiple tumor cell species has been modeled by multiphase mixture models (Ward and King, 1997; Please et al., 1998; Ward and King, 1999; Please et al., 1999; Ambrosi and Preziosi, 2002; Breward et al., 2002, 2003; Byrne et al., 2003; Byrne and Preziosi, 2003; Franks et al., 2003a, b; Roose et al., 2003; Cristini et al., 2003; Araujo and McElwain, 2005a,b; Zheng et al., 2005; Chaplain et al., 2006a; Li et al., 2007; Macklin and Lowengrub, 2007; Tosin, 2008; Wise et al., 2008; Ambrosi and Preziosi, 2009; Ambrosi et al., 2009; Preziosi and Tosin, 2009a,b; Armstrong et al., 2009; Cristini et al., 2009; Tracqui, 2009; Macklin et al., 2009; Frieboes et al., 2010; Preziosi and Vitale, 2011; Hawkins-Daarud et al., 2012). In these models, the mechanical effects of the stroma, the extracellular matrix, basement membrane and connective tissue were either neglected or highly idealized. Recently, Bresch et al. (2010) used the immersed interface boundary method to study the interactions of a growing tumor and a basement membrane, accounting for both proliferating and quiescent tumor cells, where the membrane is represented by a level set function. This work extended an approach developed by Cottet and Maitre (2004) for fluid-structure interactions, and modeled the membrane elasticity by penalizing local stretching. Two and three dimensional simulations were performed to show the effects of the membrane and nutrient heterogeneity on tumor growth. Very recently, using multiphase porous media mechanics and thermodynamically constrained averaging theory, Sciumé et al. (2013) modeled growing tumors as a multiphase medium containing extracellular matrix, tumor and host cells, and interstitial liquid. Numerical simulations were performed that characterized tumor growth as a function of the initial tumor-to-healthy cell density ratio, nutrient concentration, mechanical strain, cell adhesion and geometry. Following the approach used in Bresch et al. (2010), a multiphase mixture model was developed by Chen et al. (2013) incorporating a simple membrane elasticity where global stretching is penalized. An efficient numerical method was designed to solve the governing equations. Two and three dimensional simulations were performed and nonlinear effects of membrane elastic forces were found to either resist or enhance growth of the tumor, depending on the membrane geometry.
In this paper, we extend the model developed by Chen et al. (2013) to simulate solid tumor growth in active, complex and dynamic TMEs. The complex domain is captured implicitly using an auxiliary function, which is a smoothed characteristic function of the complex domain, and the governing equations are appropriately modified, extended and solved in a larger, regular domain. The boundary conditions appear as singular source terms in the reformulated equations. This approach, known as the diffuse domain method (e.g., Li et al., 2009; Teigen et al., 2009; Teigen et al., 2011; Aland et al., 2010), enables us to develop an efficient numerical implementation that does not depend on the space dimension or on the geometry of the microenvironment. We apply this framework to a mixture model of tumor growth in duct-like geometries, such as ductal carcinoma in situ (DCIS) of the breast (e.g., Sakorafas and Tsiotou 2000; Sanders et al. 2005). We model homotypic cell-cell adhesion and heterotypic cell-basement membrane (BM) adhesion with the latter being implemented via a membrane energy that models cell-membrane interaction (Jacqmin, 1999) in two and three dimensions. We incorporate simple models of elastic forces and the degradation of the BM and ECM by tumor-secreted matrix degrading enzymes, which allows us to model tumor invasion of the stroma. We investigate in-situ and invasive progression of tumors, and the corresponding BM dynamics, as a function of cell-BM adhesion and the stiffness of the BM. Note that Chen et al. (2013) did not consider cell-BM adhesion, the degradation of the BM and ECM, or tumor invasion of the stroma.
The paper is organized as follows. In Section 2, we develop a mathematical model of tumor growth and tumor invasion in complex, evolving geometries using the diffuse domain method. In Section 3, numerical simulations are performed to illustrate the nontrivial dependence of tumor growth and local invasiveness on the adhesive characteristics of the tumor cells and the properties of the basement membrane in two and three dimensions. Finally, in Section 4, we give some concluding remarks and future work. The details of the numerical method are presented in the Supplementary Material.
2. Mathematical model
We build upon the tumor growth models from Wise et al. (2008) and Chen et al. (2013). For completeness, these are summarized below. We consider a bounded, open tissue domain Ω ⊂ R d , d = 2 or 3 in which the tumor and membrane are evolving. The dimensionless variables defined in Ω are:
ϕV, the volume fraction of the viable tumor cells,
ϕD, the volume fraction of the dead cells,
uS , the mass-averaged cell velocity,
p, the pressure,
n, the nutrient concentration.
Following Wise et al. (2008), we assume that the volume fractions satisfy the mass conservation equations
| (1) |
where i = {V, D} are the cell types, Ji are fluxes that account for the mechanical interactions among the cell species, and the source terms Si account for the intercomponent mass exchange as well as gains due to cell proliferation and loss due to cell death. The fluxes and velocities are determined using a energetic variational argument. In Chen et al. (2013), we incorporated a simple model to simulate the effect of an embedded deformable membrane described implicitly using an auxiliary function ψ(x, t). We assume the energy of the system is a sum of the cell-cell adhesion energy Eadhesion and a simplified form of the elastic energy Eel:
| (2) |
| (3) |
| (4) |
where
| (5) |
is the total volume fraction of tumor cells and is a double-well bulk energy, which implies a well-delineated separation of the tumor ϕT ≈ 1 and the host ϕT ≈ 0. The parameters γ and ∈ measure the cell-cell adhesion strength and the thickness of the diffuse interface that separates the tumor and host domains, respectively. In Eq. (4), Ψ is a template function (e.g., Ψ(x, t) = ψ(x, 0)), and A represents the stiffness of the membrane (e.g., a simplified version of Hooke’s law).
The fluxes and velocities can be modeled as (Wise et al., 2008; Chen et al., 2013)
| (6) |
and
| (7) |
where
| (8) |
Eq. (7) is a generalized Darcy’s law that relates the velocity of the tumor cells with the pressure, cell-cell adhesive and the elastic forces. In Chen et al. (2013), an advective Cahn-Hilliard type equation is used to approximate the transport of ψ
| (9) |
| (10) |
under the assumption that the membrane moves with the velocity uS.
The sources terms are taken to be (Wise et al., 2008)
| (11) |
| (12) |
| (13) |
where the parameters λM, λA, λN and λdc are the rates of cellular mitosis, apoptosis, necrosis and dead cell clearance, respectively. 𝓗 is a Heaviside step function. It is assumed that viable tumor cells necrose based on the level of the local nutrient concentration n, i.e., when the nutrient level is below the cell viability limit nN , cells die at the rate λN.
Assuming no proliferation or death of the host tissue, the velocity is constrained to satisfy (Wise et al., 2008)
| (14) |
where ST is the sum of SV and SD
| (15) |
Combining Eqs. (7) and (14) yields an equation for the pressure
| (16) |
The nutrient is assumed to evolve quasi-statically and satisfies
| (17) |
where the nutrient uptake by host tissue is negligible compared with the uptake by tumor cells and nutrient diffusion occurs on a much shorter time scale (e.g. minute) than the cell-proliferation time scale (e.g. day or more), see Wise et al. (2008). The term D(ϕT) is the nutrient diffusion coefficient, which may be different in the tumor and host domains. The term TC (ϕT , n) represents a nutrient source (e.g., from capillaries).
2.1. Diffuse domain formulation
We next extend the model by assuming that a basement membrane (BM) bounds the domain where the tumor is growing (Fig. 1). Further, we explicitly account for cell-BM adhesion. We model the cell-BM adhesive energy as (Jacqmin, 1999),
| (18) |
where g(ϕT) is an energy density and ΓBM denotes the BM. A variational argument shows that this introduces the boundary condition (Granasy et al., 2007):
| (19) |
where n is the unit normal to the BM. Taking , where θ models the static contact angle (e.g., Jacqmin, 1999; Granasy et al., 2007; Li et al., 2009; Do-Quang and Amberg, 2009; Teigen et al., 2009; Teigen et al., 2011; Aland et al., 2010), this term reflects the difference in cell-cell, cell-ECM, and ECM-ECM adhesion energies in analogy with Young’s relation for multicomponent fluids. A small value of θ (e.g., θ < 90 °) implies that tumor cells prefer to adhere to each other rather than to the BM whereas a large value of θ (e.g., θ > 90 °) implies that tumor cells prefer to adhere to the BM.
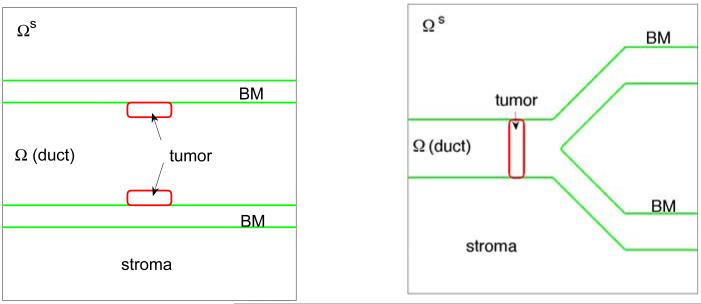
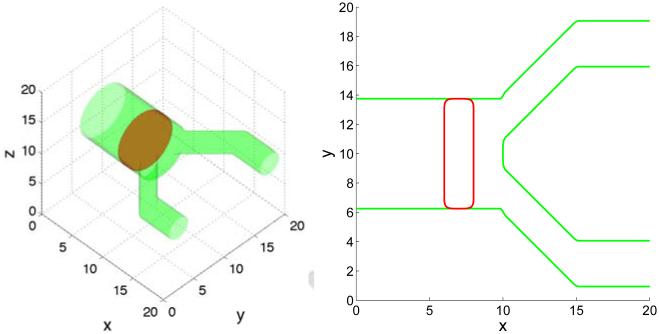
Figure 1.
The initial shape of tumor clusters (red; ϕT = 0.5 contours) and basement membranes (green; ψ = 0.5 contours) in the 2D simulations. Left: simple duct; Right: branched duct. Note that in the simple duct, the membrane thickness is explicitly modeled by introducing the inner and outer membrane boundaries.
We consider a large, regular domain Ωs containing the complex, dynamic domain Ω (Fig. 1). We represent the complex domain using a phase field function ψ, which approximates the characteristic function of the domain Ω such that ψ ≈ 1 in Ω and ψ ≈ 0 in Ωs/Ω. The boundary ∂Ω, which may be time-dependent, is described implicitly using the set ∂Ω(t) = {x|ψ(x, t) = 1/2}.
We next reformulate Eq. (1) and the boundary conditions on ∂Ω using the diffuse domain formulation (Li et al., 2009; Teigen et al., 2009; Teigen et al., 2011; Aland et al., 2010) where the equations are extended into Ω S and the boundary conditions are incorporated as singular source terms. Accordingly, we obtain
| (20) |
where we have assumed no-flux boundary conditions Ji · n = 0 on ∂Ω. To determine the fluxes Ji and the velocities ui in Eq. (20), we use an energy variation argument to derive the constitutive laws, which is consistent with a dissipative biophysical energy.
In the following we reformulate the tumor cell-cell adhesion energy Eq. (2) in the larger domain Ω s as
| (21) |
and use a surface delta function δΓ to rewrite the cell-membrane interaction forces in the domain Ωs
| (22) |
where Γ = ∂Ω and we take as a diffuse interface approximation of the surface delta function, with ∈ characterizing the width of the diffuse boundary of the domain Ω. All together, the total free energy of the system becomes
| (23) |
A variational argument gives that
| (24) |
where the term ∈g′(ϕT)|▽ψ| comes from the diffuse domain approximation of the tumor-membrane boundary condition (19).
Correspondingly, a generalized Darcy’s law gives
| (25) |
with
| (26) |
The term δΓ▽g(ϕT ) comes from the active tumor-membrane boundary, and other terms on the right hand side of v equation arise from the cell-cell adhesion.
Substituting the fluxes Ji and the velocity uS into Eq. (20), the tumor volume fraction ϕT follows the Cahn-Hilliard-type advection-reaction-diffusion equation
| (27) |
where the mass exchange term ST will be specified later in this section.
Rather than solving for the volume fraction of viable tumor cells ϕV, a dynamic equation for the volume fraction of dead cells ϕD is used instead
| (28) |
where the mass exchange term SD will be given later in this section. Knowing ϕT and ϕD, the volume fraction of viable tumor cells is calculated as ϕV = ϕT − ϕD.
Assuming, no proliferation and death of the host tissue, the velocity is constrained to satisfy
| (29) |
where τ is a small positive number.
Together, Eqs. (25) and (29) constitute a Poisson equation for the solid pressure p
| (30) |
The nondimensional quasi-steady nutrient equation is given by
| (31) |
The diffusion coefficient D(ψϕT) and nutrient capillary source term TC(ψϕT, n) are
| (32) |
| (33) |
where DH is the nutrient diffusion coefficient in the host domain, denote the nutrient-to-tissue transfer rates for the pre-existing vasculature in the tumor and host domains, and nC is the nutrient level in the capillaries. We do not model angiogenesis here, although models of angiogenesis could be incorporated. This will be investigated in future work. The interpolation function Q(ϕ) is
For simplicity, we take DH = DT here.
Eqs. (27)-(31) and (9)-(10) are valid on the extended domain Ω s and not just on the tumor volume ΩT. We choose the following boundary conditions
As long as the tumor does not intersect the boundary of the extended domain Ω s, the results are insensitive to the choice of boundary conditions on ∂Ω s.
2.2. Tumor invasion into stroma
Cancer cells have ability to invade the local tissue and spread to other tissues and organs. During this stage of growth, tumor cells secrete matrix degrading enzymes (MDEs), mainly matrix metallo-proteases (MMPs) and urokinase plasminogen activators (uPAs) that degrade the extracellular matrix (ECM) and the basement membrane (Friedl and Wolf, 2003; Friedl and Alexander, 2011; Hood and Chersh, 2002; Ilina et al., 2011). At the same time, viable tumor cells may rebuild the ECM by secreting insoluble matrix macromolecules (Carter, 1965; Quigley et al., 1983; Lacovara et al., 1984; McCarthy & Furcht, 1984; Liotta et al., 1986; Klominek et al., 1993) due to their interactions with the BM and ECM. Following recent work (Chaplain et al., 2006a; Graziano et al, 2007; Macklin et al., 2009; Giverso et al., 2010), we introduce the ECM density E, the concentration of matrix degrading enzymes m, and assume that E evolves via
| (34) |
where λmE is the matrix degradation rate by the MDEs and λvE is the production rate of ECM by the viable tumor cells. The MDE concentration m satisfies
where Dm is the diffusion coefficient, the parameter λprod is the production rate of MDEs by the viable tumor cells, mmot is a desired level of MDE, λdecay is the natural decay rate of MDEs, and the parameters λdmψ and λdmE are loss rates of MDEs due to interactions with the basement membrane and the ECM, respectively. The boundary condition for m is
We extend the cell velocity to account for active cell movement via haptotaxis by introducing a haptotaxis velocity, which is proportional to the gradient of ECM (e.g., Chaplain et al, 2006b, Macklin et al., 2009). In particular, we add the term χE ▽E to the velocity v in Eq. (26), where χE is the haptotaxis coefficient.
Finally, the model for the basement membrane is extended to include degradation by MDEs (Bresch et al., 2010)
| (36) |
where the parameter λdeg is the membrane degradation rate by the MDEs.
3. Numerical results
In order to numerically solve the governing system of equations derived in the previous section, a stable numerical scheme developed in Chen et al. (2013) is used to solve the equations. Two and three dimensional simulations are performed. Adaptive, block-structured Cartesian mesh refinement is used to increase accuracy locally (Wise et al., 2011). The details of the algorithm are given in the Supplementary Material. The parameters are given in Tables 1 and 2 and are consistent with nondimensionalizing time by the cell mitosis rate (e.g., 1 day) and space by the diffusion penetration length (e.g., approx 200μm). In two dimensions the computational domain is Ω = (0, 20) × (0, 20). The root-level grid size is 322 and we perform three levels of refinement, giving an effective spatial grid size h = 0.078. The time step size is s = 0.001. In three dimensions the computational domain is Ω = (0, 20) × (0, 20) × (0, 20). The root-level grid is 323 and there are two levels of refinement, giving an effective spatial grid size h = 0.16. In three dimensions, the time step size is s = 0.01. The time and space step sizes are sufficient to resolve the nonlinear dynamics.
Table 1.
Nondimensional parameters in the two dimensional numerical simulations.
| ∈ | 0.05 | 0.05 | |
| M | 20.0 | 20.0 | |
| γ | 0.2 | ν U | 1.0 |
| 0.2 | 0.0 | ||
| nc | 1.0 | λ M | 1.0 |
| λ A | 0.0 | λ N | 3.0 |
| λ dc | 1.0 | λ deg | 20.0 |
| λ prod | 200.0 | λ decay | 10.0 |
| λ dmψ | 1.0 | λ dmE | 1.0 |
| λ mE | 0.0 | λ νE | 0.0 |
| Dm | 0.1 | χ E | 0.1 |
| mmot | 1.0 |
Table 2.
Nondimensional parameters in the three dimensional numerical simulations.
| ∈ | 0.1 | 0.1 | |
| M | 10.0 | 10.0 | |
| γ | 0.2 | ν U | 1.0 |
| 0.2 | 0.0 | ||
| nc | 1.0 | λ M | 1.0 |
| λ A | 0.0 | λ N | 3.0 |
| λ dc | 1.0 | λ deg | 1.0 |
| λ prod | 100.0 | λ decay | 20.0 |
| λ dmψ | 1.0 | λ dmE | 1.0 |
| λ mE | 0.0 | λ νE | 0.0 |
| Dm | 0.1 | χ E | 0.1 |
| mmot | 1.0 |
3.1. Two dimensional results
We first present simulations of tumor growth in simplified 2D Cartesian domains with duct-like geometries with elastic, dynamic boundaries. We assume that the tumors (red; ϕT = 0.5 contours) start as small clusters of tumor cells, a subset of which are attached to the BM (green; ψ = 0.5 contours) since in many carcinomas, some tumor cells are able to survive without being attached to the BM (anoikis-resistance; e.g., Derksen et al. 2006; Howe et al. 2011; Taddei et al. 2012). We do not explicitly model the layer of normal epithelial cells (ECs) that are also attached to the BM (away from the tumor), but the model could be straightforwardly extended to this case. We instead assume that the normal ECs are displaced by the growing tumor. In the simple duct shown in Fig. 1 (left), we model the BM as having a finite thickness and we track the inner and outer boundaries. The tumors are initially present on the inner boundary. Although the thickness of the BM is exaggerated here, the results shown below do not depend qualitatively on the thickness of the BM. Simulating thinner BMs just requires more numerical resolution. Because tumors such as DCIS grow in breast ducts, which are examples of branched epithelial tissues, we also consider the evolution of a tumor in a simplified model of a branched duct. For the branched duct in Fig. 1 (right), we do not model the thickness of the BM and we assume that the tumor has grown across the lumen. In this case, the lumens of the secondary branches are smaller than that of the primary branch and the ratio between the lumen radii is 1.6, which is consistent with experimental observations of breast duct morphologies (Ramsay et al., 2005). In both the simple and branched ducts, we assume that nutrient is delivered uniformly to the stroma by the vasculature, which is modeled by taking the nutrient capillary source term in Eq. (33) to be .
Simple duct
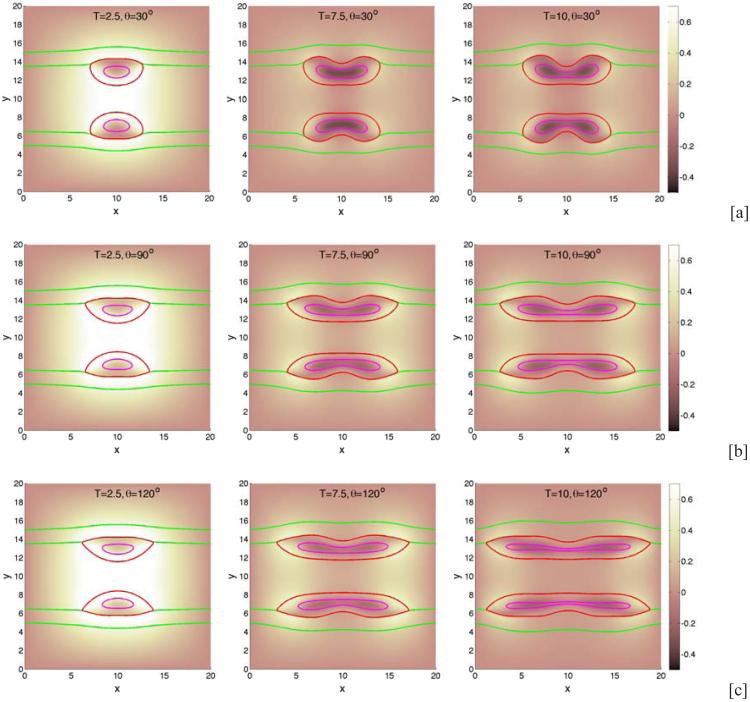
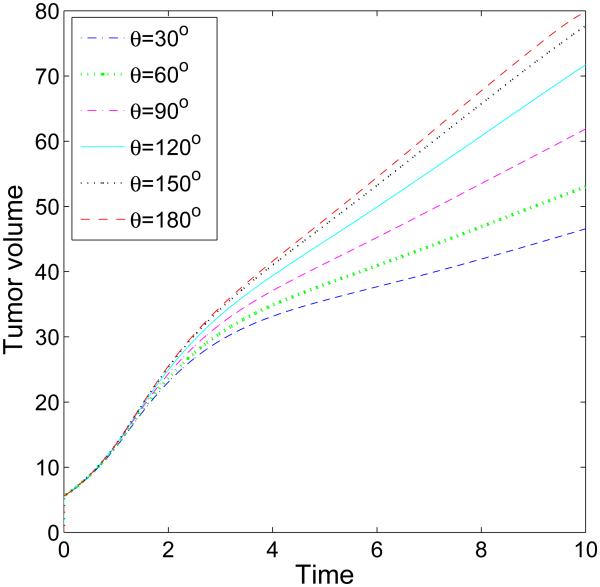
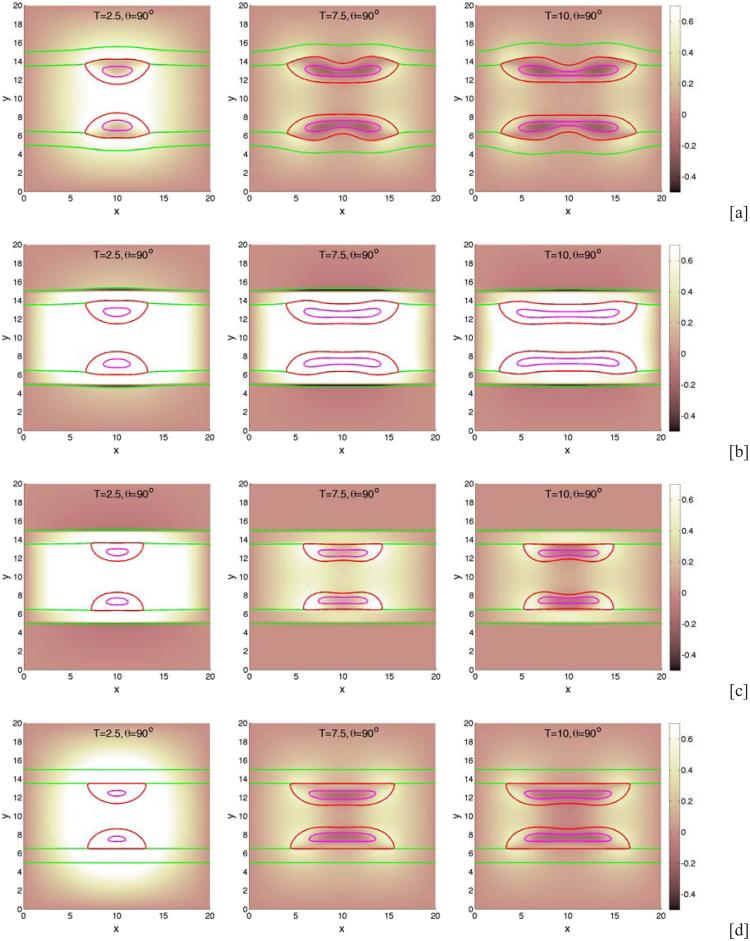
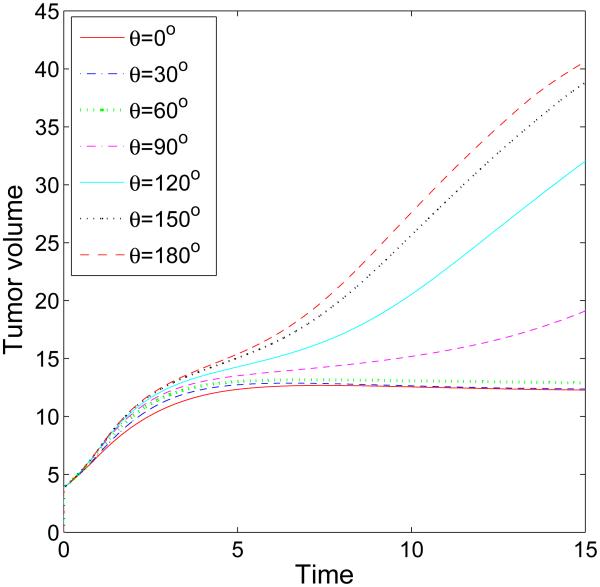
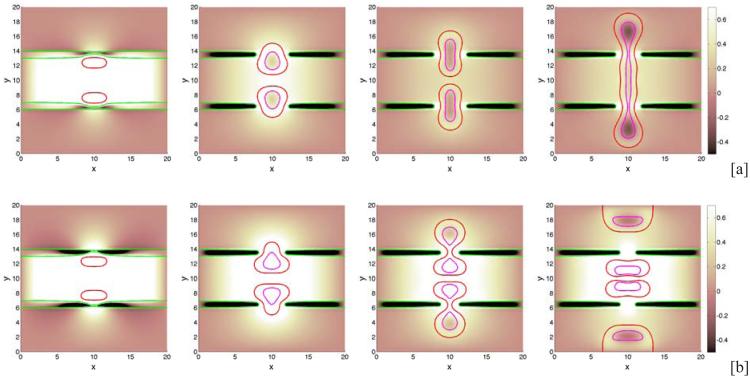
We begin by investigating the dependence of tumor growth on cell-membrane adhesion using the simple duct geometry. We do not consider the production of MDEs or haptotaxis (these are considered later below). We vary the cell-membrane contact angle θ and investigate the evolution of the small tumor clusters. Recall that for θ < 90 °, the tumor cells prefer to adhere to each other rather than to the BM while for θ > 90 °, the tumor cells prefer to adhere to the BM. In Fig. 2, characteristic evolutions of the tumor and BM are shown at different times (columns) for different contact angles (rows; [a]: 30°, [b]: 90°, [c]: 120°) for the simple duct geometry. The locations of the tumor boundaries (red), necrotic cores (magenta) and BM (green) are shown together with the contours of the pressure with levels indicated by the color bar. In Fig. 3, the corresponding contours of the nutrient distribution are shown. As the tumors grow along the BM, the BM deforms due to the pressure exerted by the tumor cells, and nutrient is depleted in the tumor centers and necrotic cores form. At early times duct deforms outward into the stroma while tumor grows along the duct and into the lumen. At later times, dimples form at tumor surface in contact with the membrane. This is due to the necrosis of cells in interior of the tumor clusters due to lack of nutrients, which diffuse in from the stroma. Necrosis generates negative pressures (dark regions in Fig. 2) due to cell death and clearance, and inward cell velocities. As the cell-BM adhesion is increased (e.g., θ increases), the tumors become more elongated and thinner. This in turn increases the availability of nutrients to the tumor cells and decreases the amount of necrosis, which results in smaller dimples. Correspondingly, as quantified in Fig. 4, the size of the tumor clusters is an increasing function of θ. Note that the growth curves of the clusters have inflection points, which are more pronounced when the cell-BM adhesion is high. This occurs when there is a transition from volumetric growth at early times to planar growth along the duct at later times. This is also observed in Fig. 6, which shows the size of the tumor clusters when the membrane stiffness is varied.
Figure 2.
Tumor cluster growth in a 2D simple duct showing the pressure field (background), tumor (red; ϕT = 0.5 contours) and BM (green; ψ = 0.5 contours) and necrotic core (magenta; ϕD = 0.5 contours) for different relative strengths of cell-BM adhesions as labeled via the contact angle θ. Increasing the cell-membrane adhesion by increasing θ leads to thinner, larger, more elongated tumors. [a]: θ = 30°; [b]: θ = 90°; [c]: θ = 120° . The membrane stiffness is A = 0.01, , and other parameters are shown in Table 1. Note that in all simulations, time is measured relative to the mitosis time (e.g., approximately 1 day) and space is measured relative to the diffusion penetration length (e.g., approximately 200μm).
Figure 3.
The nutrient distributions of the tumor cluster growth shown in Fig. 2. Nutrient diffuses from the stroma and is uptaken by tumor cells, leading to lowered nutrient concentrations in the tumor interior and the development of necrotic cores (regions inside the magenta curves).
Figure 4.
The time evolution of the volumes of the tumor clusters shown in Fig. 2 up to T = 10 (days). Increasing cell-BM adhesion by increasing θ leads to larger tumors and faster growth.
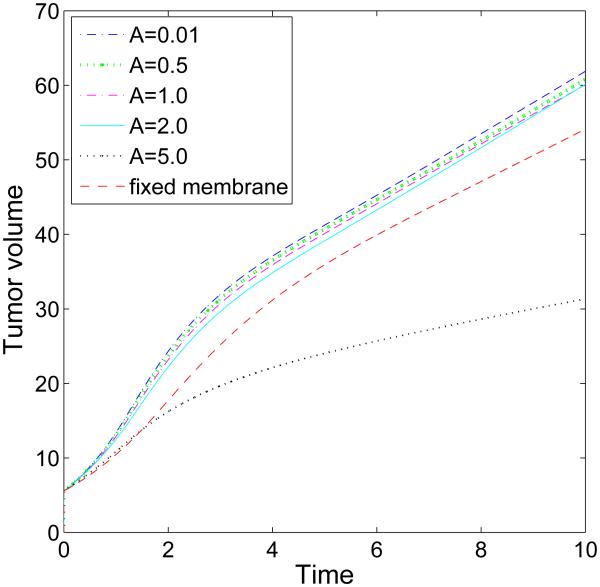
Figure 6.
The evolution of the volumes for the tumor clusters shown in Fig. 5 for different membrane stiffness A as labeled. Generally, the volume is a decreasing function of BM stiffness, although when A = 2.0 the tumor reaches the same size as that with A = 1.0 at time T = 10 (days).
Next, we examine the dependence of tumor growth on the membrane stiffness A. We fix the cell-BM adhesion and take θ = 90°. Characteristic evolutions are shown in Fig. 5 at different times (columns) and for different stiffnesses (rows; [a]: A = 0.01, [b]: A = 2.0, [c]: A = 5.0). In Fig. 5 [d], the BM is not allowed to deform and ψ = ψ is imposed. No BM-generated elastic forces are imparted to the tumor since the membrane energy Eel = 0. The figure shows that as A is increased, the BM deforms less. While the sizes of the tumor clusters are decreasing functions of A (see Fig. 6), the tumor morphologies and areas of necrosis depend non-monotonically on A. In particular, the tumor cluster with A = 2.0 in [b] extends farther along the BM than the cluster with A = 0.01 in [a], even though its overall size is slightly smaller than that in [a]. Further, in [b] and [c] small bands of negative pressure induced by elastic restoring forces from the BM are observed along the outer boundary of the BM, which are more prominent at early times and tend to disappear at later times as the BM flattens. Interestingly, the pressure inside the tumor cluster in [b] is much larger than that those in [a], [c] and [d], which reflects a difference in the overall balance of forces. When the stiffness is increased to A = 5.0, the membrane is nearly flat and the tumor is smaller and more deformed than that with A = 2.0. Compared to the tumor with A = 0.01, the dimple forms on the lumen side of the tumor in [c] rather than the BM side as observed in [a] where the BM is less stiff. Interestingly, in [d] where the membrane is fixed and there are no BM-generated elastic forces, the tumor cluster grows substantially larger than that with A = 5.0 in [c] and is nearly as large as the clusters in [a] and [b]. This is because when the membrane is fixed, there are no resistive forces imparted back to the tumor, and so the clusters grow more freely than those with large A. Further, the 90 ° contact angle between the tumor cluster and BM can be more clearly seen in [d] than the other cases since the BM does not deform.
Figure 5.
The effect of membrane stiffness on growing tumor clusters in 2D simple ducts. The cell-BM adhesiveness is fixed (θ = 90°). The pressure field (background), tumor (red; ϕT = 0.5 contours) and BM (green; ψ = 0.5 contours) and necrotic core (magenta; ϕD = 0.5 contours) are shown for different membrane stiffnesses: [a]: A = 0.01; [b]: A = 2.0; [c]: A = 5.0. In [d], the membrane is not allowed to deform and induce stresses. As A increases, the BM deformation decreases. When the membrane is fixed, there are no restoring forces and tumors grow more freely than those with large A. The contact angle θ = 90°, and other parameters are shown in Table 1.
Branched duct
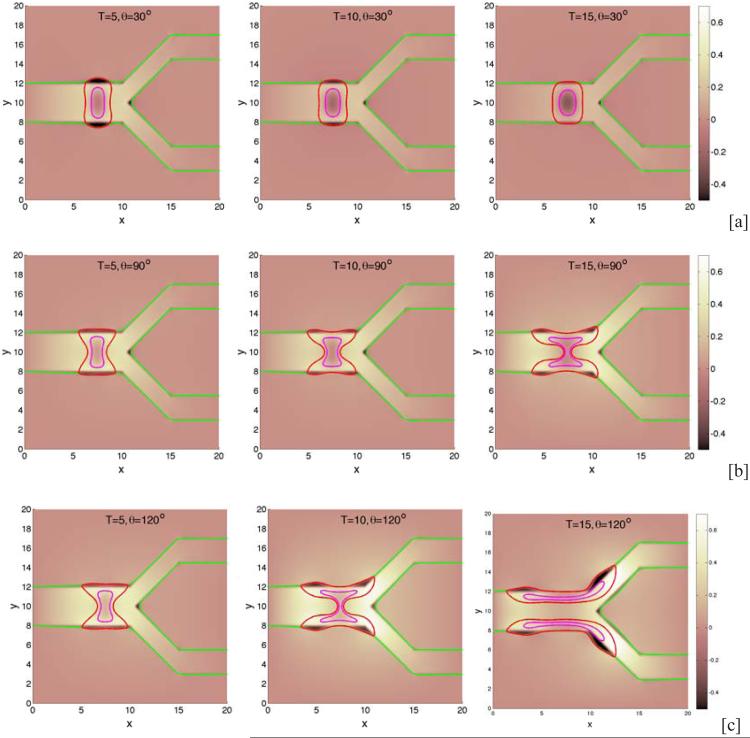
We next consider the evolution of a tumor in a branched duct. As in the single duct case, we do not consider haptotaxis and tumor invasion. In Fig. 7, characteristic tumor cluster and BM morphologies are shown together with the pressure at different times (columns) and different cell-BM adhesivities (rows; [a]: θ = 30 °, [b]: θ = 90°, [c]: θ = 120°). Interestingly, when the cell-BM is small (e.g., θ = 30 °), the tumor grows only at early times and the BM correspondingly deforms outward. At later times, however, the growth of the tumor slows as the forces of growth and necrosis balance those of cell-cell and cell-BM adhesion. The tumor spreads laterally along the BM but only to a limited extent. Eventually, the tumor reaches a steady configuration with the BM only being slightly deformed. When cell-BM adhesiveness is increased, the clusters eventually begin to grow continuously. An analysis of the volumes of the tumor clusters (see Fig. 8) indicates that the transition to growth occurs for θ between 60 ° and 90° and that tumor size positively correlates with cell-BM adhesiveness. As the clusters start to grow, necks form in the center of the clusters due to negative pressures that arise from cell death and clearance. Eventually, the necks pinch off and the clusters grow along the BM in both the primary and secondary branches. The pinch off events are controlled by the relative strengths of cell-cell and cell-membrane adhesion, the membrane stiffness, and the rates of cell proliferation, necrosis and clearance. Generally, increasing the cell-membrane adhesiveness increases the tendency of the clusters to pinchoff. As observed earlier, there is an inflection point in the growth curves at sufficiently large cell-BM adhesiveness because of the change from volumetric to planar growth of the tumor clusters. Negative pressures are also observed along the BM near the tumor cluster, and at the BM branch points, induced by the BM elastic restoring forces. The effect of BM stiffness on tumor and BM evolution is similar to that presented in Fig. 5 for the simple duct and thus is not shown here for the branched duct.
Figure 7.
The evolution of tumor clusters in 2D branched ducts. The pressure (background), tumor (red; ϕT = 0.5 contours), membrane (green; ψ = 0.5 contours) and necrotic cores (magenta; ϕD = 0.5 contours) are shown for different relative strengths of cell-membrane adhesions as labeled via the contact angle θ: [a]: θ = 30° ; [b]: θ = 90° ; [c]: θ = 120°. The membrane stiffness is A = 1, see Table 1 for the other parameters. When the cell-BM adhesion is low, the tumors grow at early times but growth is not sustained and the tumors progress to a steady state. Increasing cell-BM adhesion leads to larger, more elongated tumors and to fragmentation.
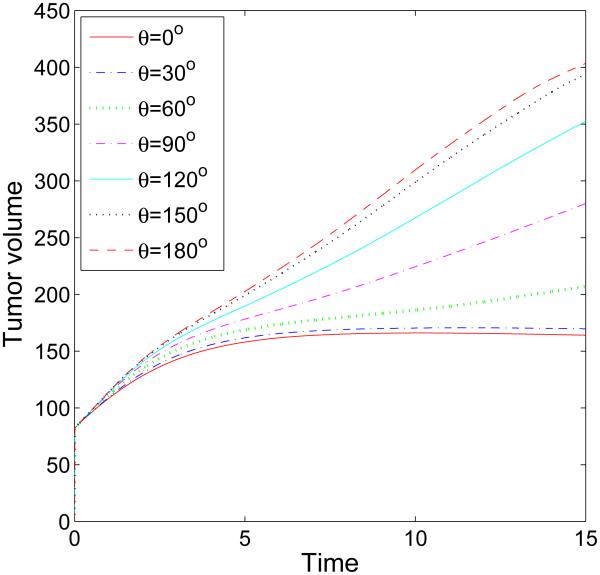
Figure 8.
The evolution of the volumes of the tumor clusters shown in Fig. 7 for different cell-membrane adhesion strengths, as labeled, up to T = 15 (days). The threshold adhesion between the progression to steady-states and sustained growth occurs between θ = 60° and θ = 90°.
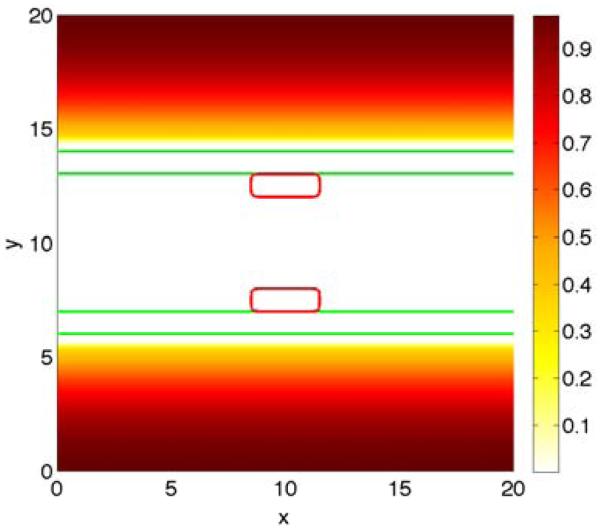
Tumor invasion
We next investigate tumor invasion into the stroma. We use the simple duct geometry and the initial condition for the tumor clusters, the BM and the ECM are shown in Fig. 9. Although we have taken a symmetric initial condition for simplicity, our model approach allows for asymmetric initial data and asymmetric evolution. Interestingly, we find that in order to be able to simulate tumor invasion numerically the cell-BM adhesion needs to be downregulated, which is consistent with experimental observations (e.g., Liotta et al., 1991; Perl et al., 1998; Wolf et al., 2007; Ilina et al, 2011). Here, we took θ = 0°, which seems to be required to simulate invasion of the stroma. In Fig. 10, the evolution of the tumor clusters and BMs are shown. In [a], the BM stiffness is A = 10 while in [b] the stiffness is A = 20. At early times, the MDEs secreted by tumor cells degrade the BM and the tumor cells detach from the BM. Eventually, the BMs are degraded and small holes form connecting the lumen with the stroma. Note that the interior part of the BM reconnects with the exterior part. Once the BM is breached, the tumor clusters squeeze through the opening, grow and migrate haptotactically into the stroma. As this process occurs, strong negative pressures develop in the BM interior due to elastic restoring forces and as a result, the hole width decreases at later times. This is particularly noticeable in [b] where the BM stiffness is larger. In [a], where A = 10, the hole in the basement membrane is larger than that in [b] where A = 20. Further, in [a] the tumor clusters connect across the lumen which limits the rate of local invasion. In [b], where A = 20, the tumor develops a narrow neck that pinches off as it squeezes through the opening in the BM. The resulting fragments grow, migrate and invade farther into the stroma than when A is small.
Figure 9.
The initial shape of tumor clusters (red; ϕT = 0.5 contours) and basement membranes (green; ψ = 0.5 contours) and ECM distribution in the 2D invasive simulations.
Figure 10.
Invasion of the stroma by tumor clusters in 2D simple ducts for different membrane stiffnesses: [a] A = 10; [b]: A = 20. In each case, the cell-BM adhesion θ = 0. The pressure (background), tumor (red; ϕT = 0.5 contours), membrane (green; ψ = 0.5 contours) and necrotic core (magenta; ϕD = 0.5 contours) are shown. A smaller membrane stiffness ([a]) leads to limited invasion and a larger membrane stiffness ([b]) leads to more invasive tumors. see Table 1 for other parameters.
3.2. Three dimensional results
We now investigate tumor growth and invasion in three dimensions by exploiting the fact that our methodology is independent of the number of space dimensions and of the geometries of the tumor and microenvironment. We first simulate tumor progression in a branched duct and then we close by modeling tumor invasion of the stroma from a simple duct.
Branched duct
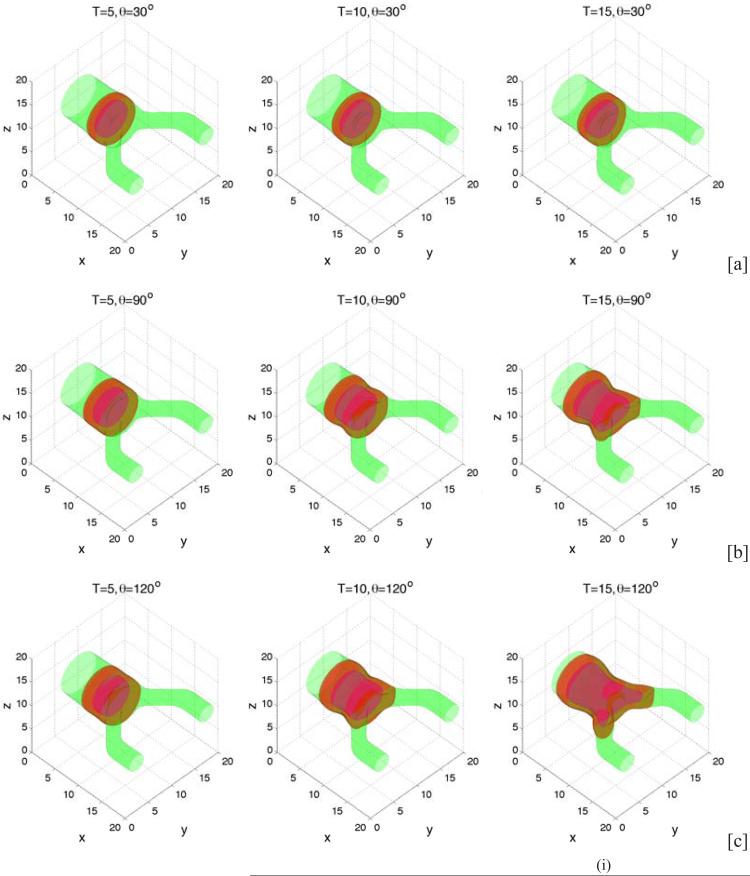
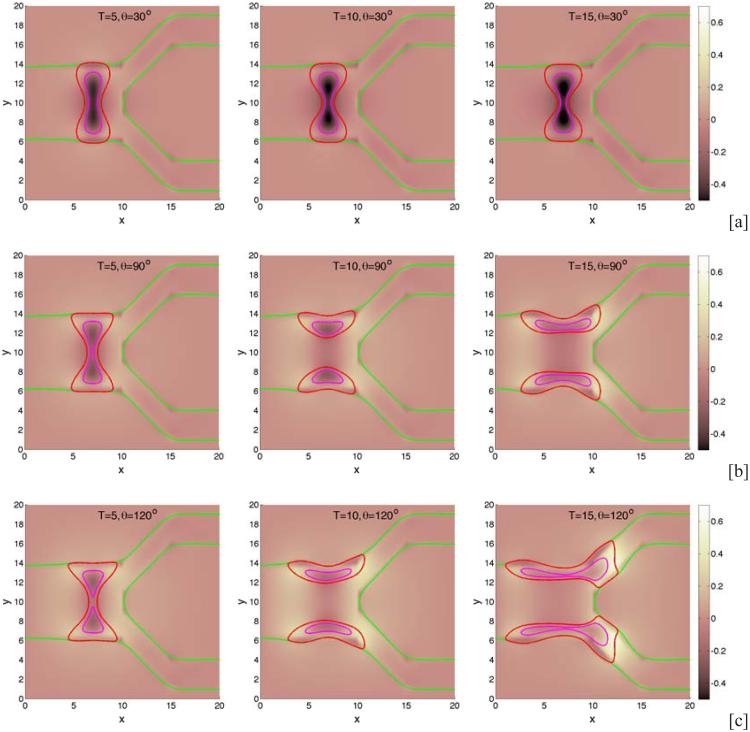
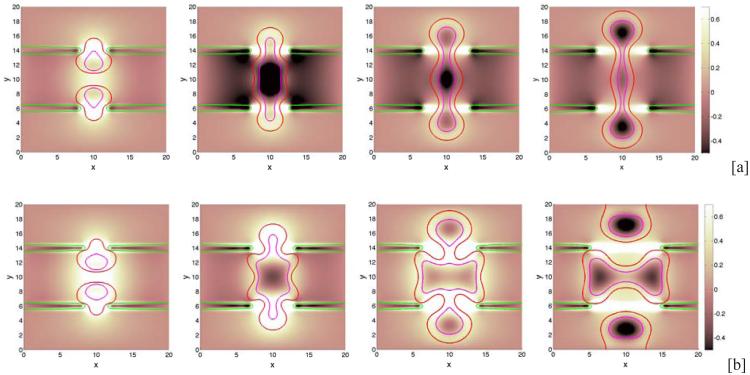
Extending the two dimensional configuration to three dimensions, we consider an initial condition consisting of a tumor cluster that has grown across the primary lumen. The lumens of the secondary branches are smaller than that of the primary branch with the ratio between their radii being 2.4. The configuration is shown in Fig. 11 where on the left, the tumor (red) is shown via the isosurface ϕT = 0.5 and the BM (green) corresponds to the isosurface ψ = 0.5. In Fig. 11 (right), a two-dimensional cross-section along the center plane (z = 10) of the three dimensional geometry is shown. In Figs. 12 and 13, which show three-dimensional results and the corresponding two-dimensional cross-sections respectively, we present characteristic tumor and BM evolutions using different cell-BM adhesiveness (rows: [a]: θ = 30°, [b]: θ = 90°, [c]: θ = 120°). As in two-dimensions, when the cell-BM adhesiveness is small (θ = 30° in [a]), the tumor grows initially before reaching a dynamic equilibrium that reflects the balance of forces. The two-dimensional slices in Fig. 13, which also show the pressure distributions, reveal that the tumor clusters develop necks due to cell necrosis and clearance that lead to negative pressures (dark regions) and to inward cell velocities. When the cell-BM adhesion is increased the tumor clusters eventually start to grow continuously. As can be seen in Fig. 14, which shows the tumor volumes, the transition to growth occurs between θ = 30 ° and θ = 60°, which suggests that continuous growth in three dimensions may occur at smaller cell-BM adhesiveness than that needed in two dimensions. As in two dimensions, tumor size is positively correlated with cell-BM adhesion. Our results also show that in three dimensions the necks pinchoff more readily than in two dimensions, which is to be expected from the additional radius of curvature, and that the tumor clusters grow continuously along the BM through both the primary and secondary ducts, and dimples form at the tumor-BM interface. In [c], where θ = 120 °, the tumor cluster grows across the lumen in the secondary duct and attaches to the inner BM.
Figure 11.
The initial tumor cluster (red; ϕT = 0.5 isosurfaces) and BM geometries (green; ψ = 0.5 isosurfaces) in a branched duct in 3D. Left: 3D geometry, Right: a two-dimensional cross-section along the center plane z = 10. As in 2D, the membrane thickness is modeled by explicit representation of the inner and outer boundaries.
Figure 12.
Evolution of tumor clusters in 3D branched ducts showing the tumor (red; ϕT = 0.5 isosurfaces), membrane (green; ψ = 0.5 isosurfaces) and necrotic core (magenta; ϕD = 0.5 isosurfaces) for different relative strengths of cell-membrane adhesions: [a]: θ = 30° ; [b]: θ = 90°; [c]: θ = 120° . In all cases A = 0.5. As in 2D (Fig. 7) when the cell-BM adhesion is low, growth ceases while at large cell-BM adhesions, growth is sustained.
Figure 13.
Two-dimensional cross-sections (z = 10) of the tumor clusters shown in Fig. 12.
Figure 14.
The evolution of the volumes of the tumor clusters shown in Fig. 12 for different cell-BM adhesion strengths, as labeled, up to T = 15 (days). The transition between progression to steady-states and sustained growth occurs between θ = 30° and θ = 60°.
Tumor invasion
We conclude our investigation of three dimensional tumor growth by modeling tumor invasion into the stroma using a simple duct geometry. Analogous to the two-dimensional study we presented in Sec. 3.1, we consider the evolution of a thin torus of tumor cells that is attached to a cylindrical BM, see Fig. 15 (left). As in 2D, we have taken a symmetric initial condition although our model allows general configurations. Fig. 15 (right) shows a two-dimensional cross-section of the tumor cells, ECM distribution and BM along the center plane (z = 10). As in two dimensions, cell-BM adhesion is down regulated (θ = 0 °) and the evolution of the tumor clusters is investigated as a function of BM stiffness. The results are presented in Figs. 16 and 17, which show the evolution in three dimensions and in two-dimension cross-sections together with the contours of the pressure, respectively. In [a], the BM stiffness A = 10 while in [b] A = 20. Overall, the results are similar to that observed in two dimensions, although the details of the evolution are a little different. As in two dimensions the tumors squeeze through the openings that form in the BM under the action of tumor-secreted MDEs. When A = 10, the reconnection of the tumors across the lumen reduces the rate of local invasion compared to that observed when the BM is stiffer (A = 20). Interestingly, when A = 20, the tumor fragment that remains in the lumen does not undergo a secondary break-up as in two dimensions but instead grows substantially and forces the opening in the BM to become even wider than that when A = 10. This increases the probability that another tumor fragment may invade the stroma at a later time.
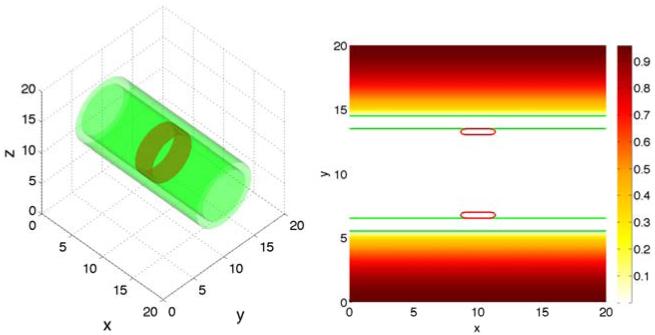
Figure 15.
The initial tumor cluster (red: ϕT = 0.5 isosurfaces) and BM geometries (green; ψ = 0.5 isosurfaces) in a simple duct in 3D. Left: 3D geometry, Right: a two-dimensional cross-section along the center plane z = 10.
Figure 16.
Invasion of the stroma by tumor clusters in 3D simple ducts for different membrane stiffnesses: [a] A = 10; [b]: A = 20. In each case, the cell-BM adhesion θ = 0. The tumor (red; ϕT = 0.5 isosurfaces), membrane (green; ψ = 0.5 isosurfaces) and necrotic core (magenta; ϕD = 0.5 isosurfaces) are shown. As in 2D, a smaller membrane stiffness ([a]) leads to limited invasion and a larger membrane stiffness ([b]) leads to more invasive tumors (see Fig. 17). see Table 2 for other parameters.
Figure 17.
Two-dimensional cross-sections (z = 10) of the simulations shown in Fig. 16, together with the corresponding pressure distribution (background).
4. Conclusion
We have developed a mathematical model of tumor growth in complex, dynamic geometries with elastic, deformable membranes using a diffuse domain approach (e.g., Li et al., 2009; Teigen et al., 2009; Teigen et al., 2011; Aland et al., 2010). In this methodology, the complex domain was captured implicitly using an auxiliary function and the governing equations were appropriately modified, extended and solved in a larger, regular domain. The boundary conditions appeared as singular source terms in the reformulated equations. The diffuse domain method facilitated an efficient numerical implementation that did not depend on the space dimension or on the geometry of the microenvironment. Although we considered simple and symmetric geometries in this paper, the model is in no way limited in this respect and can handle any microenvironmental or tumor geometry that can be represented implicitly as a level surface of a function.
We applied this framework to a mixture model of tumor growth in duct-like geometries in two and three dimensions. Such geometries arise in ductal carcinoma. We modeled homotypic cell-cell adhesion and heterotypic cell-BM adhesion with the latter being implemented via an effective contact angle between the tumor cluster and BM that arises from differences in adhesion energies. We incorporated simple models of elastic forces and the degradation of the BM and ECM by tumor-secreted matrix degrading enzymes. We investigated tumor progression and BM response as a function of cell-BM adhesion and the stiffness of the BM. We found that tumor sizes tend to be positively correlated with cell-BM adhesion since increasing cell-BM adhesion results in thinner, more elongated tumors that are easier for nutrients to penetrate. Prior to invasion of the tumor into the stroma, we found a negative correlation between tumor size and BM stiffness as the elastic restoring forces tend to inhibit tumor growth. The details of the deformation and pressure fields were found to be non-monotone, however.
In order to model tumor invasion of the stroma, we found it necessary to downregulate cell-BM adhesiveness, which is consistent with experimental observations (e.g., Liotta et al., 1991; Perl et al., 1998; Wolf et al., 2007; Ilina et al, 2011). We found a positive correlation between tumor invasiveness and BM stiffness. A stiff BM was found to promote invasiveness because at early stages the opening in the BM tends to be narrower when the BM is stiffer. This requires invading cells to squeeze through the narrow opening and thus promotes fragmentation that then leads to enhanced growth and invasion. In three dimensions, the opening in the BM was found to increase in size even when the BM is stiff because of pressure induced by growing tumor clusters. This could allow a second wave of invasive tumor cells to penetrate the stroma.
There are several ways in which the methodology described in this paper can be extended. First, the model of BM-induced forces can be made more realistic. For example, bending forces induced by the BM could be incorporated using a Helfrich-like model (Helfrich, 1973; Du et al., 2004; Torabi et al., 2009). Such a model, however, introduces higher-order derivatives and requires the development of new, stable numerical methods to simulate the dynamics of the nonlinear system efficiently. Second, local elastic stresses can be included following the approach described in Bresch et al. (2010) and Cottet et al. (2004). Third, additional cellular biophysical processes can be incorporated and specific tumor types can be modeled. For example, the framework developed here can be extended to model ductal carcinoma in situ (DCIS), which is the most common type of non-invasive breast cancer in women. In DCIS, the surface receptors e.g., E-cadherins and integrins, and subcellular structures degrade, the cell loses its liquid volume, and calcium is deposited in its solid fraction. Following the spirit of Macklin et al. (2012), who developed a mechanistic agent-based model, one can develop a continuum model for microcalcification and couple this model to the diffuse-domain framework developed herein to investigate the effect of a dynamic BM on DCIS. The model can then be used to estimate how far the tumor extends beyond the microcalcification, which is a critical variable for treatment.
Supplementary Material
Acknowledgements
YC and JL acknowledge partial funding from the National Science Foundation-Division of Mathematical Sciences (NSF-DMS). JL additionally acknowledges partial funding from the National Institutes of Health (NIH) through grant P50GM76516 for a Center of Excellence in Systems Biology at the University of California, Irvine, and NIH grant P30CA062203 for the Chao Comprehensive Cancer Center at the University of California, Irvine.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Ying Chen, Department of Mathematics, University of California, Irvine, USA.
John S. Lowengrub, Department of Mathematics Department of Biomedical Engineering Center for Complex Biological Systems University of California, Irvine, USA.
References
- 1.Aland S, Lowengrub J, Voigt A. Two-phase flow in complex geometries: A diffuse domain approach. CMES. 2010;57:77–106. [PMC free article] [PubMed] [Google Scholar]
- 2.Albini A, Sporn MB. The tumor microenvironment as a target for chemoprevention. Nat. Rev. Cancer. 2007;7:139–147. doi: 10.1038/nrc2067. [DOI] [PubMed] [Google Scholar]
- 3.Ambrosi D, Duperray A, Prschetola V, Verdier C. Traction patterns of tumor cells. J. Math. Biol. 2009;58:163–181. doi: 10.1007/s00285-008-0167-1. [DOI] [PubMed] [Google Scholar]
- 4.Ambrosi D, Presiosi L. On the closure of mass balance models for tumor growth. Math. Mod. Meth. Appl. Sci. 2002;12(5):737–754. [Google Scholar]
- 5.Ambrosi D, Preziosi L. Cell adhesion mechanisms and stress relaxation in the mechanics of tumours. Biomech. Model. Mechanobiol. 2009;8:397–413. doi: 10.1007/s10237-008-0145-y. [DOI] [PubMed] [Google Scholar]
- 6.Anderson ARA, Quaranta V. Integrative mathematical oncology. Nat. Rev. Cancer. 2008;8:227–244. doi: 10.1038/nrc2329. [DOI] [PubMed] [Google Scholar]
- 7.Araujo RP, McElwain DLS. A mixture theory for the genesis of residual stresses in growing tissues I: A general formulation. SIAM J. Appl. Math. 2005a;65:1261–1284. [Google Scholar]
- 8.Araujo RP, McElwain DLS. A mixture theory for the genesis of residual stresses in growing tissues II: solutions to the biphasic equations for a multicell spheroid. SIAM J. Appl. Math. 2005b;66:447–467. [Google Scholar]
- 9.Armstrong NJ, Painter KJ, Sherratt JA. Adding adhesion to a chemical signaling model for somite formation. Bull. Math. Biol. 2009;71:1–24. doi: 10.1007/s11538-008-9350-1. [DOI] [PubMed] [Google Scholar]
- 10.Baldock AL, Rockne RC, Boone AD, Neal ML, Hawkins-Daarud A, orwin DM, Bridge CA, Guyman LA, Trister AD, Mrugala MM, Rockhill JK, Swanson KR. From patient-specific mathematical neuro-oncology to precision medicine. Front. Oncol. 2013 doi: 10.3389/fonc.2013.00062. doi: 10.3389/fonc.2013.00062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bellomo N, Li NK, Maini PK. On the foundations of cancer modeling: selected topics, speculations, and perspective. Math. Models Methods Appl. Sci. 2008;4:593–646. [Google Scholar]
- 12.Bresch D, Colin T, Grenier E, Ribba B, Saut O. Computational modeling of solid tumor growth: the avascular stage. SIAM J. Sci. Comput. 2010;32(4):2321–2344. [Google Scholar]
- 13.Breward C, Byrne H, Lewis C. The role of cell-cell interaction in a two-phase model for avascular tumour growth. J. Math. Biol. 2002;45:125–152. doi: 10.1007/s002850200149. [DOI] [PubMed] [Google Scholar]
- 14.Breward C, Byrne H, Lewis C. A multiphase model describing vascular tumor growth. Bull. Math. Biol. 2003;65:609–640. doi: 10.1016/S0092-8240(03)00027-2. [DOI] [PubMed] [Google Scholar]
- 15.Byrne HM. Dissecting cancer through mathematics: from the cell to the animal model. Nat. Rev. Cancer. 2010;10(3):221–30. doi: 10.1038/nrc2808. [DOI] [PubMed] [Google Scholar]
- 16.Byrne HM, Alarcón T, Owne MR, Webb SD, Maini PK. Modeling aspects of cancer dynamics: a review. Philos. Trans.R.Soc A. 2006;364:1563–1578. doi: 10.1098/rsta.2006.1786. [DOI] [PubMed] [Google Scholar]
- 17.Byrne H, King J, McElwain D, Preziosi L. A two-phase model of solid tumour growth. Appl. Math. Lett. 2003;16:567–573. [Google Scholar]
- 18.Byrne H, Preziosi L. Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. 2003;20:341–366. doi: 10.1093/imammb/20.4.341. [DOI] [PubMed] [Google Scholar]
- 19.Carter SB. Principles of cell motility: the direction of cell movement and cancer invasion. Nature. 1965;208:1183–1187. doi: 10.1038/2081183a0. [DOI] [PubMed] [Google Scholar]
- 20.Chaplain MAJ, Graziano L, Presiosi L. mathematical modelling of the loss of tissue compression responsiveness and its role in solid tumour development. Math. Med. Biol. 2006a;23:192–229. doi: 10.1093/imammb/dql009. [DOI] [PubMed] [Google Scholar]
- 21.Chaplain MAJ, Lolas G. Mathematical modeling of cancer invasion of tissue: dynamic heterogeneity. Net. Hetero. Med. 2006b;1(3):399–439. [Google Scholar]
- 22.Chen Y. 2012. Ph.D. Thesis. University of California at Irvine.
- 23.Chen Y, Wise SM, Shenoy V, Lowengrub J. A stable scheme for a nonlinear, multiphase tumor growth model with an elastic membrane. Int. J. Numer. Meth. Biomed. Engng. 2013 doi: 10.1002/cnm.2624. doi: 10.1002/cnm.2624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cottet GH, Maitre E. A level-set formulation of immersed boundary methods for fluid-structure interaction problems. C.R. Acad. Sci. Paris, Ser. I. 2004;338:581–586. [Google Scholar]
- 25.Cristini V, Frieboes H, Li X, Lowengrub J, Macklin P, Sanga S, Wise S, Zheng X. Nonlinear modeling and simulation of tumor growth. In: Bellomo N, Chaplain M, De Angelis E, editors. Selected topics in Cancer Modeling: Genesis, Evolution, Immune Competition, and Therapy, in: Modeling and Simulation in Science, Engineering and Technology. Birkhäuser; Boston: 2008. [Google Scholar]
- 26.Cristini V, Li X, Lowengrub J, Wise S. Nonlinear simulations of solid tumor growth using a mixture model: invasion and branching. J. Math. Biol. 2009;58:723–763. doi: 10.1007/s00285-008-0215-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cristini V, Lowengrub JS. An integrated experimental and mathematical modeling approach. Cambridge University Press; 2010. Multiscale modeling of cancer. [Google Scholar]
- 28.Cristini V, Lowengrub J, Nie Q. Nonlinear simulation of tumor growth. J. Math. Biol. 2003;46:191–224. doi: 10.1007/s00285-002-0174-6. [DOI] [PubMed] [Google Scholar]
- 29.Deisboeck TS, Zhang X, Yoon J, Costa J. In silico cancer modeling: is it ready for prime time? Nat. Clin. Pract. Oncol. 2009;6:34–42. doi: 10.1038/ncponc1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Deisboeck TS, Wang ZH, Macklin P, Cristini V. Multiscale Cancer Modeling. Annu. Rev. Biomed. Eng. 2011;13:127–55. doi: 10.1146/annurev-bioeng-071910-124729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Derksen PW, Liu X, Sariden F, van der Gulden H, Zevenhoven J, Evers B, van Beijnum JR, Griffioen AW, Vink J, Krimpenfort P, Peterse JL, Cardiff RD, Berns A, Jonkers J. Somatic inactivation of E-cadherin and p53 in mice leads to metastatic lobular mammary carcinoma through induction of anoikis resistance and angiogenesis. Cancer Cell. 2006;10:437–449. doi: 10.1016/j.ccr.2006.09.013. [DOI] [PubMed] [Google Scholar]
- 32.Do-Quang M, Amberg G. The splash of a solid sphere impacting on a liquid surface: Numerical simulation of the influence of wetting. Physics of Fluids. 2009;21:022102. [Google Scholar]
- 33.Drasdo D, Höhme S. On the role of physics in the growth and pattern formation of multicellular systems: what we learn from individual-cell based models? J. Stat. Phys. 2007;128:287–345. [Google Scholar]
- 34.Du Q, Liu C, Wang X. A phase field approach in the numerical study of bending energy for vesicle membranes. J. Comput. Phys. 2004;198:450–468. [Google Scholar]
- 35.DuFort CC, Paszek MJ, Weaver VM. Balancing forces: architectural control of mechanotransduction. Nat. Rev. Mol. Cell Biol. 2011;12:308–319. doi: 10.1038/nrm3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fang H, DeClerck YA. Targeting the tumor microenvironment: From understanding pathways to effective clinical trials. Cancer Res. 2013;73:4965–4977. doi: 10.1158/0008-5472.CAN-13-0661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fasano A, Bertuzzi A, Gandolfi A. Mathematical modeling of tumour growth and treatment, in: Complex system in Biomedicine. Springer, Milan; 2006. pp. 71–108. [Google Scholar]
- 38.Franks S, Byrne H, King J, Underwood J, Lewis C. Modeling the early growth of ductal carcinoma in situ of the breast. J. Math. Biol. 2003a;47:424–452. doi: 10.1007/s00285-003-0214-x. [DOI] [PubMed] [Google Scholar]
- 39.Franks S, Byrne H, Mudhar H, Underwood J, Lewis C. Mathematical modeling of comedo ductal carcinoma in situ of the breast. Math. med. Biol. 2003b;20:277–308. doi: 10.1093/imammb/20.3.277. [DOI] [PubMed] [Google Scholar]
- 40.Frieboes HB, Chaplain MAJ, Thompson AM, Bearer EL, Lowengrub JL, Cristini V. Physical oncology: A bench-to-bedside quantitative and predictive approach. Cancer Res. 2011;71:298–302. doi: 10.1158/0008-5472.CAN-10-2676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Frieboes HB, Jin F, Chuang Y-L, Wise SM, Lowengrub JS, Cristini V. Three-dimensional multispecies nonlinear tumor growth-II: tumor invasion and angiogenesis. J. Theor. Biol. 2010;264:1254–1278. doi: 10.1016/j.jtbi.2010.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Friedl P, Alexander S. Cancer invasion and the microenvironment: plasticity and Receprocity. Cell. 2011;147:992–1009. doi: 10.1016/j.cell.2011.11.016. [DOI] [PubMed] [Google Scholar]
- 43.Friedl P, Wolf K. Tumour-Cell Invasion and Migration: Diversity and Escape Mechanisms. Nat. Rev. Cancer. 2003;3:362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- 44.Friedman A, Bellomo N, Maini PK. Mathematical analysis and challenges arising from models of tumor growth. Math. Models Methods Appl. Sci. 2007;17:1751–1772. [Google Scholar]
- 45.Giverso C, Scianna M, Preziosi L, Lo Buono N, Funaro A. Individual cell-based model for in-vitro mesothelial invasion of ovarian cancer. Math. Model. Nat. Phenom. 2010;5:1–21. [Google Scholar]
- 46.Granasy L, Pusztai T, Saylor D, Warren JA. Phase field theory of heterogeneous crystal nucleation. Phys. Rev. Lett. 2007;98:035703. doi: 10.1103/PhysRevLett.98.035703. [DOI] [PubMed] [Google Scholar]
- 47.Graziano L, Preziosi L. Mechanics in tumor growth. In: Mollica F, Rajagopal KR, Preziosi L, editors. Modeling of Biological Materials. Birkhäuser; Basel: 2007. pp. 267–328. [Google Scholar]
- 48.Harpold HL, Alvord EC, Jr., Swanson KR. The evolution of mathematical modeling of glioma proliferation and invasion. J.. Neuropathol. Exp. Neurol. 2007;66:1–9. doi: 10.1097/nen.0b013e31802d9000. [DOI] [PubMed] [Google Scholar]
- 49.Hatzikirou H, Chauviere A, Bauer AL, Leier A, Lewis MT, Macklin P, Marquez-Lago TT, Bearer EL, Cristini V. Integrative physical oncology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2012;4(1):1–14. doi: 10.1002/wsbm.158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hatzikirou H, Deutsch A, Schaller C, Simon M, Swanson K. Mathematical modeling of glioblastoma tumour development: a review. Math. Models Methods Appl. Sci. 2005;15:1779–1794. [Google Scholar]
- 51.Hawkins-Daarud A, Van der Zee KG, Oden JT. Numerical simulation of a thermodynamically consistent four-species tumor growth model. Int. J. Numer. Methods Biomed. Eng. 2012;28:3–24. doi: 10.1002/cnm.1467. [DOI] [PubMed] [Google Scholar]
- 52.Helfrich W. Elastic properties of lipid bilayers- theory and possible experiments. Zeitschrift für Naturforschung C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 53.Hood JD, Cheresh DA. Role of integrins in cell invasion and migration. Nat. Rev. Cancer. 2002;2:91–100. doi: 10.1038/nrc727. [DOI] [PubMed] [Google Scholar]
- 54.Howe EN, Cochrane DR, Richter JK. Targets of miR-200c mediate suppression of cell motility and anoikis resistance. Breast Cancer Res. 2011;13:R45. doi: 10.1186/bcr2867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ilina O, Bakker G, Vasaturo A, Hoffman RM, Friedl P. Two-photon laser-generated microtracks in 3. collagen lattices: principles of MMP-dependent and -independent collective cancer cell invasion. Phys. Biol. 2011;8:015010. doi: 10.1088/1478-3975/8/1/015010. [DOI] [PubMed] [Google Scholar]
- 56.Jacqmin D. Calculation of two-phase Navier-Stokes flows using phase-field modeling. J. Comput. Phys. 1999;155:96–127. [Google Scholar]
- 57.Jiang GS, Shu C-W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996;126:202–228. [Google Scholar]
- 58.Joyce JA, Pollard JW. Microenvironmental regulation of metastasis. Nat. Rev. Cancer. 2009;9:239–252. doi: 10.1038/nrc2618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kam Y, Rejiak KA, Anderson AR. Cellular modeling of cancer invasion: integration of in silico and in vitro approaches. J. Cell Physiol. 2012;227(2):431–9. doi: 10.1002/jcp.22766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Katira P, Bonnecaze RT, Zaman MH. Modeling the mechanics of cancer: effect of changes in cellular and extra-cellular mechanical properties. Front. Oncol. 2013;3:145. doi: 10.3389/fonc.2013.00145. dpi: 10.3389/fonc.2013.00145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kim Y, Stolarska MA, Othmer HG. The role of the microenvironment in tumor growth and invasion. Prog. Biophys. Mol. Biol. 2011;106:353–379. doi: 10.1016/j.pbiomolbio.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Klominek J, Robert KH, Sundqvist K-G. Chemotaxis and haptotaxis of human malignant mesothelioma cells: e?ects of fibronectin, laminin, type IV collagen, and an autocrine motility factor-like substance. Cancer Res. 1993;53:4376–4382. [PubMed] [Google Scholar]
- 63.Lacovara J, Cramer EB, Quigley JP. Fibronectin enhancement of directed migration of B16 melanoma cells. Cancer Res. 1984;44:1657–1663. [PubMed] [Google Scholar]
- 64.Li H, Fan X, Houghton J. Tumor microenvironment: the role of the tumor stroma in cancer. J. Cell. Biochem. 2007;101(4):805–15. doi: 10.1002/jcb.21159. [DOI] [PubMed] [Google Scholar]
- 65.Li X, Cristini V, Nie Q, Lowengrub JS. Nonlinear three-dimensional simulation of solid tumor growth. Disc. Cont. Dyn. Sys. B. 2007;7(3):581–604. [Google Scholar]
- 66.Li X, Lowengrub J, Räez A, Voigt A. Solving PDEs in complex geometries: A diffusion domain approach. Commun. Math. Sci. 2009;7:81–107. doi: 10.4310/cms.2009.v7.n1.a4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Liotta LA, Nageswara R, Wewer UM. Biochemical interactions of tumor cells with the basement membrane. Ann. Rev. Biochem. 1986;55:1037–57. doi: 10.1146/annurev.bi.55.070186.005133. [DOI] [PubMed] [Google Scholar]
- 68.Liotta LA, Stetler-Stevenson WG. Tumor invasion and metastasis: an imbalance of positive and negative regulation. Cancer Res. 1991;51:5054s–5059s. [PubMed] [Google Scholar]
- 69.Lowengrub J, Frieboes H, Jin F, Chuang Y-L, Li X, Macklin P, Wise S, Cristini V. Nonlinear modeling of cancer: bridging the gap between cells and tumors. Nonlinearity. 2010;23:R1–R91. doi: 10.1088/0951-7715/23/1/r01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Macklin P, Edgerton ME, Thompson AM, Cristini V. Patient-calibrated agent-based modeling of ductal carcinoma in situ (DCIS): From microscopic measurements to macroscopic predictions of clinical progression. J. Theor. Biol. 2012;301:122–140. doi: 10.1016/j.jtbi.2012.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Macklin P, Lowengrub J. Nonlinear simulation of the effect of microenvironment on tumor growth. J. Theor. Biol. 2007;245:677–704. doi: 10.1016/j.jtbi.2006.12.004. [DOI] [PubMed] [Google Scholar]
- 72.Macklin P, McDougall S, Anderson A, Chaplain M, Cristini V, Lowengrub J. Multiscale modeling and nonlinear simulation of vascular tumour growth. J. Math. Biol. 2009;58:765–798. doi: 10.1007/s00285-008-0216-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.McCarthy JB, Furcht LT. Laminin and fibronectin promote the directed migration of B16 melanoma cells in vitro. J. Cell Biol. 1984;98:1474–1480. doi: 10.1083/jcb.98.4.1474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Mueller MM, Fusenig NE. Friends or foes – Bipolar effects of the tumour stroma in cancer. Nat. Rev. Cancer. 2004;4:839–49. doi: 10.1038/nrc1477. [DOI] [PubMed] [Google Scholar]
- 75.Nagy JD. The ecology and evolutionary biology of cancer: a review of mathematical models of necrosis and tumor cell diversity. Math. Biosci. Eng. 2005;2:381–418. doi: 10.3934/mbe.2005.2.381. [DOI] [PubMed] [Google Scholar]
- 76.Perl A, Wilgenbus P, Dahl U, Semb H, Christofori G. A causal role for E-cadherin in the transition from adenoma to carcinoma. Nature. 1998;392:190–193. doi: 10.1038/32433. [DOI] [PubMed] [Google Scholar]
- 77.Pickup M, Novitskiy S, Moses HL. The role of TGFβ in the tumor microenvironment. Nat. Rev. Cancer. 2013;13:788–799. doi: 10.1038/nrc3603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Place AE, Huh SJ, Polyak K. The microenvironment in breast cancer progression: biology and implications for treatment. Breast Cancer Res. 2011;13:227. doi: 10.1186/bcr2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Please C, Pettet G, McElwain D. A new approach to modeling the formation of necrotic regions in tumors. Appl. Math. Lett. 1998;11:89–94. [Google Scholar]
- 80.Please C, Pettet G, McElwain D. Avascular tumour dynamics and necrosis. Math. Models Methods Appl. Sci. 1999;9:569–579. [Google Scholar]
- 81.Preziosi L, Tosin A. Multiphase and multiscale trends in cancer modelling. Math. Model. Nat. Phenom. 2009;4:1–11. [Google Scholar]
- 82.Preziosi L, Tosin A. Multiphase modelling of tumour growth and extracellular matrix interaction: mathematical tools and applications. J. Math. Biol. 2009;58:625–656. doi: 10.1007/s00285-008-0218-7. [DOI] [PubMed] [Google Scholar]
- 83.Preziosi L, Vitale G. A multiphase model of tumour and tissue growth including cell adhesion and phasic reorganization. Math. Models. Methods Appl. Sci. 2011;21:1901–1932. [Google Scholar]
- 84.Quaranta V, Weaver AM, Cummings PT, Anderson ARA. Mathematical modeling of cancer: the future of prognosis and treatment. Clin. Chim. Acta. 2005;357(2):173–179. doi: 10.1016/j.cccn.2005.03.023. [DOI] [PubMed] [Google Scholar]
- 85.Quigley JP, Lacovara J, Cramer EB. The directed migration of B-16 melanoma cells in response to a haptotactic chemotactic gradient of fibronectin. J. Cell Biol. 1983;97:A450–A451. [Google Scholar]
- 86.Ramsay DT, Kent JC, Hartmann RA, Hartman PE. Anatomy of the lactating human breast redefined with ultrasound imaging. J. Anat. 2005;206(6):525–534. doi: 10.1111/j.1469-7580.2005.00417.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Rejniak KA, McCawley LJ. Current trends in mathematical modeling of tumor-microenvironment interactions: a survey of tools and applications. Exp. Biol. Med (Maywood) 2010;235(4):411–23. doi: 10.1258/ebm.2009.009230. [DOI] [PubMed] [Google Scholar]
- 88.Ribba B, Alarcón K, Maini PK, Agur Z. The use of hybrid cellular automaton models for improving cancer therapy. In: Chopard B, Sloot PMA, Hoekstra AG, editors. Cellular Automata, in: Lecture Notes in Computer Science. Springer; Berlin: 2004. pp. 444–453. [Google Scholar]
- 89.Roose T, Chapman SJ, Maini PK. Mathematical models of avascular tumor growth. SIAM Rev. 2007;49:179–208. [Google Scholar]
- 90.Roose T, Netti P, Munn L, Boucher Y, Jain R. Solid stress generated by spheroid growth estimated using a linear poroelastic model. Microvasc. Res. 2003;66:204–212. doi: 10.1016/s0026-2862(03)00057-8. [DOI] [PubMed] [Google Scholar]
- 91.Sakorafas GH, Tsiotou A. Ductal carcinoma in situ (DCIS) of the breast: evolving perspectives. Cancer Treatment Rev. 2000;26:103–125. doi: 10.1053/ctrv.1999.0149. [DOI] [PubMed] [Google Scholar]
- 92.Sanders ME, Schuyler PA, Dupont WD, Page DL. The natural history of low-grade ductal carcinoma in situ of the breast in women treated by biopsy only revealed over 3. years of long-term follow-up. Cancer. 2005;103:2481–2484. doi: 10.1002/cncr.21069. [DOI] [PubMed] [Google Scholar]
- 93.Sanga S, Frieboes HB, Zheng X, Gatenby R, Bearer EL, Cristini V. Predictive oncology: a review of multidisciplinary, multiscale in silico modeling linking phenotype, morphology and growth. Neurolmage. 2007;37:S120–S134. doi: 10.1016/j.neuroimage.2007.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Sciumè G, Shelton S, Gray WG, Miller CT, Hussain F, Ferrari M, Decuzzi P, Schrefler BA. A multiphase model for three-dimensional tumor growth. New J. Phys. 2013;15:015005. doi: 10.1088/1367-2630/15/1/015005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Szabó A, Merks RMH. Cellular Potts modeling of tumor growth, tumor invasion, and tumor evolution. Front. Oncol. 2013 doi: 10.3389/fonc.2013.00087. doi: 10.3389/fonc.2013.00087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Taddei M¡, Giannoni E, Fiaschi T, Chairugi P. Anoikis: An emerging hallmark in health and diseases. J. Pathol. 2012;226:380–393. doi: 10.1002/path.3000. [DOI] [PubMed] [Google Scholar]
- 97.Teigen KE, Li X, Lowengrub J, Wang F, Voigt A. A diffuse-interface approach for modelling transport, diffusion and adsorption/desorption of material quantities on a deformable interface. Commun. Math. Sci. 2009;7:1009–1037. doi: 10.4310/cms.2009.v7.n4.a10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Teigen KE, Song P, Lowengrub J, Voigt A. A diffusion-interface method for two-phase flows with soluble surfactants. J. Comput. Phys. 2011;230:375–393. doi: 10.1016/j.jcp.2010.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Torabi S, Lowengrub J, Voigt A, Wise SM. A new phase field model for strongly anisotropic systems. Proc. Roy. Soc. A. 2009;465:1337–1359. [Google Scholar]
- 100.Tosin A. Multiphase modeling and qualitative analysis of the growth of tumor cords. Netw. Heterog. Media. 2008;3:43–84. [Google Scholar]
- 101.Tracqui P. Biophysical models of tumor growth. Rep. Prog. Phys. 2009;72:056701. [Google Scholar]
- 101.Trottenberg U, Oosterlee C, Schüller A. Multigrid. Academic Press; New York: 2001. [Google Scholar]
- 103.Tlsty TD, Coussens LM. Tumor stroma and regulation of cancer development. Annu. Rev. Pathol. 2006;1:119–50. doi: 10.1146/annurev.pathol.1.110304.100224. [DOI] [PubMed] [Google Scholar]
- 104.van Leeuwen IM, Edwards CM, Ilyas M, Byrne HM. Towards a multiscale model of colorectal cancer. World J. Gastroenterology. 2007;13(9):1399–1407. doi: 10.3748/wjg.v13.i9.1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Ward J, King J. Mathematical modelling of avascular tumor growth. IMA J. Math. Appl. Med. Biol. 1997;14:36–69. [PubMed] [Google Scholar]
- 106.Ward J, King J. Mathematical modelling of avascular tumor growth II: modelling growth saturation. Math. Med. Biol. 1999;16:171–211. [PubMed] [Google Scholar]
- 107.Wise SM, Lowengrub JS, Cristini V. An Adaptive multigrid algorithm of simulating solid tumor growth using mixture models. Math. Comput. Model. 2011;53:1–20. doi: 10.1016/j.mcm.2010.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Wise SM, Lowengrub JS, Frieboes HB, Cristini V. Three-dimensional multispecies nonlinear tumor growth-I: model and numerical method. J. Theor. Biol. 2008;253:524–543. doi: 10.1016/j.jtbi.2008.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Wodarz D, Komarova N. Computational biology of cancer: Lecture notes and mathematical modeling. World Scientific Publishing; 2005. [Google Scholar]
- 110.Wolf K, Wu YI, Liu Y, Geiger J, Tam E, Overall C, Stack MS, Friedl P. Multi-step pericellular proteolysis controls the transition from individual to collective cancer cell invasion. Nat. cell Biol. 2007;9(8):893–904. doi: 10.1038/ncb1616. [DOI] [PubMed] [Google Scholar]
- 111.Zheng X, Wise S, Cristini V. Nonlinear simulation of tumor necrosis, neovascularization and tissue invasion via an adaptive finite-element/level-set method. Bull. math. Biol. 2005;67:211–259. doi: 10.1016/j.bulm.2004.08.001. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.