Abstract
We consider the inverse and patient specific problem of short term (seconds to minutes) heart rate regulation specified by a system of nonlinear ODEs and corresponding data. We show how a recent method termed the structural correlation method (SCM) can be used for model reduction and for obtaining a set of practically identifiable parameters. The structural correlation method includes two steps: sensitivity and correlation analysis. When combined with an optimization step, it is possible to estimate model parameters, enabling the model to fit dynamics observed in data. This method is illustrated in detail on a model predicting baroreflex regulation of heart rate and applied to analysis of data from a rat and healthy humans. Numerous mathematical models have been proposed for prediction of baroreflex regulation of heart rate, yet most of these have been designed to provide qualitative predictions of the phenomena though some recent models have been developed to fit observed data. In this study we show that the model put forward by Bugenhagen et al. (2010) can be simplified without loss of its ability to predict measured data and to be interpreted physiologically. Moreover, we show that with minimal changes in nominal parameter values the simplified model can be adapted to predict observations from both rats and humans. The use of these methods make the model suitable for estimation of parameters from individuals, allowing it to be adopted for diagnostic procedures.
Keywords: Parameter estimation, Inverse problems, Model reduction, Structural correlation method, Subset selection, Simulation and modeling, Nonlinear heart rate model, Patient specific modeling
1. Introduction
Most models (including the one analyzed here) have been developed with the aim of estimating dynamics of the system studied. Often models are developed in steps including all known properties, rather than for obtaining the simplest, self contained model following the parsimonious principle. The former is essential for gaining understanding of how various mechanical or physical properties impact the system dynamics, thus having basic research as a goal. Yet it may not be practical if the objective is to study how model parameters change within and between groups of subjects, thus having an applicable or clinical goal. For the latter, a simpler self contained model with fewer states and parameters may be better. Estimation of reliable model parameters requires that sufficient data are available to identify all model parameters. Typically this is not the case because transversal experimental data are often sparse since they can be difficult and/or expensive to obtain in contrast to longitudinal data. Moreover, when it comes to biomedicine most experiments and clinical procedures are developed without regard to modeling. Consequently, as discussed in previous studies, Pope et al. (2009); Ottesen and Olufsen (2011); Olufsen and Ottesen (2013), only a subset of parameters may be identifiable. In this study we show how sensitivity and correlation analysis can be used for identifying model redundancies, which in turn can be used for model reduction. Furthermore, we show how reliable parameters can be estimated in the reduced model.
Inspired by earlier studies by Houk et al. (1966); Srinivasen and Nudelman (1972); Hasan (1983); Alfrey (1997); Ottesen (1997); Olufsen et al. (2006); Ottesen and Olufsen (2011); Bugenhagen et al. (2010) we developed a nonlinear differential equations model designed to predict baroreflex regulation of heart rate as a function of blood pressure. The model was validated by showing that it can fit experimental data obtained from rats and humans. Our objective was to develop a model that can be used to increase the scientific understanding of heart rate regulation, yet also fit experimental data from multiple species.
The model is complex consisting of 16 nonlinear differential and algebraic equations with 27 parameters. In particular our study expands and analyzes the model by Bugenhagen et al. (2010) that includes many details, but without a more comprehensive analysis, this original model cannot be adopted for reliable patient specific’ parameter estimation, i.e. fitting the model output to data. Data for the model are considered sparse since only one output quantity (heart rate) and one input quantity (pressure) are available, though both quantities are sampled at a high frequency. The model is complex since it contains nonlinear dynamics as well as several time scales, including fast inter-beat dynamics and slow dynamics associated with baroreflex regulation. Moreover, 27 parameters are needed to characterize all known properties of the system. The model is developed from first principles describing the underlying mechanisms with model parameters representing physiological quantities including arterial wall deformation, deformation of the baroreceptor nerve endings, firing of afferent neurons, prediction of neurotransmitter dynamics (acetylcholine and noradrenaline), and the impact on heart rate. Although Bugenhagen et al. (2010) showed that their model could predict measured data, no attempts were made to simplify the model or to analyze the predicted parameters.
In this study, we showed how to develop a simplified heart rate model in which all model components have biological interpretations. We demonstrate how to identify a parameter subset that can be estimated reliably given the model output and associated heart rate measurements from both rats and humans. The resulting reduced model may be considered ideal as it is a compromise between a detailed model and a crude lumped model. On one hand, sufficient details are included and on the other superfluous details are excluded. Such models are well suited for clinical use as a tool for accessing patient specific information through patient specific parameter estimation. Moreover it should be emphasized that the resulting model can predict dynamics displayed by both rat and humans.
2. Mathematical foundation for the structured correlation method
To predict sensitivities and pairwise correlations, we assume, that the model can be formulated as a system of nonlinear differential equations of the form
| (1) |
where f : R1+n+q → Rn, t ∈ R denotes time, x ∈ Rn the state vector, and θ ∈ Rq the parameter vector. Associated with the states we assume that the output vector h ∈ Rm (predicting heart rate) corresponding to the available data can be computed algebraically as a function of time t, the states x, and the model parameters θ. Finally, the output function g : R1+n+q → Rm. By construction the model output h is associated with the data H sampled at times ti. Note the sampling rate may vary between output components.
With the least squares error between measured data and model predictions of heart rate defined by
| (2) |
where denotes the heart rate data measured at time t = ti and hm(ti) denotes the corresponding model predictions.
Using this model formulation, sensitivities predicting how much the model output changes with a change in the parameters should be defined. Classically Frank (1978) the sensitivity matrix S of order m ×l ×q (where l is the sampling cardinality) is defined by
| (3) |
In this study, model parameters vary in magnitude and do not have the same units. Thus, to compare sensitivities, S was computed with respect to log-scaled parameters. For θ̃ = log(θ) the sensitivity matrix becomes
| (4) |
Finally, a sensitivity rank (for either S or S̃) can be computed as the 2-norm of the sensitivity matrix,
| (5) |
Analysis of ranked sensitivities may reveal parameters that do not affect the model output. Such parameters are denoted insensitive. For this study, insensitive parameters were kept at their a priori values, and thus, not examined further. In general, insensitive parameters can not be estimated reliably since a large change in the parameter value leads to a small or no change in the model output.
In addition to being sensitive parameters may be correlated, i.e. a change in one parameter may be offset by a change in another. This study shows how pairwise parameter correlations can be predicted from the sensitivity matrix using the structured correlation analysis method proposed by Olufsen and Ottesen (2013). As a point of departure, this method uses the model Hessian (sometimes denoted the Fisher information matrix, Cintron-Arias et al. (2009)) a positive definite symmetric matrix which for problems with constant variance σ2, can be defined as
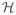 = σ−2STS
Yue et al. (2006), where S denotes the sensitivity matrix (3). Note
= σ−2STS
Yue et al. (2006), where S denotes the sensitivity matrix (3). Note
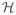 is independent of sensitivity scaling. Using
is independent of sensitivity scaling. Using
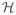 , the correlation matrix c can be computed from the covariance matrix C =
, the correlation matrix c can be computed from the covariance matrix C =
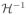 as
as
| (6) |
Note that the matrix C exists if and only if the determinant of
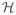 is non-vanishing. The matrix c is symmetric with elements |ci,j | ≤ 1. Parameter pairs (i, j) are denoted practically correlated if |ci,j | ≥ γ for some value of γ, e.g. γ = 0.90. For some models, the Hessian is exactly singular. This follows if two or more parameters are conditionally identifiable (perfectly correlated |ci,j | = 1), giving rise to redundancy. If H is singular, the model can be simplified by eliminating either a parameter or an equation. The latter operation should be repeated until det(
is non-vanishing. The matrix c is symmetric with elements |ci,j | ≤ 1. Parameter pairs (i, j) are denoted practically correlated if |ci,j | ≥ γ for some value of γ, e.g. γ = 0.90. For some models, the Hessian is exactly singular. This follows if two or more parameters are conditionally identifiable (perfectly correlated |ci,j | = 1), giving rise to redundancy. If H is singular, the model can be simplified by eliminating either a parameter or an equation. The latter operation should be repeated until det(
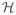 ) ≠ 0, or equivalently |ci,j | ≠ 1.
) ≠ 0, or equivalently |ci,j | ≠ 1.
Model reduction, as part of identifying a set of sensitive and uncorrelated parameters is an iterative process alternating between numerical and analytical considerations. More specifically we combined the Structured Correlation Methods (SCM) Olufsen and Ottesen (2013) with analysis of the model Hessian to identify a set of sensitive and uncorrelated parameters as follows:
Subset selection
Calculate the model Hessian
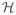 = σ−2STS, where S is the sensitivity matrix defined using (3) or (4). If
= σ−2STS, where S is the sensitivity matrix defined using (3) or (4). If
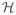 is singular, two or more parameters are conditionally identifiable. Identify what rows in S that lead to H being singular and reduce the model by eliminating either a parameter and/or an equation. Repeat this step until the Hessian
is singular, two or more parameters are conditionally identifiable. Identify what rows in S that lead to H being singular and reduce the model by eliminating either a parameter and/or an equation. Repeat this step until the Hessian
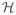 becomes non-singular, then go to step 2.
becomes non-singular, then go to step 2.Compute the correlation matrix c using (6) and identify all practically correlated parameter pairs, i.e. identify parameter pairs for which |ci,j | ≥ γ.
Sort correlated parameters according to their ranked sensitivity computed using (5). List all parameters ordered from the least to the most sensitive.
Remove the least sensitive correlated parameter from the list θ of parameters to be estimated and recompute c using (6) for the reduced parameter set (this can easily be done by deleting the corresponding column of S). The parameters removed from θ should be kept fixed at its a priori value.
Continue from 2 until |ci,j | < γ for all (i, j).
Once a reduced model and a set of identifiable parameters have been found, optimization can be employed to estimate the identifiable parameters. Assuming that the errors between the model output and data are normally distributed, parameters can be estimated via solution of the inverse problem. In this study, parameters are estimated using the Levenberg-Marquart gradient based method, which minimizes the least squares error (2) between computed and measured values of the model output (heart rate) Kelley (1999).
3. Mathematical model: Heart rate regulation
In this section we first describe the heart rate model. Second, we discuss concepts needed for prediction of sensitivities and correlations; and finally we apply these methods to analyze and simplify the heart rate model developed by Bugenhagen et al. (2010).
Heart rate is one of the most important quantities controlled by the body to maintain homeostasis. The control of heart rate is mainly achieved by the autonomic nervous system involving a number of subsystems that operate on several time and length scales. One of the major contributors to autonomic regulation of heart rate is the baroreflex system, which operates on a fast time scale (seconds). Baroreflex control consists of three parts: an afferent part, a control center, and an efferent part Ottesen (1997); Ottesen and Olufsen (2011).
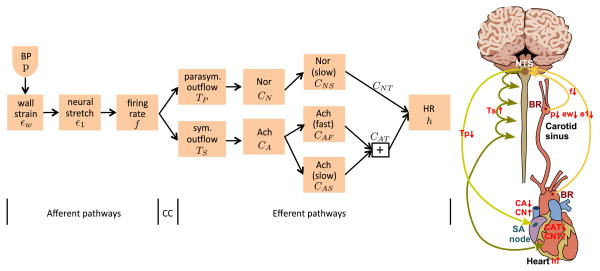
The firing rate of the afferent baroreceptor neurons is modulated by changes in the viscoelastic stretch of the nerve endings terminating in the arterial wall of the aorta and carotid sinuses. It is assumed that the deformation of the nerve endings is modulated relative to the deformation of the arterial wall, which is imposed via changes in arterial pressure. The afferent neurons terminate in the nucleus solitary tract (NTS) within the medulla. The efferent part consists of sympathetic and parasympathetic outflows (also denoted sympathetic and parasympathetic tones) generated within NTS. The parasympathetic outflow is transported along the vagal nerve, whereas sympathetic outflow is transported via a network of interconnected neurons. The main neurotransmitters involved with modulating the heart rate are acetylcholine, which is released by the vagal nerves, and noradrenaline, released from the postganglionic sympathetic nerves. This process is modeled using components summarized in Figure 1.
Figure 1.
Model components and physiological pathways. Left panel: CC denotes the control center (located within the nucleus solitary tract), which integrates all sensory inputs. Right panel: A drop in blood pressure (p) detected at aortic and carotid sinus baroreceptors causes a decrease in stretch of the vessel wall (εW) and subsequently the baroreceptor neurons (ε1), as a result afferent firing rate (f) decreases inhibiting/stimulating parasympathetic (TP) and sympathetic (TS) outflow, inhibiting/stimulating the release of acetylcholine (CA)/noradrenaline (CN). Total intercellular compounds associated with acetylcholine (CAT) and noradrenaline (CNT) are inhibited and stimulated, respectively leading to an increase in heart rate (h).
Arterial wall strain
It is commonly assumed that the wall strain can be defined as
| (7) |
where R and R0 refer to the stressed and unstressed vessel radius, respectively. This equation can be rewritten as
| (8) |
where A = πR2 represent the stressed cross sectional area. The approach originally suggested by Srinivasen and Nudelman (1972) is adopted, using the Langevin function to establish an analytic expression for the pressure-strain relationship of the sinus wall. The latter is reasonable for a thin-walled tube Valdez-Jasso et al. (2011). This corresponds to assuming a first order transient toward a static relation predicting the change in area A as
| (9) |
where Bw denotes the time scale of the transient response and cw is related to the vessel compliance. Bugenhagen et al. (2010) included (7)–(9) as separate equations, though the model can be simplified by merging equations (8) and (9) into a single differential equation that relates wall stretch and pressure
| (10) |
Note p is interpolated from blood pressure measurements sampled at time instances ti.
Neural stretch
Using the idea originally put forward by Houk et al. (1966) and Hasan (1983) later used by Alfrey (1997); Bugenhagen et al. (2010); Mahdi et al. (2013) inspired us to assume that the stretch of the baroreceptor nerve endings could be predicted by accounting for the cells embedded in the wall, which respond viscoelasticly to the vessel strain εw (7).
The deformation of the baroreceptor nerve endings is predicted using a mechanical model with three Voigt bodies in series, Fung (1993), as illustrated in Figure 2 and given by
Figure 2.
Three Voigt bodies in series. On the figure, KI denotes the spring constants and BI the dashpots characterizing the viscoelastic cell and wall components. Finally, the spring in series with the dashpots is denoted by KN.
| (11) |
For clarity (11) can be rewritten in explicit form as
| (12) |
where
Note, (12) includes six parameters, whereas the original equations in the model by Bugenhagen et al. (2010) had 7 parameters.
Afferent baroreceptor firing rate
By combining the algebraic equations in Bugenhagen et al. (2010) (equations (7)–(9)) the firing rate model can be written as one equation on the form
| (13) |
Sympathetic and parasympathetic tone
The afferent baroreceptor firing rate f (13) is integrated in the NTS, where the sympathetic and the parasympathetic outflows are generated. The model presented here only accounts for flow mediated by myelinated neurons transmitted from the nucleus ambiguus to the heart via the vagal nerve.
Assuming saturation, the sympathetic outflow TS and the parasympathetic outflow TP are predicted as functions of the afferent baroreceptor firing rate f using Hill functions of the form Olufsen et al. (2006); Ottesen and Olufsen (2011)
| (14) |
| (15) |
where subscript m refers to the minimum and subscript M to the maximum outflows, whereas η and ξ are constants predicting the steepness of the sigmoid. The parasympathetic outflow is proportional to the firing rate f, whereas the sympathetic response is inversely proportional to f. Note, the study by Bugenhagen et al. (2010) used exponential functions for prediction of sympathetic and parasympathetic outflow, which display similar behavior. The advantage of Hill functions is that the model becomes algebraic, making it feasible to exploit analytic tools to test if the model is structurally identifiable Mahdi et al. (2014).
Concentration of neurotransmitters acetylcholine and noradrenaline
The next step involves prediction of the concentration of neurotransmitters acetylcholine CA and noradrenaline CN, which can be obtained from
| (16) |
| (17) |
where qi and τi denote time scales for buildup and decay of the neurotransmitter concentrations Olufsen et al. (2006); Ottesen and Olufsen (2011).
Changes in the neurotransmitter concentrations impact the ionic stimulation of the heart. Acetylcholine binds to muscarinic receptors and noradrenaline to β1-receptors, controlling ion channels. Both acetylcholine and noradrenaline have an effect on the ion channels responsible for modifying the pacemaker potential. Both neurotransmitters interact with the G-protein coupled receptors having an inhibiting/stimulating effect, respectively, on the slow sodium channel (f-channel) affecting the slope of the depolarization of the pacemaker cells.
At low to moderate concentrations, acetylcholine reduces the heart rate by decreasing the initial slope of depolarization via increased stimulation of the f-channel only, but at higher concentrations acetylcholine also stimulates the potassium channel (K, ACh-channel) causing a further polarization of the pacemaker cells to the point where the pacemaker potentials disappear Pyetan et al. (2003); DiFrancesco (2006); Lyashkov et al. (2009); Vinogradova and Lakatta (2009).
The complexity associated with building up the action potential and thereby regulating heart rate is immense. In this study, we do not model the complexity, but only account for the overall affect. As discussed in detail in the appendix A, we assume that the occupied muscarinic and β1-receptors are in a quasi steady state and we lump all subsequent pathways into three quantities (representing artificial substances) assuming that 75% of available acetylcholine stimulates the fast channel pathways while about 25% stimulates the slower channel pathways, while for all available noradrenaline contributes to stimulating slower channel pathways. Common for all neurotransmitters stimulating the system is that the effect saturates at high concentrations. For more details see appendix A. Consequently, the noradrenaline concentration CNS can be predicted as
| (18) |
where CN (the presynaptic concentration of noradrenaline) is predicted from (17). Concentrations of acetylcholine are separated into the amount stimulating fast pathways (CAF) and that stimulating slow pathways (CAS), predicted as
| (19) |
| (20) |
where CA (the presynaptic concentration of acetylcholine) is predicted from (16), τx are time scales, F and S denote the fast and slow responses (i.e. τNS, τAS ≫ τAF), μ is a weighting parameter, and KX a parameter predicting half the max response with X = N (for noradrenaline) and X = A (for acetylcholine).
Assuming that the fast cholinergic process is almost instantaneous, (19) can be replaced by
| (21) |
Furthermore, assuming that fast and slow responses predicted by (20) and (21) are additive, the overall concentration of neurotransmitters is given by
| (22) |
In summary, the total intercellular compounds associated with the presynaptic release of acetylcholine impacting the pacemaker cells is denoted CAT, while the corresponding intercellular compounds associated with the presynaptic release of noradrenaline is denoted CNT. The intercellular compounds encompass second messengers and other bio-chemical substances constituting the intercellular pathways affecting the action potential of the pacemaker cell causing the heart to beat.
Heart rate
Inspired by De Geest et al. (1964); Levy et al. (1966); Levy and Zieske (1969); Olufsen et al. (2006); Ottesen and Olufsen (2011) we compute heart rate as
| (23) |
where h0 is the intrinsic heart rate, hM and hm denote the maximal and minimal heart rate, and CNT and CAT (predicted from (22)) denote the neurotransmitter concentrations. Assuming that hm < h < hM we rewrite h as
For CNT,CAT ∈ [0, 1], h ≥ hm, the global minima 0 is achieved for unphysiological concentrations of the neurotransmitters,
In terms of the general theory outlined above, the base model (1) can be described by n = 8 differential equations in
| (24) |
which can be solved subject to forcing by one input (pressure). The dimension of the output associated with the model is m = 1, and the output is h (heart rate). The model presented above has 30 parameters including
| (25) |
Simulations that compare the model to rat data, the nominal parameter values were set to match values reported by Bugenhagen et al. (2010). For equations where our formulation was identical to the one used by Bugenhagen et al. (2010), we used values reported in their studies. Equations that was formulated differently, estimated nominal values to make initial dynamics of the two systems match. Finally, simulations fitting the model to heart rate data from humans, changed parameters associated with prediction of the baseline unstressed vessel radius and compliance (R0, cw) as well as parameters associated with prediction of the intrinsic, minimum, and maximum heart rate (h0, hm, hM). Nominal values for these parameters were set to make the model predict average dynamics known for humans. Nominal and optimized parameter values are reported in Table 1.
Table 1.
Comparison of parameter values from Bugenhagen et al. (2010) (BM, 3rd column) with those obtained by the reduced model compared against rat (5th column) and humans (6–8th column). Initial values for the two datasets are shown in column 4. Note, except for baseline vessel radii and stiffness (encoded by parameters Kw1 and Kw2) and heart rate increments (dhM0 and dh0m), initial values were the same for both rat and human simulations. For all simulations, estimated parameters are marked in bold whereas the unbold are kept fixed at a priori values. Values marked by * are predicted to make Bugenhagen et al. (2010)’s formulation for TS, TP match our formulation. Values marked by # are calculated to convert the equations in Bugenhagen et al. (2010) to the formulation used in the simplified model. Bugenhagen et al. (2010) estimated 10 parameters, which translates to the 11 parameters marked in bold in the 3rd column. The least squares cost J (bottom row) compares the computed and measured heart rate. Values presented here were predicted for t > 20 s (rat data) and t > 50 s (human data), though it should be noted that initial values for the simplified model have been computed to predict measured heart rate values. Thus if J had been calculated from t = 0 s, the cost associated with the model by Bugenhagen et al. (2010) would have been significantly larger.
| Par | Unit | BM | SM R/H I | Rat Opt | Hum 1 Opt | Hum 2 Opt | Hum 3 Opt |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Kw1 | mmHg | 267# | 267/177 | 267 | 177 | 177 | 177 |
| Kw2 | min | 16.1# | 16.1/33.2 | 18.0 | 29.5 | 26.2 | 18.5 |
| a | min−1 | 1.5# | 1.5 | 1.54 | 1.04 | 1.75 | 0.726 |
| b | min−1 | 0.375# | 0.375 | 0.377 | 0.345 | 0.154 | 1.19 |
| c | min−1 | 0.0156# | 0.0156 | 0.0156 | 0.0156 | 0.0156 | 0.0156 |
| α1 | min−1 | 1# | 1 | 0.999 | 0.583 | 0.869 | 0.570 |
| α2 | min−1 | 0.1# | 0.1 | 0.0992 | 0.119 | 0.201 | 0.163 |
| α3 | min−1 | 0.0149# | 0.0149 | 0.0149 | 0.0149 | 0.0149 | 0.0149 |
| TSm | conc | 0.487 | 0.487 | 0.487 | 0.487 | 0.487 | 0.487 |
| TSM | conc | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 |
| TPm | conc | 0.912 | 0.912 | 0.934 | 0.377 | 0.418 | 0.365 |
| TPM | conc | 2.31 | 2.31 | 2.31 | 2.31 | 2.31 | 2.31 |
| fS | n.d. | 0.125* | 0.125 | 0.141 | 0.129 | 0.0786 | 0.0769 |
| fP | n.d. | 0.138* | 0.138 | 0.138 | 0.138 | 0.138 | 0.138 |
| η | n.d. | 15.3* | 15.3 | 11.8 | 55.7 | 31.0 | 33.6 |
| ξ | n.d. | 23.4* | 23.4 | 23.0 | 45.0 | 52.0 | 32.3 |
| τN | min | 9.1 | 9.1 | 8.53 | 50.5 | 18.2 | 17.5 |
| τA | min | 0.2 | 0.2 | 0.212 | 0.709 | 0.838 | 0.964 |
| qN | min−1 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 |
| qA | min−1 | 5 | 5 | 5 | 5 | 5 | 5 |
| KN | conc | 1.12 | 1.12 | 1.16 | 10.8 | 0.638 | 0.738 |
| KA | conc | 0.65 | 0.65 | 0.604 | 0.749 | 0.721 | 1.18 |
| τNS | min | 2.1 | 2.1 | 2.5 | 2.98 | 1.37 | 1.69 |
| τAS | min | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 |
| μ | n.d. | 0.75 | 0.75 | 0.719 | 0.291 | 0.101 | 0.114 |
| dhM0 | beats/min | 300 | 260/88.2 | ||||
| – | – | 75.8/77.8 | 217 | 197 | 68.7 | 97.7 | |
| dh0m | beats/min | 93.3 | 135/31.8 | ||||
| – | – | 44.2/42.2 | 135 | 31.8 | 44.2 | 42.2 | |
|
| |||||||
| J (10−4) | 4.25 | 4.74 | 5.25 | 2.10 | 4.56 | ||
4. Data used for model fits
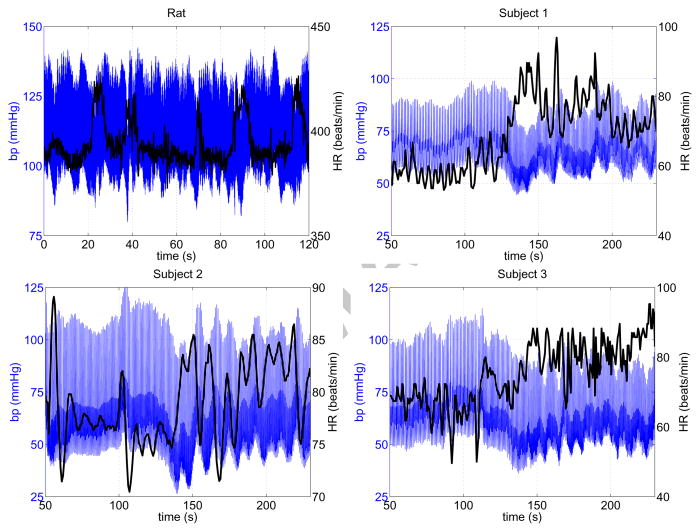
The model presented here was fitted to blood pressure and heart rate measurements from multiple datasets (shown in Figure 3), one from a Dahl salt sensitive (SS) rat (from Bugenhagen et al. (2010) and three from healthy young human subjects (from Williams et al. (2013)).
Figure 3.
Blood pressure (blue) and heart rate (black) data used for model fitting. The top left dataset, from a Dahl salt sensitive (SS) rat, was taken from the study by Bugenhagen et al. (2010). The remaining datasets are from three healthy young human subjects, recorded at the Coordinating Research Center, Frederiksberg Hospital, Denmark. The rat data show spontaneous changes in heart rate, reflecting dynamics in rats roaming freely around. The human data were measured during a head-up tilt test. More details about the human datasets can be found in the study by Williams et al. (2013).
5. Results
5.1. Model reduction: Step 1
Sensitivity analysis reveals that the sensitivity matrix S = ∂h/∂θ is singular, indicating that the model contains parameters that are perfectly correlated. From subsequent analysis of the model equations we noted two correlations. First, the equation for εw (7) can be simplified as
| (26) |
where Kw1 = R0/cw and , i.e. cw and Bw are conditionally identifiable with respect to R0. Second, substituting the expression for f (13) into the expressions for TS (14) and TP (15) shows that M is redundant. Thus the gain M may be incorporated into fS and fP, i.e. they are conditionally identifiable with respect to M. Hence the equation for f (13) reduces to
| (27) |
With these simplifications, the model (1) can be formulated using the following 28 parameters:
| (28) |
We emphasize that the resulting reduced model has a non-singular Hessian in contrast to the original model.
Initial conditions for the differential equations can be computed ensuring that the model starts in steady state and that heart rate computed at time t = 0 coincides with the measured value. First, we assume that at time t = 0 the wall is not deformed giving εw(0) = p(0)/Kw1. Initial conditions for ε1, ε2, ε3 can be computed from solving the linear system obtained by setting dεi/dt = 0 (12). These are given by
Subsequently, f(0) = εw(0) − ε1(0) can be found and from it we can predict
From the neurotransmitter equations we find
giving CNT (0) = CNS(0) and CAT (0) = CAS(0) + CAF (0).
Finally, we would like to impose that at time t = 0, the heart rate equals the data, i.e. h(0) = hd(0). This requirement allows us to eliminate one additional parameter. We have chosen to solve the equation, obtaining a closed form expression for the parameter h0. Equation (23) for heart rate can be reformulated introducing two new positive parameters dhM0 = hM−h0 and dh0m = h0 − hm. Using these parameters in place of hM and hm allows us to obtain the following quadratic equation in h0,
| (29) |
where
has two solutions, of which exactly one will be positive if γ > 0 and both β and γ are real. Hence the number of parameters reduces to 27 including
| (30) |
5.2. Practical identifiability and parameter estimation: Steps 2–5
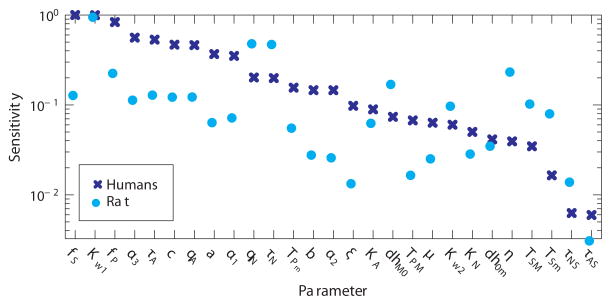
For the reduced model, the ranked sensitivities (see Figure 4) were calculated with respect to nominal parameter values for all datasets. The parameter (τAS), with a sensitivity (for all datasets) lower than 0.01, was considered insensitive, and parameters (c, α3) representing long time scales compared to available data were kept at a priori values. The figure shows average sensitivities for all three human subjects as well as sensitivities for the rat. It should be noted that the sensitivity rankings differ between the two species. This is due to the fact that nominal model parameter values differ between the two species and since the model is nonlinear sensitivities differ. Consequently, for each species or dataset we may not obtain the same set of identifiable parameters. For each correlated pair, the least sensitive parameter (determined using an average sensitivity ranking) was kept at its a priori value. All three human datasets gave the same set of 16 uncorrelated parameters, but analysis of the rat dataset gave rise to a different subset. The subset identified using the human data was a subset for the rat dataset, while the subset obtained from analyzing the rat data was NOT a subset for the human data. Consequently, we used the same subset namely the subset obtained from analyzing the human data in our further studies. The 16 parameters include:
| (31) |
Figure 4.
Ranked sensitivities. Dark blue exes show rankings for human data obtained by averaging ranked sensitivities for the three human subjects. Cyan circles denote ranked sensitivities for the rat data. Both are scaled such that the highest sensitivity has value one. Parameters associated with sympathetic activation appear more sensitive for the rat than the humans (qN, τN, dhM0, η, TSM, TSm), while other parameters appear to be ranked similarly. Parameters τNS and τAS were insensitive for all datasets, and thus kept at their a priori values.
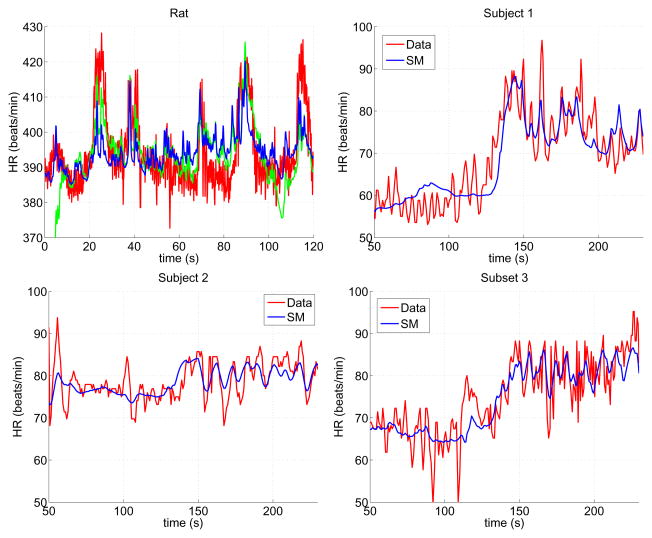
Table 1 compares parameter values from Bugenhagen et al. (2010) with those used in the reduced model, and Figure 5 shows measured and optimized blood pressure and heart rate values.
Figure 5.
Measured (red) and predicted (blue and green) heart rate for one rat (top left) and three human (top right and bottom) data sets. The blue trace shows results with the reduced model and on the top left panel green trace shows results from Bugenhagen et al. (2010).
The subset of identifiable parameters (31) were estimated minimizing the least squares error (2) between measured and computed values of heart rate. Results (see Figure 5) show that the model was able to predict dynamics for all subjects. First, it should be noted that significant variation was observed between the three human subjects, reflecting interindividual differences. However, even though parameter values vary between the human subjects, some general trends can be observed. The arterial wall parameters (Kw1 and Kw2) vary significantly between species, reflecting that vessels have different diameters and compliance, while time scales associated with viscoelastic deformation of the baroreceptor neuron (a − c, α1 − α3) are the same order of magnitude for all subjects studied. Second, it should be noted that the minimum parasympathetic outflow Tpm is about half as big in humans versus the rat, while maximum outflow TPM (not estimated) remains the same. However, parameters (ξ, η) reflecting the steepness of the sigmoid are significantly larger for humans than for the rat. Moreover, time scales for adaptation of both noradrenaline (τN) and acetylcholine (τA) are larger for humans than for the rat, and the heart rate parameters dhM0 and dh0m differ, reflecting that not only is the heart rate frequency higher but modulation of the baseline frequency also differs. Finally, it should be noted that the least squares error J (of order 10−4) was similar for all simulations, indicating that the model fits equally well to all datasets.
The differences between human and rat dynamics can also be interpreted qualitatively by comparing blood pressure and heart rate data with model dynamics (shown in Figures 3 and 5). From the blood pressure and heart rate data in Figure 3, it is observed that both data types exhibit rapid (on a time scale of a few heart beats) and medium variation (on a time scale of about 10 heart beats) while slow variation (on a time scale of more than 20 heart beats) appears in the human but not in the rat data. Oscillations in blood pressure are translated directly to the model, given that blood pressure serves as a model input. Comparing model output (heart rate), shown in Figure 5, we note that the amplitude of oscillations on a fast time scale (a few heart beats) is underpredicted whereas the amplitude on the medium and (for humans) slow time scale are more satisfactory. This result is observed for both rat and human simulations. Moreover, it should be noted that amplitude of heart rate changes is higher for the human than for the rat, reflecting that the humans have undergone an active task (head-up tilt), whereas changes observed in rat data are spontaneous in response to normal activity by a free-roaming rat. Finally, the dynamics associated with human activity (head-up tilt) occur over a longer time scale, reflected by larger parameter values for τN and τA.
6. Discussion
In this study we used structural correlation analysis to reduce and further develop an existing model for heart rate regulation developed by Bugenhagen et al. (2010). The resulting model is termed the reduced model and we refer to the method as model reduction. Assuming that initially (at time 0) the model is in steady state allowed us to predict initial values for all model states. We showed how to identify a subset of parameters that can be estimated given a model and a set of experimental data. Results showed that the model contains several parameters that are not identifiable given the model output (heart rate). We further showed that the identifiable parameters could be estimated to fit heart rate dynamics measured in a rat and three healthy young human subjects.steady state, at the measured heart rate value. The cost for all optimizations was of the same order of magnitude, reflecting that all simulations converged and that the model was able to reflect dynamics within each dataset. It should be noted that to compare results, we calculated the cost for t > 20 s to account for the fact that Bugenhagen’s simulations used generic initial conditions not specified to match data. As shown in Figure 5, their simulations display a large deviation from data in the beginning (for t < 20 s). Thus, to not bias the model predictions by Bugenhagen et al., we did excluded the initial time span in the cost function.
The rat and human heart rate values differ significantly. First, the heart beats about 5 times faster in the rat, while blood pressure is similar in both species, which may be supported by evolutionary theory. Moreover changes in heart rate observed in the human datasets reflect changes during head-up tilt, while changes in the rat heart rate dynamics reflect spontaneous changes without a specific stimulation. Even though the rat heart rate is faster, we assume that the underlying physiology associated with the baroreflex regulation is similar for both species.
However, there are at least two differences between rat and human anatomy: the length scales, e.g. diameter and length of vessels and neurons, and function. By function. we refer to the function of the autonomous nerve system, which, as part of evolution, has adapted to respond to different challenges. For example, rats make more frequent and more dramatic postural changes compared to their size, e.g. they often stand on their hind legs and sniff or make rapid head movements while orienting themselves, whereas humans change position slower and over longer time periods, giving rise to slower variations in blood pressure as illustrated in Figure 3. However, it should be emphasized that the magnitude of the pressure variation does not differ significantly between rats and humans, rather it is the timespan over which the pressure is held at an elevated level which varies. At the same time, the rat is significantly smaller and their baseline heart rate is significantly faster. Therefore, it should be anticipated that time scales associated with heart rate control is significantly faster (as evidenced by optimized parameter values). Consequently, the autonomous nerve system is exposed to different challenges and is thus likely adapted to cope with these, resulting in different responses.
On the other hand, the model presented here, a conglomerate of previous modeling efforts put together from studies from a number of species (rat, cat, dog, humans), should be general enough to represent the main features of the feedback control system, yet adaptable for studies in various species. Assuming that the system is initiated at steady state, variation within species has to be reflected by the parameter values chosen to represent the species studied. However, only a few parameters can be measured directly, but as this study has shown, estimates of a subset of parameters allowed us to recover at least some of the anticipated difference, namely that time scales are significantly larger in humans than in rats. This is also illustrated by sensitivity ranking, where some parameters were sensitive for human data, while not for rat data and vice versa. Changes in sensitivity ranking led to different subsets if chosen for humans or for rats. In this study, we selected a subset obtained by studying correlations within humans, and this subset turned out to also be valid for the rat studies. However, the subset obtained from rat sensitivity ranking was not valid when analyzed using the sensitivity matrix from the human subjects. The latter may be due to the larger variation in heart rate observed in the human data than in the rat data, which only included spontaneous changes in heart rate. It could also be a result of the fact that most parts of this model originally were developed for studying heart rate dynamics in humans.
As a side note, this study illustrates that experiments on laboratory animals may be superfluous if the goal is to gain insight into human physiology. In addition, animals are often affected by stress due to the conditions under which they are kept, which affect behavior and associated physiology, and as a result, the experimental data may be misleading. Therefore, depending on the question, one may directly model human physiological behavior rather than using data from animal experiments as an intermediary. The latter, will have the added benefit that it has potential to reduce the number of animals included in experiments, helping reach the goals recommended by the US FDA (U.S. Food and Drug Administration) and MSWG (Modeling and Simulation Working Group) under EMA (the European Medicines Agency) FDA (2011); EMA (2013).
In future studies, our objective is to use the model, parameter estimation, and model reduction methodologies developed here, combined with methods for prediction of parameter uncertainties within clinical investigations to compare parameter estimates within and between groups of patients suffering from orthostatic intolerance. Preliminary result look promising. They will be reported elsewhere along with a study of distributions of the parameter values for the groups examined. It is conjectured that using such distributions when examining subjects clinically may result in more reliable and more refined diagnoses henceforth leading to better treatment planning.
7. Limitations
When translating the model from rats to human, i.e. when attempting to use the same model including the same subset of identifiable parameters, we found that the model is suitable for some subjects but not for others. This study showed reasonable results from three healthy young human subjects. Simulations were attempted on two additional subjects, but for these parameters could not be estimated to reflect observed dynamics. More analysis is needed to understand if this is a result of the model dynamics or if data from these two subjects were too noisy and thus do not reflect hypothesis included in the model. To resolve this problem, we investigated if changing certain initial parameter values or the subset would enable the model to fit the data, but all attempts failed and optimization drove parameters to their upper and lower bounds. The study by Bugenhagen et al. (2010) used the model to fit data from six datasets, though these displayed significantly less variability than the human data. All five human datasets are shown in our previous study Williams et al. (2013). Consequently, either the subset is not suitable to capture the intervariability in humans or the model equations themselves do not capture all relevant physiology for humans. Finally, it should be noted that for one human dataset (Subject 1) the estimated parameter value for KN was significantly larger than for the rat and the two other subjects, almost reaching its upper bound. Again, additional studies are needed to more carefully analyze parameters within the subset obtained using the structured correlation method.
This study develops a mechanistic model of baroreflex regulation of heart rate.
We show how sensitivity analysis can be used for model reduction.
Subset selection is used to identify a set of parameters that is estimated rendering the model patient specific.
The model is validated against data from both human and rat studies.
A multi scale modeling approach.
Acknowledgments
We would like to thank Scott Bugenhagen and Professor Dan Beard, Department of Physiology, Medical College Wisconsin for providing data and computer code for their model analysis in this study. Olufsen and Ottesen were supported in part by National Science Foundation, under grant NSF-DMS #1022688 and by Snedkermester Sophus Jacobsen and wife Astrid Jacobsens foundation. In addition, Olufsen was supported in part by the National Institute of Health Virtual Rat Physiology center grant NIH-NIGMS #1P50GM094503-01A0 subaward to NCSU.
Appendix A. Neurotransmitters impact on ionic stimulation of the heart: A lumped model
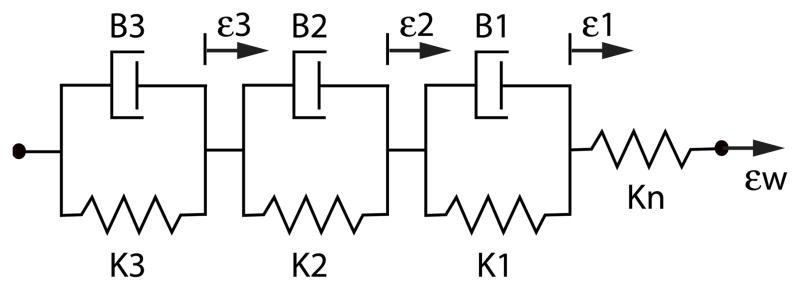
Acetylcholine binds to muscarinic receptors and noradrenaline to β1- receptors at the sinus node, controlling the ion channels within the cell membrane. The actual complexity of ion channels, taking into account the building up of action potentials, which subsequently regulate heart rate is immense. At least six ion channels are important for the generation of an action potential and hence the heart rate including f-channels (sodium channels If), cholinergic calcium channels (IK,ACh), non-transmitter dependent potassium channels (IK), L-type (long lasting) calcium channels (ICa,L), T-type (transient) calcium channels (ICa,T), and calcium sodium exchange channels (INCX) as illustrated in Figure A.6. All of these ion channels are regulated by (either inhibitory or stimulating) G-proteins: Acetylcholine binds to muscarinic receptors, downregulating cyclic AMP (cAMP) and phosphorkinase A (PKA), which upregulates Na+ (If) and downregulates K+ (IK,ACh) and Ca2+ (ICa,L), whereas noradrenaline binds to β1-receptors upregulating cAMP and PKA Pyetan et al. (2003); DiFrancesco (2006); Lyashkov et al. (2009); Vinogradova and Lakatta (2009). Common for all neurotransmitters stimulating such systems is that the effect saturates at high concentrations, which may be explained by simplifying the complex mechanisms underlying the biochemical reactions, e.g. by assuming a quasi steady state for the occupied receptors. For simplicity we imagine that two molecules of the neural transmitter (C) bind to a receptor (R) forming an occupied receptor complex in a reversible reaction with rates c+ and c− and that the occupied receptor in addition may undergo another transition to the free state, producing some substance (A) with rate c1. From Cosentino and Bates (2012); Ingalls (2013); Kremling (2014) it then follows that
We also assume conservation of the receptor type, i.e.
Hence the number of occupied receptors can be predicted by
In the quasi steady state approximation, this gives
where . It is further assumed that the occupied receptors control the states of the ion channels and thus the relevant intercellular pathways in building up the action potential. To omit this complexity, we simply lump these pathways into one or two substrates for each of the neurotransmitters, i.e. two for acetylcholine (CAF or CAS) and one for noradrenaline (CNS). Two channels are affected in response to acetylcholine, a slow sodium channel and a fast potassium channel, while noradrenaline mainly is associated with slower channels. We assume that 75% of the occupied receptors stimulate the synthesis of the substance CAF corresponding to the fast K+ channels, while about 25% stimulate the synthesis of the substance CAS corresponding to the slower Na+ channel. For noradrenaline, the full amount stimulates the synthesis of the substance corresponding to slow Na+ and Ca2+ channels. Hence, for all three substances, a fraction of the amount of occupied receptors serves as a production rate while the elimination are assumed proportional to the amount of the substance itself, thus the elimination rates are assumed constant (r),
where we use index x = A,N (denoting acetylcholine and noradrenaline) and y = F, S (denoting fast and slow, if necessary). Normalizing Cxy by r/R0 and substituting τxy = 1/r gives
Figure A.6.
Ion channels and pathways of greatest importance for the generation of the action potential and thus for the heart rate: f-channel (sodium channels If), cholinergic calcium channel (IK,ACh), non-transmitter dependent potassium channel (IK), L-type (long lasting) calcium channel (ICa,L) T-type (transient) calcium channel (ICa,T), calcium-sodium exchange channel (INCX), inhibitory G-protein (Gi), stimulating G-protein (Gs), muscarinic receptor (M2), β1-receptor, cyclic AMP (cAMP), phosphorkinase A (PKA), and phosphordiesterase (PDE).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alfrey KD. MS Thesis. Rice University; Houston, TX: 1997. A Model of the aortic baroreceptor in Rat. [Google Scholar]
- Bugenhagen SM, Cowley AW, Beard D. Identifying physiological origins of baroreflex dysfunction in salt-sensitive hypertension in the Dahl SS rat. Physiol Genomics. 2010;42:23–41. doi: 10.1152/physiolgenomics.00027.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cintron-Arias A, Banks HT, Capaldi A, Lloyd AL. A sensitivity matrix based methodology for inverse problem formulation. J Inv Ill-Posed Problems. 2009;17:545564. [Google Scholar]
- Cosentino C, Bates D. Feedback control in system biology. CRC Press, Taylor and Francis Group; Bocan Raton, FL: 2012. [Google Scholar]
- De Geest H, Levy MN, Zieske H. Carotid sinus baroreceptor reflex effects upon myocardial contractility. Circ Res. 1964;15:327–342. doi: 10.1161/01.res.15.4.327. [DOI] [PubMed] [Google Scholar]
- DiFrancesco D. Funny channels in the control of cardiac rhythm and mode of action of selective blockers. Pharmacol Res. 2006;53:399406. doi: 10.1016/j.phrs.2006.03.006. [DOI] [PubMed] [Google Scholar]
- U.S Food and Drug Administration (FDA) Advancing Regulatory Science at the FDA. 2011 www.fda.gov/regulatoryscience.
- The European Medicines Agency. First meeting of the Mod and Simul Working Group. 2013 http://www.ema.europa.eu/ema/index.jsp?curl=pages/news_and_events/news/2013/01/news_detail_001702.jsp&mid=WC0b01ac058004d5c1.
- Frank P. Introduction to sensitivity theory. Academic Press; New York, NY: 1978. [Google Scholar]
- Fung YC. Biomechanics: Mechanical properties of living tissues. Springer Verlag; New York, NY: 1993. [Google Scholar]
- Hasan Z. A model of spindle afferent response to muscle stretch. J Neurophysiol. 1983;49:989–1006. doi: 10.1152/jn.1983.49.4.989. [DOI] [PubMed] [Google Scholar]
- Houk J, Cornew RW, Stark L. A model of adaptation in amphibian spindle receptors. J Theor Biol. 1966;12:196–215. doi: 10.1016/0022-5193(66)90113-5. [DOI] [PubMed] [Google Scholar]
- Ingalls BP. Mathematical modeling in system biology: an introduction. MIT press; Cambridge, MA: 2013. [Google Scholar]
- Kelley CT. Iterative methods for optimization. SIAM; Philadelphia, PA: 1999. [Google Scholar]
- Kremling A. System biology: Mathematical modeling and model analysis. CRC press, Taylor and Francis Group; NY: 2014. [Google Scholar]
- Levy MN, Ng M, Lipman RI, Zieske H. Vagus nerves and baroreceptor control of ventricular performance. Circ Res. 1966;18:101–106. doi: 10.1161/01.res.18.1.101. [DOI] [PubMed] [Google Scholar]
- Levy MN, Zieske H. Effect of enhanced contractility on the left ventricular response to vagus nerve stimulation in dogs. Circ Res. 1969;24:303–311. doi: 10.1161/01.res.24.3.303. [DOI] [PubMed] [Google Scholar]
- Lyashkov AE, Vinogradova TM, Zahanich I, Li Yl, Younes A, Nuss HB, Spurgeon HA, Maltsev VA, Lakatta EG. Cholinergic receptor signaling modulates spontaneous firing of sinoatrial nodal cells via integrated effects on PKA-dependent Ca2+ cycling and IKACh. Am J Physiol Physiol. 2009;297:H949–H959. doi: 10.1152/ajpheart.01340.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahdi A, Meshkat N, Sullivant S. Identifiability of viscoelastic mechanical systems. PLoS One. 2014;9(2):e86411. doi: 10.1371/journal/pone.0086411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahdi A, Sturdy J, Ottesen JT, Olufsen MS. Modeling the afferent dynamics of the baroreflex control system. PLoS Comp Biol. 2013 Dec 13; doi: 10.1371/journal/pcbi.1003384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olufsen MS, Tran HT, Ottesen JT, Lipsitz LA, Novak V. Modeling baroreflex regulation of heart rate during orthostatic stress. Am J Physiol. 2006;291:R1355–R1368. doi: 10.1152/ajpregu.00205.2006. [DOI] [PubMed] [Google Scholar]
- Olufsen MS, Ottesen JT. A practical approach to parameter estimation applied to model predicting heart rate regulation. J Math Biol. 2013;67:39–68. doi: 10.1007/s00285-012-0535-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottesen JT. Nonlinearity of baroreceptor nerves. Surv Math Ind. 1997;7:187201. [Google Scholar]
- Ottesen JT, Olufsen MS. Functionality of the baroreceptor nerves in heart rate regulation. Comput Methods Prog Biomed. 2011;101:208219. doi: 10.1016/j.cmpb.2010.10.012. [DOI] [PubMed] [Google Scholar]
- Pope SR, Ellwein LM, Zapata CL, Novak V, Kelley CT, Olufsen MS. Estimation and identification of parameters in a lumped cerebrovascular model. Math Biosci Eng. 2009;6:93–115. doi: 10.3934/mbe.2009.6.93. [DOI] [PubMed] [Google Scholar]
- Pyetan E, Toledo E, Zoran O, Akselrod S. Parametric description of cardiac vagal control. Auton Neurosci. 2003;109:42–52. doi: 10.1016/j.autneu.2003.08.001. [DOI] [PubMed] [Google Scholar]
- Srinivasen R, Nudelman HB. Modeling the carotid sinus baroreceptor. Biophys J. 1972;12:1171–1182. doi: 10.1016/S0006-3495(72)86153-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdez-Jasso D, Bia D, Zocalo Y, Armentano RL, Haider MA, Olufsen MS. Linear and nonlinear viscoelastic modeling of aorta and carotid pressure-area. Ann Biomed Eng. 2011;39:1438–1456. doi: 10.1007/s10439-010-0236-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinogradova TM, Lakatta EG. Regulation of basal and reserve cardiac pacemaker function by interactions of cAMP mediated PKA-dependent Ca2+ cycling with surface membrane channels. J Mol Cell Cardiol. 2009;47:456474. doi: 10.1016/j.yjmcc.2009.06.014. t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams ND, Wind-Willassen O, Mehlsen J, Ottesen JT, Olufsen MS REU Program. Patient specific modeling of head-up tilt. Math Med Biol. 2013 doi: 10.1093/imammb/dqt004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yue H, Brown M, Knowles J, Wang H, Broomhead DS, Kell DB. Insights into the behaviour of systems biology models from dynamic sensitivity and identifiability analysis: a case study of an NFkB signaling pathway. Mol BioSyst. 2006;2:640649. doi: 10.1039/b609442b. [DOI] [PubMed] [Google Scholar]