Perspectives on the simulation of protein–surface interactions using empirical force field methods

Abstract

Protein–surface interactions are of fundamental importance for a broad range of applications in the fields of biomaterials and biotechnology. Present experimental methods are limited in their ability to provide a comprehensive depiction of these interactions at the atomistic level. In contrast, empirical force field based simulation methods inherently provide the ability to predict and visualize protein–surface interactions with full atomistic detail. These methods, however, must be carefully developed, validated, and properly applied before confidence can be placed in results from the simulations. In this perspectives paper, I provide an overview of the critical aspects that I consider being of greatest importance for the development of these methods, with a focus on the research that my combined experimental and molecular simulation groups have conducted over the past decade to address these issues. These critical issues include the tuning of interfacial force field parameters to accurately represent the thermodynamics of interfacial behavior, adequate sampling of these types of complex molecular systems to generate results that can be comparable with experimental data, and the generation of experimental data that can be used for simulation results evaluation and validation.

1. Introduction

The ability to understand and predict the interactions between proteins with material surfaces (either physically adsorbed or covalently linked) represents long-standing challenges in the fields of biomaterials and biotechnology. The behavior of proteins on material surfaces is of critical importance for numerous applications. These include the biocompatibility of materials when implanted in the body and for the function of substrates for tissue engineering, regenerative medicine, drug delivery, and bioseparations [1–8]. Protein–surface interactions also underlie the performance of biosensors, bioanalytical systems, and bioreactors as well as for the development of technologies for biodefense [9–12]. The continued growth of subfields such as nanobiotechnology and biomolecular engineering pushes the need for this understanding down to the submolecular and atomic levels in order to tap into the extreme versatility of proteins and their respective bioactive functionality. While much has been learned over the past several decades through the creative efforts of numerous research groups, the understanding of protein interactions with surfaces at the level of detail necessary to actually predict and control protein orientation, conformation, and bioactivity remains an elusive but still highly sought after goal.

The folding of a polypeptide chain into its native-state protein structure can be represented by what is referred to as the protein's folding funnel (Fig. 1a) [13–15]. This representation of the folding process depicts the relative free energy of the protein vs. its conformational state for the protein free-floating in physiological solution. The conformation of the protein that provides the minimum free energy state represents the protein's stable native-state structure. However, when a protein comes in contact with a material surface, the functional groups of the surface apply additional forces on the protein as well as causing a thermodynamic shift in the solvated state along the contacting surfaces of both the protein and the adsorbent material. These combined effects can substantially alter the shape of the folding funnel in a manner such that the native-state conformation of the protein no longer represents the lowest free energy state of the overall system. When this happens, the protein's conformation will change in a manner to cause the protein to undergo unfolding (or perhaps better thought of as ‘refolding’), toward a new low free energy state for the overall protein–surface–solvent system, as depicted in Fig. 1b. As will be addressed below, this phenomenon adds substantial additional complexity to the challenge of understanding and accurately predicting protein–surface interactions.

Fig. 1.

(a) Protein folding funnel for a protein in aqueous solution illustrating the free energy of the system as a function of the conformational state of the protein. Multiple local low-energy wells exist separated by free energy barriers, with the global low-energy state representing the native-state structure of the protein. (b) When a protein adsorbs to a surface, additional free energy contributions influence the system due to protein–surface interactions and corresponding changes in the hydration state of the protein and the surface. These combined effects cause the free energy profile to shift such that the native state of the protein is no longer the global low free energy state. The multiple low-energy adsorbed states represent different adsorbed orientations of the protein on the surface.

Protein–surface interactions have been widely studied and characterized over the past several decades in an effort to understand and control protein adsorption behavior. Methods were primarily initially developed to simply measure the amount of protein adsorbed to a surface, their competitive nature, and Vroman effects leading to the displacement of one adsorbed protein with another using techniques such as radiolabeling [16,17], surface plasmon resonance spectroscopy (SPR) [18], quartz crystal microbalance [17], and Fourier transform infrared (FTIR) spectroscopy [19,20]. Subsequently, more sophisticated experimental methods have been developed to obtain structural information regarding a protein's adsorbed orientation and conformation. These methods include circular dichroism spectropolarimetry (CD) to measure adsorption-induced changes in secondary structure [21,22], a combination of NEXAFS/SFG/ToF-SIMS to obtain information on adsorbed orientation and structure [16], FTIR for secondary structure [19], and amino-acid labeling/mass spectrometry (AAL/MS) to probe orientation and changes in tertiary structure [23,24]. These methods, however, are still very limited in their ability to provide complete residue-level detail of a protein's orientation and conformational behavior on a surface. Thus additional methods are still needed to provide a more complete depiction of protein adsorption behavior.

Empirical force field-based molecular modeling has the potential to meet this need with the inherent ability to predict molecular interactions with full atomistic detail. However, as an empirical approach, these methods must first be carefully developed and validated for specific applications. Other fields have actively taken on this challenge with great success to the point where molecular simulation methods are considered to be an indispensable resource for research and development. For example, the biophysics community has developed force field parameters and methods to represent and predict protein folding behavior in aqueous solution and when interacting with cell membranes [25,26], and the pharmaceutical field has developed force field parameters and methods for drug design [27,28]. These types of methods have similar potential for representing and predicting the interactions between peptides and proteins with material surfaces. However, this potential can only be realized if methods are developed to meet the specific needs of this type of application [29–31].

In this perspectives paper, my objective is to provide an overview of the critical issues that have to be addressed in order for simulation methods to be developed to accurately simulate protein–surface interactions. I would like to emphasize two important points regarding this overall objective. Firstly, I will not cover the closely related field of peptide–surface interactions except as it directly relates to providing information in support of the simulation of protein–surface interactions. Readers should refer to the many excellent papers that have been published in that specific area of research, which primarily focus on the atomistic-level interactions and conformational behavior between specifically sequenced peptides and various material surfaces [32–48]. Secondly, I specifically use the phrase, ‘accurately simulate’ because simulations can easily be conducted in a manner that gives completely erroneous and misleading results; often without any means to assess the reality of the predicted behavior. The real challenge for the simulation of protein–surface interactions is to develop methods that will accurately represent the behavior of a designated molecular system, and to have the ability to quantitatively verify that the results realistically represent actual system behavior. In the following sections, I present the attempts that I have made with both my experimental and computational research groups to provide this capability.

2. Methods

2.1. Overview of critical issues for empirical force field molecular simulation

In order to understand the specific issues that must be addressed for the development of empirical force field methods for the simulation of protein adsorption behavior, it is important to first understand some of the basic principles that are used for conducting this type of molecular simulation.

Two of the most important requirements that must be met to provide the ability to accurately represent molecular behavior using empirical force field methods are: (1) to have an appropriate force field equation and set of force field parameters to properly represent the interactions between the atoms contained within a given molecular system, and (2) to provide sufficient ‘sampling’ of the configurational states of the system to obtain a statistically representative depiction of the system's behavior.

2.1.1. Force field parameterization

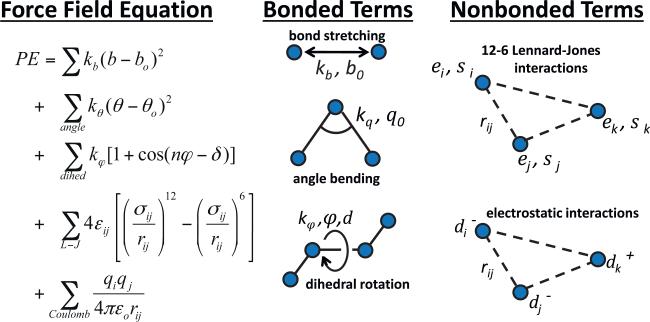
The force field used in an all-atom empirical force field simulation is an analytical expression that accounts for the potential energy (PE) contributions of each type of atomic level interaction in a given molecular system as a function of the relative position of the atoms with respect to one another [49]. The force field type typically used for simulation of biomolecules is called a Class I force field, which is represented in Fig. 2. As shown, this equation is represented by a summation of individual terms, with each term representing a specific type of interaction between the atoms in the molecular system. The first term represents the interactions between covalently bonded atoms, with a quadratic expression typically used to describe the energy related to covalent bond stretching. This term is followed by similar terms for the bending of the angle formed between three consecutively bonded atoms and the rotation of the dihedral angle formed between four consecutively bonded atoms. Although not shown in Fig. 2, additional terms are often also added to represent out-of-plane bending and coupling between bond stretching and angle bending. The bonded terms are then followed by two non-bonded terms, which are applied to atoms that are separated by more than two covalent bonds within a molecular chain, or between atoms of separate molecules. For these types of interactions, a Lennard–Jones (L–J) 12-6 potential is typically used for representing atom-atom overlap repulsion and van der Waals attraction, with a Coulombic term then used to represent electrostatic interactions between atoms. As shown in Fig. 2, each term of the force field equation involves a set of two or more force field parameters. For the bonded terms, these parameters represent the ‘stiffness’ and minimum energy position of the atoms for each type of bonded interaction. For the nonbonded terms, the L–J terms represent the radius of the atoms and the depth of the energy well when the atoms are in their minimum energy position with respect to each other, while the electrostatic term uses partial charge parameters that are assigned to each of the interacting atoms.

Fig. 2.

Typical form of a Class I biomolecular force field. The equation on the left represents the potential energy (PE) as a function of the conformation of a molecule, with the overall PE represented as the summation of contributions from covalent bond stretching, angle bending, and dihedral rotation, and a summation of nonbonded contributions from atom-atom overlap repulsion and van der Waals dispersion interactions represented by a Lennard–Jones (L–J) 12-6 potential, respectively, and electrostatic interactions represented by Coulomb's law. Force field parameters are adjusted to represent the behavior of a designated molecular system and environment. Parameters k_b and k_q represent the PE contribution for covalent bond stretching and bending as a function of the deviation of the bond length (b) and angle (θ) from a defined minimum energy position (b_o and θ_o), respectively, and k_j represents the PE contribution from dihedral rotation as a function of rotation parameters φ and δ. Parameters ε and σ represent the well-depth and atom radius for L–J interactions between pairs of atoms, with ε_ij = sqrt(ε_i × ε_j) and σ_ij = (σ_i + σ_j)/2, with r_ij representing the distance between the centers of the atoms. Each atom is then assigned a partial charge value (q_i) with ε_o being the permittivity of free space.

As an empirical force field, the force field parameters used with the force field equation are adjusted to represent the types of atoms in a given molecular system in a given molecular environment. The great advantage of the use of an empirical force field is that if the force field equation and parameter set is set up to appropriately represent the PE contributions between each of the atoms in a given molecular environment, the force field will accurately represent the atomic-level behavior for any size system of molecules within that environment. The great limitation of the use of an empirical force field is that if the force field and parameter set used does not accurately represent the interactions between the atoms in the system, the simulation will run just as well but the results will not realistically reflect actual molecular behavior. Thus selection of the appropriate force field and force field parameter set is of critical importance for the accurate simulation of any given molecular system. It should be realized that force field parameterization is specific for a given molecular environment, thus force field parameters developed for one type of molecular environment cannot be expected to perform equally well if that environment is substantially changed [50]. This principle is referred to as force field transferability. As addressed in more detail below, the general lack of force field transferability from one molecular environment to another means that parameterization developed for liquid and solid phases of a molecular system will most likely not be able to be simply combined to represent behavior at the solid–liquid interface.

The reason why the equation shown in Fig. 2 is called a force field equation rather than an energy equation is because when the expression is differentiated with respect to atomic position (x), it provides an equation that represents the force (F) that is being applied to each atom; i.e., F = −d(PE)/dx [49]. This differentiated expression is used in a molecular dynamics (MD) simulation along with Newton's laws of motion to calculate the acceleration of each atom (from F = m × a). Numerical integration is then applied over a designated timestep (typically 1–2 fs) to calculate subsequent changes in each atom's velocity and position over time. The updated positions of the atoms are then fed into the force field equation to calculate the new potential energies and force vectors for the next timestep of the simulation. In an MD simulation, this process is repeated over and over for a designated period of simulated time to predict the dynamic motion of the atoms in the system (e.g., using a 2-fs timestep for 5 million cycles predicts the motion of the atoms in the system over a simulated time of 10 ns).

This same type of force field equation is typically used in a Metropolis Monte Carlo (MC) molecular simulation, but in a completely different manner [49]. In an MC simulation, the system is not simulated in the time domain, but rather the simulation is performed ‘simply’ to evaluate the PE of a given molecular system as a function of the physical conformation of the system. Accordingly, the PE of the molecular system is first calculated using the force field equation for some designated starting molecular configuration. Small changes in the conformational state are then randomly applied and the PE of the new state is similarly determined. The PE of the new state is then compared with that of the previous state. If the PE of the new state is lower than the previous state, then the conformation of the previous state is replaced by the new state. If the PE of the new state is higher than the previous state, then the new state is accepted if it satisfies the Metropolis criterion, which represents the probability that the system should exist in that higher energy state based on statistical thermodynamics. The conformational state that is accepted after this comparison (i.e., the previous state or new state) is stored as an accepted sampled state of the system. A new conformational state is then randomly selected for comparison with the previously accepted state and the process is sequentially continued for a user-designated set of sampled states. This process ideally leads to the final development of a Boltzmann-weighted ensemble of sampled states of the molecular system.

2.1.2. Conformational sampling

As noted above, the second critical issue for performing a molecular simulation involves the conformational sampling of the system. In an experimental system, a thermodynamic property of a macroscopic sample represents the average behavior of literally many billions of molecules over timeframes typically from milliseconds to minutes. Under equilibrium conditions, this collection of molecules represents a Boltzmann-weighted ensemble of conformational states of the given molecular system. Similarly, in order to calculate an equivalent thermodynamic property from a molecular simulation, the simulation must be run in a manner to also obtain a Boltzmann-weighted set of conformational states. This presents a substantial difficulty for a complex molecular system if the system has what is referred to as a rugged conformational phase space in which there exist numerous local low-energy states that are separated by relatively high energy barriers.

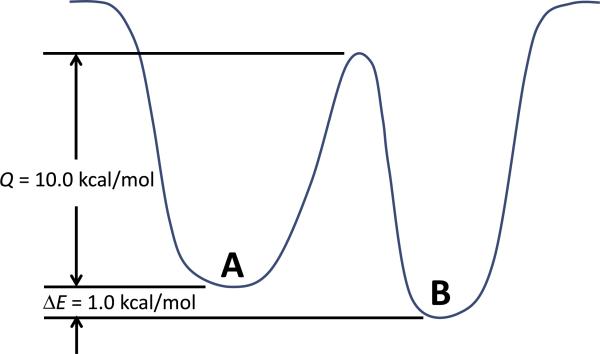
Fig. 3 depicts this problem for a simple system with two similar local low-energy wells separated by a high energy barrier. The two local low-energy wells illustrated in Fig. 3 (i.e., state A and state B) differ by only 1.0 kcal/mol (i.e., ΔE = 1.0 kcal/mol) but have a 10.0 kcal/mol energy barrier that must be surmounted to transit from state A to state B (i.e., Q = 10.0 kcal/mol). For simplicity we assume that each of these energy wells represents the same number of conformational states (i.e., equivalent degeneracy for the each well, thus equivalent entropy). Per statistical thermodynamics, the probability of the system residing in state A vs. state B at a temperature (T) of 298 K is equal to exp(− ΔE/k_BT) = 0.19, with k_B being Boltzmann's constant. In other words, under equilibrium conditions, a simulation would find that the system should reside in the energy well of state A 19% of the time and the lower energy well of state B 81% of the time. However, the probability of the system transitioning from state A to B is equal to exp(−Q/k_BT) = 5.8 × 10⁻⁸, which is equal to an average of one successful transition per 1.7 × 10⁷ attempts. To put this in perspective, this means for a conventional MD simulation with a 2 fs timestep, assuming each timestep represents an attempt to jump out of the energy well of state A into the energy well of state B, on average this event would happen about once every 35 ns of simulated time, which is on the order of the total simulated time for a typical MD simulation. The resulting ensemble of sampled states from such an MD simulation would therefore not accurately represent the proper distribution of the equilibrated states of the system. A similar problem exists for typical MC simulations as well when sampling using microscopically reversible steps, as typically used in an MC simulation for a condensed-phase system.

Fig. 3.

Illustration of two local low-energy wells representing two different conformational states (states A and B) that are 1.0 kcal/mol apart in potential energy with a 10.0 kcal/mol activation-energy barrier that must be crossed to transition from conformational state A to conformational state B.

To overcome this type of common simulation problem, more rigorous sampling methods have been developed, which are called ‘accelerated sampling’ or ‘advanced sampling’ methods. These methods typically invoke some nonphysical interaction, such as the application of elevated temperature or biasing energy to greatly accelerate the crossing of energy barriers, thus providing much more efficient sampling of a system. These nonphysical interactions are applied in a clever manner using statistical thermodynamics relationships to provide a Boltzmann-weighted ensemble of sampled states, thus providing the ability to calculate thermodynamic values from the simulation that should be comparable with those that are experimentally measured under equilibrium conditions.

Fig. 4 shows an example of this type of sampling problem for the simulation of a lysine amino acid residue, which has two main-chain dihedral angles, referred to as phi and psi [43,51]. Fig. 4a shows the equilibrated Ramachandran plot for lysine from a paper by Lovell et al. [51], which depicts the relative probability of the conformational states of the amino acid as a function of its phi and psi angles. Accordingly, each individual black dot in the figure represents the phi–psi dihedral angle combination of an individual lysine residue within a reference set of 500 proteins, thus characterizing the native-state conformational behavior of this type of amino acid. The large population of dots in the upper-left-hand corner and center-left-hand portions of the plot represent lysine configured in β-sheet and α-helix conformations, respectively. As shown in Fig. 4a, lysine has two primary high probability (i.e., low energy) states with differing regions of phi–psi angles, which are separated by a relatively high energy barrier. When using a conventional MD simulation of a simple peptide containing lysine, with the phi–psi dihedral angles of the lysine residue initially configured at either one of these low energy regions (Fig. 4c and d), the system is ‘trapped’ in its local low energy configuration for the entire simulation with the other state not being sampled over the course of the simulation, thus not properly representing the conformational behavior of the system. Fig. 4b shows the results from an MD simulation using an advanced sampling method called replica exchange MD (REMD). REMD uses multiple replicas of the same system with the replicas simulated over a range of temperatures, with exchanges made between adjacent temperature levels using a statistical thermodynamics-based exchange criterion. As shown in Fig. 4b, the use of this advanced sampling algorithm enables the system to efficiently cross energy barriers and provide sampling that closely matches the correct distribution of states of the system.

Fig. 4.

Ramachandran plots for (a) 4153 lysine residues obtained from a data base of 500 high-resolution protein structures of Lovell et al. [32] for comparison with (b) an REMD simulation, (c) a conventional MD simulation starting from a β-sheet conformation, and (d) a conventional MD simulation starting from an α-helix conformation. The accelerated sampling provided by the REMD simulation (b) enables the energy barrier separating the α-helix and β-sheet conformations of lysine to be readily crossed, providing sampling that is in close agreement with the observed conformational-state distribution (a). The MD simulations (c) and (d) result in conformationally trapped sampling that was not able to cross the energy barrier separating conformational states a and b within the timeframe of the simulation, thus improperly representing the conformational state of the system.

Reproduced with permission from Ref. [36]. Copyright 2008 American Chemical Society.

2.2. An approach to develop force field parameters for protein–surface simulations

The simulation of protein–surface interactions requires force field parameterization that not only accurately represents the conformational behavior of the protein in aqueous solution and the behavior of the atoms of the surface, but also accurately represents the interactions between the protein solution and the surface. Fortunately, the biophysics community has been diligently working on the development of force field parameters to represent protein folding behavior in aqueous solution over the past several decades and these parameter sets (e.g., CHARMM [25], AMBER [52], OPLS-AA [53] protein force fields) can be used to represent protein–solution interactions in a simulation of protein adsorption behavior. However, these parameters cannot simply be borrowed with any confidence to also represent the interactions between the protein and solution with a material surface because the molecular environment at a solid–liquid interface is distinctly different than that of the solution or surface phases themselves (i.e., force field transferability should not be assumed). A separate set of force field parameters (i.e., interfacial force field parameters) can be expected to be needed to realistically represent interfacial behavior.

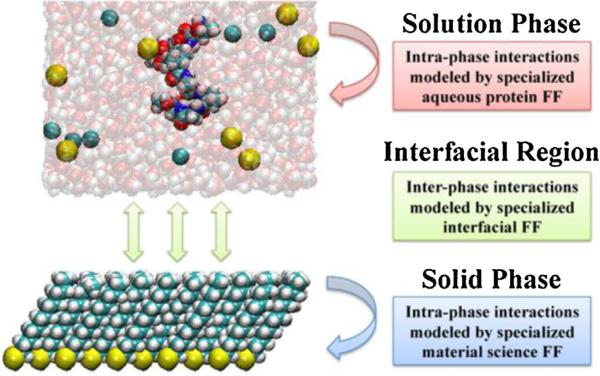
Accordingly, for the simulation of protein adsorption behavior, force field parameters must be provided not only to represent interactions between the atoms within the aqueous solution and solid material phases of the system (i.e., intraphase behavior), but also for the interactions between these two phases (i.e., interphase behavior). We refer to the latter parameter set as an interfacial force field (IFF). This concept is illustrated in Fig. 5 [54]. Accordingly, once an appropriate IFF force field parameter set can be obtained for amino acid–surface interactions for a given material surface, then it should be able to be coupled with an appropriate protein folding force field and solid material force field to accurately represent protein–surface interactions for any protein on that type of surface.

Fig. 5.

Schematic representation of the interfacial force field (IFF) method applied to a peptide adsorption simulation. The solution and solid surface phases are modeled by force fields that accurately represent their respective intra-phase interactions while interactions between atoms of the solution phase with the solid phase are represented by an interfacial force field parameter set that is tuned to accurately represent peptide adsorption free energy.

Reproduced with permission from Ref. [33]. Copyright 2012 American Chemical Society.

In order to obtain IFF parameters for the accurate representation of protein–surface interactions, three key areas of development are required. First, a data set (i.e., benchmark data set) is required that provides information concerning how amino acids actually interact with a designated material surface using a sufficiently simple system that can also be closely represented by an empirical force field molecular simulation. Secondly, a molecular simulation program must be adapted that enables IFF parameters to be independently used and adjusted while using conventional force fields to represent the conformational behavior of the amino acids in solution and the solid material surface. Thirdly, once these first two areas are addressed, then IFF parameters need to be adjusted to obtain amino acid–surface interactions that are in close agreement with the benchmark data set. Once these three objectives are met, the tuned IFF parameter set can be applied along with the parameter sets representing the behavior of the protein in solution and the material surface to realistically simulate protein–surface interactions.

2.2.1. Development of benchmark data sets to represent amino acid-surface interactions

Two approaches can be taken to obtain a benchmark data set that quantitatively characterizes the interactions between amino acids and a material surface. The first approach is to conduct experimental adsorption studies to obtain suitable data for comparison with empirical force field simulation results, and the second approach is to conduct ab initio quantum mechanical (QM) molecular simulations that do not depend on empirical parameters to calculate these types of interactions. Each of these approaches has its strengths and weaknesses. Experimental approaches have the advantage of providing data on the actual behavior of the adsorption event while being limited by the ability to obtain suitable model amino acid–surface systems and generate values that can be closely matched to parameters obtained by molecular simulation. In comparison, ab initio QM methods provide a more direct approach to create molecular models that closely match those used in an empirical force field simulation, and this approach has been used by several groups to parameterize interfacial interactions [33,38,39,45,47,55–58]. While very useful for probing the interactions for small molecular systems for interfacial force field development, highly accurate QM methods are still too limited in terms of the number of atoms that can be represented in the simulation to enable bulk water over a surface to be explicitly represented in the simulation. Because of this present limitation, lower-level QM methods must often be used as an alternative, such as density functional theory (DFT). However, while DFT can handle a sufficient number of atoms for such a simulation, the ab initio part of DFT only addresses electrostatic interactions without including electron correlation interactions that govern van der Waals dispersion effects [59,60]. Empirically fitted correction algorithms have been and are being developed and added to DFT simulations to address this limitation, which themselves need to be validated for specific types of applications [61–63]. Thus, while the use of QM methods may be the only available option if suitable experimental methods are not available to obtain benchmark data, the obtaining of an experimental data set is still the preferable option if it can be obtained.

2.2.2. Experimental benchmark data sets

We have focused on the development of two experimental methods for this purpose: surface plasmon resonance spectroscopy (SPR) and atomic force microscopy (AFM). Interested readers can refer to our publications about these methods to obtain the experimental details [64–67]. Briefly, we have used SPR to generate adsorption isotherms for a host–guest peptide model adsorbing on alkanethiol self-assembled monolayers (SAMs) formed on gold (1 1 1) surfaces and calculated the standard state free energy of adsorption (ΔG°_ads) from the isotherms [64]. The host–guest peptide was designed with a sequence of TGTG-X-GTGT, with T and G being threonine and glycine, with X (representing the mid-chain amino acid) being a varied over any of the 20 different naturally occurring amino acid types. Isotherms were generated for a set of 12 different X residues selected from each of the different types of amino acids (i.e., polar, nonpolar, +/− charged) on a set of 9 different SAM surface chemistries to provide a benchmark data set of 108 different peptide-surface combinations [65]. The use of SPR, however, has the drawback of only being applicable to materials that can be used to form nano-thick surfaces over the SPR sensor surface, thus prohibiting its use for many types of polymers, ceramics, and metals. For these other material types, we correlated the ΔG°_ads values obtained from SPR with desorption forces measured for the same set of peptide-SAM systems using AFM [66]. Using this correlation plot, we were then able to obtain effective ΔG°_ads values from desorption force measurements for materials that could not readily be used with SPR (e.g., polyethylene, poly(methyl methacrylate), Teflon®, and silica glass) [67]. With the resulting benchmark data sets, we were then in a position to evaluate and tune IFF parameter sets for empirical force field simulations from molecular models of these same peptide–surface systems.

2.2.3. Tuning IFF parameters to represent amino acid-surface interactions

Given the availability of benchmark data sets providing target ΔG°_ads values for the adsorption behavior of amino acid residues and material surfaces, IFF parameters for amino acid–surface interactions can be tuned to provide adsorption behavior to match. This process generally requires three different steps: (1) calculation of adsorption free energy values from empirical force field simulations using a selected default parameter set (e.g., CHARMM), (2) modifying the selected simulation program to enable independent use of an IFF parameter set to represent interfacial interactions, and (3) adjusting IFF parameters from the default values used in step (1) to correct the adsorption behavior of amino acids that were determined to adsorb too strongly or too weakly compared to the target benchmark data set.

There are several approaches that have been used by various groups for the evaluation of interfacial force field parameters, which typically include the calculation of characteristic properties such as the adsorption free energy of amino acids or their analogs using methods such as umbrella sampling, metadynamics, and/or replica exchange molecular dynamics (REMD)—also known as parallel tempering [39,43,46,68,69]. My group has primarily focused on the use of umbrella sampling, often in combination with REMD, to provide adequate sampling over both the designated solute's position over a surface and its conformational phase space, as briefly summarized below. Readers are again referred to publications of our methods to see the specific details that we have used to address each of these three steps [54,69,70].

For the calculation of adsorption free energy from molecular simulation, we first developed models of our hosts–guest peptides over our set of material surfaces. We then used an advanced sampling method called umbrella sampling combined with REMD to calculate adsorption free energies for comparison with our benchmark values [69]. (Most recently we have found that the REMD step is not required if umbrella sampling is applied for sufficiently long (e.g., 15 ns of MD simulation) to adequately sample the conformational behavior of the peptide in each umbrella ‘window’—unpublished data.) For step (2), we modified the source code of the CHARMM simulation program to enable IFF parameters to be included in the simulation to represent interactions between the peptide in solution with the adsorbent surface [54]. We are presently developing new modules for the LAMMPS simulation program (Large-scale Atomic/Molecular Massively Parallel Simulator; from Sandia National Laboratories) for this same purpose. We then used the modified simulation program to adjust nonbonded parameters of the IFF force field (i.e., partial charges, L–J well depth) to correct deviations found from step (1) until adsorption free energy values for each peptide were within about 0.5 kcal/mol of their respective target benchmark data set values [70].

Once an IFF parameter set is established that enables the adsorption behavior for amino acids to be in satisfactory agreement with targeted values of the benchmark data set, then the tuned IFF parameter set should be ready to be applied to simulate protein adsorption behavior. The simulation of protein adsorption behavior presents a whole set of new challenges, including how to adequately sample such a much more complex system as well as the need to obtain representative experimental data sets that can be used to evaluate and validate simulation results. These issues are addressed in the following section.

2.3. Methods development and validation for the accurate simulation of protein–surface interactions using empirical force field methods

The ability to accurately simulate actual protein adsorption behavior presents its own set of challenges that are distinctly different than those that are addressed above for the development of interfacial force field parameters. The tuning of interfacial force field parameters involves calculating the energetics of the interactions between amino acid residues and the functional groups of a surface within an aqueous solution. In contrast to this, the simulation of protein adsorption behavior primarily focuses on predicting the orientation of the protein on the surface and adsorption-induced changes in a protein's conformation and bioactivity.

As with the development of force field parameters, some defined basis is needed to characterize adsorbed protein orientation, conformation, and bioactivity in a quantitative manner so that simulation results can be confidently assessed and validated. The size of the molecular system that must be represented for a simulation of protein adsorption behavior prohibits the use of ab initio QM methods to obtain data for this purpose, thus leaving experimental approaches as the only viable option at this time.

In order for experimental data to be used to assess and validate results from a simulation of protein adsorption behavior, the experimental conditions used to obtain these data must be sufficiently similar to the conditions that are represented in a simulation for such comparisons to be meaningful. For example, presently all-atom empirical force field simulations of protein adsorption behavior are typically limited to the representation of a single protein on a surface without the presence of protein–protein effects, which can substantially alter protein adsorption behavior. Therefore experimental conditions must be used that minimize protein–protein interactions, such as by conducting adsorption experiments at sufficiently low solution concentration to enable the adsorbing protein molecules to essentially fully equilibrate on the surface in the absence of the influence of neighboring adsorbed proteins.

Likewise, it is also important to conduct a simulation in a manner that will provide data that are comparable to experimentally obtained values. For example, it must be realized that even under very dilute solution concentration conditions, experimental measurements on the orientation, conformation, and bioactivity of an adsorbed protein typically represent the average behavior of literally billions of proteins per square centimeter of surface area. In contrast, a conventional MD or MC simulation, which is run sufficiently long to achieve equilibration, will still only provide results that represent the adsorption behavior of a single adsorbed protein. Thus conventional MD or MC simulations cannot provide results that are directly comparable with experimental measurements. Instead, advanced sampling methods must be applied that do not simply provide simulation results for the adsorption behavior of a single protein on a surface, but rather provide a Boltzmann-weighted ensemble average over the whole relevant conformational phase space of the given protein–surface system. Such ensemble average properties should then be comparable to experimentally measured values obtained from an equilibrated system.

The following subsections provide a summary of the approaches that we have taken to address these challenges by attempting to generate experimental data that can be used to quantitatively assess simulation results and to conduct simulations in a manner to generate Boltzmann-weighted ensemble average values that can be directly compared with the obtained experimental data. Readers should again refer our publications of these specific methods for further details regarding these methods.

2.3.1. Experimental data sets for the evaluation and validation of protein–surface simulations

Review of the protein adsorption literature over the past several decades reveals that most of the published studies on protein adsorption behavior focus on determination of the amount of protein adsorbed to surfaces under designated conditions. Proteins typically adsorb to surfaces in an effectively irreversible manner apart from Vroman effects, and thus the amount of protein adsorbed to a surface essentially represents how protein–protein effects influence the packing arrangement of the proteins on the surface. While useful in their own right, these kinds of data, unfortunately, are of little use for the evaluation and validation of methods applied for the simulation of protein adsorption behavior. Data are instead needed that quantitatively characterize the orientation, conformation, and bioactivity of adsorbed protein in comparison to their native-state solution behavior. These factors represent parameters that can be readily determined from molecular simulation. In addition, proteins should be selected that are sufficiently small in size such that simulations can be completed within a reasonable timeframe for comparison with the experimental data obtained.

One of the main objectives of my experimental research group over the past ten years has been to develop, apply, and assess experimental methods that can quantitatively provide data on the adsorbed orientation of adsorbed protein and adsorption-induced changes in adsorbed protein structure and bioactivity. We have focused on three main techniques to obtain these kinds of data: (1) circular dichroism spectropolarimetry (CD) to measure the secondary structure composition of protein in solution and when adsorbed on a surface [21], (2) amino-acid labeling/mass spectrometry to probe both adsorbed protein orientation and adsorption-induced changes in tertiary structure [23,24], and (3) bioactivity assays for proteins in solution and in their adsorbed state [24,71]. A brief summary of each of these methods is presented below.

As noted above, a critical issue for these experimental methods is to establish conditions that minimize protein–protein effects on the surface in order for the results obtained to be comparable with simulations of protein–surface interactions for individually represented proteins. These conditions can be established by conducting a series of preliminary studies for a given protein–surface system at sequentially lower concentrations until the experimental results being obtained (e.g., the degree of adsorption-induced unfolding by CD) stabilizes to a constant value that no longer changes as solution concentration is further reduced. A critical aspect of this approach, of course, is that the solution and surface concentrations of the protein must still be sufficiently high to provide values within the limits of detection for whichever experimental method is being used. In studies with small enzymes such as lysozyme and ribonuclease A (each about 14 kDa), we have found that adsorption from solution concentrations of 0.030 mg/mL satisfy this requirement for our experimental methods [71]. Other proteins will likely result in different concentration requirements.

2.3.1.1. Circular dichroism spectropolarimetry (CD)

CD is useful for the characterization of the structure of chiral molecules, which tend to absorb circularly polarized light rotated in a clockwise direction differently from light rotated counterclockwise due to the asymmetry of the molecular structure. The secondary structural elements that make up all proteins (e.g., helices, sheets, and/or random loops) are chiral structures, each of which provides a distinct CD absorption signal over wavelengths ranging from about 190 to 250 nm. Accordingly, CD spectra can be deconvoluted to determine the percent composition of each of these kinds of structure. And, because a CD instrument performs these measurements by sending the beam of circularly polarized light through a sample with the signal primarily dependent on the amount of protein that the beam passes through, structural determination is essentially the same whether the protein is in solution or adsorbed to a surface. When used to analyze adsorbed protein, the surface plane should be placed perpendicular to the light beam to minimize diffraction. As a consequence of this, this technique is not suitable for opaque samples, or transparent samples that strongly absorb light in the 190–250 nm wavelength range. We have found this method to work very well for SAMs and nm-thick layers of metals such as gold, titanium, and chromium, as well as for many thin polymer films, such as polyethylene and poly(methyl methacrylate) [21,71]. Most importantly, CD provides a direct means of measuring adsorption-induced changes in a protein's secondary structure, which is a quantitative parameter that can also be readily calculated from simulations of proteins in solution and when adsorbed on a surface.

While CD is a very valuable method, it does not provide data on the orientation or the tertiary conformation of adsorbed protein. Other methods are therefore needed to provide these kinds of data for comparison with simulation results.

2.3.1.2. Amino-acid-labeling/mass spectrometry (AAL/MS)

In order to provide data on the adsorbed orientation and adsorption induced changes in the tertiary structure of proteins, we sought for methods that would probe changes in amino acid solvent accessibility. Accordingly, amino acids that have reduced solvent accessibility after adsorption suggest areas of the protein that are tightly adsorbed to a surface (i.e., indicative of adsorbed orientation), while those gaining in solvent accessibility after adsorption indicate areas of the protein that undergo adsorption-induced tertiary unfolding. We had initially considered hydrogen/deuterium (H/D) exchange as one of the candidate methods for these kinds of measurements. However, H/D exchange was determined to be unsuitable because of its inherent problem of rapid reverse exchange. This issue is especially problematic given the additional processing steps required to remove protein from an adsorbent surface in order to conduct MS to identify the amino acids that underwent H/D exchange.

As an alternative to this, we sought for amino acid labeling methods that could be applied under moderate conditions that would not denature the protein while covalently linking a chemical tag to the side chains of designated amino acid types that could be detected by MS. This method would then essentially serve the same purpose as H/D exchange, but in a much more robust manner such that we could be confident that the chemical labels were effectively irreversibly linked so that they would not be lost during the processing steps required for removing the protein from the surface in preparation for the MS analyses. We have found this method to be very workable for a range of amino acid residues including all of the charged amino acids (lysine, arginine, aspartic acid, glutamic acid) as well as tryptophan [23,24]. Amino acid solvent accessibility is a parameter that is also readily determined from molecular simulation, thus enabling results obtained from AAL/MS to be directly comparable to simulation results for assessment and validation.

2.3.1.3. Bioactivity assessment

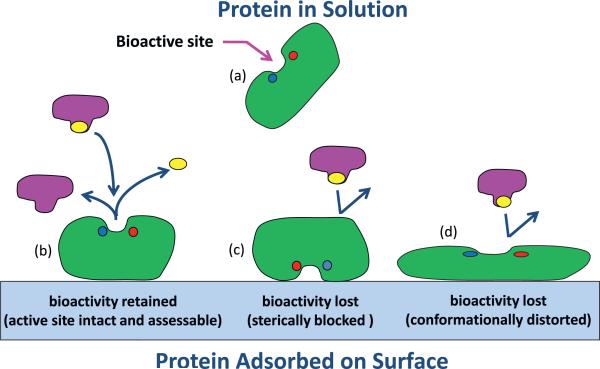
A third area of experimental studies that can provide quantitative data that can be compared with simulation results is adsorption-induced changes in bioactivity. The assessment of protein bioactivity requires the use of an enzyme as the protein model system, with a well-documented bioassay that can be performed to quantify the enzyme's bioactivity. Hen egg-white lysozyme (HEWL) and ribonuclease A (RNAsA) are excellent candidates for such studies since they are relatively small (14 kDa each) and very well characterized with readily available bioactive assays [24,71]. The assays should be run with sufficient substrate to saturate the enzyme contained in the sample, which enables a simple calibration curve to be used to determine the relative bioactivity of the enzyme when adsorbed on the surface relative to the enzyme in solution. One of the limitations of adsorbed-state bioactivity assessment is that loss in bioactivity can be due to multiple factors. For example, the bioactive site can be either sterically blocked by the surface (i.e., adsorbed orientation effect) or distorted such that its effectiveness in binding its substrate is affected (i.e., conformational effect). These two effects are illustrated in Fig. 6. However, when coupled with results from CD and AAL/MS studies, information can be gained to provide support for the mechanism involved. Bioactivity results can then be compared with simulation results related to the solvent accessibility of the protein's binding site as well as the calculation of the degree of conformational distortion of the enzyme's binding site compared to its native-state structure in solution. As our own simulations of protein adsorption of HEWL and RNAsA on various surfaces are currently ongoing, we have not yet actually applied these methods ourselves for bioactivity assessment, but are planning to do so in the near future.

Fig. 6.

Illustration of the influence of adsorption on the bioactive state of an enzyme. Enzyme in its native-state structure in solution (a) and when adsorbed (b) with its bioactive site accessible and conformationally intact, thus providing native-state bioactivity. (c) Enzyme adsorbed with its bioactive site sterically blocked by the surface, thus inhibiting substrate binding with subsequent loss in bioactivity. (d) Enzyme adsorbed with its bioactive site solvent accessible but conformationally distorted with subsequent loss in bioactivity.

At this time there are only a few reports by other groups in the molecular simulation literature that present a quantitative assessment of the bioactive state of adsorbed proteins; mostly with only qualitative comparison with experimental results. Nordgren et al. [72] and Zhou et al. [73] performed molecular dynamics simulations of cytochrome c on SAM surfaces. The bioactive state of the system was primarily characterized by the orientation and position of the heme group within the protein. Other analyses included the general structure of the protein itself, which was characterized by parameters such as the root-mean-square deviation of the adsorbed protein compared to its native structure, the protein's radius of gyration, and the orientation of the protein's dipole moment with respect to the surface plane. Others have investigated the influence of adsorption on the structure and orientation of the arginine-glycine-aspartic acid (RGD) loop of fibronectin on various types of surfaces as an approach to assess the availability of this bioactive site for cell-receptor binding [74,75].

Although apparently not yet reported in the literature, approaches involving the application of ligand-docking algorithms and scoring functions, as commonly used for drug design [76], should have substantial potential to provide more rigorous evaluations of the effect of adsorption on the bioactive state of proteins.

2.3.2. Simulation of protein–surface interactions

Given the availability of a suitable set of empirical force field parameters to represent the behavior of each phase of a protein–surface system (i.e., the protein in solution, material surface, and interface), simulations can then be conducted to explore protein adsorption behavior. The primary challenge for this type of simulation is to provide sufficient sampling to efficiently equilibrate the system within a reasonable amount of simulation time, which requires obtaining a Boltzmann-weighted ensemble of the conformational states of the system.

As illustrated above in Fig. 1b, this is particularly challenging because of the rugged potential energy phase space that can be expected for an adsorbed protein, with relatively high energy barriers separating numerous local low-energy conformations. As noted above, conventional MD and MC simulation approaches can be expected to be inadequate to provide sufficient sampling of this type of system within realistic timeframes of a simulation, at least with present computing resources. In order to predict protein adsorption behavior in a manner to provide results that can be compared with experimentally determined values, advanced sampling methods are needed that are able to provide similar Boltzmann-weighted ensemble-averaged properties.

The development of advanced sampling methods that can be applied to such large complex molecular systems with rough energy landscapes represents one of the major challenges and needs in this particular field of research. One of the most popular advanced sampling methods is temperature-based replica exchange (also called parallel tempering). Temperature replica exchange methods, however, are not suitable for very large molecular systems because the number of replicas needed for such simulations can be prohibitively large and computationally inefficient. More efficient Hamiltonian-based REMD methods have been developed to help alleviate this problem, such as replica exchange with solute tempering (REST1 [77] and REST2 [78]), which greatly reduce the number of replicas that are needed for a simulation by basing the number of replicas only on the energetic contributions of a subset of the molecular system, such as the protein. However, these methods may still become computationally too expensive for large proteins.

Our approach to address this sampling problem has been to develop a new advanced sampling method that we specifically designed for application to molecular systems that are too large to be handled using conventional replica exchange methods. We named this method Temperature Intervals with Global Exchange of Replicas, with the second version of this method being called TIGER2 [79,80]. TIGER2 is actually an empirical sampling method that approximately provides Boltzmann-weighted sampling. TIGER2 is a combined MD/MC sampling method that uses a set of replicas of the molecular system each simulated at sequentially elevated temperatures in order to rapidly overcome local energy barriers and effectively provide sampling over the entire phase space of the system. Accordingly, for a protein adsorption simulation, the minimum temperature level (or baseline temperature) is set at the desired temperature of interest (e.g., 298 K) with the maximum temperature set to a level that will fully unfold the protein, thus sampling its full conformational space. The simulation is then run as a series of cycles, with replicas rapidly heated to their assigned temperature level within about 2 ps, run under NVT MD conditions (i.e., constant number of atoms (N), constant volume (V), and constant temperature (T)) for a period of time sufficient to allow for conformational changes to occur (e.g., about 10 ps), and then rapidly quenched down to the baseline temperature and thermally equilibrated for about 3 ps. One of the quenched replicas is then randomly selected for comparison of its potential energy with the potential energy of the baseline replica using the Metropolis Monte Carlo acceptance criterion. The accepted state is then assigned to the baseline temperature for the next thermal cycle while the remaining replicas are reassigned to elevated temperature levels according to their baseline temperature potential energies, with the replica with the highest potential energy assigned to the highest temperature level.

In order for a sampling method to generate a Boltzmann-weighted ensemble of states, the sampling process should satisfy the detailed balance condition. For a TIGER2 simulation, the detailed balance relationship can be expressed as:

$$P_B\left(X_i\right)P_{E∕B}\left(X_j\right)\Pi (i\to j)=P_B\left(X_j\right)P_{E∕B}\left(X_i\right)\Pi (j\to i)$$ (1)

where P_B and P_E/B are the probabilities of selecting the conformational states of the baseline replica and the replica quenched from the randomly selected elevated temperature, respectively, X_i and X_j represent the conformational states of the selected replicas i and j, and π(i → j) and π(j → i) are the transition probabilities for exchanging states i and j and vice versa. The ratio of the transition probabilities is then given as:

$$\frac{\Pi (i\to j)}{\Pi (j\to i)}=\frac{P_B\left(X_j\right)}{P_B\left(X_i\right)}\cdot \frac{P_{E∕B}\left(X_i\right)}{P_{E∕B}\left(X_j\right)}.$$ (2)

Under the assumption that the assigned temperature levels enable the simulation to cover the complete phase space of the molecular system, then the random selection of one of the quenched replicas provides approximately equal probability for selecting either conformational state X_i or X_j (i.e., macroscopic reversibility), thus providing the relationship of P_E/B(X_i) = P_E/B(X_j). Eq. (2) then becomes:

$$\frac{\Pi (i\to j)}{\Pi (j\to i)}=\frac{P_B\left(X_j\right)}{P_B\left(X_i\right)}=\frac{\exp (-\beta E_j)}{\exp (-\beta E_i)}=\exp (-\beta \Delta E_{ij}),$$ (3)

where β is 1/k_BT_B (with k_B being Boltzmann's constant and T_B the baseline temperature). As shown by Eq. (3), the ratio of the transition probabilities of exchange represents the standard Metropolis criterion for Metropolis MC sampling, thus providing an approximately Boltzmann-weighted ensemble of conformational states at the baseline temperature.

The critical issue for the TIGER2 sampling process is then to decide how long the simulation must be run until a full equilibrated set of conformational states is achieved. Our approach to address this issue is to run multiple independent simulations of a given system while comparing the generated ensembles of sampled states using cluster analysis methods. System convergence is considered to be achieved when each independent TIGER2 simulation provides a stable, equivalent ensemble set of conformational states of the system. Once achieved, then analyses can be conducted to calculate average properties from the ensembles of sampled states for comparison with available experimental data to assess the accuracy of the simulations. These comparisons will then either validate the applied methods, or provide direction regarding what modifications may be needed to correct identified errors where predicted behavior substantially deviates from experimentally measured values.

2.4. Extension of empirical force field methods to larger time and length scales

While the development of methods to accurately predict protein–surface interactions will represent a substantial achievement and provide a basis for developing a better understanding of how surfaces can be designed to influence protein adsorption behavior, these developments only represent a starting point for the extension of methods to address higher-order time and length scales so that more complex interactions, such as protein–protein effects, can be address in a simulation.

In order to extend time and length scales for a molecular simulation for a given amount of computation resources requires a reduction in the degrees of freedom that must be represented in the simulation. Two of the most widely used methods to achieve this are by the use of implicit solvation and coarse-grained methods.

2.4.1. Implicit solvation

In order to represent bulk aqueous solution conditions in a simulation of biomolecular behavior in which the molecules of the aqueous solution are explicitly represented by individual water molecules and salt ions, it is necessary to use periodic boundary conditions along with a layer of solvent surrounding the biomolecule that extends beyond the cutoff distance that is being used for the calculation of nonbonded interactions (typically about 15 Å). For example, a spherically shaped protein with a 20Å diameter would require a solvent box of dimensions about 50Å × 50Å × 50Å = 125,000ų, with the water thus occupying about 121,000ų, or about 97% of the volume of the system. Accordingly, about 97% of the time required for the simulation will be taken up by calculating the behavior of the water with only about 3% of the time used to represent the behavior of the protein. Therefore, if the effect of the solvent environment on the behavior of the protein can be implicitly calculated through the use of some analytical function without having to explicitly represent the water and ions, then the simulation could be run about 33× faster, or a system 33× larger could be simulated within the same amount of computational time. The development and application of such analytical means of representing solvation effects (referred to as implicit solvation) is thus very desirable as a means of extending the time and length scales of a simulation.

The protein folding community has adapted and developed several implicit solvation methods over the past several decades for this purpose [81–89]. The most advanced of these methods, include energetic functions that calculate the electrostatic contribution of the solvation of partial charges as well as the representation of hydrophobic interactions as a function of solvent accessibility. Other more simplistic, and thus more unreliable methods simply include a distance-dependent dielectric constant in the Coulombic term of the force field equation to very approximately represent the solvent shielding of electrostatic effects. While very computationally efficient, this latter approach completely neglects hydrophobic interactions, which can be very important for adsorption behavior, and thus this method should be avoided as it cannot adequately represents solvation effects for an adsorbing biomolecule [90,91].

Unfortunately, none of the various implicit solvation methods have been developed and validated to accurately represent amino acid interactions with material surfaces at this time, despite the fact that publications can be found in the literature where these methods are none-the-less applied for peptide and protein adsorption simulations. We have performed evaluations of several of these methods for application to represent the energetics of amino acid interactions with material surfaces and found little consensus between the various methods [92,93]. Despite these current limitations, there is no inherent reason why accurate implicit solvent methods cannot be developed for use for the simulation of protein–surface interactions, and this thus represents an important area for further research and methods development.

2.4.2. Coarse graining methods

Another way of substantially reducing the number of degrees of freedom of a molecular system is to combine groups of atoms in selected segments of a molecular chain into single particles (or beads), which is referred to as coarse graining (CG) [94–96]. CG force field parameters are then generated for the bead segments to represent their bonded and nonbonded interactions with one another in a manner that is similar to what is used in an all-atom force field. Accordingly, CG force field parameters are typically tuned to match the behavior of all-atom simulations for the groups of atoms that the individual beads represent [97,98]. CG methods also typically include implicit solvation for the representation of solvation effects, thus further reducing the number of particles that are explicitly represented in the model system. Following a given CG simulation, the resulting CG beads can be reversed mapped back into an all-atom representation, with subsequent simulations applied to equilibrate the resulting all-atom model. Because of the inherent condensation of the degrees of freedom of a molecular system that is implemented in a CG simulation, validation of the simulation results becomes all the more important to verify that predictions realistically represent the molecular behavior of the system being modeled.

Several CG parameter sets have been developed thus far to represent peptide and protein folding behavior in solution. The most popular of these types are the MARTINI [95,99], GM [100–102], and PRIMO [94] CG force fields. Several groups have recently reported the application of CG force fields for the simulation of peptide and protein adsorption behavior to material surfaces in order to extend time and length scales of the simulation. For example, Akdim et al. [32] have investigated the use of the MARTINI force field to simulate the relatively long-term interactions (i.e., 500 ns) between 12-residue-long peptides and a graphene surface. Wei and Knotts [103] have used the GM model, with interfacial force field parameters generated based on adsorption free energies from our experimental benchmark data set for surfaces of varying hydrophobicity. Their results from simulations of lysozyme adsorption predicted increased degrees of unfolding with increased surface hydrophobicity, in general agreement with experimental observations. Vilaseca et al. [104] have conducted CG simulations to model the competitive adsorption of proteins of varying shapes and sizes with nanoparticles by representing relatively small spherical particles as albumin, larger spherical particles as immunoglobulin (IgG), and large elliptically shaped elements to represent fibrinogen. Each protein particle was represented with its own force field to vary its interactions with other proteins and the surface. MD simulations were then carried out to investigate the competitive adsorption of these three proteins as a function of their respective binding affinities and solution concentrations.

The application of CG methods can theoretically be extended to sequentially increasing levels of coarse grained modeling, with the next level of CG representation being developed to represent the general behavior of the previous level, ideally all of the way up to the macroscopic level. The development of CG methods for the simulation of protein adsorption behavior thus also represents a very promising and active area of methods development.

3. Concluding remarks

As presented above, molecular simulation using empirical force field methods represents an area of research and development with great potential to serve as a valuable resource to enhance our understanding of protein–surface interactions and as a valuable tool for material surface design to control these types of interactions. These methods are certainly not limited to applications involving proteins, but have similar potential for development to address interactions of other types of biomolecules with material surfaces including DNA, RNA, and carbohydrates, as well as the interactions between synthetic molecules and material surfaces for drug delivery applications.

Each of these types of systems presents its own unique set of challenges and problems that must be addressed for the accurate simulation of the respective type of molecular system. However, independent of the type of molecular system being represented, the accurate representation of the molecular behavior of the system will primarily be dependent on the development of reliable force field parameters, obtaining sufficient sampling of the system's conformational behavior, and attention to the application of simulation methods to generate results that are comparable with experimentally measurable behavior for the assessment and validation of simulation results.

As computational resources continue to advance at a rapid pace, the potential capabilities provided by empirical force field based methods continue to advance as well. However, these capabilities will not simply appear on their own, but rather will only be realized if time, effort, and resources are applied to develop them. In this perspectives paper, I provide an overview of the issues that I consider being most critically important for this field to continue to move forward and advance, as well as my own groups’ approaches to address these issues. Many other groups are also actively working to address these issues as well using both similar and alternative approaches. Together, I fully expect that capabilities provided by empirical force field based methods will continue to grow as a critically valuable resource for applications where the interactions between biological molecules in solution and material surfaces are important. The importance of computational approaches to predict molecular behavior will only increase over the decades ahead, especially given the trends to extend understanding down to the nanoscale and beyond. The real challenge will be whether or not molecular simulation methods will be available for use to meet these needs as they arise. Time will tell.