Prosthetic ankle push-off work reduces metabolic rate but not collision work in non-amputee walking

Abstract

Individuals with unilateral below-knee amputation expend more energy than non-amputees during walking and exhibit reduced push-off work and increased hip work in the affected limb. Simple dynamic models of walking suggest a possible solution, predicting that increasing prosthetic ankle push-off should decrease leading limb collision, thereby reducing overall energy requirements. We conducted a rigorous experimental test of this idea wherein ankle-foot prosthesis push-off work was incrementally varied in isolation from one-half to two-times normal levels while subjects with simulated amputation walked on a treadmill at 1.25 m·s⁻¹. Increased prosthesis push-off significantly reduced metabolic energy expenditure, with a 14% reduction at maximum prosthesis work. In contrast to model predictions, however, collision losses were unchanged, while hip work during swing initiation was decreased. This suggests that powered ankle push-off reduces walking effort primarily through other mechanisms, such as assisting leg swing, which would be better understood using more complete neuromuscular models.

Unilateral below-knee amputation is an increasingly common lower limb disability¹ that reduces mobility and adversely affects quality of life². Individuals with amputation expend more energy to walk³,⁴ and experience increased loading and injury of the intact limb⁵. Next-generation robotic prostheses are expected to improve these aspects of performance for amputees⁶.

The increased effort required to walk with conventional prosthetic limbs may be related to observed biomechanical changes at the hip and ankle joints. During the double-support phase of healthy human walking, the trailing limb generates positive power against the body's center of mass while the leading limb absorbs energy, referred to as push-off and collision, respectively⁷,⁸. Joint power⁹ and muscle contraction effort¹⁰ are considerably higher in the ankle than elsewhere in the legs, with most work occurring during push-off. Below-knee amputees exhibit reduced push-off in the affected limb, considering either the ankle¹¹,¹²,¹³ or the whole limb⁴,¹³, presumably as a result of the passive nature of conventional prosthetic feet¹⁴. Individuals with amputation have also exhibited increased hip power on the affected¹¹,¹²,¹³ and intact¹² limbs during early¹¹,¹² and late¹³ stance, along with increased affected-limb hip muscle activation¹⁵ during early stance. This change in hip coordination is commonly thought to be a compensation for reduced push-off from the prosthetic ankle¹¹,¹²,¹⁵. Similarly, individuals with ankle fixation exhibit reduced push-off¹⁶,¹⁷ and increased hip power in early stance¹⁷,¹⁸, usually accompanied by increased energy consumption¹⁶,¹⁷ (although not always¹⁸). Subjects with ankle push-off assistance from an exoskeleton, by contrast, have demonstrated decreased energy consumption¹⁹. These observations suggest a trade-off between ankle and hip work²⁰, leading to the hypothesis that a prosthesis which provides increased positive ankle power will decrease positive hip power, thereby reducing energy consumption.

It is not immediately clear, however, why trading ankle work for hip work would adversely effect walking efficiency. Simple dynamic models of walking, widely used in locomotion research, suggest that hip powering strategies should be less efficient than push-off powering strategies because of their disparate effects on collision losses⁷,⁸,²¹,²²,²³. In these very simple mathematical models, trailing limb push-off mitigates leading limb collision, reducing overall mechanical energy requirements, while work done at the hip does not. This concept has been used to explain observed coordination patterns in humans²¹,²²,²⁴,²⁵,²⁶,²⁷ and animals²¹,²⁸,²⁹,³⁰, and to design walking robots³¹,³²,³³,³⁴,³⁵, robotic exoskeletons¹⁹,³⁶, and robotic prostheses¹³,³⁷,³⁸,³⁹,⁴⁰,⁴¹.

The relationship between push-off and collision in these simple models has also been used to explain increased energy cost in amputees. Reduced push-off in the affected limb, presumably the result of reduced positive work at the prosthetic ankle¹⁶,¹⁷, has been implicated as the cause of the observed increases in the simultaneous intact-limb collision⁴,¹³. This has led to the hypothesis that a prosthesis which increases positive ankle power during push-off will decrease the energy dissipated during collision of the contralateral limb, thereby reducing overall mechanical work requirements and metabolic energy consumption²³,⁴².

These simple-model predictions have not yet been validated in a well-controlled experiment, and a mixture of supporting and opposing observations can be made from related studies. Some ankle fixation experiments have demonstrated increased leading limb collision losses¹⁶, while others have not¹⁸. Passive-elastic prostheses with higher rates of energy return can increase push-off somewhat⁴³,⁴⁴, but have not reduced collision losses⁴⁴ or metabolic rate⁴⁵,⁴⁶,⁴⁷ (with few exceptions⁴⁸,⁴⁹). Several robotic ankle-foot prostheses that provide ankle push-off work at levels similar to that of a healthy biological ankle have been developed¹³,³⁷,³⁸,³⁹,⁴⁰,⁴¹,⁵⁰,⁵¹,⁵², but only one of these has demonstrated improved metabolic cost when compared to conventional devices⁴¹. Such comparisons have been complicated by the many differences between devices other than ankle push-off work, such as mass, geometry, stiffness and control, any of which could be responsible for observed differences in energy use. It remains unclear whether simple model predictions about the relationship between ankle push-off, collision losses, overall mechanical work and metabolic energy cost are relevant to the design of robotic prostheses.

The aim of this study was to isolate and characterize the relationship between ankle push-off work, metabolic energy cost, and underlying mechanics in human locomotion. We performed an experiment in which ankle push-off work was varied over a wide range using a high-performance ankle-foot prosthesis emulator⁵³. Simulated amputee subjects wearing the prosthesis using an immobilizer boot walked at a fixed speed on a treadmill. We hypothesized that increased prosthesis push-off would reduce contralateral-limb collision, thereby reducing both overall mechanical energy use and the portion borne by the human user, leading to a reduction in metabolic energy consumption. We hypothesized that the proximate cause of reduced metabolic rate would be reduced positive hip work during stance. We expect the quantitative relationships determined in this study to provide new, well-controlled tests of several prevailing theories of the energetics of human walking while informing the design of improved prosthetic devices.

Results

With increasing prosthetic ankle push-off work, whole-limb push-off work on the prosthesis side increased and metabolic energy consumption decreased. Energy losses at collision were unchanged, while both contralateral-limb rebound work and the biological component of prosthesis-side push-off appeared to decrease. During prosthesis-side swing initiation, positive work at the hip joint decreased substantially and negative work at the knee increased slightly. The average stride period was 1.2 ± 0.093 s (mean ± s.d.), and did not change across conditions (P = 1).

Prosthetic ankle mechanics

Prosthesis mechanics during push-off varied widely across conditions, while behavior during the Dorsiflexion phase of stance remained consistent. As increasing values of push-off were commanded, peak prosthesis power (Fig. Ia) and measured prosthesis push-off work (Fig. Ib) increased significantly (P = 3 · 10⁻²⁵). Push-off work was significantly different from the value in the Zero work condition for all other conditions (P = 6 · 10⁻⁶, 6 · 10⁻⁶, 9 · 10⁻⁷, 4 · 10⁻⁷, 4 · 10⁻⁷, and 2 · 10⁻⁴, for comparisons to Negative Low, Low, Medium Low, Medium, Medium High, and High conditions, respectively). Negative work did not change across conditions (P = 0.9). In the Negative Low work condition, positive prosthesis work was 0.41 ± 0.082 times the positive ankle work measured in Normal Walking, negative prosthesis work was 0.69 ± 0.11 times that of Normal Walking, and net prosthesis work was −1.9 ± 0.26 times that of Normal Walking. In the High work condition, positive prosthesis work was 1.8 ± 0.32 times that of Normal Walking, negative work remained unchanged at 0.73 ± 0.11 times that of Normal Walking, and net prosthesis work was 11 ± 2.8 times that of Normal Walking. Positive work was most similar to Normal Walking in the Medium work condition (1.0 ± 0.11 times Normal Walking). Stride-averaged work rate was closest to zero in the Zero work condition (0.0078 ± 0.011 J · kg⁻¹ · s⁻¹). Positive, negative and net prosthesis work can also be visualized as the area under and between curves in torque-angle space (Fig. Ic).

Figure 1. Prosthetic ankle mechanics calculated from on-board sensor data.

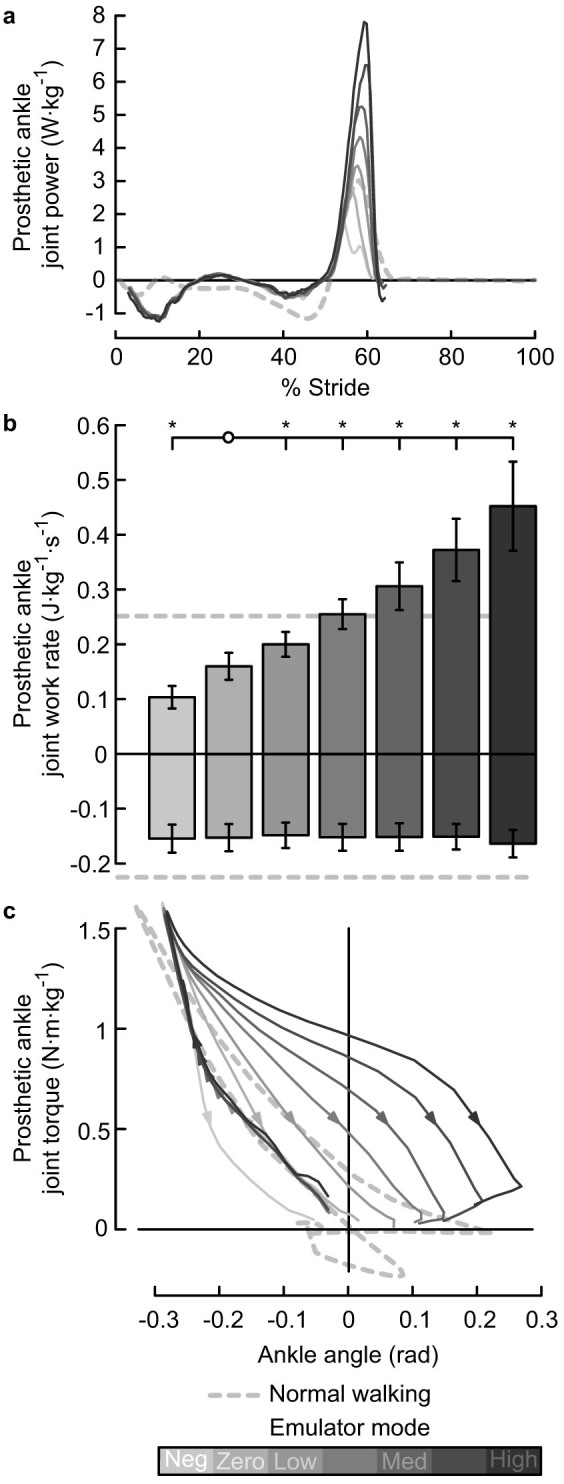
(a) Joint power. Lines indicate average trajectories for each condition, with darker lines corresponding to conditions with higher prosthesis push-off work. Dashed line indicates biological ankle joint power measured using inverse dynamics during Normal Walking. (b) Stride-averaged work rate. Positive and negative work were calculated separately. Error bars indicate inter-subject standard deviation, and *s indicate statistical significance. (c) Joint torque versus joint angle. Direction of motion indicated by arrows. Dorsiflexion curves are overlapping. The area inside each loop is the net prosthesis push-off work for that condition.

Metabolic energy consumption

Metabolic rate decreased significantly with increasing prosthetic ankle net work (P = 1 · 10⁻¹⁴, Fig. II). Metabolic rate was significantly different from the value in the Zero work condition for all other conditions (P = 4 · 10⁻³, 4 · 10⁻³, 2 · 10⁻³, 2 · 10⁻³, 1 · 10⁻⁴, 7 · 10⁻³, respectively). Least squares regression showed the best fitting exponential relationship between the change in metabolic rate, P_m, and stride-averaged prosthesis work rate, P_p, to be 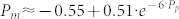(R² = 0.7, P = 1·10⁻¹⁷). This fit had less residual error than 1^st, 2^nd and 3^rd order polynomial fits. In the region between −0.05 and 0.05 J · kg⁻¹ · s⁻¹ in net prosthesis work rate, metabolic rate was reduced by approximately 4 W · kg⁻¹ for each 1 J · kg⁻¹ · s⁻¹ of additional prosthesis work per second (R² = 0.5, P = 2·10⁻⁵). This rate of return is consistent with prosthesis work directly replacing muscle fiber work (see Supplementary Fig. 1 for more details). For higher levels of net prosthesis work, metabolic rate continued to decrease but with diminishing returns. Inter-subject variability increased for high values of net prosthesis work rate; for 5 out of the 10 subjects, the greatest prosthesis work rate corresponded to the lowest metabolic rate (individual data provided in Supplementary Fig. 2). In the Negative Low prosthesis work condition the average change in metabolic rate was 0.14 ± 0.039 W · kg⁻¹, and in the High prosthesis work condition the average change in metabolic rate was −0.48 ± 0.25 W · kg⁻¹. Net metabolic rate in the Zero work condition was 3.6 ± 0.46 W · kg⁻¹ and net metabolic rate during Normal Walking was 2.7 ± 0.37 W · kg⁻¹.

Figure 2. Metabolic rate decreased with increasing ankle push-off work.

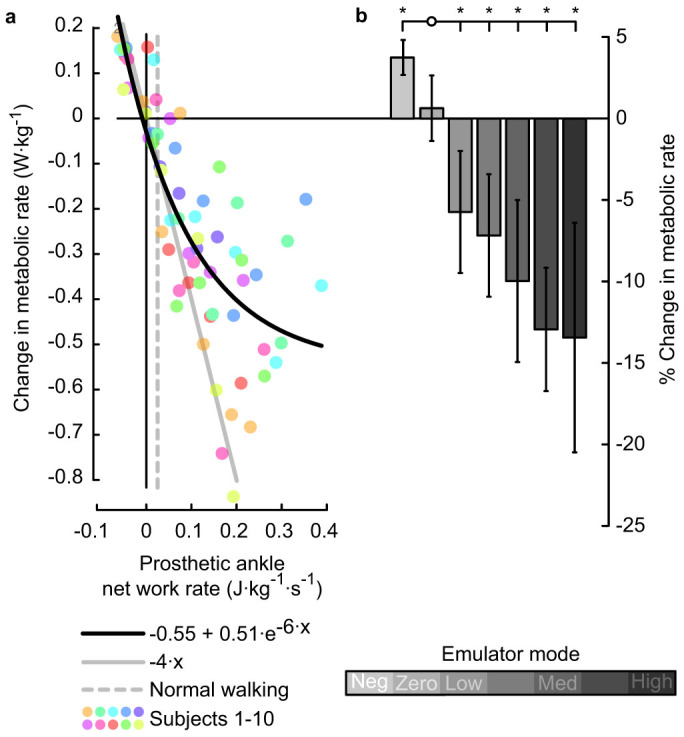
(a) Change in metabolic rate versus net prosthetic ankle stride-averaged work rate. Colored dots indicate data from individual subjects. Heavy black line is an exponential fit to the data. Solid gray line provides a reference for the rate of metabolic reduction if prosthesis work replaced muscle fiber work directly at 25% muscle efficiency. Dashed gray line indicates net biological ankle work rate in the Normal Walking condition. (b) Change in metabolic rate averaged across subjects for each condition. Shading indicates condition, error bars indicate inter-subject standard deviation, and *s indicate statistical significance. % change calculated with respect to the net metabolic rate at zero net prosthesis work.

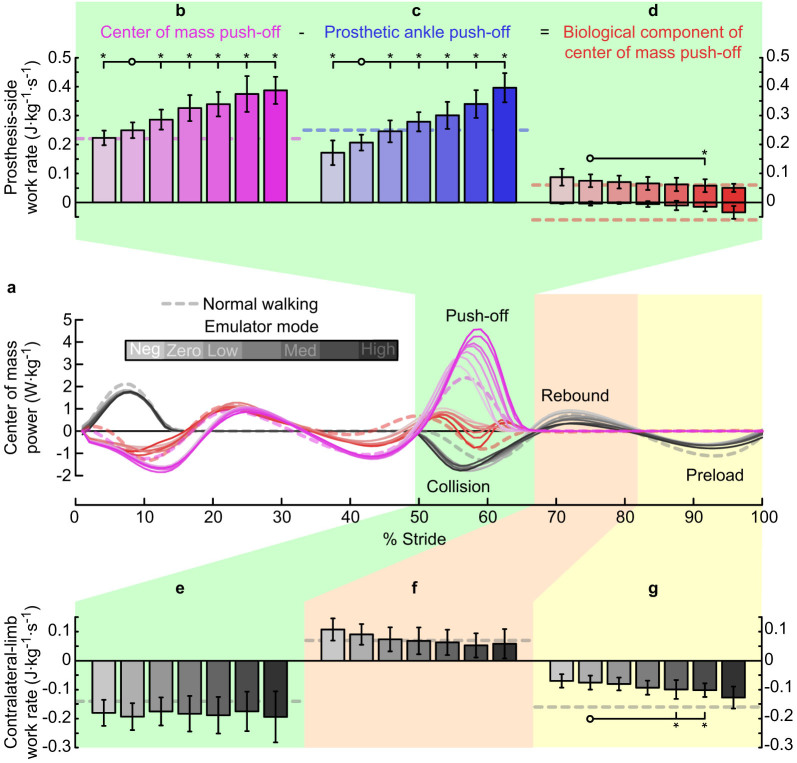
Center of mass mechanics

Increased prosthesis push-off led to increased prosthesis-side center of mass push-off, but did not decrease contralateral-limb collision work (Fig. III). Increases in whole-limb push-off work on the limb using the prosthesis were significant (P = 2 · 10⁻¹², Fig. IIIb), and push-off work was significantly different from the value in the Zero work condition for all other conditions (P = 2 · 10⁻³, 1 · 10⁻³, 2 · 10⁻³, 4 · 10⁻⁵, 7 · 10⁻⁵, and 1 · 10⁻³, respectively). The biological component of whole-limb push-off work showed a significant downward trend with increasing prosthesis push-off, in both positive and negative components (P = 0.04 and P = 4 · 10⁻⁵, respectively, Fig. IIId). In the contralateral limb, negative work during collision was unchanged across conditions (P = 1, Fig. IIIe). Positive work during contralateral-limb rebound appeared to decrease with increased prosthesis push-off (P = 0.08, Fig. IIIf). Negative work during contralateral-limb preload increased with increasing prosthesis push-off (P = 2 · 10⁻³, Fig. IIIg). Total stride-averaged positive center of mass work rate, the accumulation of all positive work done throughout the stride, increased from 0.58 ± 0.058 J · kg⁻¹ · s⁻¹ in the Negative Low condition to 0.66 ± 0.11 J · kg⁻¹ · s⁻¹ in the High prosthesis work condition, an increase of 14% (P = 0.03). The biological component of total positive work rate decreased from 0.46 ± 0.043 J · kg⁻¹ · s⁻¹ in the Negative Low condition to 0.35 ± 0.072 J · kg⁻¹ · s⁻¹ in the High prosthesis work condition, a decrease of 24% (P = 0.03), possibly indicating a reduction in associated muscular effort (Supplementary Fig. 1).

Figure 3. Center of mass power for each limb and center of mass work for key phases of the gait cycle.

(a) Center of mass power versus percent stride. Lines indicate average trajectories for each condition, with darker lines corresponding to increased prosthesis push-off work. Magenta lines are mechanical power of the prosthesis-side limb on the center of mass. Red lines are the biological component of prosthesis-side mechanical power. Gray lines are contralateral-limb power on the center of mass. Top: (b) Prosthesis-side center of mass work rate during push-off, (c) prosthetic ankle joint power during push-off, and (d) the biological component of center of mass work rate during push-off, calculated as b−c. Bottom: Center of mass work rate of the contralateral limb during (e) collision, (f) rebound, and (g) preload phases. Error bars indicate inter-subject standard deviation, *s indicate statistical significance.

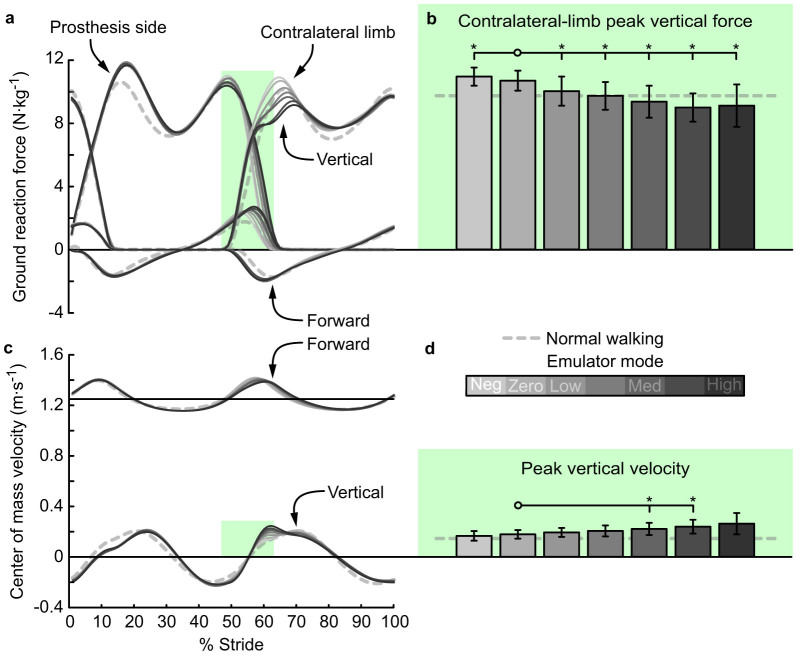
Although contralateral-limb collision work was not affected by prosthesis push-off, contralateral-limb ground reaction forces during double-support were affected (Fig. IVa). Peak vertical force decreased significantly with increasing prosthesis push-off (P = 2 · 10⁻⁵, Fig. IVb), and peak vertical force significantly differed from the value in the Zero work condition for all other conditions (P = 0.04, 2 · 10⁻³, 0.01, 2 · 10⁻⁴, 4 · 10⁻⁵, and 0.01, respectively). Center of mass velocity was oppositely affected (Fig. IVc), as peak vertical velocity increased with increasing prosthesis push-off work (P = 1 · 10⁻³, Fig. IVd).

Figure 4. Ground reaction forces and center of mass velocity were affected by increasing ankle push-off work.

(a) Ground reaction forces versus percent stride. Lines indicate average trajectories for each condition, with darker lines corresponding to conditions with higher prosthesis push-off work. (b) Peak ground reaction force on the contralateral limb during the double support period, indicated by green shading, decreased with increased prosthetic ankle push-off work. (c) Center of mass velocity versus percent stride. (d) Peak center of mass velocity during the double support period, indicated by green shading, increased with increased prosthetic ankle push-off work. Error bars indicate inter-subject standard deviation and *s indicate statistical significance.

Joint mechanics

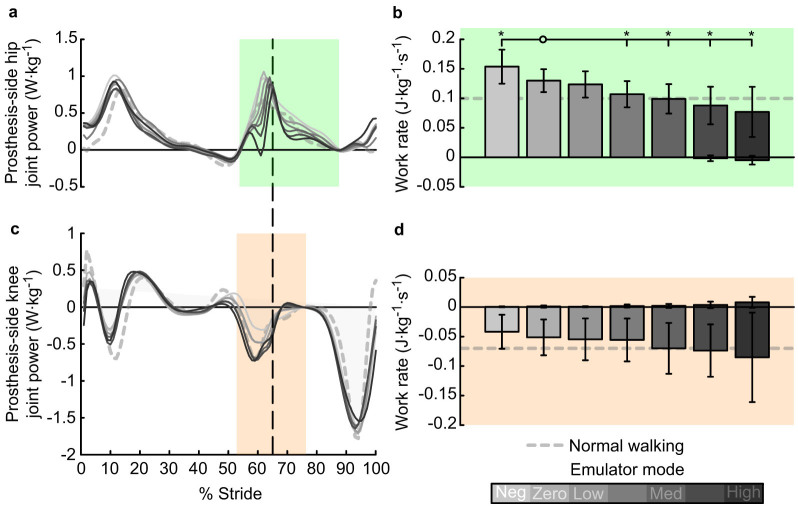
Prosthesis-side hip work during swing initiation decreased significantly with increasing prosthetic ankle push-off work (P = 4 · 10⁻⁶, Fig. Va&b). This component of hip work differed significantly from the Zero work condition in all other conditions except the Low work condition (P = 0.02, 0.2, 4 · 10⁻³, 1 · 10⁻³, 5 · 10⁻³, and 0.02, respectively). In the Negative Low prosthesis work condition, positive hip work rate during swing initiation was 0.15 ± 0.029 J · kg⁻¹ · s⁻¹. In the High prosthesis work condition, this component of hip work rate was 0.077 ± 0.043 J · kg⁻¹ · s⁻¹. Prosthesis-side knee work showed a trend toward increased negative work during swing initiation, although the trend was not statistically significant (P = 0.4, Fig. Vc&d). Total biological joint work decreased significantly with increasing prosthesis push-off (P = 7 · 10⁻¹⁴, Supplementary Fig. 1). Complete sagittal-plane joint kinematics, kinetics, and power for both limbs are included in Supplementary Fig. 4A & 4B.

Figure 5. Hip and knee joint power on the prosthesis side.

(a) Hip joint power versus percent stride. Lines indicate average trajectories for each condition, with darker lines corresponding to conditions with higher prosthesis push-off work. (b) Hip joint work rate during push-off and early swing, or the H3 region⁹ indicated by green shading, decreased with increased prosthetic ankle push-off work. (c) Knee joint power versus percent stride. (d) Negative work at the knee joint during swing initiation, or the K3 region⁹ indicated by red shading, showed a trend toward increasing in magnitude with increasing prosthetic ankle push-off work. Error bars indicate inter-subject standard deviation, and *s indicate statistical significance.

Discussion

A wide variety of mechanical designs and control approaches could be incorporated into robotic prostheses, making it difficult to select device functionalities that provide meaningful benefits to users. Simple dynamic models of walking provide predictions that could, if validated, greatly simplify this design problem. Such models have predicted a causal relationship between reduced trailing limb ankle push-off work, increased contralateral-limb collision losses, increased overall mechanical work requirements, and increased energetic cost of walking for amputees using passive-elastic prostheses. We conducted a tightly-controlled experimental test of this concept, wherein simulated amputees were presented with a broad range of ankle push-off work while gait mechanics and energy use were measured. Increased trailing limb push-off reduced the metabolic cost of walking substantially. In direct contradiction with simple model predictions, however, increased push-off did not reduce leading limb collision losses or overall center of mass work. Instead, we observed reduced prosthesis-side hip power during double support and early swing, activity associated with initiation of leg swing⁵⁵,⁵⁶. This would suggest a lower ceiling for the maximal energetic benefit of increased prosthetic ankle push-off, since muscle activity during the stance phase is thought to comprise a larger portion of the overall effort of walking than swing phase activity. These results demonstrate the need for more detailed predictive models of human walking and emphasize the value of human experiments early in the process of developing wearable robots.

In a predictive model, human-like limb segmentation and muscle-tendon actuation would likely be necessary to capture the observed changes in hip mechanics and their implications for whole-body energy cost. Such elements would also allow for catapult-like mechanics that may be important in explaining the presence of normal ankle work disproportionate to its apparent impact on metabolic rate⁵⁷. Early attempts to use this type of model to make predictions about human responses to new device designs are promising⁵⁸,⁵⁹, but have yet to be validated.

The substantial reductions in metabolic energy use with increased prosthesis work were well explained by concomitant reductions in human joint work. For Negative Low to Medium Low levels of push-off, metabolic rate decreased by about 4 W · kg⁻¹ for each additional 1 J · kg⁻¹ · s⁻¹ of net prosthesis work per second (Fig. II). This reduction is quantitatively consistent with prosthesis work directly replacing muscle fascicle work, since muscles operate at an efficiency of about 25% in converting metabolic energy into positive mechanical work⁶⁰. For higher levels of prosthesis push-off, however, metabolic energy consumption continued to decrease but at a diminished rate. The sum of all positive and negative joint work, scaled according to expected muscle efficiencies, closely corresponded to this trend, with better correlation than either direct replacement of muscle work by the device or changes in the biological component of total center of mass work (Supplementary Fig. 1). The most substantial changes in joint work occurred at the prosthesis-side hip during double-support and early swing, which accounted for approximately 60% of the change in total positive joint work (Fig. V). Increasing absorption at the prosthesis-side knee joint during the same period might also help to explain diminishing returns with increasing prosthesis push-off. These results suggest that total joint work may be a useful component of the objective function when optimizing assistive device designs in simulation, although it is unlikely that this is the precise or complete mechanism by which increased prosthesis work reduced metabolic rate.

For all subjects, energy cost was minimized when the prosthesis provided far more push-off work than the biological ankle. On average, energy cost continued to decrease even at the highest level of prosthesis work, which corresponded to 1.8 times the normal value for positive work and 11 times the normal value for net ankle work. It appears that most subjects would have benefited from even more work input (Supplementary Fig. 2). This finding seems natural in retrospect; unlike energy expended by muscles, prosthesis work incurred no additional effort to the user, shifting the balance of costs. An analogous finding was that the condition in which temporal outcomes were least asymmetric (Medium⁶¹, Supplementary Fig. 5) was not the condition with the lowest metabolic rate. Another benefit of greater-than-normal prosthesis push-off was reduced limb loading associated with osteoarthritis (Supplementary Fig. 3), confirming observations from a prior comparison of multi-featured devices⁵⁴. Imitating some aspect of unimpaired gait may be a reasonable starting point in the design of robotic prostheses, but these results demonstrate that the human-robot system can have significantly different optimal coordination patterns.

Timing of ankle push-off also seems to affect the energetics of walking, and the value applied here seems close to optimal for this system. Simple dynamic models of walking suggest that pushing off with the trailing limb just before leading limb heel strike minimizes collision losses and reduces energy cost by a factor of two to four²¹,²²,⁶². In this experiment, the onset of push-off and of collision were coincident, the observed increases in push-off work took place in the later part of collision, and peak push-off power occurred later with increasing push-off work (Fig. III). This raises the possibility that the timing of push-off was too late to have the predicted effects. Fortunately, we have also conducted a study on push-off timing that suggests the onset used here is approximately optimal. In this separate study, the timing of push-off was varied across a wide range while net push-off work was kept constant [Malcolm, P., Quesada, R. E., Caputo, J. M., Collins, S. H.]. We again found that collision work was unaffected, while metabolic rate was minimized by the latest onset of push-off work. These results are consistent with anecdotal reports of preferred timing from another robotic ankle prosthesis⁶³. It therefore seems that push-off timing is not responsible for the mismatch between trends in collision work predicted by simple models and those observed in this experiment.

Large inter-subject variability with higher push-off work suggests a need for individualized device designs. On average, metabolic rate diminished exponentially with increasing push-off, but some subjects exhibited continued improvements while others experienced increased costs and apparent local minima (Supplementary Fig. 2). These differences could be related to physiology, learning or prior experience. Individualized tuning of prosthesis behavior during prescription, check-ups or even online might therefore provide a significant benefit to users.

This experimental protocol must be performed on individuals with amputation in order to make accurate predictions about optimal push-off work in commercial robotic prostheses. People with simulated and actual amputation can exhibit qualitatively different responses to interactions with the same prostheses¹³. The immobilizer boot that subjects wore added about 2% body mass to the prosthesis-side limb, which could have increased the metabolic cost of leg swing by up to 20%⁶⁴. Hip joint mechanics, however, suggested only a 5% increase in metabolic rate in the Negative Low condition compared to Normal Walking, with hip activity lower than in Normal Walking in the High condition (Fig. V), inconsistent with the relative importance of swing being greater due to added mass. Coordination patterns could also be affected by differences in the mechanical interface with the body, differences in leg length and shoe shape, or neuromuscular differences in the residual limb. We are currently conducting this protocol among unilateral below-knee amputees, and we expect the results to provide quantitative design guidelines for powered ankle-foot prostheses.

Methods

We used an experimental ankle-foot prosthesis emulator to systematically vary ankle push-off in isolation from other prosthesis features. We controlled push-off work by setting a desired relationship between joint torque and joint angle during the push-off phase. We applied conditions with prosthesis push-off work ranging from 50% to 200% of the push-off work observed during normal walking. Ten subjects with simulated amputation completed the protocol while wearing the prosthesis via an immobilizer boot. We compared prosthesis mechanics, metabolic energy consumption, center of mass mechanics and joint mechanics across conditions.

Universal ankle-foot prosthesis emulator

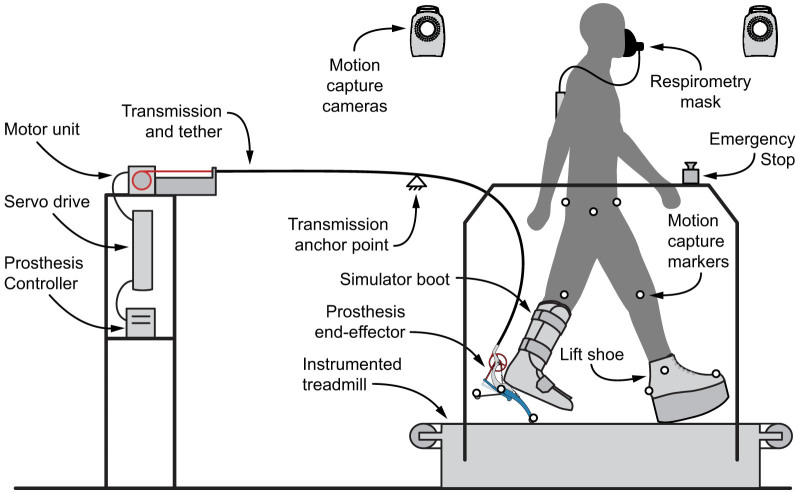
Precise regulation of push-off work across conditions was enabled by an experimental ankle-foot prosthesis emulator⁵³. The emulator provided an exceptionally broad range of push-off work, from −5 to 30 J of net work per step. Adjustments were made electronically, with all mechanical features of the prosthesis (such as size, mass, heel stiffness, and alignment) unchanged across conditions. Mechanical power and computer control of the prosthesis were generated off-board and provided via a tether as subjects walked on a treadmill (Fig. VI). The tether was supported near the subject to minimize interference with natural motions. Participants wore the ankle-foot prosthesis on their right leg via a simulator boot which immobilized the ankle. The prosthesis was attached beneath the biological limb along the centerline of the tibia. To keep leg lengths equal, a lift shoe with a rocker bottom was worn on the other leg (Fig. VI). The mass of the prosthesis, simulator boot, and lift shoe were 1.2 kg, 1.9 kg, and 1.0 kg, respectively. The length of the prosthetic foot was 0.22 m, the heel of the prosthesis was 0.070 m to the rear of the centerline, and the total added leg length was 0.13 m.

Figure 6. Schematic of the experimental setup.

The ankle-foot prosthesis emulator comprised a powerful off-board motor and controller, a flexible tether transmitting mechanical power and sensor signals, and a lightweight instrumented ankle-foot prosthesis. Measures of prosthesis function were made using onboard sensors. Human subject mechanics and energetics were calculated from data collected using a reflective-marker motion capture system, a split-belt treadmill with force sensing, and a portable respirometry system.

Prosthetic ankle joint work was regulated using impedance control in two phases. In each phase, joint torque was controlled as a function of ankle angle (Fig. VII). The Dorsiflexion phase began at heel contact and lasted until the velocity of the ankle joint reversed direction, usually around 80% of the stance period, when the prosthesis switched into the Plantarflexion phase. Dorsiflexion phase behavior was constant across conditions, while the torque profile in the Plantarflexion phase was adjusted. This changed work production during ankle push-off without altering other aspects of prosthesis function. Nominal parameters were selected to emulate the behavior of the biological ankle during normal walking at the same speed³⁸. Ankle push-off work was varied across the widest range possible without altering the controller or damaging the system.

Figure 7. Impedance control law used during walking trials.

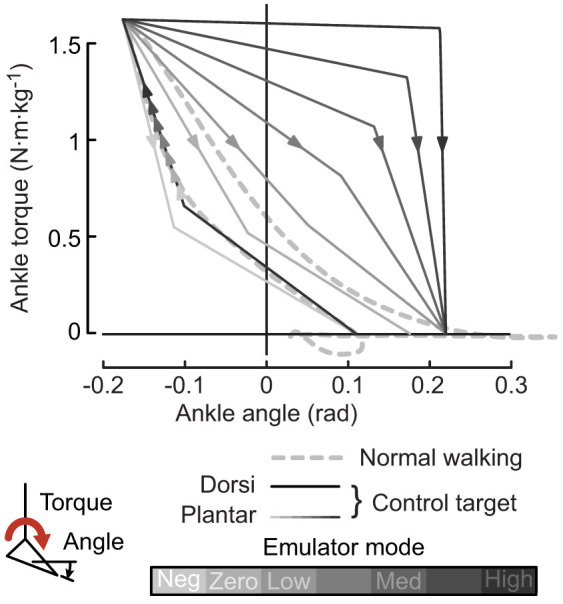
Desired torque is a piecewise linear function of ankle position, with separate dorsiflexion (negative velocity) and plantarflexion (positive velocity) phases. Gray lines indicate programmed trajectories for each condition, with darker lines corresponding to conditions with higher prosthesis push-off work. Plantarflexion segments were manipulated across conditions to alter the net positive ankle joint work over the step cycle. Dashed line indicates biological ankle joint power measured in [38].

Experimental protocol

We tested seven conditions across a wide range of net push-off work. Net work, defined as the difference between positive work during push-off and negative work during the rest of the stance period, was linearly increased from −27% to 490% of the value for normal walking (from [38]) in conditions referred to as Negative Low, Zero, Low, Medium Low, Medium, Medium High, and High, respectively (Fig. VII). Subjects also completed a Quiet Standing trial and a Normal Walking trial in street shoes. Treadmill speed was set to 1.25 m·s⁻¹. Subjects walked for 7 minutes to reach steady state. To allow adequate time for acclimation, subjects completed the entire protocol three times with one day of rest between each collection. On each day, all prosthesis conditions were presented in random order. Reported measures are from the final collection.

Ten healthy able-bodied male adults participated in the study (N = 10; age = 28 ± 4.4 yrs; body mass = 78 ± 7.7 kg; leg length = 0.87 ± 0.056 m, greater trochanter to lateral malleolus). Sample size was selected according to standard practice for locomotion research. All subjects completed all conditions except Medium Low (N = 9) and High (N = 6). Data for Medium Low were not obtained for one subject due to hardware failure. The final six subjects were presented with the High condition, which was enabled by hardware improvements midway through the study. This study was approved by the Carnegie Mellon Institutional Review Board, was carried out in accordance with the approved guidelines, and all subjects provided written informed consent. Subjects were blinded to all prosthesis conditions, but experimenter blinding was not possible while operating the control system.

Data analysis

Prosthesis power and work were calculated from on-board sensor measurements. Joint position and torque were measured using encoders and displacement of a series spring (calibrated as described in [53]). Ankle velocity was obtained by differentiating ankle position and applying a 3^rd order low-pass filter with a cutoff frequency of 50 Hz. Prosthetic ankle power was computed as the product of ankle velocity and ankle torque, and ankle work was computed as the integral of ankle power in time. Positive and negative work were considered separately, and their sum was defined as net prosthesis work. Prosthesis work is presented as stride-averaged work rate, or work divided by stride time, to allow direct comparisons with metabolic rate and to account for differences in stride time across subjects.

Metabolic energy consumption was estimated using indirect calorimetry. Gas concentrations and flow rates were measured using a commercial respirometry system. Breath-by-breath data were averaged across the last three minutes of each trial, when subjects had reached steady state, and metabolic energy consumption was then calculated using a standard formula⁶⁵. For each subject, we determined the exponential function of the form 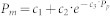that fit the relationship between metabolic rate, P_m, and net prosthesis power, P_p, with least squared error. We defined change in metabolic rate as metabolic rate minus the value of the best fit function corresponding to zero net prosthesis work rate, or P_m − (c₁ + c₂). Change in metabolic rate therefore captured the effects of adding active power to a conventional passive prosthesis. We defined net metabolic rate as metabolic rate minus the metabolic rate during the Quiet Standing trial.

We estimated mechanical power at each joint in the lower limbs using three-dimensional inverse dynamics analysis. The positions of bony landmarks on the legs, and analogous features on the robotic prosthesis, were tracked using a commercial reflective marker motion capture system. Time derivatives of position trajectories were calculated and filtered with a 3^rd order low-pass filter with a cutoff frequency of 7.5 Hz. Body segment mass properties were estimated from anthropometric regression equations⁶⁶,⁶⁷, and mass properties of the simulator boot, lift shoe, and prosthesis were determined by weighing and suspension in different configurations. Joint torques were calculated as the torques required to cause the observed segment accelerations⁶⁸. We calculated positive or negative joint work over periods of interest as the time integral of joint power over those periods. Joint work is presented as stride-averaged work rate, or work divided by stride time, to allow direct comparisons with metabolic rate and to account for differences in stride time across subjects.

We estimated work done on the center of mass by the legs using the individual limbs method. Ground reaction forces were measured using a commercial instrumented split-belt treadmill and passed through a 3^rd order low-pass filter with a cutoff frequency of 7.5 Hz. Center of mass velocity was calculated as the time integral of measured force divided by body mass, and center of mass power was calculated as the dot product of center of mass velocity and ground reaction force for each limb. The biological component of center of mass power on the prosthesis side was calculated as whole-limb center of mass power minus prosthetic ankle joint power as calculated by inverse dynamics analysis (so as to include contributions of both the actively-controlled ankle joint and the passive heel). We calculated positive or negative center of mass work as the integral of center of mass power over sequential periods of stance known as collision, rebound, preload and push-off⁸. Center of mass work is presented as stride-averaged work rate, or work divided by stride time, to allow direct comparisons with metabolic rate and to account for differences in stride time across subjects. Peak ground reaction force and center of mass velocity during the double-support period were also calculated.

We performed statistical comparisons of metabolic rate, center of mass mechanics and joint mechanics across conditions. Center of mass and joint trajectories were divided into strides, normalized in time as percent stride, and averaged across strides. Scalar values, such as work and peak force, were calculated on individual subjects' average trajectories and then averaged across subjects, so as to avoid artifacts from smoothing. Variability is represented as inter-subject standard deviation. All measures were normalized to subject body mass and averaged across subjects. Analysis of variance was used to determine the significance of each outcome. For each significant outcome, a paired t-test was then applied to compare conditions. We compared each condition to the Zero work condition, thereby capturing effects of adding or removing power from a conventional passive prosthesis. We then applied a Sidak-Holm step-down⁶⁹ and used a significance level of P ≤ 0.05.

Author Contributions

J.M.C. and S.H.C. designed the study, J.M.C. performed the experiment and analyzed the data, and S.H.C. and J.M.C. wrote and edited the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

Supplementary Information

Simulated amputee user walking with the universal ankle-foot prosthesis emulator