Automated Tract Extraction via Atlas Based Adaptive Clustering

Abstract

Advancements in imaging protocols such as the high angular resolution diffusion-weighted imaging (HARDI) and in tractography techniques are expected to cause an increase in the tract-based analyses. Statistical analyses over white matter tracts can contribute greatly towards understanding structural mechanisms of the brain since tracts are representative of the connectivity pathways. The main challenge with tract-based studies is the extraction of the tracts of interest in a consistent and comparable manner over a large group of individuals without drawing the inclusion and exclusion regions of interest. In this work, we design a framework for automated extraction of white matter tracts. The framework introduces three main components, namely a connectivity based fiber representation, a fiber clustering atlas, and a clustering approach called Adaptive Clustering. The fiber representation relies on the connectivity signatures of fibers to establish an easy correspondence between different subjects. A group-wise clustering of these fibers that are represented by the connectivity signatures is then used to generate a fiber bundle atlas. Finally, Adaptive Clustering incorporates the previously generated clustering atlas as a prior, to cluster the fibers of a new subject automatically. Experiments on the HARDI scans of healthy individuals acquired repeatedly, demonstrate the applicability, the reliability and the repeatability of our approach in extracting white matter tracts. By alleviating the seed region selection or the inclusion/exclusion ROI drawing requirements that are usually handled by trained radiologists, the proposed framework expands the range of possible clinical applications and establishes the ability to perform tract-based analyses with large samples.

1. Introduction

Due to advancements in the diffusion weighted imaging techniques, white matter (WM) structures in the human brain can now be studied in vivo at a micro-structural level (Basser et al., 1994a, 1994b). New imaging protocols such as the high angular resolution diffusion-weighted imaging (HARDI) (Tuch et al., 1999, 2002), based on their superior characterization of the complex WM structure in regions of fiber crossing, have improved the reliability of fiber tractography (Côté et al., 2013; Fillard et al., 2011; Tournier et al., 2012). This fact has led to an increasing interest in tract based analyses that have hitherto been performed over traditional (diffusion tensor based) tractography methods (O’Donnell et al., 2009; Smith et al., 2006; Snook et al., 2007). As an alternative to conventional statistical approaches such as the voxel based morphometry (VBM) (Ashburner & Friston, 2000) and the region based morphometry (RBM) (Mukherjee et al., 2001), statistical analyses over WM tracts can contribute greatly towards the structural analysis of the brain since fiber bundles are the most representative of the connectivity pathways.

In this article, we refer to each single pathway of tractography as fiber. Groups of fibers are called fiber bundles. We use the term tract to refer to a WM structure of interest such as the arcuate or the corpus callosum, which can consist of a single (the arcuate) or multiple (the corpus callosum) fiber bundles. The main challenge with tract based studies involving group or longitudinal statistics, is the extraction of the tract of interest (TOI) from the whole brain tractography results in a consistent and comparable manner over a large group of individuals. Early works on tract extraction were limited to single subject studies and big, easily discernible WM tracts like the corpus callosum due to the lack of tools that enable extracting TOIs in different individuals automatically without requiring any knowledge of detailed anatomy. Recent research on fiber clustering (Guevara et al., 2012; O’Donnell & Westin, 2007; Tunc et al., 2013; X. Wang et al., 2011; Wassermann et al., 2010) has introduced several advancements to facilitate large scale population studies, increasing the applicability of fiber clustering in the real life clinical applications. In this work, we design a framework for automated extraction of the TOIs by introducing a group-wise consistent fiber clustering approach. This consists of firstly defining a connectivity based fiber representation, then using this representation to build a fiber bundle atlas, and finally an adaptive clustering of a new subject based on this atlas.

The common approaches for tract extraction rely on fiber tractography by using either supervised or unsupervised post processing of the reconstructed fibers. Supervised methods require the placement of inclusion and exclusion ROIs (regions of interest) to extract WM tracts by eliminating the unintended fiber pathways (Mori & van Zijl, 2002; Wakana et al., 2007). This procedure can be automated by registering different scans of the subjects to a template space (Aarnink et al., 2014), thereby extracting any TOI simultaneously. Unsupervised methods, on the other hand, utilize fiber-based features within a clustering framework to automatically generate tracts that are characterized inherently by these features (Maddah et al., 2008; O’Donnell et al., 2006; Tunc et al., 2013). As an alternative to fiber tractography based approaches, another set of supervised methods have been proposed for direct segmentation of WM tracts by classification using voxel-based features such as principal diffusion direction, spherical harmonics coefficients, fractional anisotropy (FA) values, and crossing angles (Bazin et al., 2011; Ito et al., 2013; Nazem-Zadeh et al., 2011; W. Zhang et al., 2008). In this work, we use the fiber clustering approach to design an automatic tract extraction framework. We discuss other approaches in some detail, in order to put our contributions in perspective.

The most common way of tract extraction is generating fiber pathways for the whole brain and then using multiple inclusion and exclusion ROIs, that could be chosen based on an anatomical atlas that is registered to the subject (Mori & van Zijl, 2002; Wakana et al., 2007). The main drawback with these multiple regions of interest (MROI) techniques is the fact that one needs to know which ROIs are to be used specifically for each TOI, which requires a detailed knowledge of the anatomy. Several authors have proposed improvements on automating selection of initial seed points and the ROIs, and on addressing registration issues for group studies (Li et al., 2010; Suarez et al., 2012; W. Zhang et al., 2008; Y. Zhang et al., 2010). However, these improvements cannot alleviate the need for knowing the anatomy of each TOI beforehand.

Once fibers have been generated for the full brain, instead of using the supervised MROI techniques, unsupervised clustering of fibers has emerged as a promising alternative to automate tract extraction by grouping the fiber pathways according to some predefined features such as geometrical or connectivity based measures (Brun et al., 2004; Liu et al., 2012; Maddah et al., 2008; O’Donnell et al., 2006; Q. Wang et al., 2010; Wassermann et al., 2010). The resulting fiber bundles delineate different characteristics of white matter depending on which features are described by the underlying fiber representation. Fiber clustering and MROI approaches were compared in (Voineskos et al., 2009) to estimate the confidence bounds of fiber clustering with respect to the manual selection, concluding that fiber clustering can be used with a high confidence. Despite the ease of the unsupervised clustering, these methods mainly suffer from the difficulty in setting up the correspondence between subjects, or may use an incomplete representation of the underlying data, using just the shape information of fibers.

Early works on fiber clustering did not facilitate automated correspondence of TOIs across subjects. Some research has been done on establishing the correspondence across subjects after clustering each subject individually (Ge et al., 2012; Guevara et al., 2012). One drawback of these methods is that clustering of a subject is not guided in any way by the information from other subjects. Several recent works addressed the automated correspondence problem by combining fibers of different subjects and clustering them together. In (Maddah et al., 2011) registration of fibers is handled together with clustering by using the expectation maximization (EM) algorithm (Dempster et al., 1977), to generate a clustering atlas. Clustering of new subjects based on previously generated atlases is studied in (O’Donnell & Westin, 2007; X. Wang et al., 2011). These works introduced a new perspective of building clustering atlases to enable the WM tract analysis in large scale clinical studies (O’Donnell et al., 2013). In this work, we follow this new exciting path to design a fully automated TOI extraction framework.

In real life clinical applications, one requires a group wise and longitudinally consistent TOI extraction method, so that statistical analyses can be performed subsequently. Moreover, the proposed method should be able to cluster the fibers of a new subject adaptively in a way that the correspondence with other subjects in the population is automatically established, without rerunning clustering over the whole sample. We propose a clustering framework to address all these requirements. There are several methodological contributions of this work. First, we use a multinomial fiber representation that relies on the connectivity signatures of fibers to establish an easy correspondence between the individual pathways of different subjects, while utilizing the neuroanatomical attributes of fibers. Such a representation defines a hybrid model, one integrating the anatomical segmentation methods with fiber clustering (O’Donnell et al., 2013). Second, we propose the use of a Gaussian Mixture Model (GMM) (Bishop, 2006) based group-wise clustering technique that merges clusters of individual subjects to generate a fiber bundle atlas. Finally, we use an adaptive formulation of the GMM that incorporates the previously generated clustering atlas as a prior, to cluster the fibers of a new subject. We demonstrate the applicability, the reliability and the repeatability of our approach using the high angular resolution diffusion-weighted imaging (HARDI) scans of healthy individuals acquired repeatedly, establishing its use in group and longitudinal studies.

2. Material and methods

Here, we explain the proposed clustering framework that enables us to automatically and consistently extract any TOI over a large group of individuals. We first introduce the connectivity based fiber representation. This representation lets us compare or combine fibers of different subjects without utilizing their physical coordinates. Then, a fiber bundle atlas is built using the GMM. By generating an atlas, we define a prior model of the fiber bundles in the human brain. The space complexity of the atlas generation, which can be high due to a large number of subjects and fibers, is decreased greatly by an online version of the GMM that provides an incremental training scheme for the atlas building. Finally, an adaptive GMM that incorporates the generated atlas as a prior for clustering of the fibers of a new subject is introduced, so as to automatically establish the correspondence between the bundles of different subjects.

Dataset

Imaging was performed on six healthy male subjects (Age 31.25 ± 4.2 years) at three time points separated by two weeks. All participants were carefully screened to ensure that they did not have a history of current or prior neuropsychiatric symptomatology. For each subject at each time point, a whole brain HARDI dataset was acquired using a Siemens 3T VerioTM scanner using a monopolar Stejskal-Tanner diffusion weighted spin-echo, echo-planar imaging sequence (TR/TE=14.8s/111ms, 2mm isotropic voxels, b=3000 s/mm2, number of diffusion directions=64, 2 b0 images, scan time 18 minutes). A structural image was acquired, using an MP-RAGE imaging sequence (TR/TE/TI = 19s/2.54ms/.9s, 0.8mm in plane resolution, 0.9mm slice thickness) to facilitate the tissue segmentation. We generated a gray matter (GM) parcellation for each HARDI scan including 95 GM regions, by applying FreeSurfer to the corresponding T1 image (Desikan et al., 2006), which is used for the connectivity measurements. We used Camino package (Cook et al., 2006) both for tractography and connectivity analysis.

Connectivity Based Fiber Representation

Existing fiber representations mostly encode information on the geometric attributes of fibers by treating them as sampled 3D curves (Maddah et al., 2008; O’Donnell et al., 2006). Abstraction of those geometric features into other mathematical objects such as Gaussian processes (Wassermann et al., 2010) or Gaussian mixture models (Liu et al., 2012) has been practiced to extract more reliable shape information. While using high level shape information such as length and curvature may alleviate the dependence on the physical coordinates, such representations can only provide geometric features without incorporating any information related to the diffusion data such as connectivity and integrity, limiting the interpretability of the selected representation.

Analyzing fiber bundles across individuals or groups to identify the personal characteristics or the group differences requires a reliable fiber correspondence among different subjects. This is a very challenging task since it is not possible to compare fibers having different coordinate systems without registering them. We address this problem by using the connectivity signatures of fibers, by building on our formulation in (Tunç et al., 2013).

The multinomial connectivity signature of a fiber is a collection of voxels that it traverses and their corresponding probabilistic connectivity signatures. We start with defining a parcellation of the brain into regions (G_i), e.g. important cortical regions, by mapping an anatomical atlas including these regions to each subject. In our experiments, we used FreeSurfer to parcellate the brain into 95 regions (Desikan et al., 2006). Then, the connectivity signature μ(x) of each voxel x is defined as the collection of the connection probabilities of the voxel to these regions G_i, resulting in an M dimensional multinomial vector, where M is the number of regions.

$$\mathit{u}(x)\equiv [p(G_1\mid x),p(G_2\mid x),\dots ,p(G_M\mid x)].$$ (1)

Each posterior probability p(G_i|x) is first calculated by counting the number of fibers passing through the voxel x and finally connecting to the region G_i. Then, the values are normalized for each voxel so as to sum to 1.

Then, a fiber is naturally represented by a matrix having the connectivity vectors μ(x) as its rows or columns. An illustrative example for a fiber selected from the corpus callosum is given in Figure 1. As expected, the matrix clearly favors two regions, namely the ones at the ends of the fiber. The main intuition behind the probabilistic representation is the enhancement of the results of tractography with the notion of uncertainty. This enhancement is especially helpful in fiber clustering as it affords additional information for separating fibers with respect to using only the two regions marking the ends of the fiber.

Figure 1.

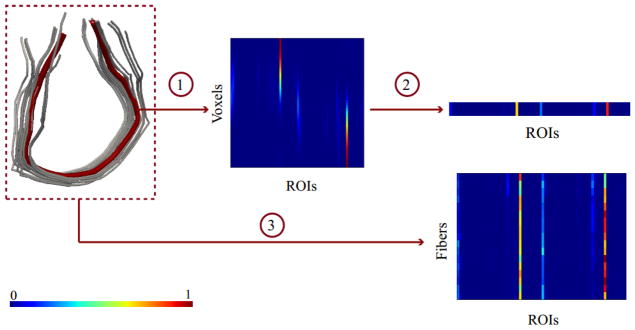
The illustration of the process to generate the connectivity based fiber representation. (1) The multinomial representation for a single fiber. The matrix is prepared by stacking connectivity vectors, corresponding to each voxel, as its rows. (2) The compact representation of the fiber is generated by averaging over voxels. (3) The same procedure is repeated for each fiber, resulting in a matrix representation of the bundle.

The matrix representation of fibers may introduce complexities with fiber clustering since we need either to define a proper metric for fibers of varying lengths or to introduce an extra fiber parameterization step to have equal lengths fibers. Hence, instead of working with the matrix representations, we take weighted average over voxels to have a compact representation of a fiber. We define different weights over voxels to emphasize the contributions of the specific voxels such as endpoints (Tunç et al., 2013). Similar to the approach used in (Q. Wang et al., 2010), we use a weight function that assigns higher weights to the endpoints and symmetrically decreases towards the center. Finally, each fiber f is represented by a single multinomial vector

$$\mathit{F}\equiv [p(G_1\mid f),p(G_2\mid f),\dots ,p(G_M\mid f)],$$ (2)

where the posterior probability p(G_i|f) is calculated by averaging over voxels of the fiber f and then by normalizing so as to sum to 1. Using the multinomial representation of fibers and the GMM as the clustering algorithm, we are able to define a clustering framework that produces highly consistent fiber bundles for a large group of individuals. We elaborate the clustering approach in the next two sections.

Fiber Bundle Atlas

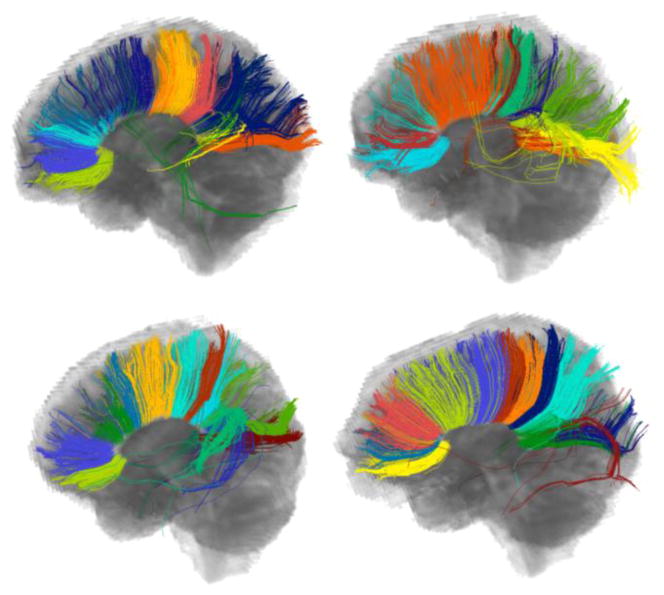
When clustered individually, fiber bundles of different subjects are mostly incompatible due to the subject specific characteristics of fibers. Figure 2 illustrates this behavior for clustering of the corpus callosum of four subjects when the GMM is employed as the clustering algorithm. Especially, the splenium and the body of the corpus callosum are clustered differently, hindering meaningful correspondences and hence comparison across subjects.

Figure 2.

The clusters of the corpus callosum for four subjects when each subject is clustered individually. The difference in clustering hinders reliable correspondence and hence comparison across the bundles of the subjects. The colors do not represent correspondence among bundles.

To assure the correspondence among subjects, we assume that each subject is an independent observation from the underlying common bundle model i.e. an atlas of fiber bundles. The easiest way to define such a fiber bundle atlas is merging fibers of all subjects and clustering over the combined set. The resulting GMM is a parameterization of the atlas, with each Gaussian representing a common fiber bundle. This approach can be applied easily to the multinomial representation (see section Connectivity Based Fiber Representation) since it does not require registration of fibers. Figure 3 shows the fiber bundles of the subjects that were used in Figure 2, after combining fibers and clustering over the combined set. The anatomical parcellation of the corpus callosum as provided in (Hofer & Frahm, 2006) is also illustrated in Figure 3 for comparison purposes. We initially clustered the corpus callosum into twenty clusters then labeled the clusters to get the best correspondence to the anatomical division.

Figure 3.

The clusters of the corpus callosum for the same set of subjects that are displayed in Figure 2 with clustering being run over the combined set of fibers collected from all subjects. The third column shows the anatomical parcellation (Hofer & Frahm, 2006) of the corpus callosum, as the proposed ground truth to be compared against. The colors are used to represent the correspondence across subjects that was achieved automatically.

When compared to Figure 2, we see a substantial improvement in consistency between fiber bundles of subjects in Figure 3. However, combining fibers of all subjects poses some challenges. First of all, individual differences may be suppressed. This hinders capturing any important anomaly in the group. Second, this procedure is space intensive as thousands (even millions) of fibers will be combined. A common approach to get around this problem is using sampling or multi-scale approaches to decrease the amount of pairwise distance calculations between fibers (Guevara et al., 2011; O’Donnell & Westin, 2007; Visser et al., 2011).

Here, we address these problems after elaborating some notations that will be used throughout this article. When using the GMM for clustering, it generates a set of Gaussian distributions parameterized by (μ_i, Σ_i, π_i), i = 1 …C, where C is the number of clusters in the mixture. Here, μ_i is the mean vector (the mean connectivity signature of the fibers assigned to the i^th cluster), Σ_i is the covariance matrix, and π_i is the prior of this cluster (the ratio of the number of the fibers assigned to this cluster over the total number of fibers of the subject). Each distribution corresponds to a cluster and therefore a fiber bundle. Each fiber f that is represented by the multinomial vector F (equation 2) is assigned to the i^th bundle by the posterior probability p(i|F, μ_i, Σ_i, π_i).

$$p(i\mid \mathit{F},{\mathit{\mu }}_i,{\mathbf{\sum }}_i,{\pi }_i)=\frac{{\pi }_{i}p(\mathit{F}\mid {\mathit{\mu }}_i,{\mathbf{\sum }}_i)}{{\sum }_j^C{\pi }_{j}p(\mathit{F}\mid {\mathit{\mu }}_j,{\mathbf{\sum }}_j)},$$ (3)

where the probability, p(F|μ_i, Σ_i) is the likelihood of the multivariate normal distribution parameterized by (μ_i, Σ_i).

We use an online version (i.e. incremental training scheme) of the GMM as defined in (Song & Wang, 2005) to decrease the space complexity of the atlas generation, which allows building the atlas incrementally by merging fiber bundles of subjects. We implemented two modifications in the original algorithm of (Song & Wang, 2005). First, a new distance measure between fiber bundles is used and second, a new decision step for merging bundles is introduced. The proposed online GMM algorithm is detailed in Table 1. Each subject is clustered individually, then fiber bundles are merged to generate a joint GMM. Given any two subjects, their fiber bundles are merged when the Fréchet distance (Dowson & Landau, 1982) between them is lower than a threshold; otherwise, both bundles are directly added to the combined model. The final joint GMM consists of the merged bundles and the remaining single bundles of both subjects. The Fréchet distance between two multivariate normal distributions D₁ and D₂ is defined as

Table 1.

Algorithm of the online GMM.

Given a set of subjects = {S1, S2, …, SL}, the number of clusters C, and the distance threshold τ, Cluster all subjects individually and parameterize results as (μij, Σij, πij), i = 1 …L; j = 1 …C Define S1 as the initial atlas, T ≡ S1 and Ĉ = C; (μTj, ΣTj, πTj), j=1…Ĉ For subjects i = 2…L Calculate distances (djk) between all pairs of bundles (μTj, ΣTj) and (μik, Σik) using the Fréchet distance (equation (4)) Match the bundles of T and Si using the Hungarian algorithm (Kuhn, 1955) If the distance djk between the matched bundles j and k is lower than τ, merge them using equations (5); add the resulting bundle as the jth bundle of the atlas Otherwise, add the bundle k directly to the atlas as a new bundle and update Ĉ, (Ĉ = Ĉ + 1) Apply steps 3[a-d] to the bundles of the final atlas to merge any similar bundles

$$d^2(D_1,D_2)={\mid {\mathit{\mu }}_1-{\mathit{\mu }}_2\mid }^2+tr({\mathrm{\sum }}_1+{\mathrm{\sum }}_2-2{({\mathrm{\sum }}_1{\mathrm{\sum }}_2)}^{\mathit{1}/\mathit{2}}).$$ (4)

The merger of the bundles is performed by calculating a new mean vector, a covariance matrix, and a prior probability using the following formulas.

$$\begin{array}{l}\widehat{\mathit{\mu }}=\frac{N_1{\pi }_{1j}{\mathit{\mu }}_{1j}+N_2{\pi }_{2k}{\mathit{\mu }}_{2k}}{N_1{\pi }_{1j}+N_2{\pi }_{2k}},\\ \widehat{\mathbf{\sum }}=\frac{N_1{\pi }_{1j}({\mathbf{\sum }}_{1j}+{\mathit{\mu }}_{1j}{{\mathit{\mu }}_{1j}}^{\prime })+N_2{\pi }_{2k}({\mathbf{\sum }}_{2k}+{\mathit{\mu }}_{2k}{{\mathit{\mu }}_{2k}}^{\prime })}{N_1{\pi }_{1j}+N_2{\pi }_{2k}}-\widehat{\mathit{\mu }}{\widehat{\mathit{\mu }}}^{\prime },\\ \widehat{\pi }=\frac{N_1{\pi }_{1j}+N_2{\pi }_{2k}}{N_1+N_2}.\end{array}$$ (5)

In the above equations, N₁ and N₂ are the total number of fibers in the datasets of the subjects. The j^th bundle of the first subject is merged with the k^th bundle of the second subject to generate a new bundle characterized by (μ̂, Σ̂, π̂). π_1j and π_2k are the prior probabilities of the bundles in their GMMs, hence the quantities N₁ π_1j and N₂ π_2k give the number of fibers in the bundles j and k, respectively. For each remaining bundle that is not merged, its new prior probability in the joint G MM is calculated as π̂ = N₁ π_1i/(N₁ + N₂) if it comes from the first subject and π̂ = N₂ π_2i/(N₁ + N₂) otherwise.

Once the atlas is generated by either combining fibers of all subjects or using the online GMM, the resulting fiber bundles (clusters) are visually inspected and assigned labels indicating the WM structures that they belong to. This guarantees the automatic labeling of the bundles of a new subject that is clustered using Adaptive Clustering (explained in section Adaptive Clustering).

Adaptive Clustering

The clustering atlas defines a common model for the fiber bundles of the human brain. Once the fiber bundles in the atlas are annotated, any TOI can be extracted simultaneously for all subjects since the TOI will be represented by the same Gaussian distribution(s) both in the atlas and in the fiber bundles set of any subject that is clustered adaptively using the atlas as a prior model.

We use the adaptive GMM (Reynolds et al., 2000) method, which is a well known technique, commonly employed in the speech recognition literature. The usual way to estimate the parameters of a GMM is using the EM algorithm to maximize the data likelihood (Bishop, 2006). When we want to introduce a prior model (bundle atlas) into clustering, the maximum a posteriori (MAP) parameter estimation (Reynolds et al., 2000) is used instead of EM. Given a new subject with a set of fibers {F₁, F₂, …, F_N}, after clusters are initiated by the parameterization of the atlas, the following quantities are estimated in the expectation step.

$$\begin{array}{l}{n}_i=\sum _{n=1}^{N}p(i\mid {\mathit{F}}_n,{\mathit{\mu }}_i,{\mathbf{\sum }}_i,{\pi }_i),\\ E_i[\mathit{F}]=\frac{1}{n_i}\sum _n^{N}p(i\mid {\mathit{F}}_n,{\mathit{\mu }}_i,{\mathbf{\sum }}_i,{\pi }_i){\mathit{F}}_n,\\ E_i[{\mathit{FF}}^{\prime }]=\frac{1}{n_i}\sum _n^{N}p(i\mid {\mathit{F}}_n,{\mathit{\mu }}_i,{\mathbf{\sum }}_i,{\pi }_i){\mathit{F}}_n{\mathit{F}}_n^{\prime },\end{array}$$ (6)

The posterior probability p(i|F_n, μ_i, Σ_i, π_i) is calculated by equation (3). Then, in the maximization step, the estimates for the parameters are adapted to the atlas as follows.

$$\begin{array}{l}{\pi }_i={\lambda }^{\pi }\frac{n_i}{N}+(1-{\lambda }^{\pi }){\pi }_{Ti},\\ {\mathit{\mu }}_i={\lambda }^{\mu }{E}_i[\mathit{F}]+(1-{\lambda }^{\mu }){\mathit{\mu }}_{Ti},\\ {\mathbf{\sum }}_i={\lambda }^{\mathrm{\sum }}{E}_i[{\mathit{FF}}^{\prime }]+(1-{\lambda }^{\mathrm{\sum }})({\mathbf{\sum }}_{Ti}+{\mathit{\mu }}_{Ti}{\mathit{\mu }}_{Ti}^{\prime })-{\mathit{\mu }}_i{\mathit{\mu }}_i^{\prime },\end{array}$$ (7)

where the parameters (μ_Ti, Σ_Ti, π_Ti) characterize the i^th cluster of the atlas. The parameters λ^π, λ^μ, and λ^Σ, with values between 0 and 1, control the tradeoff between the individual specifications of the subject and the compatibility to the atlas. Note that, π_i must be normalized so as to sum to 1, after being calculated for all clusters. Figure 4 shows the fiber bundles of two test subjects when using Adaptive Clustering. The atlas that is generated by merging four scans (see Figure 3) is used. It is clear that Adaptive Clustering provides high consistency across fiber bundles of subjects.

Figure 4.

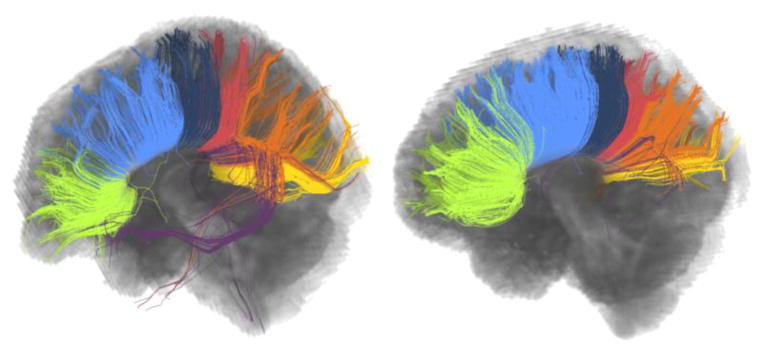
The clusters of the corpus callosum for two test subjects. Subjects are clustered adaptively, using the atlas displayed in Figure 3 as a prior model. The correspondence between the test and atlas subjects is noticeable (compare to Figure 3).

3. Results

We performed experiments to demonstrate the applicability, the reliability and the repeatability of our approach using the HARDI scans of six healthy individuals each having three scans acquired at different time points. With investigations provided below, we validate the applicability of the framework to group and longitudinal studies to extract TOIs consistently across subjects.

Validation of Adaptive Clustering

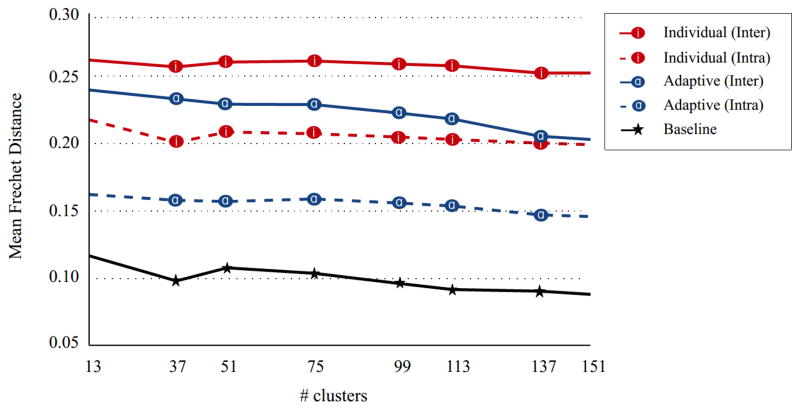
We first demonstrate that the adaptive GMM model defined in the previous sections provides an increased correspondence among fiber bundles of different subjects or time points. Two subjects were selected as the test data and the remaining data corresponding to four subjects were used for the atlas generation. A single time point of each of the four atlas subjects was selected randomly. The data acquired at all three time points of the two test subjects were clustered adaptively using the generated atlas. Fibers from the whole brain tractography were used for this experiment. The intra-person distances (the distance between the fiber bundles of different time points of the same subject) and the inter-person distances (the distance between the fiber bundles of different subjects) were calculated. When calculating the average distance between two clustering results, the fiber bundles of the subjects/time points were first matched using a linear assignment algorithm (Kuhn, 1955), then the average of the Fréchet distances between the matched bundles was computed. This experiment was repeated 100 times with the test and the atlas subjects/time points being selected randomly. The average intra- and inter-person distances were compared to those that are calculated when Adaptive Clustering is not used. Figure 5 illustrates the effect of Adaptive Clustering. When Adaptive Clustering is used, both the intra- and the inter-person distances decrease to a great degree, as expected. To provide a better interpretation of the Fréchet distances, we also provided a baseline distance (the black line in Figure 5), by running a single GMM repeatedly with random initializations and calculating the distances between different runs. The baseline distance therefore defines an approximate lower limit that can be achieved, since we used random initializations in all experiments.

Figure 5.

The effect of Adaptive Clustering on the correspondence across fiber bundles. The average Fréchet distances were computed between the matched bundles of different subjects (inter) and different time points of a single subject (intra). The baseline distance is calculated by running a single GMM with different random initializations to illustrate an approximate lower bound for the Fréchet distance. Adaptive Clustering clearly decreases the average Fréchet distance, in both cases with the inter- and intra- subject comparisons.

Invariance to Changing the Atlas Subjects

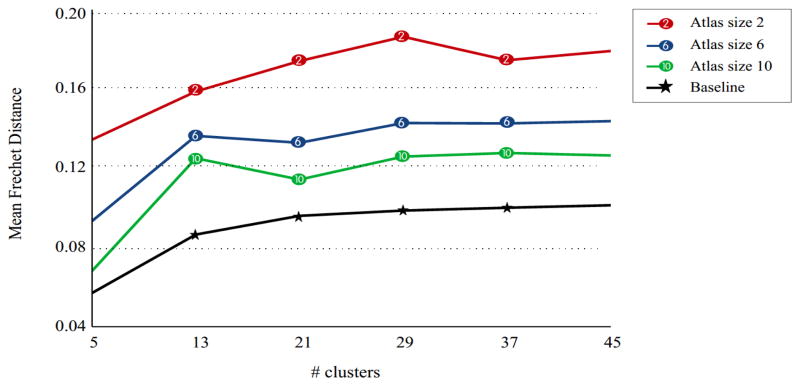
The repeatability of the framework was tested by fixing a randomly selected test subject and changing the atlas subjects repeatedly. None of the data acquired at any time point of the test subject were used in the atlas generation. The test subject was adaptively clustered, each time by a different atlas and the distances between clustering results were calculated by the Fréchet distance. The experiment was repeated with different number of clusters and atlas sizes (i.e. the number of subjects/time points used during the atlas generation). Only fibers seeded from the selected white matter regions, namely the corpus callosum, the corticospinal tract, the cingulum bundle, and the superior longitudinal fasciculus were used for this experiment. Figure 6 shows results of the repeatability experiments. As we increase the atlas size, the effect of changing the atlas subjects decreases.

Figure 6.

The effect of changing the atlas subjects for Adaptive Clustering. A fixed test subject was clustered using several atlases, each built with different subjects, and the average Fréchet distances were computed between the matched bundles. The baseline distance is calculated by running a single GMM with different random initializations to illustrate an approximate lower bound for the Fréchet distance. As we increase the atlas size, the robustness to changing the atlas subjects also increases.

The repeatability of the framework is illustrated, this time qualitatively, in Figure 7. For two test subjects, atlases were built three times by randomly changing the atlas subjects. Each time, four subjects out of the possible five subjects (excluding the subject that is used for testing) were selected with one dataset acquired at a single time point. The corpus callosum is clustered into twenty clusters, same as Figure 3 and Figure 4. The visual presentation in Figure 7 together with the quantitative analysis in Figure 6 demonstrates the high tolerance of Adaptive Clustering to changing the atlas subjects.

Figure 7.

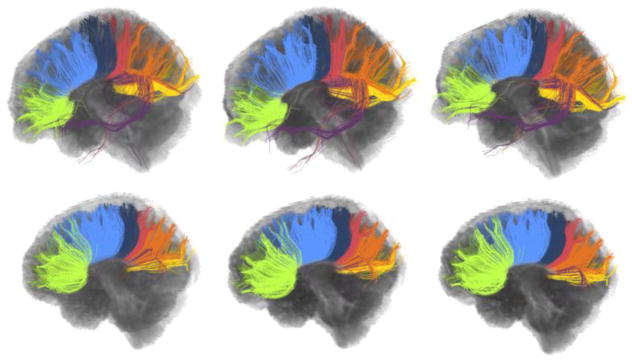
Clustering of the corpus callosum for two different subjects (top and bottom), each repeated three times by changing the atlas subjects. Each row shows the within subject variation of clustering results for a single subject while between subjects consistency is presented in the columns. The within subject variation is minimal for both subjects, showing promising robustness to changing the atlas subjects.

Reliability of the Online GMM

The online version of the GMM is proposed to decrease the high space complexity caused by combining fibers of all subjects during the atlas generation. We hypothesize that clustering results of an incremental training approach will be very similar to those that are generated by simply combining fibers. This assumption was validated by comparing the results of the traditional GMM and the online GMM. For this experiment, a test subject was adaptively clustered, first using the atlas that is generated by combining fibers of all atlas subjects, and then using the atlas provided by the incremental approach. None of the data acquired at any time point of the test subject was used in the atlas generation. The distances between the generated atlases and the fiber bundles of the test subject were calculated. The experiment was repeated 100 times with the test and the atlas subjects/time points being selected randomly. Figure 8 shows the calculated distances. In general, the difference in clustering results that are caused by using the incremental approach instead of combining fibers of all subjects, is as low as the difference that is caused by changing the atlas subjects (compare to Figure 6). Thus, the incremental training can be used to decrease the space complexity of the atlas generation without introducing critical differences in clustering results.

Figure 8.

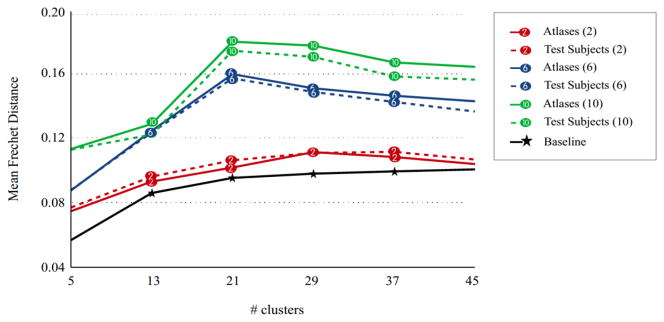
The difference between using the traditional GMM and the online GMM to build an atlas. A test subject is clustered adaptively using two atlases generated by these two approaches. The average Fréchet distances both between the generated atlases and between the fiber bundles of the test subject are given. The size of the atlas is given in parenthesis. The baseline distance is calculated by running a single GMM with different random initializations to illustrate an approximate lower bound for the Fréchet distance. The difference between the results of traditional and online GMMs increases as the atlas size increases. This introduces a tradeoff between the reliability of the online GMM and the generalizability of the resulting atlas.

Application for TOI Extraction

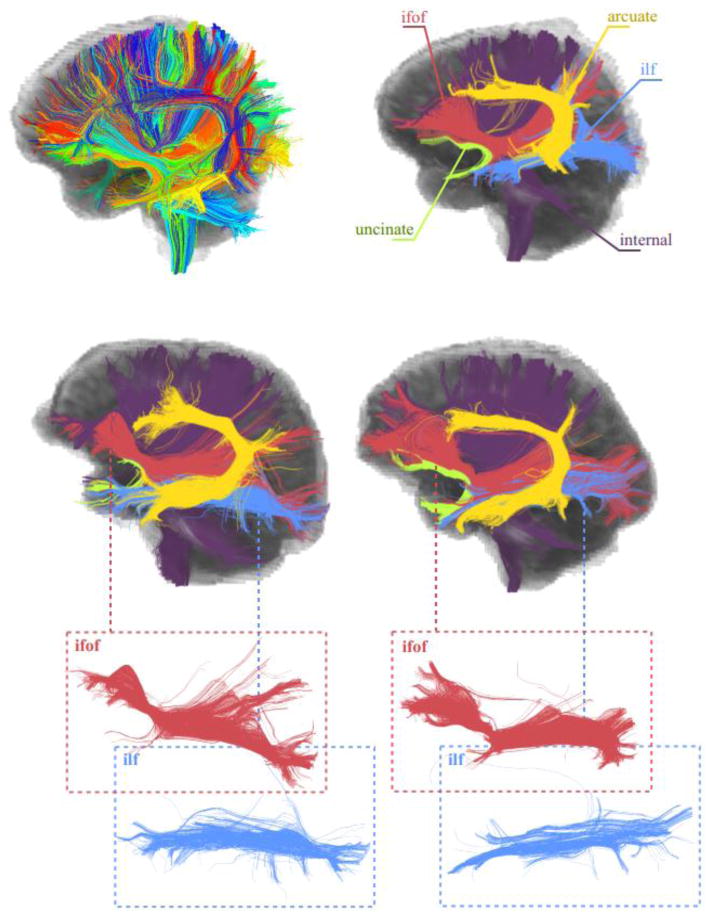
Finally, Figure 9 and Figure 10 show two successful applications of the proposed framework in group-wise consistent TOI extraction. Both experiments were performed using the whole brain tractography. An atlas was generated using four subjects and their data acquired at a single time point. Then, the data corresponding to all three time points of two test subjects were clustered adaptively. Figure 9 shows the association tracts (the inferior fronto occipital fasciculus, the inferior longitudinal fasciculus, the arcuate fasciculus, and the uncinate fasciculus) and the internal capsule for the two test subjects, selected automatically after being annotated in the atlas once. The atlas was generated by using the online GMM. For each atlas subject the number of clusters was fixed as 200. This number was determined empirically, which is large enough to catch important sub-bundles of the WM tracts. The threshold for merging the clusters was determined as 0.23 (Fréchet distance). The final number of clusters as determined automatically (see Table 1) was 327. Figure 9 shows all 327 clusters of an atlas subject together with the selected TOIs. The consistency between the fiber bundles of the test subjects and the atlas is very promising, showing the feasibility of the proposed framework.

Figure 9.

The application of Adaptive Clustering for group-wise consistent TOI extraction. The first row shows an atlas subject with all 327 clusters and selected WM tracts. Results for two test subjects are shown in the second and the third rows. The bundles (all from left hemisphere) corresponding to the internal capsule, the inferior fronto occipital fasciculus, the inferior longitudinal fasciculus, the arcuate fasciculus, and the uncinate are shown. It can be seen that while the fiber bundles are comparable, the individual variability is maintained.

Figure 10.

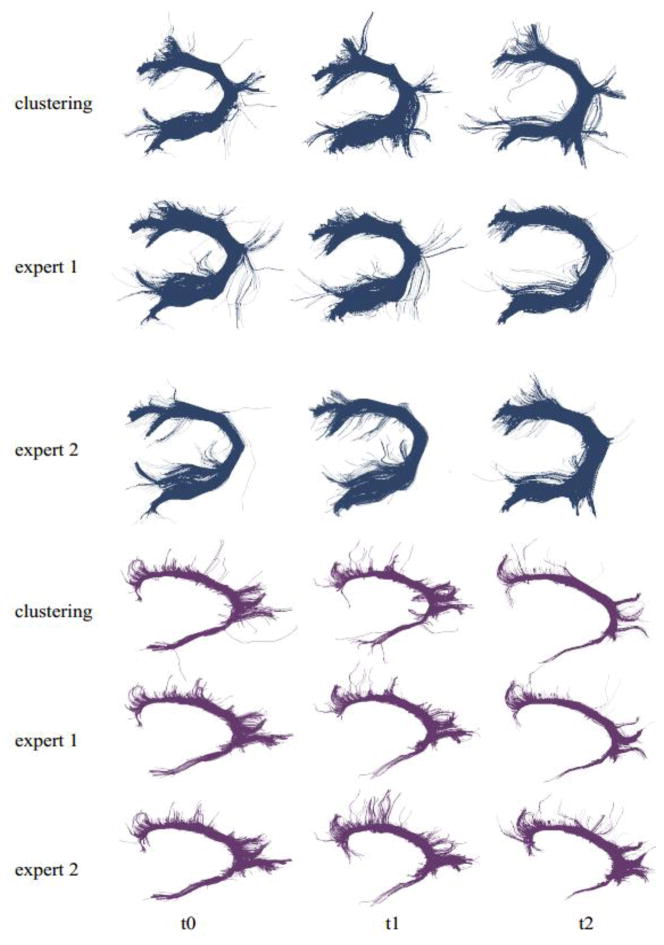
Comparison of the results of clustering with the manual reconstructions by experts. Results for the arcuate and the cingulum bundles of a single subject and three time points (columns) are given. For each bundle, the first row shows the results with clustering and other two with the expert drawings. Visual evaluation shows a big overlap between results.

In Figure 10, two automatically extracted TOIs, namely the cingulum bundle and the arcuate of one of the test subjects are compared with those that are extracted manually with the inclusion and exclusion ROIs drawn by experts. Two experts extracted TOIs for the three time points of the test subject. Figure 10 provides a visual insight into the agreement between experts and the clustering approach. As visual inspection shows, the proposed framework is successful in extracting WM tracts that are very similar to those drawn by experts with placement of the inclusion and exclusion ROIs that vary between experts. To provide a quantification of the agreement, the Sørensen Dice (SD) index (Dice, 1945; Sørensen, 1948) was used. When comparing two results (e.g. the arcuate by clustering vs. the arcuate by expert drawing), the SD index is calculated by 2c/(n₁ + n₂), where c is the overlapping tract volume (number of voxels) covered by both results and n₁, n₂ are the volumes for individual results. The SD index takes values in the interval [0,1], where 1 means a complete agreement. For the cingulum bundle, the average agreement between the clustering approach and experts was 0.81 while the average agreement between the experts was 0.89. Both agreement levels decrease significantly for the arcuate as seen in Figure 10, with a SD index of 0.62 between the clustering approach and experts and 0.73 between the experts. We also quantified the reproducibility of the expert results by calculating the SD index for their repeated drawings. The same cingulum bundle (single subject, single time point) was drawn three times separated by 1–2 days. For the first expert, the average SD index was 0.93, and 0.85 for the second one, yielding an average SD index of 0.89. This gives an intuition of the limits on the reproducibility of a single tract when drawn by experts repeatedly. When using Adaptive Clustering on the same fiber set repeatedly, the SD index is necessarily 1 (ignoring the slight variations caused by the EM algorithm). Together with the fact that the results that are provided by the proposed framework are reliable enough to perform a population study, this suggests that the proposed framework can ably assist experts in the clinical studies.

4. Discussion

We have proposed a framework for the group-wise consistent clustering of fibers. A fiber clustering atlas is generated by clustering over the combined fibers of all subjects from a healthy sample. The combination of fibers of different subjects is achieved by defining a multinomial representation for the WM fibers that uses the underlying connectivity information. Then, a new subject is clustered adaptively by taking the atlas as a prior model. Adaptive Clustering grants an automated correspondence among fiber bundles of different subjects, each “adapted” from the same atlas.

The main contribution of the framework is a new fiber representation and clustering approach to automate TOI extraction for large groups of subjects, such that the extracted tracts have a correspondence established automatically. For any study dealing with group differences or longitudinal analyses over WM tracts, this is critical such that a joint comparative analysis can be performed. The unsupervised nature of fiber clustering eliminates the need for manually drawing any inclusion or exclusion ROI to define the TOI after tractography. Similarly, the determination of proper seed points to establish a clean and complete reconstruction of the TOI is not required. Human intervention is needed only for labeling the bundles in the atlas; however, this is not a limiting feature since it enables us to define the TOIs with any precision we want.

Another important advantage of a clustering based approach over the MROI-based techniques is the ability to select the sub-bundles of large WM tracts in a very precise manner by controlling the number of clusters. For instance, when working with superior longitudinal fasciculus (SLF), a well formulated clustering scheme can extract SLF-I, SLF-II and SLF-III separately due to their different shapes or, as in our case, connectivity signatures. This improvement is essential for very large WM tracts such as the corpus callosum due to the effective heterogeneity in their neuroanatomical functioning. The usual way to study the corpus callosum is to segment it using an anatomical, geometrical, or histological parcellation. The clustering of the corpus callosum as illustrated in Figure 3, Figure 4, and Figure 7 is very similar to the anatomical segmentation of (Hofer & Frahm, 2006). The ability to pinpoint the sub-bundles helps facilitate a detailed analysis of these tracts, as the sub-bundles are also in correspondence between subjects. Measures computed over these sub-bundles have greater specificity in identifying differences between subjects, than when the measures are computed over larger, more heterogeneous WM tracts.

The number of clusters, in the current formulation, is determined in a semi-automated way. When using the online GMM, the number of clusters for each subject is fixed manually. Then, depending on the merger threshold (see Table 1), the final number of clusters in the atlas, and consequently for test subjects, is determined automatically. The initial number of clusters as well as the threshold may change the resolution of the final result. One useful heuristic is to keep the initial number of clusters large enough to catch every meaningful sub-bundle of the important WM tracts. A large number of clusters does not increase the effort as labeling of the clusters is done only once for the atlas. Nevertheless, using a Bayesian approach may contribute with fully automating the task (X. Wang et al., 2011).

The reproducibility of clustering results is critical for the most group and longitudinal studies. Considering the fact that the bundle atlas is prepared using the selected subjects, we expect that the results of Adaptive Clustering to not change substantially when we change these subjects. This expected repeatability is validated both quantitatively and qualitatively in Figure 6 and Figure 7, respectively. On comparing the Fréchet distances in Figure 6 with those of Figure 5, we observe that changing the atlas subjects causes a difference in clustering results, that is as low as the difference between the fiber bundles of different time points of a single subject. As we increase the number of subjects used in atlas building, the robustness of the atlas improves while the total inter-subject variability increases due to broader anatomical variation. This nonlinear behavior will be studied thoroughly as a future work to demonstrate the effects of changing atlases over larger samples.

The challenge of space complexity in generating the atlas is resolved by use of the online GMM, that provides an efficient clustering strategy. Experiments using the online GMM for the atlas generation showed (Figure 8) that incremental training approaches can be used instead of simply combining fibers of all subjects to generate an atlas, without causing a critical difference in the generated atlas or in clustering of a test subject. However, the difference between the atlases that are generated by the traditional GMM and the online GMM tends to increase as we increase the number of subjects used in the atlas generation. This fact defines an important tradeoff. We need to increase the number of subjects used in the atlas to make the resulting atlas a good representative of the sample (Figure 6). On the other hand, the increase in the number of subjects reduces the reliability of the incremental approach (Figure 8). We are planning to improve our strategy to decrease the space complexity in the future.

The inter- and the intra-subject differences in Figure 5 illustrate a promising aspect of the framework. Adaptive Clustering noticeably decreases both type of differences. Such a decrease in the difference of clustering results is the key element of the framework that affords group-wise consistent TOI extraction. Additionally, the fact that the intra-person differences are lower than the inter-person differences after Adaptive Clustering, provides us with possibilities of personalized applications. For instance, person specific WM integrity measures along a TOI can be calculated and compared to the distribution of the whole sample since the distinction between the typical (i.e. specific to the group) and the individual (i.e. specific to the person) attributes is preserved.

Two successful applications of the framework were demonstrated with the whole brain tractography. For both experiments, four subjects were used for the atlas generation. The fiber bundles of the generated atlas were annotated once. Then by using the atlas as a prior model, the data corresponding to two remaining test subjects were clustered adaptively. Owing to the automated nature of the bundle correspondence between the novel subjects and the atlas, the TOIs of the test subjects were extracted automatically, without any manual intervention. Several WM tracts of the test subjects are illustrated in Figure 9 and Figure 10, demonstrating the notable success of the framework in automated TOI extraction. In the absence of histology, tracts drawn by experts were considered as “groundtruth”. The comparison of the results of Adaptive Clustering with groundtruth was provided in Figure 10. The visual comparisons suggest a promising overall agreement between experts drawings and the results of the clustering approach, which was also quantified by Sørensen Dice (SD) index. Two cases were investigated, one with a low agreement (the arcuate) and one with relatively higher agreement (the cingulum bundle). The main body of the TOI was extracted successfully in both cases while several fiber pathways were mistakenly excluded or included by the proposed framework that is mainly due to the unsupervised nature of clustering, or by experts due to slight differences in the ROI placement (see Figure 9). In the absence of histology it is difficult to reach an agreement on the complete set of individual fibers. The differences could also be as a result of the way in which the atlas was generated since the tracts were labeled manually in the atlas. The imperfect agreement between the repeated drawings of experts demonstrates the indeterminacy of the WM fiber bundles, that always introduces uncertainty and thereby disagreement between any two methods of TOI extraction. Any future improvement, we believe, requires an investigation into atlas generation and subsequent improvements in fiber representation.

There are three sets of investigations that could be performed in the future. The first type of investigation can be identified as analyzing the effect of the ROI parcellation on the multinomial fiber representation. The probabilistic representation of fibers is identified by the selected cortical regions, which are used when the connectivity signature of a fiber is computed (see equations 1 and 2). Therefore, a set of empirical investigations will be carried out in the future, to study the effect of the ROI parcellation. Similarly, pros and cons of using a hierarchical clustering approach that will utilize a different representation at each level can be explored. A second future direction is performing more studies on features of clustering atlases. The generalizability of atlases based on scanner parameter changes, differences in tractography techniques, and the effect of gender or age could be analyzed. Finally, the method will be used to extract the WM tracts in a population with a pathology that affects the connectivity such as neuropsychiatric disorders and brain tumors. As the effects of these diseases on the connectivity and the geometric features can be critical, a method that extracts WM tracts automatically will be beneficial for the tract-based investigation of the pathology.

The proposed study should be considered as a generic framework that can be employed with changing components. For instance, the connectivity based fiber representation can be replaced by any other representation such as the usual geometrical ones, as long as fibers of all subjects are registered to a common template. Similarly, different models of clustering can be utilized instead of using the online GMM for atlas generation. Another possibility is using an atlas that is generated by the MROI techniques, even though such an approach is computationally intensive.

5. Conclusions

A framework for automatic group-wise consistent TOI extraction is designed and presented. The framework introduces three main components, namely a connectivity based fiber representation, a fiber clustering atlas, and Adaptive Clustering technique. The connectivity based fiber representation encodes the connectivity signatures of fibers. The clustering atlas is generated from a set of subjects, by merging fiber bundles of individuals. Finally, a new subject is clustered adaptively by incorporating this atlas as a prior model. The final achievement is the consistency among fiber bundles of subjects of large groups and automating TOI extraction.

The sensitivity and the specificity of tract extraction is assessed by its application to the dataset including the HARDI scans of healthy individuals acquired repeatedly. The results of our experiments have established the use of Adaptive Clustering in group and longitudinal studies to select TOIs that could be used for subsequent statistical analyses. The correspondence between fiber bundles of different subjects and time points are examined both quantitatively and qualitatively. The repeatability of tract extraction is validated by empirical investigations by changing the atlas subjects.

We believe that the future applications of the framework with possible improvements on the fiber representation and the atlas generation will enable new studies concentrated on the specific WM tracts, and even on their sub-bundles that could not be extracted in an automated manner before.

Highlights.

• Designed a framework for automated extraction of fiber tracts.

• Defined a fiber bundle atlas to introduce a prior model of clustering.

• Employed bundle atlas to cluster new subjects adaptively.

• Defined an automatic correspondence across tracts of large sets of subjects.

• Performed experiments on a HARDI dataset of healthy individuals.