Skip to main content
NCBI home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2014 Dec 1;21(12):947–963. doi: 10.1089/cmb.2014.0173

A Coverage Criterion for Spaced Seeds and Its Applications to Support Vector Machine String Kernels and k-Mer Distances

Laurent Noé 1,✉, Donald EK Martin 2
PMCID: PMC4253314  PMID: 25393923

Abstract

Spaced seeds have been recently shown to not only detect more alignments, but also to give a more accurate measure of phylogenetic distances, and to provide a lower misclassification rate when used with Support Vector Machines (SVMs). We confirm by independent experiments these two results, and propose in this article to use a coverage criterion to measure the seed efficiency in both cases in order to design better seed patterns. We show first how this coverage criterion can be directly measured by a full automaton-based approach. We then illustrate how this criterion performs when compared with two other criteria frequently used, namely the single-hit and multiple-hit criteria, through correlation coefficients with the correct classification/the true distance. At the end, for alignment-free distances, we propose an extension by adopting the coverage criterion, show how it performs, and indicate how it can be efficiently computed.

Key words: : coverage, alignment-free distance, spaced seeds, support vector machine

1. Introduction

To detect similarities in biosequences, in the so-called hit and extend strategy framework, spaced seeds are now a frequently used technique to define the hit (Keich et al., 2004). Several tools have been proposed that use spaced seeds (Li et al., 2004; Harris, 2007; Lin et al., 2008; Homer et al., 2009; Chen et al., 2009; Zhou et al., 2010; David et al., 2011; Kiełbasa et al., 2011; Ilie et al., 2013), or to design spaced seeds (Buhler et al., 2005; Kucherov et al., 2006; Ilie et al., 2011; Do Duc et al., 2012; Nuel, 2011; Marschall et al., 2012). Work related to spaced seeds also includes the lossless filtration problem (Burkhardt and Kärkkäinen, 2002; Kucherov et al., 2005; Farach-Colton et al., 2007; Nicolas and Rivals, 2008; Battaglia et al., 2009; Giladi et al., 2010; Egidi and Manzini, 2014a,b; Břinda, 2014), in the sense that all the alignments of a given set must be detected; the work proposed in this article can be applied to this problem too (section 3.3), but we concentrate on the lossy filtration problem in the sense that we suppose that the alignments are associated with a probabilistic model. We also mention a related work on clump statistics (Stefanov et al., 2007; Bassino et al., 2008; Martin and Coleman, 2011; Marschall et al., 2012; Régnier et al., 2014) that is close (but not similar), and that can, in some way, be complementary when both of them are considered in a more general framework.

The organization of the article is as follows. Section 2 gives notation and definitions related to spaced seeds. Section 3 defines the coverage of spaced seeds and proposes the tools used to measure it. Section 4 shows how coverage can be used in two biologically oriented applications : first, when spaced seeds are included within SVM kernels (subsection 4.1), and second, when spaced seeds are applied to measure phylogenetic distances (subsection 4.2). In this last case, we also propose a new distance based on the coverage (subsection 4.2.2) and the substantial improvement achieved. Section 5 provides, at the end, some concluding remarks.

2. Notation

We suppose here that strings are indexed starting from position number 1. For a given string u, we will use the following notation: u[i] gives the i-th symbol of u, |u| is the length of u, and |u|a is the number of symbol letters a that u contains. Also, d(u) is the prefix of length d of the string u, and (u)d is the suffix of length d of the string u. For two strings u and v, u · v is the concatenated string.

Alignments without gaps (indels) can be modeled by a succession of mismatch or match symbols, and thus be represented as a string x in a binary alphabet {0, 1}. A spaced seed can be represented as a string π, but in a different binary alphabet {*, 1}; 1 indicates a position on the seed π where a match must occur in the alignment x (it is thus called a must match symbol), whereas * indicates a position where a match or a mismatch is allowed (it is thus called a joker symbol). The weight of a seed π (denoted by w) is defined as the number of must match symbols (w = |π|1), whereas the span/length of a seed π (denoted by k) is its full length (k = |π|).

A spaced seed π of length k hits an alignment x of length n starting at position Inline graphic

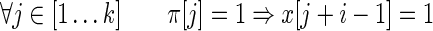graphic file with name eq2.gif

The usual requirement for a seed, when used to detect alignments x, is to have at least one hit (Keich et al., 2004) in x, the so called single-hit criterion. Several methods are also based on multiple hits, as they require more than one hit to trigger an alignment extension (Burkhardt et al., 1999; Rasmussen et al., 2006; David et al., 2011). In the next section, we extend the way to define criteria based on seed hits by measuring coverage provided by these hits.

3. Definition and Computation of the Seed Coverage

3.1. Definition of the coverage

The coverage of a seed π on an alignment x is defined by the number of 1's in the alignment x that are covered by at least one must-match symbol of one of the seed's hits (Benson and Mak, 2008; Martin, 2013; Martin and Noé, 2014).

For example, the seed π = 11 * 1 has three hits on the string alignment x = 101111001011111. The coverage provided by these hits (denoted by • symbols below) is 8.Inline graphic

The coverage concept can be generalized to multiple seed patterns. For example, the set of seeds {π1, π2} = {11 * 1, 1 * 1 * 1} has six hits on the string alignment x. The coverage provided by these hits is 11. Inline graphic

3.2. Coverage automaton

Given a seed π or a set of seeds 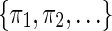Inline graphic along with an input string x, the aim of the automaton is to compute the coverage of 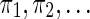Inline graphic on x, as defined in section 3.1. To fully compute the coverage, a necessary and sufficient task, typically devoted to an automaton, is to update the coverage each time we concatenate a new symbol to the right of x. For example, for the set of seeds {π1, π2} = {11 * 1, 1 * 1 * 1} and the string x = 1011110011110, we desire to determine the set of newly covered positions (denoted by two ∘ symbols below) after reading the new symbol 1 to form the extended string x′ = x · 1, together with their count to update the coverage. We will call this (+2) value the coverage increment. 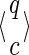Inline graphic

For a set of seeds Inline graphic with k = maxi (|πi|), first notice that a suffix of x of length (at most) k − 1 is sufficient to know which proper prefixes of one of the seeds can lead to a new hit; we will call this suffix q. Moreover, to update the coverage increment, we need to know which 1 symbols inside q have already been covered by previous hits of one of the seeds; this can be done with a binary word c of length |q| associated with q. States of the automaton are thus defined accordingly by a pair Inline graphic.

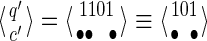For example, for the set of seeds {π1, π2} = {11 * 1, 1 * 1 * 1}, the state reached when reading the first string alignment x = 1011110011110 (used in the previous example), is represented by the pair Inline graphic, and the transition to x′ = x · 1 can be computed accordingly with the new hits of π1 and π2: Inline graphic

The new state may be represented by the pair Inline graphic with |q′| ≤ k−1. Note that q′ can even be reduced to a smaller suffix, because no proper prefix of π1 or π2 can start with q′ = 1101, but a prefix of π2 can match the first proper suffix of q′, namely 101, to initiate a hit. Thus Inline graphic; this reduction can be done easily using the fail function of the Aho-Corasick algorithm (Aho and Corasick, 1975), which is applied in classical seed automata (Buhler et al., 2005; Kucherov et al., 2007) as well as coverage automata (Benson and Mak, 2008; Martin and Noé, 2014). 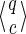We will suppose that we always apply this reduction on all the states Inline graphic.

From the point of view of the automaton definition, two finite state machines are possible: Mealy or Moore. Accordingly, the automaton must provide the coverage increment, either on each transition (for the Mealy automaton) or on each state (for the Moore automaton). For example, on the set of seeds {π1, π2} = {11 * 1, 1 * 1 * 1}, these two representations are illustrated in Figures 1 and 2; due to size, we present here the minimal version for both automata by merging equivalent states. 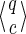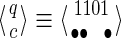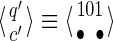For readability, when some hits occur, we have represented the states Inline graphic with their full length matching symbols of length up to k and not k − 1 (see, for example, Inline graphic and Inline graphic in the Figures 1 and 2).

FIG. 1.

FIG. 1.

Open in a new tab

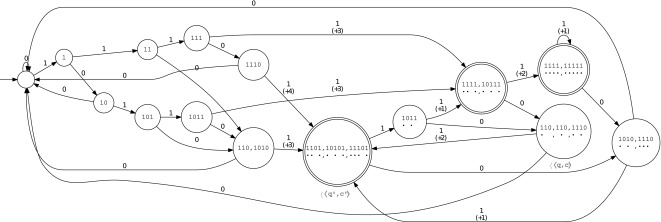
Minimized Mealy coverage automaton (count on transitions) for the seeds {π1, π2} = {11 * 1, 1 * 1 * 1}.

FIG. 2.

FIG. 2.

Open in a new tab

Minimized Moore coverage automaton (count on states) for the seeds {π1, π2} = {11 * 1, 1 * 1 * 1}.

The Mealy automaton is obviously more compact when considering the number of states. On the other hand, it requires one to store an additional value per transition [and also needs more specific algorithms; for example, the Hopcroft minimization algorithm (Hopcroft, 1971) must be adapted to the Mealy case].

Each representation has been independently implemented by one of the authors; the one based on count on transition (Mealy) is implemented in Matlab (see Martin, 2013; Martin and Noé, 2014), and code has also been tested on Octave (Octave community, 2014), whereas the other, mainly for compatibility issues, is based on count on states (Moore), and is generalized for subset seeds (slight extension of spaced seeds) with multiple seeds in mind (Kucherov et al., 2007). The “Mealy” Matlab code is available upon request from the second author, and the “Moore” code is included in the C++ Iedera program (Kucherov et al., 2014) starting from development version 1.06 α7.

Several minimizations of the states (considering both q and c) can be considered during the construction of these automata, but the details are out of scope of this article (see Kucherov et al., 2007; Martin and Noé, 2014). In practice, we use at least two methods to detect coverage strings c that are equivalent, together with the optimization of Kucherov et al. (2007) on strings q to save some memory space before completing the full automaton. Note that this last automaton, once entirely built, can always be fully reduced to its minimal form, for example, by applying the classical Hopcroft minimization algorithm (Hopcroft, 1971).

Independently, we also mention that it seems difficult, for this special coverage problem, to find an equivalent classical regular expression to help build the automata. Even classical tools (such as grep) have for example equivalent parameters to simulate a single or multiple hit, but no parameter is provided for this coverage problem.

3.3. Computation

Given a generative model for the string x, it is possible to compute the distribution of the coverage values according to a Markov process (Martin, 2013; Martin and Noé, 2014) or any model that can be represented by a nondeterministic probabilistic automaton (Kucherov et al., 2006; Nuel, 2008; Marschall et al., 2012; Martin and Noé, 2014). We don't consider directly in this article this computation, as the model used in our tests is pure Bernoulli; the computation can thus be performed directly with a simple dynamic programming algorithm on the coverage automaton of section 3.2. We refer to the aforementioned articles for more details on more complex probabilistic models.

Independently, we also mention that the work proposed here is applied on the lossy seed framework, in the sense that we consider a probability to hit (or cover) an alignment sequence x generated by a model χ. However, this work is not strictly limited to probabilities and can be easily extended, for example, to the lossless seed framework. In that case, the set of alignments is fixed, for example, by giving a fixed length together with a fixed number of errors; the problem is then to always hit (or cover) any of the alignments on this set (so without loss). This last computation can be done easily, simply by replacing the semi-ring used for probabilities by a less conventional tropical semi-ring (Simon, 1988; Pin, 1998; Mohri, 2009) used for match/mismatch scores or mismatch costs. Note also that the simple fact of counting the number of alignments, in alignment classes that have a given percentage of identity (as done in Benson and Mak, 2008) or a given coverage for a set of seeds, or any combination of these elements, is also possible, by use of a counting semi-ring adapted for this task (Huang, 2006).

4. Experiments

In this section, we consider two biological sequence oriented applications that have recently been proposed to use spaced seeds; SVM classifiers based on spaced string kernels (Onodera and Shibuya, 2013) and alignment-free distance estimators using spaced k-mers (Boden et al., 2013; Leimeister et al., 2014; Horwege et al., 2014). We show that the coverage sensitivity can be used in both cases to improve the estimators, and thus also be applied to the selection of the best seed patterns on such domains.

4.1. Coverage sensitivity and spaced seed string kernels

String kernels (Lodhi et al., 2002) are a classical model used for text classification with SVM. They have frequently been applied to biological sequence classification, as k-spectrum kernels (Leslie et al., 2002), mismatch k-spectrum kernels (Leslie et al., 2004), string alignment kernels (Saigo et al., 2004), and profile-based string kernels (Kuang et al., 2005) to cite a few examples.

The k-spectrum kernel and its derivative is mostly used with contiguous seeds; surprisingly, no spaced seeds were designed to comply with this approach. However, it has been experimentally shown (Onodera and Shibuya, 2013) that spaced seeds help decrease the zero/one misclassification rate in practice, even for the simplest kernels. The main reason of this lack might be the intrinsic difficulty to find a correct estimation criterion for spaced seed patterns, but on the other hand, not so much effort has been made to increase the diversity of criteria used. Most of the proposed algorithms to estimate spaced seed sensitivity concentrate on the single-hit criterion (“at least one hit for a seed/set of seeds”). This criterion makes sense for classical “hit and extend” alignment methods used in bioinformatics, but seems to be too restrictive for spectrum kernels that are supposed to filter the information content based of “several concordant clues.”

The multihit criterion (“at least t hits for a seed/set of seeds”) seems at first more appropriate for this task, but again has never been tried in this field of research. One possible drawback is that it does not distinguish highly overlapped hits of seeds from disjoint ones. Finally, and for the latter reason, we also decided to apply the new coverage criterion (“at least t covered 1-symbols in the alignment, each covered by at least one 1-symbol of a seed hit”) in comparison with the two others. In the two following subsections, we try to correlate these three criteria with the SVM zero/one misclassification rate.

4.1.1. SVM-benchmark and protocol

The benchmark used for this test consists of 2208 families extracted from the noncoding RNA database RFAM v11.0 (Burge et al., 2012). It represents up to 65908 sequences per family.

We decided to split each family by randomly picking 50% of its sequences for the SVM learning process and keeping the 50% remaining for the classifier to measure the zero/one misclassification rate. We use the SVMmulticlass (Joachims, 2002) package Version 2.20 (dated August 14, 2008) with the linear kernel. In each case, single or double seeds of weight 3 and span from 3 to 7 were used as a k-spectrum string kernel.

4.1.2. Seed sensitivity

In parallel, for each single or double seed we compute its “sensitivity,” either using the single-hit criterion, the multihit criterion, or the coverage criterion. Note that, for the two last criteria, we have the possibility to change the threshold t required to consider a success. We arbitrarily choose to measure these seeds on an i.i.d. alignment model of length 32 (the probability to have a 1-symbol in the alignment has been fixed at 0.7), although experiments show that this does not have much influence on the final results (data not shown).

Examples of comparative plots are given in Figure 3 for multihit and coverage-hit; a slight correlation can be seen at first sight. But we can also see that some seeds with repetitive and highly correlated patterns (e.g., 1*1*1), usually bad in theory, are in practice more efficient for the SVM classifier.

FIG. 3.

FIG. 3.

Open in a new tab

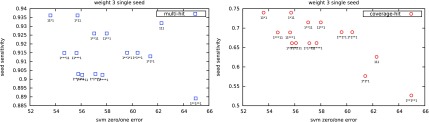
Zero/one misclassification rate vs theoretical sensitivity.

4.1.3. Correlation between zero/one misclassification and the three criteria

Finally, to determine if one of the three estimators was better suited to correlate with this SVM classifier task, we computed the sample Pearson correlation coefficient for each of the three criteria, for each set of seeds. This gives the best correlation between the theoretical seed sensitivity estimated by one of the three estimators with the experimentally measured sensitivity of the SVM classifier of each set of seeds.

For both the multiple hit and coverage criteria, we allowed the threshold parameter t for seed sensitivity to vary (x-axis). These results are illustrated in Figure 4 for single and double seeds.

FIG. 4.

FIG. 4.

Open in a new tab

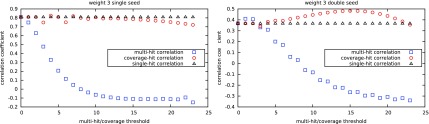
Correlation coefficient between zero/one misclassification rate and theoretical sensitivity.

Surprisingly, correlation results for the multihit criterion are not good when the number of hits required is too large. This must be taken into account when using this criterion because the multihit criterion gives the correct results for double seeds when the number of hits is, for example, at 2.

The single-hit criterion gives good results for each set. However combining single and double seeds into one set and doing the same experiment makes it the worse of the three estimators (data not shown). A carefully chosen value for the coverage criterion (here between 14 and 16) helps to reach the highest correlation of the three for double seeds. On single seeds, this is difficult to conclude, due to the few seeds of weight 3 that have been tested. Note that we also tried the same experiment for seeds of weight 4 but the dimension used here (44) makes the classifier more random without a preselection of dimensions (data not shown).

We can first notice that the correlation of the single-hit criterion is more stable than the correlation of the coverage criterion that varies more for lower thresholds. It also seems that the optimal coverage threshold is at some point a surprisingly quite regular and convex function that might be estimated when enough data is available.

4.2. Coverage sensitivity and alignment-free distance for sequence comparison

Estimating alignment-free distance is a common method used for sequence comparison in multiple alignment tools guided tree estimation (Edgar, 2004) and related phylogenetic tree estimation (Qi et al., 2004; Liu et al., 2008). Several distances are based on fixed size k-mers (Vinga and Almeida, 2003; Simsa et al., 2009) with possible mismatches allowed (Apostolico et al., 2014), or with variable length k-mers—local decoding (Didier et al., 2012), irredundant common subwords (Comin and Verzotto, 2012), etc. They are applied on assembled genomes (Haubold et al., 2005; Chor et al., 2009), protein classification (Stropea and Moriyama, 2007), and even on unassembled genomic data to estimate phylogenies (Maurer-Stroh et al., 2013). We refer to a recent special issue on alignment-free methods for more details (Vinga, 2014).

Interestingly, it's only in the last year that the use of spaced seeds has been proposed (Boden et al., 2013; Leimeister et al., 2014; Horwege et al., 2014), with recent applications for specific next generation sequencing (NGS) tasks, such as multiclonal clusterization (Giraud et al., 2014). Here again, the lack of seed criteria used in the literature didn't help the selection of good seeds for these tasks.

In subsection 4.2.1, we recall that the “classical” distance can be estimated by multihit sensitivity computation, which helps in selecting good spaced seeds. In subsections 4.2.2 and 4.2.3, we also show that coverage sensitivity can be used in a more elaborate distance; this distance can be computed using the longest increasing subsequence (LIS) of the positions of the common hits between gapped k-mers. As LIS can be computed in t · log(t) time, where t is the number of hits, it is thus a reasonable estimator in practice.

4.2.1. Multihit experimental support

One common method used to estimate alignment-free distances is based on k-mer frequency; 4k counts can be first made and used as simple feature frequency profiles (where counts are normalized to relative frequencies for any of the 4k k-mers), or more elaborate composition vectors (where normalization is done with the help of a background model). Distances can then be estimated by several models (Vinga and Almeida, 2003) to provide phylogenetic applications with an initial distance matrix. As some of these phylogenetic methods, such as unweighted pair group method with arithmetic mean (UPGMA) (Michener and Sokal, 1957), start by considering small distances, it's important to have the best estimator here and keep track of common k-mers (or spaced k-mers) and their common locations in the two sequences. One estimator that can help in that task is the number of seed hits obtained; we will call it the multihit value.

For our experiment, we use a set of seeds (627 seeds of weight 3 or 4, span up to 7, single seed or double seed patterns), a percentage of identity varying from 20% to 100% by steps of 5% each time, and we generate (for each percentage of identity) 1000 alignments of length 32. We then measure the multihit value of each alignment and compare it to the true alignment distance.

It can be shown first (Fig. 5, x-axis only) that the correlation coefficient is high (>0.9 for seeds of weight 3, less otherwise). Provided that we expect to pay a little additional cost, it is possible to improve this result, as shown in the next section.

FIG. 5.

FIG. 5.

Open in a new tab

True distance correlation with multihit (x) vs. coverage (y) distance.

4.2.2. Coverage experimental support

The distance we propose to measure is based on the number of covered 1-symbols in the alignment, each covered by at least one 1-symbol of a seed hit. We will call it the coverage value. To show how this distance better estimates the true distance (we assume here that the Hamming distance is the true distance), we are repeating the same experiment with both the multihit value and the coverage value on the set.

We use the same protocol here—the same set of seeds (627 seeds of weight 3 or 4, span up to 7, single seed or double seed patterns), the same percentage of identity varying from 20% to 100% by steps of 5% each time, and generating for each percentage of identity the same 1000 alignments of length 32 each time, we measure the multi-hit and the coverage values for each simulated alignment. Then, we compared the correlation coefficient for each of these two measures with the true percentage of identity used to simulate the alignment.

The correlation coefficient for all the seeds was 0.88 for the multi-hit value and 0.96 for the coverage value. We tried to refine this first experiment by separately measuring single seed patterns and double seed patterns and running the same test. For single seed patterns, the correlation was 0.89 and 0.94 respectively, whereas for multiple seed patterns, it was 0.89 and 0.96 respectively. We also tried to measure this correlation for each of the 627 seeds; Figure 5 plots these two correlations (pair of coordinates).

Note first that, as all the points for this plot are in the upper left region, the true distance is better estimated by the coverage value than by the multihit value. We can also notice that double seeds outperform single seeds in both cases, so that multiple seed patterns can help in estimating the distance more accurately than single seed patterns. The gain is even better for the coverage value than for the multihit value.

From the point of view of the seed weight and the number of seed patterns used, we can see that using two patterns of weight 4 gives the same correlation coefficient as using one single pattern of weight 3, but only for the coverage value, not for the multihit value. This encouraging result may help defend the idea that more patterns of larger weight will help measure a correct distance. Note that this conclusion is quite similar to the one provided 10 years ago for detecting alignments (Li et al., 2004), which was recently and independently observed in Leimeister et al. (2014); Horwege et al. (2014), but here, as the distance estimation problem is quite different from alignment detection, the seeds designed will probably be completely different from those previously seen.

From the point of view of the seed patterns, we can see in Figure 5 that, for single seeds, selection done for both values gives the same optimal seed pattern 11*1 (or its mirror) for weight 3, and the same optimal seed pattern 1*1**11 (or its mirror) for weight 4. The choice for the optimal double seed patterns differs between the multihit or coverage values, and this difference is even more marked for seeds of weight 4.

However, computing the coverage is more difficult than simply counting common k-mers. We justify in the next part that, given two easily measurable assumptions on the sequences and the k-mer weight, this task can be done efficiently.

4.2.3. Coverage algorithmic point of view

In this part, we briefly describe how coverage can be computed efficiently. Given two sequences s1 and s2 of equivalent length, we want to search for the spaced k-mers that are common to s1 and s2. But, more than establishing a frequency profile for these common k-mer codes, the main idea here is to find a set of common k-mers that have the same order of position occurrences on s1 and s2. To do so, one solution is to keep occurrences of any of the 4k possible k-mers in a reverse list of positions (given one k-mer code, we have two lists of positions where this k-mer occurs, on s1 or, respectively, on s2). Keeping the common k-mers of both s1 and s2, sorting their list of pairs of occurrence positions according to the positions of one of the two sequences (for example, positions along s1), then applying an LIS (or a windowed LIS if the two sequences are not of similar lengths) on s2, provided that spurious k-mers (those occurring randomly) are not frequent, will give a better approximation for the number of true hits and thus can be used to compute the coverage.

Note first that the LIS can be computed in t· log(t) time (Schensted, 1961), where t is the number of hits (e.g., pairs of positions for a common k-mer). This value t, provided that k is well chosen to correctly filter spurious k-mers and there is no composition bias on both sequences, must be either close to |s1| and |s2| if the s1 and s2 sequences are similar (and without self-repetitive bias/low complexity regions), or reasonably low if the sequences are nonsimilar, but can be otherwise high for low complexity/self-repeating/redundant regions that similarity search tools usually want to avoid.

Note also that, once the common and ordered hits are collected by the LIS procedure, it is possible to compute the coverage using:

  • • either a masking process using shift–or for collecting the coverage symbols, and then computing the coverage increment (which implies an additional CPU cost if no population count instruction is available),

  • • or an automaton (an example is provided in Fig. 6 for the hits of the seeds {π1, π2} = {11 * 1, 1 * 1 * 1}) that keeps the last overlapping suffix of the previously encountered hits for any of the seeds. This automaton has an alphabet of size 2#seeds, since we record whether or not there is a seed hit for each seed. Otherwise, a very similar definition to the coverage automaton holds. Once this automaton is built, it is possible to compute the coverage increment in constant time.

FIG. 6.

FIG. 6.

Open in a new tab

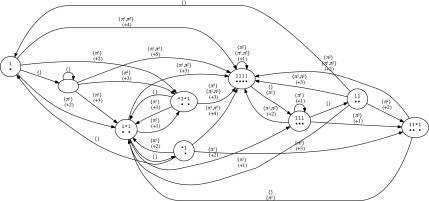
Mealy coverage increment automaton for hits of the seeds {π1, π2} = {11 * 1, 1 * 1 * 1}.

In both cases, gaps (indels) must be taken into consideration because they break—from a dot-plot point of view, diagonals—thus reinitializing the automaton or the coverage mask.

5. Concluding Remarks

We have presented how the coverage criterion (Benson and Mak, 2008; Martin, 2013) can help in measuring the seed efficiency in two recent problems: a classifier based on spaced k-mers (Onodera and Shibuya, 2013) and a k-mer alignment-free distance estimation (Boden et al., 2013 Leimeister et al., 2014; Horwege et al., 2014). We have also shown how to extend the second one to be even more sensitive.

The Moore (or Mealy) automaton obtained to measure the coverage criterion is by itself of interest for several reasons; its size seems to be bounded by polynom(w, r) × 3r even if the bound obtained now is rather limited and exponential (see the Appendix).

For example, the coverage automaton size for the PatternHunter 1 seed 111*1**1*1**11*111 is:

graphic file with name fig-8.jpg

Open in a new tab

where the current sizes for Moore and Mealy automata are respectively obtained by the Iedera tool (Kucherov et al., 2014, version 1.06 α7) or by the Matlab code (Martin and Noé, 2014) before minimization by the gap-system functionally recursive group (FR) package (Bartholdi, 2012). These sizes can be compared with those of the mere multihit automaton:

graphic file with name fig-9.jpg

Open in a new tab

Although the coverage automaton is more than 10 times larger than the equivalent multihit automaton, it is still usable for dynamic programming computation.

This is even true for multiple spaced seeds. For example, the coverage automaton size for the PatternHunter 2 seeds of weight 11: 111*1**1*1**11*111, 1111**11**1*1****1*11, 11*1****11***1*1*1111, 111*111*1***1111 (called first four in Li et al., 2004) is

graphic file with name fig-10.jpg

Open in a new tab

to be compared again with the mere multihit automaton current size (and its minimal size):

graphic file with name fig-11.jpg

Open in a new tab

Although more than 20 times larger than the equivalent multihit automaton, the coverage automaton for multiple seeds is again still usable for dynamic programming computation.

It would also be interesting (but out of the scope of this article) to consider SVM kernels or k-mer distances with subset seed (Kucherov et al., 2007; Yang and Zhang, 2008; Gambin et al., 2011; Frith and Noé, 2014) or more general vector seed (Brejová et al., 2005) techniques. Several string kernels, such as the mismatch string kernel (Leslie et al., 2004), use this general concept but generate full neighborhoods (all the words at a given distance from a given k-mer). Moreover, optimal resolution (best seed weight) (Simsa et al., 2009) remains an open problem for spaced seeds in both SVM kernels or k-mer distance problems. Note also, if one wants to avoid this optimal resolution question, seed design and increasing weight can be combined (as done in Csűrös, 2004; Kiełbasa et al., 2011), but may not be always directly compatible with the aforementioned cited works on variable k-mers.

A last idea to explore is also to merge the definition of clumps (Stefanov et al., 2007; Bassino et al., 2008; Martin and Coleman, 2011; Marschall et al., 2012; Régnier et al., 2014) with coverage, for example, by giving more significance (than a linear weight function) to coverage provided by clumps of hits than coverage provided by isolated hits.

6. Appendix

6.1. Seed coverage automaton size

We consider in this part the size of the seed automaton. Given a seed of weight w and r jokers, we are particularly interested in a bound for the size of the coverage automaton, as this can provide a limit on memory needed for future analyses.

In this section, we first solve the problem in the special case of a seed of the form 1*r1, before going to a more general case of a seed of weight w and r jokers, for which we show a more general (but less satisfying) upper bound.

6.1.1. Seed 1*r1 coverage automaton size

The 1*r1 seed family has already been shown to reach the multihit automaton size bound (Kucherov et al., 2006). As a nightmare for the classical seed design tools, such seeds are good candidates to start with.

The multihit automaton size is, in the general case, of maximal size (w + 1)2r (Buhler et al., 2005; Kucherov et al., 2006). Moreover, for seeds of the form 1*r1, this size cannot be reduced further (Kucherov et al., 2006); thus, 1*r1 always have multihit automata of size 3 × 2r (illustrated in Fig. 7a where not all the transitions are shown).

FIG. 7.

FIG. 7.

Open in a new tab

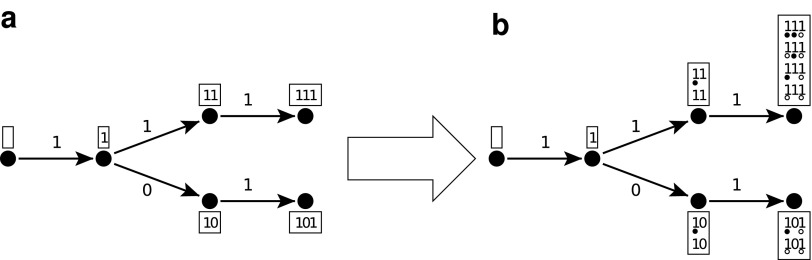
Moore multihit (a) and Moore coverage (b) automata size illustrated for the seed π = 1 * 1. In boxes are set all the seed prefixes q that can be reached for the Moore multihit (a) and the Moore coverage (b) automata. Additionally, on the coverage automaton (b), for each prefix q, we have enumerated all the possible coverage strings c that are compatible to form 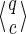Inline graphic states. This is done by substituting any non-covered 1 symbol of 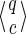Inline graphic (but the last) by a possibly covered one Inline graphic and, for final states, by considering newly covered positions Inline graphic.

The coverage automaton size for seeds of the form 1*r1 is respectively 4 × 3r for the Moore automaton, and 3 × 3r for the Mealy automaton.

Proof. We concentrate first on the Moore automaton. The set of states for the coverage automaton can be easily deduced from the multihit automaton by considering, for each of the multihit prefixes q, all the possible coverages c that are compatible with the current prefix to form reachable Inline graphic states. Any prefix q may have any of its 1-positions (but the last) covered by a previous hit of a seed if this previous hit ends at this 1-position (illustrated by the dot symbols of Fig. 7b to mark 1-positions already covered). Moreover, it must be noticed that coverage of any 1-positions inside q can be chosen independently, by making/disabling a previous hit of a seed using its first 1-position (this position is not shown on the automaton, thus not overlapping the current prefix, and does not have any side effect). Thus all the possible 1-positions (but the last) of a given proper prefix q can be chosen independently with or without coverage. Thus, for any proper prefix q of length l + 1 (0 < l + 1 < k) (q overlaps the first must match symbol, followed by Inline graphic joker symbols of the seed ongoing hit)

  • 1. the very first 1 symbol under a must match symbol can be covered or not (two possibilities: 1 or Inline graphic),

  • 2. the next l-1 symbols under joker symbols can be independently chosen as 0 or 1 (three possibilities: 0, 1, or Inline graphic),

  • 3. the very last symbol under the last joker symbol can be independently chosen as 0 or 1 (two possibilities). Note that this 1, as new, cannot be covered by a previous hit.

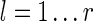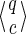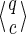For a given prefix q with Inline graphic jokers, there are thus 2 × 3l-1 × 2 = 4 × 3l-1 possible Inline graphic states. Finally, the final states can be seen as prefixes q of length k = r + 2, where the last 1 is always newly covered (one choice: Inline graphic), the r jokers can be any of 0, 1, or Inline graphic (3 choices), and the very first 1 can be previously covered or newly covered (2 choices: Inline graphic or Inline graphic when considering the Moore automaton), leading to 3r × 2 final Inline graphic states. At the end, adding the initial state for q = ε, and its next state (for q = “1” corresponding to the first must match position of the seed which cannot be covered), gives:

graphic file with name eq29.gif

Such seeds 1*r1 have thus a Moore coverage automata of size 4 × 3r.

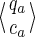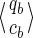Note that this size cannot be reduced. In other words, given any pair of states Inline graphic and Inline graphic on this automaton, and starting (from each of these states) a walk by reading the same (given) string u:

  • • if qa and qb are different, then it is always possible to find one string u such that only one of the two walks reaches a final state (as done in Kucherov et al., 2006).

  • • otherwise, the coverages ca and cb must be different; it is then always possible to find one string u going to two final states that have a different coverage increment for the Moore automaton.

We concentrate now on the Mealy automaton. The main difference with the Moore automaton is that suffixes of full length k (that are final states of the Moore automaton) are not represented because coverage values are set on transitions, and not on states (see Martin and Noé, 2014).

For the Mealy automaton of Martin and Noé (2014), and seeds of the form 1*r1 (of length k = r + 2 and weight 2), there are 2 × 3l proper prefixes q of length l + 1 (0 ≤ l + 1 < k):

  • 1. the first symbol must be 1 or Inline graphic (two possibilities),

  • 2. the next l symbols can be 0, 1, or Inline graphic (3l possibilities).

Adding the initial state gives:

graphic file with name eq34.gif

This bound is reached for the same reasons of nonreducibility (applied on transition labels on Mealy, and not on final state labels as in Moore).     ■

6.2. Coverage automaton size in the general case

Now consider a seed of span k with r jokers and of weight w (w + r = k). Following the previous section, 6.1, a similar reasoning gives a bound on the automaton size of 2w × 3r for the Moore automaton and of (2w−1) × 3r for the Mealy automaton.

Proof. We concentrate first on the Moore automaton. We respectively call rj and wj the number of joker symbols and must match symbols for a given seed prefix of length j (rj = j(π)*, wj = j(π)1, rj + wj = j). We don't necessarily suppose that the seed starts and ends with a must match symbol. We will show that the number of states 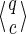Inline graphic such that |q| and |c| are ≤ j is at most Inline graphic, by induction.

  • • This is first true for j = 0, because the empty state (also called the initial state) 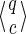Inline graphic where |q| = |c| = 0 is the only one that can match the empty seed prefix 0(π).

  • • If we suppose that it is true for a given i 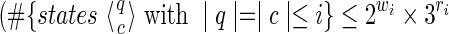Inline graphic), it can be now considered for j = i + 1. We split the demonstration for j in two parts:

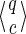  • 1. When |q| = |c| ≤ i, by taking the set of the Inline graphic possible Inline graphic states (induction hypothesis)

  • 2. Otherwise, when |q| = |c| = j, by considering and adding to this set the states 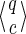Inline graphic that can be possibly reached. Two cases must then be considered:

    • (a) If the last symbol π[j] of the seed prefix j(π) is a must match, this symbol can only be compatible with a 1 on q[j] (and this 1 cannot be covered by c[j], as the last one being added).

    • (b) If the last symbol π[j] of the seed prefix j(π) is a joker, this symbol can be compatible either with a 0 or a 1 on q[j] (which cannot be covered by c[j] too).

Considering now the prefix i(π) preceding π[j], we can see that:

  • – The wi must match symbols of i(π) are compatible with a 1 or a 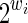Inline graphic (Inline graphic possibilities), and

  • – the remaining ri jokers of i(π) are compatible with a 0, a 1, or a Inline graphic (3ri possibilities).

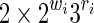Combining each of the cases (a) and (b) with the preceding prefix i(π) gives Inline graphic states for (a), or Inline graphic states for (b), respectively, when |q| = |c| = j.

At the end, because (a) wj = wi + 1 and rj = ri, or (b) wj = wi and rj = ri + 1 otherwise, we can see that summing the number of states when |q| = |c| ≤ i and when |q| = |c| = j gives the expected result 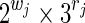Inline graphic, for non-final states.

It must then be noticed that, even for final states, new symbols that have just been covered Inline graphic are only replacing the non-covered ones (1) on a subset of the w fully determined positions given by the seed shape that are not yet covered Inline graphic; they thus don't modify the recurrence when j = |π| as they simply represent indicators to compute the coverage increment.

We concentrate now on the Mealy automaton. Again, the main difference with the Moore automaton is that suffixes of full length k are not represented because coverage values are set on transitions, but one thing to consider is that the last symbol can be covered on the Mealy automaton (see Martin and Noé, 2014). By a similar reasoning, there are thus at most 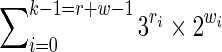Inline graphic states in the general case, and

graphic file with name eq51.gif

Note that if we suppose that the seed starts with a must match symbol, then this bound can be reduced a little more:

graphic file with name eq52.gif

    ■

We notice in practice a much smaller size, and we suspect this bound more likely to be a polynom(w,r) × 3r value, instead of exponential both in 2w and 3r. In the special case of symmetric seeds, we already have a very simple proof of this polynom(w, r) × 3r bound. This is interesting, because experimentally, seeds of the form 11u(*1u)r1 have been shown to give large coverage automata size.

Note even if not satisfying, the general result still improves on the only available “bound” proposed to date (in Benson and Mak, 2008) that can be estimated to be of order w2w4r.

Acknowledgments

D.E.K. Martin was supported in this research by the National Science Foundation under Grant DMS-1107084. L. Noé was supported by a CNRS Mastodons grant, and benefited from a half-time course buyout from the French Institute for Research in Computer Science and Automation (Inria).

Author Disclosure Statement

No competing financial interests exist.

References

  1. Aho A.V., and Corasick M.J.1975. Efficient string matching: An aid to bibliographic search. Commun. ACM 18, 333–340 [Google Scholar]
  2. Apostolico A., Guerra C., and Pizzi C.2014. Alignment free sequence similarity with bounded Hamming distance. In Proc. of the Data Compression Conf. (DCC), 183–192 [Google Scholar]
  3. Bartholdi L.2012. Functionally recursive groups. http://www.gap-system.org/Manuals/pkg/fr-2.1.1/doc/chap0.html
  4. Bassino F., Clément J., Fayolle J., et al. 2008. Constructions for clumps statistics. DIMACS Ser. Discrete Math. Theoret. Comput. Sci. AI, 179–194 [Google Scholar]
  5. Battaglia G., Cangelosi D., Grossi R., et al. 2009. Masking patterns in sequences: A new class of motif discovery with don't cares. Theor. Comput. Sci. 410, 4327–4340 [Google Scholar]
  6. Benson G., and Mak D.Y.2008. Exact distribution of a spaced seed statistic for DNA homology detection. In Proc. of the Int. Symp. on String Processing and Information Retrieval (SPIRE) 5280, 282–293 [Google Scholar]
  7. Boden M., Schöneich M., Horwege S., et al. 2013. Alignment-free sequence comparison with spaced k-mers. In Proc. of the German Conf. on Bioinformatics (GCB)34, 24–34 [Google Scholar]
  8. Brejová B., Brown D.G., and Vinař T.2005. Vector seeds: An extension to spaced seeds. J. Comput. and Syst Sci. 70, 364–380 [Google Scholar]
  9. Břinda K.2014. Languages of lossless seeds. In Proc. of the Int. Conf. on Automata and Formal Languages (AFL)151, 139–150 [Google Scholar]
  10. Buhler J., Keich U., and Sun Y.2005. Designing seeds for similarity search in genomic DNA. J. Comput. and Syst. Sci. 70, 342–363 [Google Scholar]
  11. Burge S.W., Daub J., Eberhardt R., et al. 2012. Rfam 11.0: 10 years of RNA families. Nucleic Acids Res. 41, D226–D232 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Burkhardt S., Crauser A., Ferragina P., et al. 1999. q-gram based database searching using a suffix array (QUASAR). In Proc. of the Annu. Int. Conf. on Research in Computational Molecular Biology (RECOMB), 77–83 [Google Scholar]
  13. Burkhardt S., and Kärkkäinen J.2002. Better filtering with gapped q-grams. Fund. Inform. 56, 51–70 [Google Scholar]
  14. Chen Y., Souaiaia T., and Chen T.2009. PerM: efficient mapping of short sequencing reads with periodic full sensitive spaced seeds. Bioinformatics 25, 2514–2521 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Chor B., Horn D., Goldman N., et al. 2009. Genomic DNA k-mer spectra: Models and modalities. Genome Biol. 10, R108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Comin M., and Verzotto D.2012. Alignment-free phylogeny of whole genomes using underlying subwords. Algorithms Mol. Biol. 7, 34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Csűrös M.2004. Performing local similarity searches with variable length seeds. In Proc. of the 15th Annu. Combinatorial Pattern Matching Symp. (CPM)3109, 373–387 [Google Scholar]
  18. David M., Dzamba M., Lister D., et al. 2011. SHRiMP2: Sensitive yet practical short read mapping. Bioinformatics 27, 1011–1012 [DOI] [PubMed] [Google Scholar]
  19. Didier G., Corel E., Laprevotte I., et al. 2012. Variable length local decoding and alignment-free sequence comparison. Theor. Comput. Sci. 462, 1–11 [Google Scholar]
  20. Do Duc D., Dinh H.Q., Dang T.H., et al. 2012. AcoSeeD: An ant colony optimization for finding optimal spaced seeds in biological sequence search. In Proc. of the 8th Int. Conf. on Swarm Intelligence (ANTS)7461, 204–211 [Google Scholar]
  21. Edgar R.C.2004. MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 32, 1792–1797 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Egidi L., and Manzini G.2014a. Design and analysis of periodic multiple seeds. Theor. Comput. Sci. 522, 62–76 [Google Scholar]
  23. Egidi L., and Manzini G.2014b. Spaced seeds design using perfect rulers. Fund. Inform. 131, 187–203 [Google Scholar]
  24. Farach-Colton M., Landau G.M., et al. 2007. Optimal spaced seeds for faster approximate string matching. J. Comput. and Syst Sci., 73, 1035–1044 [Google Scholar]
  25. Frith M.C., and Noé L.2014. Improved search heuristics find 20,000 new alignments between human and mouse genomes. Nucleic Acids Res. 42, e59. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gambin A., Lasota S., Startek M., et al. 2011. Subset seed extension to Protein BLAST. In Proc. of the Int. Conf. on Bioinformatics Models, Methods and Algorithms, 149–158 [Google Scholar]
  27. Giladi E., Healy J., Myers G., et al. 2010. Error tolerant indexing and alignment of short reads with covering template families. J. Comput. Biol. 17, 1397–1411 [DOI] [PubMed] [Google Scholar]
  28. Giraud M., Salson M., Duez M., et al. 2014. Fast multiclonal clusterization of V(D)J recombinations from high-throughput sequencing. BMC Genomics 15, 409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Harris R.S.2007. Improved pairwise alignment of genomic DNA. [Ph.D. thesis]. The Pennsylvania State University [Google Scholar]
  30. Haubold B., Pierstorff N., Möller F., et al. 2005. Genome comparison without alignment using shortest unique substrings. BMC Bioinformatics 6, 123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Homer N., Merriman B., and Nelson S.F.2009. BFAST: An alignment tool for large scale genome resequencing. PLoS One 4, e7767. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hopcroft J.1971. An n log n algorithm for minimizing the states in a finite automaton, 189–196. In Kohavi Z., and Paz A., eds. The Theory of Machines and Computation. Academic Press, New York [Google Scholar]
  33. Horwege S., Lindner S., Boden M., et al. 2014. Spaced words and kmacs: Fast alignment-free sequence comparison based on inexact word matches. Nucleic Acids Res. 42, W7–W11 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Huang L.2006. Dynamic programming algorithms in semiring and hypergraph frameworks. Technical report. University of Pennsylvania; Philadelphia [Google Scholar]
  35. Ilie L., Ilie S., and Mansouri Bigvand A.2011. SpEED: fast computation of sensitive spaced seeds. Bioinformatics 27, 2433–2434 [DOI] [PubMed] [Google Scholar]
  36. Ilie L., Mohamadi H., Brian Golding G., et al. 2013. BOND: Basic OligoNucleotide Design. BMC Bioinformatics 14, 69. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Joachims T.2002. Learning to Classify Text using Support Vector Machines. Kluwer: /Springer [Google Scholar]
  38. Keich U., Li M., Ma B., et al. 2004. On spaced seeds for similarity search. Discrete Appl. Math. 138, 253–263 [Google Scholar]
  39. Kiełbasa S.M., Wan R., Sato K., et al. 2011. Adaptive seeds tame genomic sequence comparison. Genome Res. 21, 487–493 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Kuang R., Ie E., Wang K., et al. 2005. Profile-based string kernels for remote homology detection and motif extraction. J. Bioinform. Comput. Biol. 3, 527–550 [DOI] [PubMed] [Google Scholar]
  41. Kucherov G., Noé L., and Roytberg M.A.2005. Multiseed lossless filtration. IEEE/ACM Trans. Comput. Biol. Bioinf. 2, 51–61 [DOI] [PubMed] [Google Scholar]
  42. Kucherov G., Noé L., and Roytberg M.A.2006. A unifying framework for seed sensitivity and its application to subset seeds. J. Bioinform. Comput. Biol. 4, 553–569 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Kucherov G., Noé L., and Roytberg M.A.2007. Subset seed automaton. In Proc. of the 12th Int. Conf. on Implementation and Application of Automata (CIAA)4783, 180–191 [Google Scholar]
  44. Kucherov G., Noé L., and Roytberg M.A.2014. Iedera subset seed design tool. http://bioinfo.lifl.fr/yass/iedera.php
  45. Leimeister C.-A., Boden M., Horwege S., et al. 2014. Fast alignment-free sequence comparison using spaced-word frequencies. Bioinformatics 30, 1991–1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Leslie C.S., Eskin E., Cohen A., et al. 2004. Mismatch string kernels for discriminative protein classification. Bioinfomatics 20, 467–476 [DOI] [PubMed] [Google Scholar]
  47. Leslie C.S., Eskin E., and Stafford Noble W.2002. The spectrum kernel: A string kernel for SVM protein classification. In Proc. of the Pacific Symp. on Biocomputing (PSB), 564–575 [PubMed] [Google Scholar]
  48. Li M., Ma B., Kisman D., et al. 2004. PatternHunter II: Highly sensitive and fast homology search. J. Bioinform. Comput. Biol. 2, 417–439 [DOI] [PubMed] [Google Scholar]
  49. Lin H., Zhang Z., Zhang M.Q., et al. 2008. ZOOM! Zillions Of Oligos Mapped. Bioinformatics 24, 2431–2437 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Liu Z., DeSantis T.Z., Andersen G.L., et al. 2008. Accurate taxonomy assignments from 16S rRNA sequences produced by highly parallel pyrosequencers. Nucleic Acids Res. 36, e120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Lodhi H., Saunders C., Shawe-Taylor J., et al. 2002. Text classification using string kernels. J. Mach. Learn. Res. 2, 419–444 [Google Scholar]
  52. Marschall T., Herms I., Kaltenbach H.-M., et al. 2012. Probabilistic arithmetic automata and their applications. IEEE/ACM Trans. Comput. Biol. Bioinf. 9, 1737–1750 [DOI] [PubMed] [Google Scholar]
  53. Martin D.E.K.2013. Coverage of spaced seeds as a measure of clumping. In JSM Proc., Statistical Computing Section. American Statistical Association, Alexandria, Virginia [Google Scholar]
  54. Martin D.E.K. and Coleman D.A.2011. Distribution of clump statistics for a collection of words. J. Appl. Probab. 48, 901–1204 [Google Scholar]
  55. Martin D.E.K., and Noé L.2014. Faster exact probabilities for statistics of overlapping pattern occurrences. Ann. Inst. Stat. Math. [Submitted] [Google Scholar]
  56. Maurer-Stroh S., Gunalan V., Wong W.-C., et al. 2013. A simple shortcut to unsupervised alignment-free phylogenetic genome groupings, even from unassembled sequencing reads. J. Bioinform. Comput. Biol. 11, 1343005. [DOI] [PubMed] [Google Scholar]
  57. Michener C.D., and Sokal R.R.1957. A quantitative approach to a problem in classification. Evolution 11, 130–162 [Google Scholar]
  58. Mohri M.2009. Handbook of Weighted Automata, 213–254 Springer, New York [Google Scholar]
  59. Nicolas F., and Rivals É.2008. Hardness of optimal spaced seed design. J. Comput. and Syst Sci. 74, 831–849 [Google Scholar]
  60. Nuel G.2008. Pattern Markov chains: optimal Markov chain embedding through deterministic finite automata. J. Appl. Probab. 45, 226–243 [Google Scholar]
  61. Nuel G.2011. Bioinformatics - Trends and Methodologies, 173–194 InTech, Rijeka, Croatia [Google Scholar]
  62. Octave 2014. GNU Octave 3.8. http://www.gnu.org/software/octave/
  63. Onodera T., and Shibuya T.2013. The gapped spectrum kernel for support vector machines. In Proc. of the Int. Conf. on Machine Learning and Data Mining in Pattern Recognition (MLDM)7988, 1–15 [Google Scholar]
  64. Pin J.-E.1998. Tropical semirings. InGunawardena J., ed. Idempotency, 11, Publ. Newton Inst., 50–69, Bristol. Cambridge University Press, Cambridge, UK [Google Scholar]
  65. Qi J., Luo H., and Hao B.2004. CVTree: A phylogenetic tree reconstruction tool based on whole genomes. Nucleic Acids Res. 32, W45–W47 [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Rasmussen K.R., Stoye J., and Myers E.W.2006. Efficient q-gram filters for finding all ε-matches over a given length. J. Comput. Biol. 13, 296–308 [DOI] [PubMed] [Google Scholar]
  67. Régnier M., Fang B., and Iakovishina D.2014. Clump combinatorics, automata, and word asymptotics. In Proc. of the Worksh. on Analytic Algorithmics and Combinatorics (ANALCO) [Google Scholar]
  68. Saigo H., Vert J.-P., Ueda N., et al. 2004. Protein homology detection using string alignment kernels. Bioinfomatics 20, 1682–1689 [DOI] [PubMed] [Google Scholar]
  69. Schensted C.1961. Longest increasing and decreasing subsequences. Can. J. Math. 13, 179–191 [Google Scholar]
  70. Simon I.1988. Recognizable sets with multiplicities in the tropical semiring. In Mathematical Foundations of Computer Science 324, 107–120 [Google Scholar]
  71. Simsa G.E., Juna S.-R., Wua G.A., et al. 2009. Alignment-free genome comparison with feature frequency profiles (FFP) and optimal resolutions. Proc. Natl. Acad. Sci. USA. 106, 2677–2682 [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Stefanov V.T., Robin S., and Schbath S.2007. Waiting times for clumps of patterns and for structured motifs in random sequences. Discrete Appl. Math. 155, 868–880 [Google Scholar]
  73. Stropea P.K., and Moriyama E.N.2007. Simple alignment-free methods for protein classification: A case study from G-protein-coupled receptors. Genomics 89, 602–612 [DOI] [PubMed] [Google Scholar]
  74. Vinga S.2014. Editorial: Alignment-free methods in computational biology. Brief. Bioinform. 15, 341–342 [DOI] [PubMed] [Google Scholar]
  75. Vinga S., and Almeida J.2003. Alignment-free sequence comparison - a review. Bioinformatics 19, 513–523 [DOI] [PubMed] [Google Scholar]
  76. Yang J., and Zhang L.2008. Run probabilities of seed-like patterns and identifying good transition seeds. J. Comput. Biol. 15, 1295–1313 [DOI] [PubMed] [Google Scholar]
  77. Zhou L., Mihai I., and Florea L.2010. Spaced seeds for cross-species cDNA-to-genome sequence alignment. Commun. Inf. Syst. 10, 115–136 [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES