Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2014 Jan 15;56(1):75–87. doi: 10.1111/jipb.12118

Genomic regions underlying agronomic traits in linseed (Linum usitatissimum L.) as revealed by association mapping‡

Braulio J Soto-Cerda 1,2,†, Scott Duguid 3, Helen Booker 4, Gordon Rowland 4, Axel Diederichsen 5, Sylvie Cloutier 1,2,*
PMCID: PMC4253320  PMID: 24138336

Abstract

The extreme climate of the Canadian Prairies poses a major challenge to improve yield. Although it is possible to breed for yield per se, focusing on yield-related traits could be advantageous because of their simpler genetic architecture. The Canadian flax core collection of 390 accessions was genotyped with 464 simple sequence repeat markers, and phenotypic data for nine agronomic traits including yield, bolls per area, 1,000 seed weight, seeds per boll, start of flowering, end of flowering, plant height, plant branching, and lodging collected from up to eight environments was used for association mapping. Based on a mixed model (principal component analysis (PCA) + kinship matrix (K)), 12 significant marker-trait associations for six agronomic traits were identified. Most of the associations were stable across environments as revealed by multivariate analyses. Statistical simulation for five markers associated with 1000 seed weight indicated that the favorable alleles have additive effects. None of the modern cultivars carried the five favorable alleles and the maximum number of four observed in any accessions was mostly in breeding lines. Our results confirmed the complex genetic architecture of yield-related traits and the inherent difficulties associated with their identification while illustrating the potential for improvement through marker-assisted selection.

Keywords: Linum usitatissimum, marker-assisted selection, quantitative trait loci mapping, yield-related traits, Favorable alleles

Introduction

Linseed (Linum usitatissimum L.) is important for the oil and nutraceutical industries (Green et al. 2008). Its oil, characterized by a high concentration of omega-3 alpha linolenic acid (∼55%), is widely recognized for its health benefits (Simopoulos 2000). A unique feature of linseed resides in the prospect of also commercializing its stems because they produce good quality fibers that have many end-uses (Czemplik et al. 2011) including paper, technical fiber, and biofuels (Diederichsen and Ulrich 2009; Cullis 2011). In 2011, the total world production of linseed reached approximately 1.6 million tons, with Canada (∼23%), China (∼21%), and the Russian Federation (∼14%) being the main producers (FAOSTAT 2013). Although Canada is the world's largest linseed producer and exporter (FAOSTAT 2013), linseed remains a minor crop, in part because its yield has been stagnating over the last decade, averaging 1.2 T/Ha compared to other oilseeds such as canola (rapeseed) that now reach 1.9 T/Ha (Statistics Canada; http://www.statcan.gc.ca).

Conventional breeding methods have been the cornerstone for linseed genetic improvement releasing new cultivars with durable resistance to diseases, agronomic fitness, and greater yield stability (Green et al. 2008). However, the narrow genetic base used for the development of Canadian linseed cultivars (Fu et al. 2002, 2003; Cloutier et al. 2009), the scarce availability of related species to incorporate new variation, the lack of hybrid production systems (Green et al. 2008), and the limited genomic tools for molecular breeding (Cloutier et al. 2011, 2012a) have hampered yield and quality improvements, limiting linseed competitiveness.

Yield is the most important and complex trait in crops that shows correlations with other traits (Li et al. 2011). In linseed, yield and its components such as 1,000 seed weight (TSW), seeds per boll (SPB), and bolls per area (BPA), are quantitatively inherited and controlled by many genes affected by multiple interactions with other genes and the environment (Shi et al. 2009; Parry and Hawkesford 2012; Cadic et al. 2013). An understanding of the genetic basis of yield-related traits is of practical value to breeders because such information assists in the design of efficient breeding strategies. This approach, focused on yield-related traits, has been embraced in oilseeds such as Brassica napus (Shi et al. 2009), soybean (Panthee et al. 2007; Liu et al. 2011), and maize (Huang et al. 2010; Peng et al. 2011) focusing on the improvement and inheritance of yield-related traits for achieving greater yield. Other important agronomic traits such as flowering time (FL), plant height (PH), plant branching (PB), and lodging resistance (LDG) may also indirectly affect yield through various physiological mechanisms (Huang et al. 2010; Li et al. 2011), allowing crop phenology and plant architecture to be adapted to regional growing conditions, thus avoiding yield and quality losses (Duguid 2009). The estimation of the positions of quantitative trait loci (QTL) with consistent effects across environments for yield and its components and other agronomic traits is of central importance for marker-assisted selection (MAS) and, ultimately, for enhancing linseed competitiveness.

In oilseed breeding, most of the QTL contributing to yield and other agronomic traits have been identified through classical linkage mapping (Panthee et al. 2007; Shi et al. 2009; Huang et al. 2010; Liu et al. 2011; Peng et al. 2011). Despite the proven usefulness of this technique to identify QTL involved in complex traits, the limited genetic diversity and recombination events accumulated in biparental populations impede the simultaneous identification of favorable alleles available to breeding programs and the precision of the location of QTL, thus weakening MAS applications (Würschum 2012). Often presented as an alternative approach, association mapping (AM) makes use of all recombination events that have occurred during the history of a germplasm collection representing a broader genetic diversity and, consequently, leading to a higher mapping resolution and the simultaneous survey of a larger number of alleles (Flint-Garcia et al. 2003; Würschum 2012). In the last decade, AM has been successfully applied to crops (reviewed in Gupta et al. 2005; Soto-Cerda and Cloutier 2012), showing that faster breeding progresses can be achieved (Myles et al. 2009; Cadic et al. 2013; Huang et al. 2013).

In 2009, the Total Utilization Flax GENomics (TUFGEN; http://www.tufgen.ca) project was initiated in Canada, generating a wealth of genomic resources with one of the main goals being applications to flax breeding (Cloutier et al. 2009, 2011, 2012a, 2012b; Ragupathy et al. 2011; Venglat et al. 2011; Kumar et al. 2012; Wang et al. 2012a). The comprehensive characterization of the Canadian flax world collection preserved by Plant Gene Resources Canada permitted the assembly of the Canadian flax core collection of 390 accessions representing the diversity from 76 countries (Diederichsen et al. 2013). This valuable genetic resource ensures a cost-effective access to the diversity harbored in the whole collection of approximately 3,500 accessions (Diederichsen et al. 2013). Further molecular characterization of the Canadian flax core collection revealed its abundant genetic diversity, weak population, and family structure, and quantified its relatively fast genome-wide linkage disequilibrium (LD) decay, all positive attributes for AM studies (Soto-Cerda et al. 2013). In the present study, we carried out AM for yield, TSW, SPB, BPA, start of flowering (FL 5%), end of flowering (FL 95%), PH, PB, and LDG on the Canadian flax core collection assessed in Western Canada over 4 years. The objective of this research was to identify QTL contributing to these agronomic traits that could be capitalized upon to assist in breeding superior linseed cultivars with improved yield and consequently market competitiveness.

Results

Agronomic traits

All agronomic traits showed significant genotype (G), location (L), and year (Y) effects (P < 0.001; Table S1). Most of the genotype-by-environment (GE) interactions (G × L, G × Y, L × Y, and G × L × Y) were significant, except for yield where only L × Y was significant. The overall means, ranges, H, and coefficient of variations are summarized in Table1. In MB, H ranged 0.15–0.83, while in SK, it ranged 0.37–0.78, indicating that the repeatability was highly variable among the agronomic traits at both locations. Among the 36 possible correlations, 25 were significant at P < 0.01 (Table2). Yield and its components were positively correlated with one another but they were negatively correlated with the phenological traits FL 5% and FL 95%, the morphological traits PH and PB, and the LDG agronomic trait.

Table 1.

Number of environments, descriptive statistics, and broad sense heritability (H) for the nine agronomic traits assessed in the Canadian flax core collection

Trait Environments Mean Range C.V. (%) H (MB) H (SK)
Yield (K/ha) 6 1312.10 565.2–2468.8 36.2 0.59 0.59
Bolls per area (bolls/m2) 6 4134.80 1653.6–6482.8 22.8 0.41 0.49
1,000 seed weight (g) 6 5.10 2.7–8.4 3.9 0.75 0.76
Seeds/boll 6 6.20 3.5–8.1 11.5 0.63 0.63
Flowering 5% (d) 7 45.10 40.0–61.9 3.3 0.83 0.47
Flowering 95% (d) 7 51.20 45.9–71.4 3.3 0.80 0.49
Plant height (cm) 6 51.30 28–92.9 11.8 0.63 0.76
Plant branching 4 3.40 1.7–5.3 23.1 0.15 0.78
Lodging 8 1.34 1.0–3.3 19.1 0.20 0.37
Open in a new tab

Table 2.

Pearson correlation coefficients amongst the nine agronomic traits in the Canadian flax core collection

Trait Yield BPA TSW SPB FL 5% FL 95% PH PB LDG
Yield —
BPA 0.528** —
TSW 0.173** −0.285** —
SPB 0.541** 0.272** −0.123* —
FL 5% −0.111* 0.029 −0.361** −0.323** —
FL 95% −0.108* 0.036 −0.352** −0.347** 0.964** —
PH −0.140** −0.046 −0.361** 0.026 0.506** 0.497** —
PB −0.073 0.007 −0.265** −0.049 0.429** 0.416** 0.633** —
LDG −0.134** −0.005 0.094 −0.354** 0.005 0.007 −0.261** −0.238** —
Open in a new tab
*

P < 0.01 and

**

P < 0.001.

Association between population structure and agronomic traits

Due to different population sizes (G1 = 153; G3 = 211) and unequal variances within the two major groups for the agronomic traits, the Kruskal–Wallis test was applied as suggested by Lin et al. (2008). Only PH showed significant differences (P = 0.03) with G1 accessions being 3 cm taller than G3 accessions (Figure S1).

Of the 92 fiber flax accessions of the core collection, 48 (36% of G1) clustered within G1 while 23 (12.8% of G3) belonged to G3, suggesting that although the coefficient of population differentiation (FST) was weak (0.09), the fiber morphotype could be the main factor responsible for the population structure of the flax core collection. We investigated the pattern of population structure within G1 and G3 separately and showed that both major groups were organized in two subpopulations (Q ≥ 0.7) and one admixed subpopulation (Q < 0.7) (Figure S2). Within G1, the two subpopulations largely corresponded to the oil and fiber morphotypes, with 91% of the fiber accessions initially clustering within G1 (Figure S2). Within G3, however, the two subpopulation clusters reflected their geographic distribution with no clear sub-clustering of the 23 fiber accessions (Figure S2). Thus, flax morphotype and geographic distribution constituted the main factors responsible for the population structure patterns observed in the Canadian flax core collection, with the Q matrix and the first three principal component analyses (PCAs) explaining 11.3% and 39% of PH variation, respectively.

AM analysis in the core collection and subgroups

As depicted by the cumulative probability–probability (P–P) plots generated using the 390 accessions (Figure 1), numerous spurious associations for all traits were observed with Q general linear model (GLM). This model was characterized by an excess of small P-values causing spurious associations. On the other hand, the PCA GLM overcorrected the majority of the small P-values with few higher P-values departing at the very end of the expected distribution. The mixed linear models (MLMs) K and Q + K performed similarly for the nine agronomic traits with their observed P-values deviating the most from the expected ones for TSW, SPB, PH, PB, and LDG, indicating that inclusion of the Q matrix brought little or no improvement to the AM model. Nevertheless, they displayed a better distribution of P-values for BPA and FL 95% (Figure 1). The PCA + K MLM had the smallest deviation from the expected distribution for all agronomic traits. The three first PCAs in combination with the K matrix were sufficient to control the majority of the potential false-positive associations created by population and family structure. Therefore, the PCA + K model was selected to conduct AM for the nine agronomic traits in the core collection.

Figure 1.

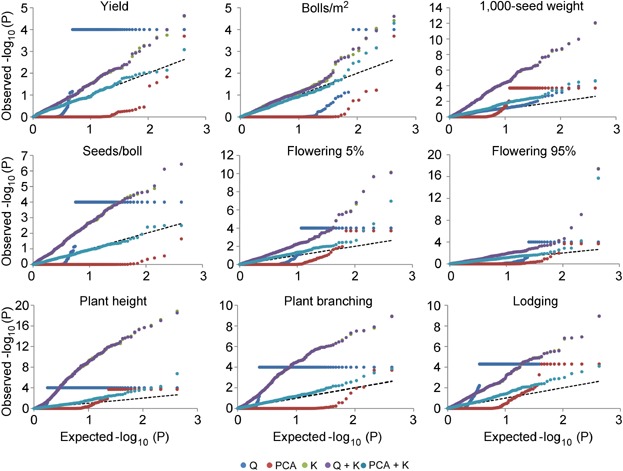
Figure 1

Open in a new tab

Probability-probability (P-P) plots of observed versus expected −log10 (P) values for nine agronomic traits evaluated with five association mapping modelsQ general linear model using the Q matrix, PCA general linear model using the principal component analysis matrix, K mixed linear model using the kinship matrix, Q + K mixed linear model using the Q and K matrices, PCA + K mixed linear model using the PCA and K matrices.

Mixed linear models may overcompensate when traits are correlated with population structure, leading to false negatives (Zhao et al. 2011). Because up to 39% of the variation for PH was explained by population structure, we conducted AM for this trait within G1 and G3 separately. The P–P plot of G1 showed an improvement for the K and Q + K models, with the latter performing as well as the PCA + K (Figure S2). On the other hand, the P–P plot of G3 exhibited a better performance for the Q + K model only, the PCA + K being the most suitable. Thus, AM model comparisons indicated that conducting subpopulation-independent AM analyses partially alleviated the effect of population structure within G1 but did not correct it for G3, making it necessary to consider population structure as a fixed covariate. Hence, AM analyses for PH were conducted using the Q + K and PCA + K models.

Marker-trait associations

After removing alleles with a minor allele frequency (MAF) of less than 0.05, 37 simple sequence repeat (SSR) markers became monomorphic, leaving 427 polymorphic loci for the AM analyses. Using the PCA + K model, a total of 12 significant marker-trait associations (estimated false discovery rate (qFDR) < 0.01) were identified as significant in at least half of the environments tested. They corresponded to 10 different markers distributed across six linkage groups (LGs). The majority of these associations remained significant even after Bonferroni correction (0.05/427 = 1.17E − 4) (Table3). Numerous other significant associations were detected but they were not consistent in at least half of the environments. This was the case for yield, SPB, and BPA, although six markers were associated with these traits in one or more of the environments.

Table 3.

Marker loci significantly associated with 1,000 seed weight (TSW), start of flowering (FL5%), end of flowering (FL95%), plant height (PH), plant branching (PB) and lodging (LDG), and their explained phenotypic variance (R2)

Trait Marker LG (cM)1 MB09 (P-value) MB10 (P-value) MB11 (P-value) MB12 (P-value) SK09 (P-value) SK10 (P-value) SK11 (P-value) SK12 (P-value) R2 (%)
TSW Lu2164 3 (76.5) N.E. n.s. n.s. 1.61E − 4 N.E. 7.50E − 5 1.10E − 8 1.10E − 4 0.50
Lu2555 6 (72.0) N.E. n.s. n.s. 1.78E − 4 N.E. 7.10E − 4 1.24E − 4 6.51E − 4 0.72
Lu2532 7 (2.7) N.E. n.s. n.s. 1.53E − 5 N.E. 9.60E − 5 2.36E − 6 7.90E − 5 8.0
Lu58a 7 (104.3) N.E. n.s. n.s. 3.92E − 4 N.E. n.s. 2.38E − 6 1.90E − 4 5.5
Lu526 9 (32.6) N.E. 4.20E − 5 n.s. 6.81E − 6 N.E. 2.27E − 4 1.10E − 4 n.s. 15.2
FL 5% Lu943 1 (149.9) n.s. 4.42E − 7 7.88E − 5 n.s. N.E. n.s. 4.34E − 5 7.35E − 7 7.1
FL 95% Lu943 1 (149.9) n.s. 2.60E − 5 8.94E − 5 n.s. N.E. n.s. 8.74E − 5 4.90E − 6 7.6
PH Lu943 1 (149.9) N.E. N.E. 1.31E − 4 n.s. 1.01E − 4 n.s. n.s. 2.31E − 4 4.6
Lu316 Unknown N.E. N.E. 1.15E − 5 9.23E − 5 n.s. n.s. n.s. 1.62E − 5 18.5
PB Lu2067a 2 (59.7) n.s. N.E. n.s. N.E. N.E. 9.08E − 5 3.35E − 5 N.E. 12.9
LDG Lu2560 6 (63.4) n.s. 4.95E − 4 n.s. N.V. N.V. 5.73E − 5 1.38E − 18 n.s. 8.9
Lu2564 6 (64.1) 1.53E − 4 8.74E − 4 9.05E − 11 N.V. N.V. n.s. 1.20E − 4 n.s. 7.1
Open in a new tab
1

Linkage group and, in bracket, loci position in centiMorgan according to Cloutier et al. (2012b). N.E., trait not evaluated; N.V., trait not phenotypically variable; n.s. non-significant. Values in bold script are significant at qFDR < 0.01 and after Bonferroni correction (0.05/427 = 1.17E − 4); those in normal script are significant at qFDR < 0.01.

A total of five significant markers were associated with TSW, together explaining approximately 30% of the phenotypic variation for the trait. Marker Lu943 was associated with FL5%, FL 95%, and PH, in agreement with their positive and significant correlations (Table2). LG6 markers Lu2560 and Lu2564 located 0.7 cM apart formed a candidate QTL for LDG. For PH AM analyses, no additional associations were identified. However, for G1, marker Lu2067a associated with PB, which was correlated with PH (r = 0.633) and showed associations in two of the six environments evaluated.

Allelic effects of significant markers

Some of the alleles significantly improved TSW. For example, the 289 bp allele of Lu526 significantly increased TSW by an average of 1.02 g (P = 8.5E − 13) across the six environments tested (Figure 2A). For Lu2532, the 270 bp allele had the largest effect, increasing TSW by 1.91 g (P = 1.7E − 6) over the 280 bp allele and 1.3 g (P = 0.003) over the 282 bp allele (Figure 2B). The 271 bp allele of Lu943 significantly shortened FL 5% by 2.13 d (P = 1.64E − 9) compared to the other two alleles (Figure 2C). These allelic differences carried through to FL 95% (Table4). A reduction of up to 23.7 cm (P = 2.2E − 13) in PH was associated with the 241 bp allele of Lu316 compared with the 223 bp allele (Figure 2D). However, this large allelic effect can be inflated by the higher PH of the fiber accessions, where the 223 bp allele was present in 33% of the fiber morphotype and only 6% of the linseed morphotype while the 241 bp allele was present in 31% of the linseed morphotype but only 7% of the fiber morphotype. The 205 bp allele of marker Lu2067a, increased PB up to 0.76 units compared with the 211 bp allele (P = 2.03E − 8) (Figure 2E). The null allele of Lu2560 decreased LDG by 0.34 units (P = 3.14E–6) (Figure 2F).

Figure 2.

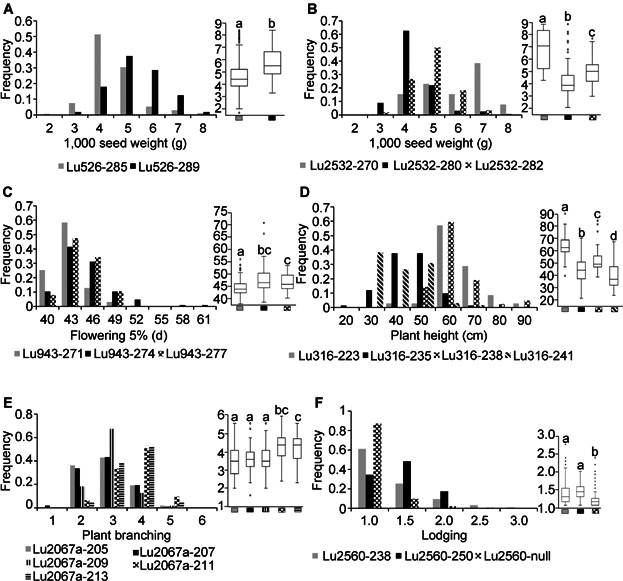
Figure 2

Open in a new tab

Comparisons of allelic effects of six associated markers with agronomic traits in linseed

(A) Lu526 and (B) Lu2532 associated with 1 000 seed weight. (C) Lu943 associated with start of flowering.(D) Lu316 associated with plant height.(E) Lu2067a associated with plant branching. (F) Lu2560 associated with lodging.Box plots followed by the same letter do not differ statistically according to the Kruskal–Wallis test (α = 0.01).

Table 4.

Favorable alleles at the ten SSR loci associated with agronomic traits, their frequencies, phenotypic effects, and stability

Trait Marker Favorable allele (bp) Frequency (%) Effecta K–W testb IPCA1c ASVd
TSW Lu2164 377 44.9 0.68 g 1.9E − 3* 0.907 3.222
Lu2555 202 47.9 0.85 g 2.1E − 12* −0.411 1.446
Lu2532 270 8.0 1.91 g 5.6E − 7* −0.729 1.537
Lu58a 209 72.5 0.72 g 3.1E − 3* 0.209 1.441
Lu526 289 15.8 1.02 g 8.4E − 13* 0.023 1.178
FL 5% Lu943 271 60.8 −2.13 d 5.5E − 5* −0.215 0.215
FL 95% Lu943 271 60.8 −2.15 d 1.2E − 9* −0.181 0.181
PH Lu943 271 60.8 −9.25 cm 8.4E − 9* 2.532 2.532
Lu316 241 17.3 −23.7 cm 1.6E − 14* −2.532 2.532
PB Lu2067a 205 27.6 −0.76 u 1.5E − 9* 0.265 0.321
LDG Lu2560 null 47.5 −0.34 u 4.7E − 8* −0.557 0.558
Lu2564 257 11.7 −0.28 u 6.4E − 4* 0.557 0.558
Open in a new tab
a

Effect of favorable alleles represented in grams (g) for TSW, days (d) for FL 5% and FL 95%, centimeters (cm) for PH, and units (u) of the respective scales for PB and LDG.

b

P-value for Kruskal-Wallis test for the allelic effect between favored alleles and others

*

*P < 0.01.

c

First interaction principal component.

d

AMMI's stability values.

Marker effect and stability

The additive main effect and multiplicative interaction (AMMI) analysis established that 1/3 of the marker-trait associations were highly stable with first interaction principal component (IPCA1) values close to ± 0.2 and that another third were moderately stable with values ranging from ± 0.25 to ± 0.6 (Table4). The AMMI stability values (ASV) parameter indicated that six marker-trait associations were highly stable with values ranging 0.18–1.17. The QTL main effect and QTL-by-environment interaction (QQE) biplot displays the average environment defined by the average IPCA1 and IPCA2 scores across environments (indicated by an open circle) (Figure 3A). The arrow passing through the biplot origin is called the AEC abscissa and points towards increasing marker/QTL main effect. The AEC ordinate line, perpendicular to the abscissa, indicates stability/instability. Highly unstable markers have longer projections on the AEC abscissa irrespective of their direction. The markers associated with TSW varied in stability. For example, Lu2532 and Lu526 were more stable than Lu2555, Lu2164, and Lu58a (Figure 3A). The intersection of the two axes defines the average marker/QTL main effect, hence, the latter three markers had effects below average; whereas, Lu2532 and Lu526 had the largest main effects on TSW across the six environments in which this TSW was tested (Figure 3A, Table4). Taking into consideration that approximately 300 accessions of the core collection are the linseed type, the favorable alleles of Lu2532 and Lu526, present in 31 and 62 accessions, respectively, clearly demonstrate that they have not been the target of intensive selection by linseed breeders to date.

Figure 3.

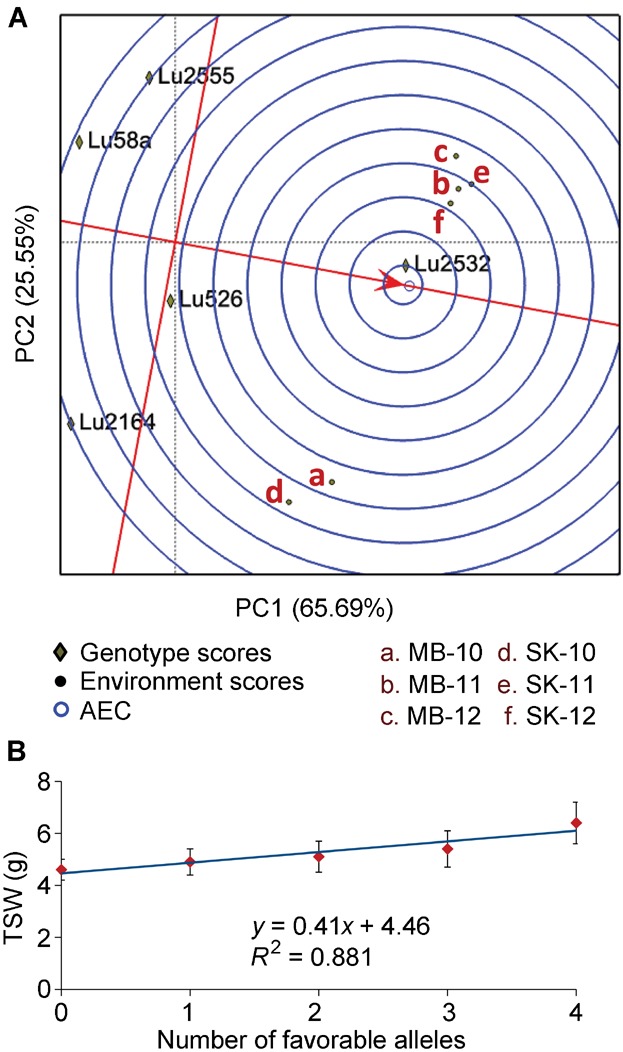
Figure 3

Open in a new tab

Marker effect and stability

(A) QTL main effect and QTL-by-environment interaction (QQE) biplot for marker/quantitative trait loci (QTL) main effect and marker/QTL stability of 1,000 seed weight. (B) Linear regression analysis of 1,000 seed weight based on six environments.

Linear regression analysis between TSW and the number of favorable alleles of associated markers showed a linear correlation, suggesting additive effects (Figure 3B). No accession had all five favorable alleles but 10 accessions had four of them. Among these, only one US modern cultivar (Maritime, mean TSW = 7.3 g) showed four alleles while the remaining nine were breeding lines including three belonging to the convar. mediterraneum characterized by its large seeds and high TSW (Figure 4). The high yielding and broadly adapted Canadian cultivar CDC Bethune (mean TSW = 5.2 g) possesses only two of the five TSW favorable alleles.

Figure 4.

Figure 4

Open in a new tab

Linseed accessions with different number of favorable alleles associated with 1 000 seed weight

(A) Accessions with zero favorable alleles. (B) Canadian cultivars with two favorable alleles. (C) Accessions with four favorable alleles.Values in brackets are the 1 000 seed weights for each accession. *Indicates the accessions that belong to the convar. mediterraneum.

Discussion

Yield is a complex trait that can be broken down into its components which are in turn affected by other traits involving diverse pathways (Shi et al. 2009). For example, seed number, seed weight, flowering time, plant height, and plant branching have all been identified as affecting yield in rapeseed (Ishimaru 2003; Salamini 2003; Ashikari et al. 2005; Clark et al. 2006; Cockram et al. 2007). Phenotypic correlations and QTL analyses suggest that yield-associated traits tend to be clustered in the genome and have pleiotropic effects (Shi et al. 2009; Li et al. 2011; Liu et al. 2011). Hence, understanding the genetic bases and relationships of yield-associated traits and agronomic traits in linseed through AM can provide the scientific background needed to devise breeding strategies that would permit and/or accelerate yield improvements beyond the 1.2 T/Ha achieved to date.

Agronomic traits

The anova showed that the genotype effect was highly significant for all nine traits, indicating that abundant and likely unexploited genetic diversity is harbored within the Canadian flax core collection (Tables1, S1). Yield, BPA, and TSW had ranges that spanned five, four, and three orders of magnitude, respectively (Table1). GE interactions also contributed significantly to trait variations highlighting the need to identify stable germplasm across environments having favorable alleles (Zhang et al. 2010).

Broad sense heritability (H) is a suitable indicator of the trait repeatability and the proportion of trait variation accounted for by genetic factors. H varied largely between traits and locations. For example, the MB and SK locations had opposite effects on FL 5%, FL 95%, PB, and LDG while their effects on yield-related traits followed similar trends (Table1). Historical meteorological data indicates that the MB location is warmer and wetter than the SK location, this was particularly true during the growing seasons of 2010 and 2011 (Agriculture and Agri-Food Canada; http://ablethr2/Weather.html). This complicates phenotypic selection of suitable parents with broad adaptation, the design of efficient breeding schemes and, ultimately, yield improvement.

Correlations among phenotypic traits are commonly observed in crops. Plant breeders need to consider trait correlations for the simultaneous improvement of numerous correlated traits or for reducing undesirable effects when the goal is to apply changes to one or a subset of the correlated traits (Chen and Lubberstedt 2010). Yield was positively correlated with its yield components and negatively correlated with FL5%, FL95%, PH, and LDG (Table2) suggesting that further yield improvement could come from the breeding of an early flowering, shorter linseed plant producing larger seeds per boll and more bolls per area. Similar phenotypic correlations among yield-related traits and other agronomic traits have been reported in soybean (Panthee et al. 2007), rapeseed (Honsdorf et al. 2010), and maize (Peng et al. 2011).

Association between population structure and agronomic traits

Correlations between population structure and variation for phenotypic traits have been reported (Camus-Kulandaivelu et al. 2006; Caniato et al. 2011; Zhao et al. 2011). In maize, a null allele of the Dwarf8 (D8idp) gene associated with flowering time was found in high frequency among Northern Flint accessions but was rare in tropical accessions (Camus-Kulandaivelu et al. 2006). In sorghum, aluminum tolerance conferred by the Sorghum bicolor multidrug and toxic compound extrusion (SbMATE) gene was almost exclusive to West African genotypes (Caniato et al. 2011). Likewise in rice, several height genes such as Oryza sativa BRI1-associated receptor kinase 1 (OsBAK1) and dwarf and gladius leaf 1 (DGL1) were population-specific and were only detected when no correction for population stratification was applied (Zhao et al. 2011). In our study, PH variation appeared to correlate with population structure caused by differences in plant morphotype because fiber flax and linseed differ considerably in morphology, anatomy, physiology, and agronomic performance (Diederichsen and Ulrich 2009). Although incorporation of population structure covariate is important to control false positives in AM, a substantial fraction of the PH variation likely remained undetected as a consequence of the morphotypes in flax (Caniato et al. 2011).

AM analysis in the core collection and subgroups

Association mapping has demonstrated its power to detect QTL across multiple plant species and germplasm collections (reviewed in Gupta et al. 2005; Soto-Cerda and Cloutier 2012). However, a potential problem of AM resides in its inherent population stratification which is recognized as a source of spurious associations because phenotypic and genotypic variations end up highly correlated between subpopulations (Würschum 2012). To circumvent this limitation, a number of approaches have been suggested (Pritchard et al. 2000; Price et al. 2006; Yu et al. 2006). For all nine agronomic traits studied herein, the PCA + K model provided the best approximation to the expected cumulative distribution of P-values (Figure 1), being superior to the K and Q + K models. This suggests that, in the case of linseed, the PCA matrix can better correct for population stratification, in line with the larger PH variation explained by the first three PCAs, which turned out to also be computationally advantageous even with thousands of markers (Price et al. 2006).

When alleles segregate across multiple subpopulations, MLMs are more powerful but when they segregate in only one or a subset of the subpopulations or, when different alleles are present in the subpopulations, MLMs will fail to detect the associations entirely (Zhao et al. 2011). Although we conducted AM for PH within each major group to minimize the confounding effects of flax morphotype and geographic distribution, it was necessary to use MLMs with population structure as covariate, but no significant associations were identified within the major groups. Because the simultaneous use of PCA and K matrices may result in overcorrection (Würschum 2012), additional PH QTL could be detected using biparental mapping populations developed from parents belonging to different subpopulations (Zhao et al. 2011) or, as recently proposed, through the design of multi-parent advanced generation intercross (MAGIC) or nested association mapping (NAM) populations (Mackay and Powell 2007; Yu et al. 2008).

Marker-trait associations

The number of significant associations varied considerably between traits, with no associations detected for yield per se, BPA, and SPB, clearly emphasizing the genetic complexity and high GE interaction of yield and its components (Shi et al. 2009). For example, five markers showed consistent associations with TSW, but more than 30 significant markers (qFDR < 0.01) were identified in at least one environment. These environment-specific associations were detected for all traits. These associations may also result from weak LD between associated markers and QTL caused by: (i) an insufficient number of markers to cover all LD blocks across the genome (Würschum 2012); (ii) low trait heritability (Pasam et al. 2012); and (iii) the removal of rare alleles with large effects excluded from the analyses for statistical reasons (Breseghello and Sorrells 2006). In our study, marker density was likely a limitation considering that our LD analysis indicated that at least 1 500 markers would be required to provide the comprehensive coverage of the genome necessary for AM in the flax core collection (Soto-Cerda et al. 2013). Trait heritability likely negatively impacted marker-trait association detection because the observed H was low to moderate for the majority of the traits which also expressed significant location effect (Tables1, S1). Other pitfalls include genomic regions close to fixation or totally monomorphic and that do not occur by chance, especially in large and diverse germplasm collections. We hypothesized that some of the 37 SSRs that became monomorphic after removal of the alleles with MAF of less than 0.05 have been selected during domestication or modern flax breeding such as the dehiscence trait, considering that they are shared across different populations (Kovach et al. 2007). As a result, they are totally uninformative using AM because the strength of LD mapping relies on polymorphisms between loci to estimate correlations between traits and their allele variants; thus, many potentially large-effect QTL were missed (Zhao et al. 2011). Genetic studies involving wild relatives, landraces, and modern cultivars should help in elucidating this question (Vigouroux et al. 2002; Würschum 2012).

Yield improvement through yield components and related traits such as flowering time and plant morphology could be advantageous because of their simpler genetic architecture and higher stability than yield per se (Peng et al. 2011). In rapeseed, 785 QTL for eight yield-related traits were identified across 10 environments, but only 85 QTL for yield, of which none were consistent across environments (Shi et al. 2009). Exploiting the phenotypic correlations between yield-related traits can facilitate the pyramiding of favorable alleles because correlations may indicate linkage or pleiotropy (Li et al. 2011; Zhao et al. 2011; Zhang et al. 2012). PH is an important developmental and yield-related trait and many genes regulating PH have been shown to affect harvest index and yield in rice (Xue et al. 2008; Xing and Zhang 2010), and yield and flowering time in soybean (Liu et al. 2011). The seemingly pleiotropic effect of the 271 bp allele of Lu943 on FL 5%, FL 95%, and PH illustrates the feasibility of developing short early flowering linseed cultivars with apparently no yield penalties using pleiotropic QTL (Li et al. 2011). Similarly, TSW is an important yield component determining yield in crops (Li et al. 2011; Liu et al. 2011; Wang et al. 2012b); thus, the combined selection of the five favorable alleles associated with TSW is a readily applicable strategy involving indirect yield improvement through yield components (Shi et al. 2009; Wang et al. 2012b).

Marker effect and stability

The majority of the associated QTL detected in biparental populations explained larger proportions of the variance than those detected in AM studies (Stich et al. 2008; Honsdorf et al. 2010; Pasam et al. 2012). Conversely, bias of biparental populations leads to an overestimation of the QTL effect, especially in small populations (Melchinger et al. 2004). In our study, the variance explained by the associated markers ranged 0.5–18.5% (Table3). Although no comparisons can be made with the non-existing previous QTL studies in flax for agronomic traits, these estimates are likely minimum estimates of the real QTL effects because incomplete LD between marker and QTL leads to an underestimation of the variance explained by the QTL (Honsdorf et al. 2010; Würschum 2012). Comparable results between biparental mapping population QTL analysis and AM should be observed when LD is perfect (r2 = 1) and the same alleles segregate in both populations (Myles et al. 2009). Even if LD was perfect, underestimation of the phenotypic variance could ensue from allelic frequency differential in the AM population (Stich et al. 2008). The maximum proportion of the variance explained by a marker is observed for allele frequencies of 0.5, as expected in biparental populations such as recombinant inbred lines or F1-derived doubled haploids. For a germplasm collection, the allele frequencies are expected to be considerably different from 0.5, especially when multi-allelic markers such as SSRs are used (Stich et al. 2008). Thus, the proportion of the variance explained by a marker is notably lower despite the same underlying allelic effect (Stich et al. 2008). As a result, when AM is conducted with suitable marker density and the phenotypes are measured in representative environments, the variance explained by the associated markers should provide a more accurate estimation of the impact that the favorable alleles will have in a breeding program.

Quantitative trait loci with major effects and stable expression across environments and genetic backgrounds are better for MAS. Associations were declared only for markers significant in at least half of the tested environments and, using multivariate analyses, we estimated their stability and effects (Table4, Figure 3A). This approach enabled the identification of MAS candidate markers such as Lu2532, Lu526, and Lu943 that exhibited both high stability and large effects on TSW and flowering traits. Other associated markers identified herein also may be useful for breeding because they all had moderate stability, although few had marginal R2-values.

Molecular breeding aims to select the most valuable genotypes or alleles and to combine them in developing a desirable cultivar (Zhang et al. 2012). The identification of favorable alleles helps in selecting parents for crosses to ensure the pyramiding of the maximum number of favorable alleles in the best genetic background. In rice, linear correlation between TSW and favorable alleles was reported (Wang et al. 2012b; Zhang et al. 2012). We observed the same in linseed, an observation that should be carefully considered because the additive effects of the five QTL could be capitalized upon to directly improve TSW and indirectly yield. Interestingly, none of the modern linseed cultivars carried the five favorable alleles, indicating that further improvement of TSW within the modern linseed gene pool is feasible by MAS. The new Canadian cultivar AAC Bravo registered in 2012, possesses high TSW (6.8 g), that is, well above the current Canadian linseed varieties ranging 5–5.5 g, and yields similar to CDC Bethune (S. Duguid, pers. comm., 2013). Independent marker testing of this variety that was not part of the core collection, showed that it possesses four of the five TSW favorable alleles (data not shown). In addition to providing validation to our TSW markers, AAC Bravo illustrates a practical example of indirect yield improvement through yield components. However, additional validation in biparental populations testing various genetic backgrounds is warranted before implementation of molecular breeding strategies.

The current study provides initial insights into the genomic regions underlying agronomics traits. Although only 12 marker-trait associations were identified for six agronomic traits, these markers were consistent across environments and mostly stable. An attribute of AM is the identification and validation of favorable alleles in germplasm collections (Wang et al. 2012b). The accessions carrying favorable alleles, especially for TSW, will be useful to ensure their transfer into the best modern linseed cultivars. To further disentangle the genetic bases of yield and yield-related traits, marker density will be increased with thousands of single nucleotide polymorphism markers obtained by the re-sequencing of the entire core collection that should enable us to take advantage of the existing and comprehensive phenotypic data and the germplasm resources represented in the Canadian flax core collection (Diederichsen et al. 2013).

Materials and Methods

Plant material, genotyping, and field trials

The Canadian flax core collection assessed in this study contains 381 accessions selected by Diederichsen et al. (2013) and nine accessions of relevance to recent Canadian flax breeding programs. The 390 accessions were genotyped with 464 SSR markers (Roose-Amsaleg et al. 2006; Cloutier et al. 2009, 2012a; Deng et al. 2010, 2011) distributed across the 15 linkage groups of flax (Cloutier et al., 2012b). All accessions were evaluated during 4 years (2009, 2010, 2011, and 2012) at the Morden Research Station, Morden, Manitoba (MB), and at the Kernen Research Farm located near Saskatoon, Saskatchewan (SK), Canada. A type-2 modified augmented design (MAD) (Lin and Poushinsky 1985) was used for the field experiments from which phenotyping data was collected for nine agronomic traits. Main plots were arranged in grids of 10 rows and 10 columns. Each main plot was divided into five paralleled subplots (2 m × 2 m with 20 cm row spacing) with a plot control (CDC Bethune) located in the center. Additional subplot controls (Hanley and Macbeth) were assigned to five randomly selected main plots.

Phenotyping of agronomic traits

Yield and its components including TSW, SPB, and BPA were obtained by harvesting two 0.5 m sections of a row from the central part of each subplot. The boll weight from each 0.5 m row was measured to obtain the BPA. Four 25 boll subsamples were counted for each 0.5 m row which were weighed and threshed. The seeds from each subsample were counted and weighed to obtain the SPB and TSW. FL 5% and FL 95% were recorded as the number of days between sowing and when 5% and 95% of the flowers had opened, respectively. Plant height (in cm) was recorded at maturity using the average of 10 plants located in the center of the subplots. Plant branching was evaluated according to Kulpa and Danert (1962) using a 1–6 scale which describes PB as the ratio of the total stem length without side branches to that with side branches as follows: 1 = 1/1, 2 = 1/2, 3 = 1/3, 4 = 1/4, 5 = 1/5, and 6 = 1/6. Plant branching ratings of five and six correspond to the typical fiber flax with long stems and bolls only in the upper part of the plants while ratings of three and four correspond to intermediate flax or linseed. Lodging resistance was scored using a 1–7 scale where 1 = upright, 3 = intermediate, and 7 = lodged. The number of environments in which each agronomic trait was assessed differed between traits as indicated in Table1.

Statistical analysis

Adjusted data was obtained for each trait as previously described based on the MAD (You et al. 2013). Normal distribution of the adjusted agronomic trait data was tested using the Shapiro-Wilk test (Shapiro and Wilk 1965) and normal probability plots. Traits with significant deviation from a normal distribution were log-transformed prior to AM analysis including FL 95% (SK12), PH (SK11), and PB (MB09, SK10, and MB11). The adjusted phenotypic values were used to estimate the variance components using the GLM procedure in SAS version 9.1 (SAS Institute 2004) as described in You et al. (2013). Broad sense heritability (H) across years within location was estimated to elucidate the location effect on each agronomic trait as follows:

graphic file with name jipb0056-0075-m1.jpg

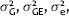where Inline graphic, e, and r correspond to the genetic variance, the genetic by environment interaction variance, the residual variance, the number of environments, and the replications per environment, respectively. Pearson's correlation coefficients were calculated to express the relationships between agronomic traits.

Population structure and LD

Population structure and LD analyses for this core collection were previously reported (Soto-Cerda et al. 2013). Briefly, the flax core collection was assessed with 259 mapped neutral SSR loci which indicated that all accessions were organized into two major groups (G1 and G3) and one admixed group (G2) with a weak population structure (FST = 0.09). G1 included mostly accessions from South Asia, Western Europe, and South America, while G3 included accessions from North America and Eastern Europe (Soto-Cerda et al. 2013). A relatively fast genome-wide LD decay of approximately 1 cM (r2 = 0.1) was estimated. To determine whether the nine agronomic traits differed between the two major groups as a consequence of the population structure, we applied the Kruskal–Wallis non-parametric test (Kruskal and Wallis 1952). For the significantly different traits (P < 0.05), a GLM was fitted to estimate the amount of phenotypic variation explained by the population structure as estimated by the membership coefficient (Q) matrix and the PCA, considering traits as dependent variables and Q and PCAs as fixed.

Association mapping

The adjusted phenotypic values of the agronomic traits were used for AM. Five AM models were tested in TASSEL 2.1 (Bradbury et al. 2007) including two GLMs and three MLMs. The first GLM incorporated the Q matrix as the fixed covariate while the second used PCA (Price et al. 2006). The first MLM incorporated the K (Yu et al. 2006) as a random effect only, while the second and third used in addition to the Q matrix and PCA as fixed covariates, respectively. The Q matrix was estimated using 259 mapped neutral SSRs (Soto-Cerda et al. 2013). The PCA matrix calculated in TASSEL 2.1 retained the first three components. The K matrix was constructed on the basis of 448 SSRs using SPAGeDi (Hardy and Vekemans 2002). All negative values between individuals were set to zero (Yu et al. 2006). The best AM model was selected using cumulative P–P plots. For the AM analysis, only MAF of more than 0.05 were retained (Breseghello and Sorrells 2006).

Association mapping analyses for the agronomic traits were carried out for each year and location independently. Correction for multiple testing was performed using the estimated false discovery (qFDR) values (Benjamini and Hochberg 1995). The q values were calculated with the Q-Value R package using the smoother method (Storey and Tibshirani 2003). Markers with qFDR of less than 0.01 in at least half of the tested environments were considered significant. For markers significantly associated with a trait, a GLM with all fixed-effect terms was used to estimate the amount of phenotypic variation explained by each marker (R2). Allelic effects of the significant marker loci were calculated as the difference between the average phenotypic values of the homozygous alleles with MAF greater than 0.05. The significant differences between the allele means were estimated by the Kruskal-Wallis non-parametric test (Kruskal and Wallis 1952) and visualized as box plots.

Stability and effect of significant markers

Marker effects were calculated as the difference between the average values of the two most contrasting homozygous classes in each environment (defined as location-year), and significance between allele means was evaluated using the Kruskal-Wallis non-parametric test (Kruskal and Wallis 1952). Marker stability was estimated using the AMMI model (Zobel et al. 1988; Gauch 1992) in GenStat 14 (VSN International 2011). Markers with an IPCA1 near zero are more stable than those with positive or negative values. The ASV (Purchase 1997) were calculated using the following formula:

graphic file with name jipb0056-0075-m5.jpg

where SSIPCA1 and SSIPCA2 are the sum of squares of the interactions of the first and second PCAs, respectively. We defined ASV values in the range of 0 to 1, as indicative of high stability across environments. In addition, the stability and effect of associated markers/QTL were graphically displayed using the QQE (QTL main effect and QTL-by-environment interaction) approach where the first two IPCAs were plotted in a QQE biplot (Yan and Tinker 2005) using GenStat 14.

Acknowledgments

The authors are grateful to Andrzej Walichnowski, Elsa Reimer, Natasa Radovanovic, Evelyn Miranda, and the breeding teams at the Morden Research Station and the Crop Development Centre for technical assistance. This work was conducted as part of the Total Utilization Flax Genomics (TUFGEN) project funded by Genome Canada and co-funded by the Government of Manitoba, the Flax Council of Canada, the Saskatchewan Flax Development Commission, Agricultural Development Fund and the Manitoba Flax Growers Association. Project management and support by Genome Prairie are also gratefully acknowledged. Braulio J. Soto-Cerda was supported by Becas Chile – Comisión Nacional de Investigación Científica y Tecnológica (CONICYT).

Supporting Information

Additional Supporting Information may be found in the online version of this article:

Figure S1

Box plots for nine agronomic traits for the two major groups G1 and G3. Significant differences for traits between major groups was tested by the Kruskal–Wallis test (P < 0.05)

jipb0056-0075-SD1.tif (12.8MB, tif)
Figure S2

Structure analysis within major groups and model comparison for plant height

(A) and (D) Estimation of the most probable number of subgroups (K) using the ad hoc ΔK (Evanno et al. 2005) for K values ranging from 1–5 within G1 and G3, respectively. (B) and (E) Estimation of the hypothetical number of subpopulations using STRUCTURE (Pritchard et al. 2000) within G1 and G3, respectively

Each individual is represented by a vertical column partitioned into K colored segments proportional to their coefficient of membership (Q) to each subpopulation. (C) and (F) probability–probability (P–P) plots of observed versus expected −log10(P) values for plant height evaluated with five association mapping models within G1 and G3, respectively. Q general linear model using the Q matrix, PCA general linear model using the PCA matrix, K mixed linear model using the kinship matrix, Q + K mixed linear model using the Q and K matrices, PCA + K mixed linear model using the PCA and K matrices

jipb0056-0075-SD2.tif (23.8MB, tif)
Table S1

anova for nine agronomic traits in the flax core collection, namely yield, bolls per area (BPA), 1 000 seed weight (TSW), seeds per boll (SPB), start of flowering (FL 5%), end of flowering (FL 95%), plant height (PH), plant branching (PB), and lodging (LDG)

jipb0056-0075-SD3.docx (17.7KB, docx)

References

  1. Ashikari M, Sakakibara H, Lin S, Yamamoto T, Takashi T, Nishimura A, Angeles ER, Qian Q, Kitano H, Matsuoka M. Cytokinin oxidase regulates rice grain production. Science. 2005;309:741–745. doi: 10.1126/science.1113373. [DOI] [PubMed] [Google Scholar]
  2. Benjamini Y, Hochberg Y. Controlling the false discovery rate—A practical and powerful approach to multiple testing. JR Statist Soc B. 1995;57:289–300. [Google Scholar]
  3. Bradbury PJ, Zhang Z, Kroon DE, Casstevens TM, Ramdoss Y, Buckler ES. TASSEL: Aoftware for association mapping of complex traits in diverse samples. Bioinformatics. 2007;23:2633–2635. doi: 10.1093/bioinformatics/btm308. [DOI] [PubMed] [Google Scholar]
  4. Breseghello F, Sorrells M. Association mapping of kernel size and milling quality in wheat (Triticum aestivum L.) cultivars. Genetics. 2006;172:1165–1177. doi: 10.1534/genetics.105.044586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cadic E, Coque M, Vear F, Grezes-Besset B, Pauquet J, Piquemal J, Lippi Y, Blanchard P, Romestant M, Pouilly N, Rengel D, Gouzy J, Langlade N, Mangin B, Vincourt P. Combined linkage and association mapping of flowering time in Sunflower (Helianthus annuus L.) Theor Appl Genet. 2013;126:1337–1356. doi: 10.1007/s00122-013-2056-2. [DOI] [PubMed] [Google Scholar]
  6. Camus-Kulandaivelu L, Veyrieras JB, Madur D, Combes V, Fourmann M, Barraud S, Dubreuil P, Gouesnard B, Manicacci D, Charcosset A. Maize adaptation to temperate climate: Relationship between population structure and polymorphism in the Dwarf8 gene. Genetics. 2006;172:2449–2463. doi: 10.1534/genetics.105.048603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Caniato FF, Guimarães CT, Hamblin M, Billot C, Rami JF, Hufnagel B, Kochian LV, Liu J, Garcia AA, Hash CT, Ramu P, Mitchell S, Kresovich S, Oliveira AC, de Avellar G, Borém A, Glaszmann JC, Schaffert RE, Magalhaes JV. The relationship between population structure and aluminum tolerance in cultivated sorghum. PLoS ONE. 2011;6:e20830. doi: 10.1371/journal.pone.0020830. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chen Y, Lubberstedt T. Molecular basis of trait correlations. Trends Plant Sci. 2010;15:454–461. doi: 10.1016/j.tplants.2010.05.004. [DOI] [PubMed] [Google Scholar]
  9. Clark RM, Wagler TN, Quijada P, Doebley J. A distant upstream enhancer at the maize domestication gene tb1 has pleiotropic effects on plant and inflorescent architecture. Nat Genet. 2006;38:594–597. doi: 10.1038/ng1784. [DOI] [PubMed] [Google Scholar]
  10. Cloutier S, Niu Z, Datla R, Duguid S. Development and analysis of EST-SSRs for flax (Linum usitatissimum L.) Theor Appl Genet. 2009;119:53–63. doi: 10.1007/s00122-009-1016-3. [DOI] [PubMed] [Google Scholar]
  11. Cloutier S, Ragupathy R, Niu Z, Duguid S. SSR-based linkage map of flax (Linum usitatissimum L.) and mapping of QTLs underlying fatty acid composition traits. Mol Breed. 2011;28:437–451. [Google Scholar]
  12. Cloutier S, Miranda E, Ward K, Radovanovic N, Reimer E, Walichnowski A, Datla R, Rowland G, Duguid S, Ragupathy R. Simple sequence repeat marker development from bacterial artificial chromosome end sequences and expressed sequence tags of flax (Linum usitatissimum L.) Theor Appl Genet. 2012a;125:685–694. doi: 10.1007/s00122-012-1860-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cloutier S, Ragupathy R, Miranda E, Radovanovic N, Reimer E, Walichnowski A, Ward K, Rowland G, Duguid S, Banik M. Integrated consensus genetic and physical maps of flax (Linum usitatissimum L.) Theor Appl Genet. 2012b;125:1783–1795. doi: 10.1007/s00122-012-1953-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Cockram J, Jones H, Leigh FJ, O'Sullivan D, Powell W, Laurie DA, Greenland AJ. Control of flowering time in temperate cereals: Genes, domestication, and sustainable productivity. J Exp Bot. 2007;58:1231–1244. doi: 10.1093/jxb/erm042. [DOI] [PubMed] [Google Scholar]
  15. Cullis C. Linum. In: Kole C, editor. Wild Crop Relatives: Genomic and Breeding Resources Oilseeds. New York: Springer; 2011. pp. 177–189. [Google Scholar]
  16. Czemplik M, Boba A, Kostyn K, Kulma A, Mituła A, Sztajnert M, Wróbel-Kwiatkowska M, Żuk M, Jan Szopa J, Skórkowska-Telichowska K. Flax engineering for biomedical application. In: Komorowska MA, Olsztynska-Janus S, editors. Biomedical Engineering, Trends, Research and Technologies. Rijeka: InTech; 2011. pp. 407–434. [Google Scholar]
  17. Deng X, Long S, He D, Li X, Wang Y, Liu J, Chen H. Development and characterization of polymorphic microsatellite markers in Linum usitatissimum. J Plant Res. 2010;123:119–123. doi: 10.1007/s10265-009-0271-3. [DOI] [PubMed] [Google Scholar]
  18. Deng X, Long S, He D, Li X, Wang Y, Hao D, Qiu C, Chen X. Isolation and characterization of polymorphic microsatellite markers from flax (Linum usitatissimum L.) Afr J Biotechnol. 2011;10:734–739. [Google Scholar]
  19. Diederichsen A, Ulrich A. Variability in stem fibre content and its association with other characteristics in 1177 flax (Linum usitatissimum L.) genebank accessions. Ind Crop Prod. 2009;30:33–39. [Google Scholar]
  20. Diederichsen A, Kusters PM, Kessler D, Bainas Z, Gugel RK. Assembling a core collection from the flax world collection maintained by Plant Gene Resources of Canada. Genet Resour Crop Evol. 2013;60:1479–1485. [Google Scholar]
  21. Duguid SD. Flax. In: Vollmann J, Rajcan I, editors. Oil Crops, Handbook of Plant Breeding 4. New York: Springer; 2009. pp. 233–255. [Google Scholar]
  22. FAOSTAT. Production of Crops: Linseed: Area Harvested and Production (tonnes) 2013. Available on-line http://faostat3.fao.org/home/index.html (accessed March 2013)
  23. Flint-Garcia S, Thornsberry JM, Bukler ES. Structure of linkage disequilibrium in plants. Annu Rev Plant Biol. 2003;54:357–374. doi: 10.1146/annurev.arplant.54.031902.134907. [DOI] [PubMed] [Google Scholar]
  24. Fu YB, Diederichsen A, Richards KW, Peterson G. Genetic diversity within a range of cultivars and landraces of flax (Linum usitatissimum L.) as revealed by RAPDs. Genet Resour Crop Evol. 2002;49:167–174. [Google Scholar]
  25. Fu YB, Rowland GG, Duguid SD, Richards K. RAPD analysis of 54 North American flax cultivars. Crop Sci. 2003;43:1510–1515. [Google Scholar]
  26. Gauch HG. AMMI analysis of yield trials. In: Kang MS, Gauch HG, editors. Genotype-by-Environment Interaction. Boca Raton: CRC Press; 1992. pp. 1–40. [Google Scholar]
  27. Green AG, Chen Y, Singh SP, Dribnenki JCP. Flax. In: Kole C, Hall TC, editors. Compendium of Transgenic Crop Plants: Transgenic Oilseed Crops. Oxford: Blackwell Publishing Ltd; 2008. pp. 199–226. [Google Scholar]
  28. Gupta PK, Rustgi S, Kulwal PL. Linkage disequilibrium and association studies in higher plants: Present status and future prospects. Plant Mol Biol. 2005;57:461–485. doi: 10.1007/s11103-005-0257-z. [DOI] [PubMed] [Google Scholar]
  29. Hardy OJ, Vekemans X. SPAGeDi: A versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol Ecol Notes. 2002;2:618–620. [Google Scholar]
  30. Honsdorf N, Becker HC, Ecke W. Association mapping for phenological, morphological, and quality traits in canola quality winter rapeseed (Brassica napus L.) Genome. 2010;53:899–907. doi: 10.1139/G10-049. [DOI] [PubMed] [Google Scholar]
  31. Huang YF, Madur D, Combes V, Ky CL, Coubriche D, Jamin P, Jouanne S, Dumas F, Bouty E, Bertin P, Charcosset A, Moreau L. The genetic architecture of grain yield and related traits in Zea maize L. revealed by comparing intermated and conventional populations. Genetics. 2010;186:395–404. doi: 10.1534/genetics.110.113878. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Huang J, Zhang J, Li W, Hu W, Duan L, Feng Y, Qiu F, Yue B. Genome-wide association analysis of ten chilling tolerance indices at the germination and seedling stages in maize. J Integr Plant Biol. 2013;55:735–744. doi: 10.1111/jipb.12051. [DOI] [PubMed] [Google Scholar]
  33. Ishimaru K. Identification of a locus increasing rice yield and physiological analysis of its function. Plant Physiol. 2003;133:1083–1090. doi: 10.1104/pp.103.027607. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Kovach MJ, Sweeney MT, McCouch SR. New insights into the history of ricedomestication. Trends Genet. 2007;23:578–587. doi: 10.1016/j.tig.2007.08.012. [DOI] [PubMed] [Google Scholar]
  35. Kruskal WH, Wallis WA. Use of ranks in one-criterion variance analysis. J Am Statist Assoc. 1952;47:583–621. [Google Scholar]
  36. Kulpa W, Danert S. Zur Systematik von Linum usitatissimum L. Kuturpflanze. 1962;3:341–388. [Google Scholar]
  37. Kumar S, You FM, Cloutier S. Genome wide SNP discovery in flax through next generation sequencing of reduced representation libraries. BMC Genomics. 2012;13:684. doi: 10.1186/1471-2164-13-684. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Li X, Yan W, Agrama H, Jia L, Shen X, Jackson A, Moldenhauer K, Yeater K, McClung A, Wu D. Mapping QTLs for improving grain yield using the USDA rice mini-core collection. Planta. 2011;234:347–361. doi: 10.1007/s00425-011-1405-0. [DOI] [PubMed] [Google Scholar]
  39. Lin CS, Poushinsky G. A modified augmented design (type 2) for rectangular plots. Can J Plant Sci. 1985;65:743–749. [Google Scholar]
  40. Lin J, Quinn TP, Hilborn R, Hauser L. Fine-scale differentiation between sockeye salmon ecotypes and the effect of phenotype on straying. Heredity. 2008;101:341–350. doi: 10.1038/hdy.2008.59. [DOI] [PubMed] [Google Scholar]
  41. Liu W, Kim MY, Van K, Lee YH, Li H, Liu X, Lee SH. QTL identification of yield-related traits and their association with flowering and maturity in soybean. J Crop Sci Biotech. 2011;14:65–70. [Google Scholar]
  42. Mackay I, Powell W. Methods for linkage disequilibrium mapping in crops. Trends Plant Sci. 2007;12:57–63. doi: 10.1016/j.tplants.2006.12.001. [DOI] [PubMed] [Google Scholar]
  43. Melchinger AE, Utz HF, Schön CC. QTL analyses of complex traits with cross validation, bootstrapping and other biometric methods. Euphytica. 2004;137:1–11. [Google Scholar]
  44. Myles S, Pfeiffer J, Brown PJ, Ersoz ES, Zhang Z, Costich DE, Bukler ES. Association mapping: Critical considerations shift from genotyping to experimental design. Plant Cell. 2009;21:2194–2202. doi: 10.1105/tpc.109.068437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Panthee DR, Pantalone VR, Saxton AM, West DR, Sams CE. Quantitative trait loci for agronomic traits in soybean. Plant Breed. 2007;126:51–57. [Google Scholar]
  46. Parry MAJ, Hawkesford MJ. An integrated approach to crop genetic improvement. J Integr Plant Biol. 2012;54:250–259. doi: 10.1111/j.1744-7909.2012.01109.x. [DOI] [PubMed] [Google Scholar]
  47. Pasam RK, Sharma R, Malosetti M, van Eeuwijk F, Haseneyer G, Kilian B, Graner A. Genome-wide association studies for agronomical traits in a worldwide spring barley collection. BMC Plant Biol. 2012;12:16. doi: 10.1186/1471-2229-12-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Peng B, Li Y, Wang Y, Liu C, Liu Z, Tan W, Zhang Y, Wang D, Shi Y, Sun B, Song Y, Wang T, Li Y. QTL analysis for yield components and kernel-related traits in maize across multi-environments. Theor Appl Genet. 2011;122:1305–1320. doi: 10.1007/s00122-011-1532-9. [DOI] [PubMed] [Google Scholar]
  49. Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
  50. Pritchard JK, Stephens M, Rosenberg NA, Donnelly P. Association mapping in structured populations. Am J Hum Genet. 2000;67:170–181. doi: 10.1086/302959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Purchase JL. Parametric Analysis to Describe G × E Interaction and Yield Stability in Winter Wheat. Bloemfontein, South Africa: Department of Agronomy, Faculty of Agriculture, University of the Orange Free State; 1997. PhD thesis. [Google Scholar]
  52. Ragupathy R, Rathinavelu R, Cloutier S. Physical mapping and BAC-end sequence analysis provide initial insights into the flax (Linum usitatissimum L.) genome. BMC Genomics. 2011;12:217. doi: 10.1186/1471-2164-12-217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Roose-Amsaleg C, Cariou-Pham E, Vautrin D, Tavernier R, Solignac M. Polymorphic microsatellite loci in Linum usitatissimum. Mol Ecol Notes. 2006;6:796–799. [Google Scholar]
  54. Salamini F. Hormones and the green revolution. Science. 2003;302:71–72. doi: 10.1126/science.1090811. [DOI] [PubMed] [Google Scholar]
  55. SAS Institute. SAS Version 9.1. Cary: SAS Institute; 2004. [Google Scholar]
  56. Shapiro SS, Wilk MB. An analysis of variance test for normality (complete samples) Biometrika. 1965;52:591–611. [Google Scholar]
  57. Shi J, Li R, Qiu D, Jiang C, Long Y, Morgan C, Bancroft I, Zhao J, Meng J. Unraveling the complex trait of crop yield with quantitative trait loci mapping in Brassica napus. Genetics. 2009;182:851–861. doi: 10.1534/genetics.109.101642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Simopoulos AP. Human requirement for N-3 polyunsaturated fatty acids. Poult Sci. 2000;79:961–970. doi: 10.1093/ps/79.7.961. [DOI] [PubMed] [Google Scholar]
  59. Soto-Cerda BJ, Cloutier S. Association mapping in plant genomes. In: Caliskan M, editor. Genetic Diversity in Plants. Rijeka: InTech; 2012. pp. 29–54. [Google Scholar]
  60. Soto-Cerda BJ, Diederichsen A, Ragupathy R, Cloutier S. Genetic characterization of a core collection of flax (Linum usitatissimum L.) suitable for association mapping studies and evidence of divergent selection between fiber and linseed types. BMC Plant Biol. 2013;13:78. doi: 10.1186/1471-2229-13-78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Stich B, Piepho HP, Schulz B, Melchinger AE. Multi-traits association mapping in sugar beet (Beta vulgaris L.) Theor Appl Genet. 2008;117:947–954. doi: 10.1007/s00122-008-0834-z. [DOI] [PubMed] [Google Scholar]
  62. Storey JD, Tibshirani R. Statistical significance for genome wide studies. Proc Natl Acad Sci USA. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Venglat P, Xiang D, Qiu S, Stone SL, Tibiche C, Cram D, Alting-Mees M, Nowak J, Cloutier S, Deyholos M, Bekkaoui F, Sharpe A, Wang E, Rowland G, Selvaraj G, Datla R. Gene expression analysis on flax seed development. BMC Plant Biol. 2011;11:74. doi: 10.1186/1471-2229-11-74. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Vigouroux Y, McMullen M, Hittinger CT, Houchins K, Schulz L, Kresovich S, Matsuoka Y, Doebley J. Identifying genes of agronomic importance in maize by screening microsatellites for evidence of selection during domestication. Proc Natl Acad Sci USA. 2002;99:9650–9655. doi: 10.1073/pnas.112324299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. VSN International. GenStat for Windows. 14th edition. Hemel Hempstead, UK: VSN International; 2011. Available on-line: http://www.GenStat.co.uk. [Google Scholar]
  66. Wang Z, Hobson N, Galindo L, Zhu S, Shi D, McDill J, Yang L, Hawkins S, Neutelings G, Datla R, Lambert G, Galbraith DW, Grassa CJ, Geraldes A, Cronk QC, Cullis C, Dash PK, Kumar PA, Cloutier S, Sharpe AG, Wong GK, Wang J, Deyholos MK. The genome of flax (Linum usitatissimum) assembled de novo from short shotgun sequence reads. Plant J. 2012a;72:461–473. doi: 10.1111/j.1365-313X.2012.05093.x. [DOI] [PubMed] [Google Scholar]
  67. Wang L, Ge H, Hao C, Dong Y, Zhang X. Identifying loci influencing 1,000-kernel weight in wheat by microsatellite screening for evidence of selection during breeding. PLoS ONE. 2012b;7:e29432. doi: 10.1371/journal.pone.0029432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Würschum T. Mapping QTL for agronomic traits in breeding populations. Theor Appl Genet. 2012;125:201–210. doi: 10.1007/s00122-012-1887-6. [DOI] [PubMed] [Google Scholar]
  69. Xing Y, Zhang Q. Genetic and molecular bases of rice yield. Annu Rev Plant Biol. 2010;61:421–442. doi: 10.1146/annurev-arplant-042809-112209. [DOI] [PubMed] [Google Scholar]
  70. Xue W, Xing Y, Weng X, Zhao Y, Tang W, Wang L, Zhou H, Yu S, Xu C, Li X, Zhang Q. Natural variation in Ghd7 is an important regulator of heading date and yield potential in rice. Nat Genet. 2008;143:1–7. doi: 10.1038/ng.143. [DOI] [PubMed] [Google Scholar]
  71. Yan W, Tinker NA. A biplot approach for investigating QTL-by-environment patterns. Mol Breed. 2005;15:31–43. [Google Scholar]
  72. Yu J, Pressoir G, Briggs W, Vroh Bi I, Yamasaki M, Doebley J, McMullen M, Gaut B, Nielsen D, Holland J, Kresovich S, Buckler E. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet. 2006;38:203–208. doi: 10.1038/ng1702. [DOI] [PubMed] [Google Scholar]
  73. Yu J, Holland JB, McMullen MD, Buckler ES. Genetic design and statistical power of nested association mapping in maize. Genetics. 2008;178:539–551. doi: 10.1534/genetics.107.074245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. You FM, Duguid SD, Thambugala D, Cloutier S. Statistical analysis and field evaluation of the type 2 modified augmented design in phenotyping of flax germplasm in multiple environments. Aust J Crop Sci. 2013;7:1789–1800. [Google Scholar]
  75. Zhang LY, Liu DC, Guo XL, Yang WL, Sun JZ, Wang DW, Zhang A. Genomic distribution of quantitative trait loci for yield and yield-related traits in common wheat. J Integr Plant Biol. 2010;52:996–1007. doi: 10.1111/j.1744-7909.2010.00967.x. [DOI] [PubMed] [Google Scholar]
  76. Zhang D, Hao C, Wang L, Zhang X. Identifying loci influencing grain number by microsatellite screening in bread wheat (Triticum aestivum L.) Planta. 2012;236:1507–1517. doi: 10.1007/s00425-012-1708-9. [DOI] [PubMed] [Google Scholar]
  77. Zhao K, Tung CW, Eizenga GC, Wright MH, Ali ML, Price AH, Norton GJ, Islam MR, Reynolds A, Mezey J, McClung AM, Bustamante CD, McCouch SR. Genome-wide association mapping reveals a rich genetic architecture of complex traits in Oryza sativa. Nat Commun. 2011;2:467. doi: 10.1038/ncomms1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Zobel RW, Wright MG, Gauch HG. Statistical analysis of yield trial. Agron J. 1988;80:388–393. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Figure S1

Box plots for nine agronomic traits for the two major groups G1 and G3. Significant differences for traits between major groups was tested by the Kruskal–Wallis test (P < 0.05)

jipb0056-0075-SD1.tif (12.8MB, tif)
Figure S2

Structure analysis within major groups and model comparison for plant height

(A) and (D) Estimation of the most probable number of subgroups (K) using the ad hoc ΔK (Evanno et al. 2005) for K values ranging from 1–5 within G1 and G3, respectively. (B) and (E) Estimation of the hypothetical number of subpopulations using STRUCTURE (Pritchard et al. 2000) within G1 and G3, respectively

Each individual is represented by a vertical column partitioned into K colored segments proportional to their coefficient of membership (Q) to each subpopulation. (C) and (F) probability–probability (P–P) plots of observed versus expected −log10(P) values for plant height evaluated with five association mapping models within G1 and G3, respectively. Q general linear model using the Q matrix, PCA general linear model using the PCA matrix, K mixed linear model using the kinship matrix, Q + K mixed linear model using the Q and K matrices, PCA + K mixed linear model using the PCA and K matrices

jipb0056-0075-SD2.tif (23.8MB, tif)
Table S1

anova for nine agronomic traits in the flax core collection, namely yield, bolls per area (BPA), 1 000 seed weight (TSW), seeds per boll (SPB), start of flowering (FL 5%), end of flowering (FL 95%), plant height (PH), plant branching (PB), and lodging (LDG)

jipb0056-0075-SD3.docx (17.7KB, docx)

Articles from Journal of Integrative Plant Biology are provided here courtesy of Wiley

RESOURCES