Drug effects on the CVS in conscious rats: separating cardiac output into heart rate and stroke volume using PKPD modelling

Abstract

Background and Purpose

Previously, a systems pharmacology model was developed characterizing drug effects on the interrelationship between mean arterial pressure (MAP), cardiac output (CO) and total peripheral resistance (TPR). The present investigation aims to (i) extend the previously developed model by parsing CO into heart rate (HR) and stroke volume (SV) and (ii) evaluate if the mechanism of action (MoA) of new compounds can be elucidated using only HR and MAP measurements.

Experimental Approach

Cardiovascular effects of eight drugs with diverse MoAs (amiloride, amlodipine, atropine, enalapril, fasudil, hydrochlorothiazide, prazosin and propranolol) were characterized in spontaneously hypertensive rats (SHR) and normotensive Wistar-Kyoto (WKY) rats following single administrations of a range of doses. Rats were instrumented with ascending aortic flow probes and aortic catheters/radiotransmitters for continuous recording of MAP, HR and CO throughout the experiments. Data were analysed in conjunction with independent information on the time course of the drug concentration following a mechanism-based pharmacokinetic-pharmacodynamic modelling approach.

Key Results

The extended model, which quantified changes in TPR, HR and SV with negative feedback through MAP, adequately described the cardiovascular effects of the drugs while accounting for circadian variations and handling effects.

Conclusions and Implications

A systems pharmacology model characterizing the interrelationship between MAP, CO, HR, SV and TPR was obtained in hypertensive and normotensive rats. This extended model can quantify dynamic changes in the CVS and elucidate the MoA for novel compounds, with one site of action, using only HR and MAP measurements. Whether the model can be applied for compounds with a more complex MoA remains to be established.

Table of Links

TARGETS	LIGANDS
α1 adrenoceptor	Amiloride
	Amlodipine
	Atropine
	Enalapril
	Fasudil
	Hydrochlorothiazide
	Prazosin
	Propranolol

This Table lists key protein targets and ligands in this document, which are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Pawson et al., 2014) and are permanently archived in the Concise Guide to PHARMACOLOGY 2013/14 (Alexander et al., 2013).

Introduction

BP and heart rate (HR) are important parameters in the safety evaluation of novel drugs for a wide variety of disorders (Guth, 2007; Gasparyan et al., 2012; Sudano et al., 2012; Cardinale et al., 2013). Although BP and HR are usually measured simultaneously, it is common practice to quantify drug effects on these haemodynamic parameters independently resulting in two separate dose/concentration–effect relationships. However, this approach disregards the interrelationship between BP and HR. As this interrelationship is complex because of the feedback mechanisms regulating the CVS, interpretation of the separate relationships can be challenging and ambiguous. With the physiology of the CVS being well understood, an integrated analysis could result in improved understanding of cardiovascular effects and the underlying mechanism of action (MoA). Moreover, it has the advantage that a single dose/concentration–effect relationship can be established. Previously, it was demonstrated that drug effects on the interrelationship between mean arterial pressure (MAP), cardiac output (CO) and total peripheral resistance (TPR) can be quantified using a systems pharmacology model (Snelder et al., 2013a). As CO equals the product of HR and stroke volume (SV), it is anticipated that this model can be extended to a more detailed level by parsing CO into HR and SV with the advantage that drug effects on MAP, CO, HR, SV and TPR can be characterized simultaneously. It has been demonstrated that the previously developed CVS model (basic CVS model) can be applied to elucidate the MoA of novel compounds (Snelder et al., 2013a). This requires continuous recording of CO. However, measuring CO has not been integrated into daily practice because of the challenges associated with invasive instrumentation procedures (Doursout et al., 2001). Therefore, it is of interest to investigate if the proposed extended CVS model can be applied to elucidate the MoA of new compounds using only HR and MAP measurements.

The basic CVS model is specific for spontaneously hypertensive rats (SHR). Thus modelling of the haemodynamic effects in normotensive rats has not been achieved. This is of interest as the prediction of haemodynamic side effects is also important for normotensive subjects. The normotensive Wistar-Kyoto (WKY) rat strain is generally accepted as the most appropriate control strain for SHR (Louis and Howes, 1990). As there are pronounced differences in MAP regulation between hypertensive and normotensive rats (Pinto et al., 1998), the magnitude of the effect of cardiovascular drugs on the different haemodynamic endpoints may vary considerably between strains. Therefore, the basic CVS model might not be directly applicable to data from normotensive rats. This is a major drawback especially for drug safety evaluations, which are usually conducted in normotensive rats. As the ultimate aim of the proposed quantitative pharmacology model is to predict clinical responses to novel pharmacologic agents, it is pivotal that the CVS model is applicable to both normotensive and hypertensive rats.

In this investigation, we describe the extension of the basic CVS model to a more detailed level by (i) parsing CO into HR and SV and (ii) quantifying differences in BP regulation between normotensive and hypertensive rats, with the aim of evaluating whether the MoA of new compounds can be elucidated using only HR and MAP measurements. To this end, data from preclinical experiments in hypertensive and normotensive rats with a training set of eight cardiovascular drugs with diverse MoAs are used. Ultimately, this quantitative pharmacology model may be used to predict, quantitatively, clinical responses to novel pharmacological agents.

Methods

Animals

For the investigations male, SHR (Taconic Farms, Germantown, NY, USA) and WKY rats (Taconic Farms) were used. All experiments were conducted in accordance with Novartis Animal Care and Use Committee protocols. These protocols have been accredited and conform to international animal welfare standards and to the Guide for the Care and Use of Laboratory Animals. The ages of the rats ranged from 41 to 54 weeks and 35 to 38 weeks for SHR and WKY rats respectively. The body weights were between 367 and 504 g and between 499 and 600 g for SHR and WKY rats respectively. Rats were housed on a 12 h light/dark cycle (light: 0600–1800 h), kept at room temperature, 22°C, and were provided normal chow (Harlan Teklad 8604; Harlan, Indianapolis, IN, USA) and water ad libitum. The studies were reported in accordance with the ARRIVE guidelines for the reporting of experiments involving animals (Kilkenny et al., 2010; McGrath et al., 2010).

Experimental procedures

For continuous recording of BP, HR and CO, rats were surgically instrumented with both an ascending aortic flow probe and a femoral arterial catheter/radiotransmitter as described by Snelder et al. (2013a).

Experimental design

The effects of a training set of compounds were obtained in two studies. In study 1, information on the effect on MAP, CO, HR, SV and TPR was obtained following a single oral administration of different doses of each drug [amiloride, amlodipine, enalapril, fasudil, hydrochlorothiazide (HCTZ) or prazosin] on separate days (Table 1). The number of dose strengths investigated varied for each drug in order to find an appropriate dose showing a clear effect, and, therefore, the duration of the study also varied for each drug. The MAP and CO measurements following the administration of amlodipine, prazosin and HCTZ (first occasion) in SHR were also used for the development of the previous CVS model (Snelder et al., 2013a). As these data are also informative for the proposed extended CVS model, they are included in this investigation as well. However, in the previous investigation, the maximum effect of HCTZ was not observed at the dose range used. Therefore, information on the influence of higher doses of HCTZ on the haemodynamic parameters was obtained in this study (second occasion) (Table 1). In study 2, the effects of atropine (10 mg kg⁻¹) and propranolol (30 mg kg⁻¹) on MAP, CO, HR, SV and TPR were measured following a single, sequential or combined oral administration of propranolol and/or atropine in eight SHR (Table 1). No WKY rats were included in this study. In the rats, repeated experiments were conducted over periods of up to 6 months. Sufficient washout between consecutive experiments was allowed. In studies 1 and 2 together, 10 SHR and two WKY rats were used. Data from one SHR (study 2) were omitted for model development as this rat learned how to disconnect its flow cable and elicited a much stronger response than all the other rats (Table 1). For practical reasons, the flow cables were disconnected from the flow probes between 1700 h and 0700 h the following morning. On the experiment days, baseline data were collected between 0700 h and 1000 h. Drug administration took place at 1000 h and 1300 h (study 2 only). Data collection was continued until 1700 h. In the period between 1700 h and 0700 h the following morning, only MAP and HR data were captured.

Table 1.

Study overview study 1 and study 2

Study 1
Study	Measures	Study designs	Compound	Dose (mg kg−1)	Strain	Number of rats
1 Single administrations of different doses on separate days	MAP, HR and SV (CO and TPR)	Day 1: vehicle Following days: a different dose each day	Amiloride	10	SHR	3
			Amlodipinec	0.3, 1, 3, 10	SHR	2
					WKY	2
			Enalapril	3, 10, 30	SHR	4d
			Fasudil	3, 10, 30	SHR	4
			HCTZa,c	0.1, 0.3, 1, 3	SHR	2
					WKY	2
			HCTZb	10, 30	SHR	4
			Prazosinc	0.04, 0.2, 1, 5	SHR	2
					WKY	1

Study 2
Study	Measures	Study designs	Number of rats (SHR)
2 Single, sequential or combined administration of atropine (10 mg kg−1) and/or propranolol (30 mg kg−1)	MAP, HR and SV (CO and TPR)	Vehicle followed by vehicle 3 h later	2
		Atropine followed by propranolol 3 h later	3d
		Propranolol followed by atropine 3 h later	3
		Combination of atropine and propranolol	1
		Atropine followed by no dosing	3d
		Propranolol followed by no dosing	3

¹First occasion.

²Second occasion.

³Data from SHR were previously used for the characterization of the CVS model (Snelder et al., 2013a).

⁴Data from one rat were excluded for model development as this rat learned how to disconnect its flow cable and responded more strongly than all other rats resulting in a low MAP.

Compounds

Amiloride HCl hydrate (Sigma-Aldrich, St. Louis, MO, USA, A7410), enalapril maleate (Sigma-Aldrich, E6888), fasudil mono HCl (LC Laboratories, Woburn, MA, USA, F-4660), atropine sulfate (Sigma-Aldrich, A0257) and propranolol HCl (Sigma-Aldrich, P0884) were dissolved in water. Amlodipine besylate (Lek Pharmaceuticals, Ljubljana, Slovenia) and prazosin HCl (Sigma-Aldrich, P7791) were homogenized in 0.5% methylcellulose (Fisher Scientific, Pittsburgh, PA, USA). HCTZ (Sigma-Aldrich, H2910) was dissolved in NaOH and diluted with filtered water (vehicle was water adjusted to pH 11). All compounds were formulated for administration at 2 mL kg⁻¹ by oral gavage.

Data analysis

The interrelationship between MAP, TPR, CO, HR and SV is expressed by the formulas (i) MAP = CO × TPR and (ii) CO = HR × SV (Levick, 2003). Previously, we developed a mechanism-based linked turnover model to describe the interrelationship between MAP, CO and TPR (Snelder et al., 2013a). This model consisted of two turnover equations, one for CO and one for TPR, which were linked by negative feedback through MAP representing homeostatic feedback mechanisms such as the baroreflex system (Cleophas, 1998) (Equation 12009).

(1)

in which, K_{in_CO} and K_{in_TPR} are the zero-order production rate constants and k_{out_CO} and k_{out_TPR} are the first-order dissipation rate constants of CO and TPR respectively. These rate constants describe the time course of the effect on CO and TPR. FB1 and FB2 are constants characterizing the negative feedback of MAP on CO and TPR.

In the present study, this model was extended by parsing CO into HR and SV. More precisely, the turnover equation for CO was replaced by two turnover equations for HR and SV (Figure 1). Therefore, the extended CVS model consisted of three linked turnover equations involving TPR, HR and SV all linked by negative feedback through MAP (Equation 2). In addition, a direct inverse relationship between HR and SV was included in the model representing the relationship between the cardiac interval and left ventricular filling time (LVFT), that is when HR increases, the cardiac interval decreases, and therefore, LVFT decreases and SV decreases (Equation 2).

Figure 1.

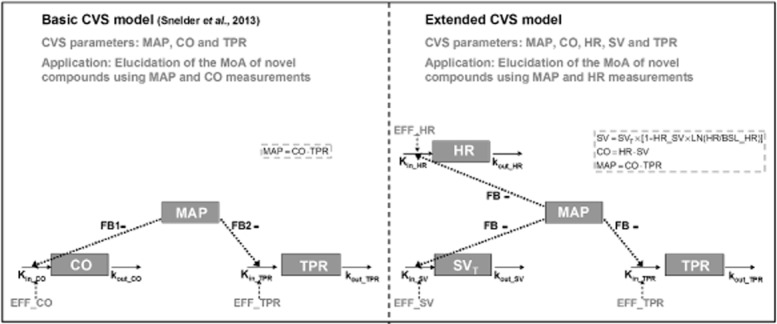
Comparison between the basic CVS model to characterize drug effects on the interrelationship between MAP, CO and TPR and the extended CVS model to characterize drug effects on the interrelationship between MAP, CO, HR, SV and TPR. Extended CVS model: CO equals the product of HR and SV (CO = HR × SV) and MAP equals the product of CO and TPR (MAP = CO × TPR). SV is influenced by indirect feedback through MAP (SV_T) and by HR through a direct inverse log-linear relationship, where HR_SV represents the magnitude of this direct effect. Effects on HR, SV and TPR are described by three linked turnover equations. In these equations, K_{in_HR}, K_{in_SV} and K_{in_TPR} represent the zero-order production rate constants and k_{out_HR}, k_{out_SV} and k_{out_TPR} represent the first-order dissipation rate constants. When MAP increases as a result of a stimulating effect on HR, SV or TPR, the values of HR, SV and TPR will decrease as a result of the action of the different feedback mechanisms regulating the CVS. In this model, the magnitude of feedback on HR, SV and TPR is represented by FB. System-specific parameters are indicated in blue and drug-specific parameters are indicated in red.

(2)

In these equations, SV^* represents the SV influenced by the negative feedback of MAP; K_{in_HR} and K_{in_SV} represent the zero-order production rate constants and k_{out_HR} and k_{out_SV} represent the first-order dissipation rate constants of HR, SV and TPR respectively. These hypothetical production and dissipation rate constants reflect the rate of change in HR, SV and TPR. FB is a constant representing the magnitude of the negative feedback of MAP on HR, SV and TPR and HR_SV is a constant that represents the magnitude of the direct effect of HR and SV. Following the criteria for statistical significance as specified in the section ‘Computation’, a linear relationship between MAP and the production rate constants of HR, SV and TPR and a log-linear relationship between HR and SV were the most parsimonious relationships that adequately captured the feedback mechanism and the direct inverse relationship between HR and SV respectively.

The circadian rhythm, which was observed in all five parameters of the CVS, was described by two cosine functions, one influencing K_{in_HR} and one influencing K_{in_TPR} (Equation 32009). As a result of the feedback through MAP, this model also describes the circadian rhythm in SV, CO and MAP in addition to that of HR and TPR.

(3)

In these equations, the parameter amp is the amplitude, t is the time and hor is the horizontal displacement of the physiological variable over time.

Brief manual restraint and oral dose administration either directly or indirectly (i.e. sensed by a bystander rat in the same room) caused a temporary increase in HR, TPR, CO and MAP and decrease in SV that was independent of drug exposure. This handling effect was described by an empirical function HD (Visser et al., 2006) influencing the K_{in_HR} and K_{in_TPR} (Equation 41990).

(4)

In this equation, P_HR and P_TPR determine the magnitudes of the handling effect on HR and TPR respectively, k_HD determines the rate of disappearance of the handling effect and t_HD equals the time of handling.

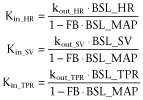
At baseline, before drug administration, the system is in oscillating steady state. This means that the values of the parameters oscillate around their baseline values. For turnover models, it is common practice to derive the steady-state conditions and to express K_in in terms of BSL and k_out (Dayneka et al., 1993). For this system, the steady-state conditions for the oscillating steady state cannot be derived analytically. Therefore, K_in was expressed in terms of BSL and k_out without accounting for the circadian rhythm (Equation 52013). To ensure that the system is in oscillating steady state at the start of pharmacological intervention, the observations where shifted 2 weeks (determined empirically), that is the system was initialized at time = 0 h and the pharmacological interventions started at time = 336 h.

(5)

In this equation, BSL_HR, BSL_SV and BSL_TPR represent the baseline values of HR, SV and TPR respectively. In the experiments, SV and TPR were derived from the directly measured MAP, CO and HR. Therefore, in the modelling, the BSL_MAP and BSL_CO and BSL_HR were estimated and BSL_SV and BSL_TPR were derived from these parameters.

To functionally characterize the system, eight different drugs with different MoA were administered. In the analysis of the data, it was assumed that the drugs (EFF) influence the production rates of HR, SV or TPR according to Equation 61998.

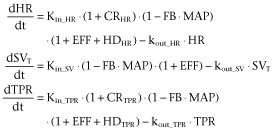(6)

The time course of the drug plasma concentrations, that is the pharmacokinetics (PK), rather than the dose, was used as a predictor for the pharmacodynamics (PD). This enables an accurate description of the time course of the drug effect. For that purpose predicted plasma concentration versus time profiles were used, which were derived from the literature (Table 2). However, for atropine and prazosin, the administration route was different from that used in these literature studies, i.v. as compared with p.o. in the present study. Therefore, for these compounds, the absorption rate was estimated based on the time course of the effect on BP in conjunction with the relevant information on the pharmacokinetics from the literature (Table 2). For atropine and prazosin, PK and PD parameters were estimated simultaneously.

Table 2.

Specification of the PK models to describe the pharmacokinetics of the effects of the six compounds selected, enalapril, fasudil, amlodipine, prazosin, propranolol and HCTZ, on the CVS

Compound	PK model	Literature model	Comments	Species
Amiloride	Two-compartmental model with liver compartment	(Segre et al., 1998) Two-compartmental model with liver compartment	–	Wistar rats
Amlodipine	One-compartmental model	(Stopher et al., 1988): Non-compartmental analysis	Ka was derived from the reported half-life, Vd, F and Tmax using Berkeley Madonna	Sprague-Dawley rats
Atropine	Two-compartmental model	(Perlstein et al., 2002) Two-compartmental model	Ka was estimated simultaneously with PD	Sabra rats
Enalapril	Two-compartmental model with Michaelis-Menten elimination	(Lin et al., 1988) and (Li et al., 2007)	Data read out from the manuscripts and a two- compartmental model with Michaelis-Menten elimination was optimized in NONMEM	Sprague-Dawley rats
Fasudil	One-compartmental model	(Ikegaki et al., 2001): Non-compartmental analysis	Ka and lag-time were derived from the reported half-life, AUC and Cmax using Berkeley Madonna	WKY rats
HCTZ	One-compartmental model	(Asdaq and Inamdar, 2009): One-compartmental model	Reported: Ke, Ka, Vd, AUC/F was calculated from these parameters	WKY rats
Prazosin	One-compartmental model	(Hamilton et al., 1985): one-compartmental model	CL, Vd; scaled to rat using allometric scaling. Ka was estimated	New Zealand white rabbits
Propranolol	Three-compartmental model	(van Steeg et al., 2010) and (Belpaire et al., 1990): three-compartmental model	Distribution and elimination parameters were fixed to van Steeg et al. Ka was estimated in NONMEM using data obtained from Belpaire et al.	WKY rats

The PK models were based on literature models. The adjustments required to account for the differences in experimental conditions and formulations in these literature studies as compared with the experiments described in this paper are described in the ‘Comments’ column. CL, clearance; F, bioavailability; Ka, absorption rate; Ke, elimination rate; Vd, distribution volume.

The concentration–effect relationships for the drug effects on HR, SV and TPR were evaluated using linear, power, E_max or Sigmoid E_max pharmacodynamic models (Equation 72010).

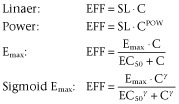(7)

In this equation, EFF represents the effect at concentration C. SL, E_max, EC₅₀ and γ represent the slope of the linear relationship, the maximum effect, the concentration at which half of the maximum effect is achieved and the Hill coefficient (sigmoidicity parameter) respectively.

For the basic CVS model, we have presented an equation to calculate TPR and CO at steady state during pharmacological intervention. For the extended CVS model, there is no analytical solution for the steady-state values during pharmacological intervention. However, these values can be simulated from the final model using the steady-state concentration C_ss.

The proposed model assumes that the time delay between concentration and effect (hysteresis) is the same for all classes of compounds influencing a certain effect site, that is HR, SV or TPR. To evaluate this assumption, for each compound, it was investigated if there was an additional delay between concentration and effect by re-evaluating the proposed model with an extra hypothetical effect compartment (Equation 82007).

(8)

In this equation, C and C_e represent the plasma concentration and the concentration in the hypothetical effect compartment, respectively, and k_e0 represents the first-order rate constant describing drug transport. This approach implies that at equilibrium C equals C_e. A significant improvement of the goodness of fit after the addition of an effect compartment indicates that there is a difference in temporal delay between plasma concentration and effect between different classes of drugs influencing the same parameter (HR, SV or TPR).

The PK and PD models were based on the assumptions described in Table 3 and discussed by Snelder et al. (2013a).

Table 3.

Model assumptions

Number	Assumption	Clarification
1	All compounds influence the production rates of HR, SV or TPR rather than the dissipation rates.	This assumption is based on the MoA of the selected compounds (Table 4).
2	For compounds for which the maximum effect was not observed, complete inhibition (i.e. Emax = 1) was assumed at infinite concentrations to ensure identification of the EC50 parameter.	The validity of this assumption was evaluated for amlodipine using the basic CVS model (Snelder et al., 2013a). The influence of different values of the Emax (i.e. Emax = 0.8) on the estimates of the system parameters was tested.
3	The PK does not differ between rat strains and can be scaled between rabbit and rat on the basis of an allometric function (West et al., 1999; Anderson and Holford, 2009).	Although published information on the PK of all selected compounds was available, the PK was often evaluated in different rat strains and, for prazosin, even in a different species (rabbit).

SHR versus WKY rats

The difference in BP regulation between hypertensive SHR and normotensive WKY rats was investigated by evaluating the system parameters per strain under the assumption that the structural model was the same for SHR and WKY rats. In addition, as the level of baseline BP, which is known to differ between and within strains (Louis and Howes, 1990), is continuously and proportionally related to cardiovascular risk (Pinto et al., 1998), we investigated whether continuous relationships between BSL_MAP and the system parameters could be identified. Linear and power relationships were investigated.

System properties

To determine whether the profiles of the time course of the drug effect on MAP, CO, HR, SV and TPR are different for compounds with a direct effect on HR, SV or TPR respectively, simulations were performed. The simulated profiles of the time course of the change in MAP, CO, HR, SV and TPR obtained are referred to as signature profiles. Distinct differences in the signature profiles for compounds with an effect on HR, SV or TPR indicate that the extended CVS model can be applied to identify the site of action (HR, SV or TPR) of novel compounds with an unknown MoA on BP. The time courses of the effects on MAP, CO, HR, SV and TPR were simulated after triggering the model by inhibiting HR, SV or TPR with a hypothetical compound after a single oral dose.

HR and MAP measurements only

Previously, it was demonstrated that measuring CO is pivotal for characterizing the system (Snelder et al., 2013a). However, at present, the measurement of CO is not a common practice because of the technical difficulties of these invasive instrumentation procedures (Doursout et al., 2001). Therefore, the question arises if the extended CVS model, which was developed using MAP, HR and CO measurements, can be used to quantify the dynamic changes in the CVS and elucidate the MoA for novel compounds using only HR and MAP measurements. This was investigated using the data from the compounds from Table 1. These data were also used for model development and, therefore, for estimation of the system-specific parameters. Hence it seems obvious that the drug effects of these compounds can be quantified using the extended CVS model. However, for model development, the site of action was assumed to be known ( Table 4). Moreover, MAP, CO, HR, SV and TPR measurements were used to quantify the drug effects. Therefore, it was not known if the site of action and the drug effect of each compound on HR and MAP can be quantified using a limited amount of data (i.e. only HR and MAP measurements). For each compound, a model-based hypothesis testing procedure was followed using the extended CVS model with the system-specific parameters fixed to values from Table 5.

Table 4.

Compounds selected to challenge the CVS with the aim of distinguishing system- from drug-specific parameters and their mechanism of action

Compound	Class	MoA	Effect
Amiloride	Diuretic	Diuretics cause blood volume contraction and lower venous pressure, which decreases cardiac filling and, by the Frank-Starling mechanism, decreases ventricular SV (Levick, 2003).	SV
Amlodipine	Calcium channel blocker	Amlodipine is a dihydropyridine that blocks voltage gated calcium channels and selectively inhibits Ca2+ influx into vascular smooth muscle cells. Calcium antagonists act by decreasing TPR to lower arterial pressure. As a consequence, reflex tachycardia, increased CO, and increased plasma catecholamine and plasma renin activity are commonly seen, particularly with the initial dose and with short-acting dihydropyridines (Michalewicz and Messerli, 1997; Perez-Reyes et al., 2009).	TPR
Atropine	M2 receptor antagonist	Muscarinic (M2) receptor antagonist (MRA) is an agent that blocks the activity of the muscarinic acetylcholine receptor. It causes tachycardia by blocking vagal effects on the sinoatrial node. Acetylcholine hyperpolarizes the sinoatrial node which is overcome by MRA and thus increases the heart rate	HR
Enalapril	Angiotensin-converting enzyme (ACE) inhibitor	ACE inhibitors competitively inhibit angiotensin I-converting enzyme, preventing the conversion of angiotensin I to angiotensin II, a potent vasoconstrictor that also stimulates release of aldosterone. Decreased levels of angiotensin II lead to decreased TPR that is unassociated with reflex stimulation of the heart (Frohlich, 1989). In addition, aldosterone acts on the distal tubules and collecting ducts of the nephron, the functional unit of the kidney. Decreased levels of aldosterone, cause the depletion of sodium, conservation of potassium, decreased water retention and decreased BP	TPR and SV
Fasudil	Rho-kinase inhibitor	Rho-kinase inhibits myosin light chain phosphatase activity and plays a key role in Ca2+ sensitization and hypercontraction of vascular smooth muscle cells. Rho-kinase inhibitors decrease TPR (Masumoto et al., 2001).	TPR
HCTZ	Diuretic	See amiloride	SV
Prazosin	Selective α1 adrenergic receptor blocker	Prazosin is a quinazoline derivative that is a specific and selective competitive antagonist of α1 adrenoceptors on vascular smooth muscle cells. Prazosin reduces BP by reducing elevated peripheral resistance and has little effect on cardiac function (Reid et al., 1987).	TPR
Propranolol	β-adrenergic receptor blocker	Propranolol is a non-selective beta blocker. It antagonizes the action of norepinephrine and epinephrine at all β-adrenergic receptors. Propranolol decreases CO and heart rate with a reflex rise in TPR (Ebadi, 2008).	HR

Table 5.

The system- and drug-specific parameter values from the extended drug-independent model used to predict effects on the CVS

Parameter	Value	RSE	LLCI	ULCI
System-specific parameters
BSL_HR_SHR (beats min-1)	310	1.12	303	317
BSL_MAP_SHR (mmHg)	155	0.684	153	157
BSL_CO_SHR (mL min-1)	69.0	4.17	63.4	74.6
BSL_HR _WKY(beats min-1)	323	1.61	313	333
BSL_MAP_WKY (mmHg)	102	0.884	100	104
BSL_CO_WKY (mL per min)	129	1.47	125	133
kout_HR (h−1)	11.6	19.1	7.27	15.9
kout_SV (h−1)	0.126	30.7	0.0501	0.202
kout_TPR (h−1)	3.58	29.1	1.54	5.62
FB0 (mmHg−1)	0.00290	5.93	0.00256	0.00324
FB0_MAP	−1.98	10.6	−2.39	−1.57
HR_SV	0.312	15.6	0.216	0.408
kHD (h−1)	4.70	8.19	3.95	5.45
PHR	0.632	9.67	0.512	0.752
PTPR	0.331	12.9	0.247	0.415
horHR (h)	8.73	3.10	8.20	9.26
ampHR	0.0918	5.15	0.0825	0.101
horTPR (h)	19.3	1.92	18.6	20.0
ampHTPRR	Fixed to ampHR
Drug-specific parameters
Amiloride: Emax model with Emax fixed to 1
EC50 (ng mL−1)	245	25.1	125 365
Amlodipine: Emax model with Emax fixed to 1
EC50 (ng mL−1)	82.8	4.99	74.7	90.9
Atropine: linear model
SL (ng mL−1)−1	0.00149	32.3	0.000547	0.00243
Ka (h−1)	1.17	59.9	–0.204	2.54
Enalapril: Emax model with Emax fixed to 1
EC50 (ng mL−1)	1200	4.03	1110	1290
ke0 (h−1)	0.163	5.07	0.147	0.179
Fasudil: Emax model with Emax fixed to 1
EC50 (ng mL−1)	0.172	18.4	0.110	0.234
HCTZ: Emax model with Emax fixed to 1
EC50 (ng mL−1)	28 900	7.65	24 600	33 200
Prazosin: power model
SL (ng mL−1)−1	0.328	5.58	0.292	0.364
POW	0.0910	6.05	0.0802	0.102
Interindividual variability
BSL_HR (CV%)	6.1		4.36	7.47
BSL_MAP (CV%)	3.7		2.67	4.49
BSL_CO (CV%)	22.7		18.09	26.57
Residual variability
Prop. Res.ErrorHR (CV%)	7.8		7.26	8.22
Prop. Res.ErrorMAP (CV%)	6.0		5.44	6.57
Prop. Res.ErrorCO (CV%)	6.9		5.72	7.83

CV, coefficient of variation; LLCI, lower limit of 95% confidence interval; RSE, relative standard error of parameter estimate; ULCI, upper limit of 95% confidence interval.

• Different hypotheses of the site of action (i.e. HR, SV and TPR) and direction of the effect (i.e. inhibiting or stimulating) were formulated, resulting in six possible combinations of effects.

• For each hypothesis, the model was fitted to the HR and MAP measurements.

• Which hypothesis resulted in the best description of the data was evaluated, as judged by the agreement between the observed and predicted direction and magnitude of effect and the lowest minimum value of the objective function (MVOF) as specified in the section ‘Computation’.

Because not all compounds were investigated in WKY rats, only data from SHRs were used.

Computation

The data from studies 1 and 2 were simultaneously analysed using a non-linear mixed-effects modelling approach implemented in NONMEM (version 7.2.0; Icon Development Solutions, Ellicott City, MD, USA). The models were compiled using Digital Fortran (version 6.6C3, Compaq Computer Corporation, Houston, TX, USA) and executed on a PC equipped with an AMD Athlon 64 processor 3200 + under Windows XP. The results from the NONMEM analysis were subsequently analysed using the statistical software package S-Plus for Windows (version 8.0 Professional, Insightful Corp., Seattle, WA, USA). Modelling techniques were as described in detail by Snelder et al. (2013a). Goodness of fit was determined using the MVOF defined as minus twice the log-likelihood. For nested models, a decrease of 10.8 points in the MVOF (corresponding to P < 0.001 in a chi-squared distribution) by adding an additional parameter was considered significant. The goodness of fit was also investigated by visual inspection of the plots of individual predictions and the diagnostic plots of (weighted) residuals (Snelder et al., 2013a).

Results

The extended CVS model as expressed by Equations 2–8 and as shown graphically in Figure 1 was used to simultaneously analyse the data from studies 1 and 2. In the analysis, interindividual variations in the baseline values of the parameters, BSL_HR, BSL_MAP and BSL_CO, were allowed (interindividual variability). The residual errors of HR, MAP and CO were best described by proportional residual error models. The residual errors of TPR and SV were derived from these parameters.

SHR versus WKY rats

The baseline parameters were found to differ in the two strains of rats, with a higher BSL_MAP and a lower BSL_CO for SHR as compared with WKY rats, whereas BSL_HR did not significantly differ between the strains (Table 5). BSL_SV and BSL_TPR were derived from these parameters, resulting in a lower BSL_SV and a higher BSL_TPR for SHR as compared with WKY rats.

In addition, for both SHR and WKY rats, FB was found to decrease with BSL_MAP according to the following relationship (Equation 92008):

(9)

In this equation, FB0, FB0_MAP, IBSL_ MAP and TVBSL_MAP_SHR represent the feedback for a typical SHR, the exponent of the power relationship, the individual baseline values of MAP and typical value of BSL_MAP in SHR respectively. Overall, the feedback is about twofold higher in WKY rats as compared with SHR. Based on the statistical findings, this model was preferred over a model with the FB estimated for each strain.

Vehicle response

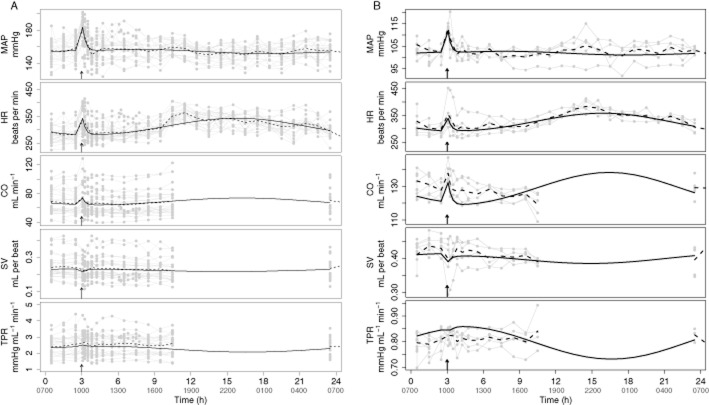
The response in the p.o. vehicle groups is characterized by circadian variation and a handling effect. The handling effect, which is visible at 3 h, was adequately described by Equation 41990 (Figure 2). The circadian rhythm, which was observed in all five parameters of the CVS, was adequately described by two cosine functions influencing K_{in_HR} and K_{in_TPR} in both SHR (Figure 2A) and WKY rats (Figure 2B). However, on two out of five occasions, CO is underpredicted between 3 and 5 h in WKY rats. In addition, in WKY rats, CO is slightly underpredicted on a population level. As TPR is derived from MAP and CO, TPR is slightly overpredicted on a population level. The amplitudes of the two cosine functions, that is amp_HR and amp_TPR, could not be distinguished and were estimated to be 0.09 indicating that the variation in K_{in_HR} and K_{in_TPR} is maximally 9% during the day. The horizontal displacement parameters of the two cosine functions, that is hor_HR and hor_TPR, were significantly different, even if one of the cosines would have been replaced by a sine (i.e. a shift of 12 h) (Table 5). In addition, omitting one of the cosine functions resulted in a decrease in the goodness of fit indicated by a significant increase in the MVOF.

Figure 2.

Description of the handling effect and circadian rhythm in MAP, HR, CO, SV and TPR in SHR (A) and WKY rats (B) after vehicle administration. Data are from study 1 and study 2 from all treatment groups. Handling of the rats caused a temporary increase in HR, TPR, CO and MAP and decrease in SV that was independent of drug exposure. The handling effect is visible at 1000 h that is when the rats were dosed with vehicle as indicated by the arrows. Two SHR were also dosed at 1300 h (not indicated in the plot). The grey dots represent the observations, which are connected by the continuous grey lines, the dashed black lines represent the mean of the observations and the continuous black lines represent the population prediction by the developed extended CVS model.

Drug effects

For prazosin, the absorption rate parameter (Ka) was found to be very high and could not be estimated with good precision. Therefore, for this compounds Ka was fixed to a high value (99 h⁻¹) before the other model parameters were estimated. Overall, fixing Ka resulted in a reduction in runtimes as correlations between drug-specific parameters were removed. For atropine, Ka was estimated simultaneously with the PD. The poor precision of the estimate with a standard error of 59.9% (Table 5) was considered acceptable as system-specific parameters were not influenced by this factor (results not shown). This was demonstrated by successively removing data from one of the compounds that were used for model development according to the methods described in detail by Snelder et al. (2013a).

The concentration–effect relationships for amiloride, amlodipine, enalapril, fasudil and HCTZ were best described by E_max models. As described previously (Snelder et al., 2013a), E_max was fixed to 1 for these compounds and EC₅₀ was estimated. Enalapril was found to influence both TPR and SV with the same EC₅₀. Initially, different EC₅₀ values were estimated. However, confidence intervals overlapped indicating that the EC₅₀ values for the two effects could not be distinguished. In addition to the turnover equations (Equation 22013), an effect compartment was used to describe the delay between change in enalapril plasma concentration and the effect on TPR and SV. The half-life of this additional delay was 4.3 h. The effect of atropine was best described by a linear concentration–effect relationship. As atropine had a stimulating effect on K_{in_HR}, applying a linear concentration–effect relationship did not result in problems with parameter optimization.

The effect of prazosin was best described by a power model. The exponent of this relationship was low (0.0910) indicating that the maximum effect was not reached for the highest dose evaluated. Finally, the effect of propranolol was too small to be quantified.

In general, the data were adequately described by the model (Figure 3 and Supporting Information Figures S1 and S2). Except for the absorption rate of atropine, all system- and drug-specific parameters could be estimated with good precision as all SEM were less than 50% of the parameter estimates (Table 5). In addition, all parameter correlations were below 0.85.

Figure 3.

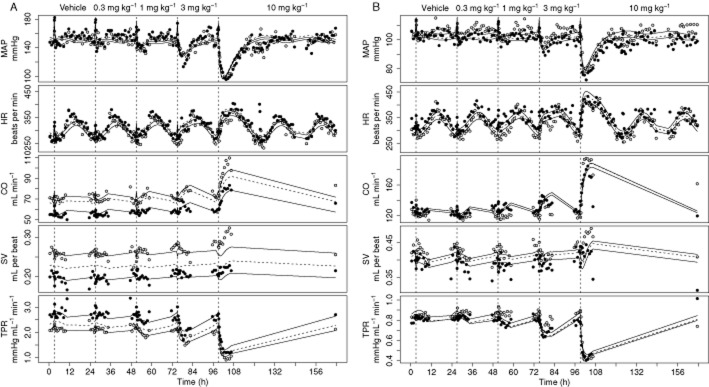
Description of the effects of amlodipine in SHR (A) and WKY rats (B). Data are from study 1, in which vehicle and a different dose of amlodipine (0.3, 1, 3 and 10 mg kg⁻¹ p.o.) were administered on separate days. Amlodipine has an inhibitory effect on TPR. Therefore, TPR decreases after administration of amlodipine. As a result of the indirect feedback, HR, SV and CO increase. In addition, the initial decrease in SV is related to the direct inverse relationship between HR and SV. MAP changes in the same direction as the initial effect that is MAP decreases. The grey and black dots represent the observations from two different rats. The continuous and dashed lines represent the effects of amlodipine on individuals and the population predicted by the developed extended CVS model.

System properties

In the simulations, distinct differences between the signature profiles of MAP, CO, HR, SV and TPR were observed for direct drug effects on HR, SV and TPR respectively. Specifically, in the simulations, it was shown that inhibition of HR, SV or TPR always results in a decrease in MAP, demonstrating that homeostatic feedback cannot be stronger than the primary effect (Figure 4). Interestingly, the delay between the stimulus and the response for MAP was longer than for the drug effect on SV as compared with TPR.

Figure 4.

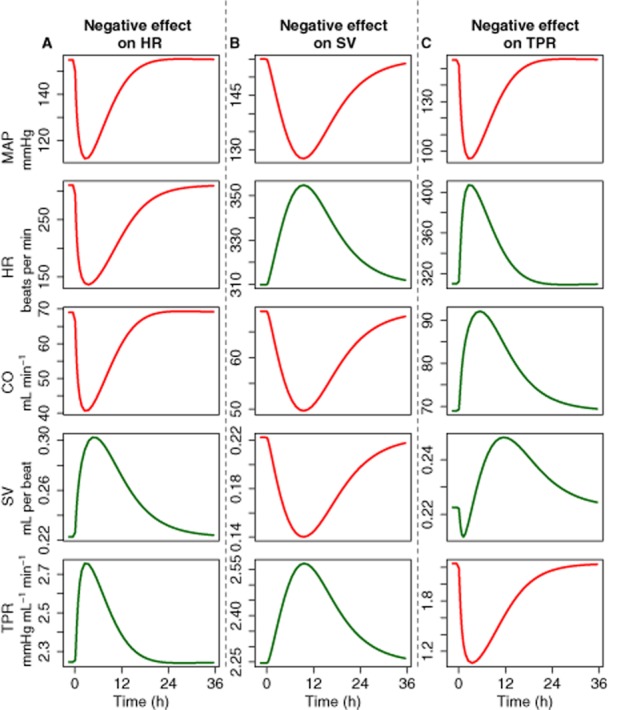
Properties of the CVS. The system properties of the CVS were investigated by simulating the response on MAP, CO, HR and TPR after inhibiting HR (A), SV (B) or TPR (C). Inhibiting HR, SV or TPR always resulted in a decrease in MAP, which demonstrates that feedback cannot be stronger than the primary effect. In addition, the delayed response of the MAP was longer when the drug effect was on SV as compared with TPR.

HR and MAP measurements only

For each compound, we investigated if the developed extended CVS model could be used to quantify the dynamic changes in the CVS and identify the site of action (HR, SV or TPR) using only HR and MAP measurements. Amlodipine was selected as a paradigm compound to illustrate the results of this analysis. It was assumed that a stimulating effect of amlodipine on HR resulted in an adequate description of the effect on HR. However, the description of the effect on MAP was inadequate as the directions of the observed and predicted effects were opposite (Figure 5). It was assumed that an inhibitory effect of amlodipine on SV resulted in an adequate description of the effect on HR and a reasonable description of the effect on MAP (Figure 5). However, the delay in effect on MAP was overpredicted. Finally, it was assumed that an inhibitory effect of amlodipine on TPR resulted in an adequate description of the effect on HR and MAP (Figure 5). Overall, the effect of amlodipine on the CVS was best described if it was assumed it had an inhibitory effect on TPR, which was confirmed by a significantly lower MVOF for the model with an effect on TPR as compared with the models with an effect on HR or SV. The estimated EC₅₀ [84.9 (confidence interval: 75.4–94.4) ng mL⁻¹] did not differ significantly from the estimated EC₅₀ from the final extended CVS model [82.8 7 (confidence interval: 74.7–90.9) ng mL⁻¹].

Figure 5.

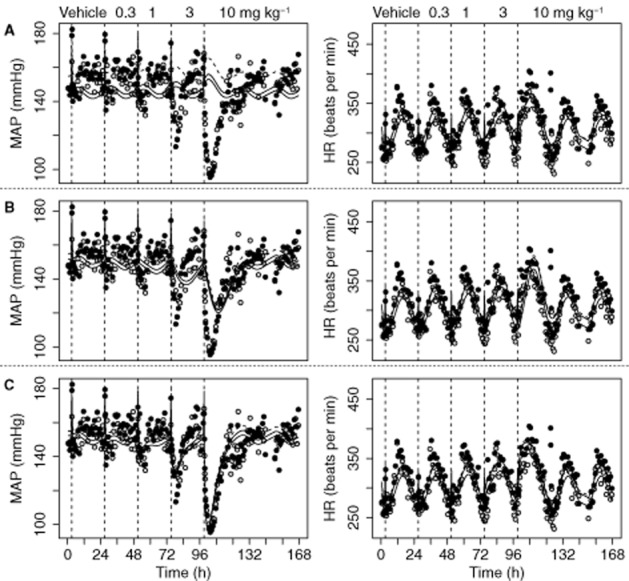
Description of the effects of amlodipine on MAP and HR using the extended CVS model with the system-specific parameters fixed to values from Table 5, while assuming a stimulating effect on HR (A), an inhibitory effect on SV (B) or an inhibitory effect on TPR (C). Data are from study 1, in which vehicle and a different dose of amlodipine (0.3, 1, 3 and 10 mg kg⁻¹ p.o.) were administered on separate days. To evaluate if the site of action of amlodipine can be identified using only MAP and HR measurements, three hypotheses were evaluated. (i) Assuming amlodipine has a stimulating effect on HR resulted in an adequate description of the effect on HR. However, the description of the effect on MAP was inadequate as the directions of the observed and predicted effects were opposite. (ii) Assuming amlodipine has an inhibitory effect on SV resulted in an adequate description of the effect on HR and a reasonable description of the effect on MAP. However, the delay in the effect on MAP was overpredicted. (iii) Assuming amlodipine has an inhibitory effect on TPR resulted in an adequate description of the effect on HR and MAP. In conclusion, this model-based hypothesis testing indicated that it is most likely that the effect of amlodipine is on TPR, which is consistent with informationavailable from the literature. This indicated that the MoA of a compound can be elucidated using only MAP and HR measurements. The grey and black dots represent the observations of two different rats. The continuous and dashed lines represent the individual and population prediction.

The effects of fasudil and prazosin on HR and MAP were best described assuming inhibition of TPR (results not shown). For amiloride, HCTZ and enalapril, the effect on HR and MAP were best described following inhibition of SV (results not shown). Finally, the effect of atropine was best described by a stimulating effect on HR (results not shown). As the effect of propranolol was too small to be quantified, propranolol was omitted from this analysis. For all compounds, the estimated drug-specific parameters did not differ significantly from the drug-specific parameters estimated by the final extended CVS model.

Discussion

Previously, a systems pharmacology model was developed that integrated a quantitative description of the physiology of the interrelationship between MAP, CO and TPR and the pharmacological effects of cardiovascular drugs in the SHR (Snelder et al., 2013a). This model can be applied for elucidation of the MoA of novel compounds, but this requires continuous recording of MAP and CO. Measuring CO has not been integrated into daily practice because of the challenges associated with invasive instrumentation procedures (Doursout et al., 2001). Therefore, the aim of this research was to evaluate if the MoA of new compounds can be elucidated using only HR and MAP measurements.

Firstly, the basic CVS model was extended by parsing CO into HR and SV. This extension was successfully established as (i) all drug effects of compounds with different MoAs were adequately described, (ii) all system-specific parameters were estimated with good precision and (iii) drug- and system-specific parameters were not correlated. Distinguishing drug- from system-specific properties is essential for mechanism-based pharmacokinetic-pharmacodynamic modelling (Danhof et al., 2007; Ploeger et al., 2009) and enables the prediction of treatment effects to later stages of development using a translational modelling approach (Danhof et al., 2008), which is an ultimate application for the quantitative systems pharmacology model developed. The system-specific parameters of the extended CVS model were comparable with the system-specific parameters of the basic CVS model (Snelder et al., 2013a) except for k_out__TPR, which was about 10-fold higher in the extended CVS model. This may be explained by the fact that in the basic CVS model k_{out_TPR} and FB2 (feedback of MAP on TPR) were highly correlated (−0.984) indicating that these parameters could not be distinguished. In the current model, the feedback parameters representing the magnitude of the feedback of MAP on HR, SV and TPR could not be distinguished. Therefore, only one feedback parameter could be estimated. As FB2 was a little higher than FB, this could well explain the difference in k_{out_TPR} between the two models.

SHR versus WKY rats

A secondary aim of this research was to quantify possible differences in BP regulation between hypertensive and normotensive rats. This is important as normotensive rats are often used for evaluating the safety of drugs and are thought to be more predictive for the effects in humans with normal BP than hypertensive rats. As expected, the baseline parameters were found to differ between the sstrain with a higher BSL_MAP and a lower BSL_CO for SHR as compared with WKY rats (Table 5). In addition, FB decreased with the higher BSL_MAP indicating impaired BP regulation in hypertensive rats. Similar findings were reported by Francheteau et al. (1993) regarding BP regulation in humans. They hypothesized that the effect of dihydropyridine drugs in hypertensive patients can be adequately predicted by assuming different baselines and lower feedback relative to normotensive subjects.

The relationship between FB and BSL_MAP was described by a hyperbolic function. It should be noted that this function is purely descriptive and was based on data from only 10 SHR and two WKY rats. Therefore, further research is required to establish the precise relationship between FB and BSL_MAP.

Vehicle response

The underprediction of CO between 3 and 5 h in WKY rats is a result of a large and highly variable handling effect. Because including interoccasion variability, which describes the variability of a parameter within a rat from one occasion to another, in the model did improve the description of the data on an individual level, but did not influence the estimates of the structural parameters, this bias was accepted. In addition, the underprediction of CO on a population level in WKY rats is a result of the fact that the population prediction is based on the observations from all rats, including the observations following active treatment, and the observed baselines of the rats following vehicle administration are in the tail of the overall baseline distribution, which is thought to be a chance finding that is related to the low number of WKY rats included in the study.

Drug effects

As the PK was not measured in these experiments, predicted plasma concentration versus time profiles were derived from the literature (Table 2). As discussed previously (Snelder et al., 2013a), the assumptions made regarding the use of PK models derived from published results may have a large effect on the PK profiles. Therefore, the PK models were descriptive and the PK and drug-specific PD parameters should only be interpreted in the context of this model. The effects of all compounds were adequately described by the extended CVS model. However, the effect of propranolol was too small to be quantified. Therefore, propranolol did not contribute to the identification of the system parameters. Enalapril was found to influence TPR and SV with the same EC₅₀. In our previous research, less detailed information on the effect of enalapril on the CVS was available as CO was not measured at that stage (Snelder et al., 2013a). Therefore, only the primary effect of enalapril on TPR was included in the model. Enalapril is an angiotensin-converting enzyme, which influences TPR and SV through the renin-angiotensin-aldosterone system (RAAS) (see Table 4 for a description of the MoA). Therefore, the effect of this compound is delayed in comparison with the effect of calcium channel blockers or selective α₁ adrenoceptor blockers, which directly influence vascular smooth muscle cell contraction. This additional delay was described adequately by an effect compartment. From a mechanistic point of view, a turnover model might be better as it has been demonstrated that the RAAS can be described by a set of turnover equations (Hong et al., 2008). However, as there was only one compound included in this research with an effect on the RAAS, the data did not contain enough information to characterize the RAAS in a mechanism-based manner.

System properties

Clear differences were found between the signature profiles of MAP, CO, HR, SV and TPR after simulating drug effects on HR, SV and TPR (Figure 4). From these simulations it can be concluded that, even if CO is not measured, it is likely that the extended CVS model can be used to elucidate the site of action of novel compounds with a simple MoA (i.e. one site of action). In summary, when the direction of the effect on HR and MAP is the same, the primary effect is on HR. When the direction of the effect on HR and MAP is opposite, the primary effect of the drug is on SV or TPR. Effects on SV and TPR can be distinguished by the delay between the perturbation and the effect on MAP, that is a long delay indicates that the primary effect is on SV and a short delay indicates that the primary effect is on TPR. These conclusions are based on the data from eight different cardiovascular drugs. To further support these conclusions, data from more compounds is required.

HR and MAP measurements only and system properties

To further evaluate if the extended CVS model can be applied to elucidate the MoA of novel compounds using only HR and MAP measurements, the effect of each compound was quantified using the extended CVS model, while assuming different sites of action and different directions of the effects. For all compounds, the site of action identified was consistent with the available information on the MoA of the compounds (Table 4). However, the effect of enalapril on HR and MAP was best described after inhibiting SV, whereas according to information from the literature, enalapril influences both TPR and SV (Table 4). Evaluating a model that is structurally comparable with the final extended CVS model, but with a combined delayed inhibitory effect on TPR and SV, improved the goodness of fit (results not shown). However, without any prior knowledge it is foreseen that it may be difficult to identify the site of action of novel compounds with unknown and more complex MoAs. Nevertheless, as the site of action of six out of seven compounds was adequately characterized, and there are pronounced differences in their signature profiles, it is anticipated that the extended CVS models can be applied to elucidate the MoA for novel compounds using only HR and MAP measurements. Before our model can be applied for that purpose, this conclusion should be validated using data from new compounds, that is compounds that were not used for model development, but with a known MoA. Recently, the extended CVS model was applied to identify the site of action of fingolimod (Snelder et al., 2013b), which is effective in the treatment of multiple sclerosis (Cohen et al., 2010), but is associated with cardiovascular effects (Kappos et al., 2006; 2010). Results indicated that the active metabolite of fingolimod, fingolimod-phosphate (fingolimod-P), has an effect on TPR in rats, and it is likely that fingolimod-P also influences HR. This is in line with the available information on the mechanisms underlying the cardiovascular effects of fingolimod-P, which indicates that the model can also be applied to provide insights into the site of action of compounds with a more complex MoA. In addition, for all compounds, the estimated drug-specific parameters did not differ significantly from the estimated drug-specific parameters from the final extended CVS model. This implies that the model also can be used to predict the dynamics of the effects on CO, SV and TPR for novel compounds using only HR and MAP measurements.

In conclusion, the extended CVS model can be applied to elucidate the MoA and to quantify drug-specific parameters for new compounds with desired and undesired effects on the CVS using only HR and MAP measurements. Applications of the developed model, using the identified set of system parameters, are limited to SHR and WKY rats. However, as a mechanism-based modelling approach was applied, it is foreseen that accurate extrapolation between different rat strains and from one species to another is possible (Danhof et al., 2008; Ploeger et al., 2009). This requires the differences in the values of the system-specific parameters between the different species to be known. An ultimate application of the extended CVS model would be to predict the change in the haemodynamic parameters in humans based on preclinical data for newly developed compounds. However, before our model can be applied for that purpose, it is necessary to predict long-term BP effects (Snelder et al., 2013a). Moreover, the model should be scaled to humans and validated for human MAP, HR and CO measurements.

Glossary

amp

amplitude

BSL_CO

baseline value of cardiac output

BSL_HR

baseline value of heart rate

BSL_MAP

baseline value of mean arterial pressure

BSL_SV

baseline value of stroke volume

BSL_TPR

baseline value of total peripheral resistance

C

drug concentration in plasma

CO

cardiac output

E_max

maximum effect

FB

negative feedback of mean arterial pressure

FB0

feedback of a typical subject

FB0_MAP

exponent of the power relationship between FB and the individual BSL_MAP

HCTZ

hydrochlorothiazide

hor

horizontal displacement

HR

heart rate

K_{in_HR}

zero-order production rate constant of HR

K_{in_SV}

zero-order production rate constant of stroke volume

K_{in_TPR}

zero-order production rate constant of total peripheral resistance

k_{out_HR}

first-order dissipation rate constant of HR

k_{out_SV}

first-order dissipation rate constant of stroke volume

k_{out_TPR}

first-order dissipation rate constant of total peripheral resistance

LVFT

left ventricular filling time

MAP

mean arterial pressure

MoA

mechanisms of action

MVOF

minimum value of the objective function

PD

pharmacodynamics

PK

pharmacokinetics

RAAS

renin-angiotensin-aldosterone system

SHR

spontaneously hypertensive rats

SV

stroke volume

t

time

TPR

total peripheral resistance

WKY

Wistar-Kyoto rats

Author contributions

N. S., B. A. P., O. L., D. F. R., D. R. S. and M. D. participated in the research design. D. F. R., F. F. and M. B. conducted the experiments. N. S., B. A. P., O. L., D. F. R., D. R. S. and M. D. performed or contributed in the data analysis. N. S., B. A. P., O. L., D. F. R., F. F., M. B., D. R. S. and M. D. wrote or contributed to the writing of the manuscript.

Conflicts of interest

None.

Supporting information

Additional Supporting Information may be found in the online version of this article at the publisher's web-site:

http://dx.doi.org/10.1111/bph.12824

Figure S1 Description of the effects of amiloride in SHR (plot A), enalapril in SHR (plot B), fasudil in SHR (plot C), HCTZ part a in SHR (plot D), HCTZ part b in SHR (plot E), HCTZ part a in WKY rats (plot F), prazosin in SHR (plot G) and prazosin in WKY rats (plot H). Data are from study 1, in which vehicle and a different dose of amiloride (10 mg kg⁻¹ p.o.), enalapril (3, 10 and 30 mg kg⁻¹ p.o.), fasudil (3, 10 and 30 mg kg⁻¹ p.o.), HCTZ (part a: 1, 3, 0.1 and 0.3 mg kg⁻¹ p.o; part b: 10 and 30 mg kg⁻¹ p.o.) or prazosin (0.04, 0.2, 1 and 5 mg kg⁻¹ p.o.) were administered on separate days. Fasudil and prazosin have an inhibiting effect on TPR. Therefore, TPR decreases after administration of these compounds. As a result of the indirect feedback, HR and CO increase. SV first decreases because of the direct inverse relationship between HR and SV. Subsequently, this decrease is reversed by the indirect feedback. Enalapril inhibits TRP. Therefore, the influence on the parameters of the CVS is similar to the influence of fasudil and prazosin. However, as enalapril also has and inhibiting effect on SV, the initial decrease is SV is not reversed by the indirect feedback. Amiloride and HCTZ have an inhibiting effect on SV. Therefore, SV and, consequently, CO, decrease after administration of these compounds. As a result of the indirect feedback, HR and TPR increase. MAP changes in the same direction as the initial effect for all compounds. The dots represent the observations of different rats (coloured in different shades of grey by rat). The continuous and dashed lines represent the individual and population predictions by the developed extended CVS model after administering amiloride, enalapril, fasudil, HCTZ or prazosin.

Figure S2 Description of the effects of atropine and propranolol. Data are from study 2, in which atropine (10 mg kg⁻¹) and/or propranolol (30 mg kg⁻¹) were administered alone, sequentially with a 3 h interval or simultaneously on separate days. Atropine has a stimulating effect on HR. Therefore, HR and, consequently, CO, increase after administration of atropine. As a result of the indirect feedback, SV and TPR decrease. MAP changes in the same direction as the initial effect. The effect of propranolol was too small to be quantified. The dots represent the observations of different rats (coloured in different shades of grey by rat). The continuous and dashed lines represent the individual and population predictions by the developed extended CVS model.