Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2014 Oct 21;23(12):1789–1799. doi: 10.1002/pro.2574

Linking 3D and 2D binding kinetics of membrane proteins by multiscale simulations

Zhong-Ru Xie 1,1, Jiawen Chen 1,1, Yinghao Wu 1,*
PMCID: PMC4253819  PMID: 25271078

Abstract

Membrane proteins are among the most functionally important proteins in cells. Unlike soluble proteins, they only possess two translational degrees of freedom on cell surfaces, and experience significant constraints on their rotations. As a result, it is currently challenging to characterize the in situ binding of membrane proteins. Using the membrane receptors CD2 and CD58 as a testing system, we developed a multiscale simulation framework to study the differences of protein binding kinetics between 3D and 2D environments. The association and dissociation processes were implemented by a coarse-grained Monte-Carlo algorithm, while the dynamic properties of proteins diffusing on lipid bilayer were captured from all-atom molecular dynamic simulations. Our simulations show that molecular diffusion, linker flexibility and membrane fluctuations are important factors in adjusting binding kinetics. Moreover, by calibrating simulation parameters to the measurements of 3D binding, we derived the 2D binding constant which is quantitatively consistent with the experimental data, indicating that the method is able to capture the difference between 3D and 2D binding environments. Finally, we found that the 2D dissociation between CD2 and CD58 is about 100-fold slower than the 3D dissociation. In summary, our simulation framework offered a generic approach to study binding mechanisms of membrane proteins.

Keywords: membrane proteins, binding kinetics, multiscale simulation, coarse-grained model

Introduction

Membrane proteins constitute a large proportion of cellular composition.1 They are responsible for various biological activities, such as transducing signals from extracellular to intracellular environments,2,3 transporting ions across membranes,4,5 and maintaining adhesion between cells.6,7 Functions of membrane proteins are implemented by their interactions, for instance, between signaling receptors and their ligands, or between adhesive proteins from apposing cell surfaces. The properties of these interactions are characterized by binding affinity and kinetic rate constants. Most experimental methods such as isothermal titration calorimetry (ITC)8 and surface plasmon resonance (SPR)9,10 measure these binding properties in solution. However, motions of proteins in solution are different from their motions on cell surfaces. Unlike soluble proteins which possess three translational and three rotational degrees of freedom, membrane proteins only have two translational degrees of freedom and experience constraints on their rotational degrees of freedom. As a result, binding properties of soluble and membrane proteins display significant differences.

Two categories of experimental studies have recently contributed to the measurements of 2D binding properties of membrane proteins. Fluorescence recovery after photo-bleaching (FRAP) microscopy has been used to detect the surface densities of T-cell receptors (TCR), peptide-bound major histocompatibility complex (pMHC) and TCR-pMHC complexes at the interface between T cells and planar bilayers.11 The 2D dissociation constant can be calculated by assuming that the receptor–ligand interactions are at equilibrium. In parallel, the “mechanical methods” were applied to study the 2D binding parameters of membrane-anchored receptors,12 including micropipettes,13,14 hydrodynamic flow chambers,15 the surface force apparatus,16 or the bio-membrane force probe. For instance, the time-dependence of cadherin's intercellular binding was evaluated by micropipette manipulation measurements.17 However, as pointed out by Dustin et al., the values of 2D dissociation constant obtained from FRAP differ by several orders of magnitude from values measured with mechanical methods.18 Therefore, it is challenging to understand how molecular binding is affected by cellular location, as well as different experimental environments.

Theoretical analysis and computational simulations serve as an alternative to approach this problem. Bell originally provided a theoretical relation between 3D and 2D dissociation constant by defining a confinement length in which anchored molecules from two opposite sides of cell membranes form interactions.19,20 Bell's theory has recently been generalized by decomposing the confinement length into different factors such as molecular flexibility and membrane-constrained rotations. By specifically applying the new theoretical framework to the cadherin system, together with a coarse-grained Monte–Carlo simulation technique, we were able to convert the 3D dissociation constant measured in solution into 2D by accounting directly for the structure and dynamics of the membrane-bound molecules.21–23 This method so far cannot provide kinetic information of binding. On the other hand, Brownian dynamic simulation,24–33 and a more recently developed method based on transient-complex theory34,35 give promising results on predicting kinetic rates of protein association. However, the extension of these methods to membrane protein association is currently under development.

To study the 2D binding kinetics of membrane proteins and quantify its relation with 3D binding of soluble proteins, a multiscale simulation method was developed in the current study. The method was applied to a specific system, the interaction between membrane protein CD2 and CD58. CD2 and CD58 are cell adhesion molecules known to mediate the activation of T cells and natural killer cells.36,37 We show that both 3D and 2D association rates can be quantitatively simulated by a coarse-grained (CG) Kinetic Monte–Carlo (KMC) algorithm. The calculated values are close to the experimental measurements. The 2D diffusion constants of proteins on membrane surfaces and the flexibility of domain linkers in the CG model were derived from all atom molecular dynamic simulations. We provide detailed analysis of how molecular diffusions and membrane fluctuations affected 2D association rates. The simulations were further extended to evaluate protein dissociation. Interestingly, we found that the 2D dissociation is about 100-fold slower than the 3D dissociation. This result is consistent with previous experimental observation.38 Potential mechanisms were proposed. Finally, we offered biological insights to the question of why binding affinity measured by mechanical methods is several orders of magnitude weaker than the affinity measured by fluorescent methods.

Results

The parameters of 2D dynamic properties derived from GROMACS

We first estimated the 2D diffusive properties of simulated proteins on membrane surfaces. The translational diffusions of the molecule can be reflected by the mean square displacements (MSD). On the basis of the 100 ns GROMACS simulation data, we traced the position of the molecule within the 2D simulation area for each snapshot of 2 fs. The center of mass for the extracellular domain of the protein was used to calculate the information of MSD along with the average simulation time (ΔT). Figure 3(a) shows the result of the MSD calculation. The slope of the MSD plots gives the 2D diffusion coefficient, which equals 1.75 Å2 ns−1. We further defined a vector to describe the rotations of the molecule along the membrane surface normal. The vector is perpendicular to the transmembrane helix and parallel to the lipid bilayer. We calculated the orientation of the vector every 10 ns along the simulations. The changes of the orientation in this time interval give the angular velocity of the molecule along the membrane surface normal. The distribution of the calculated angular velocity is shown in Figure 3(b). The standard deviation of the distribution is 12°. On the basis of the distribution, we assume that the rotational diffusion of the protein along membrane surface normal is about the range of 12° per 10 ns, leading to a rotational diffusion coefficient equal to 4 × 106 rad2 s−1. Consequently, the 2D translational and rotational diffusion coefficients derived from our simulations are much smaller than those for soluble proteins, suggesting that diffusion of proteins on cell membrane are much slower than cytoplasmic diffusion. However, these diffusion constants are still comparatively faster than experimental measurements.39 This is due to the fact that in vivo diffusion can involve other factors such as cellular crowding.

Figure 3.

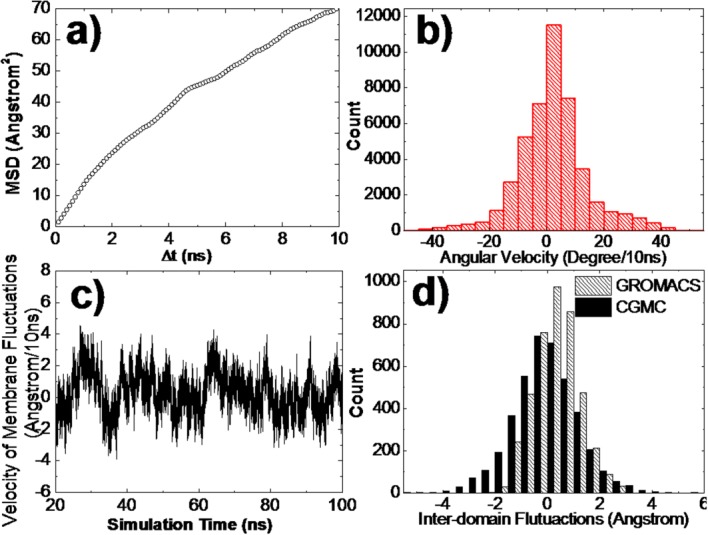
Figure 3

Open in a new tab

The 2D dynamic properties derived from GROMACS all-atom simulations include: (a) mean square displacements of protein moving on the surface of lipid bilayer which was used to calculate the translational diffusion constant; (b) the distribution of angular velocity of the protein rotated along the membrane surface normal; (c) the changes of the perpendicular position of the lipid bilayer for each snapshot of 2 fs which were used to estimate membrane fluctuations; and (d) the fluctuations of interdomain distance between center-of-mass of extracellular and trans-membrane regions in a time interval of 10 ns that were derived from GROMACS (slashed bars) and CGMC simulations (black bars).

Additionally, the GROMACS simulations provide the kinetic information of membrane fluctuations and linker flexibility. We traced the perpendicular position of the lipid bilayer for each snapshot of 2 fs. The changes of the position in a time interval of 10 ns were calculated along the entire simulation trajectory. The results are shown in Figure 3(c). The statistical analysis of the data indicates that the membrane fluctuations every 10 ns are within the amplitude of 2 Å, while the total range of the fluctuations is smaller than 10 Å. Finally, to estimate the flexibility of the linker region, we calculated the fluctuations of inter-domain distance between center-of-mass of extracellular and trans-membrane regions in a time interval of 10ns [slashed bars of Fig. 3(d)]. By adjusting appropriate parameters, a quantitatively similar distribution was achieved by randomly changing the bond angle and dihedral at the linker region [black bars in Fig. 3(d)]. The adjusted amplitudes are 0.5° per 10 ns for the variation of bond angle and 1.0° per 10 ns for the variation of dihedral. A unit of 10 ns was used here because it is the time step used in the coarse-grained simulation. Using the same value makes it easier to transfer the simulation parameters.

Linking 3D and 2D on rates of CD2/CD58 association

The 3D on rate was estimated by placing the extracellular regions of CD2 and CD58 in a cubic box with 10 nm in length. The only degrees of freedom applied to both molecules are free translational and rotational diffusions. As described in the Methods, the diffusions are guided by the energy parameter, μ, which is adjustable to mediate the constraints from native contacts. We tested different values of μ in simulations from 0.5 to 5. For each testing value, 100 simulation trajectories were generated. Each trajectory contained 104 simulation steps with a time step of 10 ns. At the end of each trajectory, we checked if an encounter complex was successfully formed. The criteria of forming an encounter complex are: (1) the distances of more than 50% native contacts are below the cutoff value, and (2) the Cα-based RMSD of the encounter complex must be lower than 7Å from the native dimer. After all 100 trajectories completed, we calculated the successful rate. The simulation results of successful rates for all tested μ are plotted in Figure 4. The figure indicates that generally the rates are higher at larger values of μ. As μ reaches 3, however, further increases of its value reduced the successful rate. This suggests that the simulations are more easily trapped at local minimal states under strong values of μ.

Figure 4.

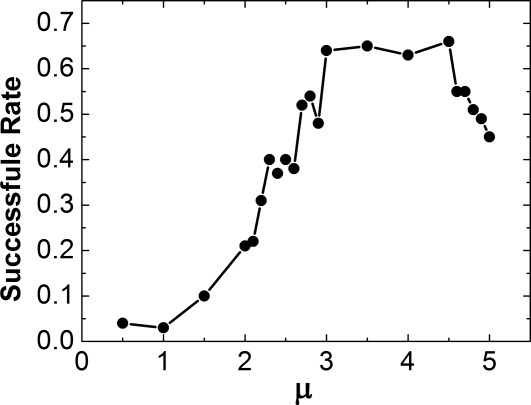
Figure 4

Open in a new tab

The successful rates of 3D association are plotted under different values of energy parameter μ. In general, the rates are higher at larger values of μ. However, as μ reaches 3, the further increases of μ value reduced the successful rate. This suggests that the proteins are more easily to be trapped at local minimal states under strong energy parameters.

By SPR measurements, the 3D CD2/CD58 binding affinity is 2 × 10−6 M and the reverse-rate is higher than 6 s−1.40,41 The ratio of reverse-rate and binding affinity gives the 3D on-rate of CD2/CD58 association of 3 × 106 M−1 s−1. Given the size of the simulation box and the length of each simulation trajectory, Eq. (4) indicates that the successful ratio should be 50% in order to have the calculated on rate comparable with the experimental value. Therefore, the value 2.7 was selected for μ under which simulations are able to reproduce the experimental 3D on-rate. Using the same binding criteria and same value of μ (μ = 2.7), we evaluated the binding kinetics of CD2 and CD58 on 2D cell surfaces. Our simulations were performed on a 2D plane with 10 nm in length. We carried out 1000 independent simulation trajectories. Each trajectory contained 104 simulation steps with a time step of 10 ns. As a result, among these 103 trajectories, we found 27 of them forming encounter complexes by the end of their simulations. This gave the 2D on rate of 0.027 μm2 s−1. If the size of simulation box was increased to 20 nm in length, we found eight encounter complexes formed among 1000 simulation trajectories, leading to a 2D on rate of 0.032 μm2 s−1. Using contact area FRAP, the 2D binding of CD2 and CD58 was experimentally studied. The measured 2D on-rate equals 0.015 μm2 s−1.38 Therefore, our simulated 2D on-rate is quantitatively close to the experimental value. Furthermore, the same energy parameters used in both 3D and 2D simulations indicate that the 2D binding rates are transferable from 3D binding, assuming the binding energy does not change in both systems.

It is worth mentioning that when two molecules freely diffuse in 3D solutions, their relative position and orientation are only described by six degrees of kinetic freedom, three for translation and three for rotation. It is equivalent to fix one of these two molecules at the origin and move the other one relative to it. In another word, binding between anchored and soluble proteins dose not shift much from the binding of two soluble proteins. Therefore, SPR experiments are able to reflect the 3D binding kinetics, although one of the interaction partners in these experiments is attached on to the gold surface. On the other hand, we can connect SPR experiments with our simulations in which both proteins diffuse and rotate in three dimensions.

Evaluating different factors that affect 2D protein association

The cell membrane is a complex system. Protein interactions in this environment are affected by many different factors. For instance, cell membranes are crowded by a large number of membrane receptors and channels. The cell surface crowding have prominent effects on the 2D diffusions of membrane proteins. Therefore, we first reduced the 2D diffusion constant by one, two and three orders of magnitude from its original value derived from all-atom simulations. For each testing value of diffusion constant, 1000 independent trajectories were generated to simulate the successful rate of 2D association. To increase the simulation efficiency, we lowered the association criteria so that now an encounter complex will be formed if the distances of 10% native contacts are below the cutoff value, instead of 50% that was used before. Under the new criteria, we found 493 encounter complexes among 1000 trajectories when the original value of diffusion constant (1.75 Å2 ns−1) was used. However, if the diffusion constant was set to 0.175 Å2 ns−1, the number of encounter complexes formed after 1000 trajectories decreased to 317. The relation between successful rate and diffusion constant is plotted in Figure 5(a). The x axis of the figure is the ratio between testing value and original value of diffusion constant (D/D0). This figure suggests that slower diffusions of membrane proteins decelerate their associations.

Figure 5.

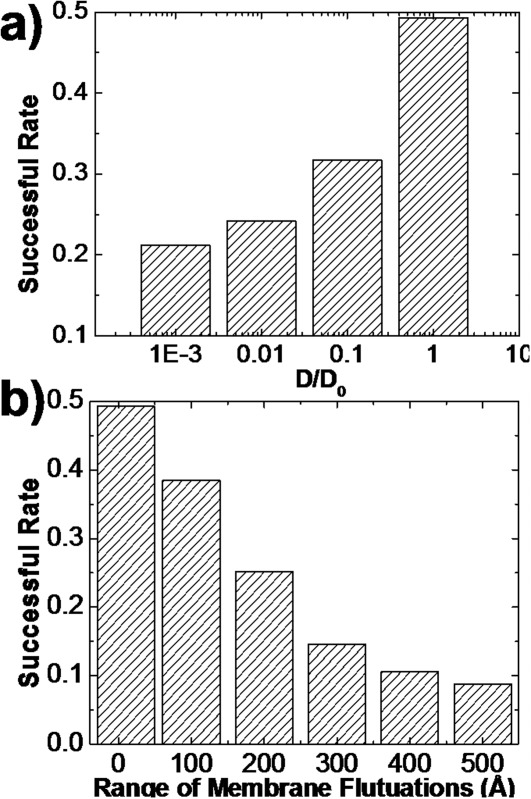
Figure 5

Open in a new tab

The relation between successful rate of 2D association and diffusion constant is plotted in (a). The x axis is the ratio between testing value and original value of diffusion constant (D/D0). The figure suggests that slower diffusions of membrane proteins decelerate their associations. Furthermore, the relation between successful rate of 2D association and total range of membrane fluctuations is plotted in (b). This figure indicates that 2D associations of membrane proteins are impeded by larger fluctuations of cell membranes.

In contrast to 3D association of soluble proteins which is only limited by diffusions, the 2D association of membrane proteins also depends on the properties of membrane fluctuations. Based on the all-atom simulation data of the lipid bilayer, the total range of the fluctuations is in the scale of 10 Å. However, the GROMACS simulation was applied to study the dynamics of the system around its equilibrium state. When proteins from two approaching cells associate, the range of membrane movements is much larger. Therefore, we increase the range of membrane fluctuations from 10 Å to 500 Å, while the amplitude of membrane fluctuations within a time step (10ns) of simulations is still 2 Å. Consequently, the relation between successful rate and total range of membrane fluctuations is plotted in Figure 5(b). This figure indicates that associations of membrane proteins are impeded by larger fluctuations of cell membranes. Overall, our simulations demonstrated that membrane protein association can be modulated by various cellular factors.

Comparing 3D with 2D dissociation between CD2 and CD58

The process of dissociation between CD2 and CD58 was further investigated. We started from simulating the 3D dissociation. To manipulate the rate of dissociation, we changed the value of μ from 1.0 to 4.0. For each data point, 1000 simulation trajectories were generated from the native structure of a dimer and the corresponding successful rate was calculated after all simulations were completed. The simulation results are illustrated in Figure 6. The figure shows the rate that CD2 successfully dissociated from CD58 under different values of μ. Overall, the successful rates decrease as μ increases, indicating that the proteins are more difficult to dissociation under stronger interactions. In specific, when μ equals to 1.75, we found CD2 and CD58 did not dissociate in only 3 out of 1000 simulation trajectories. When μ equals to 2.0, two proteins remained complex in 69 trajectories. Interestingly, previous experimental observations showed that the off-rate of 2D dissociation between CD2 and CD58 is two orders of magnitude slower than their 3D dissociation.38 Therefore, we used the same simulation criteria to study the 2D dissociation.

Figure 6.

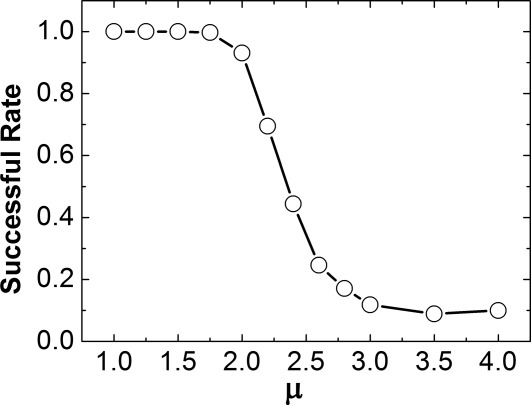
Figure 6

Open in a new tab

The 3D dissociation between CD2 and CD58 was further investigated by changing the value of μ from 1.0 to 4.0. For each testing μ, 1000 simulation trajectories were generated from the native structure of a dimer and the corresponding successful rate was calculated after all simulations were completed. Overall, the successful rates decrease as μ increases, indicating that the proteins are more difficult to dissociation under stronger interactions. The 3D dissociation was further compared with 2D dissociation and we found that 2D dissociation between CD2 and CD58 is two orders of magnitude slower than 3D dissociation.

We first assume that a large number of complexes formed and the membrane environment reaches equilibrium, so that the degrees of freedom in membrane fluctuations and linker flexibility were fixed. The only conformational perturbations applied to both molecules were small amplitude of 2D translational diffusions and rotation along the surface normal of cell membranes. Consequently, when the value 1.75 was used for μ, we found two proteins remained complexed in 870 out of 1000 simulation trajectories. While the μ value increased to 2.0 in simulations, two proteins remained complexed in 972 of 1000 trajectories. Comparing with the corresponding results of 3D dissociation, our simulations clearly indicate that the 2D dissociation between CD2 and CD58 is two orders of magnitude slower than 3D dissociation, which is quantitatively consistent with the experiments. Because the energy parameters used in both systems are the same, we therefore give supportive evidences that the reason of this difference is because the specific membrane environment makes the receptor and ligand tend to remain together. For instances, if we added membrane fluctuations and linker flexibility back to simulations of 2D dissociation, we found the numbers of trajectories in which two proteins remain complex decreased. Specifically, μ = 1.75 resulted in 216 undissociated complexes among 1000 trajectories, while μ = 2.0 resulted in 587 un-dissociated complexes. Therefore, our studies indicate that the additional degrees of freedom from the system accelerate dissociation. This will further bring insights to the question of why different experimental methods generated very different measurements to 2D binding, which will be discussed in the next section.

Concluding Discussions

Membrane proteins allow cells to communicate with their environments, therefore they are among the most functionally important proteins in cells. Binding of membrane proteins is fundamentally distinguishable from soluble protein because of the constrained motions of membrane proteins on cell surfaces. Furthermore, due to the complexity of membrane environments, there are significant discrepancies between different experimental methods that measure the 2D binding properties of membrane proteins. Computational modeling is a valuable technique that can be used to provide quantitative evaluations to these problems. In this article, we developed a multi-scale simulation framework to study the binding kinetics of membrane proteins. The diffusional properties of proteins on membrane surfaces were captured from all-atom molecular dynamic simulations, while the association and dissociation processes were implemented by a coarse-grained Monte-Carlo algorithm in both 3D and 2D environments. The binding between membrane protein CD2 and CD58 was used as a testing system. By calibrating simulation parameters to the measurements of 3D binding, we derived the 2D binding constant which is quantitatively consistent with the experimental data, indicating that the method is able to capture the difference between 3D and 2D binding environments. We also found that the 2D dissociation between CD2 and CD58 is about 100-fold slower than the 3D dissociation. We show that molecular diffusion, linker flexibility and membrane fluctuations are important factors to adjust binding kinetics. In summary, our simulation framework offered a generic approach to study binding mechanisms of membrane proteins.

The energy terms in the target function of current model are predetermined by the native contacts in the interacting proteins. Because the main focus of current study is to investigate the difference of binding between 3D and 2D systems and the different factors affecting the 2D binding, the effect of this native bias can be canceled out as long as we assume that the binding energies are the same for proteins in both 2D and 3D environments and the same energy parameters are used for both systems. Moreover, by simply adjusting the relative weights between different two energy terms, the rate constants can be easily modulated. However, this study requires that experimental data of both 3D and 2D binding are available, so that the scoring functions can be adjusted to fit the measurements. In case experimental constants are not available, the implementation of physical-based energy functions will be expected in the future to carry out more predictive simulation studies. Therefore, it would be more significant if the application of a more realistic, parameters-free coarse-grained force-field, such as MARTINI,42 can reach the binding kinetics that is equally consistent with the experimental results. There are two distinctive classes of energetic factors generally known to influence binding kinetics.43 One is geometric complementary and the hydrophobic interactions that are short range. The other one is the long range electrostatic interactions leading to the faster association which rates can always be higher than 107 M−1 s−1. A recently developed method based on transient-complex theory demonstrated that the long-range electrostatic interactions play dominant role to accelerate association processes in the diffusion-limited regime.35,44,45 It gives promising results on predicting rates of diffusion-limited protein association. However, the method is atom-based. On the coarse-grained level, a new physical-based force field, SCORPION, was recently used to simulate the recognition between barnase and barstar.46 One of the future directions includes incorporating similar physical-based force-fields into the conformational sampling of current model.

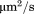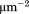The fundamental difference between 2D binding of membrane proteins and their 3D counterparts is in the units associated with the kinetic rates. The 2D on rate and affinity units are reflected by surface density of interacting molecules and are expressed in terms ofInline graphic andInline graphic, while the units of 3D on rate and dissociation constant are reflected by volumetric concentration and are expressed by M−1 s−1 and M. This difference in the units causes it very difficult to directly compare the 2D binding with 3D. By applying our coarse-grained simulations respectively to the 3D and 2D environments, we showed that the 3D binding rate can be directly transferred to the 2D rate. Therefore, the simulation studies proposed in this article provides a potential method to compare protein binding in different cellular environments. Furthermore, our simulations also showed that 2D binding of membrane proteins can be affected by various factors due to the complexity of membrane environments. For instance, we have demonstrated that membrane fluctuations were responsible in decelerating protein association but accelerate dissociation, which leads to the fact that the 2D binding affinity is higher in the environment with higher membrane fluctuations. Because it is generally believed that the membrane fluctuations in mechanical methods are much larger that fluorescence methods, our simulation data therefore explains why affinity measured by mechanical methods is several orders of magnitude weaker than the affinity measured by fluorescence methods.

Further improvements of our current simulation method will be helpful to provide insights to a number of specific biological systems. For examples, the 2D interactions between TCR and MHC are determined by the specific recognition of peptides that bind to MHC, which is required to control the appropriate immune responses at distinct stages of T-cell maturation.47–50 At the cellular interfaces of neural synapses, the 2D interactions of neural receptors and synaptic adhesion molecules are the primary determinant of establishing neuronal connectivity.51 While the quantitative examinations of these 2D binding are still under development, our computational studies can be used to estimate the 2D binding kinetics from available 3D measurements and generate mechanistic hypothesis by adjusting simulation variables. Moreover, many membrane receptors such as neurexin, integrin and cadherin form multimeric signaling complexes or clusters after binding to their ligand on cell surfaces.52,53 The interactions, aggregations and clustering of these membrane proteins are further coupled with other biological molecules. For instance, the TCR–MHC complex additionally interacts with other proteins such as CD3, CD4/8 co-receptors in the immunological synapse.54 The molecular mechanisms of all these processes are currently not well-understood. Future extension of our method to systems with multiple proteins and applications of the new method to above problems will expand our understanding of molecular interactions to the subcellular level.

Methods

Constructing the 2D model of CD2–CD58 interaction with its 2D dynamic properties

The current study focuses on a testing system, a T-cell surface receptor CD2 with its binding target CD58. Both CD2 and CD58 contain two extracellular immunoglobulin domains, a transmembrane helical domain and a connecting linker region. The complex of full-length CD2 and CD58 was constructed on the two-layer cellular interface, as shown in Figure 1(a). The structure of two-domain extracellular region for CD2 was adopted from the PDB ID 1HNF,55 while the structure of two-domain extracellular region for CD58 was generated by following PDB ID 1CCZ.56 The dimeric binding interface was modeled by following PDB ID 1QA9,57 which is a dimer consisting of N-terminal domains from CD2 and CD58. The transmembrane regions for both CD5 and CD58 were modeled as standard α-helix and the linker regions were built by the online server, ModLoop. The total residue number of CD2 in 2D simulation is 207, while the linker region connecting extracellular region and trans-membrane helix is ranged from residue 179–183. The total residue number of CD58 in 2D simulation is 200, while the linker region connecting extracellular region and trans-membrane helix is ranged from residue 171–177. Consequently, the intercellular distance derived from the model is 16 nm [Fig. 1(a)], which is consistent with previous observations.58

Figure 1.

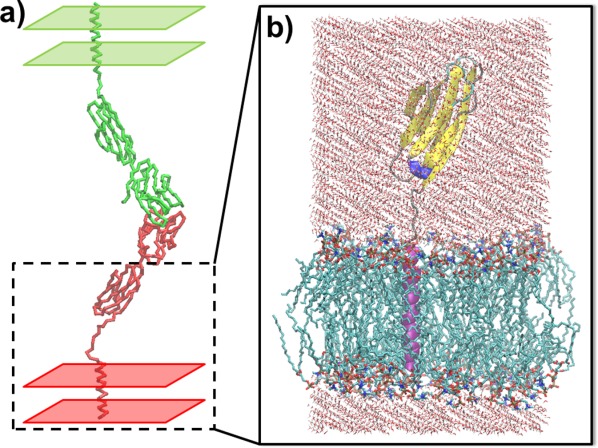
Figure 1

Open in a new tab

The complex of full-length CD2 and CD58 was constructed on two-layer cell surfaces (a). The inter-cellular distance derived from the model is 16 nm. A 100 ns all-atom MD simulation was carried out for CD2 within lipid bilayer and explicit solvent (b). The N-terminal domain was not included in the simulation for the purpose of computational efficiency.

To derive dynamic properties of our testing molecules on membrane surfaces, a 100 ns all-atom MD simulation was carried out for CD2 with lipid bilayer and explicit solvent. The N-terminal domain was not included in the simulation for the purpose of computational efficiency. We assume that the deletion of N-terminal domain will not qualitatively affect dynamic properties of the molecule on cell membranes. Specifically, the MD simulations were performed with GROMACS version 4.5.5,59 by gromos53a6_lipid.ff force field for simulating the system with both protein and lipids. The lipid bilayer in our simulations contains the structure of 128 DPPCs (dipalmitoyl phosphatidylcholine). As shown in Figure 1(b), the simulation box size was ∼64 × 64 × 115 Å, and the system contained around 35,164 atoms. A uniform integration step of 2 fs was used for all types of interactions, throughout all simulations. (A cutoff of 12 Å was used for van der Waals interactions, and electrostatic interactions were calculated with the particle mesh technique for Ewald summations, also with a cutoff of 12 Å.) A Berendsen thermostat was used to maintain a constant temperature of 300 K, and a constant pressure of 1 bar was maintained using a Berendsen barostat.

On the basis of the all-atom simulation data, we derived the diffusion coefficient for the 2D translational motions of CD2 on membrane surfaces, together with the coefficient of its rotation along the membrane normal. We further obtained the range of membrane fluctuations from the motions of the lipid bilayer. Finally, we gave the quantitative measurements to the flexibility of the linker region that connects extracellular and trans-membrane domain. Because of the structural similarity between CD2 and CD58, we assume that the properties derived from CD2 are also applicable to CD58. Specifically, based on the GROMACS simulation data, we generated a distribution of interdomain distance fluctuations. The distance was calculated between center-of-mass of extracellular and transmembrane regions in every time interval of 10 ns. A quantitatively similar distribution can be reproduced by adjusting the amplitudes that change the C-based virtual bond angles and dihedrals at the linker region. The adjusted amplitudes were then used to model linker flexibility in coarse-grained Monte–Carlo simulations. The detailed values of these dynamic properties will be given in the results section, and they will be used as parameters in our coarse-grained Monte–Carlo algorithm to simulate the 2D protein association.

Coarse-grained Monte–Carlo simulations of protein-protein association in 3D and 2D

The associations between CD2 and CD58 in 3D and 2D environments were simulated by a Kinetic Monte–Carlo algorithm. First, the 3D simulation starts from an initial conformation, in which CD2 and CD58 are randomly placed in a cubic box [Fig. 2(a)]. Only the extracellular regions are used in simulations for both molecules, and they are coarse-grained in Cα representation. Following the initial conformation, both molecules make random diffusions with the periodic boundary condition. They are treated as rigid bodies with three translational and three rotational degrees of freedom. For translational diffusions, given a discrete time step of fixed size Δt, each molecule moves along a random direction uniformly distributed over the surface of a sphere with a distance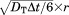Inline graphic, in which DT is the translational diffusion constant of the molecule and r is a random number generated between 0 and 2. For rotations, within each time step, the molecule randomly rotates along each Euler angle with value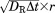Inline graphic, in which DR is the rotational diffusion constant of the molecule and r is a random number generated between −1 and 1. The translational and rotational diffusion constants for both molecules are adopted from fitting the data that were calculated by a precise boundary element method.60

Figure 2.

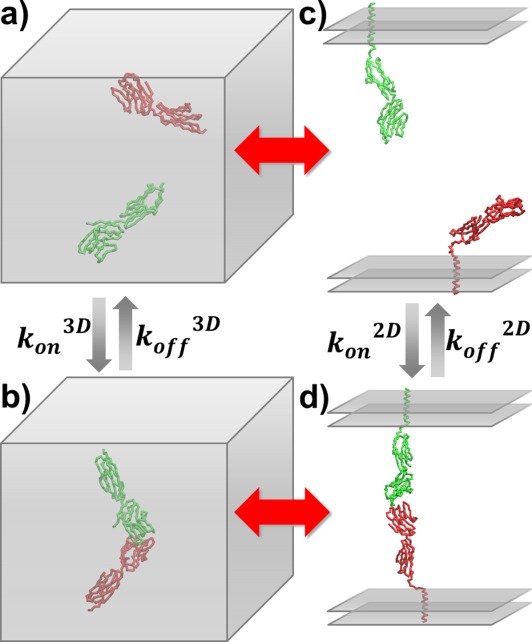
Figure 2

Open in a new tab

The association and dissociation rates were estimated by the coarse-grained simulations in both 3D and 2D environments. The 3D association starts from an initial conformation in which CD2 and CD58 are randomly placed in a cubic box (a). Kinetic Monte–Carlo algorithm was performed until two proteins form an encounter complex (b). Similarly, 2D association was initiated from a conformation in which two molecules are placed face to face on two-layer parallel surfaces with random positions (c) and the simulation terminated until CD2 and CD58 form an encounter complex at the interface region (d). On the other hand, simulations of protein dissociation were started from the native conformation of CD2/CD58 complex.

Above movements are guided by a scoring function consisting of two terms:

graphic file with name pro0023-1789-m5.jpg 1

The first term is a GO-like potential61 applied to all native contacts:

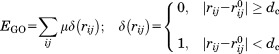graphic file with name pro0023-1789-m6.jpg 2

Here, any residue i in CD2 and j in CD58 is defined as a native contact if the corresponding Cα distance in the native structure is smaller than 7.5Å. The rij is the Cα distance between residue i and j in current conformation,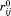Inline graphic is the distance in native structure, dc is a distance cutoff equals to 2Å, and μ is an adjustable energy parameter defines the depth of the GO-potential. The second term is a repulsive penalty effective when the Cα distance between any residue pair is smaller than 3 Å during simulations. The potential function used to guide protein-protein association in simulations is applied only to intermolecular interactions. No intramolecular potential is used because each protein is represented as a rigid body and all intramolecular degrees of freedom are fixed. After each time step, the acceptance of the random diffusions is determined by the probability:

graphic file with name pro0023-1789-m8.jpg 3

in which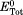Inline graphic and ETot are calculated total values of the target function before and after diffusions along the time step. After the acceptance of the diffusions, the new configuration is updated and the simulation time of the system is moved forward by adding one time step. Above process is iterated until two proteins form an encounter complex [Fig. 2(b)].

The simulations of 2D association between CD2 and CD58 are initiated from a conformation in which two molecules are placed face to face on two-layer parallel surfaces with random positions [Fig. 2(c)]. In additional to the extracellular domains, the structural models include trans-membrane helices and connecting linker regions in the Cα representation. The random diffusion for both molecules consist of 2D translational movements in the plane and rotations along the surface normal. The translational and rotational diffusion constants were derived from the all-atom MD simulations. The perpendicular positions of both molecules were also changed after diffusions in each time step to mimic the small fluctuations of membrane surfaces and inter-membrane distance. The total range and amplitude of the fluctuations were obtained from all-atom simulations. Furthermore, a residue at the linker regions from both molecules is randomly selected within each time step. The bond angle and dihedral of the selected residue is randomly changed within a specific amplitude. The amplitude was derived by fitting the data from all-atom simulations. Therefore, the flexibility of the linker region can be captured by our method. The same scoring function used in Eq. (1) is applied to guide the 2D diffusion, except that an additional term is included to evaluate the conformational preference of the flexible linker regions. A short-range knowledge-based potential developed by Bahar et al.62 is used to prevent the linkers from sampling to any unfavorable conformations. Finally, Eq. (3) is used to update conformations of the system until CD2 and CD58 form an encounter complex at the 2D interface region [Fig. 2(d)].

Simulating protein–protein dissociation in 3D and 2D

The process of dissociation between CD2 and CD58 was also simulated by a similar algorithm in both 3D and 2D environments. The simulations started from the native conformation of CD2/CD58 complex [Fig. 2(b,d)] and were followed by small translational and rotational perturbations that were applied to both molecules in each simulation time step. The amplitudes of the translational and rotational movements of these random perturbations are much smaller than what is used for simulating protein associations. For 3D dissociation, both translational and rotational perturbations are along three degrees of freedom. For 2D dissociation, translational perturbations are along two degrees of freedom in the membrane plane, while rotational perturbations are along the surface normal of the membrane plane. Depending on different experimental set-up, the intermembrane distance and the conformations of linker regions can also undergo small perturbations in 2D dissociation simulations.

After each time step, the new configuration after the perturbations described above is evaluated by the scoring function expressed in Eq. (1). The probability of accepting the configuration after perturbations follows Eq. (3). After the acceptance of the new configuration, the simulation time of the system is updated by adding one time step. Above process is iterated until the dimer dissociates into two separated monomers in 3D [Fig. 2(a)] and 2D [Fig. 2(c)] environments. The criteria of dissociation are that the distances of all native contacts are above the cutoff value. Finally, it worth mentioning that because the scoring function of current study is not a physical-based potential but biased to the native conformation, the absolute value of dissociation rate calculated from simulations is less meaningful. However, when we compared the dissociation between CD2 and CD58 in 3D solvent with their dissociation on 2D cellular interface, we assume that the differences in their dissociation rates are not caused by the binding energy. Therefore, if we used the same energy parameters in both 3D and 2D systems, the relative difference between 3D and 2D dissociation rates can be intrinsically reflected by our simulations.

Deriving 3D and 2D kinetic rate constants from coarse-grained simulations

The 3D and 2D rate constants of protein association and dissociation were calculated from statistical information of multiple simulation trajectories. In detail, to calculate the on rate, we assume that the formation of encounter complexes is rate-limiting. A total number of Ntot trajectories were generated. At the end of each trajectory, an indicator was recorded whether or not two proteins formed an encounter complex. After all simulations completed, a successful rate ρ was calculated by ρ = Non/Ntot, where Non is the number of times two proteins formed an encounter complex among all Ntot trajectories. The total simulation time ttot of one trajectory is n×Δt, in which n is the total number of simulation steps in each trajectory. The on rate of 3D protein association can be written as

graphic file with name pro0023-1789-m10.jpg 4

in which V is the volume of the simulation box, c3D is a constant that converts the unit from molecule/nm3 to M. Similarly, the on rate of 2D association can be written as

graphic file with name pro0023-1789-m11.jpg 5

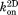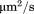in which S is the area of the 2D simulation surface. The unit ofInline graphic isInline graphic.

To derive the rate of protein dissociation, a total number of Ntot trajectories were generated. The successful rate ρ of dissociation was defined by how many times a complex broke among a total number of Ntot trajectories. Given the total simulation time ttot for each trajectory and the successful rate ρ, the 3D and 2D off rate of protein dissociation can be calculated by

graphic file with name pro0023-1789-m14.jpg 6

Finally, if rate constants are compared under the same simulation environments, it is more convenient to do so directly by using successful rates as an indicator to evaluate the kinetics of association and dissociation.

Acknowledgments

The authors thank Dr. Aviv Bergman and Daniel Biro for proofreading of this manuscript. Computational support was provided by Albert Einstein College of Medicine High Performance Computing Center.

References

  1. Singer SJ, Nicolson GL. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
  2. Packard B. Receptor phosphorylation and signal transduction across plasma-membranes. Trends Biochem Sci. 1985;10:138–138. [Google Scholar]
  3. Ullrich A, Schlessinger J. Signal transduction by receptors with tyrosine kinase-activity. Cell. 1990;61:203–212. doi: 10.1016/0092-8674(90)90801-k. [DOI] [PubMed] [Google Scholar]
  4. Doyle DA. Molecular insights into ion channel function. Mol Membr Biol. 2004;21:221–225. doi: 10.1080/09687680410001716844. [DOI] [PubMed] [Google Scholar]
  5. Chang AB, Lin R, Studley WK, Tran CV, Saier MH., Jr Phylogeny as a guide to structure and function of membrane transport proteins. Mol Membr Biol. 2004;21:171–181. doi: 10.1080/09687680410001720830. [DOI] [PubMed] [Google Scholar]
  6. Brasch J, Harrison OJ, Honig B, Shapiro L. Thinking outside the cell: how cadherins drive adhesion. Trends Cell Biol. 2012;22:299–310. doi: 10.1016/j.tcb.2012.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Atilgan E, Ovryn B. Membrane deformation at integrin adhesions. Curr Pharm Biotech. 2009;10:508–514. doi: 10.2174/138920109788922146. [DOI] [PubMed] [Google Scholar]
  8. Pierce MM, Raman CS, Nall BT. Isothermal titration calorimetry of protein–protein interactions. Methods. 1999;19:213–221. doi: 10.1006/meth.1999.0852. [DOI] [PubMed] [Google Scholar]
  9. Kersh GJ, Kersh EN, Fremont DH, Allen PM. High- and low-potency ligands with similar affinities for the TCR: the importance of kinetics in TCR signaling. Immunity. 1998;9:817–826. doi: 10.1016/s1074-7613(00)80647-0. [DOI] [PubMed] [Google Scholar]
  10. Khilko SN, Jelonek MT, Corr M, Boyd LF, Bothwell AL, Margulies DH. Measuring interactions of MHC class I molecules using surface plasmon resonance. J Immunol Methods. 1995;183:77–94. doi: 10.1016/0022-1759(95)00033-7. [DOI] [PubMed] [Google Scholar]
  11. Huppa JB, Axmann M, Mortelmaier MA, Lillemeier BF, Newell EW, Brameshuber M, Klein LO, Schutz GJ, Davis MM. TCR-peptide-MHC interactions in situ show accelerated kinetics and increased affinity. Nature. 2010;463:963–967. doi: 10.1038/nature08746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Huang J, Zarnitsyna VI, Liu BY, Edwards LJ, Jiang N, Evavold BD, Zhu C. The kinetics of two-dimensional TCR and pMHC interactions determine T-cell responsiveness. Nature. 2010;464:932–936. doi: 10.1038/nature08944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Chesla SE, Selvaraj P, Zhu C. Measuring two-dimensional receptor-ligand binding kinetics by micropipette. Biophys J. 1998;75:1553–1572. doi: 10.1016/S0006-3495(98)74074-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Langer MD, Guo HB, Shashikanth N, Pierce JM, Leckband DE. N-glycosylation alters cadherin-mediated intercellular binding kinetics. J Cell Sci. 2012;125:2478–2485. doi: 10.1242/jcs.101147. [DOI] [PubMed] [Google Scholar]
  15. Korn C, Schwarz US. Efficiency of initiating cell adhesion in hydrodynamic flow. Phys Rev Lett. 2006;97:138103. doi: 10.1103/PhysRevLett.97.138103. [DOI] [PubMed] [Google Scholar]
  16. Bayas MV, Kearney A, Avramovic A, van der Merwe PA, Leckband DE. Impact of salt bridges on the equilibrium binding and adhesion of human CD2 and CD58. J Biol Chem. 2007;282:5589–5596. doi: 10.1074/jbc.M607968200. [DOI] [PubMed] [Google Scholar]
  17. Chien YH, Jiang N, Li F, Zhang F, Zhu C, Leckband D. Two stage cadherin kinetics require multiple extracellular domains but not the cytoplasmic region. J Biol Chem. 2008;283:1848–1856. doi: 10.1074/jbc.M708044200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dustin ML, Bromley SK, Davis MM, Zhu C. Identification of self through two-dimensional chemistry and synapses. Ann Rev Cell Devel Biol. 2001;17:133–157. doi: 10.1146/annurev.cellbio.17.1.133. [DOI] [PubMed] [Google Scholar]
  19. Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
  20. Bell GI, Dembo M, Bongrand P. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys J. 1984;45:1051–1064. doi: 10.1016/S0006-3495(84)84252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Wu YH, Honig B, Ben-Shaul A. Theory and simulations of adhesion receptor dimerization on membrane surfaces. Biophys J. 2013;104:1221–1229. doi: 10.1016/j.bpj.2013.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wu HY, Vendome J, Shapiro L, Ben-Shual A, Honig B. Transforming binding affinities from three dimensions to two with application to cadherin clustering. Nature. 2011;475:510–513. doi: 10.1038/nature10183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Wu Y, Jin X, Harrison O, Shapiro L, Honig BH, Ben-Shaul A. Cooperativity between trans and cis interactions in cadherin-mediated junction formation. Proc Natl Acad Sci USA. 2010;107:17592–17597. doi: 10.1073/pnas.1011247107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Gabdoulline RR, Wade RC. Brownian dynamics simulation of protein–protein diffusional encounter. Methods. 1998;14:329–341. doi: 10.1006/meth.1998.0588. [DOI] [PubMed] [Google Scholar]
  25. Gabdoulline RR, Wade RC. Simulation of the diffusional association of barnase and barstar. Biophys J. 1997;72:1917–1929. doi: 10.1016/S0006-3495(97)78838-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Northrup SH, Luton JA, Boles JO, Reynolds JC. Brownian dynamics simulation of protein association. J Comput Aided Mol Des. 1988;1:291–311. doi: 10.1007/BF01677278. [DOI] [PubMed] [Google Scholar]
  27. Antosiewicz J, McCammon JA. Electrostatic and hydrodynamic orientational steering effects in enzyme-substrate association. Biophys J. 1995;69:57–65. doi: 10.1016/S0006-3495(95)79874-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Sharp K, Fine R, Honig B. Computer simulations of the diffusion of a substrate to an active site of an enzyme. Science. 1987;236:1460–1463. doi: 10.1126/science.3589666. [DOI] [PubMed] [Google Scholar]
  29. Schlosshauer M, Baker D. Realistic protein-protein association rates from a simple diffusional model neglecting long-range interactions, free energy barriers, and landscape ruggedness. Protein Sci. 2004;13:1660–1669. doi: 10.1110/ps.03517304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Dlugosz M, Huber GA, McCammon JA, Trylska J. Brownian dynamics study of the association between the 70S ribosome and elongation factor G. Biopolymers. 2011;95:616–627. doi: 10.1002/bip.21619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Harel M, Spaar A, Schreiber G. Fruitful and futile encounters along the association reaction between proteins. Biophys J. 2009;96:4237–4248. doi: 10.1016/j.bpj.2009.02.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Blachut-Okrasinska E, Antosiewicz JM. Brownian dynamics simulations of binding mRNA cap analogues to eIF4E protein. J Phys Chem B. 2007;111:13107–13115. doi: 10.1021/jp0758521. [DOI] [PubMed] [Google Scholar]
  33. Sept D, McCammon JA. Thermodynamics and kinetics of actin filament nucleation. Biophys J. 2001;81:667–674. doi: 10.1016/S0006-3495(01)75731-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zhou HX, Bates PA. Modeling protein association mechanisms and kinetics. Curr Opin Struct Biol. 2013;23:887–893. doi: 10.1016/j.sbi.2013.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Qin S, Pang XD, Zhou HX. Automated prediction of protein association rate constants. Structure. 2011;19:1744–1751. doi: 10.1016/j.str.2011.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Koyasu S, Lawton T, Novick D, Recny MA, Siliciano RF, Wallner BP, Reinherz EL. Role of interaction of CD2 molecules with lymphocyte function-associated antigen 3 in T-cell recognition of nominal antigen. Proc Natl Acad Sci USA. 1990;87:2603–2607. doi: 10.1073/pnas.87.7.2603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Moingeon P, Chang HC, Wallner BP, Stebbins C, Frey AZ, Reinherz EL. CD2-mediated adhesion facilitates T lymphocyte antigen recognition function. Nature. 1989;339:312–314. doi: 10.1038/339312a0. [DOI] [PubMed] [Google Scholar]
  38. Tolentino TP, Wu J, Zarnitsyna VI, Fang Y, Dustin ML, Zhu C. Measuring diffusion and binding kinetics by contact area FRAP. Biophys J. 2008;95:920–930. doi: 10.1529/biophysj.107.114447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ramadurai S, Holt A, Krasnikov V, van den Bogaart G, Killian JA, Poolman B. Lateral diffusion of membrane proteins. J Am Chem Soc. 2009;131:12650–12656. doi: 10.1021/ja902853g. [DOI] [PubMed] [Google Scholar]
  40. Dustin ML, Golan DE, Zhu DM, Miller JM, Meier W, Davies EA, van der Merwe PA. Low affinity interaction of human or rat T cell adhesion molecule CD2 with its ligand aligns adhering membranes to achieve high physiological affinity. J Biol Chem. 1997;272:30889–30898. doi: 10.1074/jbc.272.49.30889. [DOI] [PubMed] [Google Scholar]
  41. van der Merwe PA, Barclay AN, Mason DW, Davies EA, Morgan BP, Tone M, Krishnam AK, Ianelli C, Davis SJ. Human cell-adhesion molecule CD2 binds CD58 (LFA-3) with a very low affinity and an extremely fast dissociation rate but does not bind CD48 or CD59. Biochemistry. 1994;33:10149–10160. doi: 10.1021/bi00199a043. [DOI] [PubMed] [Google Scholar]
  42. Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The MARTINI force field: coarse grained model for biomolecular simulations. J Phys Chem B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
  43. Ravikumar KM, Huang W, Yang S. Coarse-grained simulations of protein–protein association: an energy landscape perspective. Biophys J. 2012;103:837–845. doi: 10.1016/j.bpj.2012.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Alsallaq R, Zhou HX. Prediction of protein-protein association rates from a transition-state theory. Structure. 2007;15:215–224. doi: 10.1016/j.str.2007.01.005. [DOI] [PubMed] [Google Scholar]
  45. Alsallaq R, Zhou HX. Energy landscape and transition state of protein–protein association. Biophys J. 2007;92:1486–1502. doi: 10.1529/biophysj.106.096024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Basdevant N, Borgis D, Ha-Duong T. Modeling protein–protein recognition in solution using the coarse-grained force field SCORPION. J Chem Theory Comput. 2012;9:803–813. doi: 10.1021/ct300943w. [DOI] [PubMed] [Google Scholar]
  47. Monks CRF, Freiberg BA, Kupfer H, Sciaky N, Kupfer A. Three-dimensional segregation of supramolecular activation clusters in T cells. Nature. 1998;395:82–86. doi: 10.1038/25764. [DOI] [PubMed] [Google Scholar]
  48. Grakoui A, Bromley SK, Sumen C, Davis MM, Shaw AS, Allen PM, Dustin ML. The immunological synapse: a molecular machine controlling T cell activation. Science. 1999;285:221–227. doi: 10.1126/science.285.5425.221. [DOI] [PubMed] [Google Scholar]
  49. Huppa JB, Davis MM. T-cell-antigen recognition and the immunological synapse. Nature Rev Immunol. 2003;3:973–983. doi: 10.1038/nri1245. [DOI] [PubMed] [Google Scholar]
  50. Dustin ML. The cellular context of T cell signaling. Immunity. 2009;30:482–492. doi: 10.1016/j.immuni.2009.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Yang X, Hou D, Jiang W, Zhang C. Intercellular protein-protein interactions at synapses. Protein Cell. 2014;5:420–444. doi: 10.1007/s13238-014-0054-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Cebecauer M, Spitaler M, Serge A, Magee AI. Signalling complexes and clusters: functional advantages and methodological hurdles. J Cell Sci. 2010;123:309–320. doi: 10.1242/jcs.061739. [DOI] [PubMed] [Google Scholar]
  53. Hartman NC, Groves JT. Signaling clusters in the cell membrane. Curr Opin Cell Biol. 2011;23:370–376. doi: 10.1016/j.ceb.2011.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Hashimoto-Tane A, Yokosuka T, Ishihara C, Sakuma M, Kobayashi W, Saito T. T-cell receptor microclusters critical for T-cell activation are formed independently of lipid raft clustering. Mol Cell Biol. 2010;30:3421–3429. doi: 10.1128/MCB.00160-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Bodian DL, Jones EY, Harlos K, Stuart DI, Davis SJ. Crystal structure of the extracellular region of the human cell adhesion molecule CD2 at 2.5 A resolution. Structure. 1994;2:755–766. doi: 10.1016/s0969-2126(94)00076-x. [DOI] [PubMed] [Google Scholar]
  56. Ikemizu S, Sparks LM, van der Merwe PA, Harlos K, Stuart DI, Jones EY, Davis SJ. Crystal structure of the CD2-binding domain of CD58 (lymphocyte function-associated antigen 3) at 1.8-A resolution. Proc Natl Acad Sci USA. 1999;96:4289–4294. doi: 10.1073/pnas.96.8.4289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Wang JH, Smolyar A, Tan K, Liu JH, Kim M, Sun ZY, Wagner G, Reinherz EL. Structure of a heterophilic adhesion complex between the human CD2 and CD58 (LFA-3) counterreceptors. Cell. 1999;97:791–803. doi: 10.1016/s0092-8674(00)80790-4. [DOI] [PubMed] [Google Scholar]
  58. Dustin ML, Chakraborty AK, Shaw AS. Understanding the structure and function of the immunological synapse. Cold Spring Harb Perspect Biol. 2010;2:a002311. doi: 10.1101/cshperspect.a002311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Hess B, Kutzner C. Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. van der Spoel. [DOI] [PubMed] [Google Scholar]
  60. Aragon S, Hahn DK. Precise boundary element computation of protein transport properties: diffusion tensors, specific volume, and hydration. Biophys J. 2006;91:1591–1603. doi: 10.1529/biophysj.105.078188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Onuchic JN, Wolynes PG. Theory of protein folding. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
  62. Bahar I, Kaplan M, Jernigan RL. Short-range conformational energies, secondary structure propensities, and recognition of correct sequence-structure matches. Proteins. 1997;29:292–308. doi: 10.1002/(sici)1097-0134(199711)29:3<292::aid-prot4>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES