Abstract
Patient-specific modeling of ventricular electrophysiology requires an interpolated reconstruction of the 3-dimensional (3D) geometry of the patient ventricles from the low-resolution (Lo-res) clinical images. The goal of this study was to implement a processing pipeline for obtaining the interpolated reconstruction, and thoroughly evaluate the efficacy of this pipeline in comparison with alternative methods. The pipeline implemented here involves contouring the epi- and endocardial boundaries in Lo-res images, interpolating the contours using the variational implicit functions method, and merging the interpolation results to obtain the ventricular reconstruction. Five alternative interpolation methods, namely linear, cubic spline, spherical harmonics, cylindrical harmonics, and shape-based interpolation were implemented for comparison. In the thorough evaluation of the processing pipeline, Hi-res magnetic resonance (MR), computed tomography (CT), and diffusion tensor (DT) MR images from numerous hearts were used. Reconstructions obtained from the Hi-res images were compared with the reconstructions computed by each of the interpolation methods from a sparse sample of the Hi-res contours, which mimicked Lo-res clinical images. Qualitative and quantitative comparison of these ventricular geometry reconstructions showed that the variational implicit functions approach performed better than others. Additionally, the outcomes of electrophysiological simulations (sinus rhythm activation maps and pseudo-ECGs) conducted using models based on the various reconstructions were compared. These electrophysiological simulations demonstrated that our implementation of the variational implicit functions-based method had the best accuracy.
Keywords: cardiac ventricular geometry reconstruction, variational implicit functions, interpolation, validation, cardiac electrophysiology
1. Introduction
State-of-the-art computer models of the heart are being used to study a wide range of phenomena in cardiac electrophysiology and electromechanics (for a recent review, see (Trayanova and Boyle 2014)). Currently, the heart is one of the most advanced “virtual organs” among computational models of various physiological systems (Trayanova 2011, 2014, Winslow et al. 2012). Recent years have witnessed the emergence of image-based models of the heart that incorporate representations of cardiac anatomy with unprecedented detail (Vadakkumpadan et al. 2010, Bishop et al. 2010, Moreno et al. 2011, Boyle et al. 2013, Hu et al. 2013a, McDowell et al. 2013, Rantner et al. 2013a, 2013b). These detailed models incorporate information on cardiac geometry, tissue heterogeneity, and muscle fiber orientation. Structural detail is acquired using Hi-res ex vivo imaging techniques, such as ex vivo diffusion tensor magnetic resonance imaging (DTMRI) and ex vivo late-gadolinium enhanced (LGE) MRI. Such ex vivo models are being applied in basic research to uncover specific mechanisms of heart dysfunction in diseases such as myocardial infarction and heart failure. For example, Arevalo et al. (Arevalo et al. 2013) employed Hi-res electrophysiological models of infarcted canine ventricles reconstructed from ex vivo imaging data that represented infarct scar and border (peri-infarct) zone to examine the role of border zone extent in arrhythmogenesis. This study established that ventricular tachycardia (VT) maintenance requires a minimum volume of remodeled but viable tissue, and that the organizing center of infarct-related VT is located within the border zone. This finding could have major clinical impact in the development of new approaches for determining the ablation target of infarct-related VT, which is the most frequent clinical ventricular arrhythmia (Stevenson et al. 1985). In other studies, a correspondence between in vivo electroanatomical and in silico voltage maps was demonstrated by Pop et al. (Pop et al. 2011) by using a model of infarcted pig ventricles reconstructed from ex vivo MRI and DTMRI data. Their simulations in two infarcted hearts successfully predicted the VT-inducibility consistent with the in vivo electrophysiological studies. Ng et al. (Ng et al. 2012) also demonstrated the feasibility of using simulations, with a model of the pig left ventricles (LV) reconstructed from high-resolution in vivo MRI data, to predict VT circuits.
The emerging field of patient-specific cardiac modeling seeks to translate the above advancements into the clinical arena. In a recent study by Ashikaga et al. (Ashikaga et al. 2013), finite element meshes of hearts from LGE MR images were created for computer simulation to non-invasively predict the VT circuits and to examine the targets for ablation of infarct-related VT. This study demonstrated that in silico prediction of the optimal ablation targets could result in much smaller lesion than those executed in the clinic. Relan et al. (Relan et al. 2011) applied a personalization framework to a clinical dataset derived from a hybrid X-ray/MRI and non-contact mapping procedure on a patient with heart failure. The results of simulations using the personalized model demonstrated that it could successfully be used to predict the induction of infarct-related VT from sites not accessible in the clinic. Vadakkumpadan et al. (Vadakkumpadan et al. 2013a) developed MRI-based heart models from 20 patients with ischemic cardiomyopathy to simulate VT inducibility. The successful prediction of arrhythmia risk may provide an opportunity to noninvasively predict the risk of sudden cardiac death in patients.
Eventually, physicians may be able to utilize the simulation tools for diagnosis and guidance of therapies in a patient-specific manner. To this end however, an interpolated three-dimensional (3D) reconstruction of the patient ventricular geometry with accurate representation of the myocardial surfaces is crucial. Specifically, electrophysiological studies have demonstrated that an edge length of 250–400 μm is needed in the finite element models to resolve wave front propagation (Plank et al. 2008, Gurev et al. 2011). However, due to limitations such as those associated with image acquisition time and patient discomfort, clinical cardiac magnetic resonance (CMR) cannot currently fulfill the resolution requirement. An inter-slice spacing of about 7 mm is the norm in routine clinical LGE-CMR and Cine MR. Although isotropic sub-millimeter whole-heart coronary MRI techniques have been developed (Akçakaya et al. 2014), these techniques use acceleration rates beyond what is available clinically. Therefore, the myocardial boundaries obtained from a clinical MR image need to be interpolated to obtain a 3D cardiac geometry reconstruction, the first step in the image-based patient-specific cardiac model generation.
Methods that combine such a reconstruction with automatic segmentation of ventricular boundaries were reviewed by Petitjean and Dacher (Petitjean and Dacher 2011). Among these methods, the atlas-based approach can reconstruct a Hi-res ventricular geometry from Lo-res cardiac images, provided that a Hi-res atlas or template is available. For example, Lamata et al. (Lamata et al. 2014) developed an atlas-based platform for the personalization of ventricular cardiac meshes. However, the method used was highly dependent on the accuracy of registration between the atlas mesh and the patient images. Notably, recent study by Paiement et al. (Paiement et al. 2014) summarized the approaches for 3D modeling from sparse medical data. They also proposed a method to integrate segmentation and interpolation into a level set framework which uses the radial basis function interpolation. While these studies have focused on automatic cardiac segmentation, manual contouring is the standard for derivation of important clinical indices such as ventricular mass and volume, and is the ground truth in the validation of automatic segmentation methods (Grosgeorge et al. 2011). Indeed, efforts to reconstruct the ventricular geometry based on manual delineation of myocardial boundaries have been undertaken for patient-specific modeling. Specifically, Mansi et al. developed a software tool to reconstruct ventricular geometry based on manual landmarking and variational implicit functions interpolation, for patient-specific simulations of pulmonary valve replacement interventions (Mansi et al. 2009). Image-based patient-specific cardiac modeling studies referred to earlier (Relan et al. 2011, Ashikaga et al. 2013, Vadakkumpadan et al. 2013a) also used a combination of manual contouring and various interpolation methods for ventricular geometry reconstruction methods. However, a thorough evaluation of reconstruction methodologies which rely on manual segmentation has not been undertaken. A study that sought to evaluate the reconstruction methodology within the software tool developed by Mansi et al. was recently conducted by Ringenberg et al. (Ringenberg et al. 2014). This validation study, however, did not examine the effect of reconstruction errors on the outcomes of simulations of cardiac electrophysiology, or of any other function of the heart. Ringenberg et al. also did not compare the variational implicit functions interpolation strategy with alternatives, or include any in vivo scans, where the shape of the heart is markedly different than in ex vivo scans.
The goal of this study is to develop and extensively evaluate a processing pipeline for obtaining an interpolated 3D reconstruction of patient ventricular geometry from low-resolution (Lo-res) clinical images. The implemented pipeline involves contouring of the epi- and endocardial boundaries of the ventricles, interpolation of the contours using the variational implicit functions method, and then merging of the interpolation results to obtain a reconstruction. To evaluate our method, we compared the reconstructed ventricular geometry to that obtained by manually segmenting Hi-res images of the same ventricles. Numerous Hi-res ex vivo and in vivo cardiac computed tomography (CT), MR, and DTMR images of pigs, canines, and humans were used. Lo-res data of the same ventricles were generated by sparsely sampling the manual contours. The performance of our approach based on variational implicit functions was compared to five other interpolation methods previously used in cardiac reconstruction, namely those based on linear, cubic spline, spherical harmonics, cylindrical harmonics, and shape-based. In all cases, performance comparisons involved similarity metrics based on ventricular geometry. Finally, the accuracy of the reconstructions was evaluated in terms of the outcomes of electrophysiological simulations at clinically observable levels, including pseudo-ECGs.
2. Methods
2.1. Hi-res Image Data
A total of 15 Hi-res cardiac images of normal and diseased hearts were made available to us for this study, as described in Table 1. The datasets included those of 1 normal canine heart ex vivo, 4 failing canine hearts ex vivo, 3 infarcted canine hearts ex vivo, 4 infarcted pig hearts in vivo, and 3 human hearts in vivo. These datasets encompass heart conditions that would most likely be encountered in patient-specific modeling. The Hi-res in vivo datasets were included in this study to increase the diversity of input data. Note that, compared to ex vivo images, the shape of the heart in in vivo scans is different due to spatial constraints imposed by the nearby organs.
Table 1.
Images used in this study.
| Dataset | Description | Image Size (pixels) | Image Resolution (mm) |
|---|---|---|---|
| Dog 1 | ex vivo CMR (Normal) | 256 × 256 × 130 | 0.31 × 0.31 × 0.80 |
| Dog 2 | ex vivo CMR (Heart Failure) | 256 × 256 × 130 | 0.31 × 0.31 × 0.80 |
| Dog 3 | ex vivo CMR (Heart Failure) | 256 × 256 × 136 | 0.31 × 0.31 × 0.85 |
| Dog 4 | ex vivo CMR (Heart Failure) | 256 × 256 × 74 | 0.31 × 0.31 × 0.80 |
| Dog 5 | ex vivo CMR (Heart Failure) | 704 × 704 × 520 | 0.25 × 0.25 × 0.25 |
| Dog 6 | ex vivo CMR (Infarcted) | 400 × 400 × 480 | 0.25 × 0.25 × 0.25 |
| Dog 7 | ex vivo CMR (Infarcted) | 480 × 480 × 480 | 0.25 × 0.25 × 0.25 |
| Dog 8 | ex vivo CMR (Infarcted) | 448 × 448 × 560 | 0.25 × 0.25 × 0.25 |
| Pig 1 | in vivo CMR (Infarcted) | 336 × 336 × 60 | 0.74 × 0.74 × 1.50 |
| Pig 2 | in vivo CMR (Infarcted) | 384 × 384 × 68 | 0.70 × 0.70 × 1.50 |
| Pig 3 | in vivo CMR (Infarcted) | 400 × 400 × 60 | 0.73 × 0.73 × 1.50 |
| Pig 4 | in vivo CMR (Infarcted) | 384 × 384 × 60 | 0.70 × 0.70 × 1.50 |
| Human 1 | in vivo CT (Heart Failure) | 175 × 175 × 83 | 0.63 × 0.63 × 1.00 |
| Human 2 | in vivo CMR (Normal) | 336 × 336 × 40 | 0.95 × 0.95 × 2.50 |
| Human 3 | in vivo CMR (Normal) | 256 × 256 × 16 | 1.37 × 1.37 × 6.00 |
The porcine datasets (Pig 1 – 4) were acquired under a protocol approved by the Institutional Animal Care and Use Committee (IACUC). The mid-left anterior descending coronary artery of a swine was occluded for 120 minutes using a balloon angioplasty catheter to create myocardial infarction (MI). Several months post-infarction, the swine underwent an in vivo imaging session. As a gold standard for infarct imaging, phase sensitive inversion recovery (PSIR) late gadolinium-enhancement imaging was performed in a 3-Tesla clinical MR system (Achieva TX, Philips Healthcare, Best, The Netherlands) (Kellman et al. 2002, Lee et al. 2011). For the canine datasets (Dog 1 – 8) as well as the Human 1 dataset, the acquisitions are described in previous studies (Vadakkumpadan et al. 2012, 2013b). We also used a publicly available human MR dataset (Human 3) from the Auckland MRI Research Group (AMRG 2014). The resolution for each image is described in Table 1. No down-sampling of the original data was done in order to retain all anatomical details.
The epi- and endocardial boundaries of the ventricles in every 2D slice of the Hi-res images were manually contoured by placing a number of landmark points along the boundaries (see Figure 1). The contouring was performed by trained experts at Johns Hopkins University. Cubic splines were then fitted to these points, and the resulting contours were assembled to create the manual ventricular geometry reconstruction, which served as the ground truth. The number of landmark points was the same in each slice of a given image. Even though semi/automatic methods could have been used to segment the ex vivo datasets for the ground truth, we did not do so as these methods segment the trabeculae from the Hi-res images, which are not visible in the clinical MR. By excluding the trabeculae, the created ground truths represented the common clinical ventricular geometries, and were appropriate for our comparative study of the patient-specific model generation.
Figure 1. Manual reconstruction of ventricular geometry.
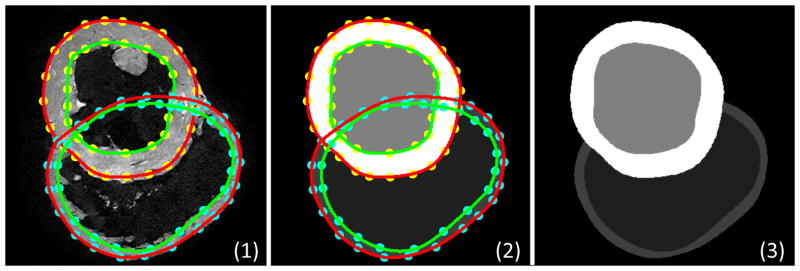
Landmark points were placed manually on the boundaries of the epi- and endocardial LV/RV in the 2D slices (1). 2D splines were fitted to the landmark points for each surface (2). The surfaces were combined to create the reconstruction of the ventricles (3).
2.2. Ventricular Reconstruction using Interpolation Based on Variational Implicit Functions
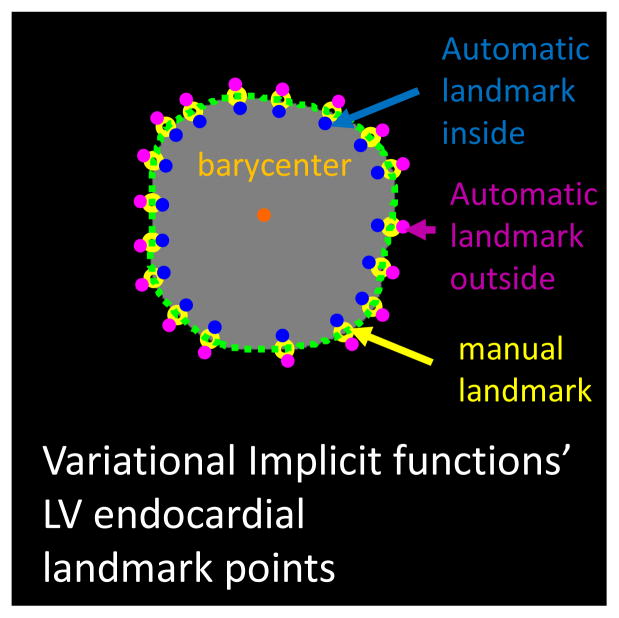
Our method is a modification of the approaches presented by Ringenberg et al. and Mansi et al. (Mansi et al. 2009, Ringenberg et al. 2014) who utilized the so-called variational implicit functions (Turk and O’Brien 1999) to reconstruct patient-specific ventricular geometries from Lo-res clinical images. In brief, to reconstruct a surface from n landmark points cj, j = 1,2, …, n, the variational implicit functions method builds a smooth function f in 3D space such that f = 0 at these landmark points. The interpolation function is expressed as where φ(x) = |x|2 log(|x|) is the radial basis function, P(x) is a 1-degree polynomial that accounts for the linear and constant portions of f(x), and dj are the weights to be computed. The weights dj are calculated by solving the linear system: where φij = φ(ci − cj), and i, j = 1,2, …, n. Additional landmark points inside the surface where the function values are set to positive or h > 0 are also required. For this, we calculated the barycenter of the landmark points in each slice using the formula , where s was the number of landmark points in the slice (see Figure 2 for the LV endocardium). The points located 1% of the way from each landmark point to the barycenter were automatically added as the points where f > 0 (see Figure 2). Similarly, the points located 1% from each landmark points away from the barycenter were automatically added right outside the surface as the points with f < 0. We performed the reconstruction separately for the epi- and endocardial left and right ventricles (LV/RV) and then merged the results to create the full ventricular geometry. Compared to the approach by Mansi et al. (Mansi et al. 2009), we automatically detected the landmark points inside and outside of each contour, rather than manually placing those points. In contrast with the technique by Ringenberg et al. (Ringenberg et al. 2014), we did not contour the same part of myocardial boundary more than once. Accordingly, we did not require the application of morphological operations to remove any erroneous pixel artifacts at the edges of the segmented regions as Ringenberg et al. described in their study. Also, we used the radial basis function |x|2 log(x) in our implementation of the variational implicit functions method, as our initial experiments showed that this radial basis function delivered slightly more accurate reconstructions than alternatives such as |x| or |x|3. One possible reason is that the level of smoothness in ventricular surfaces is best captured by the radial basis function |x|2 log(x).
Figure 2. Automatic addition of landmark points for the variational implicit functions method.
We automatically added several landmark points inside (blue) and outside (purple) based on their distance to the barycenter (orange) for each surface (epi- and endocarial LV/RV).
In this study, for all datasets, the contours of Lo-res images to use with automatic interpolation methods were mimicked, by selecting sparse samples of contours drawn on the Hires images described above. Assessment of the accuracy of reconstructions was performed by comparing the reconstructed ventricular geometry to the ground truth geometry of the same ventricles.
2.3 Alternative Ventricular Geometry Reconstruction Methods
The performance of our modified variational implicit functions method was also compared to five other interpolation methods previously used in Lo-res cardiac reconstruction, namely those based on linear, cubic spline, spherical harmonics, cylindrical harmonics, and shape-based. These are briefly described below.
2.3.1 Linear and Cubic Splines Interpolation
In the linear interpolation method, from two adjacent slices l and k containing corresponding landmark points xk and xl, we calculated xm = xl + ((m − l)/(k − l))(xk − xl) for the slices m = l, l + k, …, k − l, k, where xm is a landmark point of a slice that lied in between the two slices (Vadakkumpadan et al. 2010). The in-plane boundary contour for slice m was computed by joining the landmark points xm with straight lines. In the cubic spline reconstruction method, a cubic spline was used to find xm between xk and xl and then a cubic spline interpolation was applied in each slice to reconstruct the in-plane boundary contour. In order to incorporate an anatomically meaningful reconstruction of the apical region into the linear and cubic reconstruction methods, the location of the tip of the apex for the epicardium was automatically estimated, and an additional landmark point was placed at this location. More precisely, the in-plane coordinates of this additional landmark point were the same as those of the barycenter of the epicardial contour in the most apical slice. The out-of-plane coordinate was calculated such that the distance between the landmark point and the most apical slice was the same as the slice thickness of the Lo-res images.
2.3.2 Spherical and Cylindrical Harmonics Interpolation
In the spherical and cylindrical surface harmonics methods, the interpolation function is a linear combination of surface harmonics (Matheny and Goldgof 1995, Hopenfeld 2004). Harmonics functions are the solutions of Laplace’s equation. The landmark points were expressed in spherical and circular cylindrical coordinates, and the coefficients of the surface harmonics were calculated by fitting the solution of Laplace’s equation to all landmark points. More details are provided in the Appendix.
2.3.3 Shape-Based Interpolation
The shape-based interpolation method we implemented was originally proposed by Raya and Udupa (Raya and Udupa 1990). Brieftly, a cubic spline was fit to the landmark points in each slice, and the pixels inside the curve were marked to create a binary image slice. The binary image slice was then converted into a grayscale image by computing the 2D signed distance transform. Next, the stack of grayscale image slices was linearly interpolated, and an isosurface was extracted from the interpolated image. More details are given in the Appendix section. As in the linear and cubic spline interpolation methods, the location of the apex was estimated to ensure that the apical region was meaningfully reconstructed (see Section 2.3.1). Specifically, we added, to the apical end of the stack of binary image slices for the epicardium, a slice that contained a one pixel region at the estimated location of the apex.
2.4. Performance Evaluation of the Ventricular Geometry Reconstructions
Our pipeline for performance evaluation of the ventricular geometry reconstructions is illustrated in Figure 3. The acquired Hi-res images were used as input to the pipeline, with every slice of these images contoured, to reconstruct the ground truth ventricular geometry. To mimic the sparseness of a clinical CMR image (Lo-res), 7 to 9 evenly distributed contours were selected from each Hi-res image. Six ventricular geometry reconstruction methods, the one developed here, plus 5 others, linear, cubic spline, spherical harmonics, cylindrical harmonics and shape-based method, were used to reconstruct ventricular geometries from each Lo-res dataset. The reconstruction results obtained with our variational implicit functions method were compared to the ground truth, as well as to those obtained with the other interpolation methods.
Figure 3. Pipeline for performance evaluation of the different ventricular geometry reconstructions.
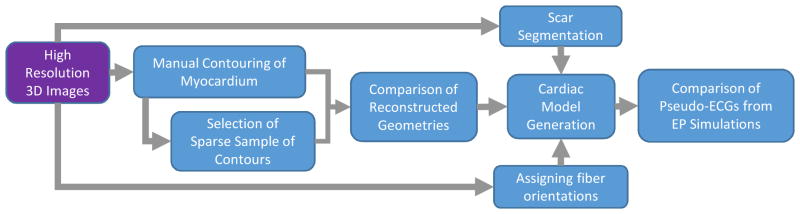
Hi-res images were used as the input in the pipeline. First, manual contouring was done on the Hi-res images for the construction of the ground truth ventricular geometry. A sparse selection of manual contours was then created as the input for the Lo-res interpolation approaches, both our method, and the 5 alternative ones. Comparisons of reconstructed geometries were then performed. Final evaluation performance was done in terms of outcome of electrophysiological simulations with geometries reconstructed with each interpolation method. This required constructing an electrophysiological model of the ventricles (including infarction remodeling, if any, and fiber orientation).
For each dataset in Table 1, we quantitatively evaluated the reconstruction methods using similarity criteria. The first quantitative measure was the Dice Similarity Coefficient (DSC) (Zou et al. 2004), which measures the spatial overlap between two sets of segmentation of the same (ventricular) geometry. It is defined as DSC = 2(Myom ∩ Myoc)/(Myom ∪ Myoc) where Myom and Myoc are the manual (ground truth) and computed (with any of the interpolation methods) ventricular geometry reconstructions. Additionally, we used the Mean Shortest Distance (MSD) metric, which is the mean of the shortest distance from each point in the surface of computed reconstruction to the surface of manual reconstruction.
The metrics of relative errors in LV chamber volume, LV mass, and myocardium mass were also used in the geometry reconstruction evaluations. For relative errors in the LV chamber volume and LV mass, the values calculated from the reconstructed ventricular geometries were compared with the values calculated from the estimates of the Simpson’s rule method, a commonly used method in the clinic, which treats each slice as a volume slab having a given thickness. In the Simpson’s rule method, the LV chamber and LV wall volume for each slice are calculated by multiplying the area of the LV chamber or the LV wall by the slice thickness, and to calculate the LV mass, the LV wall volume is multiplied by the density of myocardium.
Finally, we performed comparisons between results of electrophysiological simulations (Figure 3) conducted with the manually-reconstructed geometry (ground truth geometry), and with each of the computed geometries (using our method as well as the other methods). The aim of this comparison was to assess how sensitive the results of electrophysiological simulations were to the differences in the ventricular geometry reconstructions. Specifically, for each of the dataset in Table 1, we compared pseudo-ECGs (see Section. 2.5) calculated with ventricular models generated from the manual reconstructions and those generated from computed reconstructions. The pseudo-ECG signals were normalized so that the signal values lay within the interval [0,1]. This normalization was done to focus the evaluation on the morphology of the ECG, as opposed to actual signal values. The metrics that we used to compare normalized pseudo-ECGs were the root mean square error (RMSE), the relative error (RE), the maximum cross-correlation (MCC) = |(xm * xc)(xl)| where τ = arg maxi |(xm * xc)(i)|, and the mean absolute deviation (MAD)
where xm(i), xc(i) are the pseudo-ECGs computed from the simulation using the manual and computed reconstructions at time point i, respectively, for each dataset, and t is the signal length.
2.5 Cardiac Electrophysiological Modeling Methods and Simulations
First, for the hearts that had ischemic cardiomyopathy (the datasets Dog 6, Dog 7, Dog 8, Pig 1, Pig 2, Pig 3 and Pig 4), the infarct zones were extracted semi-automatically using an interactive level-set segmentation method (CIBC 2014). The labeling of the border zone and the infarct core zone (scar) was done by employing the full-width half-maximum algorithm (Vadakkumpadan et al. 2013b). The infarct zone reconstructions were combined with the corresponding ventricular geometry reconstructions. Then, for each dataset and each ventricular geometry reconstruction method, a volumetric mesh of the reconstructed ventricles was first generated, as described elsewhere (Prassl et al. 2009). Fiber orientation data are required to determine the directions of the cardiac electrical propagation in electrophysiological simulations. Accordingly, we acquired DTMR images for 2 of the hearts (Dog 6 and Dog 7), and used these images to assign fiber orientations to each element in the meshes for these hearts as described previously (Vadakkumpadan et al. 2010). For the other hearts, DTMRI data were not available; fiber orientations for the meshes of these hearts were computed by a rule-based algorithm (Bayer et al. 2012).
To evaluate the performance of the various reconstruction methods in terms of outcomes of electrophysiological simulations, sinus rhythm was simulated by replicating activations originating from the Purkinje network. The ventricles were activated at six locations on the endocardium: one on the RV free wall, three on the LV septum and two on the LV free wall as described previously (Gurev et al. 2010, Hu et al. 2013b, 2014). Appropriate timings of the stimuli were chosen such that the resultant 3D electrical propagation matched with experimental data (Durrer et al. 1970, Spach and Barr 1975). Electrophysiology of the healthy myocyte was represented by the ten Tusscher model of human ventricular action potential (Tusscher et al. 2004). In the infarcted heart datasets, to represent the infarct border zone, the ten Tusscher model was modified by incorporating experimentally recorded changes in the sodium (Pu and Boyden 1997) and L-type calcium currents (Dun et al. 2004), as well as in the potassium currents IKr, and IKs (Jiang et al. 2000). Transverse conductivity was also decreased by 90% to represent connexin 43 reorganization (Yao et al. 2003). Scar was modeled as an insulator collagen.
A pseudo-ECG for each simulation was obtained by calculating the difference of extracellular potentials between two points in an isotropic bath surrounding the heart. The two points were placed near the apex or the base of the heart separated by 18 cm (Vadakkumpadan et al. 2010). The electrophysiological simulations were performed using the software package CARP (CardioSolv, LLC) with the numerical methods described by Vigmond et al. (Vigmond et al. 2002). Previous studies by Rodríguez et al., Bishop et al. and Rantner et al. (Rodríguez et al. 2005, Bishop et al. 2007, Rantner et al. 2012), have validated that the electrophysiological simulations using this methodology in rabbit hearts matched the experiments conducted using optical imaging.
3. Results
3.1 Accuracy of the 3D Ventricular Geometry Reconstructions
Figure 4 shows the reconstructions of the ventricular geometry for the Dog 6 dataset, which was chosen as a good representative sample that illustrates the differences in quality between the various interpolation methodologies and the manual reconstruction (ground truth). All interpolation methods except the linear generated smooth ventricular surfaces. Interpolation artifacts are apparent as surface roughness in the shape-based interpolation. Since cylindrical harmonics method assumes that there is a periodic condition along the long-axis direction, this method did not produce physiologically meaningful reconstructions (see Figure 4).
Figure 4. Ventricular geometry reconstructions for the Dog 6 dataset.

Smooth surfaces were generated by all methods except the linear, and the shape-based. The cylindrical harmonics method reconstructed holes in the RV wall. The cylindrical harmonics method did not generate physiologically meaningful ventricular geometry.
The results of quantitative evaluation of the reconstruction methods using various geometry-based metrics are shown in Table 2. The method based on variational implicit functions generated the best overall reconstruction. It had the highest DSC, smallest MSD, and also the smallest RE on the LV chamber, LV mass, and myocardium mass. The LV chamber volume estimates for our method, and for the spherical harmonics method were the only ones not significantly different from those of the manual reconstructions (p>0.05). Cubic spline, spherical harmonics and our method provided better estimations of LV chamber volume than the clinically used Simpson’s rule. In terms of the LV mass, the cylindrical harmonics, the spherical harmonics, and our method generated better estimations than the Simpson’s rule. Even though the spherical harmonics method had the second best performance, we observed that increasing the cut-off parameter L led to the anatomically incorrect ventricular reconstructions, as illustrated in Figure 5. Our investigation revealed that, at larger values of L, a highly concave region appears at the apex of the reconstructed LV epicardium. A hole is formed when the part of this concave region falls inside the endocardial surface.
Table 2.
Quantitative evaluation of the reconstruction methods.
| Method | DSC | MSD (mm) | Relative Error (RE) | ||
|---|---|---|---|---|---|
| LV Chamber Volume (%) | LV Mass (%) | Myocardial Mass (%) | |||
|
| |||||
| 1 Linear | 0.85±0.06 | 2.46±1.58 | 9.1±5.0 | 11.5 ±8.2 | 9.2±6.9 |
| 2 Cubic Spline | 0.87±0.06 | 2.13±1.60 | 5.5±5.6 | 7.4±7.4 | 5.8±6.6 |
| 3 Variational Implicit | 0.91±0.04 | 1.05±0.70 | 1.1±1.3 | 3.0±3.8 | 2.3±2.5 |
| 4 Cylindrical Harmonics | 0.46±0.08 | 5.21±1.66 | 9.2±6.4 | 4.6±4.2 | 10.1±7.4 |
| 5 Spherical Harmonics | 0.87±0.04 | 1.49±0.92 | 1.3±1.5 | 4.4±4.9 | 3.5±3.6 |
| 6 Shape-Based | 0.86±0.06 | 2.68 ±1.78 | 9.3±5.8 | 8.1±6.9 | 6.5±5.1 |
| 7 Simpson’s Rule | - | - | 7.6±3.7 | 7.2±4.4 | - |
Figure 5. The effect of increasing spherical harmonics cut-off degree L on ventricular geometry for the Dog 6 dataset.

Increasing the cut-off degree parameter from 4 (optimal value we picked based on empirical observation) to 5 and 6, results in the anatomically-incorrect ventricular reconstruction. A hole appears at the apex of the LV when L =6 is used.
3.2 Electrophysiological Simulation Results Comparisons
Only the variational implicit function method and the spherical harmonics method, the second-best method in our evaluations of the reconstructions with geometry-based metrics (please see Section 3.1), were included in the comparison of outcomes of electrophysiological simulations. We excluded the human and pig hearts from simulations since the original images, and accordingly the manual reconstructions of these hearts, had an out-of-plane resolution above 1 mm, which is too low for resolving electrophysiological phenomena. Thus, given 3 reconstruction methods (manual, our method outlined here, spherical harmonics), and 8 hearts, we conducted a total of 24 sets of electrophysiological simulations.
As an example, Figure 6 shows results of simulations for Dog 6. The sinus rhythm activation time maps in the Dog 6 model generated with different geometry reconstruction methods were visually similar (see Figure 6). It is also evident that the pseudo-ECG corresponding to the heart geometry generated by our implementation of the variational implicit functions method (blue) was the closest to the one corresponding to the manual reconstruction (black). Table 3 and 4 show that our implementation of the variational implicit functions method outperformed the others. Overall, the proposed technique resulted in the smallest RMSE, smallest RE, highest MCC, and also the smallest MAD. We observed significant differences in Table 3, with the variational implicit method showing 31%, 31%, and 26% improvement in the means of RMSE, MAD and RE, respectively, over the spherical harmonics method. These results suggest that, in comparison with alternative methods, the variational implicit method developed here is more accurate in generating interpolated 3D ventricular geometry reconstructions from Lo-res clinical images. Our observations also suggest that relatively small global differences in geometry (see Table 2) have significant effects on outcomes of electrophysiological simulations (see Tables 3 and 4).
Figure 6. Electrophysiological simulation results for the Dog 6.
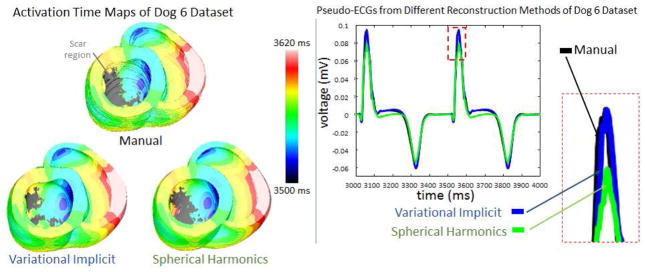
Sinus rhythm activation time maps are shown along with the pseudo-ECGs measured near the apex, for the different reconstruction methods. Using the pseudo-ECG, the difference between reconstruction methods was quantified.
Table 3.
Performance evaluation of various reconstruction methods based on simulations results of the pseudo-ECG measured near the apex.
| Method | RMSE (mV) | RE (%) | MCC (%) | MAD (%) |
|---|---|---|---|---|
|
| ||||
| 1 Variational Implicit | 0.0284±0.0441 | 4.73±5.43 | 99.83±0.38 | 6.51±9.96 |
| 2 Spherical Harmonics | 0.0410±0.0510 | 6.87±6.04 | 99.77±0.42 | 8.82±8.77 |
Table 4.
Performance evaluation of various reconstruction methods based on simulations results of the pseudo-ECG measured near the base
| Method | RMSE (mV) | RE (%) | MCC (%) | MAD (%) |
|---|---|---|---|---|
|
| ||||
| 1 Variational Implicit | 0.0178±0.0156 | 3.48±1.83 | 99.95±0.04 | 4.29±3.42 |
| 2 Spherical Harmonics | 0.0326±0.0317 | 6.30±4.07 | 99.85±0.16 | 7.56±5.79 |
4. Discussion and Conclusion
The objective of this study was to implement a processing pipeline that utilizes the variational implicit functions method for obtaining an interpolated 3D reconstruction of ventricular geometry from Lo-res clinical images, and to thoroughly evaluate the efficacy of this pipeline in comparison with alternatives. This evaluation is crucial for advancing clinical applications of patient-specific simulations, and the lack of such evaluation has been a major stumbling block in ventricular model construction for clinical applications. Addressing this need is the main contribution of this study. The comparison of the automatically reconstructed ventricular geometries generated by the various methods showed that our implementation of the variational implicit functions-based method had the best accuracy. Though the current study was focused on patient-specific cardiac modeling, our method based on variational implicit would also allow more accurate estimations of other important image-based metrics such as myocardial mass, LV chamber volume, and consequently LV ejection fraction, which are proven to be predictive of clinical outcomes.
Our evaluation showed that the spherical harmonics method performed the second best after the variational implicit functions method, in terms of the various geometry-based error metrics. However, the spherical harmonics method generated increasingly anatomically-incorrect ventricular reconstructions as the cut-off degree L parameter was increased (see Figure 5). The poor performance of the linear, cubic splines and shape-based methods was mostly due to the inaccuracy of reconstruction in the apical area. Interestingly, the cylindrical harmonics method estimated the LV mass relatively well, although it did not reconstruct meaningful ventricular geometries. Note that the variational implicit scheme that we have implemented generates a noticeable notch at the LV/RV junction. We believe that this is realistic as this notch is also observed in high resolution ex vivo data (Vadakkumpadan et al. 2010, Deng et al. 2012).
Ideally, experimental electrophysiological data should serve as the ground truth for comparing outcomes of simulations. However, such data were not available for this study, and overall, are not routinely available together with imaging data. Under this limitation, we resorted to an alternative, i.e, performing comparisons between the outcomes of electrophysiological simulations with automatic reconstruction and those with manual reconstructions. While this approach was an indirect way of evaluating outcomes of simulations with automatic reconstructions, it was the best alternative available to us, considering that the contours for the manual reconstructions were drawn by experts, and the electrophysiological simulation methodologies we used have been shown to match experimental recordings in previous studies (see Section 2.5). Note that, though the accuracies of reconstructions were evaluated with volume and geometry-based metrics (see Section 3.1), the comparison of simulation outcomes was an important part of this study, as the degree of sensitivity of the results of electrophysiological simulations to differences in ventricular geometry reconstructions was unknown. We found that relatively small global differences in ventricular geometry reconstructions can lead to significant differences in sinus rhythm pseudo-ECGs, and this underscores the need for accurate reconstruction methods in patient-specific modeling of ventricular function.
A limitation of the current study is in the use of one specific ground truth reconstruction of each heart for the evaluation, without explicitly considering any inter-subject variability in contouring. However, we believe that our conclusions are still valid, since not all datasets were contoured by the same experts, and so the variability in contouring was introduced into our analysis. The variational implicit functions reconstruction method consistently outperformed the other methods, regardless of who did the contouring. Another limitation of our study is in the exclusion of papillary muscles in the models. The reason for excluding papillary muscles was that current clinical Lo-res cardiac MR images only show partial (mostly basal) part of the papillary muscles which are connected to the endocardium. The exclusion of papillary muscles, however, has not posed a limitation thus far for patient-specific simulations since such models have been predominantly used to simulate infarct-related ventricular tachycardia, as in the study by Ashikaga et al. (Ashikaga et al. 2013). Also, the 2D manual contouring scheme brings out the details on the surface. This, combined with the fact that no constraint was applied to ensure a smooth transition of contours between adjacent slices, made the manual reconstructions less smooth. However, the manual contours do reflect experts’ observations and thus, the reconstructed surface is not far from the expected smooth surface. Furthermore, Swenson et al. (Swenson et al. 2013) demonstrated that such surface irregularities do not significantly affect the results of cardiac electrical simulations. Specifically, they compared electrical propagation simulated in non-conformal (jagged surfaces) and conformal (smooth surfaces) meshes. They found that, while local voltage patterns were affected by the mesh type, the overall electrical potential root mean squared errors was small. Finally, we mimicked the contouring of Lo-res clinical images by choosing a subset of contours drawn on the Hi-res images. The level of realism in our derivation of contours of clinical images is limited, as the contours were not directly drawn on images of clinical resolution and quality, where boundaries are difficult to delineate. Additionally, since our experts drew the contours on Hi-res images, for each contour, they had access to the contours of immediately adjacent slices, which is not the case when dealing with clinical images only. Ideally, each slice of the Lo-res clinical images should be mimicked by averaging multiple slices from the Hi-res dataset, and the contours of the Lo-res images should be generated by drawing on the averaged slices. However, this would have required additional contouring instead of utilizing the contours we obtained for the Hi-res dataset. Our experimental setup was a trade-off between accuracy in the mimicking of the contours of clinical images, and the amount of manual labor required.
Acknowledgments
This study was supported by the National Institutes of Health (NIH) Director’s Pioneer Award (DP1HL123271), NIH Grant R01-HL103428, and National Science Foundation Grant CBET- 0933029 to NAT, as well as by the American Heart Association grant 13SDG14510061 and WW Smith Charitable Trust Heart Research grant H1202 to FV.
Appendix
Spherical and Cylindrical Harmonics
For spherical harmonics, the model which represents the surfaces in spherical coordinate is r = r(θ, Ø), where for each pair of angles θ and Ø, the radial coordinate r is unique. Up to a specified cut-off, the linear combination of spherical harmonics that represents the surfaces is
where L is the cut-off degree. Features of higher spatial frequency can be better captured by increasing the cut-off degree. Pl and are Legendre polynomials, where l and m are separation constants. The coefficient parameters and are computed by fitting the model to the 3D data.
The model in circular cylindrical coordinates is ρ(z, Ø), where ρ, z, and Ø are the radial coordinate, polar angle and height, respectively. The general surface representation of the cylindrical harmonics is
where z̃ represents the period along the z axis of the solution to Laplace’s equation. Alm, Blm, Clm, and Dlm are the coefficient parameters which are found by fitting the model to the scattered 3D data, where l and m are separation constants.
Shape-based Interpolation
In shape-based interpolation, the notion of univariate data interpolation is generalized to achieve high-order interpolation between cross section of a 3D body of general topology (Raya and Udupa 1990). In our case, the set of parallel cross sections C1, C2, ···, Ck of a ventricular surface O are region contained within the in-plane boundary contours created by applying cubic spline interpolation to the landmark points in each slice z1, z2, ···, zk of the sparse sample of the manual contours. The interpolation problem is to estimate new cross sections at . To solve this, first the problem is converted into univariate interpolation problem to determine if for some fixed real number x, y and some integer j ∈ {1,2, ···, m}. This univariate interpolation problem is solved by calculating the signed distance transform di at each (x, y, zi) based on the boundary of Ci for 1 ≤ i ≤ k, where di > 0 if (x, y, zi) ∈ Ci, di < 0 if (x, y, zi) ∈ C̄l, the complement of Ci, and 0 if (x, y, zi) is a boundary point of Ci. A univariate function f is then computed by linearly interpolating d1, d2, ···, dk. The final reconstructed surface is an isosurface of the new cross section created by considering (x, y, ) to belong to if .
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akçakaya M, Basha TA, Chan RH, Manning WJ, Nezafat R. Accelerated isotropic sub-millimeter whole-heart coronary MRI: Compressed sensing versus parallel imaging. Magnetic Resonance in Medicine. 2014;71:815–822. doi: 10.1002/mrm.24683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- AMRG. The Cardiac Atlas. 2014 Download from: http://atlas.scmr.org/download.html.
- Arevalo H, Plank G, Helm P, Halperin H, Trayanova N. Tachycardia in Post-Infarction Hearts: Insights from 3D Image-Based Ventricular Models. PLoS ONE. 2013;8:e68872. doi: 10.1371/journal.pone.0068872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashikaga H, Arevalo H, Vadakkumpadan F, RCB, Bayer JD, Nazarian S, Zviman MM, Tandri H, Berger RD, Calkins H, Herzka DA, Trayanova NA, Halperin HR. Feasibility of image-based simulation to estimate ablation target in human ventricular arrhythmia. Heart Rhythm. 2013;10:1109–1116. doi: 10.1016/j.hrthm.2013.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayer JD, Blake RC, Plank G, Trayanova NA. A Novel Rule-Based Algorithm for Assigning Myocardial Fiber Orientation to Computational Heart Models. Annals of Biomedical Engineering. 2012;40:2243–2254. doi: 10.1007/s10439-012-0593-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop MJ, Plank G, Burton RA, Schneider JE, Gavaghan DJ, Grau V, Kohl P. Development of an anatomically detailed MRI-derived rabbit ventricular model and assessment of its impact on simulations of electrophysiological function. American Journal of Physiology Heart and Circulatory Physiology. 2010;298:699–718. doi: 10.1152/ajpheart.00606.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop MJ, Rodriguez B, Qu F, Efimov IR, Gavaghan DJ, Trayanova NA. The Role of Photon Scattering in Optical Signal Distortion during Arrhythmia and Defibrillation. Biophysical Journal. 2007;93:3714–3726. doi: 10.1529/biophysj.107.110981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyle PM, Williams JC, Ambrosi CM, Entcheva E, Trayanova NA. A comprehensive multiscale framework for simulating optogenetics in the heart. Nature Communications. 2013;4:2370. doi: 10.1038/ncomms3370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CIBC. Seg3D: Volumetric Image Segmentation and Visualization. Scientific Computing and Imaging Institute (SCI); 2014. Download from: http://www.seg3d.org. [Google Scholar]
- Deng D, Jiao P, Ye X, Xia L. An Image-Based Model of the Whole Human Heart with Detailed Anatomical Structure and Fiber Orientation. Computational and Mathematical Methods in Medicine. 2012;2012:16. doi: 10.1155/2012/891070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dun W, Baba S, Yagi T, Boyden PA. Dynamic remodeling of K+ and Ca2+ currents in cells that survived in the epicardial border zone of canine healed infarcted heart. American Journal of Physiology - Heart and Circulatory Physiology. 2004;287:H1046–H1054. doi: 10.1152/ajpheart.00082.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrer D, van Dam RT, Freud GE, Janse MJ, Meijler FL, Arzbaecher RC. Total excitation of the isolated human heart. Circulation. 1970;41:899–912. doi: 10.1161/01.cir.41.6.899. [DOI] [PubMed] [Google Scholar]
- Grosgeorge D, Petitjean C, Caudron J, Fares J, Dacher J-N. Automatic cardiac ventricle segmentation in MR images: a validation study. International Journal of Computer Assisted Radiology and Surgery. 2011;6:573–581. doi: 10.1007/s11548-010-0532-6. [DOI] [PubMed] [Google Scholar]
- Gurev V, Constantino J, Rice JJ, Trayanova NA. Distribution of electromechanical delay in the heart: insights from a three-dimensional electromechanical model. Biophysical Journal. 2010;99:745–754. doi: 10.1016/j.bpj.2010.05.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurev V, Lee T, Constantino J, Arevalo H, Trayanova N. Models of cardiac electromechanics based on individual hearts imaging data. Biomechanics and Modeling in Mechanobiology. 2011;10:295–306. doi: 10.1007/s10237-010-0235-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopenfeld B. Spherical harmonic-based finite element meshing scheme for modelling current flow within the heart. Medical and Biological Engineering and Computing. 2004;42:847–851. doi: 10.1007/BF02345219. [DOI] [PubMed] [Google Scholar]
- Hu Y, Gurev V, Constantino J, Bayer JD, Trayanova NA. Effects of Mechano-Electric Feedback on Scroll Wave Stability in Human Ventricular Fibrillation. PLoS ONE. 2013a;8:e60287. doi: 10.1371/journal.pone.0060287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y, Gurev V, Constantino J, Trayanova N. Efficient preloading of the ventricles by a properly timed atrial contraction underlies stroke work improvement in the acute response to cardiac resynchronization therapy. Heart Rhythm. 2013b;10:1800–1806. doi: 10.1016/j.hrthm.2013.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y, Gurev V, Constantino J, Trayanova N. Optimizing cardiac resynchronization therapy to minimize {ATP} consumption heterogeneity throughout the left ventricle: A simulation analysis using a canine heart failure model. Heart Rhythm. 2014;11:1063–1069. doi: 10.1016/j.hrthm.2014.03.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang M, Cabo C, Yao J-A, Boyden PA, Tseng G-N. Delayed rectifier K currents have reduced amplitudes and altered kinetics in myocytes from infarcted canine ventricle. Cardiovascular Research. 2000;48:34–43. doi: 10.1016/s0008-6363(00)00159-0. [DOI] [PubMed] [Google Scholar]
- Kellman P, Arai AE, McVeigh ER, Aletras AH. Phase-sensitive inversion recovery for detecting myocardial infarction using gadolinium-delayed hyperenhancement. Magnetic Resonance in Medicine. 2002;47:372–383. doi: 10.1002/mrm.10051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamata P, Sinclair M, Kerfoot E, Lee A, Crozier A, Blazevic B, Land S, Lewandowski AJ, Barber D, Niederer S, Smith N. An automatic service for the personalization of ventricular cardiac meshes. Journal of The Royal Society Interface. 2014:11. doi: 10.1098/rsif.2013.1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Schar M, Kozerke S, Harouni A, Sena-Weltin V, Zviman MM, Halperin H, McVeigh E, Herzka D. Independent respiratory navigators for improved 3D PSIR imaging of myocardial infarctions. Journal of Cardiovascular Magnetic Resonance. 2011;13:18. [Google Scholar]
- Mansi T, André B, Lynch M, Sermesant M, Delingette H, Boudjemline Y, Ayache N. Virtual Pulmonary Valve Replacement Interventions with a Personalised Cardiac Electromechanical Model. In: Magnenat-Thalmann N, Zhang JJ, Feng DD, editors. Recent Advances in the 3D Physiological Human. Springer; London: 2009. pp. 75–90. [Google Scholar]
- Matheny A, Goldgof DB. The use of three- and four-dimensional surface harmonics for rigid and nonrigid shape recovery and representation. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1995;17:967–981. [Google Scholar]
- McDowell KS, Vadakkumpadan F, Blake R, Blauer J, Plank G, MacLeod RS, Trayanova NA. Mechanistic Inquiry into the Role of Tissue Remodeling in Fibrotic Lesions in Human Atrial Fibrillation. Biophysical Journal. 2013;104:2764–2773. doi: 10.1016/j.bpj.2013.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno JD, Zhu ZI, Yang P-C, Bankston JR, Jeng M-T, Kang C, Wang L, Bayer JD, Christini DJ, Trayanova NA, Ripplinger CM, Kass RS, Clancy CE. A Computational Model to Predict the Effects of Class I Anti-Arrhythmic Drugs on Ventricular Rhythms. Science Translational Medicine. 2011;3:98ra83. doi: 10.1126/scitranslmed.3002588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng J, Jacobson JT, Ng JK, Gordon D, Lee DC, Carr JC, Goldberger JJ. Virtual Electrophysiological Study in a 3-Dimensional Cardiac Magnetic Resonance Imaging Model of Porcine Myocardial Infarction. Journal of the American College of Cardiology. 2012;60:423–430. doi: 10.1016/j.jacc.2012.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paiement A, Mirmehdi M, Xie X, Hamilton MCK. Integrated Segmentation and Interpolation of Sparse Data. Image Processing, IEEE Transactions on. 2014;23:110–125. doi: 10.1109/TIP.2013.2286903. [DOI] [PubMed] [Google Scholar]
- Petitjean C, Dacher J-N. A review of segmentation methods in short axis cardiac MR images. Medical Image Analysis. 2011;15:169–184. doi: 10.1016/j.media.2010.12.004. [DOI] [PubMed] [Google Scholar]
- Plank G, Zhou L, Greenstein JL, Cortassa S, Winslow RL, O’Rourke B, Trayanova NA. From mitochondrial ion channels to arrhythmias in the heart: computational techniques to bridge the spatio-temporal scales. Philosophical Transactions of The Royal Society A: Mathematical, Physical and Engineering Sciences. 2008;366:3381–3409. doi: 10.1098/rsta.2008.0112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pop M, Sermesant M, Mansi T, Crystal E, Ghate S, Peyrat J, Lashevsky I, Qiang B, McVeigh E, Ayache N, Wright GA. Correspondence Between Simple 3-D MRI-Based Computer Models and In-Vivo EP Measurements in Swine With Chronic Infarctions. Biomedical Engineering, IEEE Transactions on. 2011;58:3483–3486. doi: 10.1109/TBME.2011.2168395. [DOI] [PubMed] [Google Scholar]
- Prassl AJ, Kickinger F, Ahammer H, Grau V, Schneider JE, Hofer E, Vigmond EJ, Trayanova NA, Plank G. Automatically Generated, Anatomically Accurate Meshes for Cardiac Electrophysiology Problems. Biomedical Engineering, IEEE Transactions on. 2009;56:1318–1330. doi: 10.1109/TBME.2009.2014243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pu J, Boyden PA. Alterations of Na+ Currents in Myocytes From Epicardial Border Zone of the Infarcted Heart3: A Possible Ionic Mechanism for Reduced Excitability and Postrepolarization Refractoriness. Circulation Research. 1997;81:110–119. doi: 10.1161/01.res.81.1.110. [DOI] [PubMed] [Google Scholar]
- Rantner LJ, Arevalo HJ, Constantino JL, Efimov IR, Plank G, Trayanova NA. Three-dimensional mechanisms of increased vulnerability to electric shocks in myocardial infarction: Altered virtual electrode polarizations and conduction delay in the peri-infarct zone. The Journal of Physiology. 2012;590:4537–4551. doi: 10.1113/jphysiol.2012.229088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rantner LJ, Tice BM, Trayanova NA. Terminating ventricular tachyarrhythmias using far-field low-voltage stimuli: Mechanisms and delivery protocols. Heart Rhythm. 2013a;10:1209–1217. doi: 10.1016/j.hrthm.2013.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rantner LJ, Vadakkumpadan F, Spevak PJ, Crosson JE, Trayanova NA. Placement of implantable cardioverter-defibrillators in paediatric and congenital heart defect patients: a pipeline for model generation and simulation prediction of optimal configurations. The Journal of Physiology. 2013b;591:4321–4334. doi: 10.1113/jphysiol.2013.255109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raya SP, Udupa JK. Shape-based interpolation of multidimensional objects. Medical Imaging, IEEE Transactions on. 1990;9:32–42. doi: 10.1109/42.52980. [DOI] [PubMed] [Google Scholar]
- Relan J, Chinchapatnam P, Sermesant M, Rhode K, Ginks M, Delingette H, Rinaldi CA, Razavi R, Ayache N. Coupled personalization of cardiac electrophysiology models for prediction of ischaemic ventricular tachycardia. Interface Focus. 2011;1:396–407. doi: 10.1098/rsfs.2010.0041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringenberg J, Deo M, Devabhaktuni V, Berenfeld O, Snyder B, Boyers P, Gold J. Accurate reconstruction of 3D cardiac geometry from coarsely-sliced MRI. Computer Methods and Programs in Biomedicine. 2014;113:483–493. doi: 10.1016/j.cmpb.2013.11.013. [DOI] [PubMed] [Google Scholar]
- Rodríguez B, Li L, Eason JC, Efimov IR, Trayanova NA. Differences Between Left and Right Ventricular Chamber Geometry Affect Cardiac Vulnerability to Electric Shocks. Circulation Research. 2005;97:168–175. doi: 10.1161/01.RES.0000174429.00987.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spach MS, Barr RC. Ventricular intramural and epicardial potential distributions during ventricular activation and repolarization in the intact dog. Circulation Research. 1975;37:243–257. doi: 10.1161/01.res.37.2.243. [DOI] [PubMed] [Google Scholar]
- Stevenson WG, Brugada P, Waldecker B, Zehender M, Wellens HJ. Clinical, angiographic, and electrophysiologic findings in patients with aborted sudden death as compared with patients with sustained ventricular tachycardia after myocardial infarction. Circulation. 1985;71:1146–52. doi: 10.1161/01.cir.71.6.1146. [DOI] [PubMed] [Google Scholar]
- Swenson D, Levine J, Tate J, Whitaker R, MacLeod R. Impacts of Boundary Conforming Meshes on Electrical Cardiac Simulation. In: Jiao X, Weill J-C, editors. Proceedings of the 21st International Meshing Roundtable. Springer; Berlin Heidelberg: 2013. pp. 585–602. [Google Scholar]
- Trayanova NA. Whole-Heart Modeling: Applications to Cardiac Electrophysiology and Electromechanics. Circulation Research. 2011;108:113–128. doi: 10.1161/CIRCRESAHA.110.223610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trayanova NA. Mathematical Approaches to Understanding and Imaging Atrial Fibrillation: Significance for Mechanisms and Management. Circulation Research. 2014;114:1516–1531. doi: 10.1161/CIRCRESAHA.114.302240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trayanova NA, Boyle PM. Advances in modeling ventricular arrhythmias: from mechanisms to the clinic. Wiley Interdisciplinary Reviews: Systems Biology Medicine. 2014;6:209–224. doi: 10.1002/wsbm.1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turk G, O’Brien JF. Shape Transformation Using Variational Implicit Functions. Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques; New York, USA: ACM Press/Addison-Wesley Publishing Co; 1999. pp. 335–342. [Google Scholar]
- Tusscher KH, ten WJ, Noble D, Noble PJ, Panfilov AV. A model for human ventricular tissue. American Journal of Physiology - Heart and Circulatory Physiology. 2004;286:H1573–H1589. doi: 10.1152/ajpheart.00794.2003. [DOI] [PubMed] [Google Scholar]
- Vadakkumpadan F, Arevalo H, Ceritoglu C, Miller M, Trayanova N. Image-Based Estimation of Ventricular Fiber Orientations for Personalized Modeling of Cardiac Electrophysiology. Medical Imaging, IEEE Transactions on. 2012;31:1051–1060. doi: 10.1109/TMI.2012.2184799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vadakkumpadan F, Arevalo H, Jebb A, Wu K, Trayanova N. Image-Based Patient-Specific Simulations of Ventricular Electrophysiology for Sudden Arrhythmic Death Risk Stratification. Circulation. 2013a;128:A18014. [Google Scholar]
- Vadakkumpadan F, Arevalo H, Pashakhanloo F, Alers A, Dawoud F, Schuleri KH, Herzka D, McVeigh E, Lardo AC, Trayanova N. Estimation of ventricular fiber orientations in infarcted hearts for patient-specific simulations. 2013b:636–639. ISBI 2013. [Google Scholar]
- Vadakkumpadan F, Arevalo H, Prassl AJ, Chen J, Kickinger F, Kohl P, Plank G, Trayanova N. Image-based models of cardiac structure in health and disease. Wiley Interdisciplinary Reviews: Systems Biology Medicine. 2010;2:489–506. doi: 10.1002/wsbm.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vigmond EJ, Aguel F, Trayanova NA. Computational techniques for solving the bidomain equations in three dimensions. Biomedical Engineering, IEEE Transactions on. 2002;49:1260–1269. doi: 10.1109/TBME.2002.804597. [DOI] [PubMed] [Google Scholar]
- Winslow RL, Trayanova N, Geman D, Miller MI. Computational Medicine: Translating Models to Clinical Care. Science Translational Medicine. 2012;4:158rv11. doi: 10.1126/scitranslmed.3003528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao J-A, Hussain W, Patel P, Peters NS, Boyden PA, Wit AL. Remodeling of Gap Junctional Channel Function in Epicardial Border Zone of Healing Canine Infarcts. Circulation Research. 2003;92:437–443. doi: 10.1161/01.RES.0000059301.81035.06. [DOI] [PubMed] [Google Scholar]
- Zou KH, Warfield SK, Bharatha A, Tempany CM, Kaus MR, Haker SJ, Wells WM, Jolesz FA, Kikinis R. Statistical validation of image segmentation quality based on a spatial overlap index. Academic Radiology. 2004;11:178–189. doi: 10.1016/S1076-6332(03)00671-8. [DOI] [PMC free article] [PubMed] [Google Scholar]