Improved measurement of brain deformation during mild head acceleration using a novel tagged MRI sequence

Abstract

In vivo measurements of human brain deformation during mild acceleration are needed to help validate computational models of traumatic brain injury and to understand the factors that govern the mechanical response of the brain. Tagged magnetic resonance imaging is a powerful, noninvasive technique to track tissue motion in vivo which has been used to quantify brain deformation in live human subjects. However, these prior studies required from 72 to 144 head rotations to generate deformation data for a single image slice, precluding its use to investigate the entire brain in a single subject. Here, a novel method is introduced that significantly reduces temporal variability in the acquisition and improves the accuracy of displacement estimates. Optimization of the acquisition parameters in a gelatin phantom and three human subjects leads to a reduction in the number of rotations from 72–144 to as few as 8for a single image slice. The ability to estimate accurate, well-resolved, fields of displacement and strain in far fewer repetitions will enable comprehensive studies of acceleration-induced deformation throughout the human brain in vivo.

1. Introduction

Traumatic brain injury (TBI) is a major health concern in both civilian and military populations. In the United States, approximately 1.4 million TBIs are reported to occur each year (Langlois et al., 2006). The direct physical cause of TBI is the rapid deformation of brain tissue, typically in response to linear or angular acceleration of the skull (Graham et al., 1995). The effects of brain trauma may lead to neurodegenerative diseases— for example, TBI is an established risk factor for Alzheimer’s disease, especially in combination with the ε4 allele of apolipoprotein E (Mayeux et al., 1993; Mortimer et al., 1991). Contact sport participants with histories of repeated head impacts appear to have high incidence of memory impairment, depression, and dementia (Baugh et al., 2012). These symptoms have been associated with post-mortem findings of accumulated hyper-phosporylated tau and the disease protein TDP-43(Baugh et al., 2012). The mechanism of this pathology is poorly understood and the relationship between the magnitudes, locations, directions, numbers, and frequencies of the mechanical insult and the resulting neurodegeneration is almost entirely unknown.

Because experiments measuring brain deformation during injury-level events in humans cannot be performed for ethical reasons, computer simulations of brain biomechanics, e.g., (Zhang et al., 2004), have been used to estimate brain deformation in response to specific loading conditions. Solutions obtained from computer models are highly dependent on the tissue connectivity, boundary conditions, and material properties assigned to different brain regions. Experimental measurements of brain deformation during acceleration of the skull are necessary to validate such computation models of brain injury. Experiments on physical models of brain injury have been performed using gel-filled skulls, e.g., (Margulies et al., 1990; Meaney et al., 1995), and high-speed biplanar x-ray measurement of radio-opaque targets embedded in cadaver brains during skull impact (Hardy et al., 2001). However, these physical models provide only a sparse set of data points and lack many of the features of the living brain (Gefen and Margulies, 2004; Vappou et al., 2008).

Tagged magnetic resonance imaging (MRI)(Axel and Dougherty, 1989; Zerhouni et al., 1988), a noninvasive approach to track the motion of biological tissues, has been applied previously to measure brain deformation during mild linear (Bayly et al., 2005; Feng et al., 2010) and angular (Sabet et al., 2008) acceleration of the live human brain. While these studies provide useful quantitative information regarding brain deformation in response to a known loading condition, only a limited region of the brain could be examined because the subject was required to repeat the head motion 72–144 times to acquire a single data slice. A large number of rotations consumes scan time, causes fatigue in the subject, and potentially introduces artifacts caused by variability between each repetition.

This study has two major contributions. First, in imaging studies of a gelatin phantom and three human subjects during mild angular acceleration, the tagged MRI acquisition parameters were optimized to minimize the number of rotations needed to acquire a single image set. Second, a novel double trigger tagged MRI pulse sequence was developed to reduce the temporal variability between rotations during the acquisition, and thus increase the accuracy of estimated displacement fields. These contributions are important steps toward enabling increased coverage and accurate measurement of deformation throughout the human brain.

2. Methods

2.1 Subjects

Three healthy subjects, two male and one female, were consented under an IRB approved protocol and enrolled in this study. MRI scanning was restricted by the protocol to no more than 2 hours, and no subject spent more than 90 minutes in the scanner.

2.2 Head rotation device

In this experiment, a mild angular acceleration was generated after an angular rotation about the inferior-superior axis towards the subject’s left shoulder. To generate a standardized and reproducible angular acceleration of the head, a device (Sabet et al., 2008) was used to constrain head motion within the MRI scanner (Figure 1). The subject lies in the supine position and his or her head is firmly coupled to the device using side bars and a chin strap. Prior to each rotation, the subject faces forward in the rest position with the device latched at 0° (Figure 1a,c). The subject voluntarily initiates each head rotation when ready by releasing a latch to allow an active head rotation, assisted by a small counterweight. A rapid deceleration is generated by rotating into a padded stop set at approximately 32° toward the subject’s left shoulder (Figure 1b,d). This rapid deceleration is approximately 10–15% of that experienced routinely by soccer players in heading a soccer ball (Naunheim et al., 2003). The subject then pauses for 1–2 seconds before turning his or her head back to the rest position. Use of the device in the MRI environment was approved by the institutional MRI safety committee.

Figure 1.

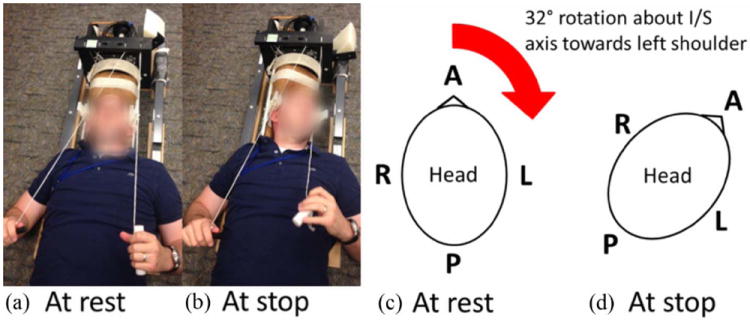
Photograph of the head rotation device and schematic of head at rest and stop positions :A mild angular acceleration was generated using an MRI-compatible head rotation device.(a,c) At rest, the subject lies in the supine position with his or her head facing straight ahead. The subject initiates the motion by releasing a latch, which allows for free rotation about the inferior(I)/superior(S) axis towards his or her left shoulder. (b,d) After a 32° rotation, the device encounters a stop, which generates a mild angular acceleration. The subject is instructed to pause for 1-2 seconds at the stop. The subject then rotates his or her head back to the rest position, and the motion is repeated when the subject is ready.

2.3 Optimization of Image acquisition

All MR images were acquired using a Siemens 3.0T mMR Biograph scanner (Siemens, Munich, Germany). Agelatin phantom was used to validate the proposed approach and to optimize the image acquisition parameters. The stiffness of the gelatin phantom was selected to be within the range of reported values for brain tissue. The gelatin phantom was prepared by filling a plexiglasscylindrical container (diameter=11.4cm, length=18.0cm) with a mixture of 103.7g of gelatin (Knox) and 1.8L of water heated to 82°C. The solution was stirred vigorously and allowed to cool at 4°C overnight. Prior to the experiment, the phantom was allowed to equilibrate to room temperature for at least 8 hours. The response of thegelatin cylinder to mild angular acceleration has previously been characterized using tagged MRI and compared to a numerical simulation (Bayly et al., 2008). Additionally, the gelatin phantom can be imaged for a longer period of time than human subjects.

All tagged MR images were acquired with a SPAMM tagging pulse (Axel and Dougherty, 1989) followed by a segmented cine gradient echo acquisition at the same slice location. Three image sets were acquired with 24 phase encode lines at 18.5 ms temporal resolution to assess the reproducibility of the acquired strain fields in vivo. The number of phase encode lines (spatial resolution) and the number of lines acquired per rotation (inversely proportional to temporal resolution) directly determine the number of rotations needed to acquire a single image set. To assess the effect of spatial resolution on the strain fields, images were acquired with 20, 24, 28, 36, and 44 phase encode lines at 12.4 ms temporal resolution (4 lines/rotation). To assess the effect of temporal resolution on the strain fields, images were acquired with 24 phase encode lines and temporal resolutions of 6.1ms (2 lines/rotation), 12.2ms (4 lines/rotation), 18.4ms (6 lines/rotation), 24.5ms (8 lines/rotation), and 30.6 ms (10 lines/rotation).

Given the differences between the live human brain and the gelatin phantom, e.g., geometry, boundary conditions, material parameters, a series of 2D tagging experiments were performed in three human subjects on two adjacent axial slices to ensure that the optimized acquisition parameters were appropriate for use in the live human brain. To assess the reproducibility of the strain fields, three image sets were acquired with 24 phase encode lines at 18.5 ms temporal resolution. To assess the effect of temporal resolution on the strain fields, images were acquired with 24 phase encode lines and temporal resolutions of 6.1 ms (2 lines/rotation), 12.2 ms (4 lines/rotation), 18.4 ms (6 lines/rotation), and 24.5 ms (8 lines/rotation).

2.4 Double trigger approach

For cine tagged MRI acquisition, only a portion of the spatial frequency domain (“k-space”) is acquired during each rotation, so that the rotation must be repeated to fill k-space and create a single cine image sequence. Previous experiments required 72–144 rotations, each corresponding to the acquisition of one line in k-space, to acquire a single cine sequence (Bayly et al., 2005; Sabet et al., 2008). For those prior experiments, the MRI scanner was triggered when the latch was released at the beginning of the head motion. Variability in the synchronization between motion and imaging can lead to image distortions, e.g., breaks in the tag lines, making the acquired images unusable. The head rotation device constrains the path of the rotation to be consistent; however, the precise temporal trajectory of each rotation is not constrained. Figure 2 (left column) shows the angular position versus time profiles of 30 rotations in the gelatin phantom and a single human subject. The motion of the gelatin phantom was very consistent between rotations, with a standard deviation to the time of peak angular acceleration of 1.4 ms. The human subject was more variable, with a standard deviation of 18.4 ms. This amount of variability would likely lead to image distortions.

Figure 2.

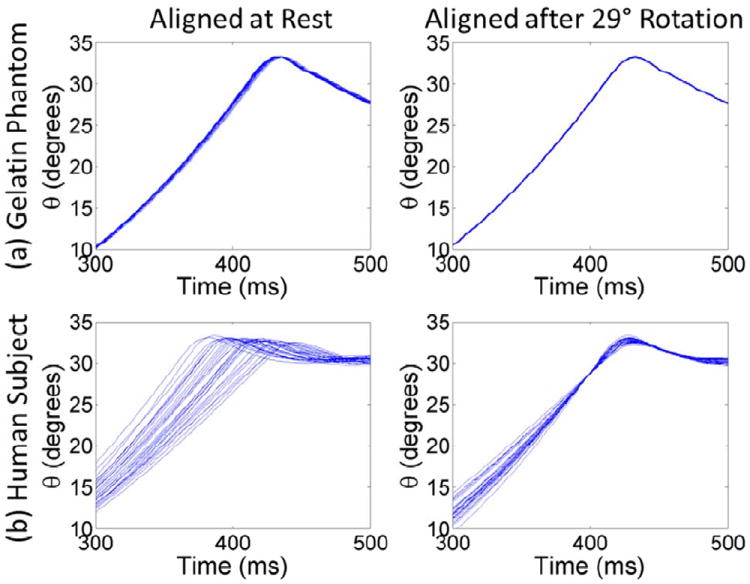
Angular position θ versus time for 30 rotations measured using an MRI-compatible angular position sensor. (a) In the gelatin phantom, the motion is highly repeatable whether the rotations are aligned at rest (0° rotation) or after a 29° rotation. (b) Rotations in live human subjects are more variable. Temporal variations can lead to image distortions. If the rotations are aligned at rest, then the standard deviation of the time to peak angular acceleration is 18.4 ms. Aligning the rotations after 29° rotation reduced the standard deviation at peak acceleration to 2.8 ms.

A novel double trigger tagged MRI pulse sequence was designed to dramatically reduce temporal variability in imaging of human head motion. An MRI-compatible angular position sensor (MICRONOR, USA) was attached to the shaft of the head rotation device. The sensor measures the angular position in real-time for each head rotation. Software from MICRONOR additionally computes acceleration versus time measurements for each head rotation.

The goal of the experiment is to quantify brain deformation after rapid angular deceleration caused by the sudden stop. The rotation from release of the latch to just prior to the stop is dominated by rigid body motion, which is not of interest. Accordingly, in the new double trigger sequence, the first trigger occurs after the subject initiates the rotation by releasing the latch. This starts the application of tag lines, but the cine image acquisition does not yet begin. A second trigger is generated by the angular position sensor when the subject rotates through a threshold value of 29°. This second trigger initiates the cine image acquisition. Thus, image acquisition is guaranteed to begin at the same angular position at a point very close to the stop. With the rotations aligned at 29°, the standard deviation in the time to peak angular acceleration was reduced to 0.4 ms in the gelatin phantom and 2.8 ms in the human subject (Figure 2). A schematic illustrating the standard and modified approaches is provided in Figure 3.

Figure 3.

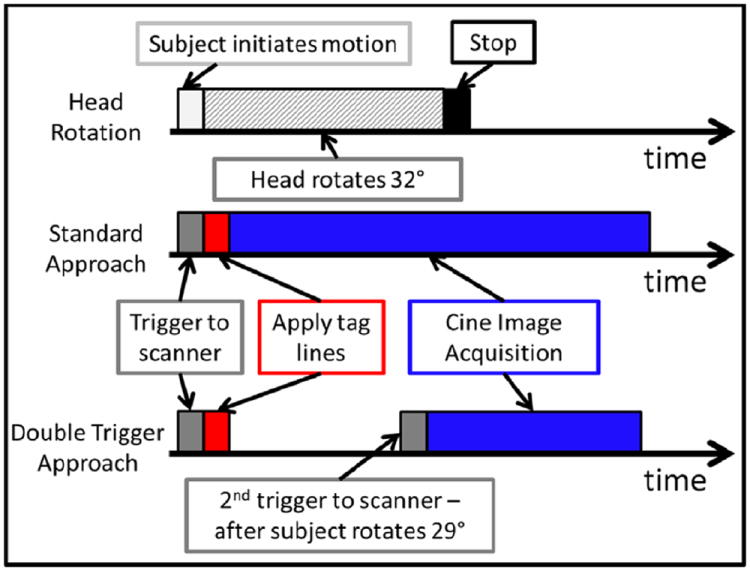
Schematic diagram comparing the timing for the standard tagging approach and proposed double trigger approach (one rotation is shown). The subject initiates the motion by releasing a latch on the head rotation device. Assisted by a counterweight, the subject rotates his or her head towards the left until the head support encounters a fixed stop at 32°. The sequence is triggered when the subject initiates the motion, and the tag lines are then applied. For the standard approach, the cine image acquisition begins immediately after the application of tag lines. For the proposed approach, the cine acquisition begins after the subject rotates through a preset threshold of 29°. An MRI-compatible angular position sensor generates the trigger when this threshold is reached.

2.5 Strain estimation

Estimation of the strain tensor for each slice was as follows. Motion was tracked between image frames using harmonic phase (HARP) analysis, which employs the phase part of the images after a bandpass filter is applied to extract offset spectral peaks in k-space (Osman et al., 1999). Because the phase value of a material point remains constant between image frames, these points can be tracked between image frames. To minimize errors from tag jumps, the shortest-path HARP refinement algorithm (Liu and Prince, 2010) was applied to derive the displacement vector (u) between each voxel center in the first image frame (X) to its corresponding location in each other image frame (x). The Lagrangian strain tensor (E) was computed from the displacement vectors at each reference point (Taber, 2004)

$$\mathit{E}=\frac{1}{2}[\nabla \mathit{u}+{(\nabla \mathit{u})}^T+(\nabla \mathit{u})·{(\nabla \mathit{u})}^T].$$ (1)

where (·)^T is the tensor transpose, and ∇ is the gradient operator. Maximum shear strain, γ_max, was computed from the strain tensor as an invariant measure of deformation:

$${\gamma }_{\mathit{max}}=\frac{1}{2}(E_1-E_2),$$ (2)

where E₁ and E₂ are the first and second principal strains, respectively.

Normalized root mean square error (NRMSE) was calculated to quantitatively compare the strain fields obtained using the standard and proposed double trigger approaches, and to assess the effects of acquisition parameters related to spatial and temporal resolution that directly affect the number of rotations

$$\mathit{NRMSE}=\frac{\sqrt{{\sum }_{i=1}^m{\sum }_{j=1}^n\frac{{\left({\gamma }_{\mathit{max},1}\left(x_i,t_j\right)-{\gamma }_{\mathit{max},2}\left(x_i,t_j\right)\right)}^2}{\mathit{mn}}}}{\max ({\gamma }_{\mathit{max},1})}.$$ (3)

Here, γ_{max, 1} and γ_{max, 2} are strain fields varying in space (x) and time (t) from two different acquisition parameter sets, m is the number of points within the material, and n is the number of time frames. Estimates obtained with the highest acquired temporal resolution (Δt=6.1 ms, 2 lines/rotation) and spatial resolution (160×44) were used as the benchmarks for comparison when adjusting each acquisition parameter, respectively. The maximum value of γ_max,1 from the benchmark data set was used for normalization. To compare the standard and proposed double trigger approaches, an image set was acquired using the standard approach with 12.2 ms temporal resolution and 160 × 44 spatial resolution (22 rotations).

3. Results

3.1 Strain estimates in gelatin phantom

Peak angular acceleration values were recorded for each rotation. For the gelatin phantom, the peak angular acceleration (ᾱ_max) was 260.1±4.0rad/s² (mean±s.d., N=200 rotations).

NRMSE values for the gelatin phantom experiments are listed in Table 1. NRMSE values ranging from 0.064–0.108 were obtained between strain fields obtained from different scans using the double trigger approach with the same acquisition parameters. These NRMSE values define the range of reproducibility of the approach. Increasing the number of lines acquired per repetition (inverse relationship to temporal resolution) and decreasing the number of lines acquired (spatial resolution) decreases the number of rotations needed to acquire a data at a single slice. When the temporal resolution is decreased, NRMSE values were in the range of reproducibility for temporal resolutions of at least18.4ms (6 lines/rotation), just outside of the upper boundary at 24.5 ms (8 lines/rotation), but well out of the range at 30.6 ms (10 lines/rotation). When the spatial resolution is decreased, NRMSE values were in the range of reproducibility for resolutions greater than 24 lines acquired, and just outside the upper boundary for 20 lines acquired. In the gel phantom, strain fields acquired using the standard and modified double trigger approaches show good agreement (NRMSE=0.111).

Table 1.

Normalized root mean square error (NRMSE) values of strain measurements obtained in a gelatin phantom using different acquisition parameters. Reduction in number of rotations (N) may be achieved by reducing temporal and spatial sampling resolution. Strain fields obtained with the highest temporal (6.1 ms) and spatial (160 × 44) resolutions were used as the benchmarks (“gold standards”). The parameters for the benchmark acquisitions are listed in parentheses in the left-most column. NRMSE values between strain fields acquired using: (1). three scans with the same acquisition parameters describe reproducibility of the strain fields, (2). temporal resolutions from 6.1 ms (2 lines/rotation) to 30.6 ms (10 lines/rotation). (3) spatial resolutions from 160 × 44 to 160 × 20, and (4). using the standard and modified double trigger tagged MRI pulse sequence.

	Scan 1 vs. 2	Scan 1 vs. 3	Scan 2 vs. 3
1. Repeat Scans (Δt=18.4 ms, 160 × 24, N=8)	0.064	0.098	0.108
	Δt=12.2 ms N=12	Δt=18.4 ms N=8	Δt=24.5 ms N=6	Δt=30.6 ms N=6
2. Temporal resolution (Δt=6.1 ms, 160 × 24, N=24)	0.083	0.096	0.0123	0.239
	160 × 36 N=18	160 × 28 N=14	160 × 24 N=12	160 × 20 N=10
3. Spatial Resolution (Δt=12.2 ms, 160 × 44, N=22)	0.063	0.081	0.094	0.125
	Δt=12.2 ms, 160 × 44, N=22
4. Standard versus double trigger approach	0.111

3.2 Strain estimates in human subjects

Average values of peak angular acceleration range from 85–246 rad/s² (Table 2). NRMSE values from strain fields obtained using the same acquisition parameters range from 0.104–0.330 (Table 3). Increasing the number of lines acquired per rotation (inversely proportional to temporal resolution) decreases the number of rotations needed to acquire strain data at a single slice. When the temporal resolution is decreased, NRMSE values were in the range of reproducibility error for temporal resolutions of at least 18.4 ms and at 24.5 ms for subjects 1 and 2 (Table 4). In subject 3, the NRMSE values at 24.5 ms temporal resolution are outside of the range of reproducibility. Raw values of maximum shearing strain versus time for each slice and subject are shown in Supplemental Figures 1–3.

Table 2.

Average statistics of peak angular acceleration (mean and standard deviation, rad/s²) of for each acquisition set in three human subjects.

	Proposed “double trigger” approach					Standard approach
	Δt=6.1 ms N=24	Δt=12.2 ms N=12	Δt=18.4 ms N=12	Δt=18.4 ms N=8	Δt=24.5 ms N=6	Δt=12.2 ms N=22
Subject 1 Slice 1	223.9±13.5	233.7±8.8	237.2±9.0	222.5±8.6	233.7±2.8	221.5±34.3
Subject 1 Slice 2	228.2±8.7	218.5±26.9	222.1±4.6	224.1±18.0	218.0±5.0	207.2±19.1
Subject 2 Slice 1	222.6±10.4	242.0±10.5	246.2±6.6	225.8±12.4	243.2±10.5	Not acquired
Subject 2 Slice 2	192.0±15.8	191.7±22.6	179.1±6.7	172.5±9.6	197.6±18.4	Not acquired
Subject 3 Slice 1	84.7±18.4	104.9±15.8	95.9±17.7	87.2±15.4	90.7±25.5	Not acquired
Subject 3 Slice 2	98.5±28.9	101.1±21.8	112.1±18.1	117.6±12.9	105.1±34.7	Not acquired

Table 3.

Normalized root mean square error of maximum shearing strain values obtained in three human subjects with the acquisition repeated three times. A temporal resolution of 18.4 ms and spatial resolution of 160 × 24 (N=8 rotations) were used for all acquisitions.

	Scan 1 vs. 2	Scan 1 vs. 3	Scan 2 vs. 3	max γmax
Subject 1 Slice 1	0.145	0.330	0.296	0.053
Subject 1 Slice 2	0.203	0.225	0.145	0.048
Subject 2 Slice 1	0.104	0.140	0.113	0.058
Subject 2 Slice 2	0.241	0.195	0.247	0.045
Subject 3 Slice 1	0.255	0.296	0.149	0.045
Subject 3 Slice 2	0.219	0.197	0.179	0.038

Table 4.

Normalized root mean square error (NRMSE) of strain measurements obtained in three subjects at different temporal sampling resolutions. Increasing the number of lines acquired per rotation decreases the number of rotations needed to acquire strain data at a single slice. The strain field obtained with the highest temporal sampling resolution (6.1 ms) was used as the “gold standard” for each subject/slice. A spatial resolution of 160 × 24 was used for all acquisitions.

	Proposed double trigger approach			Standard approach
	Δt=12.2 ms N=12	Δt=18.4 ms N=8	Δt=24.5 ms N=6	Δt=12.2 ms N=22	maxγmax
Subject 1 Slice 1	0.249	0.141	0.229	1.710	0.053
Subject 1 Slice 2	0.169	0.143	0.173	0.319	0.048
Subject 2 Slice 1	0.116	0.143	0.131	N/A	0.058
Subject 2 Slice 2	0.143	0.165	0.145	N/A	0.045
Subject 3 Slice 1	0.246	0.221	0.439	N/A	0.045
Subject 3 Slice 2	0.234	0.236	0.349	N/A	0.038

Strain fields using the standard tagged MRI approach were obtained in two slices in subject 1 for comparison with the proposed double trigger approach. NRMSE values for strain fields obtained by the standard approach, with respect to those obtained by the double trigger approach, are 1.710 for slice 1 and 0.319 for slice 2 (Table 4). NRMSE values from strain fields obtained from repeated scans by the double trigger approach, using the same acquisition parameters each time, range from 0.145–0.330 for slice 1 and 0.145–0.225 for slice 2 (Table 3). Thus the NRMSE values of the standard approach with respect to the double trigger method markedly exceed the reproducibility of the new approach. The tagged images obtained using the standard approach, particularly in slice 1, show considerable image artifacts, e.g., breaks in the tag lines, compared to the double trigger approach (Figure 4).

Figure 4.

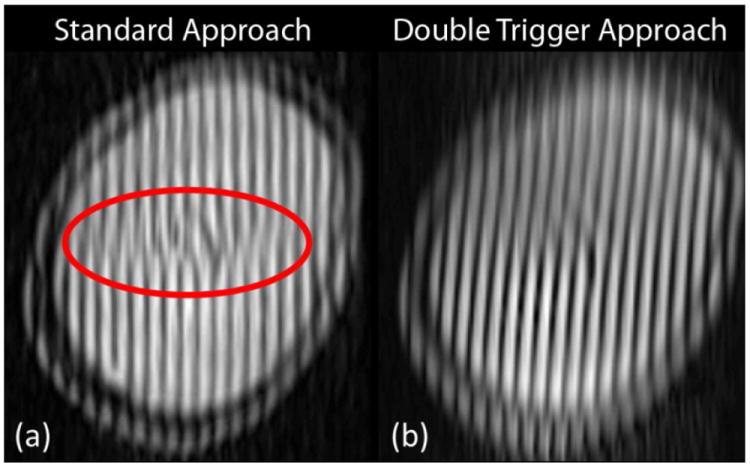
(a) Tagged MR image from subject 1, slice 1 acquired using the standard approach. Breaks in the tag line (inside the red ellipse) can occur due to highly variable motion over time. When this occurs, motion tracking will not produce reliable results. (b) Tagged MRI acquired using the modified double trigger approach in subject 1, slice 1 at the time corresponding to peak deformation. The tag lines within the brain are continuous and can be used to accurately track motion and compute strain fields over time.

The peak values of maximum shear strain used to normalize NRMSE for each subject and slice are listed in Tables 3 and 4. These values were determined from the strain fields obtained at the highest temporal resolution (6.1 ms, 2 lines/rotation). To enable a direct comparison, the same peak shear strain values were used when assessing repeatability as when assessing the effect of temporal resolution on the computed strain fields.

4. Discussion

To use tagged MRI to track motion of soft tissue, the motion being observed must be highly repeatable and precisely synchronized with image acquisition. For the angular motion in this study, the subject’s head motion was constrained by an MRI-compatible head rotation device. While head rotation is encouraged by an offset counter weight, motion is highly dependent on the subject’s active control of his or her neck muscles. Consequently, both temporal variability in impact time, and variability in acceleration amplitude between rotations in human subjects is to be expected.

The new double trigger sequence directly addresses the issue of temporal variability of impact with respect to imaging. Beginning the image acquisition portion of the pulse sequence after the subject rotates through 29° instead of immediately after the application of the tag lines removes the majority of the temporal variations between rotations. This approach makes the experiment easier for the subject and increases the likelihood of obtaining a high quality image set, which is essential to obtain measurements over the entire brain in a limited number of rotations.

Direct measurement of kinematics also allows the assessment of amplitude variability. The MRI-compatible angular position sensor provides real-time measurements of the applied loading conditions for each rotation. For the acquisition of a single slice in the gelatin phantom, the magnitude of peak angular acceleration was very consistent between rotations, with variations on the order of 1–2% of the peak value. This is expected for the phantom because it is allowed to rotate freely and the rotation is entirely driven by the offset weight. In live human subjects, the values of peak angular acceleration within a single slice acquisition are more variable. The offset weight encourages rotation of the head, but the applied torque may be resisted by the subject. Additionally, precise repetition of the rotation is highly unlikely due to human error. However, acceleration amplitude variations for most subjects were ≤ 10% of the peak acceleration, which led to good agreement in the computed strain values between parameter sets. Strain estimates are less sensitive to such variations in input amplitude than to errors in synchronization of the magnitude seen in Figure 2b/Table 2. Knowledge of the applied loading conditions will be extremely valuable for comparison with computational models of brain injury.

The temporal and spatial resolutions of tagged image acquisition directly relate to the number of rotations needed to acquire data at a single slice. Minimizing the number of rotations per image slice is necessary to increase coverage of brain within a single imaging session; however, the temporal and spatial resolutions must not be reduced so much that the strain measurements are no longer accurate. The NRMSE values for strain fields in the gelatin phantom and in human subjects provide a quantitative assessment of the effects of these acquisition parameters on computed strain values. These data, which show that strain estimates are quite robust to acquisition parameter values within reasonable limits, will be very valuable in designing future imaging studies of brain biomechanics.

Decreasing the acquired spatial resolution does not have a large effect on the acquired strain fields. In HARP analysis, a bandpass filter is applied about the spectral peaks in k-space, removing all other spatial information. The radius of the bandpass filter is determined by the tag spacing, sampling of k-space, and the type of tagged imaging pulse sequence. For our acquisition type and imaging parameters, a filter radius of 9 voxels in k-space was appropriate. Because any spatial frequency information outside of the filter is removed, reduced spatial resolution in the phase encode direction does not have a large influence on the acquired strain measurements. For this reason, the effects of decreasing spatial resolution on the acquired strain fields in human subjects was not examined.

Decreasing the temporal resolution from 6.1 ms to 18.4 ms also does not have a large effect on the corresponding strain fields. The subjects 1 and 2, strain fields acquired at a temporal resolution of 24.5 ms also show good agreement, while the strain fields obtained in subject 3 at this temporal resolution do agree well. This suggests that a temporal resolution of 24.5 ms may be pushing the boundary of what is useful in measuring deformation of the brain.

Maximum shear strain was used as the metric to quantify deformation and compare strain fields obtained using different acquisition parameters. This invariant measure combines both principal strain components. Previous studies using this device reported radial-circumferential shear strain values because this component dominates the deformation, and has a clear physical interpretation, including the meaning of positive and negative values (Bayly et al., 2008; Sabet et al., 2008). For comparison, images of the raw radial-circumferential strain values for all experiments from the human subjects are provided in Supplemental Figures 4–6.

The improved ability to obtain accurate estimates of displacement and strain with far fewer repetitions opens up a number of potential avenues for future study, primarily because it enables much greater coverage of the brain. Strain fields identified over the entire brain could then be mapped to anatomical structures, such as cortical gray matter, white matter, the corpus callosum, brain stem, etc., that can be identified using an automated segmentation algorithms applied to anatomical MR images. The information obtained from this approach may be used to understand the role that the meninges play during the brain’s response to impact (Bigler, 2008; Coats et al., 2012; Feng et al., 2010). Additionally, because the loading conditions and the displacement response are known, an inverse approach, e.g., (Augenstein et al., 2005; Moulton et al., 1995; Van Houten et al., 1999) could be applied to estimate material properties of brain tissue, possibly distinguishing between different brain structures. This type of approach would complement other techniques of material parameter estimation of brain tissue such as magnetic resonance elastography, e.g., (Clayton et al., 2012; Kruse et al., 2008; Sack et al., 2008), and ex vivo mechanical testing, e.g., (Feng et al., 2013).

The current study is restricted to 2D measurements of deformation during mild angular acceleration of the skull. Using standard tagged MRI, 3D motion tracking is possible if an additional series of tagged images is acquired in an orthogonal plane, with tag lines oriented along the z-axis. The displacement information obtained from the axial and orthogonal image planes can be combined using a post-processing technique, such as IDEA (Liu et al., 2012). Another possibility is to use a different acquisition approach, such as zHARP (Abd-Elmoniem et al., 2007; Abd-Elmoniem et al., 2005) or 3D DENSE, e.g., (Zhong et al., 2010). While these methods require twice the number of rotations per slice, they provide a 3D displacement vector over time at each image voxel. The current study was limited to pure angular rotation about the inferior/superior axis of the brain, which has the advantage of inducing primarily 2D kinematics. Future studies will examine brain deformation under different head motions, including anterior-posterior linear accelerations and angular rotations about different axes.

5. Conclusion

A novel approach was developed to improve the measurement of human brain deformation during mild angular acceleration of the head. Measurement of angular motion and estimation of loading conditions by an MR-compatible transducer and addition of a second trigger to improve the image acquisition are key advances. Using the modified approach and by optimizing acquisition parameters, the number of rotations necessary to acquire a single image slice were reduced from as many as 144 to as few as 8 while retaining high confidence in the acquired strain measurements. This significant reduction in the number of rotations needed per slice will enable complete brain coverage during a single imaging session in the future.