Patient-specific modeling of ventricular activation pattern using surface ECG-derived vectorcardiogram in bundle branch block

Abstract

Patient-specific computational models have promise to improve cardiac disease diagnosis and therapy planning. Here a new method is described to simulate left-bundle branch block (LBBB) and RV-paced ventricular activation patterns in three dimensions from non-invasive, routine clinical measurements. Activation patterns were estimated in three patients using vectorcardiograms (VCG) derived from standard 12-lead electrocardiograms (ECG). Parameters of a monodomain model of biventricular electrophysiology were optimized to minimize differences between the measured and computed VCG. Electroanatomic maps of local activation times measured on the LV and RV endocardial surfaces of the same patients were used to validate the simulated activation patterns. For all patients, the optimal estimated model parameters predicted a time-averaged mean activation dipole orientation within 6.7±0.6° of the derived VCG. The predicted local activation times agreed within 11.5±0.8 ms of the measured electroanatomic maps, on the order of the measurement accuracy.

1. Introduction

The sequence of electrical excitation in the ventricles of the heart is an important indicator of cardiac health and disease. Intrinsic cardiac electrical conduction disorders, such as left bundle branch block (LBBB), are detrimental to normal mechanical synchrony and pump efficiency. In device-based treatments for heart failure (HF) such as cardiac resynchronization therapy (CRT) (i.e. biventricular pacing), the therapeutic response is dependent on the patient-specific baseline electrophysiological substrate (Ploux et al., 2013; Varma et al., 2007). The most important electrophysiological characteristic is the myocardial activation pattern.

Electrocardiographic imaging (ECGI) (Rudy et al., 2013; Wang et al., 2011) and noninvasive imaging of cardiac electrophysiology (NICE) (Pfeifer et al., 2008) have advanced rapidly in the last decade, and their clinical use has grown. ECGI and NICE estimate distributions of extracellular potential and electrical activation times, respectively, on the epicardial surface of the heart from body-surface potential recordings on a subject’s torso. Estimates are based finding inverse solutions to the forward problem of electrophysiology:

$${\Phi }_B=Z\cdot {\Phi }_H,$$

where Φ_H is a vector of the electrical source distribution on the surface of the heart, Φ_B is a vector of the potential distribution on the body surface, and Z is the transfer matrix of the passive volumetric conduction of the thoracic cavity tissue and fluids. ECGI makes use of a pericardial potential source model for Φ_B , while NICE uses an equivalent double layer source model. The potentials Φ_B are typically sampled over the torso (~250 locations in ECGI, ~64 locations in NICE) and recorded as electrocardiograms; Z can be modeled as an isotropic conducting medium (using the boundary element method) or as a three-dimensional torso with prescribed conductivities (using finite volume or finite element methods). Though a unique relationship between body-surface and epicardial potentials exists in certain conditions (Ramanathan et al., 2003; Yamashita et al., 1982), the inverse problem is ill-conditioned and sensitive to noise in Z or Φ_B. This problem is usually handled with numerical regularization techniques (Ramanathan et al., 2003; Oster et al., 1992; Greensite et al., 1998; Messinger-Rapport et al., 1988; Tikhonov et al., 1977; Golub et al., 1970). ECGI and NICE methods have been successfully applied to a range of physiologic conditions including normal sinus rhythm, ventricular pacing, atrial flutter, ventricular tachycardia, bundle branch block (Ramanathan et al., 2004), and Wolff-Parkinson-White syndrome (Berger et al., 2006).

Preconditioning of the inverse problem may also take the form of model-based constraints by conditioning Φ_B a priori with solutions from forward models of ventricular excitation. Recent model-based approaches have been implemented and validated in animal (Han et al., 2012; Han et al., 2011; Liu et al., 2008; Zhang et al., 2004; He et al., 2002; Li et al., 2001) and human (Dossel et al., 2005) studies. Using electrical activation models based on artificial neural networks and cellular automata, the results of these studies agreed with measured surface electrocardiograms, activation times, and known source locations within reasonable error bounds. One limitation of these approaches is the computational expense of detailed excitation models. Recent advances in computing power and GPU architecture, however, make physiologically detailed forward models more feasible. Recently, Cluitmans et al. (2013) found that, compared with conventional regularization techniques alone, a training model with patient-specific epicardial geometry and FitzHugh-Nagumo (FHN) membrane kinetics optimized to match vectorcardiographic features significantly improved the agreement between recorded electrocardiograms and localization accuracy of known pacing sites compared to numerical regularization alone (Cluitmans et al., 2013).

In light of these advancements, we propose a model-based approach for estimating patient-specific myocardial electrical activation patterns. We used a forward monodomain model of human ventricular action potential propagation in patient-specific anatomical models approximated using high-order 3D biventricular geometry, human fiber architecture, and regions of heterogeneous conductivities due to the presence of myocardial infarction. From our excitation model, we approximated the total cardiac dipole at each time and compared it to the vectorcardiogram (VCG) derived from the 12-lead surface electrocardiogram (ECG). We hypothesized that the optimal combination of excitation model parameters that minimizes a VCG objective function could predict activation patterns within measurement limits. We validated computed activation patterns directly using invasive electroanatomic maps of endocardial activation isochrones.

2. Methods

2.1 Clinical study

Three male patients (ages 67, 71, 85) (74±9 years) with left bundle branch block, NYHA class III heart failure, and dilated cardiomyopathy were enrolled from the Veteran's Administration San Diego Healthcare System (San Diego, CA) into an Institutional Review Board (IRB)-approved protocol after obtaining informed, written consent. End-diastolic cardiac anatomy was obtained with CT imaging (GE Lightspeed, GE Medical Systems, Milwaukee, WI, in-plane resolution of 0.49x0.49 mm, thickness 0.625 mm). Two patients with indications for myocardial ischemia underwent nuclear perfusion imaging (technetium sestamibi, ECAM-2, Siemens Medical Solutions, Hoffman Estates, IL, resolution of 6.59x6.59x1 mm) to localize the affected regions; one patient had an inferoseptal infarct, and another an inferior infarct. In the following invasive electrophysiology study, standard 12-lead body-surface electrocardiograms were recorded (Bard Pro, Bard Electrophysiology, Lowell, MA) at 1 kHz simultaneously with non-fluoroscopic electroanatomic contact mapping (NavX, St. Jude Medical, St. Paul, MN) of biventricular endocardial geometry and activation times. The electrocardiograms were printed to XPS file format, rasterized at 600 dpi (1.6 ms, 0.004 mV), and resampled to 1 kHz. Intracardiac electrograms at the LV and RV endocardial surfaces were recorded using a roving catheter with 3D tip localization (Rotter, 2004; Wittkampf, 1999). Activation times were computed by first identifying the global activation time reference (t=0) at the earliest onset of the QRS complex in body-surface leads I, II, aVF, and V1. Local activation at the catheter in contact with the endocardial surface was then marked (with respect to the global activation time reference) by the onset of the largest deflection in the recorded electrogram.

2.2. VCG computation

The cardiac dipole or “heart vector” represents the net intracellular current that flows from regions of higher intracellular potential to regions of lower potential at the activation and recovery wave fronts at a given instant in the ventricular myocardium. The magnitude of the cardiac dipole is proportional to the effective intracellular conductivity of the tissue and the strength of the potential gradients, and its orientation is in the mean direction of the propagating wave front:

$${\Phi }_H=-{\int }_{\Omega }{\sigma }_i\nabla {\Phi }_{i}d\Omega$$

where δ_i is the intracellular conductivity, Φ_i is the intracellular potential, and Ω is the geometric domain of the ventricular myocardium. Burger was one of the first to investigate the relationship between the cardiac dipole and body-surface electrocardiogram recordings (Burger et al., 1954):

$${\Phi }_H=A\cdot {\Phi }_B$$

where Φ_H is the cardiac dipole, Φ_B is the vector of electrocardiogram recordings on the body surface (ECG), and A is the matrix of transfer coefficients accounting for the passive conductivity of the thoracic cavity tissue and fluids. This system is similar to the inverse problem with the exception of the reduced dimensionality of Φ_H as a lumped vector representing the magnitude and mean orientation of the instantaneous potential distribution in the myocardium. Prior studies (Kors et al., 1990; Dower et al., 1988; Edenbrandt et al., 1988) have determined general transformations between the cardiac dipole and surface electrocardiograms by obtaining simultaneous measurements of 12-lead ECG and Frank-lead VCG in a wide patient population and minimizing the differences between derived and measured signals. In this study, we utilize the inverse Dower and Kors transformations to derive VCGs from the surface ECGs. The transformation coefficients are given in Table 1.

Table 1.

Coefficients for the Inverse Dower and Kors ECG-VCG transformations

Inverse Dower				Kors
	X	Y	X		X	Y	Z
V1	−0.17	0.06	−0.23	V1	−0.13	0.06	−0.43
V2	−0.07	−0.02	−0.31	V2	0.05	−0.02	−0.06
V3	0.12	−0.11	−0.25	V3	−0.01	−0.05	−0.14
V4	0.23	−0.02	−0.06	V4	0.14	0.06	−0.2
V5	0.24	0.04	0.06	V5	0.06	−0.17	−0.11
V6	0.19	0.05	0.11	V6	0.54	0.13	0.31
I	0.16	−0.23	−0.02	I	0.38	−0.07	0.11
II	−0.01	0.89	0.10	II	−0.07	0.93	−0.23

2.3. Patient-specific computational model

2.3.1. Anatomical model

Patient-specific finite element meshes of ventricular anatomy were generated from the clinical CT and perfusion images together with previously described diffusion tensor magnetic resonance images (DT-MRI) from a cadaver heart (Aguado-Sierra et al., 2011). Ventricular myocardium from apex to the basal valve plane was identified in the CT images, manually segmented, and triangulated in ITK-SNAP (www.itksnap.org; Yushkevich et al., 2006). The coordinate frame of the resulting geometry was rotated to coincide with the ECG reference frame: the positive x-direction corresponds to right to left (lead I), the positive y-direction corresponds to superior to inferior (lead aVF), and the z-direction corresponds to anterior to posterior (~ lead -V1). A generic biventricular control mesh (132 elements, Δx ~12.5 mm) with linear hexahedral elements was manually overlaid onto the endocardial and epicardial surfaces of the triangulated segmentations. The resulting linear mesh was converted into a high-order cubic Hermite mesh with extraordinary vertices (Gonzales et al., 2013). The mesh was subdivided thrice in a 1-8 fashion to the final level of refinement (67,584 elements, Δx ~ 2 mm) for electrophysiology simulations.

Regions of myocardial infarction were identified from sestamibi perfusion images during stress and rest in the two ischemic patients. The boundaries of the regions were manually demarcated on the anatomical meshes by an expert cardiac electrophysiologist (DEK); Patient 1 had a posteroseptal infarction, and Patient 2 had an inferior infarction. The regions were registered in the anatomical model as a binary field of normal and infarcted tissue.

The myofiber architecture was estimated empirically using a log-Euclidean interpolation framework previously described (Krishnamurthy et al., 2012; Aguado-Sierra et al., 2011 et al; Fillard et al., 2007; Arsigny et al., 2006) for registering DT-MR measurements to the anatomical models. Briefly, DT-MR images of an isolated human donor heart were obtained. The reconstructed diffusion tensors were fitted as a field of the log-transformed components in a corresponding anatomical mesh to interpolate local fiber, sheet, and sheet-normal axes. The fiber orientations in the resulting model were mapped to each patient via large-deformation diffeomorphic mapping (Cao et al., 2005) and reoriented based on the 3D deformation gradients between the template and target patient ventricular geometries to account for the effect of ventricular shape differences on fiber orientation (Alexander et al., 2001). The resulting fiber-sheet model formed the local basis of transversely isotropic electrical conductivity with a fiber-sheet anisotropy ratio of 7.

2.3.2. Electrophysiology model

Myoctye transmembrane potentials are described by a recent model of human ventricular myocytes (ten Tusscher, 2006) which was modified to accommodate changes in channel kinetics during heart failure (Aguado-Sierra, 2011). Action potential propagation was modeled in a monodomain reaction-diffusion framework. Electrical conductivity in the ventricular domain was partitioned into LV and RV subendocardial regions (~3 mm transmurally), infarct region, and the remaining bulk myocardium. The conductivity in the endocardial regions was allowed to vary up to 10 times that of bulk myocardium (Aguado-Sierra, 2011) to account for the fast conduction of the Purkinje system which was not explicitly modeled. In infarcted regions, conductivity was isotropic and allowed to vary between 10% - 90% of that in the bulk myocardium.

2.4. Model parameter optimization to derived VCG

The electrophysiological model was parameterized by a single ectopic stimulus site and regional electrical conductivity values which were optimized to simulate an activation sequence with a VCG that best matched the measured VCG. Stimulus sites were sampled at 118 locations (~ 4 mm spacing) in the RV endocardium spanning from apex to base and anterior to posterior septal junctions. Stimuli were applied for a duration of 5 ms at a magnitude of 80,000 αA/cm³. Electrical conductivity in the sheet direction of the bulk myocardial regions (σ_bulk) was sampled in the range of 0.0001 to 0.004 cm²/ms. Electrical conductivity ratios with respect to σ_bulk in the LV (λ_LV) and RV (λ_RV) subendocardial regions were sampled in the range of 1 (myocardial conduction) and 10 (fast Purkinje conduction). A simulation database of the solutions of all possible parameter combinations (approximately 600) was created for each patient. Due to the computational cost of searching the parameter space, we made a first approximation of the optimal parameters in a coarse mesh (8448 elements, Δx ~4 mm). The approximate optimal stimulus location for the coarse mesh was found and applied in the nominal mesh. The conductivities in the nominal mesh were adjusted to match the total activation time of the initial optimal approximation.

We utilized an objective function Θ to compare the orientations of the simulated and measured cardiac dipoles:

$$=\frac{1}{\mathrm{tot}}\sum ^{t_{\mathrm{tot}}}\frac{\mid {\tilde{v}}_t^m\mid }{\mid {\tilde{v}}_p^m\mid }\left(\frac{\theta \mathrm{acos}\left(\frac{{\tilde{v}}_t^s\cdot {\tilde{v}}_t^m}{\mid {\tilde{v}}_R^s\mid \mid {\tilde{v}}_R^m\mid }\right)}{\pi }\right)$$

where at time t, ${\tilde{v}}_t^m$ is the measured dipole (VGC), ${\tilde{v}}_t^s$ is the simulated dipole, ${\tilde{v}}_R^m$ is measured dipole at R peak , and ${\tilde{v}}_R^s$ is the simulated dipole at the R peak, and t_tot is the total measured activation time. The objective function computes the weighted timeaverage of the dot products between the two dipoles. Note that Θ is computed between 3D dipoles and represents the maximal angle in the plane containing them. Weighting by the relative strength of the measured signal gives more importance to deviations between dipoles with greater magnitude.

3. Results

3.1 Clinical electrophysiological measurements

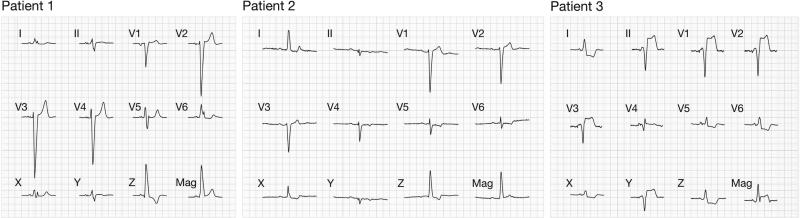
The recorded ECG and computed VCG for each patient are shown in Figure 2. Indications for LBBB (Daubert, 2012) include the following: QRS durations for Patient 1, Patient 2, and Patient 3 were 152 ms, 148 ms, and 115 ms, respectively. All ECGs exhibited rS patterns in leads V1 – V3 which transitioned into RS patterns in the lateral leads. Discordant T-waves are also a consistent feature in the precordial leads for all patients. Mid-QRS notching was present in lead I and V6 for Patient 1 and lead II for Patient 2. In Patient 3, measurements were taking during right ventricular apex pacing which closely approximates LBBB activation pattern. The RV pacing lead was positioned at the posterior septal surface near the RV apex during an ICD insertion procedure. The derived VCG loops were oriented primarily from RV to LV and apex to base, indeed confirming a right to left activation sequence. In Patient 3, the loop was oriented anteriorly. We estimated a 12.5±2.2° variability in the derived VCGs between the Kors and inverse Dower transformations by computing Θ between the two derived VCGs for each patient.

Figure 2.

Recorded surface ECG and derived VCG traces for a single beat for all three patients. The top two rows show the recorded limb leads I – II and precordial leads V1 – V6 for VCG derivation. The computed VCG components and magnitude (Kors transformation) are shown in the third row. One large grid has dimensions 200 ms × 0.5 mV.

We estimated the measurement error in the activation times and spatial coordinates of the electroanatomic contact maps. To estimate the timing error, we measured the variability of the QRS onset as automatically detected for all beats in the surface ECG for each patient and found it to be in the range of 7–11 ms. Assuming the same uncertainty in the intracardiac electrogram of the roving catheter, the combined uncertainty results in an activation time noise floor in the range of 10–16 ms. We accounted only for measurements made by physical contact with the endocardial surface in our analysis to minimize systematic and methodological bias by the electroanatomic mapping software which can densely interpolate endocardial surface geometries for the LV and RV. The total number of contact measurements were 63 for Patient 1 (25 RV, 38 LV), 21 for Patient 2 (7 RV, 14 LV), and 22 for Patient 3 (11 RV, 11 LV). The contact measurements were registered to the anatomical model by translation and rigid rotation of the interpolated endocardial surfaces to the centers of the LV and RV cavities; interpolated measurements representing the lateral walls were positioned closest to the lateral walls of the model. Separate affine transformations were applied to the LV and RV electroanatomic measurements for direct comparison to the nearest points on the endocardial surface of the anatomical model. The mean distance of the final measurement locations to the model surfaces was 5 mm.

3.2. Optimization of cardiac dipole orientation

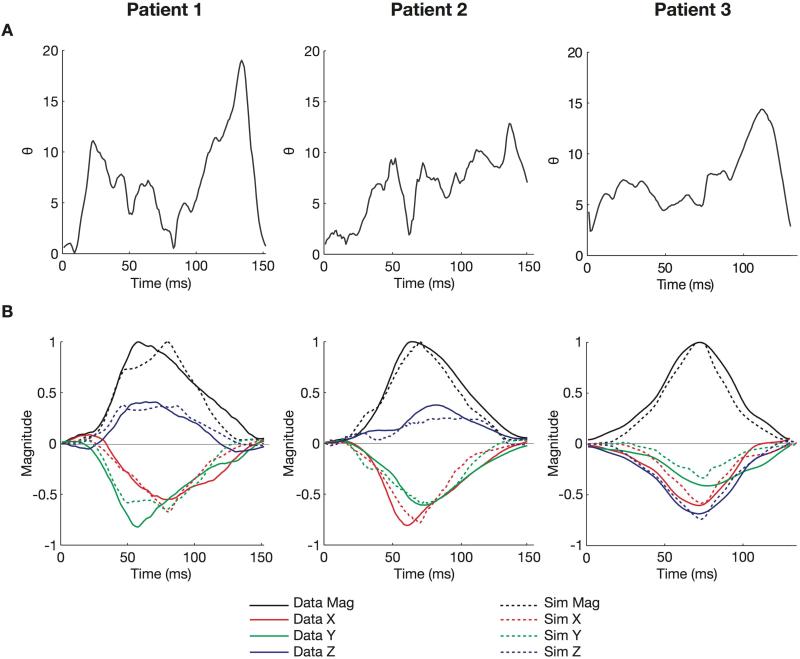
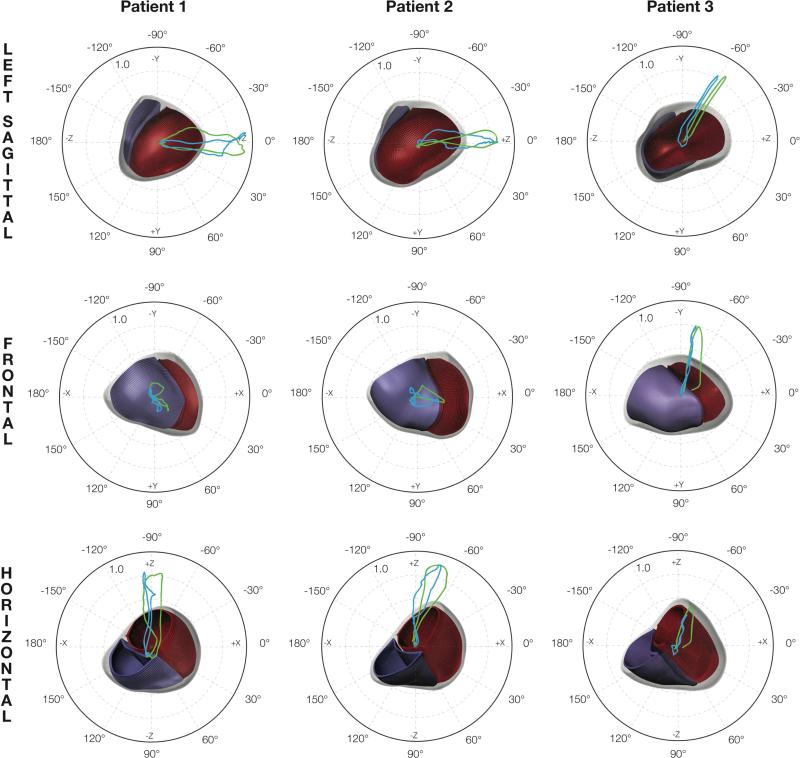
The objective Θ was computed for VCGs derived from both Kors and inverse Dower transformations. A parameter set was identified as optimal if it ranked in the top ten best parameter sets in both VCG comparisons and were within 5 ms of the measured total activation time. The simulated total activation times were 157 ms (152 ms measured) for Patient 1, 150 ms (148 ms measured) for Patient 2, and 120 ms (116 ms measured) for Patient 3. Table 3 lists the optimal parameter values and corresponding values (compared to Kors only): 7.6° for Patient 1, 6.1° for Patient 2, and 6.5° for Patient 3. The time course of is shown in Figure 3 (A). For all patients, instantaneous Θ values were typically less than 10° and deviated by no larger than 20°. The VCG traces of the measured and optimal VCG are compared in Figure 3 (B). The morphologies and relative magnitudes of the simulated VCG components agree with the measurements. The 3D orientations of the VCG loops are compared with respect to the ventricular anatomy in Figure 4. Predicted early activation sites in the RV shown in Figure 5 (B) are located anteriorly in Patient 1, laterally in Patient 2, and close to the known RV apex lead location in Patient 3.

Table 3.

Optimal electrophysiology parameter values and corresponding VCG objective (θ) and local activation time σ_AT errors. Patient 3 did not have a myocardial infarction.

Patient	Stimulus location	σbulk(cm2/ms)	λ LV	λ RV	λ scar	θ (°)	σAT (ms)
1	Anterior RV	0.0002	1	1	0.9	7.6	12.6
2	Lateral RV	0.0006	1	3.33	0.9	6.1	10.9
3	Posteroapical RV	0.0005	1	1	--	6.5	11.0

Figure 3.

Summary comparisons between optimal and measured VCGs. (A) The time course of the cost value Θ(°) during activation. (B) Comparison of the peak-normalized magnitude (Mag), X, Y, and Z components of the optimal simulated (dashed line) and measured (solid line) VCGs (for Kors transformation).

Figure 4.

Comparison between optimal simulated and measured peak-normalized VCG loops. The loops represent the spatial trajectory of the tip of the cardiac dipole with its tail at the origin. The polar plots show the projections of the simulated (blue) and measured (green) VCG loops (Kors transformation) on to the left sagittal, frontal, and horizontal planes. The relative orientation of the loops to the anatomical meshes (red – LV endocardial surface; blue – RV endocardial surface) is illustrated.

Figure 5.

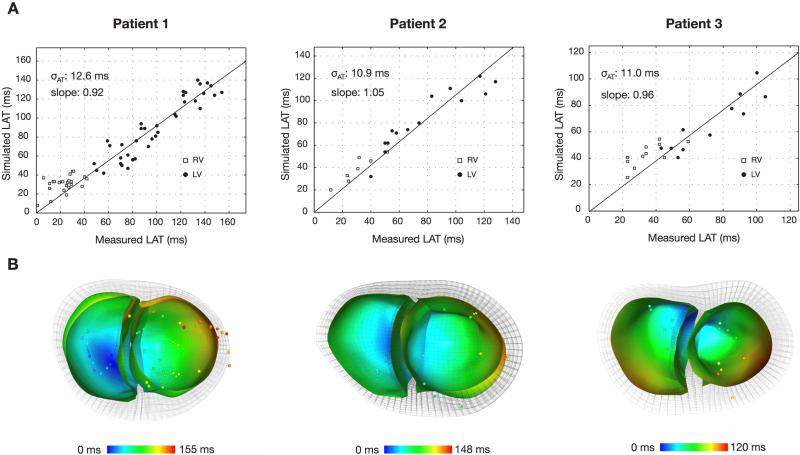
Comparison of local activation times between optimal activation patterns and electroanatomic measurements at corresponding points on the endocardial surface. (A) Plots of the simulated and measured activation times with parameters of the regression line are shown. (B) Short-axis views of the optimal activation patterns on the RV and LV endocardial surfaces of the anatomical mesh with electroanatomic measurements superimposed at corresponding locations.

3.3. Validation to electroanatomic maps

We compared the optimal activation maps with the registered electroanatomic measurements. Figure 5 shows the point-by-point comparison of the electroanatomic measurements and the corresponding nearest point on computed a linear regression of the corresponding activation times and measured the the endocardial surface. We computed a linear regression of the corresponding activation times and measured the scatter δ_AT (one standard deviation) of local activation times about the line to determine goodness-of-fit. The scatter was 12.6 ms for Patient 1, 10.9 ms for Patient 2, and 11.0 ms for Patient 3. Overall, the activation time scatter was on the order of the estimated measurement precision.

4. Discussion

In the present study, we have demonstrated that patient-specific models of ventricular depolarization can estimate LBBB and RV-paced activation sequences from VCGs generically derived from routine 12-lead body-surface ECGs within the accuracy of invasive measurements. We estimated the activation sequence of a single depolarization wave by recapitulating the time course of the total cardiac dipole with an optimal set of electrophysiology model parameters. We show good agreement between the predicted activation sequence and invasive electroanatomic measurements of endocardial activation times to within measurement precision. In addition to providing a quantitative estimation of 3D activation pattern in patient-specific ventricles, a detailed transmembrane current model which includes calcium kinetics also allows extension of the model to contractile ventricular mechanics (Krishnamurthy, 2012).

A reduced ionic model would have been sufficient to predict similar LBBB and RV-paced activation patterns as those obtained with the ten Tusscher model. Simplified FitzHugh-Nagumo-like models are of lower computational cost partly due to slower depolarization kinetics. Although the predicted activation patterns may be similar, the reduced rate of the potential upstroke at the wave front of a FHN-like model would result in different potential gradients and cardiac dipoles. This difference does not necessarily invalidate our approach, but it could obfuscate comparison of simulations to measurements.

Activation patterns were estimated on the basis of the objective function Θ which compares deviations between simulated and measured cardiac dipole orientations. Since a direct comparison of absolute time-voltage tracings was not possible due to incomplete lead position data, Θ was intended to compare the relative magnitudes of orthogonal activation dipole components. Deviations in dipole orientations are weighted by the R-peak normalized magnitude of the measured dipole. Since VCG loop shape and size are functions of the absolute dipole magnitude, it may be possible for loops of different shape and size to show good agreement if the relative ratios of the VCG components agree at times near the peaks of the measured signal.

4.1. Numerical convergence

We verified the numerical convergence of the simulated dipole orientations and activation times by comparing the results of the coarse and nominal meshes. For our purposes, a sufficiently converged wave front was taken as one that could recapitulate the dominant morphology and features of the measured VCG and produce activation patterns that were independent of mesh resolution. We compared the mean cost values in a representative solution for a coarse and nominal mesh with the same parameters (stimulus location, scar and endocardial conductivities and adjusted bulk conductivity for equal total activation time). The mean difference in dipole orientation between the coarse and nominal meshes was less than 5°. Considering that the uncertainty of the dipole orientations derived from measurements due to a generic transformation is approximately 10°, the VCGs are converged to within estimated limits of accuracy of the measured signals. The predicted activation times of the coarse and nominal meshes at corresponding anatomical locations also have a RMS difference of approximately 4 ms which is within the limits of the accuracy of the data (~10 ms).

4.2. Limitations

The validity of the activation pattern estimation approach using the VCG rests on the condition that depolarization wave dynamics can be simply approximated by a single dominant excitation wave and described unambiguously by a single rotating fixed dipole. This assumption holds for activation patterns such as true LBBB (Strauss, 2011; Auricchio, 2004; Rodriguez, 2003) and RV pacing. The electrophysiology model assumes this condition by including a single RV activation site without a detailed description of the cardiac conduction system. Intact cardiac conduction in the present model is approximated by allowing rapid electrical conduction of the LV and RV subendocardial layers relative to the bulk myocardium. Our results show that with the current degrees of freedom, the model can capture the features of a simple rotating dipole representation of depolarization in conditions of LBBB and RV-paced activation within the measurement limits of accuracy. However, most arrhythmias and activation sequences in disease states typically involve complex wave dynamics with multiple wave fronts (Vaquero, 2008). In these more general cases, a single activation site and fixed dipole equivalent source model would be unable to describe ventricular depolarization patterns in detail.

The lack of precise lead position information warranted the use of a patient-generic ECG to VCG transformation. Transformations such as Kors represent the average effects of heart size, body size, lead position, and heart orientation of a wide patient population and do not account for patient-specific torso properties. We estimated the error due to different transformations (Kors vs. inverse Dower) to approximately 10° to limit the accuracy we can expect to match measurements. We attempted to normalize out the effects of heart size, location, and body habitus by considering only the relative signal magnitudes and dipole orientation relative to the cardiac anatomy. We estimated the relative orientation of simulated dipoles to the measurements by co-registering the ventricles and VCG reference frame using the CT images. Compression of the 12-lead ECG to three orthogonal leads has been shown by factor analysis to preserve 99% of the original data content, with little information added by additional leads (Schreck et al., 1998). A full 12-lead description of the signal would be more valuable for patient-specific torso models where the individual lead positions are known. Future studies may include lead position measurements by leaving the 12-lead ECG electrodes in place during the CT scan or applying radiopaque markers in the same locations as the leads. Detailed lead position information in a patient-specific torso model would also allow direct comparison of the simulated voltage-time traces to actual body-surface electrocardiograms or invasive electrograms as an additional validation of the model.

The present model focuses on ventricular depolarization in heart failure. Heart failure is a complex disease state with changes in ventricular shape, fiber orientation, and ion channel expression remodeling. The anatomical model accounts for the gross fiber architecture remodeling in dilated ventricles by mapping the architecture of a human DT-MRI dataset according to differences in ventricular shape. Similar approaches to estimating fiber architecture have been described and validated by other groups (Vadakkumpadan et al., 2012). It is currently impractical to measure patient-specific fiber orientations using invivo DT-MRI. A generic phenotype of HF-induced electrophysiological ion channel remodeling is described by a modified ten Tusscher transmembrane current model (Aguado-Sierra et al., 2011) and does not fully account for patient-specific HF ionic remodeling. The present model may be extended to estimate ventricular repolarization and atrial activation. Transmural ion channel heterogeneities of action potential morphology in HF remodeling and more stringent steady state convergence of electrical properties (e.g. APD restitution and conduction velocity) are required for accurate steady and non-steady state predictions of T-wave morphology. A more detailed description of the geometry, conductivity, and fiber orientation in infarcted regions are also necessary to account for T- wave modulations effected by a scar. Estimation of atrial activation from the P-wave would require at least a different generic VCG transformation to account for the difference in the location of the origin of the atrial dipole from the ventricular dipole (Guillem, 2006). An appropriate anatomical model must also incorporate the geometry and fiber orientations of the valvular plane and atrial chambers.

5. Conclusion

We have described a method to estimate three dimensional LBBB and RV-paced activation patterns based on VCG derived from routine body-surface ECG using patient-specific computational models of HF electrophysiology. The early RV stimulus site and myocardial conductivities in the model are optimized by minimizing the total deviation of simulated and measured cardiac dipole orientations during activation. The activation pattern predicted by the optimal parameters agrees with invasive measurements of endocardial activation time. This approach has potential to advance solution techniques for noninvasive electrocardiographic imaging and extend the utility of patient-specific computational models in clinical diagnosis and therapy planning.

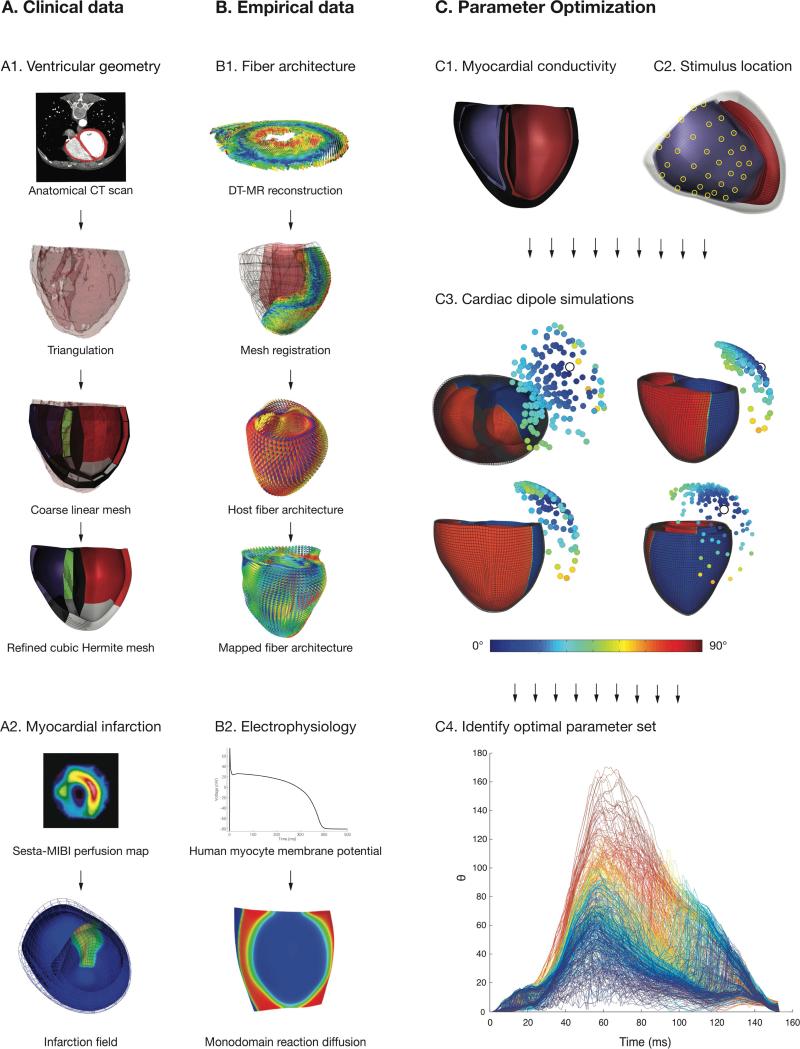
Figure 1.

Overview of the complete patient-specific computational model of LBBB activation. The four main components of the model are derived from (A) clinical measurements of (A1) ventricular geometry and (A2) myocardial infarction and (B) empirical data of (B1) fiber architecture and (B2) cellular and tissue electrophysiology. (C) Parameter optimization is performed by simulating activation from combinations of (C1) prescribed regional conductivity values and (C2) stimulus locations. (C3) The deviation (Θ) in dipole orientation between the measured and simulated dipoles during activation was computed for all parameter combinations (shown here at t = 80 ms for Patient 1; R at 56 ms); the circles represent the units vector tips of simulated dipoles, and the color (blue to green to red) reflects the orientation deviation (0° – 45° – 90°) with the measured vector (tip marked by white circle). (C4) The time course of deviations for all simulated parameter sets in one patient, with the time-averaged value of Θ(0° – 90° – 180°) for each trace represented by the color (blue to green to red); the solution of the parameter set with minimal and total activation time within 5 ms of the measured duration was chosen as optimal.

Table 2.

Range of tested electrophysiology parameter values.

Stimulus locations	σbulk(cm2/ms)	λLV, λRV	λ scar
118	1e-4 – 4e-3	1 – 10	0.1 – 0.9