A comprehensive biophysical description of pairwise epistasis throughout an entire protein domain

SUMMARY

Background

Non-additivity in fitness effects from two or more mutations, termed epistasis, can result in compensation of deleterious mutations or negation of beneficial mutations. Recent evidence shows the importance of epistasis in individual evolutionary pathways. However, an unresolved question in molecular evolution is how often and how significantly fitness effects change in alternative genetic backgrounds.

Results

To answer this question we quantified the effects of all single mutations and double mutations between all positions in the IgG-binding domain of protein G (GB1). By observing the first two steps of all possible evolutionary pathways, this fitness profile enabled the characterization of the extent and magnitude of pairwise epistasis throughout an entire protein molecule. Furthermore, we developed a novel approach to quantitatively determine the effects of single mutations on structural stability (ΔΔG_U). This enabled determination of the importance of stability effects in functional epistasis.

Conclusions

Our results illustrate common biophysical mechanisms for occurrences of positive and negative epistasis. Our results show pervasive positive epistasis within a conformationally dynamic network of residues. The stability analysis shows that significant negative epistasis, which is more common than positive epistasis, mostly occurs between combinations of destabilizing mutations. Furthermore, we show that although significant positive epistasis is rare, many deleterious mutations are beneficial in at least one alternative mutational background. The distribution of conditionally beneficial mutations throughout the domain demonstrates that the functional portion of sequence space can be significantly expanded by epistasis.

INTRODUCTION

Epistasis, within and between genes, is thought to play an essential role in the ability for protein sequences to evolve through neutral drift or adaptation [1, 2]. While contingencies in fitness limit pathways of divergence, permissive mutations reveal “cryptically beneficial” substitutions [3] that increase the number of acceptable mutations [4]. Epistasis can be explained in physical terms by investigating the biochemical effects of mutations singly and in combination [5]. Examples include evolution of a switch in glucocorticoid receptor-ligand specificity [6], increased hemoglobin affinity to O₂ in high-altitude deer mice [7], and antibiotic resistance in a β-lactamase variant [8], which all rely on non-additive combinations of mutations.

The importance of epistasis is evident for organisms such as influenza which accumulate mutations at a high rate and adapt rapidly in response to immunological and drug pressure [9, 10]. Gong et al. demonstrated how an evolutionary pathway in influenza nucleoprotein required permissive stabilizing mutations prior to gaining certain adaptive substitutions that alone disrupted protein structure [10]. Indeed, most mutations destabilize protein structures [11, 12] and directed evolution experiments show that a large fraction of mutations are deleterious for function [13]. It was recently shown that 63 of 168 mutations chosen from a homologous protein with the same function were deleterious when substituted alone and thus epistatic interactions are necessary to preserve function [14].

While these examples show epistasis is essential in individual evolutionary pathways, these examples do not address whether combinations of mutational fitness effects are typically epistatic. How likely is it that a mutation has the same fitness in two different genotypes? Historically, protein engineering experiments have shown the effects of mutations on protein function are typically energetically additive [15–18]. Furthermore, next generation sequencing technology has enabled the analysis of very large numbers of mutational pairs in experimental evolution which also show that fitness effects are usually additive [19, 20]. Here, we sought to determine whether this observation of general pairwise additivity conflicts with the apparent pervasiveness of epistasis in light of mutational sensitivity [14]. By analyzing the first two steps of all possible evolutionary pathways, we can determine the frequency of pairwise energetic non-additivity.

Such a comprehensive analysis is necessary in order to determine how often deleterious mutations can be compensated by at least one additional mutation, and, likewise, how often neutral or beneficial mutations can be negated by an additional mutation. To do this, we characterized a comprehensive fitness map of single and double mutants within protein G domain B1 (GB1) that was highly correlated to binding affinity to IgG-FC (K_A). GB1 is well characterized structurally and is a classical model protein for folding and stability studies [21–24]. While small, GB1 is a stable, compact, and highly soluble protein with no disulfide bonds. The structure includes an α-helix packed against a 4-stranded β-sheet which are connected by four short loops. This extensive structural and mutagenic characterization of GB1 provided a substantial reference for validating our fitness map.

Furthermore, we were able to use the fitness map to accurately predict the effect of all non-lethal single mutations on structural stability (ΔΔG_U). This was accomplished by identifying destabilized mutational backgrounds in which the binding data reflects a change in fraction folded upon addition of secondary mutations. Thus, our fitness map enabled us to identify common biophysical mechanisms of both negative and positive epistasis. For example, we show that exhaustion of the intrinsic stability reservoir, or threshold robustness [25–27], largely accounts for examples of significant negative epistasis. Stabilizing substitutions, which are rare, produce positive epistasis although with a smaller magnitude compared to combinations of destabilizing mutations. We also describe long-range positive epistasis that is pervasive within a highly conformationally dynamic network of residues. Our results confirm that epistasis is rare and also that many mutations are detrimental to function. However, this comprehensive fitness profile shows that many deleterious mutations are compensable by at least one of the numerous possible secondary mutations. Together these results provide an empirical, biophysical description of epistasis and resolve how rare non-additivity can contribute to the extensive divergence of protein sequences as observed in nature.

RESULTS AND DISCUSSION

High resolution GB1 double mutant affinity profile

We developed a cassette saturation-mutagenic approach for assembling a library that includes all single and double mutations within the 56 residue GB1 domain (excluding Met1) (Figure 1, Figure S1 and Table S1). Two technical hurdles were overcome in thus study: the ability to error correct and the ability to build a library that is focused on one or two amino acid mutations throughout the entire 55 codon random region. To enable sequencing error correction, each cassette included internal barcodes (Figure S1A). Linking saturation-mutagenized cassettes was accomplished in a sequence-independent manner by using a type IIs restriction endonuclease (BciVI) (Figure S1B). After digestion, a single, degenerate M (A/C) overhang on 3’ fragments enabled specific ligation to a G, T, or K (G/T) overhang on 5’ fragments.

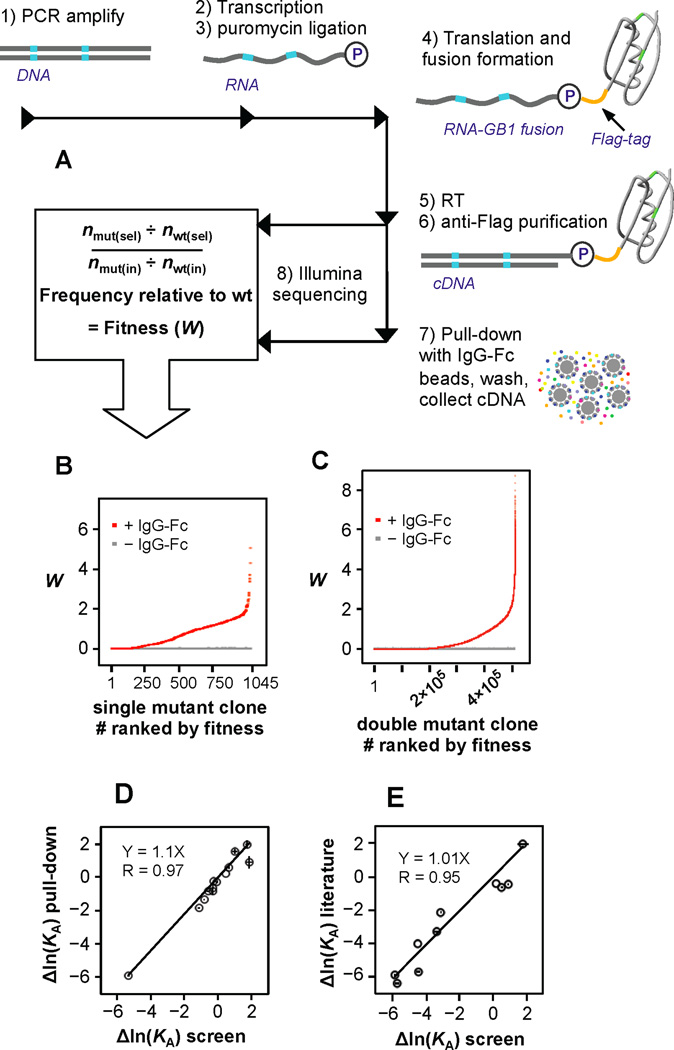
Figure 1. mRNA display fitness profile scheme.

(A) A DNA library encoding all single and double mutants in GB1 was created (See also Figure S1). mRNA display was used to profile the relative binding efficiency of all variants. After a single generation of affinity enrichment, the relative fitness (W) for each variant was determined from the change in sequence frequency as identified by Illumina sequencing. (B) The binding fitness (red dots) of each single mutant and (C) all high-confidence double mutants (see Figure S1E). The gray dots represent the contribution to W from background binding to beads which was determined from a control lacking IgG-FC. (D) Thirteen clones were constructed and expressed in vitro with a ³⁵S-Methionine label for comparison to fitness determined by the screen. Binding efficiency (see also Figure S1D) was used to estimate relative affinity (see the Experimental Procedures). Error bars representing standard deviation from the triplicated screen are shown (X-axis) and from the pull-down when performed in triplicate (Y-axis). (E) Correlation of Δln(K_A) from the screen to Δln(K_A) for 10 variants reported in the literature (see Table S3).

The use of in vitro display technologies to analyze the effects of individual mutations on binding function is well established [28, 29]. Next generation sequencing has greatly expanded the ability to analyze mutational fitness effects quantitatively [30]. In this study, relative binding affinity of all single and nearly all double amino acid mutants to IgG-FC was characterized using mRNA display [31]. mRNA display is an in vitro genetic system in which peptides are covalently linked to their encoding mRNAs (Figure 1A) typically used to evolve novel molecular recognition tools [31, 32]. Here, we used deep sequencing combined with mRNA display to monitor the evolution of GB1 mutants in real time after one generation of affinity enrichment (Figure 1A).

By measuring the frequency of each variant before and after enrichment (Table S2), we determined relative binding efficiency, or fitness (Figure 1B,C and Figure S1D, see the Experimental Procedures). While fitness is traditionally a population-genetics term, protein fitness can be defined [30, 33, 34] and here relative fraction bound is analogous to a classical definition of relative fitness (W), which is the number of progeny relative to wild type per generation. The conditions of this screen, in which the concentration of IgG-FC is below the K_D of wt GB1, provided a large dynamic range in observed fitness effects, from 100-fold below to 8-fold higher than wild type fitness (Figure 1B,C). Thus, our evolution experiment investigates affinity-based adaptation for improved or new function. We caution that this extremely simplified, noncompetitive evolutionary experiment has many differences in comparison to natural evolution and the relationship between affinity and in vivo fitness will not be directly correlated for many proteins, especially considering many proteins are multifunctional. However, there are examples in natural evolution such as viral host switching which show a relationship between affinity of host-adapted RBD variants and viral infectivity in cell culture [35].

Using a Poisson-based 90% confidence interval, we determined that the fitness effects of all 1,045 single mutants were determined with high confidence and 509,693 double mutants (95.1% of all) were characterized with high confidence (Figure S1E). Importantly, the high confidence data set includes abundant double mutants throughout all 1,485 possible positional pairs (Figure S1E). The single generation of affinity enrichment was performed in triplicate and Figure S1F shows that the single mutant fitness profiles are highly correlated (R>0.996 for all three comparisons). Thus the binding, PCR, Illumina adapter ligation, and sequencing steps are highly reproducible. Furthermore, we included a no-IgG control to show that background binding does not affect fitness calculations for any variant, including mutants known to be unfolded (Figure 1B,C).

We also show W can be used to approximate relative affinity (K_A-mut/K_A-wt) similar to the “shotgun scanning” approach [29] (see the Experimental Procedures). This was used to facilitate validation and enable the comparison of energetic effects to fitness effects. We show that Δln(K_A) values predicted by this screen are highly correlated to that of 13 single or double mutants reconstructed and analyzed for validation by an in vitro pull down assay (Figure 1D). Furthermore, Δln(K_A) predicted by the screen is highly correlated to that of an addition ten variants independently reported in the literature (Figure 1E, Table S3).

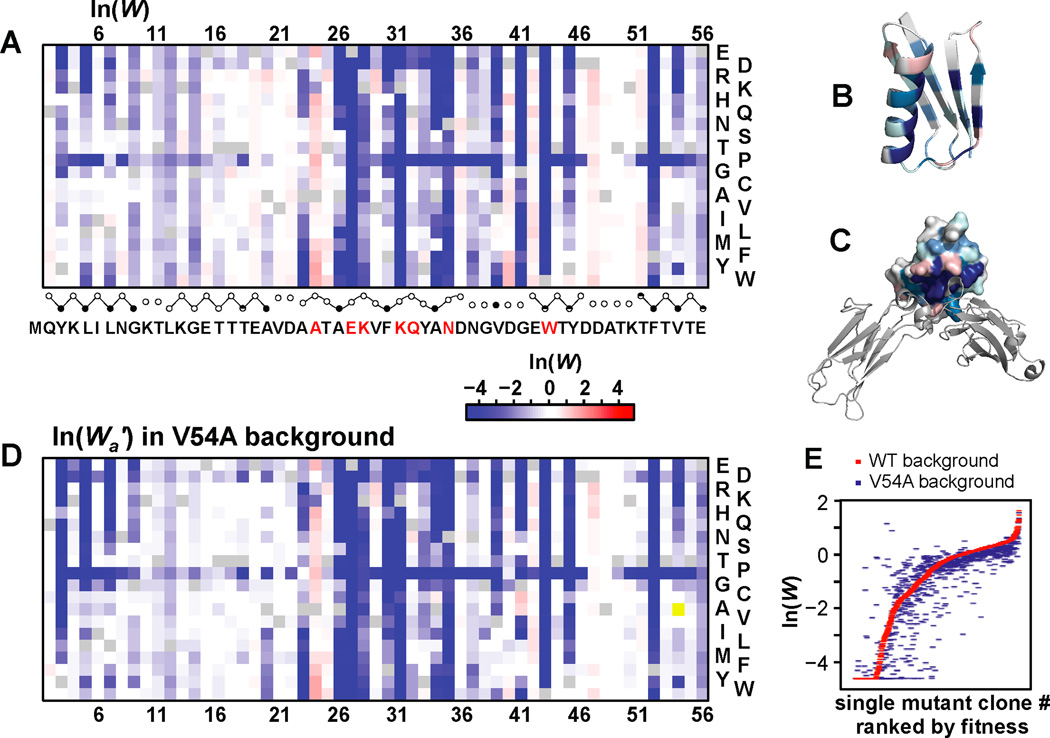
Figure 2A depicts ln(W) as a heat-map for all 19 single mutants at each position. The average ln(W) values per position are displayed on GB1 structures alone or in complex with IgG-FC (Figure 2B,C). As expected, core residues are sensitive to substitution [36] indicating severe structural destabilization or that small changes in structure that accommodate core volume changes might adversely affect binding affinity [37, 38]. Surface residues that are sensitive to mutation correlate with alanine scanning mutagenesis [39] and clarify relative importance for ligand recognition [21]. However, beneficial and detrimental surface mutations are found throughout the domain, thus highlighting the importance of such comprehensive screens for characterizing the sequence determinants of functionality [28, 30, 40–43]. For example, alanine scanning could not uncover the importance of position Thr25 where acidic substitutions are highly deleterious and basic substitutions are highly beneficial while Ala is neutral [39] (Figures 1E and 2A).

Figure 2. Affinity profile validation and fitness maps.

(A) A heat-map depicting fitness of all single mutants. Residues previously determined to interact with IgG-FC [21] are highlighted in red. The fraction side-chain solvent accessibilities (closed<0.1, partial>0.1, open>0.4 circles) are depicted below. Circles are connected by straight or curved lines to delineate β-strands and the α-helix, respectively. (B) Average ln(W) plotted on GB1 (PDB 1PGA) [54] and (C) the complex between protein G domain C2 (space filled) and IgG-FC (cartoon) (PDB 1FCC) [21]. (D) A heat-map depicting fitness of all single mutants in the background of V54A. (E) Comparison of the fitness profile to fitness effects in the background of V54A. See also Figure S2.

The double-mutant fitness landscape is depicted as a heat-map showing all high confidence double mutants (up to 361) for all 1485 positional pairs (Figure S2A). The comprehensive nature of this screen enables an alternative approach to interpret this data by showing the fitness of all substitutions (“a”) in alternative mutational backgrounds (“b”). For example we show the fitness effects of all single mutants (W_a’) in the background of V54A (Figures 2D,E). V54A alone is functionally neutral, however, certain positions become more sensitive to mutations while others change from deleterious to beneficial, notably at position Gly 41 (Figure 2D) (vide infra). Furthermore we show how the fitness of all mutations will change in the background of highly adaptive mutations, such as A24E, which is observed in nature (Figures S2B–D). In this background the functional test is less stringent (i.e. the K_D of A24E is closer to [IgG]) and thus the distribution of fitness effects (DFE) [44] shifts significantly (Figure S2E–G) as it would in a less stringent test of fitness (Figure S2H).

Frequency and proximity of epistatic interactions

Figures 2D and 2E show certain mutations display a change in fitness in combination with V54A and are thus epistatic. Various models can be used to determine whether combinations of mutations display epistasis (ε) [19, 45, 46]. The difference between the fitness in Figure 2D and the fitness in figure 2A produces one measure of epistasis [ε=ln(W_a’)−ln(W_a)], which is identical to the relative epistasis model described by Kahn et al. [ε=ln(W_ab)−ln(W_a)−ln(W_b)] [45]. We show that the relative model is suitable for the highly adaptive landscape of this experiment (Figure S3A). Here, epistasis (ε) refers to the relative model unless stated otherwise.

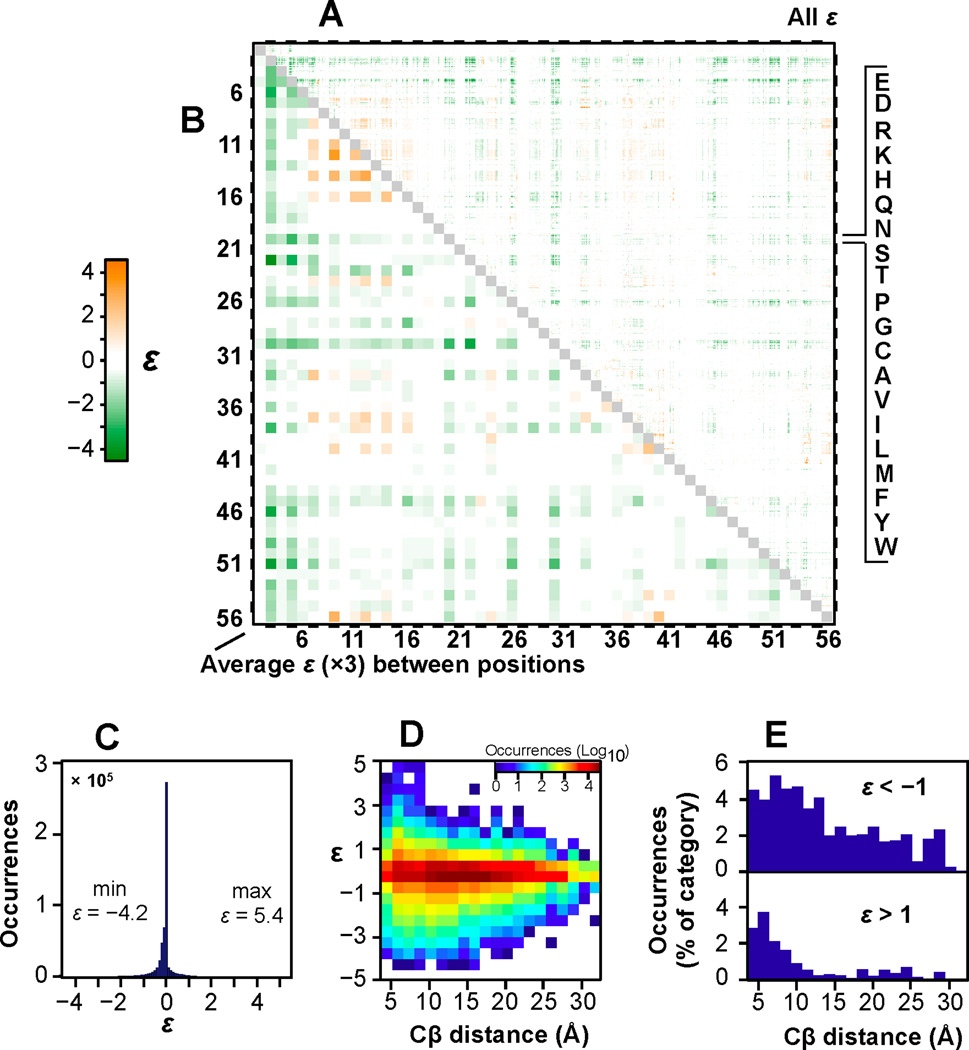
We displayed ε for all observed double mutants (Figure 3A) and the average ε for all substitutions at each pairwise positional combination (Figure 3B) as a heat map. In addition to the 509,693 high confidence variants, 7,585 variants were unambiguous in sign or significance in ε resulting in characterization of 96.5% of all pairs. The 90% confidence interval (see above and the Experimental Procedures) was used to minimize epistasis resulting from very low fitness double mutants which could display very large fold-change in observed compared to expected fitness due to statistical noise. All 1,485 pairwise positional combinations are represented (Figure S1E) thereby providing a comprehensive description of epistasis throughout the entire protein molecule.

Figure 3. Pairwise epistasis map throughout GB1.

(A) A heat-map depicting epistasis for 517,278 double mutants (96.5% of all possible). The amino acid order is listed top to bottom and is the same left to right. Each of the 1485 pairs display 19×19 sequence variants. (B) Average ε for all sequence combinations at each positional combination multiplied by a factor of 3 in order to match the range of the color bar. (C) Histogram showing extent of epistasis (increments of 0.1). (D) Two dimensional histogram relating ε to Cβ distances in 1PGA [54]. (E) |ε|>1 as a percentage of total occurrences in each Cβ distance bin. See also Figure S3.

Generally, mutational pairs interact additively or nearly additively and thus strongly epistatic pairs are rare (Figure 3C, Figure S3B–G). This observation is in agreement with two recent large scale analyses of epistasis [19, 20]. It is worth noting that while only a fraction of all double mutants display |ε|>1 (~4%), there are nonetheless thousands of such epistatic pairs (Figure S3B–C). We also show that epistasis is similarly rare when calculated using another common epistasis model, the product model (Figure S3E,F) [19]. Importantly, due to the low frequency or small magnitude of epistatic effects, the observed double mutant DFE is nearly identical to the expected distribution (Figure S3H–L). While lethal double mutants are slightly more frequent than would be predicted based on a model without epistasis (Figure S3H), this demonstrates the predictability of the distribution of multiple mutant fitness effects in this adaptive landscape. We also show that observed relative epistasis in this experiment closely matches a model of energetic non-additivity (scaled by −1/RT) (Figure S3M,N) [18]. The differences resulting from the nonlinear nature of the relationship between fraction bound and affinity are numerous but relatively small (Figure S3M). This would not be observed in a test of mutational robustness for well-adapted proteins as is depicted by the DFE in Figure S2H.

As expected, strongly epistatic pairs tend to be close in space although very large negative epistasis (ε<−3) can be long range (Figure 3D). However, most neighboring residues do not display either form of epistasis (Figure 3E). Even considering interactions within 6Å (Cβ), only 8.1% display |ε|>1. Thus, for many mutations binding fitness is independent of the background in which one appears. For positions that are energetically coupled, double mutants might be predicted to display either negative or positive epistasis depending on the physicochemical nature of the two amino acid substitutions. To highlight an example, the maps showing ln(W) and ε for all 361 amino acid combinations at positions 32 and 36 are enlarged (Figure S3O,P). However, an interesting observation from Figure 3A and 3B is that some positional combinations, including long-range combinations, display either negative or positive epistasis in general.

General negative epistasis throughout GB1

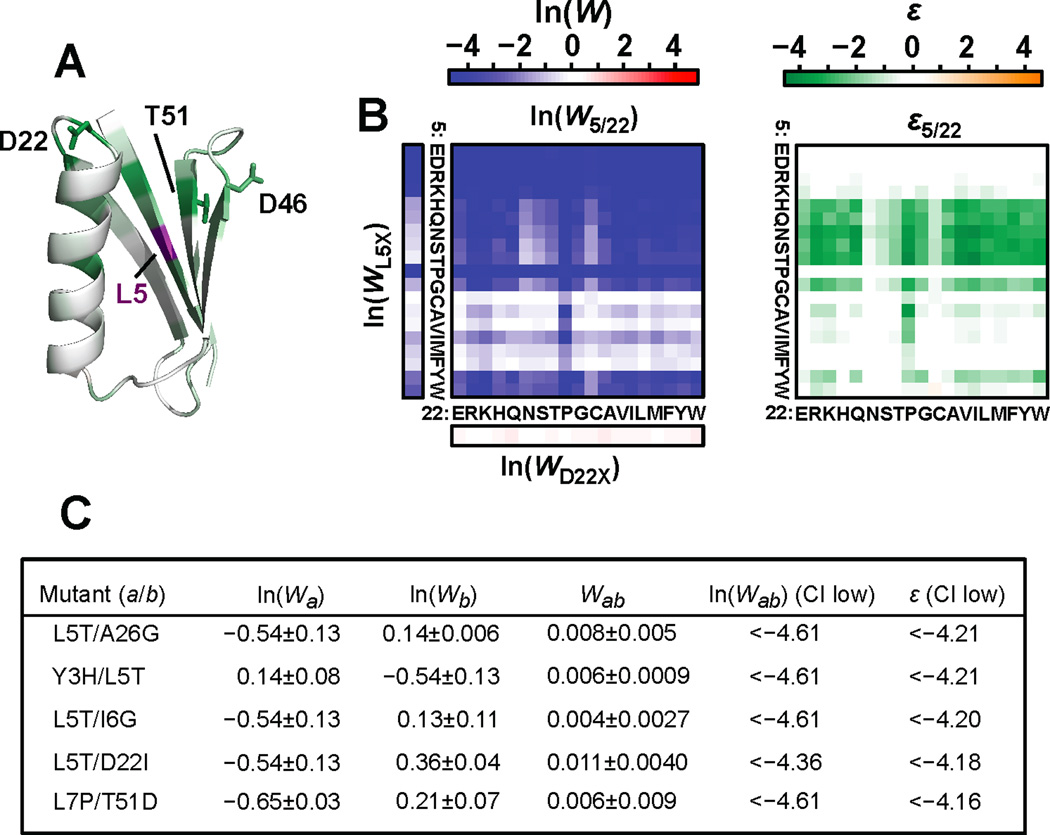
We wanted to determine what mechanism could explain general patterns of epistasis independent of specific amino acid identities. For example, core mutations, such as those at position 5 (Leu), display general negative epistasis with other positions throughout the domain (Figure 3B, 4A). In addition to general negative epistasis between substitutions at position 5 and other core positions, long-distance negative epistasis occurs between position 5 and surface positions within the stable β3–4 loop [22, 47] as well as substitutions for Asp22, a helical capping residue (Figure 4A). Figure 4B highlights ln(W) and ε for all 361 amino acid combinations within positions 5 and 22. The threshold robustness model [25–27] (Figure S4A–C) may explain the pervasive negative epistasis exhibited between these and similar residues. Most proteins are marginally stable [11, 12] yet withstand destabilizing mutations that do not significantly decrease the fraction of folded protein. However, when two such destabilizing substitutions combine, the stability “reservoir” can be exhausted thus resulting in a decrease in the fraction of native protein and a concomitant loss in function (Figure S4A–C). Thus additive stability effects produce non-additive functional effects. This model is consistent with the observation that large values of negative epistasis can be long-range (Figure 3D,E). The threshold robustness model is also consistent with the observation that the combination of buried polar residues at position 5 and substitutions at 22 that abolish a helical capping motif display some of the largest values of negative epistasis observed (Figure 4C, Figure S4D).

Figure 4. Positions display negative epistasis in general independent of amino acid combination.

(A) Average ε between position 5 and all other positions in GB1 (1PGA) [54]. Distant surface residues that demonstrate negative epistasis are labeled. (B) Binding fitness and epistasis for all 361 combinations of substitutions for Leu5 and Asp22. Leu5 is a critical core residue that is sensitive to mutation while Asp22 is part of a helix stabilizing N-capping motif near the binding surface where substitutions are generally well tolerated for binding function. (C) The most significant values of negative epistasis are listed. Each pair includes mutations that are expected to destabilize the structure but alone do not unfold the protein or significantly disrupt affinity. A Poisson-based 90% confidence interval was used to generate an upper boundary for binding fitness thereby enabling a conservative estimate of epistasis. See also Figure S4.

Structural stability and functional epistasis

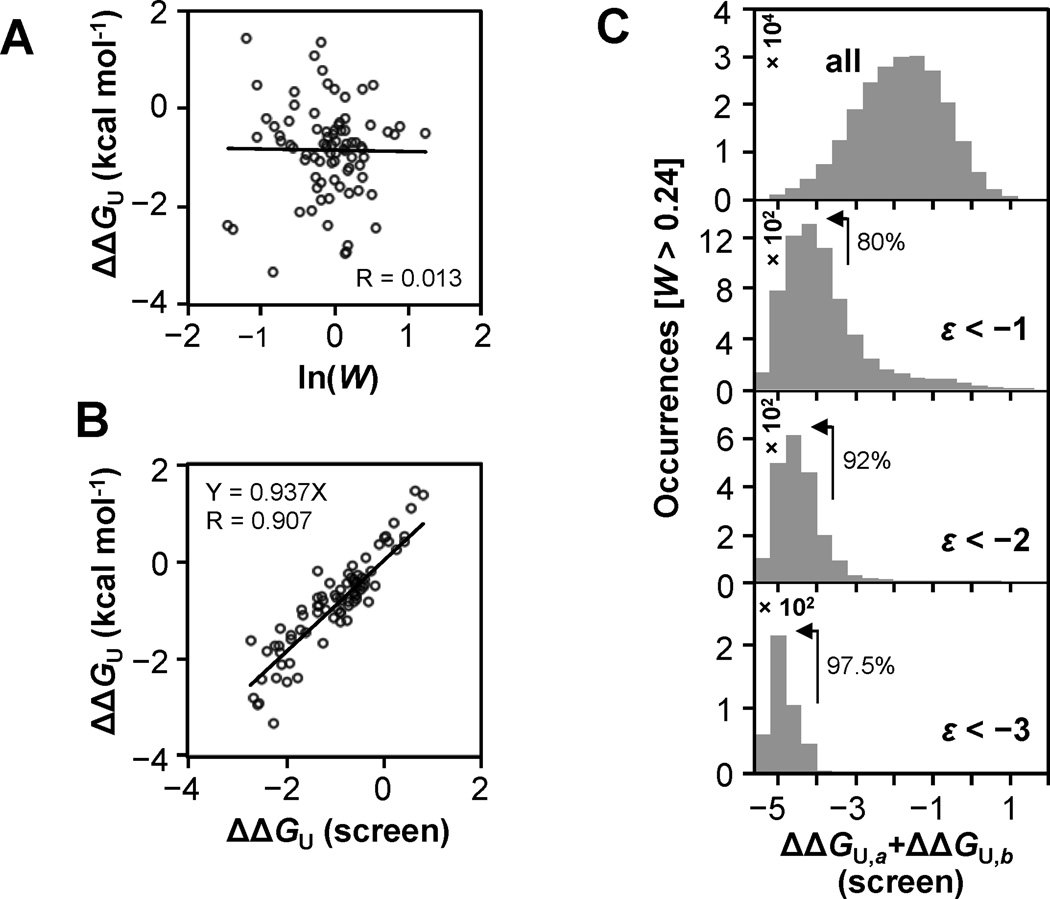
We further examined to what extent structural effects could account for examples of either negative or positive epistasis. To do this we developed a method to estimate change in free energy of unfolding (ΔΔG_U) for single mutants from the binding data. We found that ln(W) is uncorrelated to ΔΔG_U reported in the literature as expected for destabilizing mutations that remain folded at the screen temperature (Figure 5A, Figure S4A, Table S4). However, for partially unfolded mutants, addition of a second mutation will increase the fraction unfolded (f_U) if destabilizing and, conversely, will increase the native fraction (f_N) if stabilizing. As noted above, the threshold robustness effect can be explained as additive stability effects that produce non-additive functional effects (Figure S4). We hypothesized that certain mutants might be identified which satisfy the condition W_a=f_N,a and if these backgrounds are generally non-interacting other than through stability effects, we can estimate f_N,ab=W_ab/W_b. The predicted f_N,ab can then be used to estimate structural stability of single mutants (b) by ΔΔG_U=−RT×ln(f_U,ab/f_N,ab)+RT×ln(f_U,a/f_N,a).

Figure 5. Relationship between structural stability effects and epistasis.

(A) Comparison of ln(W) to free energy of unfolding relative to wild type (ΔΔG_U) reported in the literature. (B) The predicted thermodynamic stability of 82 single mutants compared to ΔΔG_U values reported in the literature (See Table S4). ΔΔG_U predicted by the screen are median values identified by estimating the change in fraction of unfolded protein in 5 destabilized mutant backgrounds. This analysis was limited to variants displaying W>0.24 (709 of 1045) as lower fitness values did not produce sufficient dynamic range to measure decreased structural stability. (C) Histograms of ΔΔG_U,a+ΔΔG_U,b showing how the distribution of predicted stability changes as the magnitude of negative epistasis increases. The percentage of each epistasis category resulting from combinations of significantly destabilized mutations (left of arrow) is listed. See also Figure S5.

The large number of GB1 variants characterized in the literature provided a substantial reference to identify stability effects from the binding data. An automated analysis was performed which identified multiple background mutations (a) that generated ΔΔG_U values that correlate well with the values found in the literature. These backgrounds therefore satisfy the conditions stated above. This method is limited however to mutants (b) with sufficient fitness to produce a dynamic range in observed fitness (ab) (those with W_b<0.24 correlated poorly). An average of the values generated from five reference backgrounds (Y3A, Y3C, L5N, L5S and F30N) were highly correlated to 82 ΔΔG_U values published in the literature with a slope of 0.94 and a correlation coefficient (R) of 0.907. We note that this correlation is very good considering variability in experimental ΔΔG_U calculations illustrated by Potapov et al. [48]. They show that the correlation (R) between 406 pairs of ΔΔG_U values reported for identical protein variants is 0.86.

In order to estimate the importance of the threshold robustness effect in shaping the GB1 double mutant fitness landscape, we estimated the structural stability of double mutants by summing ΔΔG_U and determined the number of occurrences of significant negative epistasis for different predicted double mutant stabilities (Figure 5C). For some combinations, ΔΔG_U will not be additive (Figure S5A–C, Table S5), which can mitigate the threshold robustness effect. However, as negative epistasis becomes more significant, double mutants predicted to be very unstable account for most occurrences (Figure 5C). For example, 97.5% of all double mutants displaying ε<−3 are predicted to be at least 4 kcal mol⁻¹ less stable than wt GB1. Thus, our study empirically demonstrates the extent of the threshold robustness model in functional epistasis.

It is also expected that positive epistasis will arise from stability effects. This will occur if a stabilizing mutation increases the fraction of native protein in the background of a highly destabilized mutant that is partially unfolded at room temperature. Stabilizing mutations have been shown to set the stage for evolution by permitting adaptive mutations that are destabilizing alone [10, 49, 50]. However, it is known that stabilizing mutations are lower in frequency and in magnitude compared to destabilizing mutations [12], and this is corroborated by our screen (Figure S5D). Thus, additive effects from the smaller number and magnitudes of stabilizing mutations overall contributes less to epistasis in comparison with additive effects from combinations of two destabilizing substitutions (Figure S5E–J).

General positive epistasis within a dynamic region

In addition to general negative epistasis, it is also apparent that combinations of mutations within a smaller group of positions display positive epistasis on average (Figure 3B). One position is A24, which shows positive epistasis is correlated with low fitness positions and negative epistasis is correlated with high fitness positions (Figure S6A, see also Figure S2C–D). Other positions that display positive epistasis in general include residues within the β1–2 loop (7, 9, 11), β-strand 2 (12, 14, 16), C-terminal end of the α-helix through the α-β3 loop (33, 37, 38, 40), and C-terminal β4 residues (54, 56) (Figure 3B, S6B–D). These residues participate in a network of residues that undergo correlated conformational dynamics [51–53]. Remarkably, the pattern of general positive epistasis seen in Figure 3B is very similar to that of correlated NH bond vector motions modeled by Lange et al. [53].

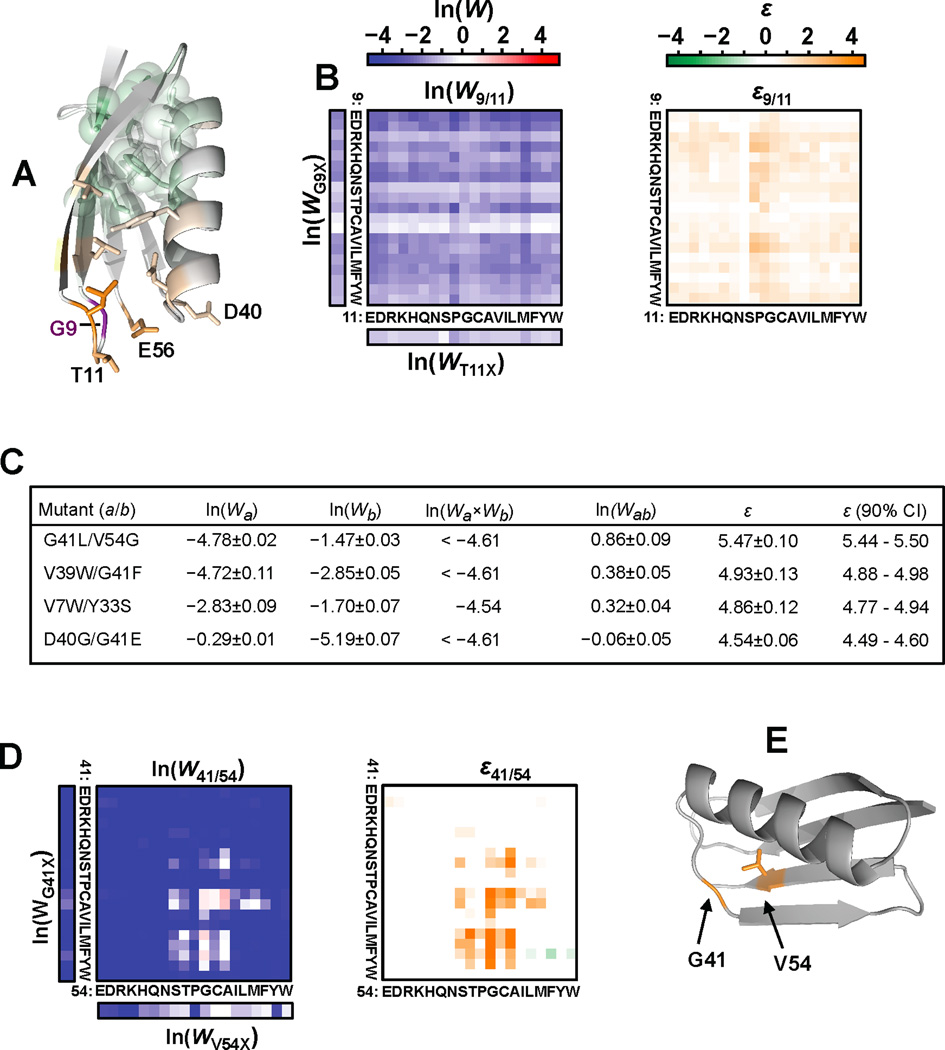
Combinations of mutations within the twelve positions listed in the dynamic region account for 49% of epistasis values >1, while accounting for only 4.4% of all pairs. Figure 6A shows the structure of GB1 depicting the average epistasis between substitutions for Gly9 and mutations at all other positions. This region directly contacts IgG-FC through a main-chain H-bond between the Val39 carbonyl oxygen and Asn434 on IgG [21]. This loop is coupled to the β1–2 loop through H-bonds between the C-terminal Glu56 carboxylate with the Asp40 and Lys10 amides [54] (Figure 6A). The dynamic region extends through β-strand 2, which is located on the opposite side of GB1 relative to the IgG-FC binding surface. Note that several mutations within this dynamic region also display slightly negative epistasis on average with substitutions in the protein core (Figure 3B, Figure 6A). This is consistent with the threshold robustness effect as such substitutions are predicted to decrease the stability of the structure.

Figure 6. Positions that display general positive epistasis independent of amino acid combination.

(A) Average ε for all pairwise combinations with position 9. Glu56, which couples the two dynamic loops through H-bonds, is highlighted. (B) Epistasis and binding fitness for all 361 combinations of substitutions for G9 and T11 which are located within the highly dynamic β1–β2 loop. (C) The 20 most significant examples of positive epistasis include double mutants from 4 pairwise positional combinations. The double mutants displaying the largest value of positive epistasis per positional pair are listed. These combinations include neighboring residues within or at the edge of the conformationally dynamic region that overall demonstrates pervasive positive epistasis (see Figure 3A,B). For calculating epistasis, we limited expected fitness by ln(W_a×W_b)≥ln(0.01) to minimize spurious epistasis values for lethal or nearly lethal double mutants resulting from non-meaningful predicted fitness values below the background (~W=0.01). (D) Fitness and epistasis for all double mutants including positions 41 and 54. (E) Exchanging volume from core residue Val54 to Gly41 demonstrates the most extreme value of positive epistasis. See also Figure S6.

Many of the residues in the coupled, dynamic region of GB1 are generally sensitive to substitution (Figure 2C). For example all 361 possible combinations of substitutions for G9 and T11 are highlighted (Figure 6B). The data shows when one mutation reduces fitness, an additional mutation in this region imparts a diminished negative effect. We constructed G9A, T11A, and the double mutant, G9A/T11A to validate this epistatic effect (Figure S3A). This validation also confirms that subtle changes in amino acid identity in this region can have a significant effect on binding fitness from a distance (Figure 2A,C).

In some cases, combinations of substitutions in the dynamic region result in dramatic reversal of lethal fitness to positive fitness (Figure 6C). The most extreme example, G41L/V54G, results in the exchange of volume from the C-terminal core residue Val54 to the α-β3 loop (Figure 6D,E). However, how the loop conformation can change to accommodate this swap is not intuitive either by manual inspection or through computational analysis using the parameters described by Kellogg et al. [55]. Interestingly, a highly diverged homolog of protein G of identical length demonstrates the sequence variation 41L/54G (Figure S6E). Furthermore, analysis by EVfold shows that this is a highly co-evolving pair [56]. In summary, this analysis has uncovered an important role for residues involved in a dynamic network in contributing to GB1 function and identified how non-additivity in this region, in some cases extreme, affects the double mutant fitness landscape.

Impact of epistasis on adaptive pathways

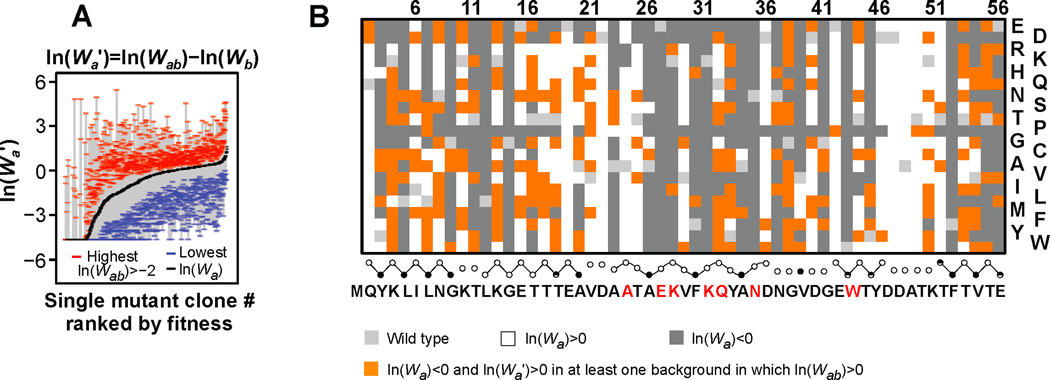
While context independent fitness effects generally dominate the mutational landscape of GB1 (Figure 3C–E), epistasis may promote or limit mutational walks in sequence space (Figure S7A). While most pairs do not display large positive epistasis, there are 37,405 pairs (7.2%) that display ε>0.15. We wanted to determine how positive epistatic effects are distributed throughout the domain. We calculated fitness for each single mutant in all alternative backgrounds [ln(W_a’)=ln(W_ab)−ln(W_b)] and show the range between the highest [if ln(W_ab)>−2] and lowest values in comparison to the fitness in the wt background (Figure 7A). Many deleterious mutations display significantly improved fitness in at least one of the 1026 possible non-wild type backgrounds. In fact, of the 678 single mutations that are deleterious in the wt background, the fitness of 429 can reverse in sign [ln(W_a’)>0] and are thus compensable. Even considering only beneficial double mutants [ln(W_ab)>0], more than a third of the deleterious mutations (240 of 678) reverse in sign in at least one alternative mutational background and are therefore “cryptically beneficial” (Figure 7B, Figure S7C).

Figure 7. The fitness effects of many mutations change dramatically depending on the background in which they appear.

(A) The range is bound by a blue dash for the lowest fitness in any of the 1026 possible alternate backgrounds, and by a red dash for the highest fitness. The highest fitness values are limited to double mutants displaying ln(W_ab)>−2. (B) A map showing deleterious single mutants that are beneficial in at least one alternative mutational background even while limiting double mutant fitness greater than wild type (orange). See also Figure S7.

DISCUSSION

Using next generation sequencing, the number of sequence variants in highly diverse populations can be counted before and after laboratory-designed tests of fitness, thereby quantifying evolution [30, 34, 40–43, 57–60]. An important question related to such studies is how often would the observed fitness effects change in the background of other mutations. Fields and colleagues have demonstrated the ability to characterize thousands of single and double mutants in segments of protein domains and thus make important conclusions on the frequency and nature of epistasis in protein function [19, 20]. In this article, we observe the first two steps of all evolutionary pathways in the recognition of IgG by GB1 and therefore observe how fitness profiles change in all alternative mutational backgrounds. This comprehensive analysis determines how often deleterious effects are compensated and beneficial effects are negated for all mutations in an entire protein molecule.

The fitness profile in Figure 1B and the DFE in figure S2E show that the stringency of this fitness challenge is analogous to evolution of new function. It is well understood that the highest affinity possible will often not be selected for function in vivo [28]. However, the beneficial mutations we identify in vitro are found in natural protein G homologs (Figure S2B) and one homolog that does not benefit from tandem duplication has 7 mutations which are all adaptive in this screen (see Figure S2B). Furthermore, there are ligand pairs that demonstrate a functional demand for exceptional affinity [61], including for IgG binding proteins similar to GB1 [62]. Such an adaptive landscape as described in this experiment could possibly be analogous to natural evolution in viral receptor host switching. For example, mutations found after adaption of SARS from civet to human show enhanced affinity to receptor in vitro and those mutations enhanced viral infectivity in cell culture [35]. Furthermore, affinity-based adaptation can occur if ligand concentrations decrease, for example, as observed in increased affinity for O₂ in high altitude deer mice hemoglobin [7].

We show common biophysical mechanisms for both negative and positive epistasis, including how additive stability effects produce functional epistasis. While the environment of the cell will modulate the concentration of functional protein compared to what is observed in vitro [63], there is a clear relationship between protein stability and fitness in cells and viruses [10, 27, 64]. The cooperative nature of protein folding creates an inherently epistatic effect from additive stability effects [25–27]. In this experiment, additive effects of destabilizing mutations account for nearly all examples of very large negative epistasis. That destabilizing mutations are both more common and larger in magnitude compared to stabilizing mutations [12] explains why there are more significant negative epistatic effects compared to positive epistatic effects in this experiment. Stabilizing mutations might display stronger epistatic effects in vivo however by counteracting degradation or aggregation, such as been demonstrated in β–lactamase evolution [8].

Furthermore, we demonstrated that long-range deleterious fitness effects throughout a dynamic region are not additive and therefore mutations in this region display positive epistasis in general. These observations mirror results from extensive characterization of PDZ domains which also display long range mutational sensitivity in dynamic regions [42, 65, 66]. This effect can be exploited for allosteric modulation in nature or through engineering [67, 68]. The most substantial occurrences of positive epistasis were found in the region between positions in which two highly deleterious mutations combine to produce neutral or beneficial double mutants. A similar “hot spot” of epistasis predicted to produce a conformational switch that removes unfavorable interactions was also seen in an exceptionally high throughput mutagenic study of an RRM domain [20].

The results of this paper reconcile observations about the importance of epistasis in adaptive evolution despite the rarity of it. We can see that while it should not be expected that mutations have different fitness in alternative backgrounds, most mutations can have a very different effect in at least one alternative genetic background. Cryptically beneficial mutations [ln(W_a’)>0 and ln(W_ab)>0] are found throughout 43 positions in the 55-residue domain. Furthermore, while wt is optimal at 17 positions, compensatory mutations reveal beneficial mutations within 10 of these 17 positions even when limiting ln(W_ab)>0. Thus, while sign epistasis limits pathways of adaptation, it at the same time facilitates sequence change in light of mutational sensitivity.

EXPERIMENTAL PROCEDURES

See the Extended Experimental Procedures in the Supplemental Information section for complete details for library construction, mRNA display and affinity enrichment, sequencing, data analysis, and validation.

Calculation of structural stability effects

In order to estimate change in fraction folded, we assumed there will be mutational backgrounds (a) in which W_ab/W_b=f_N,ab. This can occur if the reference mutations are partially folded but neutral in the native state, if the test mutant (b) is fully folded in the native state, and if the two mutations do not interact functionally (only through additive thermodynamic stability effects). Thus, these conditions mean, given that the observed W is a product of the fraction folded and fitness of the native state (W=f_N×W_N), that the background mutations must satisfy f_N,a=W_a (W_N,a=1), and the test mutants (b) must satisfy f_N,b=1. Therefore, for pairs that are energetically additive, W_N,ab=W_b. Substituting into W_ab=f_N,ab×W_N,ab gives us f_N,ab=W_ab/W_b. We automatically converted the 82 test mutants from the literature (Table S4) into f_N,ab using all suitable backgrounds (0<W_a<1) and then into relative free energy of unfolding. At equilibrium, k_F×[U]=k_Un×[N] and thus f_U,ab/f_N,ab=k_Un/k_F which by definition equals K_Un and therefore ΔΔG_U=−RT×ln(f_U,ab/f_N,ab)+RT×ln(f_U,a/f_N,a). Numerous substitutions at positions Y3, L5, F30, and A26 produced highly correlated data. The average ΔΔG_U values from the top 5 backgrounds from positions 3, 5 and 30 (Y3A, Y3C, L5N, L5S, and F30N) produced highly correlated data with a slope close to 1.