Turtle utricle dynamic behavior using a combined anatomically accurate model and experimentally measured hair bundle stiffness

Abstract

Anatomically correct turtle utricle geometry was incorporated into two finite element models. The geometrically accurate model included appropriately shaped macular surface and otoconial layer, compact gel and column filament (or shear) layer thicknesses and thickness distributions. The first model included a shear layer where the effects of hair bundle stiffness was included as part of the shear layer modulus. This solid model’s undamped natural frequency was matched to an experimentally measured value. This frequency match established a realistic value of the effective shear layer Young’s modulus of 16 Pascals. We feel this is the most accurate prediction of this shear layer modulus and fits with other estimates (Kondrachuk, 2001b).

The second model incorporated only beam elements in the shear layer to represent hair cell bundle stiffness. The beam element stiffness’s were further distributed to represent their location on the neuroepithelial surface. Experimentally measured striola hair cell bundles mean stiffness values were used in the striolar region and the mean extrastriola hair cell bundles stiffness values were used in this region. The results from this second model indicated that hair cell bundle stiffness contributes approximately 40% to the overall stiffness of the shear layer– hair cell bundle complex.

This analysis shows that high mass saccules, in general, achieve high gain at the sacrifice of frequency bandwidth. We propose the mechanism by which this can be achieved is through increase the otoconial layer mass. The theoretical difference in gain (deflection per acceleration) is shown for saccules with large otoconial layer mass relative to saccules and utricles with small otoconial layer mass. Also discussed is the necessity of these high mass saccules to increase their overall system shear layer stiffness. Undamped natural frequencies and mode shapes for these sensors are shown.

1 Introduction

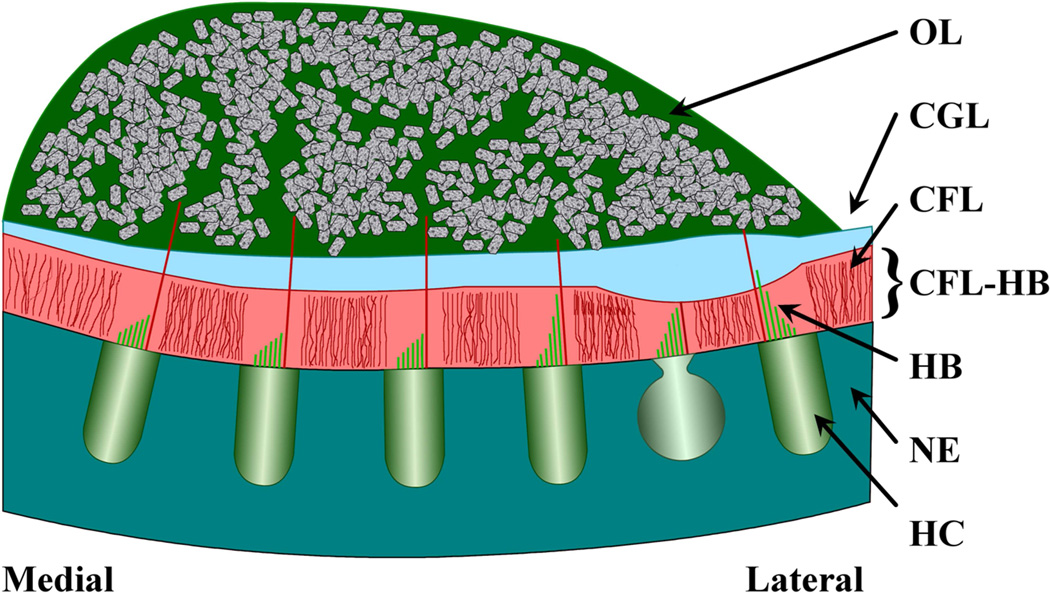
Otolithic organs are transducers of static and dynamic motion of the head (De Vries, 1951; Lowenstein et al., 1949). The most common otolithic organs are the utricle and saccule; these are acceleration sensors. They consist of a three-layered structure covered in endolymph fluid and resting atop a neuroepethelial (NE) surface. The three structural layers from the endolymph down to the NE are: an otoconial layer (OL) containing dense carbonate crystals, a compact gel layer (CGL) consisting of saccharide gel, and a column filament layer consisting of filaments of saccharide gel in which hair cell bundles (HB) are located (the CFL-HB complex) (see Figure 1). The hair cell bundles contribute to the mechanical stiffness of this CFL-HB complex (Benser et al., 1993). Head acceleration and gravity act on the dense otoconia crystals in the OL, causing a relative displacement between the OL and NE. It is this relative displacement that shears the CFL-HB complex layer. These relative displacements deflect the hair cell bundles, activating these cells, and initiating afferent neural signals.

Figure 1. Schematic cross-section of the layered structure of utricle.

This is a representative diagram of the layered structure in the Lateral-Medial Transect of the utricle. From the top down, the layers are labeled: OL for the otoconial layer; CGL for the Compact Gel Layer; CFL for the Column Filament Layer; and NE for the Neuroepithelium. Also indicated in this figure are Hair Cells (HC), which reside in the neuroepithelium.

Presented here is a macro-mechanics model of the utricle in the Red Eared Slider turtle, where the relative shear of the CFL-HB complex is examined to determine the effective modulus of this shear layer. In addition, the relative contribution of this shear layer stiffness due to hair cell bundles is determined. The only species and otolithic organ in which hair cell bundle stiffness contribution to overall CFL stiffness has been measured is in the Bullfrog Saccule (Benser et al., 1993). The saccule in the bullfrog and in many other animals has a very large OL when compared to the OL of the utricle. In most of the animals with these high mass saccules, the mass almost completely fills the membranous saccule (Lewis et al., 1985). The OL of the utricle in almost all animals is thin, reducing its mass. These mechanical properties: shear modulus and OL mass, are important to quantify in order to enhance our understanding of how these organs operate as dynamic sensors.

In earlier work, a combination of experimental and finite element modeling was used to determine material properties of the bullfrog saccule CFL-HB complex layer (Benser et al., 1993; Kondrachuk, 2000). These two studies of the stiffness of the saccule CFL-HB complex, determined hair bundles contributed from 50 to 70% of the total stiffness, and the effective Young’s modulus of the CFL-HB complex was determined to be 250 Pa. De Vries (1951) determined that fish saccules have a natural frequency of approximately 40 Hz. More recently Dunlap et al. (2012) found higher natural frequencies in turtle utricles of 363 Hz (95% confidence interval = 328 to 397). These experiments have been supplemented with lumped parameter models to quantify material physical properties of the CFL-HB complex response (De Vries, 1951; Grant et al., 1986; Grant et al., 1990; Grant et al., 1984; Grant et al., 1994; Grant et al., 1987; Kondrachuk, 2001a) showing the effective Young’s modulus for a low mass otolithic organ was probably more in the 10 Pa range. However, these otolith models generally use simplified geometry: a flat neuroepithelium with otolithic layers of uniform thickness, to quantify CFL-HB complex combined properties and response. Although this work was performed on the turtle utricle, similarities in shear layer thicknesses and hair cell bundle distribution suggest that the implications can be applied to human and/or mamallian utricles as well.

The first goal of this work was to match the natural frequency determined by Dunlap et al. (2012) of turtle utricle using a high fidelity finite element model to determine the modulus of the shear layer. The second goal was to determine the contribution of hair cell bundles to the overall stiffness of the CFL-HB complex. To achieve these goals, two modifications were made to the anatomically accurate Davis et al. (2007) model. First, the shear layer modulus was adjusted to match experimental results (Dunlap et al., 2012). Second, the CFL-HB complex is replaced with models of hair cell bundles. Natural frequencies, resulting from modal analysis of each utricle model, were compared with each other and with previous work done in the bullfrog saccule. Some key differences are discussed.

This is the first work to determine dynamic shear layer stiffness using an anatomically accurate model of a utricle and validate the model against experimental results. Results illustrate that there are significant differences in material properties between saccule and utircle organs, and that these differences may affect the transient response of the organ. This suggests these organs may be optimized for two quantities, sensitivity (or gain) and frequency bandwidth.

2 Methods

2.1 Finite Element Models

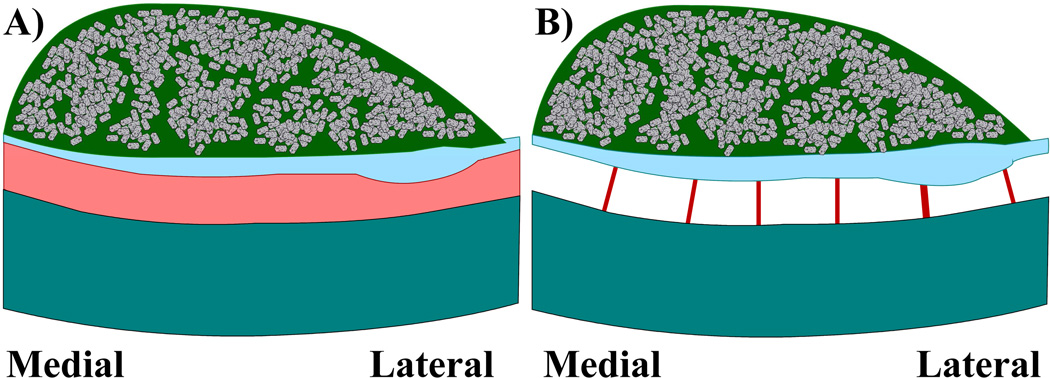
Two finite element utricle models with one very important structural difference are constructed. The first utricle model consists of three otoconial membrane (OM) layers approximated with solid finite elements and unique material properties for each layer (see Table 1) (Davis et al., 2007). Each OM layer of the model also varies thickness relative to the striolar region (Davis, 2007). Finally, while other OM models use constant OM layer thicknesses and flat epithelial surfaces and (Grant et al., 1990; Grant et al., 1984; Kondrachuk, 2000; Kondrachuk, 2001a; Kondrachuk, 2001b), this model is unique; it includes curvature of the macular surface in both the medial-lateral and anterior-posterior directions. This model may be the most geometrically accurate model of a otolith organ to date. In this first model, the modulus of the CFL-HB complex layer implicitly accounts for stiffness of hair-bundles within the layer (see Figure 2A: CFL-HB Model).

Table 1. Material Properties for otoconial membrane layers.

These data were used in each finite element model of the turtle utricle OM. Eventually we determined the modulus of the CFL-HB complex to me an order of magnitude lower.

	E (Pa)	ρ (kg/m3)	ν
CFL-HB complex	250	1000	0.45
CGL	6600	1000	0.45
OL	6.6×106	2400	0.45

Figure 2. Representation of CFL-HB and HB model adaptations.

This figure represents the difference between each adaptation of the turtle utricle OM model. In A) the CFL–HB complex is modeled with isotropic volume elements that implicitly account for the shear stiffness of the hair bundles. In B) the CFL-HB complex is removed and hair bundles are explicitly modeled with finite element Euler-Bernoulli beams. Comparing the CFL-HB model to the HB model allows for a determination of how much hair bundles contribute to the shear stiffness of the CFL-HB complex. Please note 1) the neuroepithelium is curved in both medial-lateral and anterior-posterior directions and 2) OM layers vary thickness in all directions.

The second utricle model replaces the CFL-HB complex layer with explicit representations of hair bundles modeled as Euler-Bernoulli beams (see Figure 2B: HB Model); the remaining OM layers in the model are unchanged from the previous model. The bundle models on the macular surface are unique to previous works incorporating hair bundles in OM models because striolar and extrastriolar hair bundles are modeled with different stiffness values based on their placement on the macular surface.

2.2 Modal Analysis

Modal analysis is a technique used to determine the natural frequencies and mode shapes, or vibration displacement profiles, of a structure. In this study, the first two undamped natural frequencies are of interest for three reasons:

1. These low natural frequencies require the least amount of energy to excite and thus are generally most commonly observed.

2. The displacement mode shapes (displacement profile of the whole OM at specific frequencies) corresponding to these natural frequencies represent the characteristic motion of the OM: a shearing of the CFL-HB complex.

3. The direction of displacement in modes 1 and 2 are close to the direction of maximum and minimum static deflection directions.

Undamped natural frequencies of the structure can be used to make conclusions about the stiffness of that structure. In the case of otoconial membranes it is often assumed that the hair bundles work in parallel with the surrounding CFL. This interaction has been modeled as two springs working in parallel (Benser et al., 1993). Their effective stiffness is calculated by adding the two individual stiffness values; representing both springs working in parallel.

If the total and distribution of the driving mass is the same in each model, dividing stiffness by the mass of the system can easily make the transition to natural frequencies. This ratio represents the square of the natural frequency. Therefore if hair bundles dominate the shear stiffness of the CFL-HB complex, the HB model will have natural frequencies close to the natural frequencies observed in the CFL-HB model. If the natural frequencies are not close to the observed CFL-HB model then the share of stiffness between the two sources can be evaluated.

2.3 Hair Bundle Stiffness

Typical methods that characterize bundle stiffness require measurements at the kinocilium tip: Force applied at the tip of kinocilium divided by linear displacement at the tip of kinocilium (Crawford et al., 1985; Flock et al., 1984; Howard et al., 1986; Spoon et al., 2005; Spoon et al., 2011b; Strelioff et al., 1984). These experiments are then modeled with finite elements using Euler-Bernoulli beam theory (Cotton et al., 2004a; Cotton et al., 2004b; Nam et al., 2005; Silber et al., 2004) which includes the mechanics of bundle and the effect of both moments and shear on the displacement and bending (Beer et al., 2006).

In the OM models that include explicit models of hair bundles, Euler-Bernoulli beams with uniform circular cross sections are used to model hair bundles. The same method of characterizing stiffness of individual hair bundles is used (linear force over linear displacement). Typical stiffness measurements of isolated bundles generally use a cantilever beam approximation (Spoon et al., 2005). However, in these OM models, beams are modeled with fixed boundary conditions on both ends (i.e.: no rotation at either end of the beam) in order to preserve continuity with other elements in the model. This effects how stiffness is calculated in each beam. The stiffness value, k, is calculated using the equation below

$$k=\mathit{12}{E}_{B}I/L^3$$ (1)

where: L = the beam length is assumed to be the thickness of removed the CFL-HB complex, I = area-moment of inertia = 7.85E-25 m⁴ (calculated from the 1 µm beam radius), and E_B = the effective bundle modulus determined knowing the experimentally measured stiffness for the different types of bundles. These values are summarized in Table 2.

Table 2. Geometric & Material Properties of Beam models of Hair Bundles.

We were able to differentiate between striolar and extrastriolar hair bundles in our OM models. We used two different sets of geometric and material property data to based on our OM geometry to calculate equivalent stiffness values for each set of bundles.

	Turtle Utricle (Spoon et al., 2005)
	Striola	Extrastriola
k (µN/m) [Range]	45 [40–50]	11 [9–13]
r (µm)	1	1
I (µm4)	.785	.785
L (µm)	9.5	14.5
ρ (kg/m3)	1000	1000
Number of Bundles/Macula	920	7749
Ebundle (kPa)	4.093	3.558
Number of Beams/Macula	125	1180
Ebeam (kPa)	30.13	23.37

Non-linear properties of hair cell bundle stiffness, from active tip link tensioning by the molecular motors during stimulus (Howard et al., 1988; Nam et al., 2007), were not included in this study. Any observable increase in stiffness of hair bundles during OM motion would proportionally increase the natural frequency of the OM. However, non-linear behavior was not observed in Dunlap and Grant's (2014) experimental work. We suspect any non-linear effects would be averaged out over the nueroepithelium due to the varied orientations of the bundles and the severity of the non-linear behavior relative to the overall deflection of the OM. Non-linear stiffness of hair bundles could be accounted for in both OM models (those with the implied and explicit hair cell bundles) and would proportionally effect the results. The results reported here may be considered as a conservative estimate of contribution of hair cell bundle to the overall stiffness of the OM.

2.4 Regional Variation

Turtle utricles have been shown to have hair bundles of different morphological structure depending on the location in the macula (Xue et al., 2006). The turtle macula is divided into two regions based on bundle structure: Striola and Extrastriola (Xue et al., 2003). This variation in bundle structure contributes to different hair bundle stiffness in these regions of the utricle.

These regional variations are accounted for in the FE model of the turtle utricle. In the OM finite element models, the striolar region is determined as a crescent region following the curve of the lateral edge of the maculae. Starting at about 25 microns medial to the lateral edge and being about 75 microns wide, the striola region has stiff hair bundles compared to the extrastriola region (Davis, 2007; Xue et al., 2003). Once beams in these locations are identified, they are meshed with stiffness characteristics (discussed below) based on the region in which they are located.

Striolar hair bundles tend to have more stereocilia compared to their counterparts in the extrastriola region (Xue et al., 2006). The ratio of height of tallest stereocilia to height of kinocilium is close to unity. In addition, striolar bundles have kinocilia heights that are very close to the thickness of (i.e: they do not protrude into) the CFL. These properties and the "buttressing," described in Spoon et al. (2011b) indicate the striola bundles interaction with the OM is strong. Therefore the measured stiffness (41.6 ± 25.4 pN/µm (Grant et al., 2007)) is assumed to fully contribute to the shear resistance of the CFL; that is to say the in-vitro measurement of the physiological stiffness of the hair bundle should be very close to as if it would behave in-vivo (Spoon et al., 2011b).

Extrastriolar hair bundles have different morphological structure than striolar hair bundles. Extrastriolar hair bundles tend to have a ratio of kinocilium compared to their stereocilia on the order of 2 or 3; indicating a very tall kinocilium. In addition, extrastriolar hair bundles tend to have fewer stereocilia compared to their counterparts in the striolar region (Xue et al., 2006). These morphological characteristics make them more compliant (7.6 ± 3.0 pN/µm (Grant et al., 2007)) than striolar hair bundles (Silber et al., 2004).

However, the kinocilium of extrastriolar hair bundles may at times protrude through CFL and CGL into the OL. This method of connecting to the OL may change the bundle’s stiffness contribution to shear resistance in the CFL. We used the physiologic (in-vivo) stiffness values here, (9–13 pN/micro-meter) adjusted to reflect CFL thickness (Spoon et al., 2011a; Spoon et al., 2005), to model the contribution of stiffness to the shear layer. This approximates a minimal contribution of extrastriolar hair bundles to the stiffness of the shear layer. We also consider adjusting the ES hair bundles stiffness to maximize their contribution to the shear layer in comparison to that observed in the bullfrog saccule.

In addition, due to a large variation of kinocilia heights (and bundle morphology) in extrastriolar region of the utricle, median values of stiffness are used to calculate material properties for the representative bundles (Xue et al., 2006). Stiffness of bundles located in lateral extrastriola region have been shown to have the similar range of stiffness as medial extrastriola bundles (Spoon et al., 2005). They will be treated with similar stiffness.

We estimate the total number of hair bundles in the turtle utricle model to be about 8670 bundles from Severinsen et al. (2003). This is confirmed with Rowe et al. (2006). This number is calculated from a macular area in the utricle model of 0.80446 mm² and the linearly proportional relation the macular area. Severinsen further determined hair bundles in the striolar region to account for approximately 12–13% of the total number of hair bundles on macula.

Finally, after removing solid elements representing the CFL-HB complex from the OM model, we attach finite element beams connecting the CGL to the neuroepithelial surface at finite element nodes along the top of the neuroepithelial surface and the bottom of the CGL. These beams explicitly represent hair bundles, excluding any effect of the CFL. Each beam represents the stiffness of several bundles to account for all 8670 bundles in the utricle. This assumes that the hair bundles close to one another work in parallel. The full effect of shear resistance of hair bundles is approximated by adding their individual stiffness values to each other. The result of all of these calculations, including bundle stiffness and counts, are included in Table 2 below.

3 Results

3.1 Shear Layer Modulus

In order to match the experimentally measured turtle utricle natural frequency of 363 Hz (Dunlap et al., 2012), the effective modulus of the CFL-HB complex is lowered from the 250 Pa that was used in Davis et al. (2007) (See Table 3, Row 1). Table 3 summarizes the results of the shear layer moduli and hair bundle stiffness calculations. Rows 1 through 3 includes material properties used for the CFL-HB complex. Stiffness of hair bundles is implied in each of these models (See Fig. 2A) and are presented in parentheses. First and second natural frequencies are also included. Rows 4–5 contains the results for models in which the CFL-HB complex is replaced with explicit models of hair bundles. Results from rows 4 and 5 are used to calculate stiffness contributions of hair bundles of models in rows 1 through 3.

Table 3. Properties and Natural Frequencies of Turtle Utricle models.

Rows 1,2 & 3 contain the natural frequencies of the CFL-HB complex OM models with two different moduli. The frequency results are compared with the results of two different HB models presented in Rows 4 & 5. The stiffness contribution of hair bundles relative to the CFL-HB complex are calculated.

		Effective CFL-HB Young's Modulus	Striolar HB	Extrastriolar HB	Natural Frequencies ω1 − ω2	Percent Contribution of HBs
	OM Model	Pa	µN/m	µN/m	Hz	%
1	CFL-HB	250	(45)	(11)	1530 – 1592	3.10 – 3.15
2	CFL-HB	250	(45)	(220)	1530 – 1592	42.4 – 45.6
3	CFL-HB	16	(45)	(11)	363 – 408	44.7 – 47.1
4	HBs Only	-	45	11	271 – 280	-
5	HBs Only	-	45	220	995 – 1074	-

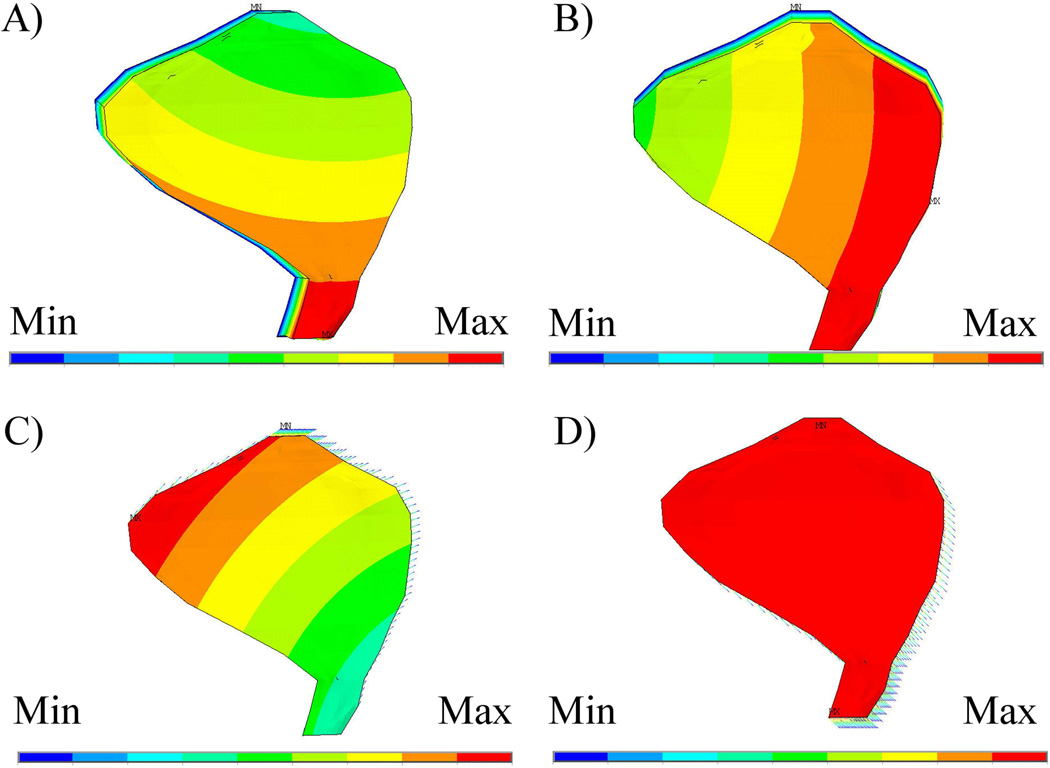
A frequency match is achieved with the turtle utricle model by using a CFL-HB complex modulus of 16 Pa (See Table 3, Row 3). This yields a result that compares well with turtle utricle experiments (Dunlap et al., 2012); opposed to a frequency of 1530 Hz using the saccule modulus of 250 Pa (See Table 3, Row 1). Of primary interest are the first two mode shapes (See Fig. 3 A and B) because they represent the biologically relevant displacement of the OM; one in which the CFL-HB complex shears and therefore excites hair bundles.

Figure 3. Displacement mode shapes for CFL-HB and the HB models of the turtle utricle.

The first two displacement modes (A-mode 1 and B-mode 2) for the CFL-HB model and the HB only model (C-mode 1 and D-mode 2) are shown here. Included in Table 3 are the matching natural frequencies for the 4 models considered in this study.

3.2 Hair Bundle Stiffness Contribution

The natural frequency results from the second utricle OM model, in which the CFL-HB complex is replaced with explicit models of hair bundles, are shown in Table 3 for comparison (Rows 4 and 5). The first two mode shapes of this model are shown in Fig. 3C and Fig. 3D. These two displacement modes represent biologically relevant motion of the OM; shearing displacement of the hair bundles. To calculate the stiffness contribution of hair bundles in the CFL-HB complex, frequencies from rows 3 and 4 are compared. These data indicate the percent contribution of hair bundles is between 45 and 47 percent

The results show that a Young's modulus of 250 Pa for the CFL-HB complex of the turtle utricle does not correlate with either the dynamic testing (Dunlap et al., 2012) nor the idea that hair bundles contribute significantly to the stiffness of the CFL-HB complex (Benser et al., 1993; Kondrachuk, 2000). Recall, we assume the striolar bundles fully contribute their stiffness to the stiffness of the CFL-HB complex. We modify ES bundles to determine how increasing their stiffness could affect overall HB contribution when the CFL-HB complex remains at 250 Pa. We discover increasing ES hair bundle stiffness an unreasonable amount of 220 times the experimentally measured stiffness is necessary to obtain the stiffness contribution observed in the bullfrog saccule (Compare rows 1 and 5 in Table 3). This supports the results of a low modulus in the utricle OM.

4 Discussion

4.1 Otolithic organs gain and bandwidth

The results presented here support a much broader realization about otolithic organs in general, their sensitivity, gain, and bandwidth. High natural frequency otolithic organs (mostly utricles) have frequencies in the 350 to 400 Hz range (Dunlap et al., 2014; Dunlap et al., 2012), and low natural frequency otolithic organs (mostly saccules) are in the 20 to 40 Hz range (De Vries, 1951; Narins et al., 1984). The undamped natural frequency of these systems are determined by the square root of the ratio of system stiffness over system mass (see appendix). The system stiffness arises from the CFL-HB complex and the system mass is that of the OL. The utricle is clearly an accelerometer with relatively high undamped natural frequency in all animals that have been investigated (Dunlap et al., 2012). Saccules can have relatively low natural frequencies in some animals (frogs, fish, and turtles), and relatively high natural frequencies in other animals (mammals and birds). However, saccules are still accelerometers irrespective of their natural frequency.

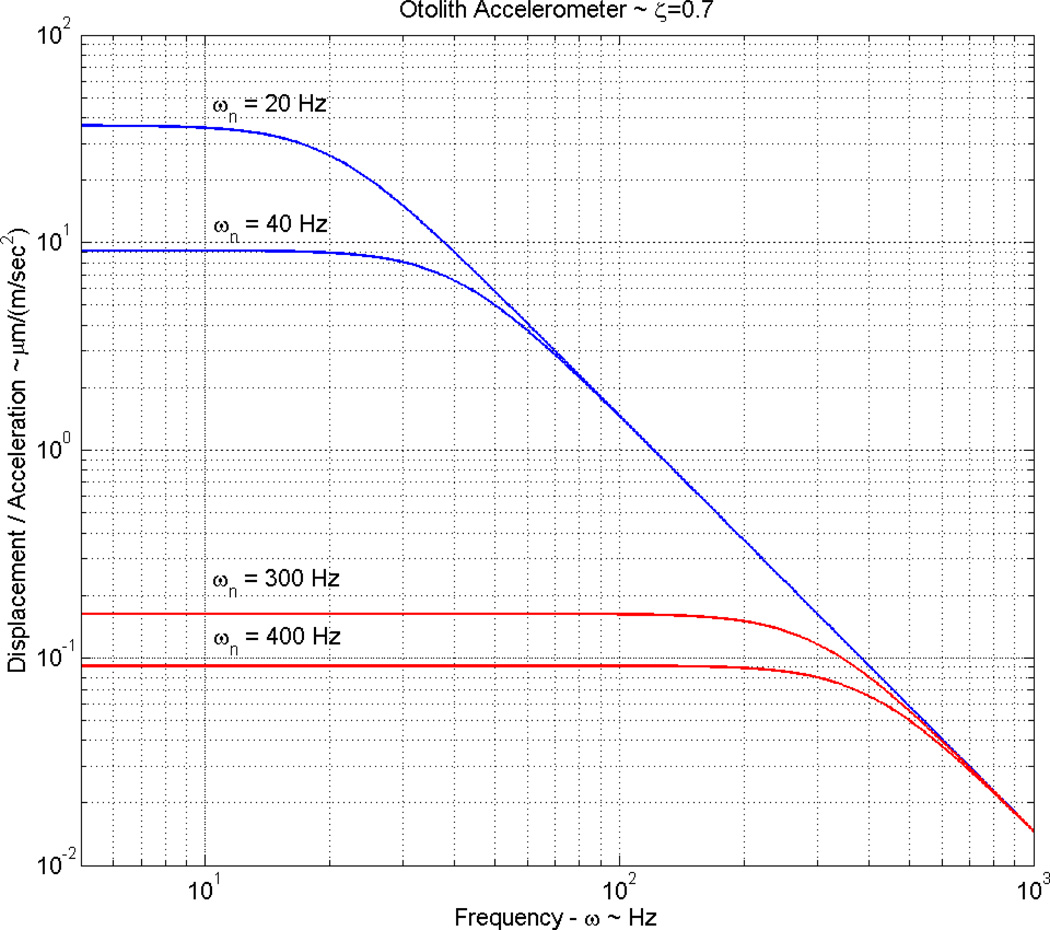
The low natural frequencies of the saccule group are achieved by having a high OL mass, decreasing the natural frequency. In most cases this high OL mass almost completely fills the membranous saccule (Lewis et al., 1985). It is the high mass in this group of saccules that increases their gain (displacement/acceleration). This increase can easily be seen in a simulation of these systems with a plot of gain versus frequency. A simulated frequency response comparing the range of natural frequencies of a high mass saccule and a low mass utricle are shown in Fig. 4.

Figure 4. Gain magnitude vs frequency for a high mass saccule and low mass utricle.

Gain (OL Displacement/ Acceleration) versus system stimulus frequency plot, indicating the basic difference in gain or sensitivity of the high mass saccules and low mass utricles. The difference shown: (1) for high mass saccules with natural frequencies in the 20 to 40 Hz range (shown in blue), and (2) small mass utricles with natural frequencies in the 300 to 400 Hz range (shown in red). It is clear from this plot that the high mass saccules have large gain or sensitivities at the sacrifice of bandwidth. Low mass utricles gain an order of magnitude of bandwidth and loose two orders of magnitude in gain to achieve the bandwidth. The increased gain of high mass saccules is apparently tied to sensing earth born vibrations, while the bandwidth of utricles appears to be needed for visual fixation purposes (linear vestibular-ocular reflex) during rapid head motion.

The derivation of the transfer function for gain that is used in this simulation is shown in appendix A. The high mass saccules in this simulation have a natural frequency in the range from 20 to 40 Hz, and the low mass utricles have a natural frequency in the range from 300 to 400 Hz. It is easily seen from this simulation that for similar acceleration stimuli the high mass saccule has an approximate 100-fold greater gain than the low mass utricle. This increased gain makes these high mass saccules extremely sensitive to small earth born vibration acceleration signals. It is also seen from this plot that achieving this high gain has sacrificed frequency response bandwidth. Accelerations from earth born vibrations have frequency content that matches the frequency bandwidth of these large mass saccules. Achieving high gain versus extending frequency bandwidth is a trade-off of system high versus low mass, and this can be moderated somewhat by system stiffness from the CFL-HB complex.

These high mass saccules are credited as being some of the most sensitive otolithic organs to detect earth born vibrations. The white-lipped frog (Leptodactylus albilabris) found in the mountains of Puerto Rico is credited as being able to detect 10⁻⁶ g of acceleration (Narins et al., 1984). The natural frequency of this white-lipped frog’s saccule was evaluated to be 20 Hz in several neuron recordings. The low natural frequencies and the high OL mass clearly establish the high gain sensitivity of these saccules. Most frogs, especially the North American bullfrog also have these large saccular masses along with most fish and turtles. These animals clearly use these as sensitive acceleration motion detectors for earth born and/or water born vibrations (Narins et al., 1984).

High mass saccule organs also have increased stiffness of the CFL-HB complex when compared to the utricle, as seen in the effective Young’s modulus in Table 3. This increased stiffness is probably required to reduce the deflections of the high mass when stimulated by gravity and/or large head acceleration. Although no evidence exists, this increased stiffness could be to control minimal deflection for hair cell stimulation or to reduce the deflections produced by the high mass when stimulated by gravity and/or large head acceleration.

It is also apparent that the utricle has evolved and is developed for transduction where large frequency bandwidth is desired or needed. This is achieved by decreasing the OL mass leading to a high natural frequency. Then in order to maintain sufficient displacement for hair cell bundle activation, the stiffness of the CFL-HB complex must also be lowered. The two requirements of larger frequency bandwidth while at the same time having enough OL deflection to achieve hair cell bundle activation are competing evolutionary pressures.

It is also important to recognize that these large mass otoconia organs are accelerometers. The relative displacement of the OL is proportional to acceleration, and the system operates below its lower corner frequency for both saccule and utricle (See Fig. 4). This allows the otolithic sensors to function from below their lower corner frequency all the way down to zero frequency, giving them the ability to sense gravity in their static state. Otolithic organs are not seismometers in which the OL displacement would be proportional to earth displacement or a seismic stimulus and would operate above their natural frequency or upper corner frequency. The results shown here support previous claims that turtle utricles, due to their relatively low OL mass, act as accelerometers in the vestibular system with broad frequency bandwidth (Davis et al., 2004; Dunlap et al., 2014; Dunlap et al., 2012; Grant et al., 1986). Afferent recordings from utricles and saccules also support the conclusion that they are accelerometers (Fernandez et al., 1976). Afferent nerve recordings also support the bandwidth conclusions about bullfrog high mass saccules where these organs are shown to have high gain sensitivity and low natural frequency (Narins et al., 1984).

Increases in CFL-HB complex stiffness of large mass saccules is probably present to control displacement magnitude. It is not clear if the stiffness increase in large mass saccules is for: (1) control of minimal displacement to initiate hair cell activation, and/or (2) to reduce maximum OL displacement. Again, it may be a tradeoff between these two parameters. Hair cell bundle operating range is defined as the displacement range from: minimal hair cell activation, up to cell saturation. It is bundle morphology that dictates this operating range (Nam et al, 2005a and 2005b). It may be that hair cell operating range also influences CFL-HB complex stiffness. Some bundles have narrow operating ranges and these are used to sense small displacements of the OL. These narrow operating range hair cells with minimal deflection sensitivity, define overall sensitivity and minimum detection of acceleration of the otolithic system. Other hair cell bundle morphology provided for broad operating ranges that allow the system to sense accelerations over large ranges. This shows that there are several overall system components that can contribute to gain and sensitivity. In addition, the stiffer CFL-HB complex in the large mass saccules may also decrease the phase lag in hair bundle afferent signals. It is known that phase leads are introduced by neurobiological mechanisms to compensate for phase lags from transmission times (Huterer et al., 2002; Songer et al., 2013). So the stiffness increases could be another mechanism to reduce phase lags in the overall transduction process.

4.2 Turtle and Human Utricle Comparison

Turtle and human utricles have similar mean otoconial layer thickness with values: human mean OL thickness = 48 µm (Rosenhall, 2011); turtle mean OL thickness = 41 µm (Davis, 2007; Xue et al., 2003), however the human thickness is somewhat constant throughout the utricle, while the turtle has increased thickness over its striolar region, tapering to a thin layer at its edges. The mean shear layer thickness of both is similar with: human SL thickness = 16 µm (Rosenhall, 2011); turtle SL thickness = 18 µm (Davis, 2007; Xue et al., 2003)] with slight variations in overall thickness throughout both utricles. However, the turtle utricle overall neuroepithelial surface is slightly convex shaped (Davis, 2007) and the human is relatively flat with one turned up end (Watannuki et al., 1976).

Comparing physical dimensions and number of hair bundles of the human utricle and another mammalian utricle (the mouse) to that of a turtle utricle shows that the human utricle is by far the largest area utricle. Here surface area is defined as the dorsal surface covered by the otoconial layer. The human utricle has the largest surface area of the three: human area = 4.30 mm² (Tribukait et al., 2001); turtle area = 0.815 mm² (Rowe et al., 2006); and mouse area = 0.185 mm² (Li et al., 2008).

Due to the larger area of the human utricle it is not surprising that the human utricle has many more hair cells than the turtle with: human utricle hair cell number = 33,100 (Rosenhall et al., 1975); turtle utricle hair cell number = 8670 (Severinsen et al., 2003) and mouse hair cell number = 3013 (Li et al., 2008). However, the hair cells per unit area are somewhat similar with: human = 7200 HC/mm²; turtle = 10,600 HC/mm² and the mouse = 19,529 HC/mm².

The larger number of hair cells in a human utricle would indicate a larger number of neural inputs to the vestibular nuclei. It is speculated that this larger neural sensory input may be required due to the upright stance of humans and more dynamic motion of the overall human torso when compared to a turtle.

5 Conclusions

We have an evidence to suggest that the effective Young's modulus for the turtle utricle CFL-HB complex should be in the range of 16 Pascals. We used a finite element model that includes variable OM layer thicknesses and accurate neuroeipthelial layer geometry including compound curvature to match dynamic response of the model with dynamic experiments. Future OM models should consider the range of modulus depending on the species and organ being modeled: 250 Pa for the bullfrog saccule and 16 Pa for the turtle utricle.

Secondly by matching the natural frequency from dynamic experiments (Dunlap et al., 2012) and with slight modifications to the finite element models we were able to determine the contribution of HBs to the overall stiffness of the CFL-HB complex. These results illustrate hair bundles account for approximately 45% of the CFL-HB complex stiffness. This is only 6% lower than the bullfrog saccule’s lower value of 48% (range 48 to 70%) (Benser et al., 1993; Kondrachuk, 2000). This indicates that HBs are not passive sensors in the OM; they do contribute to the stiffness of the organ.

Finally we suggest these results speak to the dynamic function of otoconial organs; their gains and frequency bandwidth may be controlled by the shear stiffness of the CFL-HB complex and the mass of the OL. These results suggest that utricles and saccules are accelerometers; responding to acceleration stimulus and operating between a range of zero Hertz and just below their first natural frequency.

Table 4. Morphological Values Comparing Human and Turtle Utricle Properties.

Although human utricles have much larger surface areas, turtle and human utricles share similar mean otoconial layer and shear layer thicknesses.

	Surface Area	Number of Hair Cells	Hair Cells Per unit area
	mm2		~No./mm2
Human	4.30	31,100	7,200
Turtle	0.815	8,670	10,600
Mouse	0.185	3,013	19,529

Research Highlights.

• Shear layer Young’s modulus of 16 Pa is predicted matching other work

• Experimental data used in high fidelity finite element model

• Geometrically accurate finite element models provide most accurate prediction

• FEA model natural frequency (363 Hz) matches experimental measured values (363 Hz)

• Hair bundle contribution to shear layer stiffness is predicted to be 45 to 47% of the total

• Otolithic organs are accelerometers, not seismometers

Abbreviations

NE

Neuroepithelium

HB

Hair Cell Bundle

CFL-HB Complex

Column Filament Layer and Hair Bundle Complex

CFL

Column Filament Layer

CGL

Compact Gel Layer

OL

Otoconial Layer

OM

Otoconial Membrane

Appendix A

Utricle Otolith – Lumped Parameter Model

Equation of Motion

The governing equation of motion in terms of the relative displacement, x, between the otoconial layer (OL) and the neuroepithelial layer is

$$mẍ+cẋ+kx=-m(1-\frac{{\rho }_e}{{\rho }_{OL}})(a_x-g_x)$$ (A.1)

where: the over dot notation on x represents differentiation with respect to time t, m = mass of the OL and m ẍ is the inertial term, c = damping coefficient and c ẋ is the viscous damping term, k = elastic coefficient and k x is the elastic term, $(1-\frac{{\rho }_e}{{\rho }_{OL}})$= the buoyancy term of the OL, where ρ_e = endolymph density and ρ_OL = OL density, a_x = head acceleration, and g_x = acceleration of gravity, both in the x-direction of the plane of the OL. The negative sign on the acceleration term indicates that a positive x-displacement of the OL is produced by a negative a_x and positive g_x acceleration components, where the acceleration components act in the x-direction of the plane of the OL.

System Transfer Function and Frequency Response

Taking the Laplace transform of Eqn. A.1 with zero initial conditions [x(t = 0) = 0 ; and ẋ(t = 0) = 0], where s is the Laplace transform variable, defining X(s) = ℒ[x(t)], then combining the two accelerations into a single gavitoinertial acceleration term as A(s) = ℒ[(a_x(t)-g_x(t))], and solving for the transfer function results in

$$\frac{X(s)}{A(s)}=(1-\frac{{\rho }_e}{{\rho }_{OL}})\frac{1}{s^2+\frac{c}{m}s+\frac{k}{m}}$$ (A.2)

Substituting the standard 2nd order inertial system variables shown in Eqns. A.3 and A.4 (1) undamped natural frequency, ω_n and (2) damping coefficient, ζ

$${\omega }_n^2=\frac{k}{m}$$ (A.3)

$$2\zeta {\omega }_n=\frac{c}{m}$$ (A.4)

for the coefficients of the s terms in Eqn A.2 results in Eqn. A.5, below

$$\frac{X(s)}{A(s)}=(1-\frac{{\rho }_e}{{\rho }_{OL}})\frac{1}{s^2+(2\zeta {\omega }_n)s+{{\omega }_n}^2}$$ (A.5)

From Eqn. A-5 a frequency response diagram (Bode diagram) can be constructed. This is easily done in any computational math software such as MatLab.

Only the natural frequency, ω_n, and damping coefficient, ζ, need be designated for a frequency response diagram. The gain here is the displacement, X, per unit acceleration, A, the right hand term. The frequency is the Laplace transform variable s. This function is plotted in Fig. 4. for ω_n = 40 Hz and ω_n = 400 Hz with ζ = 0.7 in both cases.